Increased inbreeding and strong kinship structure in Taxus baccata estimated from both AFLP and SSR data

Abstract

Habitat fragmentation can have severe genetic consequences for trees, such as increased inbreeding and decreased effective population size. In effect, local populations suffer from reduction of genetic variation, and thus loss of adaptive capacity, which consequently increases their risk of extinction. In Europe, Taxus baccata is among a number of tree species experiencing strong habitat fragmentation. However, there is little empirical data on the population genetic consequences of fragmentation for this species. This study aimed to characterize local genetic structure in two natural remnants of English yew in Poland based on both amplified fragment length polymorphism (AFLP) and microsatellite (SSR) markers. We introduced a Bayesian approach that estimates the average inbreeding coefficient using AFLP (dominant) markers. Results showed that, in spite of high dispersal potential (bird-mediated seed dispersal and wind-mediated pollen dispersal), English yew populations show strong kinship structure, with a spatial extent of 50–100 m, depending on the population. The estimated inbreeding levels ranged from 0.016 to 0.063, depending on the population and marker used. Several patterns were evident: (1) AFLP markers showed stronger kinship structure than SSRs; (2) AFLP markers provided higher inbreeding estimates than SSRs; and (3) kinship structure and inbreeding were more pronounced in denser populations regardless of the marker used. Our results suggest that, because both kinship structure and (bi-parental) inbreeding exist in populations of English yew, gene dispersal can be fairly limited in this species. Furthermore, at a local scale, gene dispersal intensity can be more limited in a dense population.

Introduction

Habitat availability is one of the most crucial factors shaping the natural distribution of plants. Across most of Europe, the strongest influences on contemporary plant distributions are historical and current human land-use. Exploitation of natural resources often causes habitat fragmentation, limiting species distribution and increasing the risk of extinction. The lack of spatial continuity in populations can have severe consequences, such as increased inbreeding (Ledig, 1992) and reduced effective population size (Gilpin, 1991). In effect, local populations experience loss of genetic variation, and may suffer from the reduction of both viability (Frankham, 2003) and adaptive capacity (Young et al., 1996; Willi et al., 2006).

The risk of negative consequences owing to habitat fragmentation depends particularly on dispersal capabilities (Thomas, 2000). Dispersal allows the colonization of new habitats and population spread, but, through gene flow, it also assures connectivity at a meta-population level (Travis and Dytham, 1998). In fragmented populations, gene flow within and among populations helps to maintain sufficiently large effective population sizes to preserve the genetic variation necessary for adaptive potential (Willi et al., 2006). Therefore, plants characterized by a more extensive dispersal are also expected to be less susceptible to habitat fragmentation.

Another important factor contributing to the risk of extinction is the mating system, which determines the inbreeding and kinship levels (Frankham, 1995). In species experiencing inbreeding depression, time to extinction can be markedly decreased (Brook et al., 2002). Although it is often argued that the extinction process in small endangered populations is strongly influenced by demographic or environmental factors, which act long before genetic factors become significant (Caro and Laurenson, 1994), Bijlsma et al. (2000) showed that the impact of environmental stress can become acute at higher inbreeding levels. Hence inbreeding and environmental stresses are not independent but can interact.

In Europe, Taxus baccata is among a number of tree species experiencing strong habitat fragmentation. Possible reasons include climate change and long-term human impact, such as overexploitation of yew timber in the past and more recent forest management biased towards maximization of wood production. Such fragmentation is likely to have increased the risk of negative consequences such as genetic drift and inbreeding. Moreover, low rates of natural regeneration have been observed in remnant populations (Hulme, 1996; Mysterud and Østbye, 2004; Myking et al., 2009), leading to a continuous decline in population numbers (Thomas and Polwart, 2003).

Most population genetic studies on English yew have focused on among-population genetic variation. They have shown a strong genetic structure at a meta-population level (Hilfiker et al., 2004; Myking et al., 2009; Zarek, 2009; Dubreuil et al., 2010). Interestingly, whereas populations at the centre of the natural range show rather high genetic diversity (Lewandowski et al., 1995; Hertel and Kohlstock, 1996), recent analyses have shown that genetic diversity decreases in the more peripheral areas (Myking et al., 2009; González-Martínez et al., 2010). Using allozymes low genetic diversity was found in Taxus brevifolia (El-Kassaby and Yanchuk, 1994), Taxus canadensis (Senneville et al., 2001) and especially in the Asian species Taxus cuspidata (Chung et al., 1999; Lee et al., 2000). Therefore, as compared with other yew species, T. baccata has relatively high genetic diversity, which appears comparable to that in other gymnosperms (Hamrick et al., 1992). However, because of scant information on genetic variation and the high ecological diversity of English yew habitats (Thomas and Polwart, 2003), the latter conclusion should be treated with caution.

The English yew produces fleshy-fruited seeds, which can be dispersed either by birds or by gravity (Garcia et al., 2000; García and Obeso, 2003). Besides enhancing the dispersal distance, dispersal by birds can also facilitate the germination of seeds, as seed dormancy is broken more easily if seeds have passed through the digestive tract of birds (Suszka, 1985). Nonetheless, ecological studies have shown that a majority of seeds fall beneath the mother tree (García and Obeso, 2003), although they may occasionally disperse 50–70 m away from trees (Bartkowiak, 1970). Thus, within a site, seed dispersal in English yew may be relatively restricted. Knowledge of pollen dispersal in yew is scarce. Its pollen velocity (0.023 m s⁻¹; Dyakowska, 1959) is comparable with that of birch or pine species (Levin and Kerster, 1974), showing great potential for dispersal. However, strong genetic differentiation among yew populations suggests that gene exchange is rather limited (Hilfiker et al., 2004; Myking et al., 2009; Zarek, 2009; Dubreuil et al., 2010). A possible explanation could be low pollen concentration in the atmosphere because of the scattered distribution of yew populations in a landscape. In addition, English yew is typically an understory forest species (Thomas and Polwart, 2003), and its low height may limit pollen dispersal within and among populations. For example, results from pollen trapping suggest that in dense yew populations, pollen dispersal might be quite limited, with a majority of pollen grains falling on nearby male trees (Noryśkiewicz, 2006). If seed- and pollen-mediated gene flow is limited, this would enhance the isolation-by-distance process, increasing the spatial genetic structure (SGS) and (bi-parental) inbreeding in a population.

In this study we investigated whether isolation-by-distance occurs within highly isolated populations of English yew. For this purpose, two of the largest lowland populations in Poland were sampled intensively. Using both AFLP and SSR markers, we investigated the spatial extent of SGS among individuals. Additionally, we investigated the inbreeding levels within populations, and for this purpose we developed a novel Bayesian approach in order to make within-population inbreeding inference based on dominant markers such as AFLPs. The results will be important for designing efficient conservation programs for English yew.

Materials and methods

Study sites and field work

The study was conducted at two sites, both forest nature reserves established for the protection of remnant populations of English yew (T. baccata L.) (Figure 1). The sites are both highly isolated yew patches but represent very different habitats. The first population is located near Czarne in northern Poland. The current yew population comprises 439 adult trees scattered over 26.4 ha. It is characterized by relatively low density, with about 17 per individuals per hectare. The population age is estimated to be 250 years, with the oldest trees about 300 years old. Palynological data showed that yew colonized this location during the sub-boreal period (5000–2500 year BP) (Prusinkiewicz and Biały, 1976). The second population, Wierzchlas, is the largest remnant yew forest in Poland. The forested area covers about 18.5 ha. Although the oldest individuals are 500 years old, palynological records showed that yew has been a stable component of local forests since the sub-boreal period (5000–2500 year BP) (Noryśkiewicz, 2006). This population differs from that of Czarne in its high density, reaching about 200 individuals per hectare. As a result, light availability at the forest floor is poor, limiting the occurrence of understory plants. For this and other (browsing, low groundwater level) reasons, yew does not regenerate naturally, although seeds germinate in high abundance every year (seedlings survive 2 years only). Since 1910 the number of living trees has decreased from 5533 to 2856 (excluding 397 standing dead trees), according to reserve documentation. Therefore, despite its large size, the Wierzchlas is a declining population.

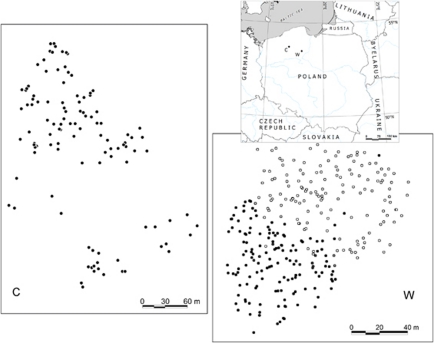
Figure 1.

Map of the location of the study populations, together with a within-plot distribution of sampled individuals: C, Czarne; W, Wierzchlas. For Wierzchlas, the dot shading reflects the probability of individual membership of one of two estimated sub-populations, according to a Bayesian clustering method applied to AFLP markers.

In Spring 2008, a study plot was established at each site, within which all mature trees were mapped using the GPS mapping system Pathfinder ProXT (Trimble, Sunnyvale, CA, USA) (Figure 1). Needles were collected from all mapped trees, immediately transported to the laboratory and stored at −80 °C until analysis. In total, 216 and 293 individuals were sampled in Czarne and Wierzchlas, respectively.

Laboratory methods

Genomic DNA was extracted by following the CTAB protocol (Doyle and Doyle, 1990), after grinding frozen tissue with a Mixer Mill (MM301; Retsch, Haan, Germany). The extracted DNA was diluted to obtain 100 ng μl⁻¹ and 10 ng μl⁻¹ solutions, which were used in AFLP and SSR analyses, respectively.

AFLP analysis

The AFLP analysis followed the original protocol by Vos et al. (1995), with some modifications introduced for analysis of large genomes (Shepherd et al., 2003). Restriction–ligation reactions were performed in a total volume of 10 μl. A single reaction contained 500 ng of genomic DNA, 5 U of EcoRI (Fermentas, Burlington, Ontario, Canada) and 5 U of Tru1I (MseI iso-schizomer) (Fermentas), 1.5 U of T4 DNA ligase (Fermentas), 1 × T4 DNA ligase buffer (Fermentas), 0.05% bovine serum albumin, 50 m NaCl, 0.5 pmol μl⁻¹ E-Adaptor and 5 pmol μl⁻¹ M-Adaptor. The reactions were performed at room temperature overnight and then diluted 5 × with H₂O in order to obtain PCR matrices (pre-matrix DNA) for pre-selective amplification.

Pre-selective amplifications were performed in 10 μl total volume. A pre-selective PCR mixture contained 2 μl of pre-matrix DNA, 1 × Qiagen Master Mix (Qiagen Taq PCR Master Mix kit), 0.5 μ E-primer (E+AC) and 0.5 μ M-primer (M+CC). Amplification was performed by using the following programme: 72 °C for 2 min; 20 cycles of 94 °C for 20 s, 56 °C for 30 s and 72 °C for 2 min; and finally 60 °C for 30 min. A product of pre-selective PCR was diluted 20 times in order to obtain a PCR matrix for selective amplification (sel-matrix DNA).

Selective amplifications were performed in 10 μl total volumes, consisting of 3 μl of sel-matrix DNA, 1 × Qiagen Master Mix, 0.5 μ FAM-labelled E-primer (E+ACG) and 0.5 μ M-primer (M+CCNN). Three M-primers, namely CCCT, CCGC and CCGT, were successfully tested and used in complete genotyping. PCRs were performed by using the following programme: 94 °C for 2 min; 10 cycles of 94 °C for 20 s, 66 °C (−1 °C per cycle) for 30 s and 72 °C for 2 min; and 20 cycles of 94 °C for 30 s, 56 °C for 30 s and 60 °C for 30 min. Both pre-selective and selective amplifications were performed using the PTC200 thermal cycler (Bio-Rad, Hercules, CA, USA).

The products of selective amplifications were sized by using the automated capillary sequencer ABI PRISM 3130XL (Applied Biosystems, Foster City, CA, USA) and the softwares GENESCAN 3.7 and Genotyper 3.7 provided by the manufacturer.

SSR analysis

All eight SSR markers published for T. baccata (Dubreuil et al., 2008) were tested. However, a preliminary analysis showed that only five (Tax26, Tax31, Tax36, Tax92, TS09) gave clearly interpretable mono-locus patterns. Therefore, to increase the genetic power, we designed five additional primers based on the sequences deposited in GenBank by Dubreuil et al. (2008) and named Tax33, Tax47, Tax70, Tax362 and Tax922 (GenBank accession numbers: EF012577, EF012579, EF012575, EF012576, EF012574 and EF012572, respectively). Of these new primers, only Tax362 gave promising amplification results (using the primers F: TTGGGTAATTGGTAATGGAAAT and R: AACTTGGTATCGTGTTGCATTTT) and was used as the additional SSR locus in this study.

Finally, six nuclear microsatellite markers were used for genotyping according to the following protocol: The total volume of the PCR mixture was 10 μl, which contained 20 ng of template DNA, 1 × Qiagen PCR buffer (Qiagen PCR Core kit), 200 n of each dNTP, 0.25 U of Taq polymerase (Qiagen PCR Core kit), 0.5 mg ml⁻¹ bovine serum albumin, 20 ng of DNA and 0.35–0.5 μ forward and reverse primers, depending on the locus. PCRs were performed based on the following programme: 94 °C for 5 min; 10 cycles of 94 °C for 30 s, 65 °C (−1 °C per cycle) for 40 s and 72 °C for 40 s; and 25 cycles of 94 °C for 30 s, 55 °C for 30 s and 72 °C for 40 s. The final extension step at 72 °C was performed for 7 min. The PCRs were performed by using PTC200 thermal cycler (Bio-Rad). The PCR products were sized by using the capillary sequencer ABI PRISM 3130XL (Applied Biosystems). The genotypes were scored by using the GENESCAN 3.7 software provided by Applied Biosystems.

Statistical methods

Genetic variation

For SSR markers the following parameters were calculated per locus: number of alleles (A), effective number of alleles (Ae), and expected (He) and observed (Ho) heterozygosity. In order to test for deviation from Hardy-Weinberg proportions, the Markov chain Monte Carlo (MCMC) version of the exact test was used. The null allele frequencies at SSR loci were estimated under the assumption of Hardy–Weinberg equilibrium by using the maximum likelihood approach. All computations were performed by using GENEPOP software (Rousset, 2008).

The AFLP markers were analysed under the assumption of a complete dominance (binary data) as pedigree data were not available (to test for the co-dominance/dominance of typed PCR products). Hence, only phenotype frequencies were known precisely and allele frequencies were estimated (together with the inbreeding coefficient) by using a Bayesian method, which is introduced in the next section.

Inbreeding coefficient

Dubreuil et al. (2008, 2010) suggested that the SSR markers used include null alleles; therefore, the inbreeding coefficient cannot be computed directly from heterozygote deficiency. Hence, the inbreeding coefficient was estimated by using the Bayesian method proposed by Vogl et al. (2002). As shown recently, the method provides robust estimates for multi-locus SSR data even in the presence of null alleles (Chybicki and Burczyk, 2009). Estimation was conducted by using the INEst software (Chybicki and Burczyk, 2009).

In this paper we apply Vogl's approach for completely dominant markers (AFLP, RAPD, iSSR etc.). In order to describe the estimation procedure, the inbreeding coefficient F is defined as the probability that two alleles randomly chosen from a population are identical by descent (ibd). A random sample of N individuals from a population may be treated as a realized sample of independent F_i, such that each F_i is the probability that two alleles at a random locus of the i-th individual are ibd. Note that F_i can be referred to as an individual inbreeding coefficient. Typically, F_i shows dispersal around a population average F; therefore, to reflect this, we assume that F_i follows a beta-distribution

The meaning of α and β parameters can be better understood by noting that the expected value of F_i, that is, a population average inbreeding coefficient F, is equal to α/(α+β), with a variance equal to αβ/[(α+β)²(α+β+1)]. A beta-distribution is chosen because it is dedicated to variables defined on the interval (0,1). Also it is quite flexible because the distribution may take the shape from concave through flat (when α=β=1) to convex. Finally, it serves as a conjugate prior for a binomial distribution, which itself is used to model proportions.

Ideally, the estimate of individual inbreeding coefficient would be F_i=X_i/L, where X_i is a number of loci having alleles ibd (out of L in total) in a genotype of the i-th individual. Assuming independence among loci, X_i follows a binomial distribution. In this way we obtain a two-stage model,

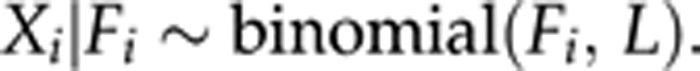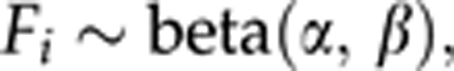that enables us to write, that

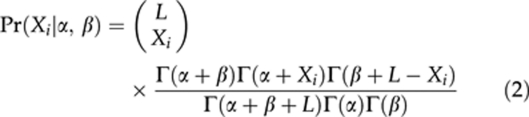that is, X_i follows a beta-binomial distribution. Given a known X_i, equation (2) would allow the estimation of a population average F (through estimation of α and β).

In the case of dominant markers, although the only observed data are binary phenotypes (neither individual proportions of alleles ibd nor genotypes are known), F_i can be inferred using a classic inbreeding model, given observed phenotypes (Appendix). A basis of this inference is the conditional probability that the i-th individual at the l-th locus has a dominant (P_il=1) or recessive (P_il=0) phenotype that can be written as

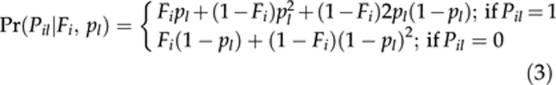where p_l is a dominant allele frequency at the l-th locus in an ancestral population. Based on equation (3) the likelihood function of the phenotypic data can be formulated as

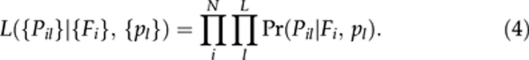In our model allele frequencies are unknown parameters to be estimated from the data. For this purpose, motivated by the findings of Wright (1931), we assume that allele frequencies in an ancestral population follow the beta-distribution

with hyper-priors α_p and β_p determining the shape of a probability distribution. We assume that α_p and β_p are shared across loci. As shown by Foll et al. (2008), making hyper-priors estimable parameters significantly improves the overall estimation procedure. Following Vogl et al. (2002), for this purpose we introduce additional variables D_l and R_l, which store a number of ancestral copies of dominant and recessive alleles (respectively) at the l-th locus. D_l and R_l are complementary variables following a binomial distribution. Therefore, we only specify that D_l follows:

Although D_l and R_l are not known directly from the data, they can be inferred in a similar way as X_i using [3], given F_i and p_l. Now, because of [5] we can write that

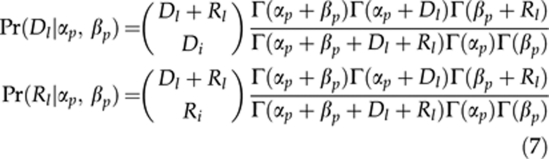The latter equations can be used to estimate α_p and β_p. The details of the inference of X_i, D_l and R_l are shown in the Appendix. Here we only describe a general estimation algorithm. The estimation procedure relies on the cyclical updating of the parameters, making proposals with (where possible) conditional distributions (Gibbs proposals) or symmetric distributions (Metropolis proposals) (known as Metropolis-Gibbs algorithm; Hoff, 2009). Given a set of parameter values at the s-th iteration {F₁^(s), F₂^(s), …, F_N^(s), p₁^(s), p₂^(s), …, p_L^(s), α^(s), β^(s), α_l^(s), β_l^(s)}, new parameter values are generated as follows:

1. Infer each X_i (i={1, …, N}), D_l and R_l (l={1, …, L}) based on equation (3), given a set of current parameter values and data.

2. For each i={1, …, N} update F_i: sample F_i^(s+1)∼beta(X_i+α, L−X_i+β)

3. For each l={1, …, L} update p_l: sample p_l^(s+1)∼beta(D_l+α_p, R_l+α_p)

4. Update α:

   • 4.1. Propose α^*∼a symmetric uniform distribution centred on α^(s)
   • 4.2. Set α^(s+1)=α^* with probability 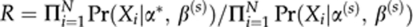and α^(s+1)=α^(s) with a probability (1−R).
5. Update β:

   • 5.1. Propose β^*∼a symmetric uniform distribution centred on β^(s)
   • 5.2. Set β^(s+1)=β^* with probability 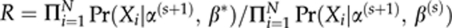and β^(s+1)=β^(s) with a probability (1−R).
6. Update α_p:

   • 6.1. Propose α_p^*∼a symmetric uniform distribution centred on α_p^(s)
   • 6.2. Set α_p^(s+1)=α_p^* with probability 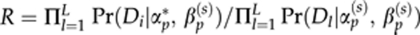and α_p^(s+1)=α_p^(s) with a probability (1−R).
7. Update β_p:

   • 7.1. Propose β_p^*∼a symmetric uniform distribution centred on β_p^(s)
   • 7.2. Set β_p^(s+1)=β_p^* with probability 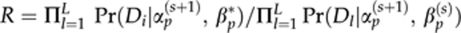and β_p^(s+1)=β_p^(s) with a probability (1−R).

The posterior marginal distributions for parameters of interest can be approximated with a large number of cycles. Then, the means and credible intervals can be extracted. The assumption of F to be beta-distributed implies that possible values of F obtained based on the full model fall always within the range (0,1). Hence, the full model cannot be used to test a null hypothesis (F=0). However, a null hypothesis can be verified through comparison of a null model (F as constants equal 0) and the full model (F as estimable parameters) using the Deviance Information Criterion (DIC) (Spiegelhalter et al., 2002) based on the likelihood function defined in equation (4).

The number of cycles (comprising Steps 1–7) applied in the analysis of the two yew populations was 60 000. However, as the Gibbs sampler requires initial guesses in order to avoid a dependence of final estimates on these initial values, we burnt-in the first 10 000 updates. Because our inference is based on prior distributions, which are not known, each analysis was repeated five times, each time starting from different initial values of parameters representing a prior distribution having the same mean (F=0.5) but differing in variance and shape (α=β={0.1, 0.5, 1, 2.5, 5}). The analyses were performed using the ad hoc computer program I4A written in Object Pascal/Delphi by IJC (freely available on at http://www.genetyka.ukw.edu.pl/index_pliki/software.htm).

In order to investigate the statistical properties of the method, a limited simulation study was conducted. In particular, we were interested in how sampling effort influences the accuracy and the precision of the estimator. Additionally, we compared the behaviour of the Bayesian estimator (hereafter ‘F_B') by the existing approach, the frequency-matching algorithm, introduced by Dasmahapatra et al. (2007) (hereafter ‘F_FM'). A detailed description of the F_FM estimator is beyond the scope of this paper, therefore only a brief description follows. F_FM relies on the assumption that at least 50% of the sampled individuals are outbred (F=0). The algorithm starts by finding the best-fitting individual inbreeding levels by comparing the observed data with a series of simulated phenotypic data differing in compositions of inbred individuals. Then, using the best-matching mean F, allele frequencies are adjusted. Finally, F_FM attempts to find the best fit of the observed phenotypes to the simulated data given adjusted frequencies.

Because the two estimators rely on specific assumptions about the distribution of F (beta-distribution for F_B and 50% non-inbred individuals for F_FM), our simulations were conducted such that neither one would be more favoured than the other. For this reason we chose the mixed mating model, in which reproduction occurs either through self-fertilization (with probability s) or random out-crossing (with probability 1−s). Then, the expected average inbreeding becomes F=s/(2−s). The simulation algorithm was as follows: (1) draw a self-fertilization rate (s) from a uniform distribution (0, 0.5) (the range implies F∈(0, 0.33)); (2) randomly generate allele frequencies at L loci; (3) attribute to each of the L loci of the T individuals a given genotype as a function of allele frequencies; (4) draw an individual (i); (5) generate a random number from a [0,1] uniform distribution (x); (6) if x>s, draw a second individual (j), otherwise take j=i; (7) for each locus take one allele at random from the i-th and the j-th individual's genotype and combine them to form the genotype of a progeny; (8) go to Step-4 T times to obtain T individuals representing the next generation (to neglect the effect of random genetic drift, here T=10 000); (9) repeat Steps 3–8 for the desired number of generations (here 30); (10) draw a sample of N individuals from the last generation and convert their genotypes so that all heterozygotes appear as dominant phenotypes.

Once phenotypes were generated they were stored as input files for estimating the inbreeding coefficient using two different applications: the FAFLPcalc Excel macro implementing the method of Dasmahapatra et al. (2007) (available at http://www.ucl.ac.uk/taxome/kanchon/#publications) and I4A, a stand-alone Windows programme implementing the Bayesian approach introduced in this paper. In the case of I4A we used the prior values of beta-distributions equal to α=β=α_p=β_p=1.0 (corresponding to an ‘uninformative' flat distribution) and 60 000 repetitions, including a 10 000-step burn-in. In the case of FAFLPcalc, we slightly modified the original estimation procedure for the two reasons given below. First, the original algorithm searches for the optimal mean F-value in discrete steps (+0.05), thus it does not allow the exploration of a continuous range of the parameter. Second, because FAFLPcalc is based on random simulations, the results show stochastic variation for successive runs so that the algorithm may occasionally find sub-optimal estimates. Therefore, in order to allow a continuous distribution of the average F-value, as well as to control for stochastic variation of the estimator, we repeated the estimation for a single data set 50 times and scored the average F-value over these repetitions as the best-matching value of the F_FM estimator.

We considered three scenarios, differing in the amount of genetic data, as follows: (a) 50 individuals genotyped at 100 dominant bi-allelic markers; (b) 50 individuals genotyped at 200 markers and (c) 100 individuals genotyped at 100 markers. In this way we were able to test the impact of sample size or number of markers on the precision and accuracy of the estimators. Because a single analysis is time consuming and joint analyses based on the two separate software tools cannot be automated easily, only 50 repetitions per scenario were conducted. For each scenario the bias and the root mean square error were estimated.

Spatial genetic structure

The SGS was assessed by using a multi-locus kinship coefficient. The analyses were performed separately for AFLP and SSR markers using the SPAGeDi ver. 1.3 software (Hardy and Vekemans, 2002). In the case of SSRs, kinship was estimated according to Nason's formula (Loiselle et al., 1995), whereas for AFLP markers a kinship coefficient was estimated according to Hardy (2003). Because the latter needs an inbreeding coefficient to be provided, we used the averaged values estimated for each population (Table 2). Correlograms were obtained by averaging kinship coefficients within 10 distance classes, each containing an even number of pairs. In order to illustrate the intensity of the SGS, therefore, we estimated Sp=−b₁/(1−f⁽¹⁾) (Vekemans and Hardy, 2004), where b₁ is the slope of a log-linear regression between observed kinship and a distance between individuals, and f⁽¹⁾ is the average kinship for the first distance class. All standard errors were estimated by jackknife procedure over loci. Additionally, to test for the presence of subtle genetic structures within a population we applied a Bayesian clustering method (Guillot et al., 2005) implemented in GENELAND ver. 3.2.4 (Guillot et al., 2008). The method was chosen because it uses geo-referenced genotypes as prior information in the estimation procedure. Also, unlike similar methods it treats a number of sub-populations (K) as an estimable parameter. The estimation procedure was based on the spatial D-model (assuming independency of allele frequencies among sub-populations). In the case of SSR data, owing to the high frequency of null alleles (see section Results) the Null Allele model was used. Estimates were obtained after 100 000 iterations (saving every 100th). Estimation was repeated five times for each data set.

Results

Genetic variation

AFLP markers

While scoring AFLP phenotypes, special care was taken in order to include only those loci that showed a stable migration pattern and peak intensity across samples. Thus, using three combinations of primers we scored 126 marker loci in total (M+CCCT, 50 loci; M+CCGC, 31 loci and M+CCGT, 45 loci). Nonetheless, in a single population the number of polymorphic loci, that is, showing more than five and less than n−5 dominant phenotypes (n: number of individuals in a population), was 114 and 115 in Czarne and Wierzchlas, respectively. On average, the frequency of a dominant phenotype was equal to 0.416 and 0.447 in the respective populations. Thus, AFLP polymorphism was comparable in the study populations, although a slightly lower polymorphism was detected in Czarne, probably because of the smaller sample and the criterion of polymorphism used.

SSR markers

The level of polymorphism in the SSR markers was high. The number of alleles per locus ranged from 12 to 35 alleles (Table 1). Interestingly, the locus designed specifically for this study (Tax362) appeared to be the least polymorphic, with only 17 detected alleles (fragment lengths ranged from 85 to 119 bp). In spite of the high average numbers of alleles (23.0 and 18.2 in Czarne and Wierzchlas, respectively), the effective numbers of alleles were relatively low, ranging from 3.5 to 9.9. This was because of the presence of many rare alleles, with some of them identified as single copy per population. On average, a substantial deficiency of heterozygotes was detected in both populations, as compared with Hardy-Weinberg expectations. The heterozygote deficiency was because of the presence of null alleles (Figure 2) and within-population inbreeding, as shown in the next section.

Table 1. Genetic structure parameters for Czarne and Wierzchlas based on SSR analysis.

Locus	A	Ae	Ho	He	HW test
Czarne
Tax31	18	6.4	0.843	0.846	0.026
Tax36	35	9.8	0.810	0.901	<0.001
Tax362	15	7.9	0.585	0.876	<0.001
Tax92	30	9.8	0.716	0.901	<0.001
Tax26	22	7.8	0.512	0.874	<0.001
TS09	18	5.7	0.643	0.826	<0.001
Mean	23.0	7.59	0.685	0.870
Wierzchlas
Tax31	15	3.5	0.720	0.720	0.304
Tax36	22	9.9	0.417	0.901	<0.001
Tax362	12	3.8	0.694	0.740	0.214
Tax92	23	5.5	0.635	0.820	<0.001
Tax26	16	6.3	0.359	0.843	<0.001
TS09	21	4.9	0.551	0.797	<0.001
Mean	18.2	5.04	0.563	0.803	<0.001

Abbreviation: HW, Hardy-Weinberg.

A, number of alleles; Ae, effective number of alleles; He, expected heterozygosity; Ho, observed heterozygosity; HW test, P-value of the test for Hardy-Weinberg equilibrium.

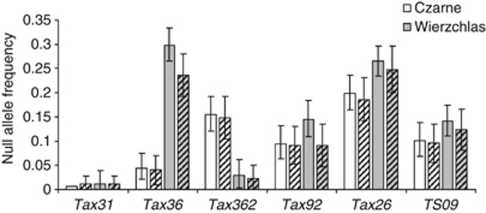
Figure 2.

The frequencies of null alleles at SSR loci in the study populations (Czarne and Wierzchlas). The clear bars indicate estimates under assumption of Hardy–Weinberg equilibrium (GENEPOP estimates), whereas the dashed bars indicate estimates that account for the within-population inbreeding (in this case both null allele frequencies and inbreeding coefficient were estimated simultaneously by a Bayesian method; INEst estimates). The whiskers indicate 95% credibility intervals.

Inbreeding and null alleles

For a given population and a given marker type we ran five independent analyses using the Bayesian approach, each starting from different initial values of the prior beta-distribution (see Materials and methods). Although these initial prior distributions differ much in shape (from concave to convex curves), the analyses conducted for a given population and marker type always converged to almost the same posterior distributions of the inbreeding coefficient (Table 2). High stability of the model can also be deduced from the behaviour of the likelihood function across different priors, for example, similar average and standard error values of LogL. The analyses showed that the inbreeding coefficient is on average higher in Wierzchlas than in Czarne. However, the difference was more pronounced for the SSR (0.016 and 0.037 for Czarne and Wierzchlas, respectively) than for AFLP markers (0.048 and 0.063 for Czarne and Wierzchlas, respectively). Nonetheless, populations did not differ statistically in F, as can be deduced from wide credibility intervals (Table 2). When averaged for two classes of markers, the inbreeding coefficient equalled 0.032 and 0.050 for Czarne and Wierzchlas, respectively. Comparison of the DIC values for the full model (F>0) and the null model (F=0) allows to conclude that inbreeding was significant in all cases except the SSR data in Czarne.

Table 2. Average inbreeding coefficient (F) estimates based on AFLP and SSR markers for the study populations.

	AFLP			SSR
	F	CI	DIC	F	CI	DIC
Czarne
Full model (F>0)
α, β
0.1	0.050	(0.003, 0.141)	20 893.7	0.018	(0.001, 0.057)	10 212.0
0.5	0.050	(0.006, 0.006)	20 889.7	0.015	(0.001, 0.049)	10 209.7
1	0.041	(0.006, 0.096)	20 898.9	0.015	(0.001, 0.050)	10 210.0
2.5	0.046	(0.006, 0.120)	20 890.5	0.015	(0.001, 0.050)	10 210.4
5	0.053	(0.011, 0.116)	20 881.3	0.016	(0.001, 0.052)	10 210.4
Mean	0.048			0.016
Null model (F=0)	—	—	20 929.2			10 203.5
Wierzchlas
Full model (F>0)
α, β
0.1	0.065	(0.035, 0.102)	27 047.8	0.039	(0.003, 0.093)	10 614.3
0.5	0.063	(0.036, 0.099)	27 047.0	0.035	(0.002, 0.085)	10 614.7
1	0.057	(0.028, 0.091)	27 048.9	0.037	(0.002, 0.088)	10 617.6
2.5	0.062	(0.033, 0.098)	27 046.6	0.037	(0.003, 0.087)	10 615.1
5	0.065	(0.034, 0.102)	27 048.2	0.036	(0.003, 0.086)	10 615.9
Mean	0.063			0.037
Null model (F=0)	—	—	27 266.1			10 635.4

Abbreviation: CI, confidence (credibility) interval.

α, β, values of the α and β parameters of the prior beta-distribution used to infer F; 95% CI, 95% credibility interval around F; DIC, Deviance Information Criterion measuring the overall fit of a model to data (the smaller the DIC, the better the fit). DIC values for the null model (F=0) are also presented.

The Bayesian approach used in this paper allowed the simultaneous estimation of inbreeding coefficients and allele frequencies in AFLP and SSR loci, including also null alleles. The most interesting results were those regarding null alleles in SSRs, because, as shown in the previous section, in both populations we detected a high deficiency of heterozygotes. Estimates based on the Gibbs sampler confirmed that there was a high frequency of null alleles in the study populations (Figure 2). On average, the highest proportion of null alleles was estimated for locus Tax26. On the other hand, consistently the lowest frequency of null alleles was found for Tax31, which in both populations was not significantly different from 0. Interestingly, the locus designed in this study, Tax362, showed a non-significant frequency of null alleles in Wierzchlas, whereas a relatively high frequency in Czarne. The null allele frequencies estimated when accounting for inbreeding were consistently lower as compared with EM (expectation-maximization) estimates based on the model assuming Hardy-Weinberg equilibrium (Figure 2).

In silico behaviour of the inbreeding estimator based on AFLP

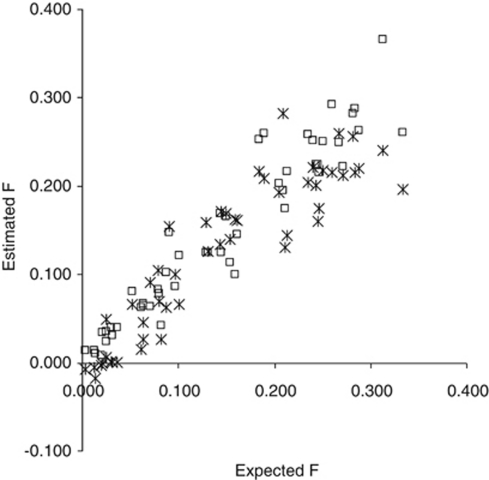
Simulations showed that the Bayesian approach F_B provides a consistent estimator of the average inbreeding coefficient so that an increasing amount of data results in both increased accuracy and precision. The study showed that F_B generally behaves better when compared with F_FM among all scenarios considered (Table 3), showing consistently lower root mean-square error. Importantly, F_B provided almost unbiased estimates, whereas F_FM tended to slightly underestimate the average inbreeding coefficient. Simulations also showed that increasing the number of individuals resulted in greater accuracy and precision than increasing the number of loci. However, the last conclusion applies mainly to the Bayesian method (F_B). Finally, we did not observe any clear relationship between the bias or root mean-square error and the expected inbreeding coefficient for the two methods (Figure 3), which indicated that the estimators are fairly robust across a wide range of possible inbreeding levels.

Table 3. The bias and RMSE of the two estimators of the average inbreeding coefficient for simulated AFLP data.

N	L		FFM	FB
50	100	Bias	−0.030	−0.010
		RMSE	0.055	0.041
50	200	Bias	−0.019	−0.003
		RMSE	0.048	0.035
100	100	Bias	−0.021	0.000
		RMSE	0.044	0.028

Abbreviation: RMSE, root mean square error.

N, sample size; L, number of loci; F_FM, the frequency-matching estimator (Dasmahapatra et al., 2007); F_B, the Bayesian estimator (developed in this study). The results are based on 50 repetitions for each scenario.

Figure 3.

Results of the simulation study for the scenario N=100, L=100 (see Materials and methods). The asterisks indicate the frequency-matching algorithm and the open squares indicate the Bayesian method introduced in this paper.

Spatial genetic structure

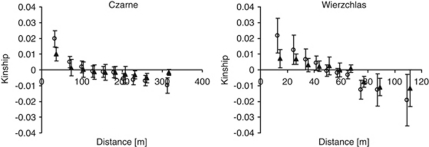
Regardless of the marker type used, both populations showed a strong SGS. All descriptive measures of SGS were significantly different from 0 (Table 4). The nearest neighbours showed the highest kinship, which then decreased with distance (Figure 4). Both AFLP and SSR markers showed that, in Wierzchlas, clustering of related individuals was more intensive than in Czarne. However, the slope parameters (b₁) for Wierzchlas were not significantly greater than those for Czarne (Table 4). Interestingly, in both populations AFLP markers showed more intensive structuring than SSRs. All three parameters illustrating SGS, that is, kinship among nearest neighbours (f_ij(1)), slope of log-linear regression (b₁) and the SGS intensity measure (Sp) were significantly higher for AFLP than for SSR markers (Table 4).

Table 4. Summary statistics of the SGS estimated for the two study populations.

	fij(1)	b1	Sp
Czarne
AFLP	0.020 (0.003)	−0.012 (0.001)	0.012 (0.002)
SSR	0.010 (0.002)	−0.006 (0.001)	0.006 (0.001)
Wierzchlas
AFLP	0.022 (0.005)	−0.019 (0.006)	0.019 (0.004)
SSR	0.007 (0.003)	−0.009 (0.003)	0.009 (0.003)

Abbreviation: SGS, spatial genetic structure.

f_ij(1), the average kinship in the first distance interval; b₁, slope of the log-linear regression between distance and kinship; Sp, descriptive measure of SGS intensity. The standard errors are in parentheses.

Figure 4.

Correlograms depicting the relationship between distance and kinship. AFLP-based correlograms are represented by the open circles and SSR-based correlograms are represented by the full triangles. Note that the correlograms for the two populations differ in spatial scale owing to sampling properties. The whiskers indicate 95% confidence intervals around the average kinship for a given distance interval.

Generally, the application of the GENELAND software showed that Czarne behaves as a single genetic unit (the most likely K=1), regardless of the markers used. On the other hand, a more complex pattern was estimated for Wierzchlas. When analysed with SSRs, Wierzchlas showed no genetic substructure (K=1). However, for AFLP markers, GENELAND showed that the sample consisted of two sub-populations forming two spatial clusters (Figure 1). A total of 151 and 130 individuals were assigned to the first and the second genetic cluster with a probability exceeding 80% thus only 12 individuals (4%) showed ambiguous membership.

Discussion

Inbreeding and SGS

One of the objectives of this study was to determine the inbreeding levels in remnant English yew populations. Knowledge of inbreeding patterns in English yew is scarce (Lewandowski et al., 1995; Myking et al., 2009; see also Dubreuil et al., 2010). For example, Lewandowski et al. (1995), studying a sample of 41 trees from Wierzchlas using isozymes, detected no inbreeding at the adult stage. However, the F_IS estimated based on the embryos of 400 seeds collected from those trees was equal to 0.049. Myking et al. (2009) suggested that inbreeding may vary significantly among populations. Possible factors contributing to this variation may include establishment history (number of colonizing individuals), size, density and the isolation level of a population. Recently, Dubreuil et al. (2010) studied the genetic structure of English yew populations in Spain using SSR markers. They noted significant deficiency of heterozygotes, which could not be attributed solely to inbreeding, as the SSRs used in that study were strongly affected by null alleles (Dubreuil et al., 2008).

In this paper we estimated the levels of inbreeding in the two yew populations using SSR and AFLP markers, and a Bayesian approach that takes full advantage of the power of multi-locus data. The main benefit of this method was that it provided simultaneous (and unbiased; see Chybicki and Burczyk, 2009) estimates of the average inbreeding coefficient and allele frequencies, including null alleles. Generally, our estimates of inbreeding coefficients were similar to those found in the literature (Lewandowski et al., 1995; Myking et al., 2009), reaching up to 0.063 in Wierzchlas. Thus, although the estimated null allele frequencies at SSR loci were high in both populations, the deficiency of heterozygotes observed in the Wierzchlas population was because of both the presence of null alleles and inbreeding. Similar, but tentative, conclusions were reached by Dubreuil et al. (2010) about Spanish populations.

Elevated inbreeding levels have been found in other Taxus species. For example, in the North American species Taxus brevifolia, El-Kassaby and Yanchuk (1994) observed high F_IS values, with the extreme mean reaching 0.472. Similar observations were also reported for T. cuspidata (F_IS=0.229; Chung et al., 1999). These studies, along with the results available for T. baccata, suggest that in spite of predominant dioecy, yew is not prevented fully from inbreeding.

One possible explanation for inbreeding is mating between relatives, which could take place in highly isolated populations, given that pollen flow is spatially restricted and populations show a kinship structure (Vekemans and Hardy, 2004). In the case of yew, the SGS has been studied only at an among-population scale (Hilfiker et al., 2004; Myking et al., 2009; González-Martínez et al., 2010). Therefore, although yew shows clear structuring at a regional scale, knowledge of within-population SGS has still been lacking. Only recently Dubreuil et al. (2010) suggested a strong tendency towards clustering of genetically similar individuals within populations. Our results fully support their conclusion, showing that a significant SGS can extend up to 50 and 100 m in Wierzchlas and Czarne, respectively (Figure 4).

Interestingly, AFLP markers showed stronger patterns of genetic structure than the SSR markers. This observation was common in both populations and concerned both inbreeding estimates and SGS. In particular, the spatial structuring parameters estimated for AFLPs were significantly greater than those for SSRs (Table 4), a phenomenon that has occasionally been noted in the literature (Jump and Peñuelas, 2007). AFLPs also provided higher, although not significantly higher, estimates of F as compared with SSR-based estimates. Reasons for the differences in genetic structure characteristics between AFLP and SSRs are multiple. AFLP markers are widely known for a high risk of homoplasy (that is, lack of homology of co-migrating fragments), which is not attributed to SSRs. Other possible explanations are differing genome coverage rates or differences in mutation rates between the two types of markers. Also, AFLP fragments show a tendency towards co-variation, which can increase estimates of SGS and inbreeding, owing to violation of the assumption on linkage equilibrium.

Bayesian clustering based on AFLP data showed that Wierzchlas is probably a mixture of two discrete genetic units, whereas SSR markers showed no structuring. This could explain a linear rather than a log-linear relationship between kinship and distance observed for AFLP markers in Wierzchlas (Figure 4) (Born et al., 2008). Nonetheless, the lack of concordance between AFLPs and SSRs points to some ambiguity in the pattern, which cannot be resolved using the available data. Possible reasons include the differing discriminating power of the two marker types (for example, high proportions of null alleles in SSRs lower discrimination power), or different responses to environmental selection (AFLPs are more likely to be linked to loci under selection owing to random coverage of a genome; Gaudeul et al., 2004). The distribution of clusters does not overlap with any evident ecological factor, apart from distance from a nearby lake (Mukrz). However, given the fine spatial scale, the impact of the lake cannot solely explain the observed pattern. Another possible reason could be the history of colonization and/or exploitation of the population in the past. Palynological data suggest that the presence of yew in Wierzchlas has changed in time because of variable human activity (interchanged periods of more and less intensive exploitation) (Noryśkiewicz, 2006). Thus, the presence of two sub-populations in Wierzchlas could be the result of independent colonization events.

Inbreeding and SGS were more evident in Wierzchlas than in Czarne. Although the observed differences were not significant, they might be related to differences in density between the sites. Population density has often been recognized as a crucial factor of genetic structure (El-Kassaby and Jaquish, 1996; Angelone et al., 2007). Density influences mating patterns within populations primarily by determining the distances between mates (Tomita et al., 2008). As a result, with all other factors being equal (for example, a level of flowering synchrony, variance in reproductive success), the effective dispersal of genes is negatively related to density (the lower the density, the larger the dispersal distance) (El-Kassaby and Jaquish, 1996). Thus, in the presence of kinship structure, increased density may enhance bi-parental inbreeding within a population (Zhao et al., 2009). On the other hand, as Wright's neighbourhood size Nb is proportional to (effective) the density of a population (Wright, 1946), one can expect a decrease in the rate of local genetic drift together with an increase in density. Thus, density may theoretically influence the spatial genetic structuring (as measured by Sp index) and inbreeding levels in opposite directions (Vekemans and Hardy, 2004). This was not the case in our study, although the populations differed in density about 10-fold. One possible explanation could be lack of a drift–dispersal equilibrium (Hardy et al., 2006). However, we cannot exclude additional forces that may interfere with gene dispersal during the development of a genetic structure, such as non-random mating or selection. The latter seems a likely additional force especially in the case of the AFLP data, as noted earlier.

Methodological considerations

AFLP markers are widely used in population genetics, because their use does not require costly initial steps, that is, a genome-specific marker design (like in case of SSRs). Although estimation of inbreeding levels is the aim of many genetic studies (especially in endangered species), AFLP markers are typically considered to be poorly informative about inbreeding owing to low polymorphism (bi-allelic system) and complete dominance (Holsinger et al., 2002). In this paper we introduced a Bayesian method for inference of the within-population inbreeding coefficient that takes full advantage of multi-locus phenotypes derived from dominant markers. Although an exhaustive study of the statistical behaviour of the method is difficult because the algorithm is a time-consuming approach, we put some effort into studying simulated data sets to uncover the most important features of the estimation procedure. Generally, 50 individuals typed at ⩾100 dominant loci allowed a quite good approximation of a true average inbreeding coefficient. However, accurate estimates of individual inbreeding coefficients require a much larger sampling effort (towards increasing a number of loci). In order to increase the precision of the estimate of the average inbreeding level, increasing the number of individuals seems to be more efficient than increasing the number of loci. This is probably because of the fact that sampling more individuals reduces the stochasticity of the average inbreeding coefficient as estimated based on individual inbreeding levels (F_i). On the other hand, increasing the number of loci will increase the accuracy of individual inbreeding estimates (F_i). However, even highly accurate F_i estimates may poorly reflect the population average if the number of individuals is small. Our method (F_B) provides somewhat better estimates of the average inbreeding as compared with the method proposed by Dasmahapatra et al. (2007) (F_FM). The two methods differ fundamentally, because, whereas the F_B estimator is well founded in the Bayesian statistical methodology, F_FM is rather a heuristic approach, in which the Method-of-Moments estimator is adjusted based on the specific assumptions. A clear advantage of the Bayesian approach is that, unlike F_FM, the F_B estimate is accompanied by posterior confidence (credibility) intervals, allowing insight into the precision of an estimate. Nonetheless, more extensive study should be made of the general statistical properties of each method.

Another important estimation problem (not considered in the simulation study), which unfortunately cannot be minimized by increasing sampling effort, is distribution (variance) of the actual within-population inbreeding coefficient. We expect that the methods work reasonably well if the actual inbreeding coefficient shows high variance (that is, individuals differ a lot in their inbreeding levels F_i). This is because low inbreeding variance leads to invariable realizations of inbreeding at the individual level. At the extreme, if all the F_i values in our model (see for example, equation (1)) were the same across all individuals, they would behave as a single parameter F. Such an F would be near-impossible to estimate, because it could take any value easily counterbalanced by specific allele frequencies to give the same likelihood. The same property makes the simultaneous maximum likelihood inference of F and allele frequencies based on dominant markers impossible (Holsinger et al., 2002). However, as long as some variation in F_i is expected (for example, owing to mixed mating system), the algorithm proposed in this study provides robust estimates of within-population inbreeding.

Recently, Foll et al. (2008) raised the problem of ascertainment bias in AFLP markers, which can introduce severe bias to F_IS estimates. The ascertainment bias arises from violation of assumptions about allele frequencies in AFLP markers. Although our simulation study did not show such behaviour in the F_B estimator, additional study should be undertaken to assess this problem. However, even if F_B also suffers from ascertainment bias, the estimator can be modified according to the ABC solution provided by Foll et al. (2008). Ascertainment bias could be another reason for the discrepancy between estimates for SSRs and AFLP mentioned earlier.

Finally, the statistical properties of the F_B estimator are generally independent of the actual inbreeding level (Figure 3), unless actual F is near its extrema (0 or 1). This behaviour is expected because of the assumed prior distribution of F (beta), which is bounded within (0,1) interval. This makes it impossible to get results for F outside the interval, leading to biased estimates at the extrema. The problem could be potentially resolved using a less constrained proposal distribution for F (for example, Ayres and Balding, 1998).

Final remarks

In Poland there are about 250 natural populations of English yew (Iszkuło and Boratyński, 2005). However, the majority are rather small (ca. 25 individuals) and highly isolated one from another. In this study, we showed that a significant kinship structure and inbreeding can be present in large yew populations. These effects are presumably even more pronounced in small patches leading, together with genetic drift, to reduction of genetic variation. The loss of genetic variation often drives the loss of adaptive potential in a population (Willi et al., 2006). Additionally, genetic relatedness among adults can cause inbreeding depression in their progeny (Hirao, 2010). From this perspective, in situ conservation of remnant yew populations needs extended studies to assess the real risk arising from a SGS.

Appendix

Here we describe the algorithm used to infer the hidden variables X_i, D_l and R_l introduced in the Materials and methods section. For the i-th individual X_i=Σ_l x_il, where an indicator x_il=1 if, at the l-th locus, two alleles are identical by descent and 0 otherwise. Using equation (3) (under Materials and methods), one may see that x_il follows a Bernoulli distribution with the probability that x_il=1 being

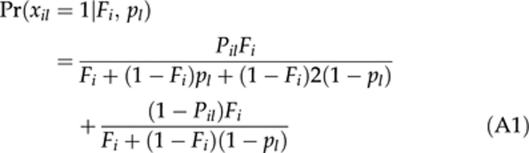Similarly, for the l-th locus D_l=Σ_i d_il and R_l=Σ_i r_il, where the indicator variables d_il and r_il store a number of copies of ancestral alleles at the i-th individual's genotype. The two indicators are inferred jointly based on equation (3). If the i-th individual has a dominant phenotype at the l-th locus (that is, P_il=1), {d_il, r_il} would take one of three possible combinations of values (d_il, r_il)={(1,0),(2,0),(1,1)} the with respective probabilities as follows:

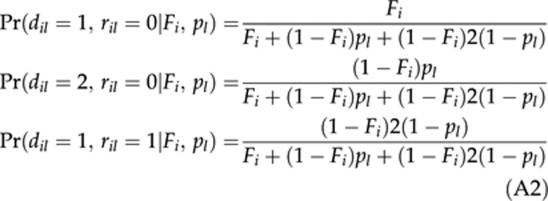If the i-th individual has a recessive phenotype at the l-th locus, then the indicator variables would take one of two possible combinations of values (d_il, r_il)={(0,1),(0,2)}, with the respective probabilities as follows:

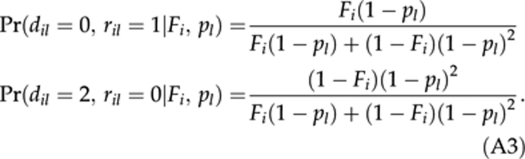Given known F_i and p_l, the indicators x_il, d_il and r_il are inferred for each individual and each locus as random samples from the respective distributions [A1], [A2] or [A3].

The authors declare no conflict of interest.