Abstract
In this paper we develop a framework to analyze the behavior of contagion and spreading processes in complex subpopulation networks where individuals have memory of their subpopulation of origin. We introduce a metapopulation model in which subpopulations are connected through heterogeneous fluxes of individuals. The mobility process among communities takes into account the memory of residence of individuals and is incorporated with the classical susceptible-infectious-recovered epidemic model within each subpopulation. In order to gain analytical insight into the behavior of the system we use degree-block variables describing the heterogeneity of the subpopulation network and a time-scale separation technique for the dynamics of individuals. By considering the stochastic nature of the epidemic process we obtain the explicit expression of the global epidemic invasion threshold, below which the disease dies out before reaching a macroscopic fraction of the subpopulations. This threshold is not present in continuous deterministic diffusion models and explicitly depends on the disease parameters, the mobility rates, and the properties of the coupling matrices describing the mobility across subpopulations. The results presented here take a step further in offering insight into the fundamental mechanisms controlling the spreading of infectious diseases and other contagion processes across spatially-structured communities.
Keywords: Mathematical epidemiology, metapopulation model, reaction-diffusion process, contagion process, infectious disease
1. Introduction
In recent years, reaction-diffusion processes have been used as a successful modeling framework to approach a wide array of systems that, along with the usual chemical and physical phenomena [1, 2], includes epidemic spreading [3–10], human mobility [6–9], and information and social contagion processes [11–16]. This paradigm is extremely useful in the case of populations characterized by a highly fragmented environment in which the population is structured and localized in relatively isolated discrete patches or subpopulations connected by mobility of individuals. In this case, the spatial structure of populations is known to play a key role in the system’s evolution and the reaction-diffusion dynamics is integrated in a metapopulation modeling scheme in which different subpopulations are coupled together by the mobility or migration patterns of individuals [17–20]. Classic metapopulation dynamics focuses on the processes of local extinction, recolonization and regional persistence [21, 22] as the outcome of the interplay between migration processes and population dynamics, and has been successfully applied to understand the epidemic dynamics of spatially-structured populations with well-defined social units (e.g., families, villages, towns, cities, regions) connected through individuals’ mobility [3–9, 23–28]. The metapopulation dynamics of infectious diseases has generated a wealth of models and results that consider both mechanistic approaches that take the movement of individuals explicitly into account [9, 29–34] and effective coupling approaches wherein the diffusion process is expressed as a force of infection coupling different subpopulations [6, 8, 35–39]. Recently, the metapopulation approach has been implemented in data-driven computational models for the large-scale analysis of the geographical spreading of infectious diseases [28, 40–45].
In large-scale systems, the metapopulation approach amounts to a particle-network description in which each subpopulation populated by a certain number of individuals is connected to a set of other subpopulation by mobility flows. The particle-network framework has stimulated the broadening of reaction-diffusion models in order to deal with complex network substrates and complex mobility schemes, which has in turn allowed for the uncovering of new and interesting dynamical behaviors as well as providing a rationale for the understanding of the emerging critical points underpinning some interesting characteristics of techno-social systems [46–49]. In particular, it has been shown that along the local epidemic threshold, which depends only on the disease parameters and is responsible for the epidemic outbreak within each subpopulation, structured populations may exhibit a global invasion threshold [47, 48, 50–52] that determines whether the metapopulation system is globally invaded by the contagion process. This novel threshold depends on the mobility rates and patterns of individuals and cannot be uncovered by continuous deterministic models as it is related to the stochastic effects of the reaction-diffusion process that describe the contagion process.
Metapopulation epidemic models, especially at the mechanistic level, are based on the spatial structure of the environment and the detailed knowledge of transportation infrastructures and movement patterns. However, the recent accumulation of large amounts of human mobility data [53–59] from the scale of single individuals to that of entire populations presents us with new challenges related to the high level of predictability and recurrence [60–62] found in the mobility and diffusion patterns in real data. For instance, commuting mobility – denoted by recurrent bidirectional flows among locations – dominates the human mobility network at the scale of census areas defined by major urban areas by one order of magnitude [59]. Highly predictable or recurrent mobility patterns do not find an easy representation in the particle-network framework as the framework is based on reaction-diffusion processes that in most cases exploit Markovian diffusion properties [47, 48, 63]. The description of mobility processes with memory and their importance in epidemic processes have been put forward in detail in the seminal paper of Ref. [7]. The effect of recurrent and predictable mobility patterns of individuals on the onset of the global invasion behavior of contagion processes is just recently being studied both analytically and numerically [64–67].
Here we develop a framework based on a time-scale separation technique to analyze the behavior of contagion and spreading processes on a network of locations where individuals have memory of their location of origin. We focus on the prototypical example of the spreading of biological agents in populations characterized by bidirectional commuting patterns. We assume that individuals of a subpopulation will visit any one of the connected subpopulations with a per capita diffusion rate σ. As we aim at modeling commuting processes in which individuals have a memory of their location of origin, displaced individuals return to their original subpopulation with a per capita return rate τ. The mobility parameters σ and τ influence the probability that individuals carrying infection or information will export the contagion process to nearby subpopulations. If the diffusion rate approaches zero then the probability of contagion of neighboring subpopulations goes to zero as there are no occasions for the carriers of the process to visit them. On the other hand if the return rate is very high then the visiting time of individuals in neighboring populations is so short that they do not have time to spread the contagion in the visited subpopulations. This implies the presence of a transition [47, 48, 50–52] between a regime in which the contagion process may invade a macroscopic fraction of the network and a regime in which it is limited to a few subpopulations. The presented results extend and generalize the analysis of [47, 48, 64, 65] and we include in the analytical treatment the heterogeneity of the subpopulation network and find an explicit expression for the threshold separating a regime in which the spreading phenomenon affects a macroscopic fraction of the system and a regime in which only a few locations are affected. The invasion threshold depends on the mobility parameters, providing guidance on how to control disease spreading by constraining mobility processes. The results are confirmed by mechanistic Monte Carlo simulations for the infection dynamics in synthetic metapopulation systems in which each single individual is tracked in time to account for the discreteness of the processes involved. Heterogeneous connectivity patterns among subpopulations are modeled and different values of the parameters involved are considered to validate the theoretical results. The theoretical approach presented in this paper extends and generalizes the results presented in Ref. [64] opening the path to the inclusion of more complicated mobility or interaction schemes and at the same time provides a general framework that may be used not just as an interpretative framework. Understanding the effect of mobility and interaction patterns on the global spreading of contagion processes can then be used to enhance or suppress spreading by adjusting the basic parameters of the system in the appropriate ways.
The paper is organized as follows. Section 2 introduces the basic formalism for recurrent mobility patterns and the time-scale separation approximation that defines mixing subpopulations. Section 3 generalizes the formalism to the case of complex subpopulation networks by using a mean-field degree-block variables description equivalent to a mean-field description that includes the network heterogeneity. Section 4 incorporates the disease spreading into the mobility processes. Stochastic effects and discrete descriptions of the processes are considered with a tree-like approximation for the analysis of the invasion dynamics at the level of subpopulations. The effects of diffusion properties on the invasion dynamics are analyzed and related to the existence of an invasion epidemic threshold for the metapopulation system. In Section 5 we report extensive mechanistic Monte Carlo simulations which confirm the analytical findings of the previous sections.
2. Mobility processes with memory and commuting networks
In order to describe the mobility process induced by the commuting pattern of people among subpopulations let us consider a metapopulation system with V distinct subpopulations, each of which has a population size Ni (i = 1, …, V). The subpopulations form a network in which each subpopulation i is connected to a set of other subpopulations ν(i). The edge connecting two subpopulations i and j indicates the presence of a flux of commuters. We assume that individuals in subpopulation i will visit any one of the connected subpopulations with a per capita diffusion rate σi. As we aim at modeling commuting processes in which individuals have memory of their residence, displaced individuals return to their original subpopulation with a per capita rate τi. The simple case of two connected subpopulations is shown in Fig. 1. In the case of each subpopulation i connected with ki other subpopulations we assume that each commuting individual can visit a specific subpopulation j with rate σij with the obvious condition that Σj∈ν(i) σij = σi. The rate σij accounts for different attractiveness of each subpopulation and may depend on variables such as the population Nj, the actual distance, and other demographic or economic factors. We will provide two basic cases in which the rate σij depends on the number of individuals at origin and destination subpopulations in analogy with the classic gravity law [68, 69] used in transportation sciences. For the sake of mathematical simplicity, however, we neglect the impact of actual distance between the origin and destination subpopulations, which is a key ingredient of gravity laws used to describe mobility fluxes among spatially structured populations.
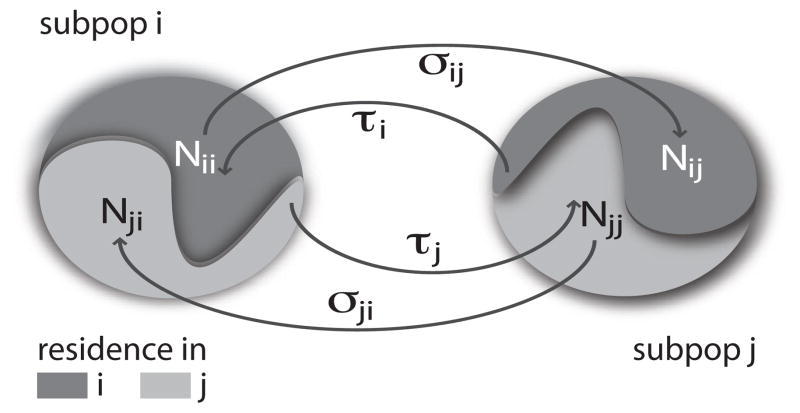
Figure 1.
Illustration of commuting and subdivision of population. At any time each subpopulation is occupied by its own residents plus visitors from its neighbors. For instance, the population in subpopulation i is divided between individuals who reside and are present in the subpopulation (Nii) and those who are residents in subpopulation j but present in subpopulation i(Nji). Different classes of people move between connected subpopulations along the edges at the rates shown.
At any moment in time, each member of subpopulation i is either in the subpopulation of residence or outside and visiting one of the neighboring subpopulations j. By using the approach developed in [7, 9], we may group the members of i according to the location in which they are actually present at a given time t, Nii(t) and Nij (t) with j ∈ ν (i) (see Fig. 1). The rate equations for the population sizes of different subgroups can be readily written by explicitly taking into account the mobility rates along the edges of the subpopulation network. This system of rate equations has a characteristic relaxation time that can be obtained by solving the differential equations, as reported in A. In particular, it is possible to show under the general assumption of σi ≪ τi that the relaxation characteristic time is and that the mixing subpopulations reads as
| (1) |
This implies that in the regime σi ≪ τi, {Nij (t)} represent a small perturbation to the overall subpopulation size Ni.
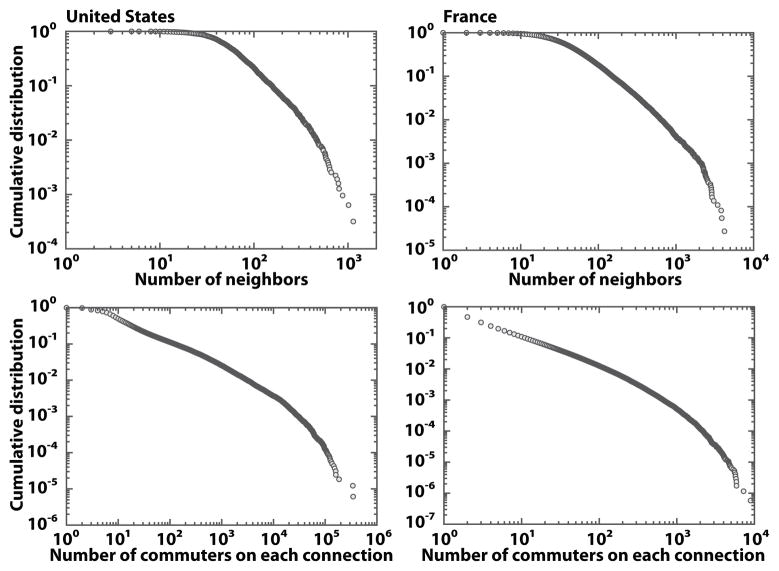
From the above considerations it appears that most of the system complexity is encoded in the subpopulation connectivity matrices that determine the σij and the corresponding populations at the equilibrium (see A). A wide range of networks that represent activity and interaction patterns of individuals [70, 71], transportation fluxes, and population movements on local and global scales [53–59] have been found to exhibit complex features encoded in large-scale heterogeneity, self-organization, and other properties typical of complex systems. In particular, air-travel patterns between urban areas [54, 55] and commuting patterns in the scale of intra- and inter-urban areas [53, 56–59] have been shown to exhibit connectivity patterns varying over orders of magnitude. In order to provide empirical evidence of the connectivity patterns observed in real commuting networks we analyze the commuting fluxes in several countries. In Fig. 2 we display the cumulative distributions of the number of connections per administrative unit and the flux of commuters on each connection in the United States and France. The networks exhibit important variability in the number of connections per geographical area, spanning three to four orders of magnitude. Similarly, the number of commuters on each connection is highly heterogeneous, distributed in a wide range of four to six orders of magnitude. These properties, often mathematically encoded in a heavy-tailed probability distribution, have been shown to have important consequences for dynamical processes on contact networks [72–77] as well as on subpopulation networks [46–48], altering the threshold behavior and the associated dynamical phase transition. It has been shown [47, 48] in particular that topological fluctuations in subpopulation networks favor global spreading of infectious diseases by lowering the global epidemic threshold and suppressing the phase transition at the infinite size limit of the network.
Figure 2.
Statistical properties of commuting networks in the United States and France. Cumulative distributions of the number of connections per administrative unit and the number of commuters on each connection are displayed. The networks are highly heterogeneous in the number of connections per geographical area as well as in the flux of individuals on each connection.
3. Mobility processes with memory in heterogeneous networks
In order to gain analytic insight into the case of subpopulation networks with highly heterogeneous connectivity patterns we rely on the assumption of statistical equivalence of subpopulations with similar degree. This is a mean-field approximation that considers all the subpopulations with same degree as statistically equivalent, thus allowing the introduction of degree-block variables that depend only upon the subpopulation degree. While this is an obvious approximation to the system description, it has been successfully applied to many dynamical processes on complex networks [46–48].
Imagine a random subpopulation network with given degree distribution P(k) and denote the number of subpopulations with k connections by Vk. By using the statistical equivalence of subpopulations with the same degree k, we can express the average population in each node with degree k as a degree-block variable,
| (2) |
where the sum runs over all the subpopulations with degree k, and attribute it to all such nodes. The above degree-block variable defines a mean-field approximation within each degree class, while relaxing the overall homogeneity assumption valid in homogeneous systems.
In the following we will consider that the degree-block variable N̄k has a prescribed functional form identifying the stationary distribution of the population within the system, which does not change over time. In other words we assume that any mobility time scale is much shorter than the demography time scale of the population. For the sake of analytical calculation we will assume the functional form
| (3) |
where N̄ = Σk N̄kP(k) is the average number of individuals per node in the subpopulation network. This expression is obtained as the stationary population distribution in the case of simple random diffusive processes where the diffusion rate of individuals along each link leaving a node of degree k has the form 1/k [48]. Moreover, the empirical data from various sources suggest similar population scaling as a function of the connectivity to other subpopulations [45, 54, 78]. While the population N̄k of each node is assumed to be fixed, each individual in a subpopulation of degree k is assumed to commute to a neighboring subpopulation of degree k′ at rate σkk′ and to return to the origin of her trip at rate τk. We thus also assume that the only dependence for the mobility rates is through the degrees of the nodes.
Following the same approach in the previous section we partition the individuals of a subpopulation with degree k according to classes identified by the degree of the subpopulation in which they are present at a given time t. Namely we define N̄kk(t) as the average number of individuals of any subpopulation k present in the subpopulation k and N̄kk′ (t) as the average number of individuals of any subpopulation k present in the subpopulation k′. It is worth noting that N̄kk′ (t) is also a degree-block variable evaluated over all the connections k → k′. The rate equations defining the commuting dynamics among subpopulations can be formalized by using the variables N̄kk(t) and N̄kk′ (t). Considering Eq. (3) for N̄k, the set of differential equations leads to the equilibrium solutions
| (4) |
| (5) |
as detailed in B. In the above expressions ρk is the ratio of per capita total diffusion rate to return rate of residents of a subpopulation with degree k,
| (6) |
The expressions (4–5) are valid for the stationary states and are good approximations to the system description under the general assumptions that σk ≪ τk and that the system can equilibrate in a time interval larger than . Analogously to the calculation originally presented by Keeling and Rohani [9], these expressions allow us to consider that the subpopulation k has an effective number of individuals N̄kk′ in contact with the individuals of the neighboring subpopulation k′ in a quasi-stationary state that is reached whenever the time scale of a second dynamical process that we study is larger than . This is extremely important in the case of disease dynamics, for which when the time scale of the disease is large enough compared to one can generalize the quasi-stationary state expressions for all population compartments and obtain the effective force of infection or the number of individuals exposed to infection in the neighboring subpopulations. In the next section we will lever on this approximation to obtain explicit analytical conditions for the occurrence of epidemic outbreaks involving a finite fraction of subpopulations in the thermodynamic limit, the so-called ‘invasion threshold’ [47, 48, 50–52].
4. Epidemic spreading and the invasion threshold
Here we want to consider that an infectious disease has been introduced in one or a tiny number of subpopulations. For the sake of analytical simplicity we assume the usual susceptible-infectious-recovered (SIR) model [77] for the disease. The SIR compartmental model classifies at any time t each individual by one of the disease compartments: susceptible (S); infectious (I); recovered (R). Susceptible individuals acquire infection in the case of contact with an infectious individual at a per capita rate β. An infectious individual permanently recovers at a rate μ, and from then on is immune to the disease and is not contagious. In a completely susceptible subpopulation, the spreading of the disease is determined by the basic reproduction ratio R0, which is defined as the average number of secondary (infectious) cases generated by the introduction of a single typical infectious individual [77]. Assuming homogeneous mixing of the population, the basic reproduction ratio is given by R0 = β/μ. When R0 > 1 the infectious disease spreads inside the subpopulation and causes an appreciable fraction of the population to acquire the infection during its entire progression.
In the case of metapopulation models, however, the spreading of the disease is determined not only by the local parameter R0, but by the diffusion process and the topology of the underlying network as well. This can be readily understood in the case of no mobility across subpopulations since the disease cannot invade other subpopulations and therefore remains constrained to a single subpopulation. In the case of a very small diffusion of individuals the disease generally dies out, depleting the susceptible pool of individuals before it can generate an epidemic in neighboring subpopulations. On the contrary, in the case of sustained mobility across subpopulations many infectious individuals can export the disease to other subpopulations thus generating a global outbreak in the metapopulation system. This implies that there must be a second reproductive number at the subpopulation level R* that depends on the mobility parameters and defines a threshold for the epidemic invasion of a finite fraction of subpopulations [47, 48, 50–52]. Here we want to investigate the dependence of R* on the commuting dynamics of individuals, thus taking into account the non-Markovian nature of the mobility process.
Imagine to introduce an infectious disease to a single subpopulation of degree k and size N̄k. Given that the local threshold condition is satisfied (R0 > 1), the epidemic will spread globally in the metapopulation systems if each infected subpopulation is able to trigger the start of an epidemic in at least one other subpopulation. This amounts to the derivation of a subpopulation reproductive number that expresses the average number of infected subpopulations generated by a typical infected subpopulation in a fully susceptible metapopulation system. We may describe the early stage of the disease spreading at the level of the metapopulation system as a branching process [47, 48, 50, 79, 80]. The process starts with a set of initially infected subpopulations { }, each of which during the course of the epidemic transmits the disease to a set of its non-infected neighboring subpopulations defining the set { } at the next generation. Let us denote the number of diseased subpopulations with degree k at the nth generation by and derive the relation between subsequent generations and . If we consider the case that we are just above the local epidemic threshold, R0 − 1 ≪ 1, and that there are no correlations between the degrees of connected nodes, then it is possible to show that
| (7) |
where λk′k is the number of infectious individuals which can be generated and sent by a diseased subpopulation (source) with degree k′ to a non-diseased subpopulation (target) with degree k and we made use of the fact that the probability of triggering an outbreak in the non-diseased subpopulation is [81]. (see C). In order to write an explicit form of the above expression we need to explicitly define λk′k. This quantity can be expressed in terms of the number of individuals living in one of the subpopulations and visiting the other by
| (8) |
where α is the fraction of individuals that is affected by the disease by the end of the SIR epidemic and can be approximated by for R0 ≃ 1 [77]. The first term on the right-hand side of λk′k accounts for the total visits of infectious people from the source to the target subpopulation, while the second term accounts for the visits of individuals from the target to the source subpopulation during which they acquire infection and carry the disease back to their origin. If the time scale of the disease in each individual μ−1 is much larger than the time scale of the visits to neighbors τ−1 (i.e., μ−1 ≫ τ−1), we can then use the stationary solutions for N̄k′k and N̄kk′ in Eq. (5). Furthermore we are assuming that there are no restrictions on the mobility of infectious people. This is generally not true even though for many diseases like influenza [82, 83] it is well known that a large fraction of clinical cases keep their regular habits as well as infectious asymptomatic cases. For other diseases this may not be a realistic assumption, but the following calculations can be performed by considering exposed or latent individuals as the disease carriers as long as the characteristic time of these disease states is larger than the mobility time scale.
In the following we will assume that the return rate τk is independent of the subpopulation degree, i.e., τk = τ. This implies that the time scale of commuting is basically the same across all the subpopulations, a reasonable assumption as the return rate is mostly defined by universal features such as work hours per day. For the commuting rates we instead assume the form
| (9) |
where the denominator corresponds to the total average population of subpopulations in the neighborhood. This term just represents a normalization factor so that the total commuting rate per capita is the same σk = σ across all the subpopulations. The above relation states that the total number of individuals commuting between subpopulations k and k′ is proportional to the product of the two populations. This is a simple case of the gravity law [68, 69] used in transportation studies. We use this form for the sake of mathematical simplicity, but more complicated functions of populations can be considered both analytically and numerically. We should note however that more realistic models consider also the actual distances between subpopulations [59, 84] in order to describe mobility fluxes among spatially structured populations.
Using all the assumptions above, the dynamical behavior of the iterative system (7) is determined by the branching ratio
| (10) |
where ρ ≡ σ/τ is the ratio of commuting to return rate, as shown in C. In the above expression f is a function only of the moments of the degree distribution of the subpopulation network,
| (11) |
The infectious disease will spread globally in the metapopulation system only if R* > 1. This is equivalent to defining a subpopulation reproductive number [47, 48, 50–52] that in structured metapopulation systems is the average number of infected subpopulations generated by a typical infected subpopulation in a fully susceptible metapopulation system. Thus, by setting R* = 1, we can define an epidemic threshold relation for the mobility ratio ρ,
| (12) |
below which the infection remains confined to a small number of subpopulations. In an infinite metapopulation system the threshold is defined rigorously and the fraction of infected subpopulations is zero below the threshold and finite only if the mobility parameters set the ratio ρ above the threshold value.
The threshold value is defined for the ratio between the rates characterizing the mobility process. We can therefore obtain two different threshold conditions on the mobility dynamics if we fix one of the two parameters σ and τ, and let the other parameter free. The threshold relation for σ is σc = ρc τ,
| (13) |
This intuitively states that the rates of diffusion to nearby subpopulations has to be large enough (σ > σc) to guarantee the spreading of the disease. Interestingly, however, we can also define the threshold relation for τ−1, ,
| (14) |
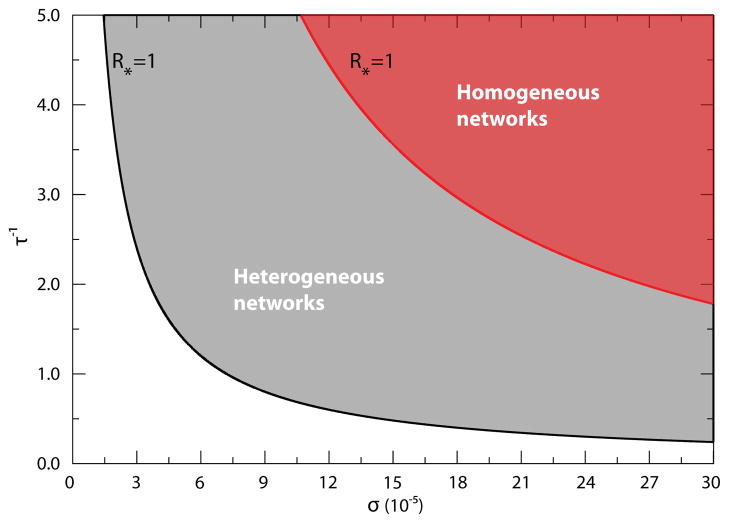
that tells us that the global spreading of the disease can be achieved by reducing the return rates of individuals – in other words by extending the visit times of individuals in nearby subpopulations ( ). However, this last condition breaks down when τ−1 gets much larger and becomes comparable to the disease time scale, thus breaking the time-scale separation assumption used here. In Fig. 3, we assume μ−1 very large, and draw the phase diagram separating the global invasion regime from the extinction regime in the σ-τ−1 plane, with the global epidemic threshold curve defined by the relation R* = 1.
Figure 3.
Phase diagram on the σ-τ−1 plane for the case of Eq. (9) in heterogeneous and homogeneous subpopulation networks. The phase diagram separating the global invasion from the extinction regime is shown on the σ-τ−1 plane assuming Eq. (9) for commuting rates. The solid lines correspond to the solution R* = 1 of Eq. (10), above which the infection spreads at the metapopulation level as indicated by the shaded areas. We can easily see an increase of about one order of magnitude in the critical values of mobility rates as we switch from a heavy-tailed to a Poisson degree distribution. Networks have the same average degree and contain V = 104 subpopulations in which the heavy-tailed network assumes P (k) ~ k−2.1. Each subpopulation accommodates a degree-dependent population of N̄k = N̄k/〈k〉 individuals with N̄ = 104. Moreover the disease is characterized by R0 = 1.25 and μ−1 = 15 days.
Another very interesting feature of the above threshold value ρc is the explicit effect of the network topology encoded in the moments of degree distribution 〈k〉, 〈k2〉, etc. As has been already observed in the Markovian diffusion case, the heterogeneity of the network favors the global spread of the epidemic by lowering the threshold value. Indeed, for heavy-tailed degree distributions P (k) ~ k−γ with γ > 1 and kmin ≤ k ≤ kmax, the nth moment scales as if n ≥ γ − 1 and kmax ≫ kmin. This means that for n ≥ γ − 1, the nth moment of the degree distribution tends to diverge at the infinite size limit of the network, as in this limit kmax → ∞, virtually reducing the threshold to zero. In particular, if the exponent γ < 5, then f (〈k〉, 〈k2〉, 〈k3〉, 〈k4〉) tends to diverge in the limit of infinite network size, which in turn pushes the threshold value ρc to zero, as reported in D. Even at finite size, however, the threshold value is generally smaller the higher the network heterogeneity is (see D for various examples). In Fig. 3 we compare the epidemic threshold curves in the space of the mobility parameters for a Poisson network and a heavy-tailed network with degree distribution P (k) ~ k−2.1.
While the previous R* and threshold conditions have been obtained in the case of a very simple σkk′ resulting in σk = σ independent of the subpopulation index, very similar expressions can be obtained in more complicated mobility schemes. For instance, we can consider the case
| (15) |
that assumes that the per capita mobility rate is rescaled by the number of individuals in the subpopulation [9], thus leading to σk that decreases as N̄k increases. This behavior accounts for the effect introduced by large subpopulation sizes; the overall per capita commuting rate outside of the subpopulation generally decreases in large populations as individuals tend to commute internally. In this case we can repeat the above calculations, finally obtaining
| (16) |
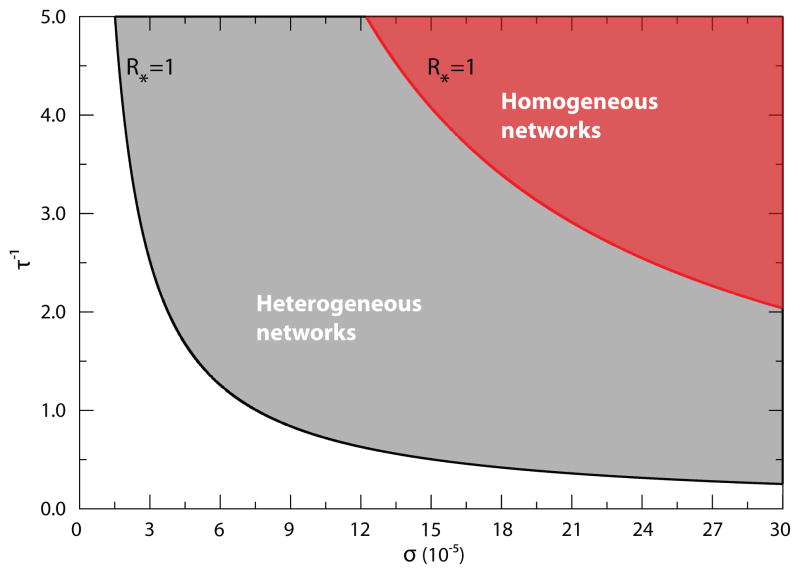
The above expression recovers global epidemic threshold conditions very close to those obtained previously, supporting the general robustness of the presented results. In Fig. 4 we draw the phase diagram separating the global invasion regime from the extinction regime in the σ-τ−1 plane, with the global epidemic threshold curve defined by the relation R* = 1 for the case of Poisson and heavy-tailed networks. Also, in this case the global epidemic threshold is a function of the mobility parameters and the network topology.
Figure 4.
Phase diagram on the σ-τ−1 plane for the case of Eq. (15) in heterogeneous and homogeneous subpopulation networks. The phase diagram separating the global invasion from the extinction regime is shown on the σ-τ−1 plane assuming Eq. (15) for commuting rates. The solid lines correspond to the solution R* = 1 of Eq. (16), above which the infection spreads at the metapopulation level as indicated by the shaded areas. The diagrams should be compared with Fig. 3.
It is worth stressing again that the previous expressions are derived under the assumption of equivalence of degree-block variables, valid only at the limit in which a small fraction of the subpopulations in the system is affected and in which R0 − 1 ≪ 1 and τ−1 ≪ μ−1. However, it is extremely relevant that metapopulation systems intrinsically have two epidemic thresholds in the case of mobility processes with memory. The emergence of a global epidemic is first constrained by the intrinsic epidemic threshold within each subpopulation, R0 > 1. If the epidemic process satisfies this condition, then each time an infectious individual seeds an epidemic within a subpopulation there is a finite probability that a macroscopic fraction of the population will be affected by the outbreak. While this condition guarantees the intra-population spreading of the epidemic, the inter-population spreading is controlled by the coupling among subpopulations as quantified by the rates of the commuting dynamics. The global invasion threshold condition R* > 1 provides an estimate of the diffusion and return rates of individuals above which the epidemic is able to affect a macroscopic fraction of subpopulations defining the metapopulation system.
5. Stochastic Simulations
In the following we provide extensive numerical simulations to support the theoretical picture described above. We present in detail the mechanistic numerical simulations where each single individual is tracked in time, during both the infection dynamics and the diffusion processes, and the synthetic subpopulation networks. We report results from Monte Carlo simulations in a variety of different cases and compare them with the analytical findings.
5.1. Computational model and synthetic subpopulation networks
We construct the network of V subpopulations from a pool of N̄V people. Population size Ni assigned to each subpopulation i is chosen at random from a multinomial distribution with probability proportional to ki, which ensures that the metapopulation system obeys Eq. (3). In order to compare with theoretical calculations, the subpopulation network structure has been generated by wiring the subpopulations according to two different random graph topologies:
Erdős-Rényi graphs [85] have been synthetized by assigning a link between each pair of nodes with probability 〈k〉/(V − 1), where 〈k〉 is a prescribed average node degree;
Networks with power-law degree distribution, P (k) ~ k−γ with kmin ≤ k ≤ kmax, have been generated by an uncorrelated configuration model [86, 87]. All the scale-free networks have been generated by setting γ = 2.1 and kmin = 2.
For the sake of comparison, the average degree of Erdős-Rényi graphs has been set to that of scale-free networks.
As detailed in E, we adopt mechanistic numerical simulations in which each individual is tracked in time during both the commuting and the infection dynamics. The rate σij at which a resident of subpopulation i commutes to a neighboring subpopulation j ∈ ν(i) assumes Eq. (15):
| (17) |
Each resident in subpopulation i leaves her origin and visits subpopulation j with probability σij Δt, where Δt is the time interval considered. A commuter in subpopulation j returns back to her permanent subpopulation i with probability τΔt. Inside each subpopulation we consider an SIR epidemic model in which each individual is classified by one of the discrete disease states at any point in time. The rate at which a susceptible person in subpopulation i acquires the infection, the so-called ‘force of infection’ λi, is determined by interactions with infectious individuals. The force of infection λi(t) acting on each susceptible individual in subpopulation i at time t has been assumed to follow the mass-action principle
| (18) |
where β is the transmission rate of infection and is the prevalence of infectious individuals in the subpopulation. Given the force of infection λi(t) in subpopulation i, each person in the susceptible compartment (S) contracts the infection with probability λi(t)Δt and enters the infectious compartment (I). Each infectious individual permanently recovers with probability μΔt and enters the recovered compartment (R).
5.2. Numerical results
The epidemic invasion threshold at the metapopulation level is determined by reproduction ratio R0, commuting ratio ρ, and the architecture of the commuting networks. In the following we present extensive numerical simulations in order to demonstrate these dependencies and verify the analytical result of Eq. (16).
Simulations have been initialized with I(0) = 10 infectious individuals, seeded randomly in a single subpopulation of degree kmin, while the rest of the population is assumed to be susceptible to infection. Since we aim at determining the global invasion threshold, we have let the metapopulation system progress until the infection dies out. In the results we present here all the realizations resulting in at least one diseased subpopulation have contributed to the statistical analysis unless stated otherwise. For each set of parameters we have generated at least 2, 000 system realizations. Since the subpopulation networks and dynamical processes on them are subject to fluctuations, we have sampled at least 10–20 network realizations and 100–200 dynamical realizations on each of them.
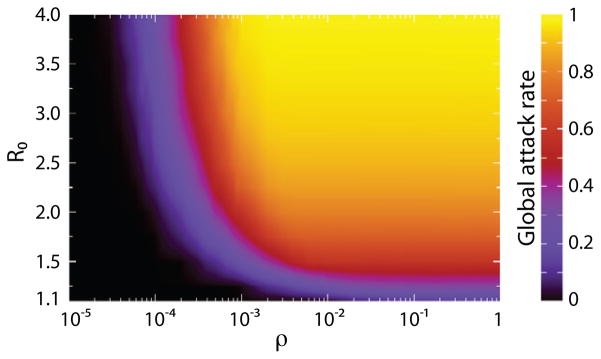
Let us first turn our attention to the effects of ρ and R0 on the global attack rate as shown in Fig. 5. We can clearly see the dependence of the critical value of ρ on R0, consistent with the analytical result of Eq. (16). The lower the basic reproduction ratio the higher the commuting ratio needed for the infection to spread successfully at the metapopulation level. Another observation is that if ρ is far from its critical value (below or above), then the global attack rate is not altered by further changes in ρ. Hence we can conclude that the attack rate is determined only by local parameters in subpopulation systems coupled with commuting.
Figure 5.
Average global attack rate as a function of ρ and R0 in homogeneous subpopulation networks. The figure codes with color the average fraction of individuals infected by the outbreak in the space of ρ and R0. For smaller values of R0 larger values of ρ are needed for the infection to spread at the global scale. Once ρ is well below or above its critical value its precise value does not affect the attack rate. In order to vary ρ, we have fixed the return rate τ at 1/day and changed the value of the commuting rate σ. Networks are made of V = 104 subpopulations, each of which accommodates a degree-dependent population of N̄k = N̄k/〈k〉 individuals with N̄ = 104. The infectious period is set to μ−1 = 3 day.
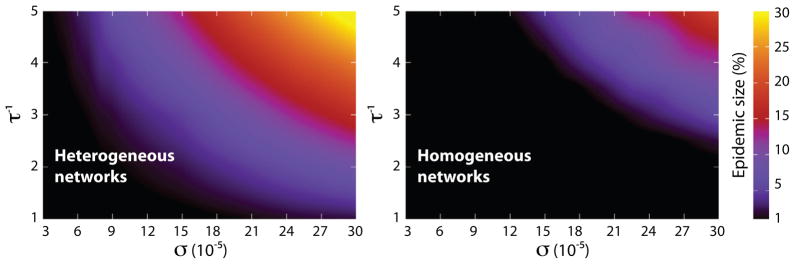
In order to uncover the dependence of invasion threshold on the individual mobility rates numerically, we have simulated epidemics on homogeneous and heterogeneous subpopulation networks. In Fig. 6 we display the variation in epidemic size as a function of σ and τ−1. Consistent with the phase diagrams of Fig. 4, the smaller the commuting rate the longer the duration of visits needed to enable the infection to invade an appreciable fraction of subpopulations. We can also easily notice the one order of magnitude difference in the critical values of σ and τ−1 as the degree distribution of subpopulation networks changes.
Figure 6.
Average epidemic size as a function of σ and τ−1 in heterogeneous (left) and homogeneous (right) subpopulation networks. Each figure shows via a color map the average percentage of subpopulations affected by the outbreak in the space of σ and τ−1. The lower the commuting rate the longer the visiting time is needed for the infection to spread to a finite fraction of subpopulations. The figure should be compared with the phase diagrams of Fig. 4. Networks are composed of V = 104 subpopulations, each of which with a degree-dependent population of N̄k = N̄k/〈k〉 residents with N̄= 104. Disease is characterized by R0 = 1.25 and μ−1 = 15 day.
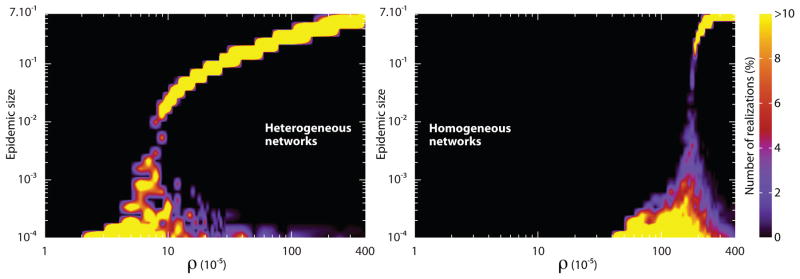
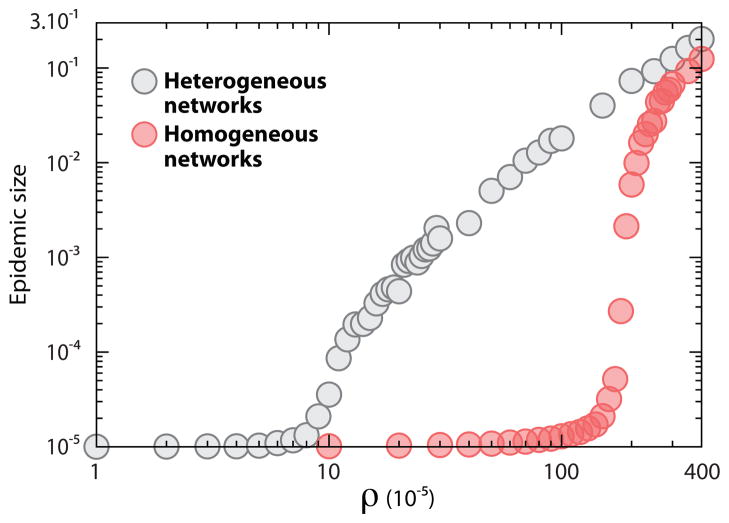
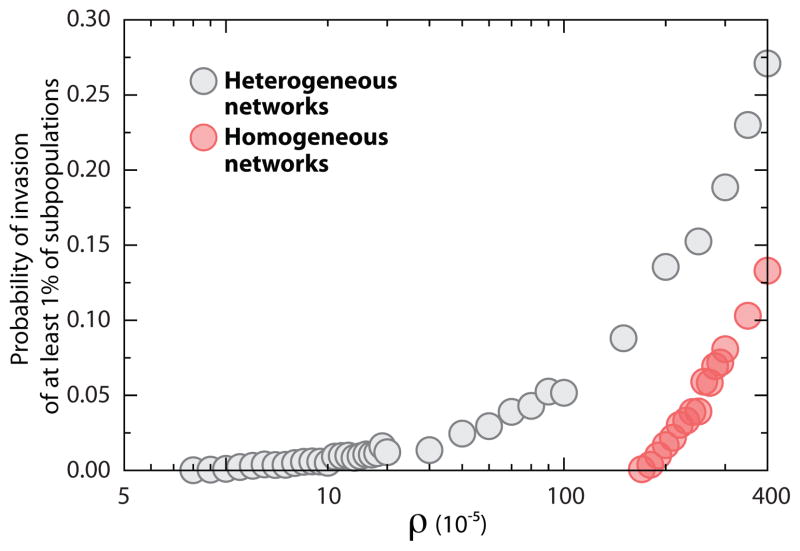
We have stressed the importance of network topology on the spreading of infectious agents at the metapopulation level. In order to verify the analytical result of Eq. (16), in Figs. 7–9 we compare homogeneous and heterogeneous subpopulation networks. In Fig. 7 we display the distribution of epidemic sizes as a function of ρ. We are performing stochastic simulations and, as it is well known also for the single population, the threshold condition R* > 1 on the subpopulation reproductive number is not a sufficient condition for an outbreak. If we start with a single infected subpopulation, stochastic fluctuations may lead to the extinction of the epidemic with a probability that is larger the more R* approaches the threshold from above. By considering the same expression obtained in the single population case and by using a coarse grained perspective on the subpopulation spreading the probability of observing a global outbreak is [81]. In Fig. 8 we show that the probability of having a macroscopic outbreak is null below the values close to the global threshold observed in the epidemic size plot. Above the threshold the probability increase slowly as we start in all simulations with a single diseased subpopulation. The probability of outbreak approaches a step function at the threshold by increasing the initial number of diseased subpopulations. For the completeness of comparisons we also display the average epidemic size as a function of ρ in Fig. 9. One readily notices an increase by more than one order of magnitude in the critical value of ρ as we move from a heavy-tailed to a Poisson degree distribution. The heterogeneity in the degree distribution favors the spreading process at the metapopulation level, leading to ρc → 0 at the infinite size limit.
Figure 7.
Distribution of epidemic sizes in heterogeneous (left) and homogeneous (right) subpopulation networks as a function of ρ. Each color map shows the probability of observing a fraction of subpopulations affected by the outbreak as a function of commuting ratio. Each figure readily shows a critical point of ρ, below which most of the epidemics are confined to a few number of subpopulations. Above the critical point most of the realizations affect almost the entire set of subpopulations. In order to highlight the differences with respect to network topology, realizations resulting in epidemics confined to less than ten subpopulations have been excluded from the analysis of size distributions. The critical value of the commuting ratio differs more than one order of magnitude as we switch from a heavy-tailed to a Poisson degree distribution. Since the precise value of the return rate does not alter the results, we have set τ−1 = 1 day and changed σ in order to vary ρ. Both networks contain V = 105 subpopulations, each of which accommodates a degree dependent population of N̄k = N̄k/〈k〉 inhabitants with N̄ = 103. The disease is characterized by R0 = 1.5 and μ−1 = 5 day.
Figure 9.
Average epidemic size in heterogeneous and homogeneous subpopulation networks as a function of ρ. Figure displays the average fraction of subpopulations affected by the outbreak as a function of commuting ratio. We have set τ−1 = 1 day and changed σ in order to vary ρ. Both networks contain V = 105 subpopulations, each of which accommodates a degree dependent population of N̄k = N̄k/〈k〉 inhabitants with N̄ = 103. The disease is characterized by R0 = 1.5 and μ−1 = 5 day.
Figure 8.
Probability of invasion of at least 1% of the subpopulations in heterogeneous and homogeneous networks as a function of ρ. Figure shows the fraction of realizations in which at least 1% of the subpopulations are invaded by the epidemic process as a function of commuting ratio. For clarity, the data points corresponding to zero values of probability have been excluded from the figure. We have set τ−1 = 1 day and changed σ in order to vary ρ. Both networks contain V = 105 subpopulations, each of which accommodates a degree dependent population of N̄k = N̄k/〈k〉 inhabitants with N ¯= 103. The disease is characterized by R0 = 1.5 and μ−1 = 5 day.
6. Conclusions
In this paper we have set a mathematical framework to investigate the conditions of global epidemic invasion in the case of subpopulations coupled with recurrent mobility patterns. On one hand we have extended the mathematical framework of degree-block variables [47, 48] to gain insight into the impact of a non-Markovian mobility process on epidemic extinction/persistence, while on the other hand we have extended the time-scale separation approach of Ref. [9] to complex settings in which subpopulations exhibit heterogeneous demographic and mobility properties.
The basic reproduction ratio is responsible for an epidemic to take off within a single subpopulation. Our analytical approach however derives the expression of a global invasion threshold parameter that depends on the disease parameters, the mobility parameters and the network architecture. Once the network structure and the disease dynamics are fixed, there exists a critical value of the mobility ratio below which the disease dies out before reaching an appreciable fraction of subpopulations. This indicates the importance of both of the commuting and return rates. In other words, the time individuals spend in temporary subpopulations is as important as the rate at which they visit a neighboring subpopulation. The network architecture also has substantial impact on the spreading dynamics. We have shown that the heterogeneity in the commuting matrices favors global spreading by lowering the critical values of the threshold parameters. In principle, the epidemic threshold is suppressed at the infinite size limit of the subpopulation network. Given that real commuting networks are highly heterogeneous, this has important consequences on the dynamical processes and explains the ineffectiveness of mobility restrictions in the containment of emergent infectious diseases [88].
Although our theoretical contribution provides a first theoretical framework for the analysis of global threshold phenomena in systems with recurrent mobility patterns, there are still theoretical and practical issues to address. We have assumed that the mobility rates only depend at most upon the population sizes of the origin and destination subpopulations. In realistic cases, however, the rates may also depend on other social and economic factors as well as the geographical distance between communities. We have also considered a very simplistic case of the dynamics within each subpopulation, ignoring possible intra-population heterogeneities such as different levels of susceptibility and infectiousness [89], or heterogeneous mixing among individuals [90, 91]. All these factors could introduce the need for more sophisticated theoretical approaches. While most of the studies in defining epidemic thresholds have been focused on single populations, it is clear that more attention has to be devoted to the study of spreading in structured populations. In this case the understanding of the invasion threshold is crucial to the analysis of large-scale spreading across communities and subpopulations. Accurate data on human mobility patterns have been increasingly available in recent years, enabling us to gain insight into the statistical laws governing their properties. Given that the spreading of human infectious diseases is only possible through movements of individuals across different geographical regions, it is crucial to explore the consequences of different types of movement patterns for the dynamical processes like epidemic spread. The theoretical framework presented here is thus very important for the development of realistic computational approaches in the study of structured metapopulation systems as well, which are good candidates for capturing fundamental aspects of interacting human communities.
A. Time-scale separation and stationary population
Mobility and infection dynamics detailed in previous sections have been assumed to operate at different time scales. In particular we have restricted our calculations to a regime in which the commuting is much faster than the infection dynamics. In the following we consider the temporal progression of subpopulation sizes and evaluate the relaxation time to an equilibrium configuration.
The rate equations governing the spatial distributions Nii(t) and Nij (t) of residents of subpopulation i can be readily written by explicitly taking into account the diffusion rates along the edges of the subpopulation network. For each subpopulation i the diffusion equations describing the system dynamics are
| (19) |
| (20) |
The first equation evaluates the variation of Nii(t) as the net balance of individuals diffusing away or returning to the subpopulation i according to the rates σi and τi, respectively. The second equation considers the change in the population size Nij(t) as the net balance of individuals of subpopulation i leaving to and returning from subpopulation j. Using the relation for the total population size of subpopulation i,
| (21) |
we can derive the closed expression
| (22) |
The solution of this first order differential equation is
| (23) |
where the constant Cii is determined by the initial condition Nii(0), leading to
| (24) |
We can similarly solve the differential equation for the population size of the residents of subpopulation i present at subpopulation j, obtaining
| (25) |
The relaxation times of Nii(t) and Nij (t) to their equilibrium configurations are thus (τi + σi)−1 and , respectively. The former term is dominated by if the relation τi ≫ σj holds. In the case of commuting, σi = Σi∈ν(i) σij, which equals the daily total commuting rate per resident of subpopulation i. Such the rate is always smaller than 1 since only a fraction of the local population commutes, and it is typically much smaller than the typical return rate τi ≃ 3 − 10 day−1 of such visits. Therefore the relaxation characteristic time can be safely approximated by . Hence for we can approximate the population sizes Nii(t) and Nij (t) with their equilibrium values, and recover the Eq. (1) reported in the main text. This approximation, originally introduced by Keeling and Rohani [9], allows us to consider each subpopulation i as having an effective number of individuals Nij in contact with the individuals of the neighboring subpopulation j. In practice, this is equivalent to consider an infinite time-scale separation between the commuting time scale and the other time scales in the problem (e.g., infection dynamics).
In the case of influenza-like illnesses, the typical time-scale separation between τi and the compartmental transition rates is close to one order of magnitude or even larger. Eq. (1) can then be generalized in the time-scale separation regime to all traveling compartments X obtaining the general expressions
| (26) |
while Xii(t) = Xi(t) and Xij (t) = 0 for all the other compartments which are restricted from traveling. While the approximation holds exactly only in the limit τi → ∞, it is good enough as long as τi is much larger than the typical transition rates of the disease dynamics.
B. Stationary population in heterogeneous networks
In our mean-field description the total number of individuals within a subpopulation of degree k is given by
| (27) |
where the sum in the second term accounts for the average total number of residents of subpopulation k visiting any of its neighbors. This term is proportional to the number of neighbors k and the average number of residents N̄kk′ traveling on each connection k → k′. Thus the sum is performed over all the possible connections through the degrees weighted by the conditional probability P (k′|k) that represents the conditional probability that any given edge departing from a node of degree k is pointing to a node of degree k′ [92]. The rate equations defining the commuting dynamics among subpopulations can be defined using the variables N̄kk(t) and N̄kk′ (t) as
| (28) |
| (29) |
where σk = kΣk′ σkk′P (k′|k) expresses the per capita diffusion rate for individuals in a subpopulation of degree k. In this case we also have considered that the diffusion rate σkk′ is averaged over all possible k′ according to the probability P (k′|k) that a given edge departing from a node of degree k is pointing to a node of degree k′. The above set of equations leads to the equilibrium condition
| (30) |
and using the expression of Eq. (27) we obtain the following equilibrium expressions
| (31) |
| (32) |
Considering in the above expressions the functional form of Eq. (3) for N̄k leads to Eqs. (4–5).
C. Branching process and epidemic invasion threshold
The expression for the number of infected subpopulations with degree k at the nth generation reads as
| (33) |
where each diseased subpopulation of degree k′ at the n − 1th generation may seed its k′ − 1 non-infected neighbors (all of its neighbors minus the one from which it got the infection). Here λk′k is the number of infectious seeds that are introduced into a fully susceptible population, and the probability of observing an outbreak in this case is [81]. The probability that the neighboring subpopulation has not already been infected in the earlier generations is . In the early stage of the epidemic we can assume that . We will also consider the case that we are just above the local epidemic threshold, R0 − 1 ≪ 1, so that the outbreak probability can be approximated by
| (34) |
In the following we will ignore the degree correlation between neighboring nodes. In this case the conditional probability P (k′|k) does not depend on the originating node, i.e., P (k′|k) = k′P (k′)/〈k〉 [92]. This relation simply states that any edge has a probability of pointing to a node with degree k′ that is proportional to the degree of the node to which it points. By using this form of the conditional probability we obtain Eq. (7).
In order to write an explicit form of the above expression we need to explicitly define λkk′. If the time scale of the disease in each individual μ−1 is much larger than the time scale of the visits to neighbors τ−1 (i.e., μ−1 ≫ τ−1), we can then use the stationary solutions for N̄kk′ and N̄k′k in Eq. (5). If we also consider the approximate expression for α in the SIR case for R0 ≃ 1, then we obtain
| (35) |
If we substitute this expression for λk′k in Eq. (7) we obtain the explicit expression
| (36) |
that depends only on the precise definition of the commuting rates σkk′ and τk. In the following we will assume that τk = τ and σk = σ in all the subpopulations. For the commuting rate σkk′ on each connection k → k′ we instead assume the form of Eq. (9). In this case by defining ρ ≡ σ/τ we can write the basic branching process equations at the metapopulation level as
| (37) |
In order to write a closed form of the above iterative process we introduce the variables and whose next generation equations are defined as
| (38) |
where the matrix G is
| (39) |
and c is a constant, defined by the following expression:
| (40) |
The dynamical behavior of the system is determined by the largest eigenvalue R* of the matrix G, leading to Eq. (10).
D. Impact of heterogeneity on epidemic invasion
Remember that Eq. (11) encodes the dependence of global epidemic invasion threshold R* on the topology of subpopulation networks. In the following we consider three different uncorrelated random network topologies.
Heavy-tailed degree distribution
We would here like to turn our attention to the scaling of f (〈k〉, 〈k2〉, 〈k3〉, 〈k4〉) with system size for heavy-tailed degree degree distributions P (k) ~ k−γ with γ > 1 and kmin ≤ k ≤ kmax. For very large system sizes, and in the case that 1 < γ < 2, f scales as
| (41) |
In the case that 2 < γ < 3, the second moment 〈k2〉 in the denominator and higher moments in the numerator dominate, leading to the scaling relation:
| (42) |
In the range 3 < γ < 4, only the third moment 〈k3〉 in the numerator dominates, thus
| (43) |
In the range 4 < γ < 5, only the fourth moment 〈k4〉 in the numerator dominates, leading to
| (44) |
The above expressions state that for any heavy-tailed degree distribution with exponent γ < 5, f (〈k〉, 〈k2〉, 〈k3〉, 〈k4〉) tends to diverge in the limit of infinite network size, which in turn pushes the threshold value ρc to zero. If γ > 5, then f (〈k〉, 〈k2〉, 〈k3〉, 〈k4〉) has a finite value.
Poisson degree distribution
Now let us consider a Poisson degree distribution with average degree λ. By using the generating function, Mk(τ) = eλ (et−1), we can calculate the nth moment as
| (45) |
We only need to know the first four moments in order to calculate f, which are 〈k〉 = λ,
| (46) |
Then f is
| (47) |
The global invasion threshold parameter in this case is
| (48) |
Finally the critical mobility ratio is given by
| (49) |
Equal degrees
If all the nodes have the same degree λ, then the nth moment of degree distribution is simply 〈kn〉 = λn. In this case, f is
| (50) |
The global epidemic threshold parameter R* is then
| (51) |
Notice what this expression tells us about the system: For any λ ≤ 1, global epidemic spread is not possible (as in this regime R* ≤ 0). If λ > 1, then the critical value of mobility ratio ρc is
| (52) |
If we assume that ρ is fixed, then we can also calculate the critical value of λ above which the epidemic will spread globally:
| (53) |
E. Infection and commuting dynamics
Since all the individuals with the same three indices (X, i, j) are identical in terms of the dynamical processes, we are going refer to the number of such individuals at time t by Xij (t). Then, by definition, the instantaneous compartment size in subpopulation j can be expressed as
| (54) |
and the total number of individuals as
. The number of individuals in each compartment X with a residence in i and present in j is subject to discrete and stochastic dynamical processes defined by disease and transport operators. The disease operator
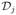 represents the change due to the compartment transition induced by the infection dynamics, and the transport operator ΩX represents the variation due to mobility.
represents the change due to the compartment transition induced by the infection dynamics, and the transport operator ΩX represents the variation due to mobility.
The term
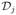 can be written as a combination of a set of transitions {
can be written as a combination of a set of transitions {
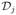 (X, Y)}, where
(X, Y)}, where
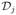 (X, Y) represents the number of transitions from compartment X to Y and is simulated as an integer random number extracted from a multinomial distribution. Then the change due to infection dynamics reads as
(X, Y) represents the number of transitions from compartment X to Y and is simulated as an integer random number extracted from a multinomial distribution. Then the change due to infection dynamics reads as
| (55) |
As a concrete example let us consider the temporal change in the infectious compartment. There is only one possible transition from the compartment, which is to the recovered compartment. The number of transitions is extracted from the binomial distribution
| (56) |
which is determined by the transition probability
| (57) |
and the number of individuals in the compartment Iij (τ) (its size). This transition causes a reduction in the size of the compartment. The increase in the compartment size is due to the transitions from the susceptible to infectious compartment. This is also a random number extracted from the binomial distribution
| (58) |
given by the chance of contagion
| (59) |
and the number of attempts equal to the number of susceptibles Sij (t). After extracting these numbers from the appropriate distributions, we can calculate the total change
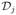 (I) in the infectious compartment as
(I) in the infectious compartment as
| (60) |
Transport operator ΩX expresses the total change in compartment sizes due to the commuting of permanent residents of subpopulation i back and forth. The variation in Xij can be decomposed into and as
| (61) |
The first term represents an increase that is caused by the departing residents of subpopulation i to visit subpopulation j. The is a random number extracted from the multinomial distribution
| (62) |
determined by the probability of commuting to subpopulation j
| (63) |
and the number of such trails Xii(t). The second term corresponds to a reduction in Xij and is due to the return trips from subpopulation j to permanent subpopulation i. The is also a random number extracted from the binomial distribution
| (64) |
given by the probability of returning home
| (65) |
and the size of the compartment Xij (τ). We have assumed that the infection does not alter people’s behavior, i.e., all the compartments are identical in their mobility. Recognize that the stochastic state variables {Sij (τ), Iij (τ), Rij (τ)} define a multivariate Markov chain [93–95] in which the present state of the system is determined only by the state of the system in the previous time step.
Highlights.
We model the contagion spreading mediated by recurrent mobility patterns.
We characterize analytically a phase transition between two regimes of spreading.
We derive the threshold values in mobility rates that ensure the global spreading.
Acknowledgments
We would like to thank Vitaly Belik and Dirk Brockmann for sharing their results on a closely related work. We would also like to thank Chiara Poletto and Vittoria Colizza for interesting discussions during the preparation of this manuscript. This work has been partially funded by the NIH R21-DA024259 award and the DTRA-1-0910039 award to AV; The work has also been partly sponsored by the Army Research Laboratory and was competed under Cooperative Agreement Number W911NF-09-2-0053. The views and conclusions contained in this document are those of the authors and should not be interpreted as representing the official policies, either expressed or implied, of the Army Research Laboratory or the U.S. Government.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Marro J, Dickman R. Nonequilibrium Phase Transitions in Lattice Models. Cambridge University Press; Cambridge: 1999. [Google Scholar]
- 2.van Kampen NG. Stochastic Processes in Physics and Chemistry. North-Holland; Amsterdam: 1981. [Google Scholar]
- 3.Anderson RM, May RM. Spatial, temporal and genetic heterogeneity in host populations and the design of immunization programs. IMA J Math Appl Med Biol. 1984;1:233–266. doi: 10.1093/imammb/1.3.233. [DOI] [PubMed] [Google Scholar]
- 4.May RM, Anderson RM. Spatial heterogeneity and the design of immunization programs. Math Biosci. 1984;72:83–111. [Google Scholar]
- 5.Bolker BM, Grenfell T. Chaos and biological complexity in measles dynamics. Proc R Soc London B. 1993;251:75–81. doi: 10.1098/rspb.1993.0011. [DOI] [PubMed] [Google Scholar]
- 6.Bolker BM, Grenfell T. Space persistence and dynamics of measles epidemics. Philos Trans R Soc London B. 1995;348:309–320. doi: 10.1098/rstb.1995.0070. [DOI] [PubMed] [Google Scholar]
- 7.Sattenspiel L, Dietz K. A structured epidemic model incorporating geographic mobility among regions. Math Biosci. 1995;128:71–91. doi: 10.1016/0025-5564(94)00068-b. [DOI] [PubMed] [Google Scholar]
- 8.Lloyd AL, May RM. Spatial heterogeneity in epidemic models. J Theor Biol. 1996;179:1–11. doi: 10.1006/jtbi.1996.0042. [DOI] [PubMed] [Google Scholar]
- 9.Keeling MJ, Rohani P. Estimating spatial coupling in epidemiological systems: a mechanistic approach. Ecol Lett. 2002;5:20–29. [Google Scholar]
- 10.Watts D, Muhamad R, Medina DC, Dodds PS. Multiscale resurgent epidemics in a hierarchical metapopulation model. Proc Natl Acad Sci USA. 2005;102:11157–11162. doi: 10.1073/pnas.0501226102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Rapoport A. Spread of information through a population with socio-structural bias: I. assumption of transitivity. Bull Math Biol. 1953;15:523–533. [Google Scholar]
- 12.Goffman W, Newill VA. Generalization of Epidemic Theory: An Application to the Transmission of Ideas. Nature. 1964;204:225–228. doi: 10.1038/204225a0. [DOI] [PubMed] [Google Scholar]
- 13.Goffman W. Mathematical Approach to the Spread of Scientific Ideas – The History of Mast Cell Research. Nature. 1966;212:449–452. doi: 10.1038/212449a0. [DOI] [PubMed] [Google Scholar]
- 14.Dietz K. Epidemics and Rumours: A Survey. J of Royal Stat Soc A. 1967;130:505–528. [Google Scholar]
- 15.Tabah AN. Literature Dynamics: Studies on Growth, Diffusion, and Epidemics. Ann Rev Inform Sci Technol. 1999;34:249–286. [Google Scholar]
- 16.Daley DJ, Gani J. Epidemic Modeling: An Introduction. Cambridge University Press; Cambridge: 2000. [Google Scholar]
- 17.Hanski I, Gilpin ME. Metapopulation Biology: Ecology, Genetics, and Evolution. Academic Press; San Diego: 1997. [Google Scholar]
- 18.Tilman D, Kareiva P. Spatial Ecology. Princeton University Press; Princeton: 1997. [Google Scholar]
- 19.Bascompte J, Solé RV. Modeling Spatiotemporal Dynamics in Ecology. Springer; New York: 1998. [Google Scholar]
- 20.Hanski I, Gaggiotti OE. Ecology Genetics and Evolution of Metapopulations. Elsevier, Academic Press; Amsterdam, New York: 2004. [Google Scholar]
- 21.Levins R. Some demographic and genetic consequences of environmental heterogeneity for biological control. Bull Entomol Soc Am. 1969;15:237–240. [Google Scholar]
- 22.Levins R. Extinction, Lecture Notes in Mathematics. 1970;2:75–107. [Google Scholar]
- 23.Hethcote HW. An immunization model for a heterogeneous population. Theor Popul Biol. 1978;14:338–349. doi: 10.1016/0040-5809(78)90011-4. [DOI] [PubMed] [Google Scholar]
- 24.May RM, Anderson RM. Population biology of infectious diseases part II. Nature. 1979;280:455–461. doi: 10.1038/280455a0. [DOI] [PubMed] [Google Scholar]
- 25.Grenfell BT, Harwood J. (Meta)population dynamics of infectious diseases. Tree. 1997;12:395–399. doi: 10.1016/s0169-5347(97)01174-9. [DOI] [PubMed] [Google Scholar]
- 26.Grenfell BT, Bolker BM. Cities and villages: infection hierarchies in a measles metapopulation. Ecol Lett. 1998;1:63–70. [Google Scholar]
- 27.Ferguson NM, Keeling MJ, Edmunds WJ, Gani R, Grenfell BT, Anderson RM. Planning for smallpox outbreaks. Nature. 2003;425:681–685. doi: 10.1038/nature02007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Riley S. Large-scale transmission models of ingectious disease. Science. 2007;316:1298–1301. doi: 10.1126/science.1134695. [DOI] [PubMed] [Google Scholar]
- 29.Baroyan OV, Genchikov LA, Rvachev LA, Shashkov VA. An attempt at large-scale influenza epidemic modelling by means of a computer. Bull Int Epidemiol Assoc. 1969;18:22–31. [Google Scholar]
- 30.Rvachev LA, Longini IM. A mathematical model for the global spread of influenza. Math Biosci. 1985;75:3–22. [Google Scholar]
- 31.Grais RF, Hugh Ellis J, Glass GE. Assessing the impact of airline travel on the geographic spread of pandemic influenza. Eur J Epidemiol. 2003;18:1065–1072. doi: 10.1023/a:1026140019146. [DOI] [PubMed] [Google Scholar]
- 32.Longini IM. A mathematical model for predicting the geographic spread of new infectious agents. Math Biosci. 1988;90:367–383. [Google Scholar]
- 33.Flahault A, Valleron A-J. A method for assessing the global spread of HIV-1 infection based on air-travel. Math Popul Stud. 1991;3:1–11. doi: 10.1080/08898489209525336. [DOI] [PubMed] [Google Scholar]
- 34.Ruan S, Wang W, Levin S. The effect of global travel on the spread of SARS. Math Biosci Eng. 2006;3:205–218. doi: 10.3934/mbe.2006.3.205. [DOI] [PubMed] [Google Scholar]
- 35.Earn DJD, Rohani P, Grenfell BT. Persistence chaos and synchrony in ecology and epidemiology. Proc R Soc London B. 1998;265:7–10. doi: 10.1098/rspb.1998.0256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Rohani P, Earn DJD, Grenfell BT. Opposite patterns of synchrony in sympatric disease metapopulations. Science. 1999;286:968–971. doi: 10.1126/science.286.5441.968. [DOI] [PubMed] [Google Scholar]
- 37.Keeling MJ. Metapopulation moments: coupling, stochasticity and persistence. J Anim Ecol. 2000;69:725–736. doi: 10.1046/j.1365-2656.2000.00430.x. [DOI] [PubMed] [Google Scholar]
- 38.Park AW, Gubbins S, Gilligan CA. Extinction times for closed epidemics: the effects of host spatial structure. Ecol Lett. 2002;5:747–755. [Google Scholar]
- 39.Vázquez A. Epidemic outbreaks on structured populations. J Theor Biol. 2007;245:125–129. doi: 10.1016/j.jtbi.2006.09.018. [DOI] [PubMed] [Google Scholar]
- 40.Grais RF, Ellis JH, Kress A, Glass GE. Modeling the spread of annual influenza epidemics in the US: the potential role of air travel. Health Care Manage Sci. 2004;7:127–134. doi: 10.1023/b:hcms.0000020652.38181.da. [DOI] [PubMed] [Google Scholar]
- 41.Cooper BS, Pitman RJ, Edmunds WJ, Gay NJ. Delaying the international spread of pandemic influenza. PLoS Med. 2006;3:e12. doi: 10.1371/journal.pmed.0030212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Hollingsworth TD, Ferguson NM, Anderson RM. Will travel restrictions control the international spread of pandemic influenza? Nat Med. 2006;12:497–499. doi: 10.1038/nm0506-497. [DOI] [PubMed] [Google Scholar]
- 43.Hufnagel L, Brockmann D, Geisel T. Forecast and control of epidemics in a globalized world. Proc Natl Acad Sci USA. 2004;101:15124–15129. doi: 10.1073/pnas.0308344101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Colizza V, Barrat A, Barthélemy M, Valleron A-J, Vespignani A. Modeling the worldwide spread of pandemic influenza: Baseline case and containment interventions. PLoS Medicine. 2007;4:e13. doi: 10.1371/journal.pmed.0040013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Colizza V, Barrat A, Barthélemy M, Vespignani A. The role of the airline transportation network in the prediction and predictability of global epidemics. Proc Natl Acad Sci USA. 2006;103:2015–2020. doi: 10.1073/pnas.0510525103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Colizza V, Pastor-Satorras R, Vespignani A. Reaction-diffusion processes and metapopulation models in heterogeneous networks. Nat Phys. 2007;3:276–282. [Google Scholar]
- 47.Colizza V, Vespignani A. Invasion Threshold in Heterogeneous Metapopulation Networks. Phys Rev Lett. 2007;99:148701. doi: 10.1103/PhysRevLett.99.148701. [DOI] [PubMed] [Google Scholar]
- 48.Colizza V, Vespignani A. Epidemic modeling in metapopulation systems with heterogeneous coupling pattern: Theory and simulations. J Theor Biol. 2008;251:450–467. doi: 10.1016/j.jtbi.2007.11.028. [DOI] [PubMed] [Google Scholar]
- 49.Vespignani A. Predicting the behavior of tecno-social systems. Science. 2009;325:425–428. doi: 10.1126/science.1171990. [DOI] [PubMed] [Google Scholar]
- 50.Ball F, Mollison D, Scalia-Tomba G. Epidemics with two levels of mixing. Ann Appl Probab. 1997;7:46–89. [Google Scholar]
- 51.Cross P, Lloyd-Smith JO, Johnson PLF, Wayne MG. Duelling timescales of host movement and disease recovery determine invasion of disease in structured populations. Ecol Lett. 2005;8:587–595. [Google Scholar]
- 52.Cross P, Johnson PLF, Lloyd-Smith JO, Wayne MG. Utility of R0 as a predictor of disease invasion in structured populations. J R Soc Interface. 2007;4:315–324. doi: 10.1098/rsif.2006.0185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Chowell G, Hyman JM, Eubank S, Castillo-Chavez C. Scaling laws for the movement of people between locations in a large city. Phys Rev E. 2003;68:066102. doi: 10.1103/PhysRevE.68.066102. [DOI] [PubMed] [Google Scholar]
- 54.Barrat A, Barthélemy M, Pastor-Satorras R, Vespignani A. The architecture of complex weighted networks. Proc Natl Acad Sci USA. 2004;101:3747–3752. doi: 10.1073/pnas.0400087101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Guimerá R, Mossa S, Turtschi A, Amaral LAN. The worldwide air transportation network: anomalous centrality, community structure, and cities’ global roles. Proc Natl Acad Sci USA. 2005;102:7794–7799. doi: 10.1073/pnas.0407994102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Brockmann D, Hufnagel L, Geisel T. The scaling laws of human travel. Nature. 2006;439:462–465. doi: 10.1038/nature04292. [DOI] [PubMed] [Google Scholar]
- 57.Patuelli R, Reggiani R, Gorman SP, Nijkamp P, Bade F-J. Network analysis of commuting flows: A comparative static approach to German data. Networks Spatial Econ. 2007;7:315–331. [Google Scholar]
- 58.González MC, Hidalgo CA, Barabási A-L. Understanding individual human mobility patterns. Nature. 2008;453:779–782. doi: 10.1038/nature06958. [DOI] [PubMed] [Google Scholar]
- 59.Balcan D, Colizza V, Gonçalves B, Hu H, Ramasco JJ, Vespignani A. Multiscale mobility networks and the spatial spreading of infectious diseases. Proc Natl Acad Sci USA. 2009;106:21484–21489. doi: 10.1073/pnas.0906910106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Wang P, González MC. Understanding spatial connectivity of individuals with non-uniform population density. Phil Trans R Soc A. 2009;367:3321–3329. doi: 10.1098/rsta.2009.0089. [DOI] [PubMed] [Google Scholar]
- 61.Song C, Qu Z, Blumm N, Barabási A-L. Limits of Predictability in Human Mobility. Science. 2010;327:1018–1021. doi: 10.1126/science.1177170. [DOI] [PubMed] [Google Scholar]
- 62.Song C, Koren T, Wang P, Barabási A-L. Modelling the scaling properties of human mobility. Nat Phys. 2010;6:818–823. [Google Scholar]
- 63.Ni S, Weng W. Impact of travel patterns on epidemic dynamics in heterogeneous spatial metapopulation networks. Phys Rev E. 2009;79:016111. doi: 10.1103/PhysRevE.79.016111. [DOI] [PubMed] [Google Scholar]
- 64.Balcan D, Vespignani A. Phase transitions in contagion processes mediated by recurrent mobility patterns. Nat Phys. 2011;7:581–586. doi: 10.1038/nphys1944. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Belik V, Geisel T, Brockmann D. Natural human mobility patterns and spatial spread of infectious diseases. Phys Rev X. 2011;1:011001. [Google Scholar]
- 66.Danon L, House T, Keeling MJ. The role of routine versus random movements on the spread of disease in Great Britain. Epidemics. 2009;1:250–258. doi: 10.1016/j.epidem.2009.11.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Keeling MJ, Danon L, Vernon MC, House TA. Individual identity and movement networks for disease metapopulations. Proc Natl Acad Sci USA. 2010;107:8866–8870. doi: 10.1073/pnas.1000416107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Erlander S, Stewart NF. The Gravity Model in Transportation Analysis. VSP; Utrecht: 1990. [Google Scholar]
- 69.de Dios Ortúzar J, Willumsen LG. Modelling Transport. Wiley; Chichester: 2001. [Google Scholar]
- 70.Liljeros F, Edling CR, Amaral LAN, Stanley HE, Aberg Y. The web of human sexual contacts. Nature. 2001;411:907–908. doi: 10.1038/35082140. [DOI] [PubMed] [Google Scholar]
- 71.Schneeberger A, Mercer CH, Gregson SAJ, Ferguson NM, Nyamukapa CA, Anderson RM, Johnson AM, Garnett GP. Scale-free networks and sexually transmitted diseases. Sexually Transmitted Dis. 2004;31:380–387. doi: 10.1097/00007435-200406000-00012. [DOI] [PubMed] [Google Scholar]
- 72.Pastor-Satorras R, Vespignani A. Epidemic spreading in scale-free networks. Phys Rev Lett. 2001;86:3200–3203. doi: 10.1103/PhysRevLett.86.3200. [DOI] [PubMed] [Google Scholar]
- 73.Pastor-Satorras R, Vespignani A. Epidemic dynamics and endemic states in complex networks. Phys Rev E. 2001;63:066117. doi: 10.1103/PhysRevE.63.066117. [DOI] [PubMed] [Google Scholar]
- 74.Moreno Y, Pastor-Satorras R, Vespignani A. Epidemic outbreaks in complex heterogeneous networks. Eur Phys J B. 2002;26:521–529. [Google Scholar]
- 75.Lloyd AL, May RM. How viruses spread among computers and people. Science. 2001;292:1316–1317. doi: 10.1126/science.1061076. [DOI] [PubMed] [Google Scholar]
- 76.Barthélemy M, Barrat A, Pastor-Satorras R, Vespignani A. Dynamical patterns of epidemic outbreaks in complex heterogeneous networks. J Theor Biol. 2005;235:275–288. doi: 10.1016/j.jtbi.2005.01.011. [DOI] [PubMed] [Google Scholar]
- 77.Keeling MJ, Rohani P. Modeling Infectious Diseases in Humans and Animals. Princeton University Press; Princeton: 2008. [Google Scholar]
- 78.Colizza V, Barrat A, Barthélemy M, Vespignani A. The modeling of global epidemics: stochastic dynamics and predictability. Bull Math Biol. 2006;68:1893–1921. doi: 10.1007/s11538-006-9077-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Harris TE. The theory of branching processes. Dover Publications; 1989. [Google Scholar]
- 80.Vázquez A. Polynomial growth in age-dependent branching processes with diverging reproductive number. Phys Rev Lett. 2006;96:038702. doi: 10.1103/PhysRevLett.96.038702. [DOI] [PubMed] [Google Scholar]
- 81.Bailey NT. The Mathematical Theory of Infectious Diseases. Macmillan; New York: 1975. [Google Scholar]
- 82.Longini IM, Halloran ME, Nizam A, Yang Y. Containing Pandemic Influenza with Antiviral Agents. Am J Epidemiol. 2004;159:623–633. doi: 10.1093/aje/kwh092. [DOI] [PubMed] [Google Scholar]
- 83.Carrat F, Vergu E, Ferguson NM, Lemaitre M, Cauchemez S, Leach S, Valleron A-J. Time Lines of Infection and Disease in Human Influenza: A Review of Volunteer Challenge Studies. Am J Epidemiol. 2008;167:775–785. doi: 10.1093/aje/kwm375. [DOI] [PubMed] [Google Scholar]
- 84.Viboud C, Bjørnstad ON, Smith DL, Simonsen L, Miller MA, Grenfell BT. Synchrony, Waves, and Spatial Hierarchies in the Spread of Influenza. Science. 2006;312:447–451. doi: 10.1126/science.1125237. [DOI] [PubMed] [Google Scholar]
- 85.Erdős P, Rényi A. On random graphs. Publ Math. 1959;6:290–297. [Google Scholar]
- 86.Molloy M, Reed B. The Size of the Largest Component of a Random Graph on a Fixed Degree Sequence. Combinatorics, Probab Comput. 1998;7:295–306. [Google Scholar]
- 87.Catanzaro M, Bogunã M, Pastor-Satorras R. Generation of uncorrelated random scale-free networks. Phys Rev E. 2005;71:027103. doi: 10.1103/PhysRevE.71.027103. [DOI] [PubMed] [Google Scholar]
- 88.Bajardi P, Poletto C, Ramasco JJ, Tizzoni M, Colizza V, Vespignani A. Human Mobility Networks, Travel Restrictions, and the Global Spread of 2009 H1N1 Pandemic. PLoS ONE. 2011;6:e16591. doi: 10.1371/journal.pone.0016591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Miller JC. Spread of infectious disease through clustered populations. J R Soc Interface. 2009;6:1121–1134. doi: 10.1098/rsif.2008.0524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Meyers LA, Pourbohloul B, Newman MEJ, Skowronski DM, Brunham RC. Network theory and SARS: predicting outbreak diversity. J Theor Biol. 2005;232:71–81. doi: 10.1016/j.jtbi.2004.07.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Lloyd-Smith JO, Schreiber SJ, Kopp PE, Getz WM. Super-spreading and the effect of individual variation on disease emergence. Nature. 2005;438:355–359. doi: 10.1038/nature04153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Barrat A, Barthélemy M, Vespignani A. Dynamical Processes on Complex Networks. Cambridge University Press; Cambridge: 2008. [Google Scholar]
- 93.Gani J, Jerwood D. Markov chain methods in chain binomial epidemic models. Biometrics. 1971;27:591–603. [PubMed] [Google Scholar]
- 94.Longini IM. Chain binomial models. In: Armitage P, Colton T, editors. The Encyclopedia of Biostatistics. Vol. 1. Wiley; NY: 1998. pp. 593–597. [Google Scholar]
- 95.Halloran ME, Longini IM, Struchiner CJ. Design and Analysis of Vaccine Studies, Statistics for Biology and Health. Springer; New York: 2010. Binomial and stochastic transmission models; pp. 63–84. [Google Scholar]