A Discriminative Approach to EEG Seizure Detection

Abstract

Seizures are abnormal sudden discharges in the brain with signatures represented in electroencephalograms (EEG). The efficacy of the application of speech processing techniques to discriminate between seizure and non-seizure states in EEGs is reported. The approach accounts for the challenges of unbalanced datasets (seizure and non-seizure), while also showing a system capable of real-time seizure detection. The Minimum Classification Error (MCE) algorithm, which is a discriminative learning algorithm with wide-use in speech processing, is applied and compared with conventional classification techniques that have already been applied to the discrimination between seizure and non-seizure states in the literature. The system is evaluated on 22 pediatric patients multi-channel EEG recordings. Experimental results show that the application of speech processing techniques and MCE compare favorably with conventional classification techniques in terms of classification performance, while requiring less computational overhead. The results strongly suggests the possibility of deploying the designed system at the bedside.

Introduction

Chronic repetitive seizures (epilepsy) affect approximately 3 percent of the United States population, with the majority being children and the elderly^[1]. Seizures are sudden abnormal discharges in the brain represented often times by convulsions or loss of consciousness. This brain abnormality is represented in electroencephalogram (EEG) recordings by frequency changes and increased amplitudes^[2]. The ability to accurately capture the frequency and amplitude changes are key to detection of seizure and non-seizure states.

EEG is a measure of the electrical activity of the brain. Surface EEG electrodes are measuring activity from a large number of neurons in underlying regions of the brain. Each neuron is generating a small electrical field that changes over time. The source of current causing the fluctuating scalp potential is primarily the pyramidal neurons and their synaptic connections to deeper layers of the cortex^[1]. The oscillations are a result of the reciprocal interaction of excitatory and inhibitory neurons in circuit loops.

Visual inspection of EEG signals for seizures is cumbersome for long recordings and prone to error. The development of a real-time seizure detection system has potential for use in neurological intensive care units where the accurate detection of a seizure can make the difference in the care that is provided^[3,4,5,6]. Several techniques capable of classifying seizure and non-seizure states from EEG signals have been presented in the literature^{[7,8,9,10,11]}. Si et al.^[7] reports on an automated pediatric seizure detector based on fuzzy logic and neural networks with 91% overall recognition. Faul et al.^[9] uses Gaussian Process (GP) modeling theory to detect neonatal seizures. The GP EEG measure, Gaussian variance, provided a classification accuracy of 82.8%. Thomas et al.^[10] obtained a 79% detection rate using Gaussian mixture models and frequency, time, and information theory domain features for neonatal seizures. Expanding on this work, Temko et al.^[11] incorporated automatic speech recognition features to classify neonatal seizures using a support vector machine classifier. Assessing the area under the Receiver Operating Curve (ROC), they obtained 93.1% with spectral enveloped based features and Cepstral coefficients.

While all of these approaches have made contributions towards a real-time system, the challenges of unbalanced data (seizure and non-seizure events) and system computational efficiency still remain. The rare occurrence of a seizure over hours of EEG recordings makes training and testing of the model difficult due to the potential class bias towards the non-seizure state. System computational efficiency becomes a challenge when moving the system to the bedside. The large number of EEG channels requires a system capable of simultaneously extracting features across EEG channels and then conducting classification.

Our approach to this problem is rooted in speech processing techniques. The efficacy of the application of speech processing techniques (e.g., real Cepstrum) to discriminate between seizure and non-seizure states in EEG signals is reported. Specifically, we report on the use of the Minimum Classification Error (MCE) algorithm applied on Gaussian mixture models for the real time classification of seizures. We compare the efficacy of MCE with two classification schemes, including support vector machines and standard Gaussian mixture models. The MCE algorithm specifically targets the constraint of unbalanced data. To enable the potential deployment of our system in live settings (e.g., in intensive care units), we utilize a real-time stream computing paradigm to build an experimental test-bed for EEG analysis addressing the challenge of computational efficiency.

Despite both speech and EEG signals having significant spectral characteristics the application of automatic speech recognition (ASR) features for biological data has only recently been investigated. Preliminary research has looked at the application of the Cepstrum to extracellular neural spike detection^[12] and neonatal EEG signals for seizure detection^[11]. The current paper adds to the body of work with the incorporation of the MCE algorithm applied on Gaussian mixture models to classify seizure and non-seizure states using Cepstral analysis. Our approach is novel in that we account for the challenge of unbalanced datasets (seizure and non-seizure), while also showing a system capable of real-time feature extraction.

Analytics for Seizure Detection

Detection of seizure and non-seizure states was performed with two different classifiers, a Support Vector Machine (SVM) and a Gaussian Mixture Model (GMM). The goal in classification is to reduce classification error. Different classifiers go about achieving this goal in different ways.

Support Vector Machine

Given a set of observations each of m input features, x_i ∈ R^m, with corresponding class labels, y ∈ {+1, −1}, the SVM attempts to define a hyperplane, y(x) = w^T x + w₀, that discriminates between the two classes. To minimize generalization error, the SVM selects the hyperplane with the largest margin, where the margin is the distance between the closest members from the two classes. Generally speaking, most data are not linearly separable, thus in these cases a soft margin SVM is used which allows some data points to be misclassified. The soft margin SVM solves the optimization problem, $\mathit{min}\left\{\frac{1}{2}{\mathbf{w}}^T\mathbf{w}\right\}+C{\sum }_i{\varsigma }_i$, for all {(x_i, y_i)}, y_i {w^T x_i + w₀) ≥ 1 − ς_i.

The parameter C is a regularization parameter which controls trade off between complexity of the machine and the number of non-separable points. If C becomes too large, the classifier can suffer from over-fitting. If C becomes too small the training error can potentially be large. The parameters ς_i are the slack variables which correspond to the deviation from the margin borders and control the allowable error.

The non-linear SVM maps the input vector of features into vectors in a high-dimensional feature space to perform classification in the high dimensional space. The data cast nonlinearly into a high dimensional feature space is more likely to be linearly separable there than in a lower-dimensional space^[13]. A kernel function is used to do the mapping. Kernels are able to operate in the input space, where the solution of the classification problem is a weighted sum of kernel functions evaluated at the support vector.

Discriminative training of Gaussian Mixture Models (GMMs)

The generative and discriminative approaches to classification problems are two competing philosophies in machine learning. The generative approach attempts to directly fit a model to training data on a category-per-category basis, typically based on the Maximum Likelihood (ML) criterion or Mean Square Error. Classification is done by comparing the score of each model and choosing the classes whose model yields the optimum score. In contrast, the discriminative approach tries to directly estimate the boundaries between classes.

In this paper, we use the Minimum Classification Error (MCE) criterion as our choice of a discriminative technique based on its success in speech and usability across a broad range of classifiers. The choice of the MCE approach is motivated by its straightforward applicability to various types of classifier, and its flexibility in tuning the learning parameters to achieve the targeted performance. In addition, MCE training has found a range of applications in various areas including speech recognition, feature extraction, and handwriting recognition.

MCE minimizes a smooth approximation of the error rate^[14] and unlike ML, MCE does not attempt to fit a distribution, but rather to discriminate against competing models^[14]. MCE training is more directly aimed at reducing the recognizer’s mistakes. MCE has been found efficient in handwriting recognition^[15] and feature extraction^[16] and to our knowledge has never been applied to seizure detection. This section describes the MCE application to Gaussian Mixtures Models (GMMs).

GMM-based seizure detection

Model-based seizure detection uses a classification approach to the problem. A model is created for each category (seizure or non-seizure) and detection is based on the optimum score of a category given a sample. Gaussian Mixture Models (GMMs) are a widely used modeling approach, typically applied to clustering or pattern classification, in particular in the context of speaker identification, language identification, or image segmentation. Its attractiveness is due to its ability to approximate the data distribution of a given class, making it a judicious choice for detection problems that exhibit differences in distribution across categorical data.

Formally, a GMM represents the probability density function (pdf) of a random variable, x ∈ R^d, as a weighted sum of k Gaussian distributions:

$$p(\mathbf{x}|\mathrm{\Theta })=\sum _{m=1}^k{\alpha }_{m}p(\mathbf{x}|{\theta }_m),$$ (1)

where Θ is the mixture model, α_m corresponds to the weight of component m and the density of each component is given by the normal probability distribution:

$$p(\mathbf{x}|{\theta }_m)=\frac{{|{\mathrm{\Sigma }}_m|}^{-1/2}}{{(2\pi )}^{d/2}}\text{exp}\left\{–\frac{1}{2}{(\mathbf{x}–{\mu }_m)}^T\sum _m^{–1}(\mathbf{x}-{\mu }_m)\right\}.$$ (2)

The Maximum Likelihood Criteria (MLE) is the standard estimation approach for GMM in which the parameters α, μ and ∑ are iteratively estimated via the Expectation Maximization (EM) algorithm in order to maximize the log-likelihood of the model. Theoretically, an MLE-trained GMM can approximate any probability distribution, provided the availability of a sufficiently large training set and an optimal choice of the model order (number of mixtures k). However, in practical situations, the training set is usually not sufficiently large, or the optimal model order is unknown. Furthermore, by estimating the model of each category separately, the MLE only provides an indirect approach to the detection task. To remedy these deficiencies, we employ the Minimum Classification Error (MCE) algorithm to correct and enhance a given MLE-trained GMM, based on an optimization criterion that closely reflects the error rate on a training set.

Minimum Classification Error training of Gaussian Mixture Models

The MCE learning paradigm provides a correction of the MLE-estimation techniques by its focus on directly improving the detection capabilities of the GMM. We are given a two-class problem in which the goal is to classify data between seizure and non-seizure states. The two categories C₁ and C₂ are represented by two GMMs of parameters Θ₁ and Θ₂. We also define Θ = {Θ_i} for i = 1, 2, as the parameter space of the overall recognizer. Given a feature vector X, the MCE training procedure is implemented as follows.

First, the discriminant function of category C_i as defined as

$$g_i(X;{\mathrm{\Theta }}_i)=\text{log}p(\mathbf{x}|{\mathrm{\Theta }}_i)+\text{log}P(C_i)$$ (3)

where P (C_i) is the prior probability of the category C_i ; this probability is estimated from training data. The discriminant function is the score generated by the GMM of category C_i, given a sample X; it is an estimation of how likely the given sample belongs to that category (seizure or non-seizure). Decoding is done by choosing the category that has the highest discrimination measure (the highest score). That is,

$$\text{choose}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{C}_i\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{if}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}i=\text{arg}\underset{1,2}{\text{max}}{g}_j(X;{\mathrm{\Theta }}_j).$$ (4)

Second, assuming that X belongs to C_i, we define the misclassification measure of C_i as

$$d_i(X;\mathrm{\Theta })=–g_i(X;{\mathrm{\Theta }}_i)+g_{j,j\ne i}(X;{\mathrm{\Theta }}_j).$$ (5)

This misclassification measure estimates how the model of category C_i can discriminate against another category, given a sample data. The sign of the misclassification measure reflects the performance of the model. A negative sign means a correct detection and a positive sign is an incorrect detection. Finally, the MCE loss assigned to X is defined as ℓ(X; θ) = ℓ(d_i(X; θ) where ℓ(·) is a smooth approximation of the step-wise 0 − 1 loss function, typically chosen to be a sigmoid:

$$\ell (d)=\frac{1}{1+\text{exp}(-\alpha d)}$$ (6)

with a positive α, chosen to allow for reasonable degree of smoothness. The MCE loss is a smooth approximation of the 0-1 loss, which reflects a correct versus incorrect decision made by the system.

The method optimizes the classification by minimizing the expected loss L(Θ), defined as a functional of the overall parameter set:

$$L(\mathrm{\Theta })=\sum _{i=1}^2{\int }_{X\in C_i}\ell (X;\mathrm{\Theta })P(X)dX$$ (7)

In practice, MCE training focuses on the minimization of the MCE average loss defined over a body of training data of size N as

$$L_N(\mathrm{\Theta })=\frac{1}{N}\sum _{i=1}^M\ell (X;\mathrm{\Theta }).$$ (8)

Clearly, L_N (Θ) approximates the empirical error rate, given a body of training data and its evolution closely reflect the performance of the system on the training set. By minimizing L_N (Θ), the error on the training is more directly minimized than when done with the standard MLE technique.

To minimize L_N (Θ), we used a gradient descent approach in which the parameters Θ of the system are iteratively updated as follows:

$${\mathrm{\Theta }}_{\tau +1}={\mathrm{\Theta }}_{\tau }–\mu \nabla L({\mathrm{\Theta }}_{\tau })$$ (9)

where μ is a learning rate, determining the rate of convergence of the algorithm.

A System for Real-Time Analysis of EEG Signals

To efficiently explore EEG signals for the real-time detection of seizures, several system requirements must be addressed. We aimed at developing not only an exploration platform leveraging novel machine learning approaches, but also a platform capable of analyzing and detecting seizures in real-time. Consequently, 2 sets of design requirements have been considered for the development of this system:

• Exploration of large amounts of streaming data: Streaming data have a temporal dimension differentiating these data from conventional data typically mined. As a result, large amounts of time-series data are required to be analyzed to detect patterns of interests. It becomes important to be equipped with IT systems capable of handling these large volumes of data at every stage of the exploration process: pre-processing, feature extraction and modeling. At the feature extraction stage, features are commonly extracted from windows of data. The exploration platform should facilitate the computation of statistics on arbitrary windows of time series data.

• Real-time stream processing: Once interesting patterns have been identified, it is imperative to be able to detect the occurrence of these patterns in real-time on live patient data. The traditional ”store and analyze” approach, typically used in data mining, is not naturally designed for such problems. The volume and rates of incoming data makes it cumbersome to persist the data for real-time analysis. To address this challenge, we impose stream computing requirements on our system since the stream computing paradigm has been developed for the analysis of data in motion, as it flows through the system.

Analytics softwares like Matlab^[17], R^[18], SPSS^[19] and Weka^[20] do not address the requirements listed above. Despite often being used for real-time deployments, these software tools were not really designed for real-time analysis in production environments. Also, despite their very good modeling capabilities some of these tools struggle to explore large data sets.

To address these problems, we have leveraged the IBM InfoSphere Streams (Streams) platform to build an experimental test-bed for EEG analysis. Streams is a highly scalable and programmable stream computing software platform allowing application developers to process structured, as well as unstructured streaming data. It provides several services on top of its analytical capabilities, including fault tolerance, scheduling and placement optimization, distributed job management, storage services, and security. Streams is designed to scale to a large collection of computational nodes, simultaneously hosting multiple applications. It can be configured on a variety of hardware ranging from stand alone Linux PCs to shared-nothing clusters of workstations or even large supercomputers (e.g., IBMs Blue Gene). Our use of it has been exclusively on clusters of Linux machines running RedHat 5.3.

Streams applications are represented as directed data flow graphs consisting of a set of processing elements (PEs) connected by data streams. Each data stream carries a series of stream data elements. A PE implements data stream analytics and is the basic execution container that is distributed over computational hosts. At the operating system level, PEs live in their own processes and communicate with each other via their input and output ports, using the TCP/IP network stack. Input and output ports are connected by streams to form these directed data flow graphs.

Application developers are not required to interact with Streams at the PE level and build PEs to specify the business logic of their applications. Streams comes equipped with a declarative programming language called SPADE ^[21] shielding developers from the complexity of the PE programming interface. SPADE applications are essentially directed graphs of SPADE operators that encapsulate some business logic. With these SPADE operators, the developer designs her application by reasoning and integrating the small building blocks needed to perform a computation. While a precise definition for what an operator does might be hard to formulate, in most application domains, application engineers typically have a good understanding about the collection of operators that they routinely use. For example, database engineers typically conceive their applications in terms of the relational operators encapsulating relational algebra. Similarly, MATLAB programmers have several toolkits at their disposal, ranging from numerical optimization to symbolic manipulation, signal processing and machine learning. Just like MATLAB, the SPADE language is extensible and allows developers to augment it with either legacy code or with specialized functions that they intend to re-use within or across applications. We have extended SPADE with a toolkit of operators specialized for time series and signal processing operations. Using this toolkit, we have prototyped all the stream pre-processing and feature extraction operations in this work.

Experiments

A dataset of pediatric EEG recordings obtained from the Physionet on-line database^[22] was used in the present study to test the effectiveness of our analysis approach. The database included recordings from 22 subjects (males: n=5, ages 3–22; females: n=17, ages 1.5–19) recorded at the Children’s Hospital Boston. Recordings were of 23 surface EEG channels sampled at 256 Hz, from subjects with intractable seizures. The data consisted of 182 seizures with approximately 6 hours of data per subject.

Experimental Setup

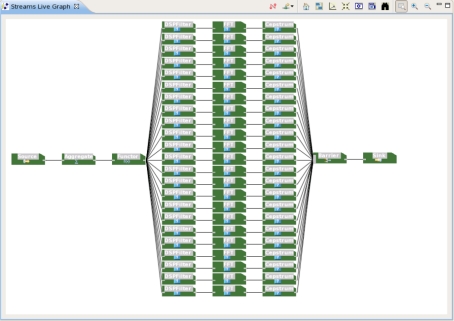
Extracting features on many hours of multi-channel EEG signals is computationally expensive. Our attempts to extract features from windows of several EEG signals have been unsuccessful with Matlab simply because of the computational burden that this step was putting on our computing systems. As a result all features in this study were extracted using IBM InfoSphere Streams, with the SPADE application shown in Figure 1. In this figure, streaming data flow from left to right. The process starts with a source operator, responsible for streaming data from files of EEG data. The next operator filters the data for noise with the 4th order Butterworth filter, using a generic DSP filtering operator that is part of our time series toolkit. This filter is a bandpass (0.5 – 55 Hz) filter. Next, 10-second sliding windows with a 3 second window slide (resulting in a 66% overlap in consecutive windows) are computed with a SPADE aggregator operator. Binary labels are then assigned to each window of EEG samples, following a simple majority rule. If in the time domain, less than 50% of the EEG samples in a given window belong to a segment of seizure activity, the window takes the label of class C1. Otherwise, the window is labeled with class C2. We then split the data into 23 branches, each one corresponding to an EEG channel. On each of these channels, a series of SPADE operators is applied to perform a Cepstral transformation on windows of EEG data.

Figure 1:

SPADE analysis graph for EEG filtering, feature extraction and labeling.

The Cepstral transformation is well known for its ability to preserve the envelop of the spectrum. It provides a compact representation of the spectrum into a small set of features that are well de-correlated. Cepstral analysis is used in speech processing to cancel out noise contribution in the signal from recording voices using multiple speakers. Speech recognition considers the frequency content of different sounds; therefore features that provide spectral information (i.e. FFT) are desired, just as in EEG analysis. For this reason, the Cepstrum is often computed to extract the spectral information from the speech signal. The computation of the spectrum can be related to a deconvolution of the signal. The deconvolution of the speech signal to remove the noise is applicable to removing the inherent environmental noise associated with recording EEG. As in speech recognition, neural changes in EEG are dominant in the frequency domain.

For our experiments, the first 12 Cepstral coefficients were retained on each EEG channel, resulting in feature vectors containing 276 features. This feature vector is produced in our SPADE graph by a SPADE barrier operator capable of synchronizing all features from all 23 EEG channels. The resulting feature vectors are then stored on the file system using a SPADE sink operator. While the feature extraction computation could have been performed sequentially one EEG channel after another, we have parallelized the Cepstral transformation step to improve the performance of the system. Indeed, we have encapsulated each Cepstral transformation for each channel in dedicated PEs running in separate processes on our system.

Supervised learning algorithms have been applied to this feature set to classify windows of EEG data. Standard algorithms implemented on SPSS^[19] and Weka^[20] (e.g., decision trees, multi-layer perceptrons, support vector machines) have been made available in our exploration platform. Streams allows the real-time scoring of such models obtained by modeling software like SPSS with a stream mining toolkit capable of interpreting models exported in the Predictive Modeling Mark-up language (PMML)^[23]. To score models trained by Weka in real-time, we have developed a user defined operator in Java leveraging the Weka Java API. Similarly, custom implementations of GMMs and MCE were also used in our test bed and the real-time scoring of these custom models does require the extension of SPADE with appropriate user-defined operators.

Classification Results

Unlike, several studies in this area, training and testing of the sets was performed on separate groups of patient data. Splitting subject data to include portions of each patient in training and testing does not support the generalization of results. However, separating patients can make creating a methodology with low misclassification errors more challenging. Our feature vectors were classified using standard Gaussian Mixture Models (GMM) using ML and MCE applied to these standard GMMs. The GMM modeling was performed by optimally growing the number of Gaussians up to 32. MCE training starts from the ML-estimated GMM model and adjusts the parameters of that model to generate a more performing model on the training set. A 10-fold cross validation approach has been used.

Application of the real Cepstrum and GMM showed comparable accuracy results (overall 91.7% recognition with standard GMM) to the use of the same dataset for seizure/non-seizure classification, but with time and frequency domain features (overall 95.0% recognition)^[8]. The recognition rates with the standard GMM were 92.2% for non-seizure windows and only 64.2% for the rare seizure events (Table 1). The low frequency of seizure events in the data set makes it hard for the classifier to have good detection accuracy for seizure events. However, the application of MCE to better discriminate (account for the unbalanced seizure/non-seizure states) between these two classes significantly boosted the seizure detection accuracy. With MCE applied to the GMM model described above, we slightly decreased the recognition accuracy of non-seizure events, while significantly boosting the recognition accuracy of seizure events by 42.4% in comparison to the standard GMM. The SVM classifier using RBF achieved a comparable recognition rate for the non-seizure class in comparison to the standard GMM, but the result for the seizure class was inferior to the accuracy reached with MCE on the seizure class.

Table 1:

Classification Results

	Non-Seizure	Seizure
SVM	90.0%	81.0%
standard GMM	92.2%	64.2%
GMM + MCE	84.9%	91.4%

These results confirm prior comparative results of the two techniques^[24,25]. The MCE efficiency is due to its ability to make use of lightweight classifier for maximum efficiency. This is specially appealing in the context of real-time seizure detection, in which a smaller, less complex, but highly efficient classifier is adapted more to lightweight devices used by medical staffs for patient care. This result is in line with the MCE philosophy as it emphasizes all classes equally, weighting them for minimum error purposes.

Systems Results

From a system perspective, we were able to reach high levels of data throughputs on an X86 machine with 8GB of RAM and 4 dual core processors. We were able to ingest an average of 10 MBytes per seconds of EEG data for this exploration phase, for each SPADE graph. By deploying several SPADE graphs for multiple patients on the same machine, much higher data processing rates can be achieved. These input rates can be multiplied further by deploying our SPADE graphs on multiple machines, an operation that is fully supported by our system.

Conclusion

We presented a novel machine learning approach to seizure classification utilizing a platform capable of analyzing and detecting seizures in real-time. We described an application of Cepstral analysis and the Minimum Classification Error (MCE) training scheme to the problem of EEG seizure detection. The MCE criterion was used to estimate the Gaussian Mixture Models (GMM) parameters for the task of classifying seizure episodes in EEG data. Experimental results showed that the MCE algorithm accounted for the unbalanced data and improved the performance of the classifier. Additionally, the stream computing paradigm accounted for the computational efficiency required for a system to be taken to the bedside. In the future, we plan on extending our feature set with time domain features to further improve the accuracy of the classification. We also hope to have the opportunity to deploy this system in the real-world for prospective studies on seizure detection.