Graphical Methods for Reducing, Visualizing and Analyzing Large Data Sets Using Hierarchical Terminologies

Abstract

Objective:

To explore new graphical methods for reducing and analyzing large data sets in which the data are coded with a hierarchical terminology.

Methods:

We use a hierarchical terminology to organize a data set and display it in a graph. We reduce the size and complexity of the data set by considering the terminological structure and the data set itself (using a variety of thresholds) as well as contributions of child level nodes to parent level nodes.

Results:

We found that our methods can reduce large data sets to manageable size and highlight the differences among graphs. The thresholds used as filters to reduce the data set can be used alone or in combination. We applied our methods to two data sets containing information about how nurses and physicians query online knowledge resources. The reduced graphs make the differences between the two groups readily apparent.

Conclusions:

This is a new approach to reduce size and complexity of large data sets and to simplify visualization. This approach can be applied to any data sets that are coded with hierarchical terminologies.

Introduction

An image consisting of nodes and links, commonly referred to as a graph, is often used for depiction and presentation of complex data sets. The graph representation has advantages in providing direct, simplified, intuitive and human-friendly images to help users comprehend data sets. However, graphs will help with comprehension only if the size and complexity of the data set are within human capacity for understanding.

One application of graphs is to understand data sets that are related to attacks on computers. Computer attack graphs represent actual or possible attacks through a network. Humans are easily overwhelmed by a moderate sized graph and its complexity^{1, 2}. Reducing the size and simplifying the complexity of a graph is very important in analyzing a large data set. In computer attack research, researchers have explored methods such as grouping similar attacks into virtual nodes² or aggregating non-overlapping sub-graphs of the attack graph to single vertices (nodes)¹. Attack graphs after complexity reduction have been demonstrated that a compressed view helps humans better understand attacks.

In biomedicine, there are often large data sets obtained from using specific applications, such as a literature search tool or an electronic health record (EHR). Some of these data sets are aggregated counts of events, such as occurrences of diseases or findings or entries of search terms by users. The terminologies used to code these events, such as The International Classification of Diseases-9 (ICD-9), Medical Subject Headings (MeSH), and Systematized Nomenclature of Medicine-Clinical Terms (SNOMED CT), can be used to organize and browse these data sets, so the counts can be distributed in hierarchical structures. Terminologies can help users understand the data sets and ultimately understand the corresponding applications in the semantic contexts.

However, sometimes humans have difficulty comprehending the essence of a terminology even with the help of visualization approaches. For example there were more than 290 thousand medical concepts in the 2011 release of SNOMED CT, so the size of the terminology graph can overwhelm any human who tries to comprehend it without reduction or partition. Gu and her colleagues used a partitioning method to divide a huge terminology structure into smaller parts to provide better understanding of the terminology.^{3, 4} Gu’s approach has been applied to a complex terminology graph to help reduce the size of the terminology graph. However, her method was not applied to large data sets represented with the terminology, only to the terminology itself.

In this paper we introduce graphical methods to provide a better understanding of large data sets by simplifying the graph based on the hierarchical structure of the terminology and the data themselves. Our methods combine data presentation and terminology presentation into one graph with the objective of reducing the original data set to a manageable size. This approach is intended to depict, highlight and distinguish the important nodes and links within the hierarchal structure.

Methods

For the purpose of this paper, we consider data sets that consist of data about individual events and a hierarchical terminology that can be used to code the individual events. Every data element in the data set has a frequency and a term name. The frequencies are counts that start from 0 and the terms have parent-child relationships.

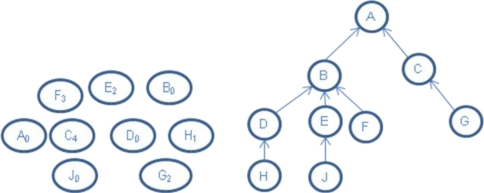
We use a small sample data set to illuminate the graphical approaches for reducing and visualizing larger data sets. Table 1 lists the sample data set with frequencies and Table 2 lists the parent-child relationships between the terms in the terminology used to code the sample data set. Figure 1 shows the graphs with frequency only or with hierarchy only for the sample data set.

Table 1.

Frequencies of the sample data set

Term name	A	B	C	D	E	F	G	H	J
Frequency	0	0	4	0	2	3	2	1	0

Table 2.

Parent-child relationships of sample terms

Parent	A	A	B	B	B	C	D	E
Child	B	C	D	E	F	G	H	J

Figure 1.

Left: sample data set with frequencies only; Right: the hierarchy of sample terms

1). Frequency only without terminology (Meth 1)

The simplest method to reduce a large data set is to set a frequency threshold (T_f) to filter each node (n) for which the frequency (F_n) is below T_f. We use the following statement to judge if a node will be shown in the graph produced by this method.

If F_n is equal to or greater than T_f, then display node n.

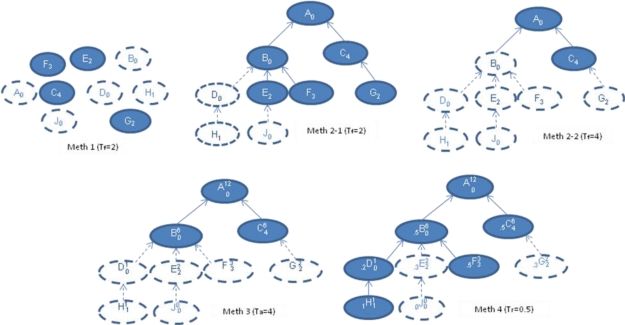
Figure 2 shows the graph produced by this method as Meth 1. The advantage of this method is that the algorithm is intuitive and straightforward. The disadvantage of this method is that the relationships between the terms are not considered, so all the nodes have been isolated and distributed randomly.

Figure 2.

Graphs before (all nodes) and after (nodes filled with blue) filtering by different reduction methods

Meth 1 shows the frequencies of each node and the nodes that meet the condition T_f = 2; Meth 2 shows the frequencies of each node and the hierarchical structure of the terms; Meth 2-1 shows nodes that meet the condition T_f =2 and Meth 2-2 shows nodes that meet the condition T_f =4; Meth 3 shows terms, frequencies (right subscripts), aggregated frequencies (right superscripts) and all nodes that meet the condition T_a = 4; Meth 4 shows terms, frequencies (right subscripts), aggregated frequencies (right superscripts) and ratio of aggregated frequencies of child nodes vs aggregated frequencies of parent nodes as left subscripts; Meth 4 shows the nodes that meet the condition T_r (AF_n /AF_p) = 0.5 and all the ancestors of such nodes. Note that Meth 4 used alone does not consider absolute values of F or AF, so nodes such as D and H are not filtered.

2). Frequency with terminology (Meth 2)

Our next method shows data sets in a terminological structure, i.e. terms with data as nodes in a hierarchical terminology. Like Meth 1 we show all the nodes for which F_n is equal to or greater than T_f. In addition, we show ancestors of such nodes and all the links between displayed nodes. We use the following statement to judge if n will be shown in the graph.

If F_n is equal to or greater than T_f, then display n and all the ancestors of n in the terminological structure.

Figure 2 shows the graphs as Meth 2-1 and Meth 2-2 with different thresholds. Compared to Meth 1, Meth2 displays not only the data and term names within nodes, but also the relationships between nodes. Like Meth 1, Meth 2 displays important nodes based on their F_n; it also displays nodes that have no significant F_n for themselves but that subsume significant nodes. For example: nodes A and B are not displayed in Meth 1 because their frequencies are 0, but they are displayed in Meth 2-1 because each of them has significant descendant nodes. We notice, however, that some nodes may subsume multiple nodes whose F_n are closer to but below T_f (we call these nodes “semi-important nodes”). We therefore sought a method that would allow display of what we consider to be potentially interesting parts of the data set.

3). Aggregated frequency with terminology (Meth 3)

In order to show nodes that subsume important areas of the data set, we introduce the concept of aggregated frequency of n (AF_n,), which is the sum frequency of n and the frequencies of all of n’s descendants, i.e. AF_n=F_n1+F_n2+F_n3…F_nk, where k is the number of n’s descendents (shown as the following function).

$${\text{AF}}_{\mathrm{n}}=\sum _{\mathrm{i}=1}^{\mathrm{k}}{\mathrm{F}}_{\text{ni}}$$

Table 3 shows aggregated frequency of each node in the sample data set. In this method we use T_a (threshold for aggregated frequency) as new threshold and use following statement to judge if n should be shown in the graph.

Table 3.

Aggregated frequencies of the sample data set

Term name	A	B	C	D	E	F	G	H	J
Aggregated frequency	12	6	6	1	2	3	2	1	0

If AF_n is equal to or greater than T_a, then display n and all the ancestors of n in the terminological structure.

Meth 3 in Figure 2 shows the graph that is produced by this method (Table 3 data set). Node B is displayed in Meth 3 although B has no important descendant (none of the decedents meets T_f=4 in Meth 2-2, so this area is filtered in Meth 2-2), however B does have several semi-important nodes and so Meth 3 includes it.

Unlike Meth 2, in which F_n is used, AF_n is used in Meth 3 to highlight the important upper level nodes, i.e. nodes with multiple semi-important descendants will not be omitted. However, we notice that some descendants are contributing a disproportionally larger share of frequency to the parents’ aggregated frequency. These semi-important nodes that contribute more to their parent level nodes among the whole set of sibling level nodes cannot be highlighted by this method, but may nevertheless be interesting as well.

4). Aggregated frequency of a child vs. aggregated frequency of the parent (Meth 4)

In order to highlight the important sibling level nodes that contribute more to their parent level node, we introduce Meth 4. In this method we calculate a ratio value for n (RV_n), which is the ratio between the aggregated frequency of the node (AF_n) and the aggregated frequency of its parent (AF_p), as shown by the following formula.

$${\text{RV}}_{\mathrm{n}}={\text{AF}}_{\mathrm{n}}/{\text{AF}}_{\mathrm{p}}$$

In this method, the ratio threshold T_r is the new threshold and we use the following statement to judge if n will be displayed in the graph.

If RV_n is equal to or greater than T_r, then display n and all the ancestors of n in the terminological structure.

Figure 2 shows the graph produced by this method as Meth 4 (sample data sets from Tables 1 and 3). The ratio indicates the relative importance of a child among all its siblings. This method highlights important contributions of children nodes to their parents’ nodes; for example, node F is important to node B in Figure 2 Meth 4.

5). Representation of data sets

Another dimension used for highlighting the visualization of data sets is visual representation the attributes of nodes in graphs. In the following case study we use colors of the nodes, colors of the arrows, arrow heads’ sizes and their directions to represent different F, AF and RV. The use of color, size and directionality adds dimensions to the graphs without increasing the structural complexity.

Case Study

The four methods described above each have strengths and weaknesses. Our methods allow different thresholds to be used in combination to produce different reduction results. We find this to be particularly useful for analysis of large data sets.

We illustrate these methods by applying them to data sets consisting of concepts of interest derived from use of Infobuttons,⁵ which are links between clinical information systems and online knowledge resources. The concepts of interest are data elements from patients’ records. In the data sets we used, these elements are coded with a hierarchical terminology called the Medical Entity Dictionary (MED).⁶ One data set contains information about how physicians query online knowledge resources and the other data set contains information about nurses as users. The data sets are derived from log files, which have been described previously.⁷

The physicians’ data set includes 2425 records and the nurses’ data set includes 2034 records. Each record contains the MED term for the concept of interest and a frequency count of its occurrence in the original infobutton log file. The frequency counts in the data sets range from 0 (some upper level nodes may have large aggregated frequencies but 0 frequencies) to 9254. We use an open source graph visualization software package called GraphViz⁸ to produce the graphs using the layout engine (called “DOT”) that we find most suitable for displaying hierarchical structures.

Figure 3 shows a part of the original graph of the physicians’ data set without any reduction. In fact, this is produced by Meth 1 with T_f =1. The original size of the graph is too large to be shown; Figure 3 is only 4% of the original data set. The size and complexity of the graph makes it challenging not only for humans to comprehend but for display facilities (monitors or printers) to produce.

Figure 3.

Part DOT lay out of the original physicians’ data set with Meth 1 and T_f =1 (this is about 4% of the original graph length; each node displays a mnemonic or ID for its corresponding term although these are not visible at this resolution of the graph)

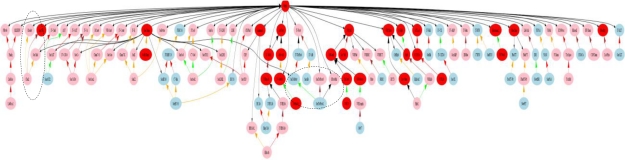
In order to provide a general overview, we apply our methods to remove the unimportant areas based on the term frequencies. However, the application of any single method fails to yield satisfactory results. For example: Meth 1 will provide randomly distributed nodes that will not help us understand the data set in any semantic context; Meth 2 produces a better look at the lower level nodes; however, it will tend to show single important leaf nodes with corresponding single paths to the root node, failing to show higher level nodes with semi-important descendents; Meth 3 provides a better depiction of the higher level nodes; however, it may omit important child level nodes; Meth 4 will highlight the relative contributions from child level nodes to parent level nodes; however, it does not consider the nodes’ actual F or AF. We therefore use a combination of thresholds to achieve our objectives in the two data sets. We choose thresholds by considering the distribution of the frequencies in the original data sets as the starting point, and then we perform a series tests to find the cutoff point for the threshold in the data set. We continue to refine the thresholds until we produce graphs that contain between 100–150 nodes. Figure 4 is a graph of the physicians’ data set after reduction. We use a combination of Meth 3 and Meth 4 to produce Figure 4 with T_a=75 and T_r=0.4. The nodes after filtering meet the conditions: its RV is greater than 0.4 and AF is greater than 75, and all the ancestors of such nodes. There are 2425 nodes before reduction and 137 nodes after reduction including 41 leaf nodes for the physicians’ data set. Figure 4 shows the reduced version of the original full graph. Some attributes of the graph are listed in the note for Figure 4.

Figure 4.

The graph with DOT layout after reduction by Meth 3 and Meth 4 from the physicians’ data set with T_a=75 and T_r=0.4 (the mnemonics are likely too small to be read, but are unimportant for the purpose of illustrating differences to the next graph). Areas of the graph outlined with dashed lines are sections that differ from the nurses’ graph (see text for details).

Note: all the colors of the nodes, colors of the links, arrows’ directions, sizes and colors represent different meanings, node colors: AF > 200, red; 200≥AF>100, pink; 100≥AF>50, light blue. For arrows: RV=1, red, double arrow head and backwards; 1>RV≥ 0.9, orange, double arrow head and backwards; 0.9>RV≥0.7 green, double arrow head and backwards; 0.7>RV≥0.5, brown, double arrow head and backwards; 0.5>RV≥0.3, black, double arrow head and backwards; RV <0.3, black, single arrow head and forwards.

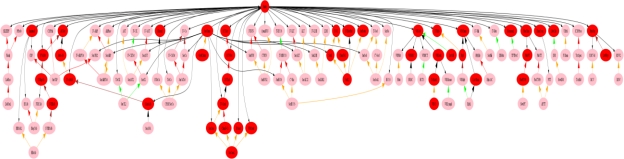
The nurses’ data set contained generally higher frequencies and a different distribution across the hierarchy. In order to get comparable graphs (similar number of nodes), we had to modify the threshold for the nurses’ data set. Figure 5 is a graph from the nurses’ data set after reduction. Method 3 and 4 are combined to get Figure 5 with T_a= 100 and T_r=0.4. There are 2034 nodes before reduction and 139 nodes after reduction including 35 leaf nodes for nurses’ data set.

Figure 5.

The graph with DOT layout after reduction by method 3 and 4 from the nurses’ data set with T_a=100 and T_r=0.4 (all annotations of the attributes in the graph are the same as Figure 4)

These reductions make the comparison of the two graphs much easier. Generally, the overlap between the two graphs is over 70%. From this we can see that similar concepts are of interest to both nurses and physicians. However, because the term in the nurses’ data set generally have higher frequencies, if we apply the physicians’ thresholds to the nurses’ data set it will produce a much larger graph with 187 nodes, while the nurses’ thresholds applied to the physicians’ data set produced a very limited graph with 92 nodes. Two of the most obvious differences between the graphs are paths to “Chol2” and paths to “SerTotProt2” in the physicians’ graph (see the two dashed circle areas in Figure 4), neither of which is displayed in the nurses’ graph. The specific differences between nurses’ and physicians’ infobutton use have not yet been analyzed comprehensively but graphs such as these will help identify different areas of interest among the concepts in the MED.

Discussion

Without reduction or visualization, a large data set can be analyzed by statistical methods and a general view of the data set can be obtained, such as the most often used term or the average use of the terms. However for detailed analysis, such as the different use of the terms and their hierarchies by physicians and nurses in our case study (i.e. to consider the terminological context and analyze the meaning of the data), pure statistical methods will not solve the problem. The reduction and visualization methods discussed in this paper are complementary methods that provide a new perspective in analyzing and interpreting large data sets.

We are exploring methods to visualize large data sets with hierarchies and reduce data sets based on data and hierarchies. The case study is an example of using the above methods and different thresholds in combination; we believe that the graphs after reduction are much easier and simpler to comprehend.

1). Comparison to related work

Gu and her colleagues ^{3, 4, 9} developed a partitioning method for large vocabulary comprehension. Their approaches included: 1) displaying only the higher priority properties and 2) dividing large networks into disjoint and logical units by following predefined rules. The main objective of their research was to understand large vocabularies. Our research also uses terminological structure; however, we have a different objective: to use terminological structure to display large data sets and to understand and interpret data sets within the terminological context. Terminology is thus one of our tools to provide simpler and easier graphic layouts for interpretation of data, although we reduced size and complexity of the terminology set as well.

Homer and colleagues² used formal and logic-based approaches to simplify computer attack graphs. In their research they 1) reduced data by identifying and trimming useless portions of graphs and 2) grouped similar attack steps to increase understandability. In our methods we used both quantitative thresholds (F, AF and RV) and hierarchical structure to filter data.

Noel and colleague¹ collapsed non-overlapping sub-graphs in order to get compressed and summary views of the original graphs. The authors built a framework based on their method to manage complexity of computer attack graphs. We faced a similar problem, with large original graphs and we had a similar objective to get a summary view of an original graph. However, we used different approaches, quantitative indicators and hierarchical structure in our case to achieve our objectives. In the above case study, our methods take advantage of the medical semantics among terms, which are usually not considered in pure mathematical methods, such as clustering algorithms¹⁰.

2). Significance

We use a controlled terminology to organize large data sets to assist our comprehension of those sets by putting the data into semantic contexts. We believe this approach will be especially helpful if we want to analyze data sets in a detailed manner. While the use of graphs to depict large data sets is not novel by itself, the combination of data sets (frequency counts) and terminology (structure) distinguish our work from the work of others. For example: if we analyze infobutton data sets without the terminological structure, the graph would consist of thousand nodes with no obvious patterns. By considering both data and terminology, we get the graphs with higher level concepts and small numbers of fine-grained concepts. The graphs make the difference between different user groups more apparent.

The combination of multiple features for filtering is a common approach to improve data visualization. However, we believe that the use of aggregated frequencies and ratio values, and especially their combination, are novel. The aggregated frequencies allow individual concepts that do not seem important on their own to contribute to the apparent importance of higher level concepts. Conversely, the ratio values permit these higher level concepts to give “credit” to particular contributors, allowing them to be included in the display when they would not otherwise qualify on their own.

3). Potential applications

The methods described in this paper can be applied to the analysis of large data sets in many different fields. Many health applications produce large data sets, ranging from users’ search terms in MEDLINE/PubMed (coded in MeSH), to patient data coded with other hierarchical terminologies such as ICD, SNOMED, or the Gene Ontology (GO). With mandatory demands for standardization, sharability and communication of clinic data and the meaningful use of EHR, we believe that controlled terminologies will be applied more extensively in operational systems. Our methods will be well-suited to the visualization and analysis of data from such systems. Furthermore the methods are not restricted to the medical applications. As long as the data set can be mapped to a hierarchical structure and has frequencies, our methods can be applied.

4). Limitations

We have not conducted a formal evaluation of the graphs after reduction, so the precise conclusions we can draw from the study are limited. The reduction of the massive graphs to smaller, simpler ones is an objective finding. It is easier and faster for us to identify the similar areas and different areas across different data sets after reduction; however, we lack a well-designed and comprehensive evaluation to support a more precise conclusion. For example: it is hard to know the exact proportion of useful or important nodes that have been filtered out and the proportion of retained nodes that are unimportant.

Another limitation of this study is that there is not a single, straightforward way to combine filtering methods and set thresholds. The current approach is somewhat trial-and-error. The analysis and selection of thresholds would be much easier, consistent, reliable and reproducible if we are able to “tune” the thresholds freely and get the reduced graphs in real time.

5). Future research

The methods described in this paper are ready to be applied to a number of data sets as mentioned above. Our methods are basic elements that can be combined to display specific data sets. It is not our intention to provide a one-size-fits-all solution for any data sets. On the contrary, additional work is needed to develop a reproducible method for setting and combining thresholds. Meanwhile, we will also explore generic formulas for combing different methods under different circumstances for different data sets, i.e. to explore various formulas and the specific suitable conditions under which the formulas can be used.

We used GraphViz⁸ to produce graphs for our case study and chose the “DOT” layout engine after exploring and comparing several available layout engines. The graphs produced by DOT provided the clear presentation of the directional and hierarchical data for our case study data. However, the exploration of other visualization techniques and layout engines is an appropriate topic for future research.

Another important area for future research is the evaluation of our overall approach. Without a formal and meaningful evaluation, no precise conclusion of the usefulness of the reduced graphs can be drawn. We believe that an “objectivist, comparison-based approach”¹¹, in which specific aspects of graphs, such as their similarity to a gold standard or the difference in information content between graphs generated with different methods and thresholds, are measured in a quantitative, reproducible manner. There are two dimensions to such an evaluation. One is to compare the graphs produced by our methods with the gold standard set by domain experts. The second approach compares different graphs produced by a variety of different visualization techniques to assess which one performs better (i.e., its usefulness). Both dimensions depend on the context of the data and the intended purpose of the graphs.

Comparison of reduced graphs with a gold standard will require identifying objective measures of what is “important” in a graph; such an evaluation will have to involve meaningful data sets and subjects with sufficient expertise to appreciate the reductions. In our case study we have two objectives in getting a better sense of clinical information seeking patterns: 1) including the most important contributors to the data set, which is comparable to “sensitivity”; 2) minimize the inclusion of unimportant contributors to the data set, which is comparable to “specificity”. In the case study data set, the important parts are the concepts that subsume terms that are used more often and the unimportant parts are concepts that subsume terms that are used less. A variety of ways can be used to obtain the gold standard, such as asking domain experts to rate concepts and compare the results to the graphs produced by our methods.

The evaluation of performance could explore various visualization techniques to compare the graphs produced by these techniques. In our case, the study could evaluate the hypothesis that the graphs by our methods will help users to predict or interpret different information seeking patterns in different user groups easily.

Conclusion

We present a new approach to combine large data sets with hierarchical terminologies to reduce and visualize data sets based on the terminology hierarchies and data themselves. Alone or in combination, our methods can be applied to produce graphs of a desirable size, which is necessary but not sufficient for comprehension. We believe this method reduces size of data sets in meaningful ways that will help us to identify important subsets easily and allow us to distinguish the differences between data sets in a way that is not readily accomplished with traditional statistical methods.