Interoperability of medical databases: Construction of mapping between hospitals laboratory results assisted by automated comparison of their distributions

Abstract

In hospital information systems, laboratory results are stored using specific terminologies which may differ between hospitals. The objective is to create a tool helping to build a mapping between a target terminology (reference dataset) and a new one. Using a training sample consisting of correct and incorrect correspondences between parameters of different hospitals, a match probability score is built. This model also enables to determine the theoretical conversion factor between two parameters. This method is evaluated on a test sample of a new hospital: For each reference parameter, best candidates are returned and sorted in decreasing order using the probability given by the model. The correct correspondent of 14 among 15 reference parameters are ranked in the top five among more than 70. All conversion factors are correct. A mapping webtool is built to present the essential information for best candidates. Using this tool, an expert has found all the correct pairs.

Introduction

It is worth noting that the term “variable” refers thereafter to items used in the regression model (there is thus on one side a variable to predict and on the other side several explanatory variables) and the term “parameter” refers to a kind of laboratory result.

Building inter-hospital databases

The construction of inter-hospital databases gives the opportunity to analyze larger databases and thus gain more power in analysis. The European PSIP project (1), which this work is part of, is a recent example of construction of such database. The aim of this project is to detect and prevent the occurrence of adverse drug reactions by analyzing large datasets using data-mining methods (2).

The construction of inter-hospital databases clearly benefits from syntactic interoperability (ie between databases) and several standards have emerged for that purpose including Health Level 7 (3). On the other hand, once the database constructed, its analysis requires semantic interoperability, which can be reached using common terminologies. Several terminologies are widely used, such as the International Classification of Diseases (4) (ICD) for diagnoses or the Anatomical Therapeutic Chemical classification (5) (ATC) for drugs. However, the encoding of laboratory results is still an issue in this context and semantic interoperability of laboratory results is effectively rarely reached yet.

Terminologies for laboratory results

The structured description of laboratory results is based on different terminologies. Several international standards exist, such as Logical Observation Identifiers Names and Codes (LOINC®) (6–8), SNOMED-CT (9) or International Union of Pure and Applied Chemistry (IUPAC) (10,11). Unfortunately, most of the time a local terminology is used with low accuracy level (i.e. less detailed) and only adapted for clinical use. As a consequence, the same parameter stored in one system is named differently between two different hospitals and it requires a manual time-consuming work to build a mapping between all the existing terminologies and a unique reference (target terminology). The main issues to map a local to an international terminology are detailed by Lin and al. (12) analyzing the correctness of the LOINC mappings of 3 large institutions.

Background

Several tools can be used to build mappings between these terminologies. Those tools are based on character string recognition in the label of parameter or in reports.

• “The Map to LOINC” presented by A.N. Khan (13) uses an automatic mapping tool to map local laboratory labels to LOINC. Initially, two experts manually assign LOINC codes to the tests in a master merging laboratory tests names and synonyms. Then an automated mapping tool is developed to map local laboratory test names to LOINC using the mappings specified in the master file. Evaluation goes on 4,967 laboratory active tests, 67% are mapped automatically, 19% manually and 14% are considerated as uncodable parameters. The local naming choice is the main cause of failure (including variant due to a different facility convention of naming).

• K.N. Lee and al. (14,15) have built a tool based on the 6 attributes of the LOINC terminology. Each LOINC code is based on a unique combination of 6 attributes so each code can be thought as having a unique set of 6 relationships, one to each attribute. All this sets are stored in a knowledge base with also synonyms and rules. For a new laboratory result, a set of relationships is created based on information given by laboratory (like unit) and a tool compares the set of relationships of the new entrant to all the sets of relationships in the knowledge base. In this way, exact LOINC code can be found. This method requires a manual work to create lists of synonyms and rules.

• Two more projects can be cited. Their objective is to map local radiology terms into LOINC (16) and to map clinical terms into LOINC (17). They don’t concern laboratory results specifically.

Labels of laboratory results are not explicit in many cases: For example in databases, the parameter “total bilirubinemia” is described using the label “BT” in a first database, “Bilirubins” in another one, and “Bilirubine totale” in a third one. Most of labels are not explicit enough and, for this reason, when experts are in charge of finding the correct correspondence they use the units, the normality range and the statistical distribution of the parameters. These steps are very useful for expert validation, so it might be useful to automatically compare the statistical distributions of parameters to develop a new kind of mapping tool. The formulated hypothesis is that the characteristics of statistical distributions are specific to a parameter.

In this context, Zollo and al. (18) defined each parameter using “name, frequency, unit, code, co-occurences” and also “mean and standard deviation”, these two last elements describing some parts of statistical distribution for a parameter.

Objective

The objective is to create a tool helping to construct a mapping between a reference parameter (associated with a target terminology) and a new parameter from an incoming data using any different terminology. The target terminology has to be simple for clinical use and ready to use for data-mining. Two steps are planned:

1. The first step consists in constructing a model giving a probability of correspondence of two parameters. The approach is not to use the labels but rather to compare the statistical distributions of parameters. This model must also be able to identify the conversion factor between the two parameters.

2. The second step consists in presenting the results and the discriminant information using a webtool which could help an expert to build this mapping.

Material

Here are presented the datasets used in this project. All datasets are completely de-identified, i.e. the identifiers of the patients and the hospital stays are removed from the database before any analysis, as well as indirect personal identifiers. The datasets are described in Table 1.

Table 1.

Description of the datasets used in the study

Hospital Center	Year	Use Name	Hospital stays	Number of records	Number of parameters	Selected parameters	Terminology
Denain (FR)	2009	Reference set Target	9,991	667,388	233	15 (to match)	Target terminology
Rouen (FR)	2007	Learning set Newcomer 1a	1,286	213,151	421	74	Local terminology
Copenhagen 1 (DK)	2009	Learning set Newcomer 1b	11,104	513,675	205	71	IUPAC
Copenhagen 2 (DK)	2009	Validation set Newcomer 2	5,469	128,077	346	74	IUPAC

Reference dataset with target terminology

The reference dataset is extracted from Denain’s (FR) general hospital. This dataset contains the reference distributions of laboratory results. From this reference data, a simple target terminology is manually created. This target terminology could be replaced by an existing international terminology. Among the 233 parameters found, 15 most used (in databases) parameters are selected for this study. These 15 parameters are the target to match with the other datasets.

Learning sets “newcomer 1a” and “newcomer 1b” used to build the model

The two datasets used in addition to the dataset of reference for learning phase contain different terminologies. Only the parameters having a number of values above 1‰ of the total number of laboratory results are retained. This limit is chosen in order to have a good representation of the distribution and to ignore too rare parameters. The learning sets are the datasets of Rouen hospital center and Copenhagen hospital 1. Table 2 illustrates the terminologies used to represent the same laboratory results (sodium ion and glycemia) in the three different datasets.

Table 2.

Examples of representation of the same laboratory results in different datasets

Kind	Hospital center	Terminology	Label of parameter	Value	Unit
Glycemia	Denain	Reference	GLY1	1.23	g/l
	Copenhagen 1 & 2	IUPAC	DNK35842	7.2	mmol/l
	Rouen	Local	Glycémie	7.2	mmol/l
Sodium ion	Denain	Reference	NA1	135	meq/l
	Copenhagen 1 & 2	IUPAC	NPU03429	135	mmol/l
	Rouen	Local	Sodium	135	mmol/l

Validation set “newcomer 2” used to test the model

The evaluation is done with a dataset from a second hospital of Copenhagen (DK). Its laboratory results are encoded using the IUPAC classification, but this setting will not be used obviously to make the correspondence between pairs of parameters, but only to check the quality of the correspondences found using the tool.

Method

Introductory example

A comparison of the distributions of two parameters with variable size and variable units is performed. Explicit units or normality ranges are found only for some parameters.

In the example displayed on Figure 1, it is easy to see that “Kalemia” and “Potassium ion” are very close (left part of Figure 1), while “Kalemia” and “Neutrophilocytes” are very different (right part of Figure 1). The main idea is to incorporate robust variables describing these charts into a model.

Figure 1.

Examples of estimated probability density functions of parameters

Construction of the model

Construction of variables to summarize distribution of parameters

The comparison of distributions is strongly linked with the detection of theoretical conversion coefficient between two parameters.

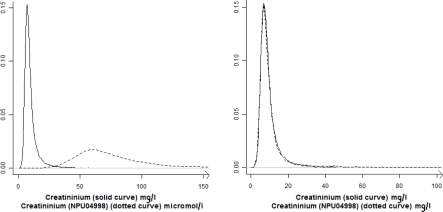
For each reference parameter, the possible theoretical conversion coefficients are known. For example, international unit for creatininium is micromoles per liter (μmol/l), but a lot of hospitals use milligrams per liter (mg/l). The theoretical conversion coefficients are “1” if the two parameters have the same unit, “8.85” (from μmol/l to mg/l) and “1/8.85” (from mg/l to μmol/l). Figure 2 illustrates this point: On the left part of Figure 2 is presented the creatinemia distribution from two different datasets with two different units. On the right part of Figure 2, the creatinemia from the second dataset is multiplied by the nearest theoretical conversion coefficient, which makes the distributions overlap. For many parameters that correspond to a count of elements (for example the number of red blood cells), all the powers of 10 are possible coefficients. It is the same with some concentrations as hemoglobin that may be in gram per liter (g/l) or in gram per deciliter (g/dl).

Figure 2.

Effect of the use of conversion coefficient on the probability density functions of parameters

To determine the nearest theoretical conversion coefficient, all theoretical coefficients (known for each reference) are compared with the ratio of medians between the reference and the candidate. This nearest theoretical conversion coefficient is used to multiply the values of a new entrant parameter and thus the two parameters have the same scale. Variables describing the distribution are evaluated after this conversion i.e. for each parameter compared to the reference parameter, a conversion factor is chosen and applied (all laboratory results of this parameter are multiplied by this factor) prior to all other calculations.

Five robust and discriminating variables are retained to describe the distribution of a laboratory result:

• Kolmogorov test’s statistic

• 10^th, 65^th and 85^th quantiles ratio of the 2 compared parameters

• R squared of the linear regression (with quantile new variable as dependent variable and quantile reference variable as independent variable).

Many variables are tested but not retained, such as Skewness measure, Kurtosis measure, other quantiles ratios (counting by fives from 5 to 95), etc. The two main arguments for keeping variables are their significance in bivariate statistical tests (with the variable to predict) and their significance in the final model. The possible collinearity between the five selected variables is not an obstacle to the convergence of the model and all the explanatory variables kept are significant (α=0.05) in the final model. The three “quantiles ratio” chosen in the model reflect the potential asymmetry of the distribution.

Learning phase: Construction of logistic model and score

The 5 variables presented above are the explanatory variables. In the table containing training data, each line corresponds to the values obtained for a pair of parameters (target vs. newcomer 1a & 1b). This table also contains a column for the binary dependent variable “couple” that indicates whether the correspondence of the couple (seen on the line) is true or false. The variable “couple” is the variable to predict. This table contains 435 lines from which 29 have the value “1” in the column “couple”. An extract of this table is presented in Table 3.

Table 3.

Extract of table containing training data

reference set - learning set	couple	R squared	Kolmogorov test	10th quantile ratio	65th quantile ratio	85th quantile ratio
kalemia - natremia	0	0.33	0.99	38.24	33.10	30.87
kalemia - kalemia	1	0.43	0.03	1.03	1.00	1.00
kalemia - calcemia	0	0.78	0.99	1.70	1.87	1.97
calcemia - natremia	0	0.52	0.97	1.71	1.60	1.56
calcemia - kalemia	0	0.30	0.99	1.74	1.93	2.02
calcemia - calcemia	1	0.95	0.26	1.05	1.03	1.03

A logistic regression is performed with these variables and a model is obtained. The model built directly returns a score describing the probability of match for a pair of tested parameters. Table 4 presents the estimated coefficient and the significance obtained for each explanatory variable in the logistic model. Validity and robustness of the resulting model are analyzed. All analyses are performed with R software version 2.11.1 (19) on windows XP (20) on a processor running at 2 GHz with 4GB of RAM.

Table 4.

Coefficients associated with variables of the model

Variables	Estimate	Pr(>|z|)
(Intercept)	−0.87	0.465
R squared	2.95	0.023
Kolmogorov test	−6.10	< 0.001
85th quantile ratio	−1.66	0.025
60th quantile ratio	2.04	0.023
10th quantile ratio	−0.76	0.047

Validation of the logistic model and the associated probability score

This score is then evaluated on a test sample of a new hospital (Newcomer 2). As presented in Table 1, the validation set contains 5,469 hospital stays with 128,077 records of laboratory results. Among 346 different found parameters, 74 are kept for the evaluation. These 74 parameters are those with a number of values above 1‰ of the total number of records of laboratory results. For each reference parameter, a table identical to Table 3 (except the column “couple” which is predicted by the model) is built. The best candidates are returned and sorted in decreasing order using the probability given by the logistic model. All results are saved using a XML format (21).

Webtool

A mapping webtool (using directly XML results files) is built to present the essential information of best candidates. This tool is designed to help an expert to take a decision. At this stage of development, this tool is a web prototype which is used on a local server. The display only requires the use of a web browser.

For each reference parameter, the web interface shows:

• A classification of best candidates sorted in decreasing order using the probability given by the logistic regression. Only the candidates with a probability above a limit score are retained.

• Their graphic distribution: The graphics display the estimated density probability of the reference parameter and the estimated density probability of the new parameter multiplied by the nearest theoretical conversion coefficient.

• Their names and a few describing attribute aggregating the main information required to validate the visual impression: Number of values, nearest theoretical conversion coefficient and, if available, explicit unit and normality range.

Evaluation of the webtool

An evaluation is performed on the database from Newcomer 2. For a given reference parameter, the short list of potential candidates is presented to an independent expert who has also labels of the considered parameters. He is then responsible for assigning to each reference the correct parameter among the pre-selected candidates. The couples formed by the expert are then verified using IUPAC code contained in the dataset Newcomer 2.

Results

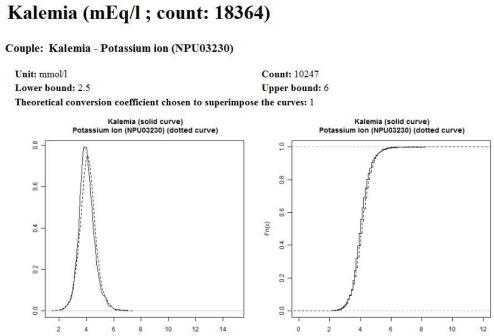
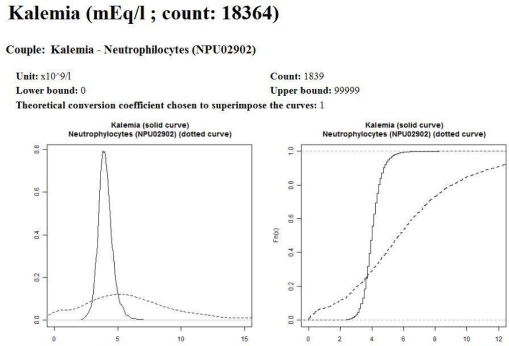
For each reference, all correct parameters are returned among the short list candidates and the median number of candidates is 6. The main result is, for each target parameter, the rank given by the model to the correct correspondent from Newcomer 2. Among 15 target parameters, the correct candidate is in first position in 7 cases, and the correct candidate is in the top five in 14 cases. The worst rank is 8, obtained for 1 couple. All conversion factors found for these parameters are correct. These results are presented in Table 5. For a given reference (Kalemia in this example), the candidates that get the maximum probability are presented. Two main graphics are presented with information about distribution allowing to choose the correct correspondent parameter. It is easy to observe that the parameter compared in Figure 3 is the correct parameter, while the parameter compared in Figure 4 doesn’t match. Using this tool, the independent expert has found all the correct couples.

Table 5.

Rank and conversion coefficient returned by the model for the correct correspondent parameters

Reference data compared to Newcomer 2		Results given by the model for the correct candidate
Parameter	Reference unit	Rank (over 74)	Conversion coefficient	Correct candidate unit
					Sodium Ion	mEq/l	1	1	mmol/l
Kalemia	mEq/l	1	1	mmol/l
Creatininium	mg/l	1	0.113	umol/l
Haemoglobin	g/dl	1	1.667	mmol/l
Leukocytes	/mm3	1	1000	109/l
C Reactive Protein	mg/l	1	1	mg/l
Carbamide	g/l	1	16.6	umol/l
Calcemia	mg/l	2	40	umol/l
Creatin Kinase	ui/l	2	1	ui/l
Aspartate transaminase	ui/l	2	1	ui/l
Glycemia	g/l	4	0.18	mmol/l
Erythrocytes	tera/l	4	1	tera/l
Alanine transaminase	ui/l	4	1	ui/l
International		5	1
Normalized Ratio
Bilirubins	mg/l	8	0.585	umol/l

Figure 3.

Reporting results on webtool, example with correct correspondence for kalemia

Figure 4.

Reporting results on webtool, example with kalemia vs. neutrophilocytes

Discussion

A logistic model based on the comparison of distributions of laboratory results is built. It is then used to select a short list of compatible parameters for each of the target parameters. All relevant parameters are among the top 8 candidates and all the pre-selected conversion factors are correct. A short list of candidates is then presented via a webtool allowing to an independent expert to find all the correct pairs.

To map each of the target parameters, an expert who would perform a work of mapping without assistance would necessarily review all parameters of the new database (more than 70 in this example). Using the tool, the time of review is reduced since a very short list is proposed for each reference parameter. The fact to find immediately the correct conversion factor also reduces the time of the review since such information is required to merge different databases. Finally, the tool provides the expert with valuable information, enabling him to make a choice. With this short list, an expert has always found without any problem the correct correspondence: Even when the distributions are considered similar by the model, a human can easily perform the match by looking at the statistical distribution (in particular). The expert review is essential since the model does not work in some cases but also because the consequences of a mismatch can be severe: In the PSIP project mentioned in the introduction, the lack of monitoring of laboratory results can be an obstacle to the detection of the occurrence of an adverse drug event.

The construction of a score based on the comparison of distributions gives both good sensitivity and good robustness in the model. Indeed, unlike the comparison of character strings, the response is not a binary response but a probability, so that all parameters of interest are in the short list.

In this study, the training sample is small and the model could be improved by increasing the size of the training dataset, i.e. the number of correct pairs. The use of the tool should enable to regularly enrich the learning dataset by incorporating the data so mapped.

Other statistical methods of classification such as regression trees (CART) have been tested in constructing a tree heavily penalizing the real couples misclassified and thus having a sheet containing at least the real couples: This alternative to the logistic regression hasn’t achieved the desired results. The number of reference parameters is reduced and related only to common parameters, that are well described in the dataset. For this reason, only the parameters representing more than 1‰ of the records of the database are analyzed. It is possible that this model has lower performance on rare parameters like troponin or thyroid hormones. Some identical parameters (with same unit) have sometimes very different distribution and are thus difficult to compare with this method. For example, in one of the hospitals the INR (international normalized ratio) is systematically calculated when a prothrombin time is measured, as in other hospitals it is calculated only when prescribed, mainly for patients under vitamin K antagonist treatment. Thus, the distributions are very different between these places. Another example concerns the C reactive protein which shows various distributions between hospitals: A first hypothesis is that the practices are different, another hypothesis is that the populations are different, and a third one is that it comes from the measurement tool. Finally, this method is not able to map laboratory results that consist of textual information, such as some results of bacteriology.

This analysis has focused on the comparison of distributions, but hasn’t tried to model the distribution of each parameter individually. This complementary approach is perhaps a way to improve the method. Moreover, it seems possible to use a meta-rule that would organize the allocation of the same parameter between many references. For example, the parameter A is ranked first among candidates for a reference 1 and only the fifth candidate for reference 2 so it seems reasonable to exclude the parameter A from the list of candidates for reference 2 and to keep it only in the list of candidates for reference 1.

The fact to report on a webtool the short list of candidates (given by the model for one reference parameter) gives a real help to map a new terminology to a target terminology, the final decision being left to an expert. One of the interests of the mapping tool is to be used with any local or international terminology.