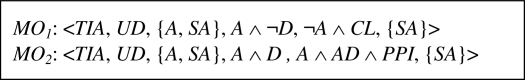Reconciling Pairs of Concurrently Used Clinical Practice Guidelines Using Constraint Logic Programming

Abstract

This paper describes a new methodological approach to reconciling adverse and contradictory activities (called points of contention) occurring when a patient is managed according to two or more concurrently used clinical practice guidelines (CPGs). The need to address these inconsistencies occurs when a patient with more than one disease, each of which is a comorbid condition, has to be managed according to different treatment regimens. We propose an automatic procedure that constructs a mathematical guideline model using the Constraint Logic Programming (CLP) methodology, uses this model to identify and mitigate encountered points of contention, and revises the considered CPGs accordingly. The proposed procedure is used as an alerting mechanism and coupled with a guideline execution engine warns the physician about potential problems with the concurrent application of two or more guidelines. We illustrate the operation of our procedure in a clinical scenario describing simultaneous use of CPGs for duodenal ulcer and transient ischemic attack.

Introduction

A clinical practice guideline (CPG)¹ is a disease-specific patient management tool created with the help of experts’ consensus and medical evidence extracted from document repositories² (i.e. The Cochrane Library). A CPG encapsulates best practices in collecting patient data, drawing conclusions from this data with regards to possible diagnoses and prescribing the most effective treatment plan. It is generally agreed that the use of CPGs at the point of care has a positive impact on a patient’s outcomes and providing guidelines to physicians in a computer executable format advances their adherence to standards of practice and improves quality of care³. There is a significant number of formal (computer-based) representations of CPGs (see⁴ for a review), however none of them is a uniformly adopted de facto standard⁵. This lack of standardization as well as other factors impacting the use of CPGs by physicians are discussed in⁶. Widely used representations either do not support computer execution of the CPG (e.g., GEM⁷), are mostly concerned with representing the underlying clinical algorithms (e.g., GELLO⁸), or are not suited for representing complex, multi-step guideline structures (e.g., Arden syntax⁹).

In the following brief review we focus on executable CPG models (see ¹⁰ for a more comprehensive review). Such models are augmented by application independent¹¹ “execution engines” that constitute computing environments for modeling and executing CPGs. The Arezzo¹² system is a commercialization of the PROforma13 project and it allows for the creation of a guideline, testing its logic, and running a guideline model taking into account patient data. In terms of system architecture, Arezzo’s design follows the autonomous agent model. The PROforma representation is also used in the HeCaSe2 system¹⁰ that implements an agent-based paradigm to modeling guidelines and their interactions with external entities. Executable graph-based models of the CPGs are used by GLARE¹⁴ and GLIF3¹⁵. While GLARE’s execution engine is part of the computing environment, GLIF3 relies on an external execution module (GLEE or GESDOR¹⁵). A similar approach of using an add-on library for guideline execution is implemented in DeGeL¹⁶, a web-based system designed to facilitate the conversion of textual CPGs to a formal representation (in Asbru¹⁷). Its run-time application allows making inferences with regards to the CPG conditions and their satisfaction. Finally there is SAGE¹⁸, one of the most complete and comprehensive guideline modeling and execution environments developed thus far. It builds on previous work on guideline modeling (including PROforma, GLIF3, and Asbru) and expands it. SAGE uses a task-network model to specify activities and decisions associated with complex patient management, and relies on standardized terminologies (SNOMED CT and LOINC) to encode guidelines and patient data.

While the ability to execute a CPG for available patient data plays an important role in guideline uptake by the medical profession, it does not yet address the issue of using guidelines on patients with comorbidity. Such a need is especially clear for elderly patients– several studies^{2, 19, 20} have shown that about 50% of people 65 years or older have more than one chronic disease, each of which is a comorbid condition. The concurrent application of disease-specific guidelines for such patients may not only have an undesired impact on the patient’s care but may also result in an unnecessarily increased financial burden placed on the patient²¹. Despite these factors, there is little research (apart from clinical studies on comorbidity and treatment of chronic diseases) on (semi-) automatic reconciliation of multiple, concurrently used CPGs so they can become active support tools assisting physicians at the point of care. Most of the research in this area is focused on semantic or functional interoperability of concurrently used guidelines and the resulting alignment of actions²². Guidelines are usually represented as ontological models and different alignment strategies are proposed to produce a cohesive recommendation.

The methodology presented in this paper relies on a solvable computer model that combines multiple CPGs associated with comorbid conditions. This model follows the constraint logic programming (CLP) mathematical paradigm allowing us to identify conflicts associated with potentially contradictory and adverse activities resulting from using multiple guidelines on the same patient and providing ways to address them. In our approach we automatically construct solvable CLP guideline models from any guideline formalism that distinguishes between action (activity) and decision steps, and we refer to the constructed models as CLP-CPG models. From a practical point of view we see our proposal as an “early alerting system” that could be combined with an execution guideline to warn the physician about possible conflicts that may occur when multiple guidelines are applied simultaneously to the same patient, and to suggest solutions to these conflicts. Considering the complexities associated with the identification and resolution of these interactions, we limit our study to reconciling pairs of CPGs. Moreover, we are concerned with CPGs related to acute conditions that are applied at the point of care during a single patient-physician encounter, thus we discard the temporal aspects of guideline modeling and execution.

The research described in this paper partially relies on our earlier work related to identifying conflicts in pairs of CPGs²³. However, it expands it significantly by assuming a more complex flowchart-based representation of CPGs with several paths being pursued in parallel (this requires a more comprehensive transformation from a CPG to a CLP-CPG model) as opposed to the simplified representation used earlier. Additionally, we propose a procedure for modifying CLP-CPG models in order to address identified conflicts.

This paper is organized as follows. We start by briefly describing the CLP methodology and explaining how it can be applied to identify conflicts between concurrently applied CPGs. Then, we introduce our approach for mitigating conflicts between guidelines. Next, we illustrate the operation of our approach using a clinical scenario. We conclude with a discussion and present areas for future research.

Methodology

Generally speaking, Constraint Logic Programming (CLP) unifies logic programming (LP) and a constraint satisfaction problem (CSP) by using LP as a constraint programming language to solve a CSP²⁴. A logic program is seen as logical theory composed of a set of rules called clauses. A clause is a disjunction of literals (an elementary proposition or its negation) and each literal is an n-ary predicate where the n terms can be a variable, constant, or an n-ary function. A CLP extends a logic program by including constraints in the body of clauses and querying the program about the provability of a goal produces a solution to the CLP. The proof for the goal is composed of clauses whose bodies are satisfiable constraints and literals.

A CLP model follows the CSP nomenclature. As such it is made up of a set of variables and their respective domains, a set of constraints that restrict the possible combinations of values assigned to variables, and a set of clauses, including a goal to be satisfied, that define the logic program. The predicates of the logic program define the set of variables and the logic used (i.e. binary for two-valued, non-binary for others) defines variables’ domains. The clauses in the program capture the relationships between value assignments for variables and the set of satisfied clauses makes up a solution.

In previous work²³ we described how a single CPG can be represented and solved using the CLP paradigm, and how individual CLP-CPG models are combined to produce a model for a patient with comorbidity. Two essential components of the CLP-CPG model are a set of Boolean variables V and a set of constraints CL. Solving a CLPCPG model entails assigning a value to each variable from V such that no constraints from CL are violated (all clauses are satisfied). Variables related to available information (known patient data) are instantiated prior to solving the model and cannot be revised by the solving procedure. For a patient with comorbidity, when individual CLPCPG models are independent of each other (they contain no shared variables or constraints affecting both models) each model can be solved independently. However, there are situations where interactions between the individual models exist (through shared variables and/or unifying constraints). Subsequently an individual CLP-CPG model may explicitly identify value(s) for a variable(s) that are infeasible for variable(s) defined in another individual CLPCPG model. This scenario leads to the combined CLP-CPG model having no solution and the identified source of the infeasibility constitutes a point of contention (POC). More formally, we define a POC as a set of variables, whose domains are annihilated (reduced to the empty set) while solving the combined model, resulting in the absence of a solution. In order to obtain a solution, the POC needs to be addressed and we refer to this process as the reconciliation of CPGs. In the following sections we describe an automatic procedure that implements this process.

Reconciliation Process

Our proposed approach can be used with any CPG formalism that distinguishes between action and decision steps, which according to the review by Isern and Moreno¹⁰ is common for most representations. While some formalisms introduce additional steps (e.g. query steps in PROforma and GLARE, route steps in SAGE or branch and synchronization steps in GLIF3) they are discarded when constructing CLP-CPG models.

Our approach assumes that at some point a CPG is given as a flowchart and we refer to this flowchart as an activity graph (AG). More specifically, AG is a directed graph that consists of context, action and decision nodes. A context node is the root node in AG and it defines a clinical context that triggers a specific CPG (i.e., diagnosing a patient with a specific disease). In other words, the context node defines an entry point in the AG. An action node corresponds to an action step from a CPG and it is a container that holds a collection of one or more tasks. Finally, a decision node corresponds to a decision step and it indicates a choice among several alternative choices that are linked to specific arc starting from the decision node. For flexibility, we allow for two types of decision nodes – OR and XOR and we introduce a split property associated with each decision node that indicates its type. In case of the OR split property, conditions associated with more than one choice can be satisfied, thus it is possible to purse several parallel paths. On the contrary, the XOR split property indicates exactly one choice may be satisfied. The majority of CPG formalisms employ only XOR decision nodes, however, there are some (e.g., SAGE) that allow for both types.

We need to note a few simplifications introduced by our approach. We do not currently consider temporal aspects of CPGs and assume that they are executed sequentially (this is a reasonable assumption for point of care encounters). Also, we do not currently consider sub-guidelines and instead amalgamate them into a CPG (however, it is possible that our approach is first applied to the sub-guidelines, and once all conflicts on this lower level have been identified and addressed, the top level guideline is processed). We discuss future work in supporting temporal actions and sub-guidelines in the Discussion section.

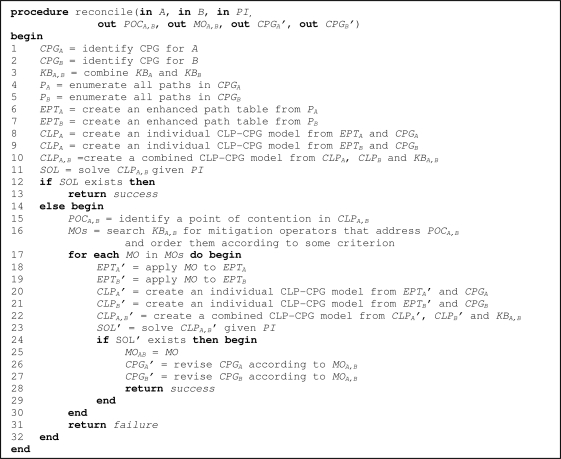
Our procedure to reconcile a pair of CPGs given in the form of AGs is summarized in pseudo-code in Figure 1. The procedure assumes a patient suffers from two comorbid conditions (labeled A and B) and is treated according to two concurrently applied CPGs (CPG_A and CPG_B) – these two disease labels together with available patient information (PI) constitute the input parameters. The reconcile procedure consists of two main phases. In the first phase (lines 1–13) it checks for possible conflicts between CPGs. If a POC has been identified, the second phase starts (lines 14–32), where the procedure tries to mitigate the POC by modifying the CPGs according to available domain knowledge. This knowledge on how to modify CPGs given POCs is encapsulated in mitigation operators (MOs) – defined later in the text.

Figure 1.

Pseudo-code for the reconcile procedure

The procedure returns success if no POC has been encountered or it has been successfully mitigated, and failure otherwise. It also provides additional output information – the POC (POC_A,B), the MO used to mitigate the encountered POC (MO_A,B) and the revised CPGs (CPG_A’ and CPG_B’) that have been modified by the MO. All these outputs are set to null if no POC is encountered during reconciliation. MO_A,B, CPG_A’ and CPG_B’ are also set to null if a POC has been discovered, but the procedure has failed to resolve it and returned failure. Our procedure uses the open source constraint programming system ECLiPSe (http://www.eclipseclp.org) for solving the CLP-CPG models. We chose ECLiPSe for its robustness and available interfaces enabling us to eventually integrate our proposed procedure into the MET3 point of care system²⁵.

The reconcile procedure assumes that there is a unique mapping between a disease label and a CPG, thus it is possible to identify CPGs for A and B (CPG_A and CPG_B respectively, lines 1–2). The procedure also relies on the availability of knowledge bases (KBs) associated with both diseases (KB_A and KB_B). These KBs unify internal and external knowledge sources and contain knowledge that is not explicitly represented in a CPG. They are represented as a collection of facts (i.e., clauses with an empty body) with different types of facts corresponding to different types of knowledge – specifically, facts that describe adverse tasks (related to treatment-treatment and treatment-disease interactions), contradictory tasks (e.g., both prescribing and stopping the usage of a specific medication) and MOs are included. Such a representation (similar to a Prolog database²⁶) allows for a flexible representation of the knowledge and efficient querying of the KB. To facilitate the querying and retrieval of required information from the KB, the procedure introduces a common view that logically combines KBs for both processed CPGs (KB_A,B, line 3).

In lines 4–5 the procedure enumerates paths in CPG_A and CPG_B (both given in the form of an AG) and represents them as logical expressions (conjunctions). It starts by associating each choice and task with a unique Boolean variable (a choice or task variable respectively). The true logical value indicates that a task represented by a task variable should be conducted, or the criterion for a choice associated with a choice variable is satisfied. On the contrary, false means that a task shouldn’t be conducted or the choice criterion is not satisfied. All possible paths in both underlying AGs are enumerated by traversing from the root node to the leaves, and then transformed into logical expressions – conjunctions of choice/task variable-value pairs. A path including nodes N₁, N₂,..N_k is translated into a conjunction according to the following rules:

• If N_i is a context node, then it is discarded,

• If N_i is a decision node, then (C_i,j = true) is added to the conjunction, where C_i,j is a choice variable linked to the traversed outgoing arc,

• If N_i is an action node, then (T_i,1 = true) ∧ (T_i,2 = true) ∧ … ∧ (T_i,m = true) is added to the conjunction, where T_i,1,…T_i,m are task variables associated with the tasks specified in the node.

For the sake of brevity in all logical expressions presented in the text, we will use a simplified notation, i.e., V = true is written as V, while V = false as ¬V.

In lines 6–7 all conjunctions representing paths in the processed CPGs are collected together in enhanced path tables (EPTs) – EPT_A stores paths from CPG_A, and EPT_B from CPG_B. Rows in the EPT correspond to conjunctions, and columns to variables. Following the categorization of variables, columns are grouped into choice and task ones. A cell in the EPT associated with a conjunction and variable V stores the value of V as it appears in this conjunction, otherwise V is not involved in the conjunction and the cell contains a null value that is interpreted as a “don’t care”. Intuitively, when considering a particular path, we focus on choices and tasks that are explicitly indicated in the corresponding conjunction and ignore the others.

In lines 8–9 the procedure constructs individual CLP-CPG models (CLP_A and CLP_B) from EPTs (EPT_A and EPT_B) and CPGs (CPG_A and CPG_B). The set V in an individual CLP-CPG model includes choice and task variables corresponding to all columns in the EPT. Constraints in the set CL are created from the EPT and the CPG (underlying AG). The procedure starts by creating a constraint that models paths in the AG. First, it identifies subsets of paths that may be followed together (in parallel) – some of these subsets may include a single path, if no other paths are allowed at the same time. This identification relies on the split property of individual decision nodes from the AG. Then the procedure creates a logical representation of each path subset using the EPT. If the subset contains a single path, it is represented as a conjunction of variable-value pairs from an EPT row corresponding to this path. Otherwise, each path from the set is represented as an implication with the premise being a conjunction of choice variable-value pairs, and the consequence being a conjunction of task variable-value pairs from the appropriate EPT row. These implications are combined into a conjunction that represents parallel path subsets. Representing parallel paths as a conjunction is driven by the fact that not all parallel paths have to be followed (depending on the evaluation of choices appearing in these paths) and the CLP representation has to account for that. Finally, logical representations of all path subsets are combined into a disjunction to ensure that one path must be followed.

Subsequently, the procedure creates and adds constraints to CL that model how specific decision nodes handle associated choices. The procedure checks each decision node N_i in the AG and introduces one of two constraints depending on the split property specified for N_i (in both constraints C_i,1,…, C_i,m are choice variables associated with choices in N_i):

• If the split property is OR, then (C_i,1 ∨ C_i,2 ∨ … ∨ C_i,m) is introduced to indicate that at least one choice has to be pursued,

• If the split property is XOR, then (C_i,1 ⊕ C_i,2 ⊕ … ⊕ C_i,m), where ⊕ denotes exclusive disjunction (or exclusive or), is introduced to indicate that exactly one choice should be pursued.

In line 10 the procedure merges CLP_A and CLP_B into a combined CLP-CPG model (CLP_A,B) to test for the possible adverse interactions between concurrent CPGs (in the following text, when referring to the V and CL sets in individual and combined models we add the proper subscripts for the model’s identification). The sets of variables and constraints in the combined model are unions of the appropriate sets from single models (V_A,B = V_A ∪ V_B, CL_A,B = CL_A ∪ CL_B). In order to complete the construction of the combined model, the procedure augments CLP_A,B with constraints corresponding to adverse and contradictory tasks that are created on the basis of appropriate facts retrieved from KB_A,B.

In line 11 the reconcile procedure invokes the solver to find a single solution of CLP_A,B given PI (variables instantiated according to PI). If a solution exists (line 12), the procedure reports success and terminates (line 13) – in this case all output parameters are null. Otherwise, the procedure starts the second phase by identifying in line 15 the POC causing the conflict (POC_A,B), and in lines 16–30 it tries to mitigate it by using available MOs to revise CPGs in question (more precisely, MOs modify corresponding EPTs and these changes are further propagated in revised individual and combined CPG-CLP models).

Each MO is formally defined as 6-tuple: <BD, TD, POC^*, LHS, RHS, MT>, where:

• BD and TD indicate labels of base and target diseases accordingly, for which associated EPTs are modified by the operator. Base disease refers to a disease for which the EPT requires more extensive changes in order to mitigate the POC and target disease refers to a disease for which these changes are minor or not required at all;

• POC^* defines the POC mitigated by the operator (it specifies a set of variables that constitute the POC);

• LHS and RHS describe modifications to be performed on the EPT_BD. They are represented as conjunctions of task variable – value pairs. LHS is a pattern of values that occurs in a single row of EPT_BD (we assume that false in LHS matches null values in the EPT), and once this pattern is located, it is replaced by the pattern defined by RHS;

• MT is a set of task variables represented as the columns in the EPT_TD that need to be removed. In other words, MT indicates mitigated and discarded tasks in the CPG for TD. MT = ∅, if no tasks are discarded.

The operation of replacing LHS by RHS in EPT_BD is governed by the following principles:

• If a variable V appears in LHS only (i.e., it has been eliminated from RHS), then the value in the located row and column corresponding to V is set to false;

• If a variable V appears in both LHS and RHS or it appears only in RHS and a column in EPT_BD corresponding to V exists, then the value of V in the located rows is updated according to RHS;

• If a variable V is present in RHS only and EPT_BD does not have a column corresponding to V, EPT_BD is expanded with a new task column with null values and the value for V in the located row is set to the value indicated in RHS.

The reconcile procedure queries KB_A,B for facts associated with MOs such that POC_A,B ⊆ POC^*, and BD = A, TD = B or BD = B, TD = A (line 16). Identified MOs are ordered to make the mitigation process more efficient. The ordering criterion can be domain-specific, e.g., cost or extent of modifications implied by the MO, or domain-independent, e.g., the number of modified variables in the target disease EPT.

In lines 17–30 the procedure iteratively applies each of the MOs following their ordering and checks if a revised CLP_A,B’ model has a solution. During this process, a given MO is applied to the EPTs associated with both CPGs – this results in revised EPTs (EPT_A’, EPT_B’, lines 18–19) that are used in lines 20–22 to revise individual and combined CLP-CPG models (CLP_A’, CLP_B’ and CLP_A,B’). Since applying the MO may result in removing and/or adding task variables, CLP_AB’ is likely to include different constraints corresponding to adverse and contradictory tasks when compared to the original CLP_AB.

The procedure again invokes the solver to solve CLP_A,B’ given PI (line 23). If a solution exists (line 24), then the current MO is retained as one of the output parameters (MO_A,B, line 25) and it is applied in lines 26–27 to CPG_A and CPG_B in order to create revised versions (CPG_A’ and CPG_B’ respectively) that are communicated to the physician. If MO_A,B eliminates a task column from the EPT or assigns false to a task variable in the EPT, then an associated task is removed from the CPG. If it assigns true to a task variable in the EPT, then a new task is added to the CPG. Finally, if removing tasks results in an empty action node, it is removed from the CPG as well. After revising the CPGs the reconcile procedure terminates and returns success (line 28). A revised CPG given as an AG needs to be additionally reviewed by the physician in order to avoid clinically inaccurate suggestions (CLP-CPG models are used internally by the reconcile procedure and due to their complexity are not presented to the physician). If possible revisions (described by candidate MOs) do not produce a solvable combined CLP-CPG model, the procedure returns failure (line 31).

Clinical Scenario

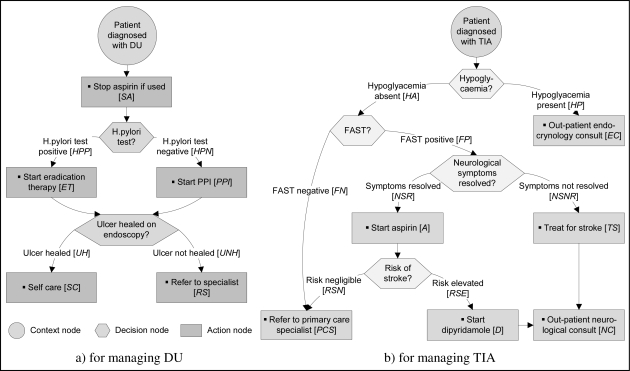
We have applied our proposed approach to multiple clinical scenarios using anonymized patient data. For clarity and brevity, we present a simple clinical scenario where a patient with an underlying chronic condition of a duodenal ulcer (DU – an ulcer placed in the duodenum) experienced a transient ischemic attack (TIA – a transient stroke that lasts only a few minutes and occurs when the blood supply to part of the brain is briefly interrupted). CPGs for DU and TIA patient managements represented as AGs are given in Figure 2. We highlight specific choices by labeling corresponding arcs starting at a decision node. Moreover, we indicate tasks defined within an action node by displaying them in the form of a bulleted list. A quick look at Figure 2 reveals that in both guidelines each action node is associated with a single task and each decision node is associated with two choices. All decision nodes have an XOR split property.

Figure 2.

CPGs in the form of AGs

Upon closer examine we find that the guidelines contain adverse interactions between treatments applied to the same patient; aspirin if used to treat TIA will exacerbate ulcer symptoms and promote gastrointestinal bleeding. The clinical resolution of this contradiction involves stopping the administration of aspirin and switching to clopidogrel, otherwise the continued use of aspirin needs to be combined with the administration of proton pump inhibitors (PPI) for gastro-protection. To identify and resolve this adverse interaction we begin by assuming that both guidelines are applied to an ulcer patient (chronic condition) diagnosed with TIA (comorbid condition) and characterized by the following patient information (PI): no signs of hypoglycemia, successfully passed FAST (Face Arm Speech Test), and resolved neurological symptoms. We use this information together with labels of both diseases (where A = DU and B = TIA) as input parameters to the reconcile procedure presented in Figure 1.

The procedure starts by locating CPG_UD and CPG_TIA, constructing KB_DU,TIA, and identifying the choice and task variables. These variables are indicated in Figure 2 in square brackets next to the description of a corresponding choice or task (e.g., HPP is associated with the “H.pylori test positive” choice, while A is associated with the “Start aspirin” task). Then the procedure identifies all paths in both guidelines and uses them to construct EPT_DU and EPT_TIA that are presented in Table 1 and 2 respectively.

Table 1.

EPT for DU (EPT_DU)

Choices				Tasks
HPP	HPN	UH	UNH	SA	ET	PPI	SC	RS
true		true		true	true		true
true			true	true	true			true
	true	true		true		true	true
	true		true	true		true		true

Table 2.

EPT for TIA (EPT_TIA)

Choices								Tasks
HA	HP	FN	FP	NSR	NSNR	RSN	RSE	EC	A	TS	PCS	D	NC
true		true									true
true			true	true		true			true		true
true			true	true			true		true			true	true
true			true		true					true			true
	true							true

Subsequently the procedure constructs CLP_DU and CLP_TIA (due to space limitations these are not presented here) and CLP_UD,TIA, presented in Figure 3. This model has 23 variables and 9 constraints. The first 8 constraints come from the individual CLP-CPG models and the last one (¬(A ∧ SA)) is created using a fact retrieved from KB_UD,TIA that describes the previously identified contradictory tasks. This constraint indicates that it is not possible to give aspirin (A) and stop using aspirin (SA) at the same time. There are no constraints corresponding to adverse tasks, as they are not present in this scenario.

Figure 3.

Combined CLP-CPG model for DU and TIA (CLP_DU,TIA)

The reconcile procedure invokes ECLiPSe to solve CLP_DU,TIA with variables instantiated according to the PI (HA = true, FP = true and NSR = true). No solution exists, variables A and SA are identified as the sources of an adverse interaction, and they define a POC (i.e., POC_DU,TIA={A, SA}). The procedure searches KB_DU,TIA for MOs that are applicable to POC_DU,TIA and finds two MOs that are presented in Figure 4 (in both cases BD = TIA and TD = UD). Both MOs imply removing SA from EPT_DU. Operator MO₁ modifies EPT_TIA by replacing aspirin with clopidogrel (RHS = ¬A ∧ CL) assuming that the administration of aspirin is not combined with dipyridamole (LHS = A ∧ ¬D). Operator MO₂ implies augmenting the administration of aspirin (LHS = A ∧ D) with PPI (RHS = A ∧ D ∧ PPI). According to the assumed criterion that simpler modifications (smaller number of modified variables) are better, MO₂ is ordered first. This is because MO₂ introduces a single task while MO₁ introduces one task and discards another one.

Figure 4.

MOs for TIA and UD addressing POC with {A, SA}

The reconcile procedure iteratively applies MOs from Figure 4 to address the POC_DU,TIA starting with operator MO₂. First, MO₂ is applied to revise EPT_TIA and EPT_DU what results in EPT_TIA’ and EPT_DU’ respectively. In comparison to EPT_TIA in EPT_TIA’ a new task column has been added (PPI) and row 3 has been modified by storing the true value in the new column, and EPT_DU’ no longer includes the column for SA.

The revised EPTs are used to construct revised individual CLP-CPG models (CLP_DU’ and CLP_TIA’) further combined into the revised CLP-CPG model (CLP_DU,TIA’) given in Figure 5. In comparison to CLP_DU,TIA (see Figure 3) it has less variables and does not include the constraint with contradicting tasks A and SA, because SA has been removed. ECLiPSe is able to solve CLP_DU,TIA’ given PI, hence, the other mitigation operator (MO₁) does not need to be considered.

Figure 5.

Revised combined CLP-CPG model for DU and TIA (CLP_DU,TIA’), application of operator MO₂

Finally, the reconcile procedure revises CPG_DU and CPG_TIA according to MO₂ resulting in AG_UD’ and AG_TIA’. In CPG_UD’ the task corresponding to variable SA is removed. Since this leads to an empty action node, it is also removed. In CPG_TIA’ an additional task “start PPI” corresponding to variable PPI is introduced – it is placed in the action node that already contains the “start dipyridamole” task. In the last step the procedure informs the physician that both CPGs can be applied simultaneously (success) despite the identified POC (POC_UD,TIA). Revisions of the CPGs according to MO₂ are also presented (CPG_UD’ and CPG_TIA’) and the physician reviews them for clinical validity. Both revised CPGs are presented as flowcharts in the same format as the original CPGs (refer to Figure 2), so they are more comprehensive than the CLP-CPG models used internally by the reconcile procedure. Moreover, the physician is also presented with the POC ({A, SA}) to better understand why and how the CPGs have been revised. This information enables a fully informed review of the revised CPGs.

Discussion

In this paper we present an automatic procedure that uses the CLP methodology to reconcile multiple clinical practice guidelines given as flowcharts (AGs). The main goal of the proposed approach is to facilitate the use, at the point of care, of guidelines for a patient with comorbidity. The key to developing a treatment regimen for such a patient is the ability to mitigate conflicting treatment plans suggested by individual CPGs. Towards this end we present the reconcile procedure that mitigates identified conflicts (called here POCs) and uses mitigation operators combined with information from external knowledge bases to suggest a possible reconciliation. Once the procedure terminates successfully, revised CPGs are constructed and presented to a physician for review. However, when the procedure terminates in failure (i.e., despite applying mitigation operators, the combined CLP-CPG does not have a solution), a physician is alerted to the identified POC and informed about the unsuccessful mitigations. This information helps in patient management by providing guidance during the manual search for alternative treatment regimens.

We are currently working to improve the reconciliation process by addressing five key issues. First, we are expanding our approach to work with more than two CPGs at a time. Second, we are exploring ways to apply Temporal Constraint Logic Programming (TCLP) to express durative actions often present in CPGs and time spans between specific actions. Third, sub-guidelines are an important feature of more complex CPGs and we are looking at the most effective way of modifying CLP-CPG to support these sub-guidelines as part of the solution process. Fourth, we want to address the issue of dosages of medication (especially when the same medication in different dosages is recommended by different guidelines) by moving beyond Boolean CLP-CPG models. Finally, we want to introduce automatic procedures to expand external knowledge bases with information on resolving drug-drug and drug-disease interactions searched and retrieved from repositories with clinical evidence.