Temporal Evolution of Biomedical Research Grant Collaborations across Multiple Scales – A CTSA Baseline Study

Abstract

The evolution of biomedical research grant collaborations (BRGC) across time (2006, 2009) and hierarchically related scales (Staff, Department) at the University of Arkansas for Medical Sciences (UAMS) is investigated using network abstractions. This baseline study is a part of the Clinical Translational Science Award (CTSA) efforts in promoting team science and exploring network science approaches for CTSA evaluation. The BRGC data were retrieved from the internally developed grants management system (Automated Research Information Administrator, ARIA). Our analysis revealed the BRGC networks to be disconnected with mutually exclusive research clusters. However, a dominant weakly-connected cluster with positively skewed degree centrality and betweenness distribution was observed across scales and time. Variation in the centrality measures, clustering coefficient, and the impact of perturbing the most-influential nodes as a function of time and scale is investigated. The results presented provide novel insights into the complex nature of BRGC networks that may persist across similar settings.

Introduction

One of the primary objectives of the Clinical Translational Science Award (CTSA) funded by the National Center for Research Resources (NCRR, NIH) is to support multi-disciplinary collaborations that can transform biomedical research, training and facilitate novel scientific initiatives. With the 2010 awardees, the number of CTSA institutions has reached fifty-five institutes. Social network analysis metrics and network science approaches have been recommended by the CTSA key function committees for understanding collaborations and even as a possible CTSA evaluation tool (e.g. www.ctsaweb.org, under Evaluation Key Function Committee). The need for team science is especially exemplified by recent cross-disciplinary funding opportunities and joint solicitations by agencies such as the National Institutes of Health and the National Science Foundation. Independent studies have also provided compelling evidence on the recent ‘shift’ towards collaborative research that transcend geographical barriers [1, 2].

Real world entities interact with one another and work as a system and not in isolation [3–8]. The behavior of such systems is complex and in most cases cannot be inferred from its parts. More importantly, these systems challenge reductionist approaches and fail to obey the principle of superposition that attempts to infer the behavior of the system from that of its parts. System-level understanding can reveal important global properties, generating mechanisms and can be an important step prior to developing meaningful interventions [3–5]. Networks have proven to be convenient abstractions of such systems where the nodes represent the entities of interest and the edges their interactions or relationships [1]. These edges in turn can be directed or undirected with directed edges capturing possible causal relationship between the nodes. Such networks also provide convenient visualization of complex high-dimensional data. For instance, the nodes may be molecular entities such as genes/proteins in which case, the corresponding network is essentially an abstraction of a signaling mechanism/biological pathway [6]. On a related note, substituting the molecular entities with researchers and establishing their links using suitable criteria such as co-authorship results in a scientific collaboration network. Recent studies on scientific collaboration networks using co-authorships provided novel insights into their topological structure, statistical properties, and possible generating mechanisms [7]. This was accomplished by mining published literature residing in biomedical research archives such as MEDLINE [7].

The proposed study is possibly the first of its kind that investigates the evolution of Biomedical Research Grant Collaboration (BRGC) across multiple scales and time using network abstractions. While BRGC may be related to scientific collaboration network, there are subtle differences. For instance, collaborative research manuscripts might not necessarily translate into collaborative research grants. This inherent limitation may be attributed to several factors including the nature of the research area and the extent of collaborations between scientists that might warrant a more serious undertaking in the form of a collaborative research grant. Unlike scientific collaboration network that identifies relationships based on their joint participation in a given manuscript (co-authorship), relationships in BRGC networks are based solely on joint participation in a research grant and were retrieved from an internally-curated research grants management database (ARIA). Several interesting properties in real-world networks such as power-law degree distribution, preferential attachment, and small-world phenomena have been reported in the past across a number of real-world settings [3–8]. Power-law degree distributions in networks have been attributed to the presence of a small number of highly influential nodes. This feature in turn renders such networks tolerant to random perturbations. Preferential attachment has been proposed as a possible generating mechanism of networks exhibiting power-law degree distributions, where new nodes have a tendency to attach to most influential nodes [3–5]. Small-world networks [8] that exhibit characteristic clustering have especially been shown to capture scientific collaborations [7]. While any of the above observations may be a plausible explanation of BRGC networks, their extension is neither immediate nor straightforward for the following reasons: (i) Size of the BRGC networks are considerably smaller compared to many of the real world networks studied thus far. This in turn may mask subtle features that may be evident in larger networks; (ii) Connectivity in a BRGC network can be significantly affected by changes in university policies, leadership, organizational structure, economic slowdown, and other forms of internal and external perturbations; (iii) Evolution of BRGC networks is accompanied by addition of new nodes as well as deletion of existing nodes in a non-constant manner leading to considerable fragmentation. While addition of a new node can be an outcome of new faculty hire/formation of a new Department/Division, deletion of an existing node can be attributed to the departure of a faculty/dissolution of a Department/Division.

The objective of the present study is to gain preliminary insights into the properties of the BRGC networks as a function of scale (Staff, Department) and time (2006, 2009). The organization of this report is as follows. The attributes of interest are first retrieved from the ARIA database. Subsequently, the BRGC networks are investigated for connectivity. Degree centrality, Betweenness Centrality and clustering coefficient and their evolution across time and scale are investigated for the weakly connected dominant cluster in the BRGC network. Finally, a perturbation approach is used to elucidate the critical role of the most-influential node in the networks.

Methods

Description of the BRGC data retrieved from ARIA

The Automated Research Information Administrator (ARIA) is an internally-developed system at the University of Arkansas for Medical Sciences that provides an integrated environment for the exchange of information across the various entities that play a critical role in grant development and submission. These include the Office for Research and Sponsored Programs (ORSP), Institutional Review Board (IRB) and the Office for Clinical Trials. ARIA development and maintenance is partly supported by National Center for Research Resources (NCRR/NIH). A Principal Investigator in a grant is required to furnish all the mandatory information with regards to the grant through password-protected online forms in ARIA as a part of the grant submission. This information is reviewed subsequently for compliance and correctness prior to the grant submission. In the present study, the attributes of interest retrieved from ARIA across the years (2006–2009) are shown in Table 1. Each grant is identified by a unique ID (Grant Number), funded by a specific agency (Awarding Agency) in a given year (Grant Year) and has an award amount (Total Cost) associated with it. The Awarding Agencies considered in the present study predominantly consists of institutes and centers at the National Institutes of Health (NIH). Each grant may have one or more Staff (Staff ID) participating in a particular role given by the (Staff Role). Examples of Staff Role may include (Principal investigator, Co-investigator, Research Assistant, Technician, Graduate Assistant, and Primary Contact). The present study considers only the following Staff Roles (Principal investigator, Co-investigator) because these Staff Roles comprise basic scientists and clinical faculty who play a critical role in building successful collaborations across the five Colleges. Such a constraint is expected to enhance the connectivity of the network. The attributes of interest were retrieved across the years (2006–2009).

Table 1.

Attributes retrieved from the Automated Research Information Administrator (ARIA)

Attribute	Format	Example
Grant Number	Numeric	102412
Awarding Agency	Text	National Cancer Institute
Staff ID	Text	SID000001
Staff Role	Text	Principal Investigator
Department	Text	Biomedical Informatics
Grant Year	Date	01/01/2006
Total Cost	Numeric	400000

Multiscale Network Abstraction of BRGC

Staff Network.

A node in the BRGC network represents a Staff (Staff ID, Table I) participating in a grant either as a principal investigator or co-investigator (Staff Roles, Table I). An edge between a given pair of staff (Staff ID, Table I) occurs when they participate in the same grant application. The direction of the edge is always from the Principal Investigator(s) to the Co-Investigator(s). Thus the resulting network is directed and asymmetric by definition. Also, it is important to note that a Staff can participate in multiple roles across multiple grants. For instance, Staff A can be a co-investigator with Staff B as the Principal Investigator in a given grant (G1), whereas their roles may be completely reversed in another grant (G2). Therefore, the presence of cycles cannot be ruled out in BRGC networks.

Department Network

Multiscale abstraction of the BRGC network can be realized by replacing the (Staff ID, Table I) by their respective Department or Division names (Department, Table I). Such an approach essentially provides a coarser resolution of Staff collaborations since Department and Staff ID are hierarchically related with one or more Staff IDs belonging to a single Department (Staff ID ⊂ Department). While a Staff’s assignment to a Department can certainly change with time, a Staff can belong to only one Department (i.e., primary appointment) at any given time. This in turn renders the Departments to be mutually exclusive entities by definition. It is important to appreciate that a network consisting solely of Staff ID’s fails to distinguish intra- and inter-departmental collaborations. In contrast, the network of Departments/Divisions is useful in assessing inter-departmental collaborations, justifying the choice of a multiscale approach.

In the above network abstractions, out-degree of a node represents its ability to lead collaborative grants as Principal Investigator, whereas in-degree captures its ability to participate in collaborative grant as support personnel (co-investigator). The degree of a node in general is the sum of its out-degree and in-degree. Multiple collaborations between a given pair of nodes at a given time and scale in the same direction is not accounted for in the present analysis.

Results

Since the temporal changes in the network properties showed no abrupt changes across adjacent years (2006–2009) and some of the funded grants persisted for several years, we present the results only across the years 2006 and 2009.

Connectivity

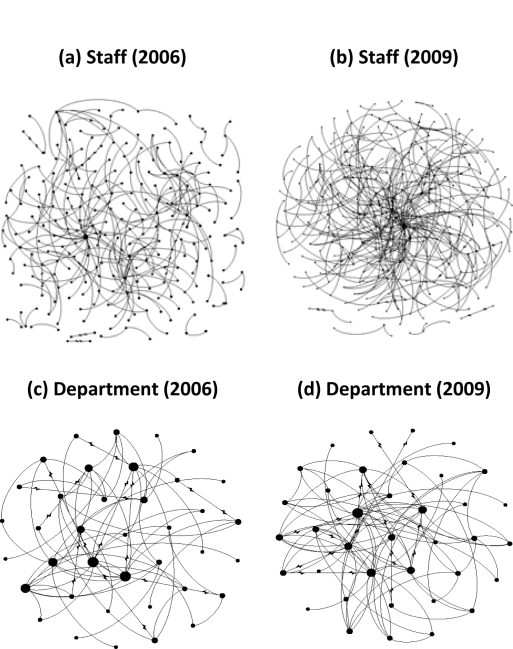
Connectivity is a fundamental aspect of networks and its understanding is critical prior to more advanced analysis. Unlike some of the real-world networks [3–5], the Staff and Department networks revealed disconnected clusters (not shown in Fig. 1). Further investigation revealed that the disconnected clusters were an outcome of mutually exclusive collaborations (i.e. isolated clusters) and singleton nodes in the network. Singleton nodes included newly hired and junior faculty yet to establish collaborations. Isolated clusters on the other hand included research groups in specialty areas that may not demand extensive collaborations across the spectrum of researchers. However, a dominant cluster was observed across the scales (Staff, Department) and across time (2006, 2009). This dominant cluster was weakly connected i.e. the undirected graph representation of the dominant cluster is connected. All subsequent discussions across Staff and Department will focus on the corresponding weakly-connected dominant cluster. The proportion of nodes in the dominant cluster to the total number of nodes showed a marked increase from 2006 (∼22%) to 2009 (∼37%) across Staff. A similar analysis of the Department network showed a decrease in the proportion of the nodes in the dominant cluster to the total number of nodes between (2006, ∼70%) and (2009, ∼57%). A possible explanation of this decrease can be attributed to the development of new satellite campuses geographically dispersed across the state, Area Health Education Centers (AHEC), and specialty departments with administrative services with minimal participation in BRGC. The dominant clusters across scales (Staff, Department) Fig. 1 generated using the open-source visualization platform (Gephi 0.7) with Fruchterman-Reingold layout showed marked topological changes between the years 2006 and 2009. Fig. 1. The clustering coefficient [3] for the Staff network increased from (∼0.054) in 2006 to (∼0.133) in 2009. The small clustering coefficient in 2006 unlike 2009 may indicate possible random graph like behavior of Staff collaborations at initial stages of collaborations. Analysis of the Departmental network showed similar increasing trend in the clustering coefficient from (∼0.15) in 2006 to (∼0.21) in 2009. In Fig. 1, the size of the nodes is proportional to the number of edges incoming or outgoing from that edge. The emergence of dominant nodes in the network is especially clearer in 2009, Fig. 1.

Figure 1.

Fruchterman-Reingold layout of the BRGC network across years (2006, 2009) and across hierarchically related scales Staff (a, b) and Departments (c, d). In each subplot, the size of a node is proportional to the number of edges incident upon it. The size of the nodes is not normalized across the plots. Some of the isolated clusters in the Staff network are shown on the periphery of the dominant weakly-connected cluster.

Centrality

In order to obtain better insight into the topological properties of the Staff and Department networks we chose to investigate the degree and betweenness centrality distributions [9] of the dominant clusters and the impact of the most-influential node across the Staff and Department networks.

Degree Centrality

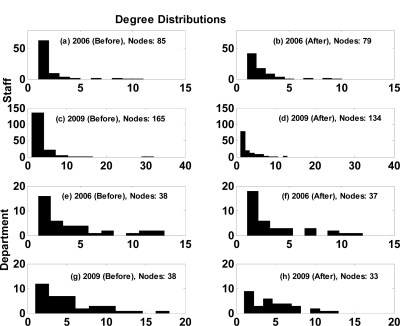
Degree centrality distributions were found to be positively-skewed across the dominant cluster in the Staff and Department networks indicating only a handful of nodes were highly connected comprising the tail of the distribution, Fig. 2. The tail of the distribution consisted of nodes with high in-degree as well as out-degree revealing the critical role of collaborators and principal investigators in orchestrating BRGC. Positively skewed distributions such as power-law degree distributions have been widely reported across a number of real-world scenarios [3–5] and exhibit properties different from those of classical random graph (Erdős–Rényi) [10]. Power-law degree distributions are heavy-tailed and have a small number of nodes with high-degree centrality comprising the tail of the distribution. This in turn renders these networks resilient to random perturbations. Generating mechanisms such as preferential attachment, where new nodes have a tendency to collaborate with nodes with high degree centrality have also been proposed as a possible explanation of power-law degree distribution. Such theories may be quite relevant in BRGC, where nodes with a history of successful collaborations have more visibility and thus are likely to attract new nodes into direct or indirect collaborations. While methods have been proposed in the literature to minimize spurious estimation of the power-law exponent [11], statistical justification of power-law degree distribution from the observed data set for the most part has proven to be elusive. This can especially be attributed to small sample size and lack of adequate samples in the tail of the distribution which plays a critical role in discerning power-law from other distributions. Also, several families of distributions (e.g. extreme-valued distributions) and more complex scenarios may exhibit characteristics similar to power-law. Our initial investigation of the log-log plot of the degree centrality distributions revealed a linear trend. However, the behavior in the tail of the distribution was unclear to allow any meaningful conclusions. Therefore, rather than argue for the presence of power-law, we investigate the statistical properties of the degree distribution and its variation using two popular measures, namely: skewness (α₃) and kurtosis (α₄). These measures for the Staff degree distribution showed a marked increase between 2006 (α₃ ∼ 2.5, α₄ ∼ 8.9) and 2009 (α₃ ∼ 5.1, α₄ ∼ 42.7) with the latter being heavily skewed and with a more pronounced peak, Figs. 2a, 2c. The larger values of these measures in 2009 may also indicate the emergence of dominant nodes in the network. A similar analysis of the Department degree distribution across 2006 and 2009 resulted in (α₃ ∼ 1.26, α₄ ∼ 3.5) and 2009 (α₃ ∼ 1.30, α₄ ∼ 3.9) respectively, Figs. 2e, 2g. Unlike the Staff network, the Department network failed to show a marked change in these statistical measures across time. Alternatively, there were no appreciable changes in the degree distribution corresponding to inter-departmental collaborations across the years as reflected by the statistical measures (α₃, α₄).

Figure 2.

The degree centrality distribution of the dominant clusters before (Before) and after (After) perturbing the most influential node (i.e. node with the highest degree) across hierarchically related scales Staff (a–d) and Department (e–h), and across time (2006, 2009). The axes in each row are represented on the same scale to enable direct comparison.

Betweenness Centrality

While degree centrality rank can provide insight into highly connected nodes it may not necessarily provide insight into dominant mediators. The role of dominant mediators may be especially critical since they orchestrate connections between disparate groups in the network. Therefore, we chose to investigate the betweenness centrality distribution of the undirected BRGC network across Staff and Department. The Staff betweenness distribution showed a marked increase in skewness and kurtosis from 2006 (α₃ ∼ 1.2, α₄ ∼ 4.0) to 2009 (α₃ ∼ 5.7, α₄ ∼ 42.6). The increase in skewness indicates the emergence of dominant mediators in 2009 in contrast to 2006. A similar analysis of the Department degree distribution across 2006 and 2009 resulted in (α₃ ∼ 1.2, α₄ ∼ 2.9) and (α₃ ∼ 2.30, α₄ ∼ 8.3) respectively. Therefore, the emergence of dominant mediating Staff was also accompanied by the emergence of dominant mediating Departments across the years. Ranking the Staff and Departments by their betweenness centrality scores revealed dominant mediating Staff emerging from dominant mediating Departments. The correspondence between the dominant mediators across scales may indicate that Staff with high betweenness centrality as possible mediators of inter-departmental collaborative grants that may demand complementary expertise and team-science.

As noted above, nodes that are highly connected need not necessarily be dominant mediators in a BRGC network. For the Staff network, we found the number of nodes with non-zero betweenness score was considerably lesser than the number of nodes with non-zero degree. Therefore, to obtain preliminary insight into this aspect we chose to determine possible overlap between the Top 20 nodes (i.e. STAFF20) ranked by their degree centrality (ST20^D) as well as betweenness centrality (STAFF20^B) across the years (2006 and 2009). For the Staff network, we found ∼60% overlap between (STAFF20^B and STAFF20D) for 2006. This percentage of overlap remained unchanged for the year 2009, although there was a marked change in the investigators in STAFF20^B and STAFF20D across the years (2006, 2009). The overlap list essentially consisted of senior faculty with a track record of funding and faculty from departments that are actively involved as collaborators in grants on a regular basis. A similar analysis for the Top 10 Departments ranked by their degree centrality (DEP10^D) and betweenness centrality (DEP10^B) revealed around ∼70% overlap in 2006 and ∼80% overlap in 2009. Unlike the Staff network, the Top 10 nodes in the Department network did not show any appreciable change across the years.

Perturbing the most-influential node

To obtain a better insight into the topological structure of the dominant cluster, we re-investigated its statistical properties after perturbing the node with the highest degree centrality (i.e. deleting the most-influential node). This was done independently across the hierarchically related scales (Staff, Department) and time (2006, 2009). As expected, perturbation of the most-influential node resulted in fragmentation of the network into mutually exclusive clusters. As earlier, the following discussion is restricted only to the dominant cluster identified from the mutually exclusive clusters. The resulting degree distributions are shown to the right of the unperturbed distributions in Fig. 2. The statistical measures (α₃, α₄) upon perturbation of the Staff network were (α₃ ∼ 2.5, α₄ ∼ 9.2) for 2006 and (α₃ ∼ 1.8, α₄ ∼ 7.2) for 2009, see Figs. 2b and 2d. Comparing these values to those estimated earlier on the unperturbed counterparts reveals marked change in 2009 as opposed to 2006. More specifically, targeted removal of the most-influential node seems to have a significant impact on the network topology in 2009 indicating possible hub-like behavior of this node. A similar analysis of the Departmental network for the years 2006 and 2009 resulted in values (α₃ ∼ 1.2, α₄ ∼ 3.6) and (α₃ ∼ 0.8, α₄ ∼ 3.0). This removal of the most-influential Department did not sufficiently affect the network’s statistical properties for 2006 whereas for 2009 the skewness and kurtosis were comparable to that of a symmetric distribution (α₃ ∼ 0.8, α₄ ∼ 3.0) indicating possible transition to classical random graph (Erdős–Rényi) [10] like behavior.

Discussion

The importance of team science and a shift towards collaborative research has also been embraced by major funding agencies and CTSA leadership. Network analysis has been identified as an important tool in assessing collaborations and team science by the CTSA key function committees. The present CTSA baseline study investigated the evolution of BRGC across multiple scales (Staff, Department) and time (2006, 2009) using the data retrieved from our internal research grant database ARIA. While the Staff network captured the collaborations between the principal investigators and co-investigators in a grant, the Department network specifically targeted inter-departmental collaborations with multiple Staff belonging to a given Department. To our knowledge, this is the first study on understanding the evolution of BRGC across scales and time. As noted earlier, BRGC networks have unique characteristics different from those of the established real-world networks. Therefore, extending some of the established theories of large real-world networks to BRGC networks may not be fairly straightforward. Our preliminary investigation BRGC networks revealed them to be disconnected with mutually exclusive groups and a dominant weakly connected cluster. Identifying these mutually exclusive groups and clusters may be an important step prior to developing suitable strategies for their possible integration with the dominant cluster. The clustering coefficient of the dominant cluster was found to increase with time in the Staff as well as Department network. This increasing trend is a potential indicator of improving collaborations as a function of time. While we did not observe small-world phenomena with this limited data, the increasing clustering coefficient certainly points towards this possibility. The degree centrality distributions were positively skewed unlike classical random graphs (Erdős–Rényi). Such positively-skewed distributions are usually accompanied by a small number of highly connected nodes orchestrating collaborations comprising the tail of the distributions. While it is tempting to conclude possible presence of power-law, the small size of the network and the lack of adequate information in the tail may challenge such conclusions. A perturbation approach was subsequently used to investigate the impact of the most-influential node on the network characteristics and statistical properties (skewness and kurtosis). The changes upon perturbation were especially evident in the Staff collaboration network indicating possible hub-like structures in these networks at the later date (2009) as opposed to the earlier date (2006). These influential nodes can prove to be effective dissemination points and can be useful in orchestrating new research collaborations across more distant entities in the weakly connected cluster. Our investigation also revealed that the betweenness centrality distribution to be positively skewed indicating prominent mediators in the BRGC network. Interestingly, we also found significant overlap in the dominant nodes ranked by their degree centrality as well as betweenness centrality. This behavior persisted at the Staff as well as the Department scales elucidating existence of possible inter-departmental collaborations that may be an outcome of complementary expertise and team effort approach in the funded grants.

Some of the limitations of the present study are as follows: (i) Percentage effort of the Staff in a given grant was not included. Percentage effort may be directly proportional to the extent or strength of collaboration in a given grant. Not accommodating this information implicitly assumes uniform strength across all the investigators. (ii) Exact time stamps as to when the investigators joined or left the grant were not included. This can have a profound impact on the overall success of the grant and possible future collaborations. (iii) The nodes in the Staff network were restricted solely to principal investigators and co-investigators. This implicitly assumes that the other Staff Roles do not contribute to the collaboration. (iv) Only one instance of collaboration between a given pair of Staff members was considered. Addressing the above limitations can certainly be useful in uncovering patterns not discussed in the present study. However, some of the results presented in this study are likely to persist across BRGC across similar settings. We believe that there are several grant databases that contains information similar to ARIA that may encourage a direct adoption of the presented approach. Further investigation can help in identifying universal characteristics that serve as benchmarks in assessing/evaluating BRGC. More importantly, these characteristics may elucidate a universal generating mechanism underlying BRGC networks and its evolution.