Improving Predictions in Imbalanced Data Using Pairwise Expanded Logistic Regression

Abstract

Building classifiers for medical problems often involves dealing with rare, but important events. Imbalanced datasets pose challenges to ordinary classification algorithms such as Logistic Regression (LR) and Support Vector Machines (SVM). The lack of effective strategies for dealing with imbalanced training data often results in models that exhibit poor discrimination. We propose a novel approach to estimate class memberships based on the evaluation of pairwise relationships in the training data. The method we propose, Pairwise Expanded Logistic Regression, improved discrimination and had higher accuracy when compared to existing methods in two imbalanced datasets, thus showing promise as a potential remedy for this problem.

Introduction

Many medical applications of machine learning classifiers attempt to identify rare events (e.g., readmission rates, adverse medical events) from large datasets^1,2,3,4,5. These datasets are highly imbalanced, with only a small minority of “positive” cases. Usually class imbalance is ignored when researchers choose a learning algorithm⁶. However, the performance of Logistic Regression (LR)⁷ and Support Vector Machines (SVM)⁸ can be significantly hindered by class imbalances^9,10,11.

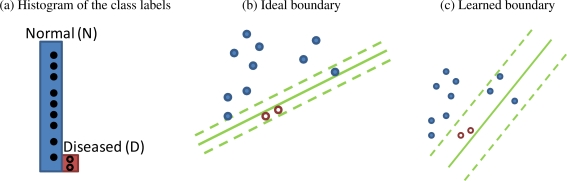
The class imbalance problem will likely become even more common as electronic health record (EHR) systems that routinely collect large volumes of patient information start to get used to study a wide range of diseases¹². The resulting datasets may be overwhelmed by the non-diseased or “normal” cases. The models created from these datasets can exhibit poor discrimination (e.g., predict most cases as normal) as well as poor calibration (e.g., scores are heavily biased towards the normal cases). Figure 1 illustrates an example when a soft margin SVM fails to distinguish the diseased cases from the normal ones because the soft margin SVM maximized its margin at the cost of a “small” total error.

Figure 1:

Learning a model from highly imbalanced training data may lead to significantly biased outputs. Classifiers like soft-margin SVM are often overwhelmed by the high percentage of normal cases, and classify everything as normal because the margin is maximized at the cost of small total error. (a) Class distribution in an imbalanced training set. (b) Ideal boundary of a soft margin SVM. (c) Learned boundary of a soft margin SVM.

To compensate for imbalanced data, naive methods such as oversampling the abnormal cases¹³ or undersampling the normal cases^14,15,16 have been used in practice. A major disadvantage of these approaches is that their results are non-deterministic¹⁷. This type of sampling may also introduce unacceptable errors when estimating the risk of diseases.

Alternative methods using neural networks (NN) have been suggested to tackle this problem^18,19. Ohno-Machado et al.²⁰ demonstrated that a hierarchical neural network approach could learn more accurately and in shorter training times than ordinary NNs. However, the performance of all these NN-based methods is limited because the backpropagation algorithm often converges to local optima.

Other systematic methods like cost-sensitive learning^21,22 could be helpful if the investigators clearly know the weights for type I and type II errors. Unfortunately, this is not always the case. Yet another approach to tackle the class imbalance problem is used in the Ranking Support Vector Machine (RSVM)²³, which is closely related to the approach we propose. RSVM takes pairs of training samples to construct an expanded training set from which it learns the partial ordering instead of class labels. However, RSVM only considers pairs of cases that induce a partial ordering (e.g., case A has a class label “1”, thus it ranks higher than case B, which has a class label “0”). Assume the dataset consists of |𝒟| diseased cases and |𝒩| negative cases, RSVM constructs and trains itself on an expanded training set of size 2|𝒟||𝒩|. Even though the size of this set is larger than that of the original training set (|𝒟| + |𝒩|), it still does not make full use of the information because it ignores pairs that share the same class label. In addition, calibration of an RSVM model is difficult. The model outputs cannot be interpreted as probabilities, even if they are normalized.

Our goal was to develop an approach to improve both the discrimination and predictive accuracy of models created from highly imbalanced datasets. In addition, we sought to minimize the effort required by users to apply and understand the new method. We hypothesized that we could create an approach based on ordinary logistic regression that utilized a pairwise expanded training set to improve handling of imbalanced data.

Methods

We developed a model that allows for classification of normal and diseased populations at a finer granularity. Specifically, we leveraged the logistic regression model to learn a fully pairwise-expanded version of the ordinary training set. Then, we computed a new observation’s class membership by synthesizing estimated similarity between the new observation and the ordinary training set. The rest of this section will introduce the details of our approach.

Notation

Conventionally, a training set is denoted as D = {X, Y}, where $\mathbf{X}={\left\{{\overrightarrow{X}}^l\right\}}_{l=1}^L$ represents features and $\mathbf{Y}={\left\{Y^l\right\}}_{l=1}^L$ represents their corresponding class labels. Here l is the index of data entries and L is the size of the training set. Note that X⃗^l = {x₁, . . . , x_i, . . . , x_n} corresponds to a n-dimensional feature vector. The training data can be further decomposed into the normal set (D^𝒩 = {X⃗^l, Y^l}_l∈𝒩) and the diseased set (D^𝒟 = {X⃗^l, Y^l}_l∈𝒟), depending on the class membership Y_l, e.g., Y_l ∈ 𝒟 if Y_l = 1, or Y_l ∈ 𝒩 if Y_l = 0.

Pairwise Expansion of Training Set

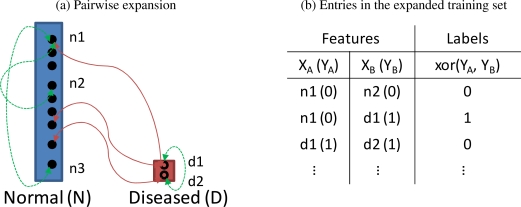
We used every possible pairwise combination (i, j) of the training data to construct the expanded training set as {[Xⁱ, X^j], xor(Yⁱ, Y^j)}. If the labels of two entries i and j agreed, their exclusive disjunction xor(·, ·) was 0, otherwise 1. Figure 2 illustrates the pairwise expansion procedure. Note that only a few pairs are shown for clarity.

Figure 2:

Visualization of the pairwise expansion. In (a), the green arrows indicate two data points agree with each other, thus xor(Yⁱ, Y^j)=0. The red arrows indicate two data points disagree with one another, thus xor(Yⁱ, Y^j)=1. In (b), we summarize the class labels of the expanded training set. Note that the number in the parentheses represents the class label of the corresponding case in each cell.

We denote [X⃗ⁱ, X⃗^j] as Z⃗^k and xor(Yⁱ, Y^j) as C^k. Then our new training set becomes $D*={\{{\overrightarrow{Z}}^k,C^k\}}_{k=1}^{\left(\begin{array}{c}L\\ 2\end{array}\right)}$, whose feature dimension is two times larger than that of D (i.e., Dim(Z⃗^k) = 2Dim(X⃗ⁱ), ∀k, i), and the size of the dataset equals $\left(\begin{array}{c}L\\ 2\end{array}\right)$, the number of unique data pairs.

The expanded dataset provides finer granularity of information when compared to the original training set that only depicts the class labels. Specifically, the expanded dataset describes the relationships between pairs, such as normal-normal, diseased-diseased, or one of each. The model built upon such expanded training set is thus capable of learning the similarity or dissimilarity on a case-by-case basis.

Model Formulation

Given D*, our model Pairwise Expanded Logistic Regression (PE-LR) learns a mapping f : Z⃗^k → C^k, where C^k ∈ {0, 1} is the class label and ${\overrightarrow{Z}}^k=<z_1^k,\dots ,z_{2n}^k>$ is the feature vector of an entry k. The model assumes a parametric form for the distribution P(Z⃗^k|C^k), which can be defined as:

$$P(C^k=0|{\overrightarrow{Z}}^k)=\frac{1}{1+\text{exp}(w_0+{\sum }_{i=1}^{2n}{w}_i{z}_i^k)},$$ (1)

$$P(C^k=1|{\overrightarrow{Z}}^k)=\frac{\text{exp}(w_0+{\sum }_{i=1}^{2n}{w}_i{z}_i)}{1+\text{exp}(w_0+{\sum }_{i=1}^{2n}{w}_i{z}_i^k)},$$ (2)

The above equations can also be expressed as a Generalized Linear Model (GLM) linked by a logit function:

$$\text{ln}\left(\frac{P(C^k=1|{\overrightarrow{Z}}^k)}{1-P(C^k=1|{\overrightarrow{Z}}^k)}\right)=w_0+\sum _{i=1}^{2n}{w}_i{z}_i^k.$$ (3)

The parameters W⃗ = {w₀, . . . , w_2n} can be estimated by maximizing the following equation using the Maximum Likelihood Estimation (MLE) criteria⁷.

$$\overrightarrow{W}\leftarrow {\text{argmax}}_{\overrightarrow{W}}\prod _k^{\left(\begin{array}{c}L\\ 2\end{array}\right)}P(C^k|{\overrightarrow{Z}}^k,\overrightarrow{W}).$$ (4)

The appendix displays the details of parameter estimation.

Model Testing

To test our model, we created an expanded feature set for each new data point X⃗⁺, and denoted it as F⁺ = {(X⃗*; X⃗⁺)|X⃗* = X⃗^l, l = 1. . . L}. Note that the test point contains the feature vector for the new case combined with the feature vector from one case from the training set. So each test case becomes L points in the test set, and each of these points has a dimension of twice the number of features, analogous to the expanded training set. The following function

$$P(\text{xor}(Y^l,Y^{+})=1|[{\overrightarrow{X}}^l;{\overrightarrow{X}}^{+}])=\frac{\text{exp}(w_0+{\sum }_{i=1}^n{w}_i{x}_i^l+{\sum }_{i=n+1}^{2n}{w}_i{x}_{i-n}^{+})}{1+\text{exp}(w_0{\sum }_{i=1}^n{w}_i{x}_i^l+{\sum }_{i=n+1}^{2n}{w}_i{x}_{i-n}^{+})},$$ (5)

estimates the probability for the exclusive disjunction (between the observed class label Y^l in the training set and the unknown class label Y⁺ of the new data point). As our goal is to estimate the probability of P(Y⁺ = 1|X⃗⁺), we need to integrate the probabilities of each pairwise comparison to get a final probability estimation. The following formula computes the marginal probability of Y⁺ = 1 conditioned on its feature set X⃗⁺, using estimated exclusive disjunctions between data points in the training set and the new data point.

$$\begin{array}{l} E(Y^{+}=1|{\overrightarrow{X}}^{+})\hfill \\ =\int P(\text{xor}(Y^l,Y^{+}),Y^{+}=1|[{\overrightarrow{X}}^l;{\overrightarrow{X}}^{+}]){\mathit{dY}}^{l}d\text{xor}(Y^l,Y^{+})\hfill \\ =\frac{1}{L}\sum _{l=1}^L[P(\text{xor}(Y^l=0,Y^{+})=1|[{\overrightarrow{X}}^l;{\overrightarrow{X}}^{+}])\hfill \\ +P(\text{xor}(Y^l=1,Y^{+})=0|[{\overrightarrow{X}}^l;{\overrightarrow{X}}^{+}])].\hfill \end{array}$$ (6)

This integration step sums up the contribution from all L points induced by the expansion procedure for each test point. If one of these L points was comprised of a training point X⃗^l (with a class label Y^l = 1) and the test point X⃗⁺, we could infer the probability of Y⁺ = 1 (conditioned on this particular feature [X⃗^l; X⃗⁺]) as the conditional probability of xor(Y^l, Y⁺) = 0. The reason is that xor(Y^l = 1, Y⁺) = 0 if and only if Y⁺ = 1. Similarly, we could infer the conditional probability of the test point’s class label Y⁺ = 1 as the conditional probability of xor(Y^l, Y⁺) = 1, given the corresponding class label Y^l = 0. The maximum likelihood estimator for Y⁺ = 1 conditioned on its feature set is thus the result of Equation 6.

Model Evaluation

In classification, the area under the ROC curve (AUC) is often used as a one-number summary of discrimination²⁴ as follows:

$$\text{AUC}=\int (\text{TPR})\hspace{0.17em}d(\text{FPR}),$$ (7)

where TPR indicates the true positive rate and FPR corresponds to the false positive rate at different cutoff points. That is, the AUC describes how well a model ranks diseased and normal cases. Ideally, if every diseased case is ranked higher than all the normal cases, the model has perfect discrimination. We thus adopted this measure to evaluate the model’s discrimination performance. To evaluate the model’s predictive accuracy, we used the Brier score²⁵, which measures the mean squared deviation between predicted outcomes for a set of cases and their outcomes. Note that a lower Brier score represents higher accuracy. This measure is closely related to the calibration of predicted outcomes.

$$ℬ=\frac{1}{L}\sum _{l=1}^L{(E(Y^l=1|X^l)-Y^l)}^2.$$ (8)

We used two real-world datasets, “Hospital Discharge” and “Myocardial Infarction” to evaluate the efficacy of our model. Along with Pairwise Expanded Logistic Regression (PE-LR), we compared four other models: Logistic Regression (LR), Support Vector Machine (SVM), Ranking Support Vector Machine (RSVM), and SVM training on imbalanced datasets proposed by Morik et al (Morik’s algorithm)²⁶.

Hospital Discharge dataset

The first data set was collected for predicting potential follow-up errors related to postdischarge microbiology results²⁷. It contains results for microbiology cultures performed at a teaching hospital in 2007. There are ten feature variables, of which eight are categorical and two are numerical. The target variable is a binary, and it corresponds to whether each observed case is a potential follow-up error. In 8, 668 cases, 385 were considered to be potential errors.

Myocardial Infarction dataset

The myocardial infarction dataset corresponds to clinical and electrocardiographic records collected by Kennedy et al.²⁸ to support early diagnosis of acute myocardial infarction. The data contains records of 500 patients admitted with chest pain to the emergency department of a large medical center in Sheffield, Great Britain. The feature size is 54, and the target is a binary variable indicating whether a patient had a myocardial infarction (MI). Table 1 summarizes both data sets.

Table 1:

Real-world data sets used. % POS indicates the percentage of positive cases.

Datasets	Features	Size	%POS
Hospital Discharge	22	8,668	4.5%
Myocardial Infarction	54	500	30%

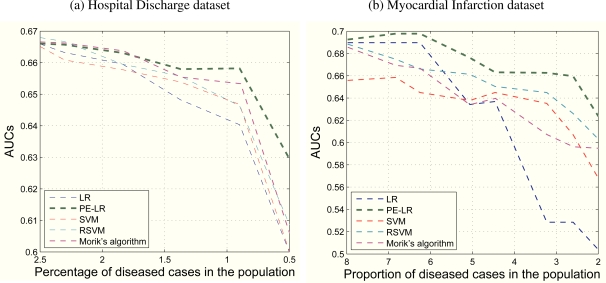
We divided both datasets into the meta-training and test sets using a random (20%/80%) split. Within the meta-training set, we separated the observations into normal and diseased populations. We adjusted the percentage of diseased cases in the training sets by gradually adding diseased cases to a fixed number of normal cases. Then, five types of models (LR, PE-LR, SVM, RSVM, and Morik’s algorithm) learned from these training sets were applied to the test set. The AUCs on the test set were computed and plotted in Figure 3 with the X-axis being the percentage of diseased cases in the training population. Note that we reverse the X-axis to show that LR and SVM deteriorated much faster than the other two methods. RSVM did slightly better but still not quite as well as PE-LR.

Figure 3:

AUCs of five models at decreasing percentages of diseased cases observed in the training population. Note that both figures were truncated on the left side to highlight the areas that show the differences.

Specifically, in subfigure (a), all five methods showed similar AUCs (0.665) at a 2.5% diseased rate in their training population. LR and SVM’s performances dropped down quickly as the percentage of diseased cases decreased. At a 0.5% diseased percentage, LR, SVM, RSVM, and Morik’s algorithm had AUCs below 0.6 while PE-LR’s AUC was 0.63. Similarly in subfigure (b), PE-LR outperformed LR, SVM, RSVM, and Morik’s algorithm consistently from an 8% diseased percentage to a 2% diseased percentage. At the extreme end of this plot, PE-LR still held an AUC of 0.63 versus LR (0.51), SVM (0.57), RSVM’s (0.60), and Morik’s algorithm (0.59). The PE-LR showed more stability under various percentages of the diseased cases in the training population. We performed a one-tailed paired-sample t-test against alternative hypothesis that the AUCs of PE-LR are larger than the AUCs of the other four models. As indicated in Table 2 and 3, the discrimination of PE-LR was comparable to RSVM and Morik’s algorithm for the hospital discharge dataset, but the improvements over LR and SVM were statistically significant (p < 0.05). For the myocardial infarction dataset, the improvements to all the other models were statistically significant (p < 0.05).

Table 2:

Results of a one tailed t-test that compare AUCs of different models using the hospital discharge dataset.

t-test	(PE-LR - RSVM)>0	(PE-LR - LR)>0	(PE-LR - SVM)>0	(PE-LR - Morik’s)>0
P-value	0.0634	0.0396	0.0493	0.1350

Table 3:

Results of a one tailed t-test that compares AUCs of different models using the myocardial infarction dataset.

t-test	(PE-LR - RSVM)>0	(PE-LR - LR)>0	(PE-LR - SVM)>0	(PE-LR - Morik’s)>0
P-value	0.0125	<0.0001	0.0012	0.0051

We also evaluated the Brier score, sensitivity, and specificity of all five models under extreme conditions (i.e., when a minimum percentage of diseased cases were included in the training set), as indicated in Table 4. Note that the sensitivity and specificity are obtained at cutoff points (i.e., points that maximize the Youden’s index) on individual ROC curves of these models. In the hospital discharge dataset, PE-LR showed the lowest Brier score (0.0803), the highest sensitivity (0.7464), and the second highest specificity (0.5737). In comparison, LR had a slightly larger Brier score and SVM based approaches (i.e., SVM, RSVM, and Morik’s algorithm) showed much larger Brier scores. Regarding the experiment using myocardial infarction dataset, PE-LR again showed the lowest Brier score (0.1765) and highest sensitivity (0.7674). Its specificity, however, is lower than three of the other methods (i.e., RSVM, LR, and Morik’s algorithm).

Table 4:

The Brier score, sensitivity, and specificity of all five models at the smallest percentage of diseased cases in the population. Note that the numbers in the parentheses are percentages of diseased cases included in the training sets.

	Hospital Discharge dataset (0.5%)			Myocardial Infarction dataset (2%)
	Brier Score	Sensitivity	Specificity	Brier Score	Sensitivity	Specificity
SVM	0.3684	0.6765	0.5370	0.4018	0.6536	0.4450
RSVM	0.2898	0.6634	0.5830	0.3460	0.6307	0.5067
LR	0.0812	0.6386	0.5560	0.1800	0.2320	0.8544
Morik’s algorithm	0.1160	0.6766	0.5673	0.3472	0.5948	0.5453
PE-LR	0.0803	0.7464	0.5737	0.1765	0.7674	0.4916

Discussion

This article describes a novel approach PE-LR, and compares it to several other learning models using class imbalanced real-world datasets. To better distinguishing negative cases from positive cases, we developed a pairwise expansion technique to exploit the relationships between every pair of observed cases. The experiments showed that PE-LR consistently outperformed LR, SVM, RSVM, and Morik’s algorithm in both discrimination and Brier score at various percentages of diseased cases.

Our results indicated that considering these types of relationships (i.e., normal-normal, diseased-diseased, and diseased-normal) between pairs of cases can result in models that can outperform existing approaches (e.g., SVM and LR that only deal with individual cases, and RSVM). Our method also distinguished itself from the RSVM as it made better use of the data by also evaluating relationships between cases in the same class. Our expanded training set considered every pair of cases, thus the total size is $\left(\begin{array}{c}\left|𝒟\right|+\left|𝒩\right|\\ 2\end{array}\right)$, assuming |𝒟| and |𝒩| are the numbers of the diseased and normal cases in the original training population. This size is much larger than 2|𝒟||𝒩|, the size of the training set constructed by RSVM, which only considers pairs that induce a partial ordering. By introducing more information from the training set (Equation 6), our model seems to be less susceptible to outliers and noise when compared to the simple linear weighting scheme (e.g. Y = W^TX) adopted in RSVM. Finally, our approach provided more accurate probability assessments than RSVM, as indicated by the Brier score results in Table 4.

Many medical datasets used to study readmission rates, adverse medical events, disease surveillance, etc. have imbalanced data. It is important to have not only good discrimination but also accurate risk assessment in learning models. Our approach, PE-LR, demonstrated the lowest Brier scores under extreme conditions in both experiments.

Despite these merits, we acknowledge some limitations and suggest possible extensions of this work. First, the pairwise expansion is an expensive operation, which could increase the size of the training set substantially. However, in many cases, this cost could be absorbed by pre-computing the expanded training set and storing the acquired model in memory. The testing phase can be quite efficient. However, an online setting scenario might introduce additional challenges, where new entries with labels enter the database periodically. In this case, models have to be updated quickly, and we cannot afford to pre-compute the entire model. If an approach could be designed to handle per-instance updates on the fly, our model could be applied more widely.

Additionally, this approach requires that the test case be transformed into L test points, and the estimates on these points combined to generate an estimate for the test case. Although it is not computationally expensive, it is not a simple application of an equation as in conventional LR. Furthermore, LR is a semi-linear model that cannot handle non linearly separable problems unless data are transformed in certain ways or interaction variables are used.

Finally, we estimate the exclusive disjunctions between pairs of cases. However, the outputs of such a function do not distinguish between these two situations: normal vs. normal and diseased vs. diseased, for which both are set to be equal to zero. This could be a limitation on the flexibility of PE-LR, as this representation does not capture the three states of pairwise relationships. A solution to this might involve kernel transformations, which we plan to pursue in future research.

In conclusion, we developed a new approach to tackle the class imbalance problem, which is frequent in medical datasets. Experiments using two real-world datasets demonstrated the performance advantage of PE-LR when it is compared to LR, SVM, and RSVM. We demonstrated improvement in both discrimination and the Brier score even in cases where the dataset was highly imbalanced. The proposed approach thus shows promise, although further research in this area is certainly warranted.

Appendix

Parameter Estimation

The description below is a slight modification of the regular parameter estimation in logistic regression.

Our goal is to infer the parameter set W⃗ = {w₀, . . . , w_2n} that maximizes the likelihood function represented by Equation 4. Because the natural logarithm does not change the parameters of the objective function (Equation 4), it is more convenient to deal with the following log-sum formulation (Equation 9) instead of the likelihood function defined by products (Equation 4).

$$\overrightarrow{W}\leftarrow {\text{argmax}}_{\overrightarrow{W}}\sum _k^{\left(\begin{array}{c}L\\ 2\end{array}\right)}\text{ln}P(C^k|{\overrightarrow{Z}}^k,\overrightarrow{W}).$$ (9)

We denote the log-likelihood function as $l(\overrightarrow{W})={\sum }_k^{\left(\begin{array}{c}L\\ 2\end{array}\right)}\text{ln}P(C^k|{\overrightarrow{Z}}^k,\overrightarrow{W})$. This function can be explicitly expanded as:

$$l(\overrightarrow{W})=\sum _k^{\left(\begin{array}{c}L\\ 2\end{array}\right)}\left[C^k\hspace{0.17em}\text{ln}P(C^k=1|{\overrightarrow{Z}}^k,\overrightarrow{W})+(1-C^k)\hspace{0.17em}\text{ln}P(C^k=0|{\overrightarrow{Z}}^k,\overrightarrow{W})\right],$$ (10)

which can be further reorganized using Equation 1, 2 as:

$$l(\overrightarrow{W})=\sum _k^{\left(\begin{array}{c}L\\ 2\end{array}\right)}\left[C^k(w_0+\sum _{i=1}^{2n}{w}_i{z}_i^k)-\text{ln}(1+\text{exp}(w_0+\sum _{i=1}^{2n}{w}_i{z}_i^k))\right],$$ (11)

where $z_i^k$ indicates the i-th feature of the k-th training point (i.e., a pair). Model parameters meeting the maximum likelihood criteria are estimated using the gradients, which are the partial derivatives of W⃗. Note the i-th component of the partial derivative is represented in the following equation:

$$\begin{array}{lll}\frac{\partial l(\overrightarrow{W})}{\partial w_i}\hfill & =\hfill & \sum _k^{\left(\begin{array}{c}L\\ 2\end{array}\right)}{z}_i^k\left(C^k-\frac{\text{exp}(w_0+{\sum }_{i=1}^{2n}{w}_i{z}_i)}{1+\text{exp}(w_0+{\sum }_{i=1}^{2n}{w}_i{z}_i^k)}\right),\hfill \\ \hfill & =\hfill & \sum _k^{\left(\begin{array}{c}L\\ 2\end{array}\right)}{z}_i^k(C^k-\widehat{P}(C^k=1|{\overrightarrow{Z}}^k,\overrightarrow{W})),\hfill \end{array}$$ (12)

where P̂(C^k = 1|Z⃗^k, W⃗) are predictions of Logistic Regression using the current W⃗ estimates. To consider w₀ (e.g., the intercept of a linear model) in the derivatives, we include an illusory $z_0^k=1$ for all data instances $k\in \left(1,\left(\begin{array}{c}L\\ 2\end{array}\right)\right)$. As the log-likelihood function (Equation 11) is concave, Equation 13 is guaranteed to converge if we keep moving towards the direction of the gradient, $\frac{\partial l(\overrightarrow{W})}{{\partial w}_i}$, in the following manner:

$$w_i\leftarrow w_i+\eta \sum _k{z}_i^k(C^k-\widehat{P}(C^k=1|{\overrightarrow{Z}}^k,\overrightarrow{W})),$$ (13)

where η denotes a constant step size.