Complex dynamics of semantic memory access in reading

Abstract

Understanding a word in context relies on a cascade of perceptual and conceptual processes, starting with modality-specific input decoding, and leading to the unification of the word's meaning into a discourse model. One critical cognitive event, turning a sensory stimulus into a meaningful linguistic sign, is the access of a semantic representation from memory. Little is known about the changes that activating a word's meaning brings about in cortical dynamics. We recorded the electroencephalogram (EEG) while participants read sentences that could contain a contextually unexpected word, such as ‘cold’ in ‘In July it is very cold outside’. We reconstructed trajectories in phase space from single-trial EEG time series, and we applied three nonlinear measures of predictability and complexity to each side of the semantic access boundary, estimated as the onset time of the N400 effect evoked by critical words. Relative to controls, unexpected words were associated with larger prediction errors preceding the onset of the N400. Accessing the meaning of such words produced a phase transition to lower entropy states, in which cortical processing becomes more predictable and more regular. Our study sheds new light on the dynamics of information flow through interfaces between sensory and memory systems during language processing.

1. Introduction

The high processing speed of the visual system contributes to form the experience that, in reading, information intake is almost instantaneous, and that the meanings of words are given to us as though they were part of the sensory input. That this is a phenomenological illusion can be seen by trying to approach a text in a foreign language sharing the same writing system as ours: although we may still be able to establish word boundaries, aspects of word-internal structure, and to some extent syntactic categories based on word-length cues, we will not be capable of assigning a definite meaning to words. This shows that word reading is rather a process that unfolds in time and that relies on the integrity of several interacting cognitive brain components dealing with specific levels of word representation [1].

Electroencephalogram (EEG) data provide detailed information on the time course of cognitive processing. A number of electrodes placed at the surface of the head can be used to record voltage changes while participants perform a task, such as silent reading. Averaging amplitude values over EEG segments time-locked to the onset of a stimulus of interest, such as a written word, produces subject-specific event-related potentials (ERPs) for a given experimental condition. Grand-average ERPs are obtained averaging over subject-specific ERPs. Importantly, EEG activity that is not time-locked to the stimulus must be quantified using different methods, such as frequency analyses of phase-locked responses and nonlinear measures of signal variability within a time series. Measures derived from the EEG have poor spatial resolution, as the transmission of electrical fields across distant regions of the brain (volume conduction) makes it impossible to provide unique solutions to the problem of reconstructing source activity from the observed scalp patterns.

Research using ERPs has provided increasing support for the notion that stages of word reading are mapped onto distinct phases of cortical processing. In a now classical experiment, Kutas & Hillyard [2] demonstrated that semantically anomalous sentence endings (‘He spread his warm bread with socks’) elicit larger negative-going modulations of the ERP relative to appropriate sentence-final words. The observed ERP waves peaked around 400 ms from word onset, hence the name ‘N400’. In the same experiment, it was shown that the N400 is not a generic response to deviant stimuli, and that its amplitude varies with the strength of the mismatch between the word's semantics and the sentence context.

Parallel to developments in ERP research on language processing, studies using intracranial recordings provided evidence that, within the ventral visual stream in the inferior temporal cortex, two anatomically adjacent circuits exist, carrying out different computations that contribute to visual word recognition [3–5]. Portions of the posterior fusiform gyrus respond preferentially to all types of letter strings but not to other visual stimuli, generating fast potentials that peak around 200 ms from stimulus onset. In more anterior regions of the fusiform gyrus, evoked responses are larger for content words compared with function words, they are absent for non-words and other visual stimuli, and they are reduced or abolished by semantic priming. Such potentials peak around 400 ms from stimulus onset, suggesting that the anterior fusiform gyrus is among the neural generators of the N400.

Written word comprehension, therefore, appears to rely on two coarsely defined processing stages, with likely further internal subdivisions and complications: (i) a modality-specific perceptual phase, indexed by a cascade of evoked responses in inferior temporal cortices between 100 and 300 ms from word onset and by scalp ERPs sensitive to word form features [3,6–9]; (ii) a conceptual phase that results in the activation or construction of word meanings, with evoked responses peaking at 400 ms in distributed perisylvian regions [10–14], generating the scalp N400. Semantic access introduces a flexible, context- and task-dependent boundary between (i) and (ii): during phase (i), semantic access may be initiated based on word envelope, graphemic familiarity and other pre-lexical cues [15] but only in (ii) access is completed and its outcome is used in discourse-level unification [16]. Thus, for the purposes of the present study, phase (i) may be best described as largely perceptual, and phase (ii) as largely conceptual.

Considerable progress has been made in mapping semantic memory access in brain space and time. However, much remains to be found out about the changes that accessing a word's meaning brings about in cortical dynamics. In this paper, we describe an application of tools borrowed from nonlinear dynamical systems theory to study fast changes in scalp EEG responses elicited by written words.

There are reasons, with associated methodological caveats, to apply nonlinear tools to the study of online cognitive change. That the brain is a system of coupled components interacting nonlinearly does not imply that its observable output is nonlinear too [17]. For instance, the amplitude of the N400 is an inverse quasi-linear function of word expectancy [18]. The usage of nonlinear methods should be justified by the data, rather than by claims regarding the underlying system's dynamics. When nonlinear interactions between neuronal sources are reflected in the EEG data, however—and this finds support in surrogate data testing [19–21]—a discerning combination of linear and nonlinear techniques is recommended. The argument that perturbations owing to noise may be mistaken for true nonlinearity does not apply to studies, such as the present one, using repeated experimental trials in which the effects of stochastic processes are controlled for by averaging, statistical testing and robustness analyses over neighbouring regions of a measure's parameter space [22].

In our study, subjects read sentences presented one word at a time on a display. In each trial, a word occurred that could either make its host sentence true (e.g. ‘In July it is very warm outside’) or false (‘In July it is very cold outside’) in a situation model barring unforeseen circumstances. Critical words were close associates (e.g. via the antonym relation), but their meanings had different consequences at the level of interpretation. This manipulation was intended to maximize our chances of eliciting post-access processes that were (i) diverging in the two experimental conditions, so as to induce a bifurcation in the system's dynamics, and (ii) closer to ordinary language comprehension, and therefore more ecologically valid than would be the use of pseudo-words or words making their host sentence senseless. Note that we do not commit to the assumption that the N400 here reflects sentence verification, for this has been shown to be incorrect [23].

We used ERPs to estimate the temporal locus of the boundary after which word meanings become available to be used in sentence-level unification. We tracked power changes in different frequency bands over time. Furthermore, we applied at each side of the boundary three nonlinear measures of predictability and complexity of the system's trajectory in phase space, reconstructed from individual EEG trials. The first measure is cross-prediction error (CPE), introduced by Schreiber [24] as a test of stationarity for time series, including physiological signals [22,25]. CPE is a measure of similarity between pairs of segments from a time series that are not necessarily adjacent in time. The second measure, known as auto-prediction error (APE), determines how accurately the upcoming temporally adjacent data point can be forecast based on the preceding section of the time series. Phase transitions are revealed by pattern changes in the two-dimensional CPE matrix, whereas non-stationary behaviour will produce changes in APE. The third measure—and the only complexity measure proper—is sample entropy (SampEn) by Richman & Moorman [26], intended as an improvement over approximate entropy [27–29]. SampEn quantifies, in a logarithmic scale and with a match tolerance (more in §2), changes in the recurrence rate of the system's states for successive dimensions of the phase space. Sample entropy is derived from Kolmogorov–Sinai entropy [30] via the Eckmann–Ruelle method [31]. Like the original measures, SampEn captures the irregularity or the rate of information generated by the system. However, SampEn is specifically designed to deal with finite samples of nonlinear processes.

2. Methods

2.1. Participants

Twenty-four right-handed native speakers of Dutch (13 female, mean age 22, age range 18–28) gave written informed consent and took part in the study.

2.2. Materials

We constructed 80 sentences in Dutch stating ordinary facts such as ‘In July it is very warm outside’. For each sentence, a false or implausible version was created by replacing a single non-final noun or adjective with another word of the same syntactic category, for instance, an antonym: ‘In July it is very cold outside’. Critical words (e.g. ‘warm’/‘cold’) were matched on average length in characters, lemma and word form log frequencies per million words (permutation t-tests, all comparisons p > 0.1) using the CELEX corpus for Dutch [32]. Two lists of sentences to be used in the EEG session were produced, each containing 40 items per condition (either the true or the false version of each sentence) and 160 fillers with variable syntactic structure, content and length. Critical sentences and fillers were preceded by a two-sentence mini-discourse, which was identical in the true and false conditions. After each trial, subjects could move on to the next one by pressing a key on a button box.

The present stimuli differ in some respects from the stimuli used in other N400 studies. First, the critical words used in the classical paradigm [2] are sentence-final words. Constraints on expectancy grow as the sentence unfolds word by word [33], whereas predictive contexts in the current design are identical across conditions, but vary unconstrained relative to critical words. Second, the critical words in a classical paradigm are equated for cloze probability, and anomalous words are random repairings within stimulus lists, such that the set of critical words remains the same, and only the context (as apt or unpredictive) varies across presentation lists. In the current study, processing trajectories have to be nearly identical up to word recognition, at which point they are expected to diverge. Hence, here the between-participant comparison of true and false words uses two different sets of words [34,35], which are nonetheless matched for length and frequency.

2.3. Recording

The EEG/EOG (electrooculography) was recorded using 32 sintered Ag/AgCl electrodes, amplified by a multi-channel BrainAmp DC system with a 500 Hz sampling rate, a low pass filter at 125 Hz, and a 10 s time constant. The EEG was sampled from 28 scalp sites, arranged according to the conventions of the American Electrophysiological Society: Fp1, Fp2, F7, F3, Fz, F4, F8, FC5, FC1, FCz, FC2, FC6, T7, C3, Cz, C4, T8, CP5, CP1, CP2, CP6, P7, P3, Pz, P4, P8, O1, O2. Two additional electrodes were placed on the left and right mastoids, the former serving as reference during the measurement. All channels were re-referenced off-line to a linked mastoid.

2.4. Event-related potentials

Segments were extracted from the EEG at each channel starting 200 ms before and ending 600 ms after the onset of each critical word, and were baseline-corrected using the 200 ms pre-stimulus interval. Artefact rejection was done in two steps: (i) trials containing activity exceeding a ±100 µV threshold were detected; (ii) segments containing eye movements were identified by means of thresholding the z-transformed values of the 1–15 Hz band-pass filtered EOG. Trials selected in steps (i) and (ii) were discarded. ERPs were obtained by averaging over trials in each condition for each participant separately. Grand-averages over participants were only used to produce figure 1. The onset of amplitude differences between conditions was estimated using the following randomization procedure [36,37]. ERP averages for each participant from both conditions were collected in a single set, which was randomly partitioned into two equally sized subsets. A dependent-samples t-test was used to compare the means of the resulting subsets. The procedure was repeated 10 000 times, and p-values were estimated as the proportion of random partitions that resulted in a larger t-statistics than the observed one. The first point in the time series showing a significant difference (at p < α = 0.05) between conditions in a cluster of two neighbouring centro-parietal electrodes was chosen as the onset of the ERP effect. Conversely, the last point in the ERP series with that property was selected as its offset.

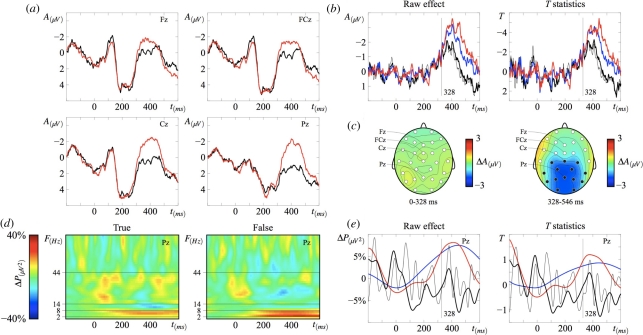
Figure 1.

(a) Grand-average ERP waveforms (N = 24) in the two experimental conditions from four electrode sites on the midline. The onset of critical words (‘In July it is very warm/cold outside’) is at 0 ms. The critical word that makes its host sentence false (‘cold’) evokes a larger N400 when compared with the true condition (‘warm’). (b) N400 effect in ERPs evoked by the critical word in the false minus the true condition (left) and t-values from time-resolved randomization statistics (right) for each midline electrode. The first data point at which the N400 effect is statistically significant over two neighbouring centro-parietal sites is at 328 ms and the last one is at 546 ms. (c) Topographic maps showing the mean difference between ERPs evoked by critical words in the false minus the true condition before (0–328 ms) and during (328–546 ms) the N400 effect, which is largest over electrode Pz. Dark circles represent the electrodes over which the effect is statistically significant. (d) Grand-average (N = 24) wavelet-based time-frequency representations (TFRs) from Pz showing a power increase in the false condition relative to the true condition and to baseline in the δ−θ (2–8 Hz) range, and a α (8–14 Hz) power decrease in the true condition relative to the false condition and to baseline. Both effects occurred after 328 ms. No other effects were found at higher frequency bands up to 125 Hz. (e) Raw power changes relative to baseline (left) and t-values from randomization statistics (right) at four selected frequency bands from Pz. (a) Black line, true; red line, false. (b) Red line, Pz; blue line, Cz; black thick line, FCz; black thin line, Fz. (e) Red line, 2–8 Hz; blue line, 8–14 Hz; black thick line, 14–44 Hz; black thin line, 44–80 Hz.

2.5. Time–frequency analysis

EEG time series from all channels was convolved with complex Morlet wavelets with a seven cycle width for frequencies ranging from 1 to 125 Hz in 2 Hz steps [38]. The resulting time–frequency representations (TFRs) were averaged over trials in each condition, for each subject separately. Mean power was expressed as a percentage change relative to baseline (−200 to 0 ms prior to critical word onset). Based on a visual inspection of grand-averaged TFRs, four bands containing qualitatively distinct patterns of oscillatory activity were identified: 2–8, 8–14, 14–44 and 44–80 Hz. The non-parametric randomization tests used for the statistical analysis of ERP data were applied to TFRs too. However, non-time-resolved average t-values in each of the two intervals (56–328 and 328–600 ms) and each of the frequency bands mentioned above were computed instead. The same procedure was repeated for the electrode Pz only, and the resulting t-values were used to calculate the per cent contribution of activity at Pz to overall phase-locked EEG activity.

2.6. Phase-space reconstruction

For each artefact-free EEG time series X = {x₁, … , x_n} (n = 400 time points), we reconstructed its phase space:

2.1

with i = 1, … , n − (m − 1)τ. Two parameters occur in this expression: the time delay τ and the embedding dimension m [39,40]. One way of estimating the optimal is to use the minimum mutual information [41] between the sets {x_i} and {x_i+τ}, for i = 1, … , n − τ. Once the delay is set, one chooses a range of values for embedding dimension and, for each m, one looks for close vectors in X(m,τ) that are no longer close in X(m + 1,τ). Those vectors are called ‘false neighbours’, and the optimal 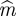is the one providing the minimum amount of them [42]. Instead of that procedure to estimate the embedding parameters τ and m, which does not take into account their correlation, we followed the Gautama–Mandic–Hulle (GMH) method based on the non-parametric Kozachenko–Leonenko (KL) estimator [43]

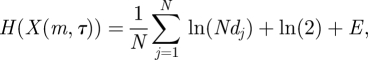2.2

where X(m,τ) is the phase space of reconstructed vectors, N = n − (m − 1)τ is the number of reconstructed vectors, d_j is the distance between the vector x_j and its nearest neighbour, and E is Euler's constant. GMH defines the ratio:

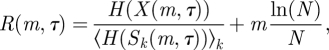2.3

where S_k are surrogates of X (see §2.10) preserving both its power spectrum and probability distribution [19]. The second additive term introduces a penalty for higher embedding dimensions. Thus, equation (2.3) is a standardization of the KL estimator that makes use of average estimate values over the reconstructed phase space for surrogates. The optimal 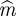and 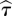are obtained as the minimum of R(m,τ), computed for each EEG time series, in each interval (56–328 and 328–600 ms) for the value ranges m = [1, 10] and τ = [1, 10]. The largest value of embedding dimension obtained across intervals, trials and participants was m = 3, and the most frequent time lag was τ = 1. The robustness of the nonlinear measures employed here was tested on other values of τ and m as well.

2.7. Time-series normalization

Each EEG time series was normalized by subtracting its running mean and then dividing the result by the time series' running standard deviation [24–25]. This standard procedure is applied to ensure that nonlinear measures are comparable across intervals in which the original time series exhibits different linear properties such as range of amplitude values, mean and variance.

2.8. Cross-prediction and auto-prediction errors

Given a time series X, we construct i equal-length windows W with size l in time points:

2.4

In a 1-step-ahead forecasting problem, one is interested in estimating w_k+1 given the subset W_ik = {w₁, … , w_k}, for k = 1, … , l − 1. In CPE, however, W_ik is not used as a prediction basin. Instead, the set W_jk, i ≠ j is used to calculate prediction errors. Given a pair of l-windows (W_i, W_j), i ≠ j, such that

2.5

and given the reconstructed vector subsets (see equation (2.1))

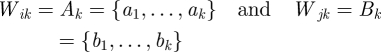2.6

an estimate for a_k+1 ∈ A (k = 1, … , l − 2) is defined as the mean 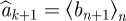over the index set n, such that ||a_k − b_n|| < ɛ. Estimates are computed on all B_k vectors that are neighbours of a_k by a tolerance ɛ. The calculation fails when a_k+1 has no ɛ-neighbours in B_k. In that case, we set 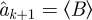. CPE is defined as

2.7

In general, γ(W_i, W_j) and γ(W_j, W_i) are evaluated in different vector subsets in phase space, hence γ(W_i, W_j)≠γ(W_j, W_i). However, if i = j, γ(W_i, W_i) is called diagonal prediction error or APE. APE fluctuations reveal non-stationarity in the time series [22,24]. We computed CPE and APE in each interval (56–328 and 328–600 ms), each subject and each condition, using 34 windows of length l = 4 time points. Average CPE and APE for each participant were compared between conditions using permutation paired-samples t-tests.

2.9. Sample entropy

Based on the vector subsets as reconstructed by equation (2.1), for each state x_i, we define its ɛ-recurrence set

2.8

where the tolerance is set to ɛ = 0.25 for the normalized time series. The probability distribution of x_i is given by

2.9

where # is the cardinality operator. The mean recurrence probability of a state in embedding dimension m is, therefore, 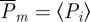. Performing the same computation for (m + 1)-embedding, we define sample entropy as

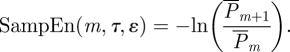2.10

Average sample entropy over trials for each interval (56–328 and 328–600 ms) was compared between conditions using permutation paired-samples t-tests.

2.10. Surrogate time series

Surrogates of the EEG time series X in the intervals 56–328 and 328–600 ms were constructed preserving the power spectrum and probability distribution of X [19], via the following iterative procedure. Given the time series' segment X = {x₁, … , x_n} (n = 136 points), we calculated its sorted values X_S and its discrete Fourier transform amplitudes:

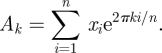2.11

We obtained X⁽⁰⁾ by performing a permutation of X without replacement and then we iterated the following steps: (i) we calculated the Fourier transform of X⁽⁰⁾ and replaced its amplitudes with the original amplitudes A_k; the resulting time series is denoted as X⁽¹⁾; (ii) we computed a probability distribution correction by applying to X⁽¹⁾ the rank ordering of X_s; the outcome is called X⁽²⁾. The first step, resulting in X⁽¹⁾, changes the probability distribution of the states; the second step, producing X⁽²⁾, changes the signal's power spectrum. Both steps are repeated until the error

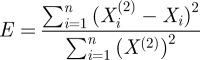2.12

is less than α = 0.05. For surrogates, CPE and APE were computed for m = 2 and τ = 1, and sample entropy was calculated for m = 3 and τ = 1. Nonlinear measures for the surrogates were compared with CPE, APE and sample entropy in the original EEG data using paired-samples permutation t-tests. The procedure was applied to X⁽¹⁾ and X⁽²⁾ surrogates separately.

2.11. Cross-measure correlations

Average values for each participant in each interval (56–328 and 328–600 ms) and each experimental condition were compared across the following measures: amplitude (µV), power (µV²) in four frequency bands (2–8, 8–14, 14–44 and 44–80 Hz), CPE, APE and SampEn. Four cross-correlation matrices were constructed, one for each combination of interval and experimental condition. Eight vectors (measures) with 24 elements each (participants) were fed intoa multiple rank-correlation test algorithm computing Spearman's ρ coefficient for all 8² pairs of measures. The resulting p-values were Bonferroni-corrected.

2.12. Further multi-electrode and moving-window analyses

Additional analyses with APE, CPE and SampEn were carried out using the methods described above on an extended set of electrodes—F7 (left frontal), Fz (midline frontal), F8 (right frontal), T7 (left temporal), Cz (midline central), T8 (right temporal), P7 (left parietal), Pz (midline parietal) and P8 (right parietal)—to determine the approximate topographic characteristics of nonlinear effects observed at Pz and associated with the largest N400 amplitudes, and to establish whether such effects are unique to the selected midline parietal site or whether instead they are consistent with a broader scalp pattern.

A moving-window approach was used to study the temporal evolution of nonlinear measures: starting from the pre-access interval (56–328 ms, see §3), a 272 ms window was moved forward in time in 10 ms (5 data points) increments, computing APE, CPE and SampEn for m = 3 and τ = 1 at each increment, to reach the post-access interval as a final window (328–600 ms).

3. Results

A larger N400 is evoked by critical words in false (‘In July it is very cold outside’) when compared with true sentences (‘In July it is very warm outside’; figure 1a). The effect shows a central–parietal topographic distribution, similar to what has been amply documented in the literature [2,34,35] (figure 1b,c). The earliest cluster of two neighbouring electrodes at which waveforms reliably diverge is at 328 ms (figure 1b), and the latest cluster is at 546 ms (t = −5211.9, p < 0.001). In the 328–546 ms window, the N400 effect has a symmetrical topographic distribution, with the largest difference over electrode Pz (figure 1c). Two aspects of ERP data were retained for subsequent analyses: (i) the estimated onset time of the N400 effect (328 ms), which will here be considered as a proxy of the time course of semantic memory access: by 328 ms, representations of the meaning of critical words have become available for further processing stages; (ii) the electrode at which the N400 effect is largest (Pz).

Two temporal intervals of equal size were defined at each side of the semantic memory access boundary: the first interval starts at 56 ms and ends at 328 ms; the second interval starts at 328 ms and ends at 600 ms; both intervals are 272 ms (i.e. 136 time points) long. These two windows correspond to a pre-access phase (56–328 ms), in which semantic memory access may be initiated, though processing will be primarily concerned with the visual, orthographic and phonologic aspects of word recognition, and a post-access phase (328–600 ms), during which word meanings are largely activated and participate in associative and combinatory semantic processes. In each interval, in addition to mean ERP amplitudes, we quantified modulations of the power spectrum over time, and we measured the signal's predictability and complexity using nonlinear methods. Our aim was to characterize the changes in cortical dynamics associated with semantic access, by comparing each measure's behaviour at each side of the 328 ms boundary.

Pre-access phase-locked responses produced no significant differences in power between true and false critical words¹ in any of the frequency bands (2–8, 8–14, 14–44 and 44–80 Hz) identified based on a visual inspection of TFRs at Pz (figure 1d; non-parametric t-tests, P > 0.1). Oscillatory activity is modulated by semantic access in the 2–8 Hz frequency range: power increases for false words (328–600 ms; t = 3795.6, p = 0.036) with a 5 per cent contribution of Pz to the overall EEG response pattern (t = 192, p > 0.1; figure 1d,e). Post-access power differences between true and false words were also observed in the 8–14 Hz band(t = 5752.5, p = 0.012), with a power decrease relative to baseline in true sentences (figure 1d), and a minor contribution from Pz (0.05%, t = 3.02, p > 0.1). Changes in EEG time-locked and phase-locked responses following semantic access, therefore, amount to an N400 amplitude increase and a δ − θ (2–8 Hz) power increase for false relative to true words [34,35], and an α (8–14 Hz) power decrease for true words relative to baseline and to false words.

We carried out further data analyses to determine whether these effects are the product of a linear Gaussian process—such as the gradual increase of activation levels in a brain network—or whether, instead, the underlying cortical dynamics displays complex nonlinear behaviour. For that purpose, the object of quantitative analysis is no longer the recorded EEG time series, but the trajectory of the system in phase space, reconstructed based on the observed data [39,40]. This requires the setting of two parameters: m (embedding dimension), i.e. the number of dimensions of the target space, equal to the length of the vectors whose elements (representing coordinate values in phase space) are drawn from the original time sequence; and τ (time delay), the distance in time points between each value in the original time series used as a vector element. We estimated the optimal m and τ (see §2.6) to be 3 and 1, respectively, we reconstructed the phase space for every individual EEG trial, and we computed mean prediction errors and sample entropies.

The results are reported in table 1 for neighbouring values of the reconstruction parameters, and shown in figure 2 for the optimal τ = 1 and m = 3. CPE increases from pre-access to post-access, but the change is significant only in the false condition. As can be seen in figure 2b, showing the reconstructed phase space for a pair of trials from both conditions exhibiting a prototypical N400 response, the system's trajectories in the false condition exhibit different attracting sets: pre-access and post-access processes occupy different regions in phase space. Such topological segregation of attractors is not seen in the true condition, and this is reflected in average CPE values (figure 2a and table 1). APE, represented by the diagonal array in CPE matrices (figure 2b), has a different pattern of effects: APE increases, though not significantly, for true words from pre-access to post-access, whereas it decreases post-access relative to pre-access in false words (figure 2a and table 1). Besides, a pre-access difference in APE between conditions was found (table 1). Sample entropy (SampEn, figure 2a) is similarly reduced following semantic access in false words (table 1). These results are robust across different values of the embedding parameters (table 1).

Table 1.

Summary of permutation statistics for CPE, APE and SampEn across different values of the reconstruction parameters time delay (τ) and embedding dimension (m). Numbers in cells are t-values. Statistical significance codes: *p < 0.05, **p < 0.01, ***p < 0.001.

			m = 1	m = 2	m = 3
CPE	τ = 1	True: 56–328 ms versus 328–600 ms	−1.3543	−1.5142	−1.478
		False: 56–328 ms versus 328–600 ms	−3.2905**	−2.57*	−2.3326*
		56–328 ms: True versus False	0.5302	1.0531	1.3844
		328–600 ms: True versus False	2.8991**	2.7086*	2.9771*
APE	τ = 1	True: 56–328 ms versus 328–600 ms	0.4425	−1.9503	−1.5131
		False: 56–328 ms versus 328–600 ms	2.8389*	3.3606**	2.8185**
		56–328 ms: True versus False	0.5743	3.2087**	3.2221**
		328–600 ms: True versus False	−1.3058	−0.9148	−1.6906
SampEn	τ = 1	True: 56–328 ms versus 328–600	−0.0968	0.3758	0.3409
		False: 56–328 ms versus 328–600	3.7623**	3.4942**	4.8056***
		56–328 ms: True versus False	1.2987	0.6903	1.0651
		328–600 ms: True versus False	−1.8001	−1.9114	−2.2903*
SampEn	τ = 2	True: 56–328 ms versus 328–600	−0.2457	0.5878
		False: 56–328 ms versus 328–600	4.1907***	4.264***
		56–328 ms: True versus False	1.516	1.7875
		328–600 ms: True versus False	−2.2594*	−0.8286
SampEn	τ = 3	True: 56–328 ms versus 328–600	−0.1012	0.825
		False: 56–328 ms versus 328–600	4.1582***	4.7972***
		56–328 ms: True versus False	1.7137	1.3771
		328–600 ms: True versus False	−2.1626*	−1.4607

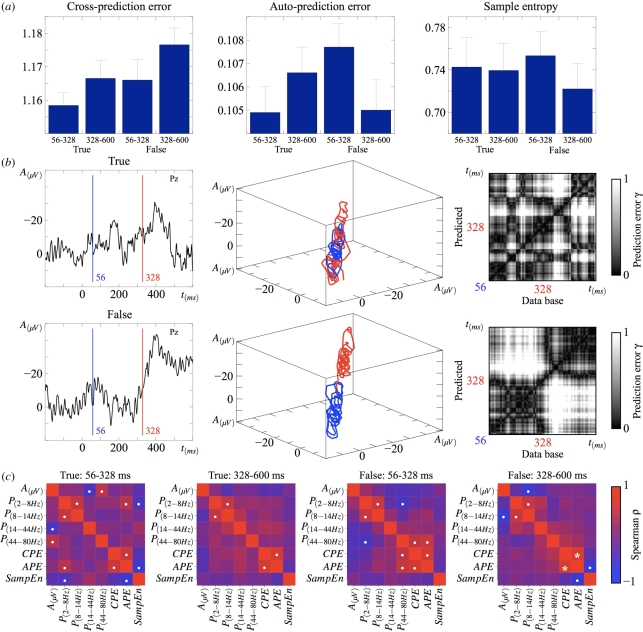
Figure 2.

(a) Mean (N = 24) cross-prediction error (CPE), auto-prediction error (APE) and sample entropy (SampEn) calculated for the optimal values τ = 1 and m = 3 in the two experimental conditions in two time intervals of equal size separated by the onset of the N400 effect at 328 ms. Whiskers represent standard errors of the mean. CPE increases significantly after 328 ms in false sentences. APE is largest before 328 ms in false relative to true sentences, and decreases in the second interval. SampEn is also reduced after 328 ms in the false condition only. These effects were significantly altered or eliminated in surrogate data preserving only the linear properties of the original signal. (b) Single EEG trials showing characteristic N400 responses from the two experimental conditions (left); reconstructed trajectories in phase space in the two intervals (blue 56–328 ms; red 328–600 ms) for τ = 1 and m = 3 (centre); greyscale matrices showing prediction errors normalized to [0 1] (right). (c) Cross-measure correlation matrices for Spearman's ρ. Dots indicate significant effects for uncorrected p-values. A positive correlation between APE and CPE after 328 ms in the false sentence passed Bonferroni correction (asterisk).

To show that the measures employed here are sensitive to nonlinear dynamics, we constructed surrogate time series [19,20] preserving both the power spectrum and probability distribution of the original EEG time series (X⁽²⁾ surrogates in table 2; see §2) or only its power spectrum (X⁽¹⁾ surrogates). CPE, APE and SampEn were computed for both surrogate types for τ = 1 and m = 3. Differences between surrogates and the original EEG data were found in most comparisons (table 2), and were especially strong for SampEn. Comparing pre-access and post-access intervals yields both qualitatively and quantitatively different effects than those seen in the original data (table 2). For instance, APE effects are reversed for both types of surrogates, and SampEn effects are reduced for X⁽²⁾ surrogates and disappear altogether for X⁽¹⁾ surrogates. These statistically significant differences entail a rejection of the null hypothesis of a Gaussian linear process measured by a monotonous function. This is a sufficient basis for claiming that the application of nonlinear measures was justified [20–21].

Table 2.

Summary of permutation statistics for CPE, APE and SampEn for τ = 1 and m = 3, comparing the original time series X with surrogates preserving only the power spectrum (X⁽¹⁾) or both the power spectrum and the probability distribution (X⁽²⁾) of X. Numbers in cells are t-values. Statistical significance codes: *p < 0.05, **p < 0.01, ***p < 0.001.

	Cross-prediction error	Auto-prediction error	Sample entropy
56–328 ms: X versus X(1)	2.5079*	−1.2955	−19.1824***
56–328 ms: X versus X(2)	3.4628**	−5.6917***	− 26.5761***
328–600 ms: X versus X(1)	2.4796*	−5.9648***	−20.3898***
328–600 ms: X versus X(2)	1.5396	−15.0138***	−17.0309***
X: 56–328 ms versus 328–600 ms	−2.332*	2.8185**	4.8062***
X(2): 56–328 ms versus 328–600 ms	−5.3173***	−4.9702***	3.6474**
X(1): 56–328 ms versus 328–600 ms	−3.7062**	−1.2848	0.8949

Multiple-correlation analyses (figure 2c) show that the different measures used here to detect and characterize change around the semantic access boundary (ERP amplitude, power changes, CPE, APE and SampEn) are statistically independent. The only correlation that passed Bonferroni correction was between CPE and APE post-access in false sentences (ρ = 0.681, S = 774, p = 0.0004). Prior to corrections for multiple comparisons, correlations between linear (amplitude and power) and nonlinear (CPE, APE and SampEn) measures were seen only in the pre-access interval. In particular, SampEn correlates with a linear measure in just one case: with δ − θ (2–8 Hz) power changes in the pre-access interval for true sentences (ρ = −0.419, S = 3263.128, p = 0.042 uncorrected). The effect persists using Kendall's rank correlation coefficient (τ = −0.302, z = −2.061, p = 0.039 uncorrected) but not using Pearson's correlation test (r =−0.108, t = 1.3711, p = 0.1842 uncorrected). Given the higher sensitivity to monotonic nonlinear relations between variables of ρ and τ over r, this effect shows the inverse correlation between δ − θ power and SampEn in the pre-access interval in the true condition is nonlinear in nature.

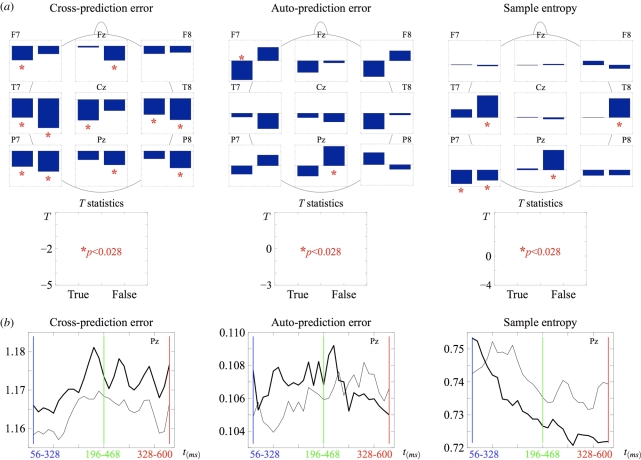
Multi-electrode analyses (figure 3a) show that, for CPE, the same effect observed at Pz—a larger CPE increase in the false than in the true condition—can be found at five other recording sites: the effect is largest at the electrode T7, over one known cortical source of the N400. As for APE, the only statistically significant difference between pre- and post-access in the false condition was found at Pz. A significant difference in the true condition can be seen at a left frontal site (F7), with a pattern that is identical to that observed at site Pz (figure 3a), albeit stronger: APE increases from pre-access to post-access. The same pattern of SampEn effects observed at Pz can be seen at two out of the three other recording sites at which significant effects were found. Taken together, these further analyses indicate that, where a broader topographic pattern is present, the nonlinear effects observed at Pz are consistent with it. We conclude that time series from Pz, selected based on N400 amplitude maxima in order to avoid the multiple comparisons problem that would arise from searching the entire electrode space, represent the most salient effects that can be observed in the analysed data.

Figure 3.

(a) Paired-samples t-tests comparing CPE, APE and SampEn values between pre-access and post-access intervals in the true and false conditions over nine scalp electrodes. Significance values passing Bonferroni correction are marked with an asterisk. (b) Results of a sliding-window analysis of Pz data using a 272 ms time interval moved forward in 10 ms (five data points) increments. Mean CPE, APE and SampEn (N = 24) were computed for the optimal values of the reconstruction parameters m = 3 and τ = 1 at each increment. The window centred on the 328 ms boundary is shown in green. (b) Grey line, true; black line, false.

A similar conclusion can be drawn in the time domain from the moving-window analysis. In figure 3b, the initial (56–328 ms) and final (328–600 ms) values of the data series are those shown also in figure 2a. Crucially, the direction of the effects remains stable throughout large portions of the original time series. This suggests that the effects reported above and in figure 2 are not an artefact of the chosen time intervals for pre- and post-access phases. Furthermore, CPE in the false condition peaks in a time window which is two-steps (20 ms) earlier than the one centred on the 328 ms boundary (196–468 ms), and APE peaks two-steps later than the intermediate window (196 –468 ms). This indicates that 328 ms, given the present experimental conditions and statistical sensitivity, is a reasonable approximation of the time at which the relevant phase transition may occur.

4. Discussion

Biological time series such as EEG signals typically fail to fulfil the requirements of low noise and long length, necessary in order to classify the system's dynamics via fractal dimension, Kolmogorov–Sinai entropy, or Lyapunov spectrum [21,22]. Nonlinear analyses of experimental data do not support inferences about chaos or the existence of strange attractors. Nonetheless, measures like CPE, APE and SampEn can be applied to short EEG time series to characterize transient changes in cortical responses associated with changes in linear measures such as ERPs. Given the vast parameter space within which nonlinear effects could be found, linear measures provide the necessary constraints to avoid a multiple comparisons problem, such as spatial and temporal information guiding the application of nonlinear measures. Conversely, it is also important to demonstrate that constraints from linear analyses do not bias inferences drawn from nonlinear measures, and that the latter do not just recapitulate the former. Here, we presented several further analyses addressing such potential pitfalls.

The nonlinear and linear measures employed here are statistically independent in our dataset. Moreover, nonlinear measures are sensitive to changes that are not reflected in ERPs and power spectrum above statistical threshold. Pre-access APE is larger for false than for true words, suggesting that the system starts to process the violation earlier than is revealed by amplitude or by power changes. The time course of this effect is consistent with a timely interaction of contextual expectancy and word form processing. In contrast with previous studies that relied on overt tasks to produce rapid lexico-semantic effects in evoked EEG and magnetoencephalography (MEG) responses [44–47], our APE data indicate that similar effects can be found also in the absence of a task. Higher mean APE values, in particular, suggest that a signature of word recognition in the pre-access interval for contextually unexpected words is a less predictable non-stationary signal [24]. This suggests either that during the early, largely perceptual phase, conceptual-semantic processing may occur, or that sensory processing is responsive to violations of sentence-level meaning. Both possibilities are consistent with interactive accounts of word processing, in which there is immediate and continuous exchange of information between sensory and memory systems.

CPE indicates that pre-access and post-access trajectories in phase space are less similar for the false word than for the true word, suggesting a more marked phase transition is brought about by accessing the meaning of a critical word that makes its host sentence false or implausible. Relative to the pre-access time frame, in the false condition, APE decreases while CPE increases: it is easier to forecast the next point in time, but more difficult to predict non-adjacent points. This dissociation of CPE and APE is not inconsistent with a positive ρ-coefficient, which emphasizes a different aspect of the statistical dependence of the two measures. This pattern of effects suggests that accessing the meaning of an anomalous word (e.g. ‘cold’ in ‘In July it is very cold outside’) produces a transition (increasing CPE) to a phase in which cortical processing is more predictable (decreasing APE) and more regular (decreasing SampEn) when compared with the pre-access phase.

5. Conclusion

In this study, we combined and compared linear and nonlinear measures to detect and characterize change in cortical activity following a critical cognitive event such as semantic memory access. We showed that activating the meaning of a word that makes its host sentence false produces a phase transition to lower entropy states, in which cortical processing is more predictable and more regular. In the target phase, the system generates information at lower rates compared with the stages preceding semantic access. This finding sheds new light on the dynamics of information flow through interfaces between sensory and memory systems in language processing, and may help constraining computational models of word comprehension.