Abstract
Brain–machine interfaces (BMIs) should ideally show robust adaptation of the BMI across different tasks and daily activities. Most BMIs have used overpracticed tasks. Little is known about BMIs in dynamic environments. How are mechanically body-coupled BMIs integrated into ongoing rhythmic dynamics, for example, in locomotion? To examine this, we designed a novel BMI using neural discharge in the hindlimb/trunk motor cortex in rats during locomotion to control a robot attached at the pelvis. We tested neural adaptation when rats experienced (1) control locomotion, (2) “simple elastic load” (a robot load on locomotion without any BMI neural control), and (3) “BMI with elastic load” (in which the robot loaded locomotion and a BMI neural control could counter this load). Rats significantly offset applied loads with the BMI while preserving more normal pelvic height compared with load alone. Adaptation occurred over ∼100–200 step cycles in a trial. Firing rates increased in both the loaded conditions compared with baseline. Mean phases of the discharge of cells in the step cycle shifted significantly between BMI and the simple load condition. Over time, more BMI cells became positively correlated with the external force and modulated more deeply, and the network correlations of neurons on a 100 ms timescale increased. Loading alone showed none of these effects. The BMI neural changes of rate and force correlations persisted or increased over repeated trials. Our results show that rats have the capacity to use motor adaptation and motor learning to fairly rapidly engage hindlimb/trunk-coupled BMIs in their locomotion.
Introduction
Brain–machine interfaces (BMIs) promise to provide, or augment, functions for spinal-injured patients (Hochberg et al., 2006; Acharya et al., 2008; Giszter, 2008; Scherberger, 2009). Successful BMIs require reliable neural decoding for stable behaviors, and/or a subject's adaptation of the interface across ongoing tasks. Different BMI control schemes might best fit different situations (Kositsky et al., 2009). To date, most efforts in BMI have used mechanically isolated contexts and concentrated on overtrained manipulation tasks of the forelimb (Chapin et al., 1999; Serruya et al., 2003; Velliste et al., 2008). They have mostly neglected locomotion, trunk, body, or substrate interactions (but see Fitzsimmons et al., 2009; Song et al., 2009). However, future BMI applications for lower limb control would require management of on-line motor adaptations and integration of lower limb BMI control into whole-body control.
The robustness of a BMI will depend on how reliably neuronal information can be used. The relative stability of cortical neural responses underlying similar behaviors remains an open problem (Fujisawa et al., 2008). Some studies suggest cells (prefrontal and M1) are functionally stable, and so BMI systems could maintain performance across days with the same decoder (Serruya et al., 2003; Greenberg et al., 2004; Chestek et al., 2007). However, significant neural plasticity (M1) has also been reported non-BMI force field adaptation experiments and in BMI systems (Li et al., 2001; Carmena et al., 2005; Zacksenhouse et al., 2007 ; Jarosiewicz et al., 2008; Ganguly and Carmena, 2009). Differential plasticity of different body representations and tasks might occur (Aflalo and Graziano, 2006; Chen et al., 2008). Furthermore, after overtraining, if switching among BMI controls is achieved easily, issues remain in integrating and adapting the controls to new tasks and mechanical contexts in activities of daily living. Conceivably, overtrained and specialized BMI designs and sophisticated decoding algorithms could affect or impede subsequent improvement of the BMI control in dynamic environments using intrinsic brain plasticity and adaptation. An alternative strategy might provide simpler interfaces (Fetz, 1969; Moritz et al., 2008) and allow the plasticity of the brain to adapt and incorporate the novel actions.
To test a trunk/hindlimb-based BMI framework in rats, we examined whether rats could learn to maintain their pelvis in a comfortable position using a novel BMI-driven mechanical action made available to them, to offset loading. Cortical modulations during locomotion in rats (Hermer-Vazquez et al., 2004) and other quadrupeds (Beloozerova et al., 2003; Bretzner and Drew, 2005; Drew et al., 2008a,b; Lajoie et al., 2010) are well documented, although rats are able to walk on flat surface after cortical ablations (Hicks and D'Amato, 1975). Nonetheless, trunk/hindlimb cortex in rodents may significantly impact recovery after spinal cord injury (Giszter et al., 2008, 2010). We chronically implanted tetrode arrays, to record single-neuron and multineuron discharge from trunk/hindlimb motor cortex in rats, during locomotion with a robot attached at pelvis, both to load the rat and provide BMI actions. As a BMI, we use a simpler interface strategy to generate a neural force from the robot, somewhat like Fetz and colleagues (Moritz et al., 2008). We tested this BMI in a dynamic environment. Rats were exposed to three conditions during treadmill locomotion: (1) control (baseline, no load), (2) simple elastic loading, and (3) BMI with elastic load in which BMI lifting control was made available in parallel with the elastic load used in (2). Our results will show that rats can adapt to these BMI actions, incorporate the BMI into their locomotion, and mostly offset an applied load. Cells recorded and used in the BMI show significantly different modulations during the adaptation processes in the BMI condition compared with loading alone.
Materials and Methods
Animals
Eleven adult female Sprague Dawley rats, weighing 250∼300 g, were used in these experiments. Seven rats meeting our criteria of good neural activity and consistent motivated locomotion on the treadmill provided the data set analyzed. Four rats not meeting these criteria were excluded from the analysis. Care and treatment of the animals during all stages of the experiments conformed to the procedures approved by the University Laboratory Animal Resources and Institutional Animal Care and Use Committee of the College of Medicine of Drexel University, and with established U.S. Department of Agriculture and U.S. Public Health Service standards.
Tetrode array fabrication
Neural activity was obtained with tetrodes organized in arrays. The tetrode arrays were custom-made by twisting or braiding four strands of polyimide-coated nichrome wires (13 μm outer diameter) together. Wires were cut with a sharp carbide scissor and left ∼2 inches long. Six tetrodes were attached around a spike-shaped tungsten shaft with microsuture thread. The final diameter of the tetrode array was ∼150 μm. The impedances of the tetrode wires were set around 1 MΩ at 1 kHz by controlled gold plating. The tetrode arrays were implanted in the trunk/hindlimb M1/S1 area of cortex in a region between −1.6 mm rostrocaudal (RC) and 2.0 mediolateral (ML) relative to bregma and the midline (see below).
Surgical procedures
Two implantations were performed in each rat consecutively in a single surgery. A pelvic orthosis implantation was performed first, followed by a cortical recording electrode implantation. Dexamethasone (5 mg/kg) was injected 12 h preceding the surgery to prevent brain swelling after opening the skull. Rats were anesthetized by using 1.0 ml/kg of a “KXA” mixture (dosage: 63 mg/kg ketamine, 6 mg/kg xylazine, 0.05 mg/kg acepromazine) initially and subsequently 0.38 ml/kg was administered each hour for maintenance of stable anesthesia. For pelvic implantation, a 1.5 cm angled incision (45°) was made on each side through the skin ∼1 cm behind the pelvic process. The skin around the incision was blunt dissected. The gluteus muscle was also blunt dissected toward the pelvic bone on each side to create a pair of windows for the implant. The implants, which should be perpendicular to the animal's pelvis and angled relative to one another, were placed under the bone of the pelvis on either side separately. The sides of the implant were pressed together as tightly as possible without bone trauma and fastened with screws. Finally, epoxy cement (J-B Weld) was applied to the joint where the pelvic implant parts were conjoined to fix the structure. This made it rigid and prevented any displacement as the animal moved after screw release. Implants integrated with the pelvic bone and provided a rigid frame for force application. This setup ensured the robot was able to apply forces effectively and directly to the skeleton.
After the pelvic implantation, the rats' heads were mounted in a stereotaxic frame and a round hole (3 mm in diameter) was drilled in the skull using a trephine. Three stainless-steel screws were placed around the hole evenly. Ketamine (24 mg/kg) was used for anesthesia maintenance after the skull was opened. After a window in the dura was removed, the tip of the tetrode array was lowered in the hindlimb/trunk region (2.0 mm lateral of the midline, 1.6 mm caudal to the bregma, and ∼1.5 mm in depth, to give recording sites at ∼1.1 mm depth). An exposed length of Teflon-coated stainless-steel wire was wrapped around a skull screw to provide the signal ground. Then, crumbled moistened Gelfoam was gently placed in the window in the skull to exclude the subsequently applied dental dement. Dental acrylic cement was built around the tetrode array and screws so as to firmly attach the electrode assembly in place and anchor it to the skull. After the cement was completely set, there were no sharp edges or cement crevices over or underneath the skin that could allow infections and irritate the animal. The skin was then loosely sutured around the cortical implant. The animal was then put back into the cage on a heating pad and observed until it was sternally recumbent. After the surgery, analgesics (Buprenex; 0.05 mg/kg) and antibiotics (ampicillin; 37.5 mg/kg) were administered to the recovering animals for 2 and 7 d, respectively. Recording began 7 d after implantations.
At the end of the final recording session, electrolytic lesions were made by passing 200 μA anodal current through one tetrode wire for 2 min. After injection of overdose anesthetic (Euthasol; 0.3 ml), the animal was perfused by using saline followed with 4% paraformaldehyde. Brain slices were cut in 40 μm sections to validate electrode placement using the electrode track and lesion area.
Neural recording and off-line sorting
Neural data were recorded using a Cerebus system (Cyberkinetics/Blackrock Microsystems) commencing 1 week after animals recovered from surgery. In each recording session, rats were first lightly anesthetized with isoflurane gas, and a unity gain preamplifier headstage (Neuralynx HS-27 micro) was connected with the tetrode array via flexible wire cables. After animals fully recovered on the treadmill surface, recordings began. Neural signals were bandpass filtered (300 Hz to 7.5 kHz) and digitized at a sampling frequency of 30 kHz. Spikes were detected on-line when above or under thresholding levels. The detected spikes could be automatically classified on-line after setting the templates of each waveform. The on-line sorted spikes were used in a BMI with elastic load control. The detected spike trains, as well as all the thresholded spike waveforms, were saved for off-line analysis. Multiple single units were isolated off-line using a commercial off-line sorter (Plexon Neurotechnology Research Systems) using the t-distribution expectation maximization sorting from features of the tetrode waveforms [an implementation of the approach of Shoham et al. (2003)]. The threshold interspike interval for a single unit was set at >1.6 ms. Only single units that were isolated by these criteria are presented here. Up to 24 channels of neural activity at a time in a single array could be recorded, and one or two individual cells from most wires of the tetrodes could be recorded. A total of 573 well isolated cells from seven rats recorded across 23 sessions from the M1/S1 trunk hindlimb area was used in our analysis. As there is no assurance that the spikes recorded on different days were the same, we did not track cells across days. We simply isolated cells afresh each day. We treated these isolations as different cells, although some of them had the same waveforms across days. However, we subsequently reviewed recordings off-line and confirmed that all statistics reported here remained significant if cells judged similar across days were instead treated as single cells (thereby reducing numbers of observed cells).
We also tested microwire arrays with 500–700 μm spacing between 16 wires in a 2 × 8 array in rats not reported here. The basic BMI observations reported here did not differ between the recording designs. However, levels of correlation among neurons after off-line sorting in the two recording methods were significantly different. Correlations were much lower in the microwire arrays. The analysis of correlation in Results and in Figure 10 holds only for the tetrode system recordings (see supplemental figure, available at www.jneurosci.org as supplemental material, showing microwire correlations).
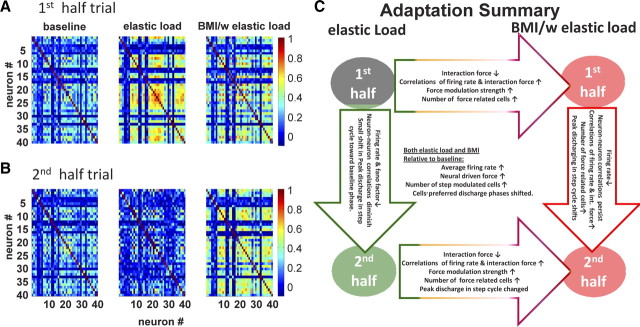
Figure 10.
Cell pair correlation coefficient and a sketch of the neural adaptation process. The cell pair correlation coefficient in half-trials across conditions (∼120 steps). A, The first half. B, The second half. The cell pair correlation matrix showed different patterns in different adaptation fields during locomotion. In the baseline condition (BL column), cell pair correlations showed a steady state across the whole trial (first half-trial vs the second half-trial). In the simple elastic load condition (E column), the cell pair correlations increased sharply in the first half-trial compared with baseline and then decreased to below the baseline condition in the second half-trial. In the first half-trial of the BMI with elastic load condition (BMI/E column), there was a moderate increase in the cell pair correlations compared with the baseline condition and the elastic load field condition, whereas in the second half-trial the cell pair correlations persisted rather than returning to the baseline condition like the simple elastic load condition. C, A simple diagram summarizes the overall neural modulation changes and differences that occurred under different field conditions and over time during the locomotion adaptation processes.
Robot controls and virtual forces
The detailed robotic BMI system has been described previously by Giszter et al. (2005). In brief, a Phantom 1.0 model A or T robot interacts with the rat as it walks on a treadmill. Mechanical interaction occurs through an implanted pelvic orthosis. The robot actions at the pelvis in this study were determined by the combination of two independent (stable) controllers, each of which emulates a passive viscoelastic system at any instance in time. Before the robot force fully engaged, there was a 2 s ramp period to minimize the interference to the locomotion of rats. The data in this transient period are not part of the analyses presented here. The control scheme of the robot is organized to manage the robot kinematic transforms and any other frame of reference transforms used for the controls. The viscoelastic controllers were added to a control stack, and the two were then combined to generate the interactions with the rat. In principle, in our robot system, there can be multiple instances of a given type of controller with different parameters on the stack. However, in this study, the design was simpler, with only fixed parameter single instances of the two qualitatively different controls (simple elastic load and BMI driven) combined in the design of our experiments:
Robot alone.
In experiments termed here “simple elastic load,” robot tip position/data and coordinate frame data were passed to the controller at each control cycle (1 ms), and force was computed and returned in the robot frame, according to Equation 1 below,. Forces were added from all controllers in the stack (one in this case), and the resultant was then transformed to torques and delivered to the robot motors.
BMI control.
In experiments termed here “BMI with elastic load,” neural information was used in this control. Neural spikes from each channel were sorted in real-time with multiple threshold windows on the Cerebus system (Cyberkinetics), and the identified binary spike-occurrence events sent to the corresponding robot controller via an RS422 serial port at each control cycle (1 ms). At the robot controller, the binary spike-occurrence data were masked for the individual controller, and a simple integration was used to obtain a scalar control variable. Spikes were aggregated in a 100 ms window to calculate the scalar variable. This was applied to the base control field of the controller to modulate the stiffness of the field following Equation 2 below. The stiffness of the neural driven elastic field (generating neural driven force Fn) was modulated by the aggregate firing rate of the masked channels, calculated according to Equation 2. The total interaction force (Ftot) was computed as the sum of the elastic force (Fe) and the neural driven force (Fn) as in Equation 3 below. This total force (Ftot) was then directly applied on-line by the robot control in effect.
where Ke and Kn are the stiffness of the elastic force (Fe) and neural driven force (Fn), respectively; Xe0 and Xn0 are the equilibrium positions set for the elastic and neural driven force fields, respectively; and X is the observed robot position. The neural multiplier parameter Naf is the aggregate firing rate, which is calculated as spike counts in the 100 ms integration window from all recorded channels chosen. We chose an elastic interaction to mimic muscle-like effects. The scalar control variable from neural activity could have been used to regulate force directly, to regulate position directly, whereas the elastic field method represents a muscle-like effect. For an elastic field interaction there are two options: we could regulate either the equilibrium position or the stiffness of an elastic field. We chose the stiffness modulation strategy in the BMI control here. We chose the elastic interaction method because we believed faster force or position transients in the other strategies might cause reflex responses and startle reactions and distract the attention or behavior of the rats using the neural firing rate to control the robot.
Virtual forces.
Using the neural activity in the simple elastic load, and applying this activity off-line after data collection in Equation 2, an instantaneous “virtual neural driven force” could be calculated at each time point: this was the instantaneous or momentary neural driven force that would have resulted if the neural control were in effect and the rat kinematic behavior were unaltered at that moment. In simple elastic load, Fn was zero in the on-line robot control—there was no neural force in the actual experiment. However, applying the virtual neural force estimation procedure, as in Equation 3, at each instant in time a “virtual total force” could be obtained for a simple elastic load trial: this was the total interaction force that would have resulted if the neural control were in effect and the rat's kinematic behavior were unaltered. Comparisons of the real forces, and the virtual forces were instructive in analyzing the rats' adaptations and BMI use.
Experiment design
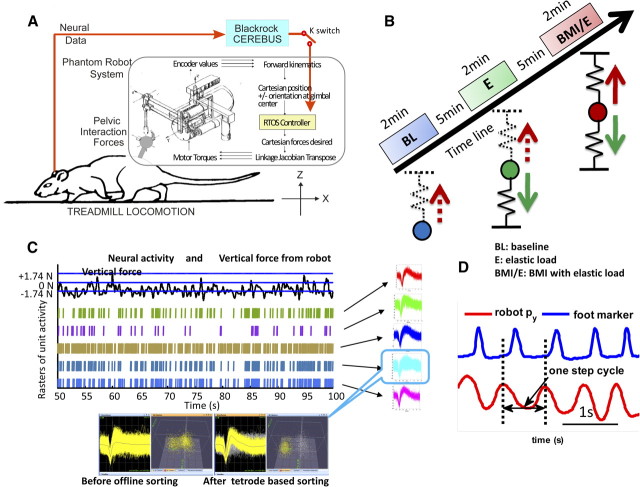
The rats were trained to walk on a treadmill. The robot position and force data were recorded simultaneously at 1 kHz for off-line analysis, together with synchronized recordings of neural activity (at 30 kHz). The speed of the treadmill, which was adjusted depending on the normal preferred walking speed of individual rats, was set in the range of 0.1–0.14 m/s, within which all rats preferred speed lay. One daily experimental session was divided into three trials: (1) baseline trial, in which rats walked on treadmill without any force; (2) simple elastic load trial, in which elastic force (Fe) was applied according to Equation 1; (3) BMI with elastic load trial, in which a neural driven elastic force (Fn) was combined with the above simple elastic force (Fe), and both forces were applied simultaneously. The speed of the treadmill was held constant throughout. The experimental setup and protocol are as shown in Figure 1. In our current experiments, the elastic force field used as a load field (Fe) was specified with a stiffness Ke of 50–90 N/m and by setting its equilibrium point 13 mm under the rat's normal pelvic height, whereas the neural driven force (Fn) with the potential maximum stiffness Kn of 200–450 N/m was used as lift by setting the equilibrium point 50 mm above normal pelvis height. Each session thus consisted of three 2 min trials of treadmill walking (∼120 steps) and 5 min intervals of rest that occurred between each trial. In total, 23 sessions or data sets were obtained in seven normal rats during different recording sessions. Our rationale was that rats will adapt locomotion in simple elastic load (2), thus expressing some differences in neural activity compared with baseline (1). In the BMI with elastic load (3), the BMI control was provided in parallel with the elastic load. The rat must adapt to both. In two additional rats, we performed repeated exposures to the sequence of three conditions on a single day to examine whether task repetitions in a day altered responses. We used these experiments to further test whether rats adapted to the BMI differently from load alone, and whether the differences might carry forward and be accentuated as rats experienced repeated sessions of load and BMI exposures in a single day. Figure 1 shows the setup and design of the study, and examples of data types.
Figure 1.
Experimental setup and training protocol. A, Rats were trained to walk on a treadmill with robot attached to the pelvis through a pelvic implanted orthosis, and neural activities were recorded from the motor cortex of the hindlimb/trunk area. The BMI could be engaged or disengaged (“switch K”) while a simple elastic load was applied to a rat. RTOS, Real-time operating system of robot. Blackrock Cerebus, Neural acquisition system. B, Training sessions were composed of three trials with 2 min baseline (BL), 2 min simple elastic load (E) trial, and 2 min BMI with elastic load trial (BMI/E) with 5–10 min resting time between trials. The elastic load on the rat and the interaction force differed in each case: in baseline there was no force, but kinematics of the pelvis were collected with the robot; in simple elastic load trials, interaction force was an elastic load (solid downward green arrow) and there was no BMI effect; in BMI with elastic load trials, interaction force was the sum of the simple elastic load (green arrow) and a neural driven BMI elastic force (solid red arrow). The neural driven force in the control was calculated from the aggregate firing rate in a 100 ms window, which modulated the stiffness of a lifting elastic field (solid red arrow) in BMI with elastic load condition. The instantaneous virtual neural driven force in baseline and simple elastic load could be calculated off-line from neural firing and kinematics (upward dotted red arrows). C, Individual neurons were detected based on the waveforms of the spikes and used in the BMI. The on-line detected spikes from five channels are shown before off-line sorting. One unit is shown before and after off-line sorted is shown below with the scatter plot of the first two tetrode principal components. Neural firing was recorded and could be correlated to kinematics or interaction forces when the rats adapted in different conditions. D, The step cycle was identified from robot tip motion py position (red), collected at 1 kHz, which corresponds to the pelvis lateral motion or step width, and this measure correlated well to video tracking as checked by toe marker from our video tracking system (blue).
Data analysis
Behavior performance criteria.
To date, most BMI systems tested use manipulation tasks of the forearm or a robotic upper arm “proxy,” and the performance of the behavior or BMI is defined by the successful correct hit rate for targets in the task. This requires skilled practice and overtraining of the animal. Currently, there is no similar criterion for the performance evaluation of locomotor BMI systems available. It is known that most animals pick speeds, gaits, and kinematics in locomotion that minimize energy usage or neuromuscular “effort” (Cavagna et al., 1977). Thus, we used the following criteria for the evaluation of performance: (1) the real (total) interaction force of the robot with the rat, which is a load that we expected the rat to seek to minimize and which was directly observed, and (2) the real neural driven force contribution, and (3) the virtual neural driven force and (4) the virtual total interaction force from application of Equation 3 to neural data collected in simple elastic load. These two latter were purely virtual forces derived from recordings for the simple elastic load condition in which the BMI control was not engaged, a type of analysis strategy that has been used in virtual sensory tracking (Suminski et al., 2009). In contrast, (2) was a real neural driven force for the BMI with elastic load condition. (All were calculated by using Equation 2 in conjunction with the kinematics and activity of the recorded channels of neural data chosen for the BMI.) Force patterns through a step cycle were also calculated as in Figure 2C.
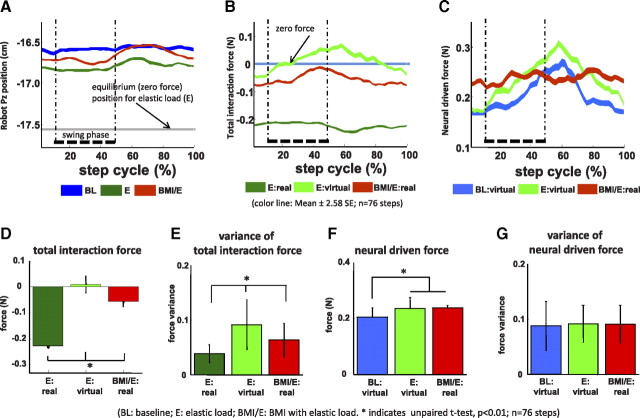
Figure 2.
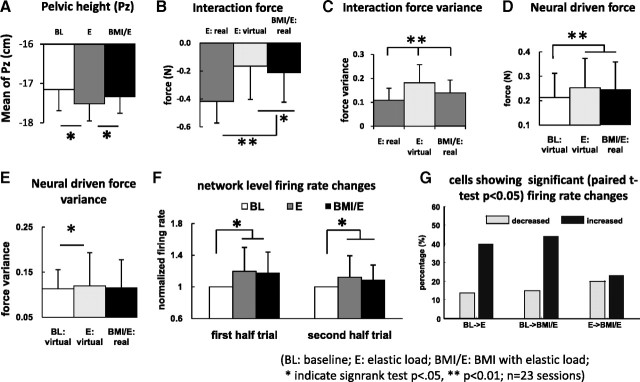
Example of robot position patterns and forces patterns in one session in a rat (also shown in Figs. 4, 5, data). BL, Baseline; E, elastic load; BMI/E, BMI with elastic load. A–C, The average robot position (A), total interaction force (B), and neural driven force (C) in the step cycle (n = 76 steps) showed different patterns in the baseline, simple elastic load, and BMI with elastic load conditions. The equilibrium position of the load field (A, gray line) for the elastic load field in simple elastic load and BMI with elastic load conditions is shown in A. The thick dotted vertical lines correspond to the right leg swing phase in the average cycle. Colored ribbon lines shown corresponds to mean ± 2.58 SE. The rat showed more normal pelvic kinematics and less loading in BMI/E compared with E. D–G, Comparisons of mean and variance of interaction forces and neural driven forces in step cycle (n = 76 steps). D, There was a significantly decrease in the BMI with elastic load trials in mean interaction force compared with the preceding simple elastic load trials. The average total virtual interaction forces in simple elastic load (E:virtual), which were calculated by supposing the rats engaged in BMI with elastic load, were also significantly different from the real interaction forces in BMI with elastic load trial. E, The variances of the interaction force under elastic load and BMI with elastic load conditions were also significantly different and were highest in E:virtual. F, The mean virtual neural driven forces in baseline were significantly different from the mean virtual neural driven forces in simple elastic load and the mean real neural driven forces in BMI with elastic load. G, The variances of the neural driven forces were not significantly different (p > 0.05) between simple elastic load, baseline, and BMI with elastic load conditions. Statistics was applied by two-sample t test (*p < 0.01; n = 76 steps). Thus, the different offset of force and reduced variance of interaction force seen in BMI with elastic load compared with E and E:virtual was likely attributable to specific coordination patterns, as suggested in C. Error bars indicate SD.
In other BMI work, it has been reported that cells in animals using a BMI showed both long-term and shorter-term changes (Wirth et al., 2003; Okatan et al., 2005; Jarosiewicz et al., 2008; Ganguly and Carmena, 2009; Carmena and Ganguly, 2010). However, the adaptation of human locomotion to altered split treadmill behaviors can be mostly achieved in around a hundred steps (Lam et al., 2006). We used these observations to guide our data analysis. To see how cells adapted and modulated their activity with the passage of time spent in each trial condition, we divided trials in two halves, each containing >100 steps.
Parameters of the firing pattern of the cell.
The modulation characteristics of each cell in step cycles and through adaptation processes were examined using the following: (1) average firing rate; (2) Fano factor, which is a statistical measure of the dynamics of the firing rate of a cell (Churchland et al., 2010); (3) correlation coefficient calculated between the rates of cell pairs; (4) correlation coefficient of the firing rate of cell with kinematics or kinetic parameters; (5) strength of relationship to interaction force amplitude; (6) peak firing phase in a step cycle; and (7) phases that “bursts” (defined below) spanned in a step cycle.
- Average firing rate was calculated as follows:
where N(n) is the spike counts in 100 ms time window and M is the total window sample number.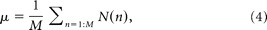
- Fano factor is defined as follows:
where σ2 is the variance and μ is the mean of a random spike count process, here in a 100 ms time window. μ was defined as in Equation 4.
- Correlation coefficient (ρij) of firing rates for cell pairs (i,j) was defined (Mazzoni et al., 2007) as follows:
where Ni(n) and Nj(n) are firing rate computed as spike counts in 100 ms time window, μi, and μj donates the mean value in a trial for neuron i and j, respectively. After testing with different length windows and considering the bins used in decoding, we set the window length to 100 ms (following Song et al., 2009). This window length was used when calculating the average firing rate, the cross-correlation coefficient among cell pairs and between cells and other movement-related variables.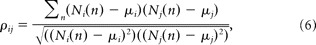
- The correlation coefficients of the firing rate with the movement parameters were defined as follows:
where Nj(n), μj are the same as in Equation 6. Ki(n), ki are movement parameters (e.g., position Px, Py, Pz) averaged in the same 100 ms time window and the mean of these parameters in a trial, respectively.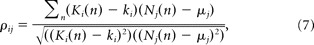
Strength of relationship to interaction force amplitude was defined as the best-fitted “slope coefficient” of the linear regression of the firing rate of a neuron with the robot–rat interaction force amplitude (for example, as in a typical session shown in Fig. 8A).
Peak firing phase was defined as the step phase in each step cycle, where neurons peak of firing rate occurred.
Bursts were defined as periods in which firing rate exceeded 75% of the difference between the maximal and minimal frequencies in the poststep phase histogram (PSPH) following Beloozerova et al. (2003). The step phases spanned by bursts of a cell were examined.
Figure 8.
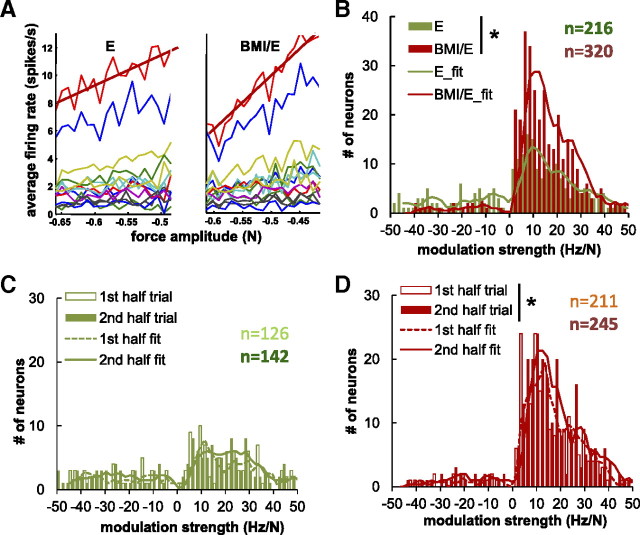
Force/rate amplitude modulation examined in detail. A, The firing rate of cells demonstrated linear correlation with force amplitude as seen in a typical session (same data set as in Fig. 4). The modulation strength was calculated as the linear coefficient of regressed firing rate with force amplitude (slopes of the regression, red lines). B, The complete population of neurons: The numbers of neurons with significant rate modulation with force amplitude was observed to be much larger in BMI with elastic load condition than in the simple elastic load condition. More cells were force amplitude modulated under BMI with elastic load condition (320 of 573) than under simple elastic load (216 of 573) condition. C, D, The distribution of modulation strength under simple elastic load condition (C) and under BMI with elastic load condition (D) in successive half-trials. Significantly more cells became significantly force related in the second half of the trial in BMI with elastic load condition (from 211 to 245) than were significantly force related in the first half of the trial (D) (binofit, p < 0.05). In contrast, this change was weaker under simple elastic load condition (from 126 to 142) and not significant (C) (*binomial test, p < 0.05).
In addition to the above single-cell level firing patterns, we also calculated how the firing pattern changed at the high population or network level. Similar to Mazzoni et al. (2007), aggregate firing rate and average cell pair correlation coefficients were calculated by averaging, respectively, the firing rates of all the cells and the correlation coefficients of all the cell pairs (ρij) in each trial.
Relationships of peak firing phase and burst spanned phase in the step cycle.
As limb and body kinematics are rhythmic during locomotion, it is to be expected that firing pattern of cells may also show some rhythmicity and consistent phase relationships. Modulations of cell firing with the step cycle and with the interaction force pattern in the step cycle were calculated. The step cycle was derived from the robot position parameter py, which corresponds to pelvic lateral motion. This is precisely synchronized with step phase during normal walking. To identify step cycles from interactive robot motion, the parameter py was first bandpass filtered (Butterworth, 0.3∼5 Hz). One step cycle was then identified by two consecutive peaks or valleys of the filtered py. This estimate of step phase matched well with foot marker motion and toe touch when checked with the video tracking system (95% step cycles from video match with step cycles from robot with an accuracy of ±0.01 step cycle). To remove anomalous or outlier steps, step cycles obtained in this way that lay outside 2 SD of the mean value were discarded from the subsequent calculations. Then, each step cycle was divided into 50 equal bins and these phases were used for statistical analysis. The PSPH was calculated from 40 to 100 steps to examine parameters relative to step phase. The phases spanned by the burst activity were tallied and the distributions of numbers of burst occurrences in each phase were obtained. The normalized PSPH in a step cycle was calculated by applying a scaling and offset that resulted in mapping the firing rate between minimum and maximum to the range of 0 to 1. The population average (mean normalized firing pattern) of this measure in each step was calculated, as shown in Figure 3. We also examined the peak firing phase and phases spanned by the burst.
Figure 3.
Changes of force and variance of pelvic motion (Py) and mean neural firing rates across all rats and sessions. A, The rats in simple elastic load (E) showed a significantly depressed pelvic mean position, compared with baseline (BL), whereas BMI with elastic load (BMI/E) showed a height that was not significantly different from baseline but significantly different from E. The rats in BMI with elastic load normalized pelvic height. B, Mean interaction force loading in E was significantly greater than in BMI/E:real and also greater than the calculated E:virtual. C, Interaction force variance in E:virtual was greater than either BMI/E:real or E:real. D, Mean neural driven force in BMI with elastic load matched E:virtual neural driven force. Both were significantly larger than baseline (BL:virtual) neural driven force. E, E:virtual neural driven force variance was significantly greater than baseline virtual force (BL:virtual) but not BMI with elastic load (BMI:real). F, Mean neural firing rates normalized to baseline in both the first half-trial and second half-trial differed significantly in E and BMI/E compared with BL, consistent with D (neural driven forces). Both were slightly but not significantly reduced in the second half-trial compared with the first. Differences were tested by signed rank test in A–F (*p < 0.05; **p < 0.01). G, Individual cell significant rate changes obtained with paired t tests showed high percentages of cells with significant rate increases (>40%) compared with decreases (>20%) from BL to E and BL to BMI/E, but ∼25% increase and 25% decrease in comparisons from E to BMI/E. The mean and variance of the interaction forces and neural driven forces in step cycle across all sessions and rats showed similar patterns of variation and statistics as in the single trial in Figure 2 (Fig. 2D–G), except that the variance of the neural driven force also showed some differences. Neural rates showed changes consistent with these effects. Rats in BMI with elastic load normalized their pelvic height kinematics, but at the same time increased neural firing rates and reduced interaction force loads, thus differing from both simple elastic load and baseline in various ways. Error bars indicate SD.
Statistical analysis.
To know how firing rate modulation changed under different conditions or in different training conditions, the following statistics were used: (1) circular Rayleigh tests (Fisher,1996) were used for testing the significance of the uniform discharging of cells versus directional discharging in a step cycle (Drew and Doucet, 1991; Berens, 2009). A modality test was performed on the step phase to estimate the number of modes. The test was based on kernel density estimate method with von Mises distribution as a kernel (Fisher, 1996). These were used to test whether the mean firing phases under two conditions were different or not using the Watson–Williams test (Fisher, 1996) (MATLAB). Watson's U2 statistic was computed as a goodness-of-fit test statistic to obtain p value through a bootstrapping procedure. (2) A paired t test was used to see whether the firing rates and correlation coefficient of a cell were significantly different or not under different conditions and whether force pattern (mean or variance) changed or not, and a circular t test (Fisher, 1996; Berens, 2009) was used when examining step cycle data. (3) Two-sample Kolmogorov–Smirnov tests (kstest2, MATLAB) were performed to compare whether two conditions variables were likely to have come from the same continuous distribution or not. All the significance levels of the above tests were set at 0.05, unless stated otherwise. (4) Regressions were analyzed by using the statistics toolbox (regression, MATLAB). (5) Variance comparisons occurred as follows: We found that interaction force data was non-Gaussian, so F test comparisons were not strictly applicable and somewhat suspect. Accordingly, comparisons of variance of neural firing, real and virtual neural driven force, and real and virtual interaction forces were made by obtaining the variance of each single trial and then using a paired nonparametric rank test (signrank, MATLAB) to compare the populations of such variances. (6) A runs test was used to check whether there was significant structure in changes in the force pattern in a step cycle among conditions (runstest, MATLAB). All data analysis was performed using MATLAB.
Results
We wanted to test whether the rats could learn to maintain their pelvis in a comfortable position using a BMI. We recorded kinematics, interaction forces, and neural activity as the rats walked on a treadmill in three conditions: (1) baseline (no load), (2) simple elastic load, and (3) BMI with elastic load. In the last condition, the BMI was engaged during locomotion, and the recorded neural activity modulated the stiffness of an elastic field [applied in parallel with the same elastic load as in (2)], which could consequently (potentially) offset the simple elastic load. A total of 573 isolated cells was recorded from the M1/S1 trunk hindlimb area (coordinates, 1.6 mm RC and 2.0 ML) in seven rats during these experiments and were used in the analysis here. We examined the load and firing pattern changes that occurred between the first half of the trial and the second half of the same trial, in addition to calculating the average changes that occurred between the three different conditions in trials in individual rats and across all tested rats.
We hypothesized that, if the rat used and incorporated the BMI actions effectively, it would offset the load and maintain pelvic height, and also that the load offset and neural activity expressed would differ from that observed in the previous elastic load trial activity and the rat's adaptation to it.
Load offset in the BMI with load condition
What happens to the rats' interaction forces with the robot across the three conditions? In particular, is a rat able to adapt to the BMI used to offset load? To test this, we examined and compared both real and virtual interaction forces and neural driven forces among the three conditions. Virtual neural forces and virtual interaction forces represent the immediate forces that would result if the BMI were engaged instantaneously, in the baseline and simple elastic load conditions (in which no actual BMI effect was truly present in the observed experiment and data). Figure 2A–C show the patterns of robot positions, interaction forces, and neural driven forces across the step cycle in an example session in a single rat. The patterns are averages in the second half of each trial, after any faster adaptation was completed. These differed during the different conditions. The rat pelvic height (Fig. 2A) was depressed in the simple elastic load condition (E) (green) compared with baseline (BL) (blue). In the BMI condition (BMI/E) (red), the rat showed less depression of pelvic height across the step cycle (and no depression in some phases). The load the rat experienced in the step cycle was obviously zero in the unloaded baseline (Fig. 2B, blue). It was large in the simple elastic load (Fig. 2B, dark green trace) and smaller in BMI with elastic load (Fig. 2B, red trace). This was a significant mean difference (Fig. 2D, E-real and BMI-real). Figure 2C shows the real BMI neural driven force in this rat, compared with the virtual neural driven forces that would have resulted if the BMI was momentarily engaged for baseline and simple elastic load. These virtual neural forces also allow calculation of “virtual interaction forces” (obtained as described in Materials and Methods). As described above and in Materials and Methods, virtual interaction forces represent the total robot forces on the rat that would result if the BMI were engaged instantaneously in baseline and simple elastic load conditions (in which no actual BMI effect was truly present in the real experiment and data). When we calculated the virtual neural driven interaction forces for simple elastic load (Fig. 2B, light green), we observed that this derived variable showed reversals of the sign of the virtual interaction forces across the step cycle. The animal would have experienced both load and lift forces from the robot, a result that was never seen in the actual BMI condition (Fig. 2B, red), and in addition the virtual forces had larger peak-to-peak excursions than real BMI forces. Furthermore, in BMI, the neural driven force contributions themselves were less variable across the step cycle than the virtual neural forces calculated for either baseline or simple elastic load (Fig. 2C). Figure 2D–G shows the statistics of the changes in the means and variances of these real forces, neural driven forces, and of our estimates of “virtual neural forces” and virtual interaction forces in this example rat and session. There were significant reductions in total interaction force in BMI and also in the virtual interaction force for simple elastic load (Fig. 2D) (t test, p < 0.05). The mean reduction in the virtual interaction force was closer to complete in the virtual interaction calculations for simple elastic load, but consistent with the plots in Figure 2B, the variance of these virtual interaction force around this mean value was significantly greater than variances of the real interaction forces for both simple elastic loading and BMI with elastic load (Fig. 2E) (t test, p < 0.05). This difference appeared to arise from the relationship of neural driven force, the elastic load, and the kinematics. The mean virtual neural driven force contributions in simple elastic load were comparable with real neural driven effects in BMI with elastic load and both were significantly larger than baseline virtual neural driven force (Fig. 2F) (t test, p < 0.05), and surprisingly neural driven force variances did not differ significantly between both real (BMI) and virtual neural driven forces (for baseline and simple elastic load). These observations together suggest that the decreased interaction force variance in the real BMI must have arisen from the better coordination of the real neural driven force and the step cycle. The interaction force variance is a measure of the stability and dynamic behavior of the robot system perturbations to the rat. High variance indicates higher fluctuations for which control of which more energy would be needed. The fluctuation and variance of the total interaction forces derive from the coordination of neural and kinematic behavior. Thus, the force variance differences in real and virtual interaction forces shown in Figure 2E likely arose from differences of the patterns of coordination of neural activity and driven forces with robot elastic load and step cycle compared with simple elastic load patterns. This idea is tested in more detail below.
Similar to the single session and exemplar rat that is shown in Figure 2, Figure 3 shows the statistics of the means and variances of total interaction forces and neural driven force across all the rats and all sessions, using data for whole trials. We hypothesized that animals would adapt their neural activity patterns and locomotion differently under the simple elastic load and the BMI with elastic load conditions. The data in Figure 2 for an example rat supported this idea. Similarly, across the group of rats, we found that the mean pelvic height was significantly depressed in simple elastic load compared with baseline and BMI, whereas in contrast the mean pelvic height was not significantly different between baseline and BMI in the group analysis (Fig. 3A). The rats thus normalized their average pelvic height in the BMI condition, despite the load. Other kinematic features were unremarkable in this analysis. Despite the normalized pelvic height in BMI with elastic load, the mean interaction force load (mean force from the robot) significantly decreased in the BMI with elastic load trial compared with the preceding simple elastic load trial for all rats across all the sessions (Fig. 3B) (Wilcoxon's signed-rank test, p < 0.05). Again, as in the individual rat in Figure 2, the mean virtual interaction force calculated from simple elastic load was significantly smaller (closer to zero) than the real observed BMI interaction force (Fig. 3B) (Wilcoxon's signed-rank test, p < 0.05), but also, again as in the Figure 2 rat, it was also significantly more variable than the real BMI interaction force (Fig. 3C) (Wilcoxon's signed-rank test, p < 0.05). Real, or virtual, neural driven forces from BMI and simple elastic load were both larger than baseline virtual neural driven forces (Fig. 3D) (Wilcoxon's signed-rank test, p < 0.05). Variances of BMI neural driven forces differed from neither the virtual neural driven force derived from simple elastic load, nor baseline. Thus, they were not different in the group (Fig. 3E), as they had been for some individual rats (Fig. 2E). However, the variances of virtual neural driven forces in simple elastic load differed significantly from the virtual neural forces in baseline (Fig. 3E) (Wilcoxon's signed-rank test, p < 0.05). However, as noted, despite this absence of any difference between neural driven force variances in BMI and the calculated virtual neural driven force from simple elastic load, the virtual interaction forces calculated for simple elastic load in the group again were significantly larger compared with variances of the real forces in simple elastic load and BMI (Fig. 3C). The group data thus again likely indicate a tighter coordination of neural drive, force, and kinematics across rats in the real BMI that was absent in the virtual data derived from simple elastic load recordings. However, it should also be noted that in the group data, the real BMI interaction force variance was slightly higher than the real interaction force variance observed in simple elastic load in Figure 3C, although the real mean force level was much reduced in BMI. These latter data suggest that the engagement of the BMI could add to variability and increase the dynamic complexity of the behavior of the rat's locomotor system while at the same time allowing the significant force offset adjustments observed.
These results strongly suggest that, in the BMI condition, the rats learned to adjust their neural activity and the associated brain-driven lifting force generation through the phases of the step cycle to counteract the elastic loading forces experienced in the BMI with elastic load condition. Examining data across the group of rats, we did indeed find that the temporal pattern (i.e., the force modulation, peak amplitude, and phase) of the virtual neural driven forces in simple elastic load and the real BMI neural driven forces in BMI with elastic load which immediately followed differed significantly during the step cycle for all experiments (23 of 23; runstest, MATLAB; p < 0.001) (Fig. 2B,C). The neural driven force patterns in the simple elastic load condition and in the BMI with elastic load condition also differed from the virtual neural driven force pattern obtained in baseline across all trials (23 of 23; runstest, MATLAB; p < 0.001). Thus, altered coordination of neural activity, kinematics, and interaction force in the presence of the BMI was supported on several levels in our data.
In summary, at the task level, in the three conditions the rats' real or virtual neural driven forces differed from one another in their pattern across the step cycle in magnitude and patterning. At the same time, in BMI with elastic load, the effects of these various changes were that the interaction forces were significantly reduced and the vertical kinematics better matched to (i.e., statistically not different from) baseline kinematics compared with the forces and kinematics of elastic load alone.
Overall neural firing rate changes between conditions
Neural pattern differences must likely be the key to the performance changes seen in BMI with elastic load conditions and achievement of normal vertical kinematics, reduced interaction force, and reduced variance of interaction forces documented in Figures 2, A, B, D, and E, and 3A–C. In what systematic ways do the patterns of neural activity alter between the rat experiencing a simple elastic load and the rat with the BMI engaged? The mean neural rates in both simple elastic load and BMI with elastic load were significantly elevated compared with baseline, both in the first and second half of the trial (Fig. 3F) (t test, p < 0.05), but these were not different from one another. However, individual neurons contributing to these rate differences behaved differently between simple elastic load and BMI with elastic load (Fig. 3G). Individually, >40% of neurons significantly increased firing rates from the baseline to the other two conditions. However, these conditions differed: in the transition between these conditions going from the simple elastic load to BMI with elastic load, we observed that cells significantly increased rates (∼20%) and decreased rates (∼20%) in equal measure, again suggesting there might be an alteration of individual neural contributions and coordination.
Changes in firing rate and Fano factor of cells through the adaptations
The mean firing rate and the Fano factor of a cell, when combined, provide estimates of the dynamics of the firing of the cell under different conditions (Churchland et al., 2010). Within a trial, cells rates varied from baseline to simple elastic load to BMI with elastic load conditions as described in Figure 3, F and G. However, the firing rates of individual cells varied from session to session across days. When considering the whole collection of trial intervals as populations, the daily variation was such that the combined distribution of the firing rates in baseline, simple elastic load, and BMI with elastic load of the cells was not significantly different (Kolmogorov–Smirnov, MATLAB kstest2, p > 0.05). In half-trail analysis, we found that significant alterations both in rates and in Fano factors occurred throughout a trial (paired t test, p < 0.05). In the second half-trial, we expected a more adapted locomotion. We found that most cells first significantly increased their firing rate when they transitioned from baseline to simple elastic load and then to BMI with elastic load conditions (paired t test, p < 0.05). In baseline conditions, the neural rates slightly increased in the second half-trial. Although this was not significant. In contrast, in the two test conditions of simple elastic load and BMI with elastic load was significantly decreased in the second half-trial, compared with the first half-trial (paired t test, p < 0.05). This significant relaxation of firing rates occurred in both simple elastic load and in BMI with elastic load trials, reducing rates by 30 and 34%, respectively. However, the rates that occurred in both the first half-trial and in the second half-trial of both simple elastic field and BMI with elastic load were significantly higher than the matching baseline rates (paired t test, p < 0.05). The different baseline changes observed might arise from an initial process of adaptation to treadmill speed and perhaps a change in arousal. Any baseline adaptation could only involve the passive interactions of the robot with the pelvis, as there were no forces generated from the robot controller and there was no active constraint from the robot. Variance changes in firing rates accompanied the overall rate changes. Within conditions, the Fano factors in the first half- and second half-trial were always significantly different for baseline, for simple elastic load and for BMI with elastic load (paired t test, p < 0.05). When the rats transitioned from baseline to the simple elastic load test, the Fano factor significantly increased between the two conditions within the first half-trial (paired t test, p < 1e-10), and then decreased over the second half of the trial. Surprisingly, the Fano factors of neurons in BMI with elastic load were not significantly different from baseline Fano factors (paired t test, p > 0.05) when compared in either the first half-trial or the second half-trial. As Fano factor represents aspects of the dynamic characteristics of cell firing, our results suggest that firing rates were very dynamic and were modulated highly as rats experienced any new condition and change in environment. Our results mostly match with observations in the previous reports on motor performance and motor learning during cells initial adaptation to an external force field (Li et al., 2001; Rokni et al., 2007) and to results in BMI-using experiments (Carmena et al., 2005; Zacksenhouse et al., 2007), but also show such alterations of neurons firing rates and variance might often happen on a shorter timescale of approximately a hundred step cycles during locomotion in new contexts, and then relax back to a default dynamics without other constraints.
Changes in burst behavior and preferred phases across the step cycle
Figure 4A shows examples of normalized average firing of 13 neurons across the step cycle in the three different conditions in the same trial and sample rat used in Figure 2. This rat was one in which all neurons recorded had somewhat similar phase preferences. Adaptive processes altered the neural firing pattern that was seen during locomotion in both simple elastic load and in BMI with elastic load conditions. Individual cells showed a particular phase preference in the step cycle (Fig. 4A–C). The average waveform of the ensemble firing in this individual rat had different width (at one-half of the peak value) in the two different conditions. This half-peak width increased by 150% (Fig. 4E,F, indicated by the horizontal bold line) in elastic load or BMI with elastic load compared with the baseline condition (Fig. 4D). This suggested that strong step phase modulation changes occurred in neurons under the different conditions. To examine these changes further, we compared the half-trial averages. The group averaged modulation plots for first and second halves of trials (Fig. 4E,F) provided additional evidence that modulation was changing over time in a trial as a result of adaptation, and firing more dispersed in phase. However, we also observed that, in half-trials, the firing pattern changes in BMI with elastic load persisted more in the second half-trial, whereas those of simple elastic load became weaker and firing much more dispersed over time (compare elastic load vs elastic load with BMI) (Fig. 4C,F).
Figure 4.
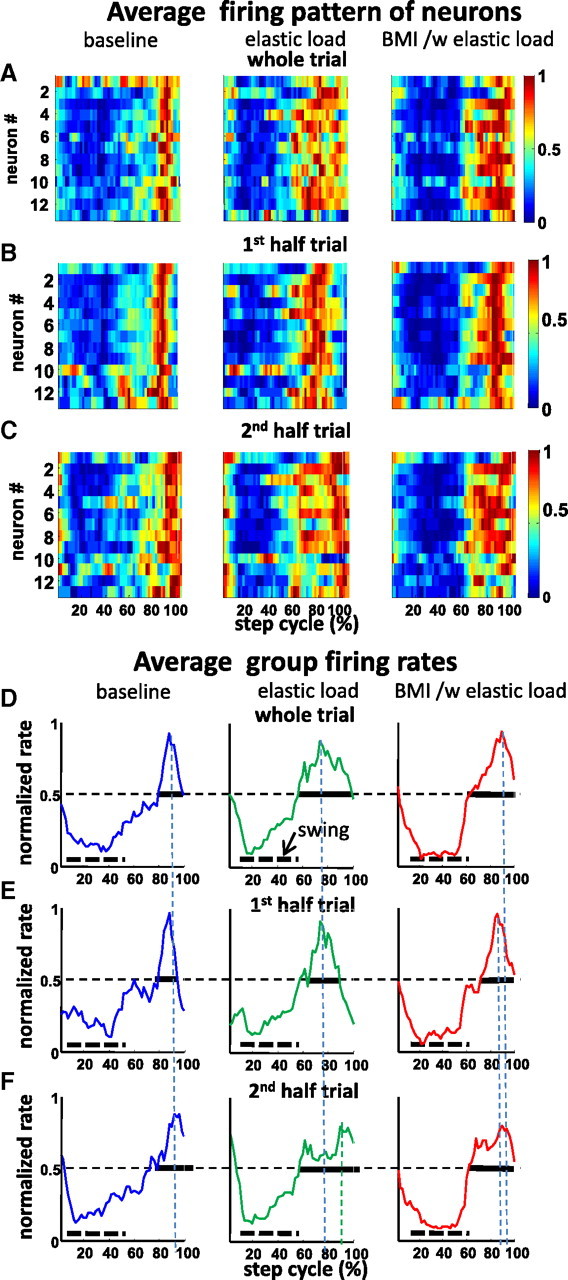
The ensemble firing patterns in the step cycle in each condition in the rat and trial also displayed in Figures 2 and 5. A, The normalized firing rates of neurons shown as a thermogram and as the average of the ensemble firing rate in the step cycle, respectively. These showed different patterns under baseline (BL), simple elastic load (E), and BMI with elastic load conditions (BMI/E). The average firing rate was normalized to the firing rate peak across baseline, elastic load, and BMI with elastic load conditions. B, First half-trial in each condition shown as a thermogram. C, Second half-trial in each condition shown as a thermogram. D, E, The whole-trial average rates normalized to the whole-trial peak in each condition. Vertical dotted lines, Peak timings; dotted horizontal bars, average swing phase; solid horizontal bars, full width at 0.5. D, Whole trial. E, First half-trial. F, Second half-trial. In each half-trial, cells demonstrated different firing patterns in different adaptation fields as well as different training phases during locomotion. In the baseline condition, cells fired at specific preferred step phases in the first half and then increased phase dispersion to spread much broader in the second half-trial. In the simple elastic load condition, these cells have wider firing phase dispersion initially and then also spread in the second half-trial, although there were still clear firing phases. In the BMI with elastic load condition, there were strong firing phase preferences in both the first half-trial and the second half-trial.
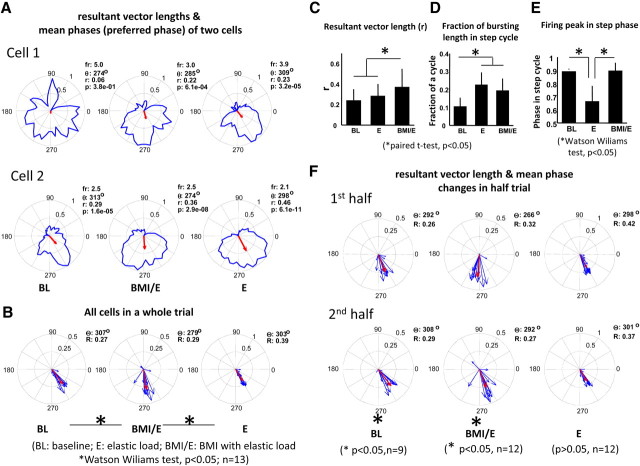
We found that many individual cells of motor cortex in all rats were significantly modulated with the step rhythm and they often fired preferentially at one phase of the step cycle. As an example, in Figure 5A, we show two individual example neurons data drawn from the session of the rat shown in Figures 2 and 4. Cell 1 is untuned to step phase in baseline but shows tuning in the two load conditions. Cell 2 is tuned in all three conditions but alters preferred phase in simple elastic load compared with the other two conditions. The step-related phase discharge patterns observed are consistent with the patterned activity data reported from previous experiments on cats (Armstrong and Drew, 1984; Beloozerova and Sirota, 1993a). We also observed that, although in some cells high discharge phasing was fixed across different trial conditions, in others there were progressive phase shifts, or weakened phase preferences (or more complex changes) when transitioning from baseline to simple elastic load and then to BMI with elastic load conditions (Fig. 5A). In different neurons in the rat, the ensemble of the recorded neurons demonstrated significant phase shift between BMI with elastic load and both simple elastic load and baseline (example cells in Fig. 5A and the rat's aggregate plots in Fig. 5B) (Watson–Williams test, p < 0.05). The resultant vector length for the population, an indication of phase coherence among the neural firing, was significantly higher in BMI with elastic load condition than either baseline or elastic load condition (Fig. 5C), indicating stronger firing phase coherence of neurons in BMI. The fraction of the bursting length in the step cycle was significantly higher in both simple elastic and BMI with elastic load condition compared with baseline condition (Fig. 5D). An example of a neuron quite different from that of Figure 5A is seen in Figure 5D. In different neurons in the rat, the peak activity could occur at widely different times during the step cycle (Fig. 5E). BMI with elastic load thus differed strongly from the other conditions in a range of ways.
Figure 5.
Examples of single-cell firing pattern in the step cycle in a session (same data sets as Figs. 2, 4). A, Cells changed firing patterns in different ways (fr, firing rate in spikes/second; r, resultant vector length; θ, mean phase of the firing rate; p, p value of the nonuniformity Rayleigh test) under different conditions. The red arrow indicates the mean preferred firing phase and the resultant vector length. Cell 1 and cell 2 show common patterns of increasing and changing phase modulations. B, The firing pattern of the ensemble of all cells (n = 13) in a session. Cells showed different nonuniform discharge patterns in the different conditions (BL, 11; E, 12; BMI/E, 12). In the cell ensemble, there was a significant mean firing phase shift (nonuniform firing cells at each of the comparing conditions) between simple elastic load and either baseline or BMI with elastic load (Watson–Williams test, p < 0.05; n = 11). The red arrows indicate the mean of the ensemble preferred firing phase and the resultant vector length. C, For the same trial and population of cells (n = 13), there was significant increase in the resultant vector length during BMI with elastic load compared with either baseline or simple elastics load conditions (paired t test, p < 0.05). D, The fraction of the cycle with bursting was significantly increased during simple elastic load and BMI with elastic load condition compared with the baseline (paired t test, p < 0.05). E, The mean phase of the firing peak in the step cycle was significantly different between simple elastic load compared with either baseline or BMI with elastic load conditions (Watson–Williams t test, p < 0.05). F, Single-cell firing patterns in step cycle during the first half and the second half of trial. The blue arrows indicate the mean preferred firing phase and the resultant vector length of each cell. There was no significant difference in resultant vector length between the first half-trial and the second half-trial, but there was significant difference in the mean preferred phase of the ensemble (red arrow) between first half-trial and the second half-trial during both baseline condition (Watson Williams test, p < 0.05; n = 9) and BMI with elastic load condition (Watson Williams test, p < 0.05; n = 12). Error bars indicate SD and asterisks indicate significant difference (p < 0.05).
We next compared the first half-trial and the second half-trial for the ensemble of cells (n = 13) to examine firing and tuning changes in detail in this rat. Major effects are shown in Figure 5F. We found that bursting duration and resultant vector length were not significantly different among half-trials under all conditions (signrank or paired t test, n = 13). However, firing peak and mean phase were significantly different between first and second half-trials in the simple elastic load condition (Watson–Williams test, p < 0.01; n = 13). For the nonuniform discharging cells (9 of 13 in baseline and 12 of 13 in other conditions), we observed that there was a significant difference in the mean preferred phase between half-trials in baseline and BMI with elastic load conditions, but not under the simple elastic load condition in which phase changes from the first half-trial were preserved in the second (Fig. 5F).
The results for the majority of the recorded cells across all rats (Fig. 6A) resembled those in Figure 5. Together, all rats showed significantly nonuniform aggregate firing rate distributions in the step cycle (circular Rayleigh test, p < 0.05). In a first pass analysis of group data, we examined the entire population of neurons recorded, and the entire interval of each condition, with no division into half-trials. We first focused on phase of peak firing, and the phases spanned by bursts as shown for the single rat example in Figure 5, D and E (these were defined using the Beloozerova criteria) (see below and Materials and Methods). Using the PSPH, bursts were defined as the portion of the step cycle where the activity level exceeded 75% of the difference between the maximal and minimal frequencies in the histogram (Beloozerova et al., 2003). The phases in which bursts occurred were then examined.
Figure 6.
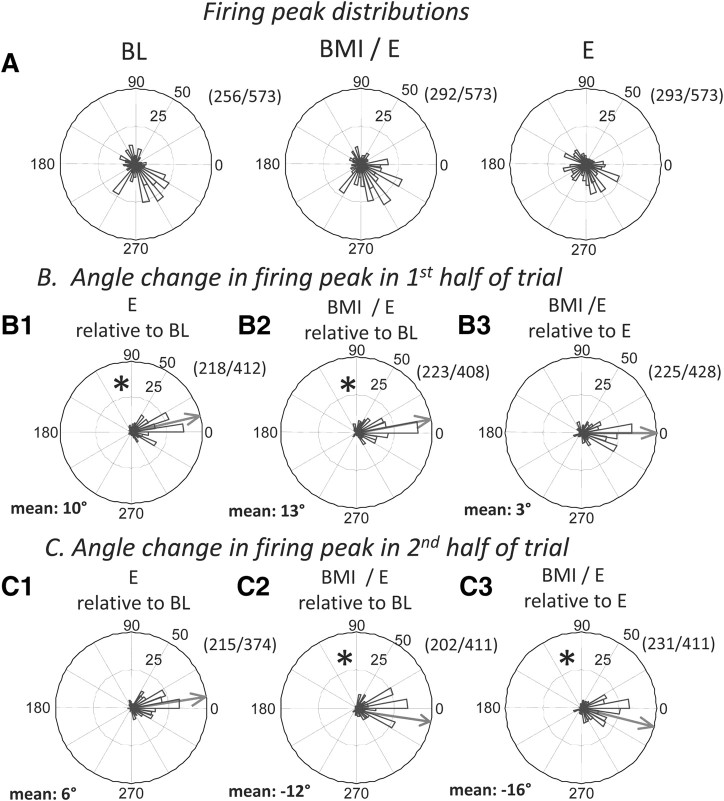
Peak firing phases in the step cycle and peak firing phase changes during adaptations in the combined data from all rats. A, Distribution of nonuniformly firing cells peak firing. Some cells preferentially fired at particular step phases under different conditions (BL, 256; E, 292; BMI/E, 293 of the total 573 cells; all with Rayleigh test, p < 0.05). Among these, 216 of 573 showed nonuniform discharging in step cycle across all conditions, whereas 96 of 573 showed uniform discharging across all conditions. We subtracted peak phases of cells which showed nonuniform discharging between conditions to examine peak phase shifts (i.e., changes in peak phase angles between conditions in B and C). Thus, 0 phase shift after subtraction indicates no change in peak phase. The numerator in the fraction number in each B and C was the number of cells shown nonuniform discharging at both conditions, and denominator was the number at either conditions. B1–B3, Differences in cell peak firing phases in first half-trial. Mean phase differences are shown by the gray arrow in each panel. In the first half-trial, there were significant changes of firing peak phase between baseline and both simple elastic load (B1; *circular t test, p < 0.05) and BMI with elastic load (B2; *p < 0.05), whereas there was no significant difference between simple elastic load and BMI with elastic load (B3; no phase shift, circular t test, p > 0.05). C1–C3, Differences in cell peak firing phases in second half-trial. Mean phase differences are shown by the gray arrow in each panel. In the second half-trial, there was no significant difference in the firing peak phases between simple elastic load and baseline (C1; no phase shift, circular t test, p > 0.05), but a significant difference persisted between BMI with elastic load and baseline (C2; *p < 0.05), and between BMI with elastic load and simple elastic load (C3; *p < 0.05). The data were consistent with a transient peak phase shift in simple elastic load condition and a longer term peak phase shift in firing in BMI with elastic load condition (*circular t test, p < 0.05), which reversed compared with the initial changes (compare B2 and C2 measured relative to baseline).
In a second-pass analysis, instead of examining the whole population of neurons as an ensemble, we selected only those neurons with a significant phase preference as indicated by the Rayleigh test (p < 0.01), and hence only neurons with clear phase modulation (shown in Fig. 6A). We reasoned that perhaps some significant effects in phase-modulated cells responses were “washed out” when these were examined in combination with nonmodulated cells. We compared the changes in peak firing behavior of such cells in the both first and second half of each adaptation trial and at baseline as a population (Fig. 6B1–B3,C1–C3). Across conditions, we observed significant shifts of the peak firing phases (circular t test, p < 0.05) when comparing baseline, and simple elastic load and BMI with elastic load conditions. This population showed significant changes in both simple elastic load conditions, and BMI with elastic load conditions that were clearly detectable with circular parametric statistics. In the first half-trial, the mean phase of peak firing for these neurons was significantly different between the baseline and simple elastic load conditions (Fig. 6B1) (circular t test, p < 0.05), which differed in the early phase of adaptation (Fig. 6B1), but was not significantly different in the second half-trial (Fig. 6C1) (circular t test, p > 0.05), the mean relaxing back to the baseline pattern. In contrast, the mean phase of peak firing was significantly different between baseline and BMI with elastic load conditions in both the first and the second half-trial but shifted significantly across the half-trials relative to baseline (Fig. 6B2,C2) (circular t test, p < 0.05) (Fig. 4). Comparing the simple elastic load condition and the BMI with elastic load condition showed that these peak firing phases were only significantly different from one another in the second half-trial [Fig. 6, compare B3 (not significant), C3] (circular t test p < 0.05) after the late BMI peak shift, and the relaxation of the simple elastic load peak changes. Thus, both simple elastic load and BMI with elastic load both showed similar significant changes in peak phases relative to baseline in the first half-trial, which then persisted and altered further in BMI, but which relaxed back in simple elastic load. At the population level, the neurons thus tended to have their peak firings in a particular step phase, and there was thus a minor but significant persistent peak phase shift for each neuron between baseline, simple elastic load, and BMI with elastic load condition (Kolmogorov–Smirnov test, MATLAB kstest2, p < 0.05). The changes of mean phase of peak firing of the subpopulation that occurred with onset persisted in the BMI with elastic load condition (Fig. 6C2,C3). Our data are consistent with rats using different strategies in the early and later stages of adaptation in the BMI with elastic load and simple elastic load conditions, with different delaying and advancing of peak firing phases. However, these peak firing differences in step phase across all conditions, although significant, were modest (<10% of a step cycle).
We found that the distributions of the timing of bursting behavior of the cells within step phases were not significantly different between baseline and simple elastic load tests. However, there was a clear significant difference both in timing of bursting and in the percentages of the step cycle spanned by bursting between the BMI with elastic load condition and both the simple elastic load condition and the baseline condition (Kolmogorov–Smirnov test, kstest2, p < 0.05). Conversely, when considering the phase of peak firing from the entire trial, simple elastic load trials differed significantly from both BMI and baseline. However, surprisingly, there were no significant differences between BMI with elastic load and the baseline trials. These patterns of alteration suggest that the simple elastic load locomotor adaptation that was used to achieve the gait modification involved a neural strategy that still strongly resembled baseline activity in phasing of bursty neural activity. In contrast, in the BMI with elastic load condition, the locomotor adaptation to the BMI needed a more complex strategy and significant burst duration and phasing differences from the other conditions, in order adapt to both the BMI and the applied load force field.
The data were thus consistent with a transient phase shift of the activity of neurons in simple elastic load conditions and a longer-term phase shift of the activity of neurons in BMI with elastic load conditions.
Changes in cross-correlation of firing rate with movement-related variables
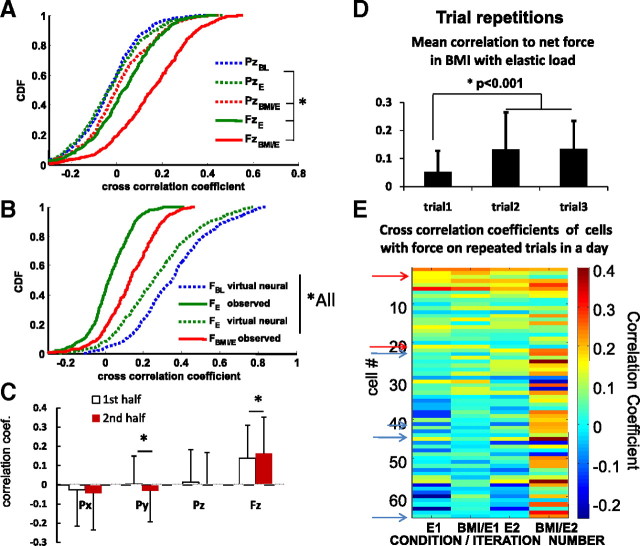
Multiple kinematics and kinetic variables are likely encoded in the cells of motor cortex. To make an initial assessment of these in our data and how they might alter, we calculated the cross-correlation coefficients of the individual neural firing rates with movement-related and force variables. We found that the spike activity of single cells was differently correlated with different variables. The population of cells showed a range of correlations with both vertical force and position of the pelvis, as obtained from the robot system (Fig. 7A). These were all significantly increased in BMI with elastic load when compared with simple elastic load and baseline (Fig. 7A) (kstest, p < 0.05), whereas lateral and rostrocaudal motion correlations showed little change (data not shown). More cells were correlated positively and more strongly with vertical force than with vertical position in both simple elastic load and BMI with elastic load conditions (paired t test, p < 0.0001) (Fig. 7A) (kstest, p < 0.05). Individual cells were on average better related to vertical force than to vertical position (paired t test, p < 0.0001). However, the numbers of significantly force-related cells also increased in BMI with elastic load conditions: 40 and 56% of cells showed significant modulation of firing in relation to force amplitude in simple elastic load and BMI with elastic load, respectively (Fig. 7A). We speculated this increase in correlation to force could be a simple consequence of an enforced correlation arising from the addition of the BMI action for the rat. We explored this possibility using the data in Figure 7B and were forced to reject this idea. The cross-correlations calculated from instantaneous virtual interaction forces assuming a BMI action for baseline and simple elastic load data sets greatly exceeded the correlations actually observed for real BMI and simple elastic load without BMI. Furthermore, the correlations to force observed in the BMI with elastic load tests significantly increased from first half-trial to second half-trial in BMI with elastic load, but were unaltered for vertical position, and decreased significantly for lateral position (Fig. 7C) (paired t test, p < 0.05). BMI imposed gain effects on the relationships of neurons with force were fixed throughout the first and second half-trials of BMI and repeat trials (see below) and thus could not account for these differences.
Figure 7.
Correlations of individual neural firing rates with kinematic and kinetic parameters examined at the whole-population level (n = 573). A, The correlation coefficients of the firing rate of cells with both vertical force (FzBMI/E) and vertical position (PzBMI/E) were significantly increased in BMI with elastic load (red) compared with simple elastic load (FzE and PzE) (green; *kstest2, p < 0.05). Cells also tended to be more correlated with force (Fz) than with position (Pz) in both simple elastic load and BMI with elastic load conditions (*kstest2, p < 0.05). The distribution of correlation coefficients between the robot position (Pz) and firing rate was not significantly different between baseline and simple elastic load (PzBL vs PzE, kstest2, p > 0.05). B, The distribution of correlation coefficients between firing rate and measured forces or derived forces (virtual forces) under different conditions: virtual force in baseline (FBL virtual neural), virtual neural driven resulting interaction force in simple elastic load (FE virtual neural), and real total interaction force in elastic load (FE observed) and real interaction force in BMI with elastic load (FBMI/E observed). All were significantly different (*kstest2, p < 0.05). Correlations with virtual forces were much larger than actually observed. C, Changes in mean correlations with kinematic and force parameters in the BMI/E condition. In half-trial comparisons, the correlation coefficient of firing rate with force was significantly increased from the first half-trial to the second half-trial in BMI/E, whereas other kinematics parameters were either not significantly different or significantly decreased (e.g., Py) (*paired t test, p < 0.05). D, In two rats with multiple iterations of the baseline→simple elastic load→BMI with elastic load presentations in succession, the mean correlation of neurons to force was significantly altered between first and second iterations and then persisted in both rats (data for a single rat also shown in E; t test, p < 0.001). E, The correlation of neural firing to net force on the first and second iterations of presentations summarized as mean correlations in D. Note the general increase in BMI correlation over iterations. Some cells alter correlation sign between iterations, with two marked on the figure changing from positive to negative (red arrows) and four from negative to positive (blue arrows). Error bars indicate SD.
In two rats, in an additional series of tests, we repeated the baseline, simple elastic load, and BMI with elastic load series as a block, three times in succession in a day, to examine any transfer of the changes observed in a block between the block repetitions. We found that, in the BMI with elastic load condition, the mean neural correlations to force significantly increased on the subsequent repetitions (Fig. 7D) (t test, p < 0.001). These mean correlation increases in block repetitions were visually apparent in color thermogram plots of individual neuron force correlations (Fig. 7E). The mean change comprised both significantly increased positive correlations with repeat exposures, as well as significant increases in numbers of correlated cells in BMI. Some cells altered the sign of their correlation with repetition. A few cells changing the sign of their correlation between blocks are indicated in Figure 7E, with blue arrows for cells changing from negative to positive and red arrows for cells changing from positive to negative. These rats' responses thus show the rats transferred experience between the block repetitions and the framework we used here can capture adaptations on timescales of both immediate and repeated exposure to the BMI actions.
Changes in modulation strength and numbers of force-related neurons in BMI
In addition to examining changes in the correlation coefficients for neurons, we also examined their modulation strengths, as estimated from the slope of the linear regression between neurons and force amplitude (see Materials and Methods). We used this to examine how the behavior of cells changed across trials, as shown in Figure 8. Correlation coefficients could increase by a reducing variance, or an increasing slope, or both. Slopes of the force relationships increased in the BMI with elastic load condition compared with the simple elastic load condition, as shown in a typical session in Figure 8A. More cells showed higher neuronal firing rate linear slope (from linear regression, MATLAB) with force amplitude in the BMI with elastic load condition than in the simple elastic load condition using the entire trial (Fig. 8B) (kstest, p < 0.05). We then also examined the change between each half-trial in the number of force correlated cells and the distributions of their modulation strength (Fig. 8C, elastic load; D, BMI with elastic load). Some cells lost correlation and their slopes were no longer significant between half-trials. During simple elastic load, the number of cells with significant correlation with force increased slightly but not significantly, from 26% in the first half-trial to 29% in the second half-trial (Fig. 8C). In contrast, in BMI with elastic load, we observed that more cells had initial significant correlations with force than in simple elastic load: 38% in the first half-trial, presumably because of the BMI action. However, this number then increased significantly to 44% in the second half-trial (Fig. 8D) (kstest, p < 0.05).
The correlation of the firing rates of the cells with nonvertical movement kinematics were either not significantly different or were significantly decreased in the second half-trial compared with the first half-trial under the two adaptation conditions (paired t test, p < 0.05), as shown in Figure 7C. In contrast, in the cells significantly correlated with force in the both the first half and the second half-trial, their correlations were significantly increased in the second half-trial under both the simple elastic load (paired t test, p < 0.05) and BMI with elastic load conditions (paired t test, p < 0.003).
The shapes of the distributions of positively correlated modulation of cells in Figure 8 do not appear to change over half-trials, or between conditions, only the numbers of cells in the distributions. We explored this in more detail for the transition from simple elastic load to BMI with elastic load. We classified the changes in numbers of force-correlated and strongly force-modulated cells as rats went from simple elastic load to BMI with elastic load. Figure 9 shows the analysis of these changes. BMI with elastic load had more strongly positively modulated and fewer negatively force-modulated neurons than simple elastic load (Fig. 9C) (kstest, p < 0.05). This difference in distributions arose from three classes of neurons (Fig. 9B): neurons that lost significant force modulation in BMI after modulation in simple elastic field (Fig. 9A, group I, 13% of neurons, 5% positive and 8% negative modulation), neurons significantly modulated in both (Fig. 9A, group II, 22% all positive and 4% switching sign), and neurons that only became modulated in BMI (group III, 28% positive, 2% negative). The distribution of modulation in group I neurons (modulation lost in BMI) differed significantly from that in group II (modulated in both), being fairly uniform (Fig. 9D) (kstest, p < 0.05). Drop out of neurons in BMI was thus uniform across strengths of modulation. The group II distributions seen in the simple elastic load and BMI with elastic load did not differ (Fig. 9E). Thus, the distributions of modulated neurons seen in both conditions were similar, despite significant increases in modulation of some neurons, and the effect of the BMI. Moreover, the modulation strength change in this group on moving from simple elastic load to BMI with elastic load was centered on 0 and not significantly different from zero (Fig. 9F). The percentage of cells significantly modulated in relation to force thus increased in BMI with elastic load (Fig. 8B) (t test, p < 0.05) compared with simple elastic load by recruiting additional neurons (group III). The number of these neurons was further increased over time so that the percentage in the second half-trial in BMI with elastic load was significantly increased (Fig. 8D) (t test, p < 0.05). However, the overall shape of the distribution of modulation strengths of positively force-correlated neurons thus did not differ between half-trials in either simple elastic load or BMI with elastic load, even as significantly more neurons became more significantly force related (Fig. 9E,F).
Figure 9.
Distribution changes of force-modulated cells between conditions and particularly in BMI. A, B, Of the 573 cells examined, ∼30% of the cells showed no modulation in either simple elastic load or BMI with elastic load conditions (gray). Thirteen percent showed force modulation only in simple elastic load (orange type I, Esig→BMI/Ensig), 30% showed force modulation only in BMI with elastic load condition (green type II, Ensig→BMI/Esig), and 30% showed modulation in both simple elastic load and BMI with elastic load condition (violet red type III, Esig→BMI/Esig). Cells could be either positively or negatively modulated. A small number of modulated cells (2%) in elastic load condition reversed their modulation strength from negative to positive, whereas most of the cells (24%) kept the modulation direction (positive to positive or negative to negative). B, Most of the positively force-modulated cells in BMI with elastic load condition came from new cells that had showed no force modulation in the simple elastic load condition. Thirteen percent of cells showed significant modulation under elastic load only (type I, Esig→BMI/Ensig); 30% of cells showed BMI with elastic load only (type II, Esig→BMI/Esig); 28% of cells showed both elastic load and BMI with elastic load (type III, Ensig→BMI/Esig). More condition specific cells were recruited during BMI with elastic load condition than during elastic load condition. C, There was significant difference in the cumulative distribution of modulation strength for force-modulated cells between simple elastic and BMI with elastic load (kstest2, p < 0.05). More cells were positively force-modulated in the BMI with elastic load condition than simple elastic load. D, There was a significant difference in the distribution of the type I and type II cells. Type I cells (drop outs of significance) were evenly distributed in modulation strength, whereas type III cells (cells newly significantly force related in BMI/E) were most likely positive-force related. E, There was no significant difference in the overall cumulative distribution of modulation strengths of type II cells (cells significantly correlated in both E in BMI/E) between the conditions of elastic field and BMI with elastic field (*significant difference with kstest2, p < 0.05). F, There was no significant modulation strength change of the individual neurons in group II between simple elastic load and BMI with elastic load.
In summary, more cells became more strongly tuned to force through the adaptation in the BMI with elastic load, despite the fact that the total force range experienced was less in the BMI with elastic load than in the simple elastic load. These changes were progressive throughout a trial and also on repeated trials. Together, these data were consistent with active use of the BMI provided for load compensation and increasing recruitment of neurons into stable force-related ensembles in the BMI with elastic load condition.
Changes in network correlations through different adaptations
Did interrelated neural ensembles alter in the different conditions? We examined neuron-to-neuron correlation changes in our data using a window of 100 ms, testing network correlations during adaptation to simple elastic load and BMI with elastic load. Example matrices of cross-correlations expressed as thermograms in half-trials of each condition are shown in Figure 10, A and B. We observed that, when all cell pair data were combined, the distributions of the firing rate correlation coefficients of the individual cell pair were significantly changed from the first half-trial to the second half-trial in all conditions (paired t test, p < 1e-4). The ensemble of individual cell pair correlation coefficients in the first half and second half-trials were also significantly different between baseline, simple elastic load, and BMI with elastic load (paired t test, p < 0.05). On this basis, every half-trial and condition differed. However, the cell pair correlations used in these group tests were not truly independent observations within each matrix of a rat, and the combined analysis performed in this way is therefore statistically partly flawed.
To examine systematic correlation matrix changes, we next tested whether the average correlation between neurons in the different matrices differed significantly, between half-trials or across conditions. Significant average changes might indicate a systematic overall strengthening and weakening change of the networks over adaptations. We found that the averaged cell pair correlation coefficient was only significantly different between the first half-trial of baseline and first half-trial simple elastic load (paired signrank, and t test, p < 0.05) and everywhere else was not different (e.g., no difference in BMI with elastic load condition). The average network correlations increased only in the first half of simple elastic load and then relaxed back to close to the level observed in baseline. However, this measure averaged both significant and insignificant neural correlations and failed to consider possible rearrangements of significant correlations.
We finally examined the consistency of correlations and their changes across rats and sessions. In a day's session, we pairwise compared the upper-half off-diagonal elements of the matrix correlations across half-trials and conditions in each rat on a daily basis using paired t tests, while treating each pair element as an independent observation as in the initial analysis (and again not strictly correct). To examine consistency, we evaluated the numbers of significant and nonsignificant test results in each type of comparison. We first examined baseline and observed that, for the baseline half-trials tested with paired t tests in this way, the correlation matrices were as likely to differ significantly as not between the half-trials. We assumed this to be the baseline variation and compared the other matrix correlation changes against this baseline variation. To next determine whether there was significant consistency in correlation matrix changes over conditions in the group of rats as a whole, we therefore used a binomial test and examined the numbers of matrices showing significant correlation changes in the paired t tests for the group. From the baseline data, we assumed equal likelihood of both the significant and nonsignificant change in the matrix element comparisons obtained using paired t tests. Thus, for a consistent significant difference of correlation matrices between conditions to be accepted, the number of significant changes in correlation matrices between the conditions had to exceed (i.e., had to occur often enough across all trials) to lie outside the 95% bounds of the binomial distribution defined by the baseline variations. We found that the correlation matrices of the second half-trials of simple elastic load adaptation differed significantly from baseline matrices (binomial test, p < 0.05). Furthermore, the first and second half-trials of BMI with elastic load adaptation were also significantly different from the baseline matrices (binomial test, p < 0.05). Together, the overall results of all of these statistical tests are captured graphically in a single rat in Figure 10, A and B. Correlations in this example clearly also increased in the first half of simple elastic load adaptation, matching the averaged correlation test results, but unlike the results of the binomial test comparison for the group. These differences were clear using the original naive t test approach or a local binomial test (paired t tests, p < 0.05). The most common pattern of significant change in the second half of simple elastic load compared with baseline was a decreased correlation, as is also observed in the rat in Figure 10, A and B. This significant decrease was observed in 15 of 21 cases (binomial test, p < 0.05) in comparing the second half of the simple elastic load to baseline matrices. In considering these matrix correlation results, and their variations through adaptations, it is important to note that our recordings were very spatially focused in cortex (i.e., all 24 tetrode sites were arranged around a 150–200 μm diameter disc parallel to the pial surface). Data presented here on neural correlations thus support the idea of changes in spatially local network correlations in adaptation to either a simple elastic load or the BMI with elastic load conditions, which are then sustained in the BMI with elastic load compensations.
Discussion
Our data show that a robotic action can be added at the trunk/pelvis and placed under BMI control from hindlimb/trunk cortex neurons in rats. The rats experienced the BMI as an augmentation, which provided new elastic force production at the pelvis in addition to regular musculoskeletal controls. Rats adapted to the BMI and incorporated it in locomotion. We compared baseline controls, a simple elastic load condition, and BMI with elastic load. When the BMI control was provided in parallel with the simple elastic load, the rats could offset the load, their pelvic height was not significantly different from normal baseline, and the load offset and activity patterns differed from those predicted from load trial neural activity. The differences in BMI adaptation compared with the simple load involved alterations in firing patterns and relationships among neurons, but not average firing rates compared with elastic loading. We observed changes in the number of force-related neurons, their peak firing and burst activity timing in the step cycle (Fig. 10C). Our data represent the first example of an interactive robotic BMI controlling elastic or muscle-like trunk actions, and first testing of active BMI/robot systems directly mechanically coupled to ongoing locomotion in vivo.
Unique features and caveats of this study
Our experiments and apparatus were unique in several ways. These influence interpreting our results. First, most of our recordings were made using a localized tetrode system that focused recordings to a patch of cortex 200–350 μm in diameter (estimated as the 150–200 μm diameter of probe ± 50–75 μm pickup distance). Cell isolation used tetrode cluster cutting off-line. This was not available on-line in the Cyberkinetics system. Given the combined rate use in neural control by the BMI here, this difference posed no significant difficulty in interpretation or analysis. However, cells with high amplitude representation on multiple channels of a tetrode were effectively more highly weighted in the combined rate data filter, since they were not combined on-line as a single unit. Since virtual forces from off-line analysis were generally higher than on-line BMI forces, despite cluster cutting removal of redundancy, and the on-line bias given to strongly emphasize multiple-channel cells effectively increased BMI gain (and forces) our results are not impacted by this bias. The neuron correlations changes reported here could indicate features of local versus distant cortical processing (Hatsopoulos et al., 2007; Hatsopoulos, 2010), observed in spatially focused electrode designs. A better understanding of local and distant cortical activity dynamics during adaptation might come from analyses in more depth of our data at the single spike and point process level [e.g., by general linear model approaches (Truccolo et al., 2005; Czanner et al., 2008; Stevenson and Körding, 2010)].
Our BMI augmented locomotion. Most BMIs use a framework of instrumental conditioning of a voluntary task and many repetitions. In our study, the rats instead simply adapted to the BMI robot augmenting their locomotion. We do not as yet know whether the rats here can generalize nor whether they can identify, estimate, and in novel ways voluntarily use the adapted controls that they used here. To best design BMI/neuroprostheses for restoration of activities of daily living, we need to understand both these voluntary and adaptive processes, that is, (1) processes of voluntary and conscious identification estimation and instrumental employment of a neurorobotic prosthesis, and (2) processes of adaptation and integration of the actions and mechanics of neurorobotic prostheses into other ongoing behaviors and the body scheme. Our data address the latter—adaptations—with the caveat noted regarding voluntary use and generalization, which remain to be explored.
A final caveat is that the physically connected BMI here operated in parallel with high bandwidth sensory feedback. All proprioceptive information for the rat was intact—significant normal feedback from the body mechanics was available to modulate the target cortical area (Gosselin et al., 2009). In this way, our rats did not face the larger inverse problem potentially posed by a completely novel and potentially high degree of freedom interface without such feedback (Héliot et al., 2010). We chose trunk/hindlimb cortex because previous work has demonstrated it plays a significant role in recovery and development of function in neonatal spinalized rats (Giszter et al., 1998, 2007a,b, 2008, 2010). However, trunk/hindlimb cortex in rats is a sensorimotor overlap area. Thus, inputs from deep trunk/proximal limb afferents that were close to the mechanical interface of the BMI may have played a significant role in the modulation of cells in this trunk sensorimotor cortex area and their adaptations. The strong roles of afferent input in the trunk/hindlimb sensorimotor amalgams in trunk cortex could have assisted rapid adaptation and incorporation of the BMI into locomotion. The controls adapting the BMI here could thus potentially have used both altered sensory filtering and altered motor outflow to modulate the recorded neural activity and control the interface, which used activity integrated over 100 ms. Furthermore, one means of altering sensory feedback could have been subtle alterations in executed motions or in gamma motoneuron spindle controls to alter feedback and thereby accomplish the cortical neural changes that were effective in reducing load in the BMI. Understanding these different possible aspects of BMI integration and use are important future issues for any physically integrated feedback-based BMI.
Roles of hindlimb trunk cortex activity of rats during locomotion, in load adaptation and BMI
Neural circuits for forelimbs have differences from those controlling trunk/hindlimb (Jankowska et al., 1974; Jankowska and Edgeley, 1993; Alstermark et al., 2007). The role of cortex in quadruped locomotion generally is an area of active investigation (Armstrong and Drew, 1984; Beloozerova and Sirota, 1993a,b; Drew et al., 2008a,b). The involvement of the cortex during locomotion has been examined mostly thoroughly in cats, in which roles are clear (Beloozerova and Sirota, 1993a,b; Drew et al., 2008a,b; Lajoie et al., 2010) (but see Fitzsimmons et al., 2009). It remains controversial as to precisely how the cortex is involved in different aspects of locomotion across different species. Not much work is available in rats. It has been argued that motor cortex in rats may be very little involved during simpler locomotion tasks (Hicks and D'Amato, 1975). However, our data show significant cortical engagement is certainly possible in rats (Giszter et al., 2008, 2010). Trunk and pelvis control might be monitored in trunk/hindlimb cortex even when less actively controlled. Cortex engagement likely occurs during adaptation of locomotion in novel contexts. The BMI use here exploits this idea and confirms strong engagement of cortex can occur during locomotor adaptations in intact rats. The data are in agreement with previous reports of preferential firing phases of cortical cells seen in forelimb areas of cat motor cortex (Beloozerova and Sirota, 1993b). The neural activity in hindlimb/trunk cortex of rats was strongly modulated during adaptation to a simple elastic load force field applied in locomotion. Furthermore, from simple elastic load to the BMI with elastic load condition additional significant shifts in preferred peak phase of neurons occurred with adaptive consequences.
BMI implications
Teasing apart sensory and motor drive effects in any closed-loop BMI task is potentially complex (Stevenson et al., 2008; Suminski et al., 2009; Héliot et al., 2010). Our approach to testing motor outflow effects was to estimate the instantaneous force effect that the BMI would have provided if briefly engaged in the baseline, or simple elastic load conditions, which we termed “virtual neural driven forces” and examine such virtual effects during the step cycle and on average, compared with the real BMI. This approach matches the analysis of visual feedback contributions to a BMI used by Hatsopoulos and colleagues (Suminski et al., 2009). However, more complex analyses and perturbation studies are likely necessary in the future.
Decoding neural information from motor cortex of forearm areas for BMI manipulation control have been tested extensively in rats, monkeys, and humans (Chapin et al., 1999; Taylor et al., 2002; Serruya et al., 2003; Carmena et al., 2005; Francis and Chapin, 2006; Hochberg et al., 2006; Velliste et al., 2008; Fagg et al., 2009). Few studies have used the trunk/hindlimb cortex in this way, which might be necessary for restoring locomotion (Fitzsimmons et al., 2009; Song et al., 2009). We have shown multiple movement-related variables can be decoded from activity of cells in the hindlimb/trunk area of the motor cortex of rats (Song et al., 2009). We here chose a proximal elastic mechanical interaction to be driven through the BMI. This was based on (1) a strong force and proximal representation in trunk/hindlimb cortex in rat (Song et al., 2009), (2) the notion of testing real biomechanically relevant actions in a BMI, (3) the idea that the cortex may best represent muscle-like features (Sergio et al., 2005; Kim et al., 2007; Morrow et al., 2007, 2009; Pohlmeyer et al., 2007, 2009; Drew et al., 2008b), and (4) choice of viscoelastic actions resembling the grouped output of muscles and spinal mechanisms (Cappellini et al., 2006; Giszter et al., 2007; Drew et al., 2008a,b; Hart and Giszter, 2010).
Instead of explicitly decoding kinematic parameters from the neural activity, we adopted strategies similar to those of Fetz and colleagues (Jackson et al., 2006; Moritz et al., 2008) using a simple linear filter to control the robot. The learning of arbitrary BMI transforms may often be easier for BMI representations of more distal than proximal biomechanics and musculature (Radhakrishnan et al., 2008). Our system used a proximal BMI effector. However, within 100–200 steps the rats operated consistently with the BMI and elastic load interactions. It remains a topic of investigation how much proximal and distal motor effectors and BMI targets differ in adaptation processes, and their voluntary flexibility and control. The differences between open-loop BMIs, BMIs with feedback, physically connected BMIs, and between BMIs for proximal locomotion versus distal reaching are not well understood (Héliot et al., 2009; Scherberger, 2009). However, these different effects may become crucial as various feedback-based BMIs are introduced and the range and scope of available BMI prosthetic devices increases (Fitzsimmons et al., 2007; O'Doherty et al., 2009).
Adaptation processes
Recent studies showed that cells in the primary motor cortex demonstrated learning-related plasticity during force field adaptation (Li et al., 2001). However, a stable relationship between neural activity and behavior can clearly be established in well trained animals (Serruya et al., 2003; Greenberg and Wilson, 2004; Chestek et al., 2007). Moritz et al. (2008) demonstrated that individual cells can be rate modulated to control functional electrical stimulation. Variations of neural firing patterns in such differing adaptation processes are not well understood at this point. For example, patterns might differ between novel voluntary tasks and more vegetative “built-in” or evolutionarily older tasks, such as locomotion. Many cells here clearly adapted, and responded differently between conditions and comparing first half-trials and second half-trials. The cell firing rates increased in each context switch (e.g., as rats transited from baseline to simple elastic load condition). In each case, the increased rates partly relaxed in the second half-trials, although BMI rate changes remained significantly different from baseline. A recent report from Zacksenhouse et al. (2007) showed that there are firing rate changes in the early sessions with other BMI experiments, and this matches a general observation about novel motor tasks. Our experiments also confirm other early firing changes: the Fano factor and the cross-correlation of cell pairs altered from early to later in each trial of treadmill locomotion with or without loads or BMI. These alterations accompanied coding changes.
Our earlier analysis of hindlimb kinematics (Song et al., 2009) showed that trunk/hindlimb cells were often better related to pelvic motion than to the hindlimb joint angles, and that these correlations increased during load conditions compared with normal control conditions. Our results here showed that, for some kinematics variables, less related to the load experienced, cells modulated strongly during the first half-trial periods, but this decreased in the second half of each trial. However, we observed an increase in force-related neural modulation and in the numbers of force-related cells in the BMI condition. Furthermore, these increasing numbers were not instantaneously engaged, which could happen simply as a result of the BMI role in perforce coupling neural activity and forces through its operation. Instead, cells became more significantly correlated throughout the trial, numbers increasing significantly in the second half of a trial. This progressive recruitment of neurons was accompanied by significant alterations in the individual neuron-to-neuron network correlations. In simple elastic load, this engagement was more transitory with more rats significantly losing correlation in the second half, whereas in BMI the strengthened network correlations persisted. Our data thus show that cortical activity during use of a BMI differs in several ways from cortical activity in baseline and in the “normal” (non-BMI) load adaptation processes in hindlimb trunk cortex.
Conclusions
When animals adapt their locomotion to new environments, initially cortex becomes more activated and engaged. Engaging a BMI in this period appears to alter and at least briefly stabilize the changes involved in the adaptation of neural activity. Despite the small role of cortex in the normal locomotion of rats, cortex can be engaged in a BMI augmenting locomotion during this adaptation. Our data thus support the idea that activity normally involved in monitoring, or simply correlated with and not normally driving a behavior in an animal, can nonetheless be engaged through motor adaptation processes to drive behavior in a BMI. We do not know whether this “adaptation-based” route of engagement of a neural interface can then be generalized to support more novel voluntary acts. Clearly, this is an important issue for future research.
Footnotes
This work was supported by National Institutes of Health Grants NS44564 and NS54894, The Craig Neilsen Foundation, and the Pennsylvania Department of Public Health.
References
- Acharya S, Tenore F, Aggarwal V, Etienne-Cummings R, Schieber MH, Thakor NV. Decoding individuated finger movements using volume-constrained neuronal ensembles in the M1 hand area. IEEE Trans Neural Syst Rehabil Eng. 2008;16:15–23. doi: 10.1109/TNSRE.2007.916269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aflalo TN, Graziano MS. Partial tuning of motor cortex neurons to final posture in a free-moving paradigm. Proc Natl Acad Sci U S A. 2006;103:2909–2914. doi: 10.1073/pnas.0511139103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alstermark B, Isa T, Pettersson LG, Sasaki S. The C3–C4 propriospinal system in the cat and monkey: a spinal pre-motoneuronal centre for voluntary motor control. Acta Physiol (Oxf) 2007;189:123–140. doi: 10.1111/j.1748-1716.2006.01655.x. [DOI] [PubMed] [Google Scholar]
- Armstrong DM, Drew T. Locomotor-related neural discharges in cat motor cortex compared with peripheral receptive field and evoked movements. J Physiol. 1984;346:497–517. doi: 10.1113/jphysiol.1984.sp015037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beloozerova IN, Sirota MG. The role of the motor cortex in the control of accuracy of locomotion movements in the cat. J Physiol. 1993a;461:1–25. doi: 10.1113/jphysiol.1993.sp019498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beloozerova IN, Sirota MG. The role of the motor cortex in the control of vigour of locomotor movements in the cat. J Physiol. 1993b;461:27–46. doi: 10.1113/jphysiol.1993.sp019499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beloozerova IN, Sirota MG, Swadlow HA, Orlovsky GN, Popova LB, Deliagina TG. Activity of different classes of neurons of the motor cortex during postural corrections. J Neurosci. 2003;23:7844–7853. doi: 10.1523/JNEUROSCI.23-21-07844.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berens P. CircStat: a MATLAB toolbox for circular statistics. J Stat Softw. 2009;31:1–21. [Google Scholar]
- Bretzner F, Drew T. Contribution of the motor cortex to the structure and the timing of hindlimb locomotion in the cat: a microstimulation study. J Neurophysiol. 2005;94:657–672. doi: 10.1152/jn.01245.2004. [DOI] [PubMed] [Google Scholar]
- Cappellini G, Ivanenko YP, Poppele RE, Lacquaniti F. Motor patterns in human walking and running. J Neurophysiol. 2006;95:3426–3437. doi: 10.1152/jn.00081.2006. [DOI] [PubMed] [Google Scholar]
- Carmena JM, Ganguly K. Large-scale reshaping of cortical networks during neurophrosthetic control. Paper presented at 20th Annual Meeting of Society for the Neural Control of Movement; April; Naples, FL. 2010. [Google Scholar]
- Carmena JM, Lebedev MA, Henriquez CS, Nicolelis MA. Stable ensemble performance with single-neuron variability during reaching movements in primates. J Neurosci. 2005;25:10712–10716. doi: 10.1523/JNEUROSCI.2772-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cavagna GA, Heglund NC, Taylor CR. Mechanical work in terrestrial locomotion: two basic mechanisms for minimizing energy expenditure. Am J Physiol. 1977;233:R243–R261. doi: 10.1152/ajpregu.1977.233.5.R243. [DOI] [PubMed] [Google Scholar]
- Chapin JK, Moxon KA, Markowitz RS, Nicolelis MA. Direct real-time control of a robot arm using signals derived from neuronal population recordings in motor cortex. Nat Neurosci. 1999;2:664–670. doi: 10.1038/10223. [DOI] [PubMed] [Google Scholar]
- Chen Y, Martinez-Conde S, Macknik SL, Bereshpolova Y, Swadlow HA, Alonso JM. Task difficulty modulates the activity of specific neuronal populations in primary visual cortex. Nat Neurosci. 2008;11:974–982. doi: 10.1038/nn.2147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chestek CA, Batista AP, Santhanam G, Yu BM, Afshar A, Cunningham JP, Gilja V, Ryu SI, Churchland MM, Shenoy KV. Single-neuron stability during repeated reaching in macaque premotor cortex. J Neurosci. 2007;27:10742–10750. doi: 10.1523/JNEUROSCI.0959-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Churchland MM, Yu BM, Cunningham JP, Sugrue LP, Cohen MR, Corrado GS, Newsome WT, Clark AM, Hosseini P, Scott BB, Bradley DC, Smith MA, Kohn A, Movshon JA, Armstrong KM, Moore T, Chang SW, Snyder LH, Lisberger SG, Priebe NJ, et al. Stimulus onset quenches neural variability: a widespread cortical phenomenon. Nat Neurosci. 2010;13:369–378. doi: 10.1038/nn.2501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Czanner G, Eden UT, Wirth S, Yanike M, Suzuki WA, Brown EN. Analysis of between-trial and within-trial neural spiking dynamics. J Neurophysiol. 2008;99:2672–2693. doi: 10.1152/jn.00343.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drew T, Doucet S. Application of circular statistics to the study of neuronal discharge during locomotion. J Neurosci Methods. 1991;38:171–181. doi: 10.1016/0165-0270(91)90167-x. [DOI] [PubMed] [Google Scholar]
- Drew T, Andujar JE, Lajoie K, Yakovenko S. Cortical mechanisms involved in visuomotor coordination during precision walking. Brain Res Rev. 2008a;57:199–211. doi: 10.1016/j.brainresrev.2007.07.017. [DOI] [PubMed] [Google Scholar]
- Drew T, Kalaska J, Krouchev N. Muscle synergies during locomotion in the cat: a model for motor cortex control. J Physiol. 2008b;586:1239–1245. doi: 10.1113/jphysiol.2007.146605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fagg AH, Ojakangas GW, Miller LE, Hatsopoulos NG. Kinetic trajectory decoding using motor cortical ensembles. IEEE Trans Neural Syst Rehabil Eng [Erratum (2009) 17:606] 2009;17:487–496. doi: 10.1109/TNSRE.2009.2029313. [DOI] [PubMed] [Google Scholar]
- Fetz EE. Operant conditioning of cortical unit activity. Science. 1969;163:955–958. doi: 10.1126/science.163.3870.955. [DOI] [PubMed] [Google Scholar]
- Fisher NI. Statistical analysis of circular data. Cambridge, UK: Cambridge UP; 1996. [Google Scholar]
- Fitzsimmons NA, Drake W, Hanson TL, Lebedev MA, Nicolelis MA. Primate reaching cued by multichannel spatiotemporal cortical microstimulation. J Neurosci. 2007;27:5593–5602. doi: 10.1523/JNEUROSCI.5297-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fitzsimmons NA, Lebedev MA, Peikon ID, Nicolelis MA. Extracting kinematic parameters for monkey bipedal walking from cortical neuronal ensemble activity. Front Integr Neurosci. 2009;3:3. doi: 10.3389/neuro.07.003.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Francis JT, Chapin JK. Neural ensemble activity from multiple brain regions predicts kinematic and dynamic variables in a multiple force field reaching task. IEEE Trans Neural Syst Rehabil Eng. 2006;14:172–174. doi: 10.1109/TNSRE.2006.875553. [DOI] [PubMed] [Google Scholar]
- Fujisawa S, Amarasingham A, Harrison MT, Buzsáki G. Behavior-dependent short-term assembly dynamics in the medial prefrontal cortex. Nat Neurosci. 2008;11:823–833. doi: 10.1038/nn.2134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ganguly K, Carmena JM. Emergence of a stable cortical map for neuroprosthetic control. PLoS Biol. 2009;7:e1000153. doi: 10.1371/journal.pbio.1000153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giszter S, Davies MR, Ramakrishnan A, Udoekwere UI, Kargo WJ. Trunk sensorimotor cortex is essential for autonomous weight-supported locomotion in adult rats spinalized as P1/P2 neonates. J Neurophysiol. 2008;100:839–851. doi: 10.1152/jn.00866.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giszter SF. Spinal cord injury: present and future therapeutic devices and prostheses. Neurotherapeutics. 2008;5:147–162. doi: 10.1016/j.nurt.2007.10.062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giszter SF, Kargo WJ, Davies M, Shibayama M. Fetal transplants rescue axial muscle representations in M1 cortex of neonatally transected rats that develop weight support. J Neurophysiol. 1998;80:3021–3030. doi: 10.1152/jn.1998.80.6.3021. [DOI] [PubMed] [Google Scholar]
- Giszter SF, Hart CB, Udoekwere UI, Markin S, Barbe C. A real-time system for small animal neurorobotics at spinal or cortical level. Paper presented at Second International IEEE/EMBS Conference on Neural Engineering; March; Washington, DC. 2005. [Google Scholar]
- Giszter SF, Davies MR, Graziani V. Motor strategies used by rats spinalized at birth to maintain stance in response to imposed perturbations. J Neurophysiol. 2007a;97:2663–2675. doi: 10.1152/jn.00308.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giszter SF, Patil V, Hart C. Primitives, premotor drives, and pattern generation: a combined computational and neuroethological perspective. Prog Brain Res. 2007b;165:323–346. doi: 10.1016/S0079-6123(06)65020-6. [DOI] [PubMed] [Google Scholar]
- Giszter SF, Hockensmith G, Ramakrishnan A, Udoekwere UI. How spinalized rats can walk: biomechanics, cortex, and hindlimb muscle scaling—implications for rehabilitation. Ann N Y Acad Sci. 2010;1198:279–293. doi: 10.1111/j.1749-6632.2010.05534.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gosselin-Kessiby N, Kalaska JF, Messier J. Evidence for a proprioception-based rapid on-line error correction mechanism for hand orientation during reaching movements in blind subjects. J Neurosci. 2009;29:3485–3496. doi: 10.1523/JNEUROSCI.2374-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grabiner MD, Troy KL. Attention demanding tasks during treadmill walking reduce step width variability in young adults. J Neuroeng Rehabil. 2005;2:25. doi: 10.1186/1743-0003-2-25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greenberg PA, Wilson FA. Functional stability of dorsolateral prefrontal neurons. J Neurophysiol. 2004;92:1042–1055. doi: 10.1152/jn.00062.2004. [DOI] [PubMed] [Google Scholar]
- Hart CB, Giszter SF. A neural basis for motor primitives in the spinal cord. J Neurosci. 2010;30:1322–1336. doi: 10.1523/JNEUROSCI.5894-08.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hatsopoulos NG. Columnar organization in the motor cortex. Cortex. 2010;46:270–271. doi: 10.1016/j.cortex.2008.07.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hatsopoulos NG, Xu Q, Amit Y. Encoding of movement fragments in the motor cortex. J Neurosci. 2007;27:5105–5114. doi: 10.1523/JNEUROSCI.3570-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Héliot R, Ganguly K, Jimenez J, Carmena JM. Learning in closed-loop brain-machine interfaces: modeling and experimental validation. IEEE Trans Syst Man Cybern B Cybern. 2010;40:1387–1397. doi: 10.1109/TSMCB.2009.2036931. [DOI] [PubMed] [Google Scholar]
- Hermer-Vazquez L, Hermer-Vazquez R, Moxon KA, Kuo KH, Viau V, Zhan Y, Chapin JK. Distinct temporal activity patterns in the rat M1 and red nucleus during skilled versus unskilled limb movement. Behav Brain Res. 2004;150:93–107. doi: 10.1016/S0166-4328(03)00226-2. [DOI] [PubMed] [Google Scholar]
- Hicks SP, D'Amato CJ. Motor-sensory cortex-corticospinal system and developing locomotion and placing in rats. Am J Anat. 1975;143:1–42. doi: 10.1002/aja.1001430102. [DOI] [PubMed] [Google Scholar]
- Hochberg LR, Serruya MD, Friehs GM, Mukand JA, Saleh M, Caplan AH, Branner A, Chen D, Penn RD, Donoghue JP. Neuronal ensemble control of prosthetic devices by a human with tetraplegia. Nature. 2006;442:164–171. doi: 10.1038/nature04970. [DOI] [PubMed] [Google Scholar]
- Jackson A, Mavoori J, Fetz EE. Long-term motor cortex plasticity induced by an electronic neural implant. Nature. 2006;444:56–60. doi: 10.1038/nature05226. [DOI] [PubMed] [Google Scholar]
- Jankowska E, Edgley S. Interaction between pathways controlling posture and gait at the level of spinal interneurones in the cat. Prog Brain Res. 1993;97:161–171. doi: 10.1016/s0079-6123(08)62274-8. [DOI] [PubMed] [Google Scholar]
- Jankowska E, Lundberg A, Roberts WJ, Stuart D. A long propriospinal system with direct effect on motoneurones and on interneurons in the cat lumbosacral cord. Exp Brain Res. 1974;21:169–194. doi: 10.1007/BF00234388. [DOI] [PubMed] [Google Scholar]
- Jarosiewicz B, Chase SM, Fraser GW, Velliste M, Kass RE, Schwartz AB. Functional network reorganization during learning in a brain-computer interface paradigm. Proc Natl Acad Sci U S A. 2008;105:19486–19491. doi: 10.1073/pnas.0808113105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim HK, Carmena JM, Biggs SJ, Hanson TL, Nicolelis MA, Srinivasan MA. The muscle activation method: an approach to impedance control of brain-machine interfaces through a musculoskeletal model of the arm. IEEE Trans Biomed Eng. 2007;54:1520–1529. doi: 10.1109/TBME.2007.900818. [DOI] [PubMed] [Google Scholar]
- Kositsky M, Chiappalone M, Alford ST, Mussa-Ivaldi FA. Brain-machine interactions for assessing the dynamics of neural systems. Front Neurorobotics. 2009;3:1. doi: 10.3389/neuro.12.001.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lajoie K, Andujar JE, Pearson K, Drew T. Neurons in area 5 of the posterior parietal cortex in the cat contribute to interlimb coordination during visually guided locomotion: a role in working memory. J Neurophysiol. 2010;103:2234–2254. doi: 10.1152/jn.01100.2009. [DOI] [PubMed] [Google Scholar]
- Lam T, Anderschitz M, Dietz V. Contribution of feedback and feedforward strategies to locomotor adaptations. J Neurophysiol. 2006;95:766–773. doi: 10.1152/jn.00473.2005. [DOI] [PubMed] [Google Scholar]
- Li CS, Padoa-Schioppa C, Bizzi E. Neuronal correlates of motor performance and motor learning in the primary motor cortex of monkeys adapting to an external force field. Neuron. 2001;30:593–607. doi: 10.1016/s0896-6273(01)00301-4. [DOI] [PubMed] [Google Scholar]
- Mazzoni A, Broccard FD, Garcia-Perez E, Bonifazi P, Ruaro ME, Torre V. On the dynamics of the spontaneous activity in neuronal networks. PLoS One. 2007;2:e439. doi: 10.1371/journal.pone.0000439. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moritz CT, Perlmutter SI, Fetz EE. Direct control of paralyzed muscles by cortical neurons. Nature. 2008;456:639–642. doi: 10.1038/nature07418. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morrow MM, Jordan LR, Miller LE. Direct comparison of the task-dependent discharge of M1 in hand space and muscle space. J Neurophysiol. 2007;97:1786–1798. doi: 10.1152/jn.00150.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morrow MM, Pohlmeyer EA, Miller LE. Control of muscle synergies by cortical ensembles. Adv Exp Med Biol. 2009;629:179–199. doi: 10.1007/978-0-387-77064-2_9. [DOI] [PubMed] [Google Scholar]
- O'Doherty JE, Lebedev MA, Hanson TL, Fitzsimmons NA, Nicolelis MA. A brain-machine interface instructed by direct intracortical microstimulation. Front Integr Neurosci. 2009;3:20. doi: 10.3389/neuro.07.020.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Okatan M, Wilson MA, Brown EN. Analyzing functional connectivity using a network likelihood model of ensemble neural spiking activity. Neural Comput. 2005;17:1927–1961. doi: 10.1162/0899766054322973. [DOI] [PubMed] [Google Scholar]
- Pohlmeyer EA, Solla SA, Perreault EJ, Miller LE. Prediction of upper limb muscle activity from motor cortical discharge during reaching. J Neural Eng. 2007;4:369–379. doi: 10.1088/1741-2560/4/4/003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pohlmeyer EA, Oby ER, Perreault EJ, Solla SA, Kilgore KL, Kirsch RF, Miller LE. Toward the restoration of hand use to a paralyzed monkey: brain-controlled functional electrical stimulation of forearm muscles. PLoS One. 2009;4:e5924. doi: 10.1371/journal.pone.0005924. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Radhakrishnan SM, Baker SN, Jackson A. Learning a novel myoelectric-controlled interface task. J Neurophysiol. 2008;100:2397–2408. doi: 10.1152/jn.90614.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rokni U, Richardson AG, Bizzi E, Seung HS. Motor learning with unstable neural representations. Neuron. 2007;54:653–666. doi: 10.1016/j.neuron.2007.04.030. [DOI] [PubMed] [Google Scholar]
- Scherberger H. Neural control of motor prostheses. Curr Opin Neurobiol. 2009;19:629–633. doi: 10.1016/j.conb.2009.10.008. [DOI] [PubMed] [Google Scholar]
- Sergio LE, Hamel-Pâquet C, Kalaska JF. Motor cortex neural correlates of output kinematics and kinetics during isometric-force and arm-reaching tasks. J Neurophysiol. 2005;94:2353–2378. doi: 10.1152/jn.00989.2004. [DOI] [PubMed] [Google Scholar]
- Serruya M, Hatsopoulos N, Fellows M, Paninski L, Donoghue J. Robustness of neuroprosthetic decoding algorithms. Biol Cybern. 2003;88:219–228. doi: 10.1007/s00422-002-0374-6. [DOI] [PubMed] [Google Scholar]
- Shoham S, Fellows MR, Normann RA. Robust, automatic spike sorting using mixtures of multivariate t-distributions. J Neurosci Methods. 2003;127:111–122. doi: 10.1016/s0165-0270(03)00120-1. [DOI] [PubMed] [Google Scholar]
- Song W, Ramakrishnan A, Udoekwere UI, Giszter SF. Multiple types of movement-related information encoded in hindlimb/trunk cortex in rats and potentially available for brain–machine interface controls. IEEE Trans Biomed Eng. 2009;56:2712–2716. doi: 10.1109/TBME.2009.2026284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stevenson IH, Körding KP. On the similarity of functional connectivity between neurons estimated across timescales. PLoS One. 2010;5:e9206. doi: 10.1371/journal.pone.0009206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stevenson IH, Rebesco JM, Miller LE, Körding KP. Inferring functional connections between neurons. Curr Opin Neurobiol. 2008;18:582–588. doi: 10.1016/j.conb.2008.11.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suminski AJ, Tkach DC, Hatsopoulos NG. Exploiting multiple sensory modalities in brain-machine interfaces. Neural Netw. 2009;22:1224–1234. doi: 10.1016/j.neunet.2009.05.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor DM, Tillery SI, Schwartz AB. Direct cortical control of 3D neuroprosthetic devices. Science. 2002;296:1829–1832. doi: 10.1126/science.1070291. [DOI] [PubMed] [Google Scholar]
- Truccolo W, Eden UT, Fellows MR, Donoghue JP, Brown EN. A point process framework for relating neural spiking activity to spiking history, neural ensemble, and extrinsic covariate effects. J Neurophysiol. 2005;93:1074–1089. doi: 10.1152/jn.00697.2004. [DOI] [PubMed] [Google Scholar]
- Velliste M, Perel S, Spalding MC, Whitford AS, Schwartz AB. Cortical control of a prosthetic arm for self-feeding. Nature. 2008;453:1098–1101. doi: 10.1038/nature06996. [DOI] [PubMed] [Google Scholar]
- Wirth S, Yanike M, Frank LM, Smith AC, Brown EN, Suzuki WA. Single neurons in the monkey hippocampus and learning of new associations. Science. 2003;300:1578–1581. doi: 10.1126/science.1084324. [DOI] [PubMed] [Google Scholar]
- Zacksenhouse M, Lebedev MA, Carmena JM, O'Doherty JE, Henriquez C, Nicolelis MA. Cortical modulations increase in early sessions with brain-machine interface. PLoS One. 2007;2:e619. doi: 10.1371/journal.pone.0000619. [DOI] [PMC free article] [PubMed] [Google Scholar]