Abstract
Background and Aims
Flower shapes are important visual cues for pollinators. However, the ability of pollinators to discriminate between flower shapes under natural conditions is poorly understood. This study focused on the diversity of flower shape in Primula sieboldii and investigated the ability of bumblebees to discriminate between flowers by combining computer graphics with a traditional behavioural experiment.
Methods
Elliptic Fourier descriptors described shapes by transforming coordinate information for the contours into coefficients, and principal components analysis summarized these coefficients. Using these methods, artificial flowers were created based on the natural diversity of petal shape in P. sieboldii. Dual-choice tests were then performed to investigate the ability of the bumblebees to detect differences in the aspect ratio of petals and the depth of their head notch.
Key Results
The insects showed no significant ability to detect differences in the aspect ratio of the petals under natural conditions unless the morphological distance increased to an unrealistic level. These results suggest the existence of a perception threshold for distances in this parameter. The bumblebees showed a significant preference for narrow petals even after training using flowers with wide petals. The bumblebees showed a significant ability to discriminate based on the depth of the petal head notch after training using artificial flowers with a deep head notch. However, they showed no discrimination in tests with training using extreme distances between flowers in this parameter.
Conclusions
A new type of behavioural experiment was demonstrated using real variation in flower corolla shape in P. sieboldii. If the range in aspect ratios of petals expands much further, bumblebees may learn to exhibit selective behaviour. However, because discrimination by bumblebees under natural conditions was low, there may be no strong selective behaviour based on innate or learned preferences under natural conditions.
Key words: Bumblebee, computer graphics, elliptic Fourier descriptors, flower corolla shape, Primula sieboldii, principal components analysis, visual cue
INTRODUCTION
Intraspecific diversity in the phenotypic characteristics of flower corollas, such as colour, shape and pattern, has been widely observed in entomophilous plants. Many ecologists have focused on this diversity in the context of co-evolution of wild plants and their insect pollinators. The colour, shape and pattern of flower corollas are considered to be important visual cues that attract their pollinators (Dafni et al., 1997; Giurfa and Lehrer, 2001). Among the several visual cues, many studies have investigated the discrimination ability of pollinators with respect to colour, and revealed that pollinators such as bees, flies and butterflies show strong preferences for a particular colour, and can discriminate among flowers based on differences in this characteristic (e.g. Lunau, 1990; Giurfa et al., 1995; Johnson and Dafni, 1998; Gumbert, 2004). Several studies also investigated the ability of pollinators to discriminate among flowers based on shapes and patterns using behavioural studies that employed artificial variation in these characteristics (Gould, 1985; Dafni et al., 1997; Johnson and Dafni, 1998; Giurfa and Lehrer, 2001). However, the ability of pollinators to discriminate among the shapes of flower corollas under natural conditions has not yet been supported by a large body of evidence. The present study focused on the impact of variation in flower corolla shapes in Primula sieboldii, used as a model flower, to determine whether bumblebees could discriminate between flowers based on shape characteristics. To do so, computer graphics were combined with a traditional behavioural experiment.
Numerous researchers have performed behavioural experiments using artificial flowers to investigate the ability of insect pollinators to discriminate among flower shapes or patterns (Gould, 1985; Johnson and Dafni, 1998; Hempel de Ibarra and Giurfa, 2003). The main advantage of using artificial flowers is that they allow researchers to standardize the flower characteristics and focus on a single target characteristic. However, the artificial flowers used in these studies sometimes bear little resemblance to real flowers (e.g. they may be squares, discs or triangles), and the results cannot be easily applied to the true interaction between flower shape and insect behaviour that is observed under natural conditions. In contrast, many behavioural experiments have used real flowers. However, in this approach, it is difficult to standardize flower characteristics other than the target characteristic, such as the reward (pollen and nectar), plant architecture and odour. Therefore, the results of these studies are distorted to a greater or lesser extent by variations in characteristics other than the target characteristic. Bradshaw and Schemske (2003) overcame this problem by using near-isogenic lines (NILs) that differed only in the target characteristic in their pollination study of monkeyflowers (Mimulus spp.). However, because it takes a prohibitive amount of time to breed NILs with specific floral characteristics, it is almost impossible in practice to use NILs in this manner for species with long generation times, such as perennial herbs and trees. Therefore, performing behavioural experiments with these species requires an effective alternative to these two traditional approaches.
Recent improvements in digital image processing and in digital imaging hardware and software may allow researchers to develop new methodologies for behavioural experiments. For example, much progress has been made in quantifying the shapes of plant organs based on image information (McLellan, 1993; Furuta et al., 1995; Horgan, 1998; McLellan and Endler, 1998; Theobald et al., 2004; Langlade et al., 2005), and these techniques have been used in genetic, developmental and evolutionary studies of organ shapes (Yamanaka et al., 2001; Iwata et al., 2002; Langlade et al., 2005; Yoshioka et al., 2005, 2006). Of these methods, a combination of elliptic Fourier descriptors and principal components analysis (EF-PCA) appears to be most effective for quantitative evaluation of organ shapes. EF-PCA describes the overall shape of an organ mathematically by transforming coordinate information for its contours into elliptic Fourier coefficients (Kuhl and Giardina, 1982), then summarizes these coefficients by means of principal components analysis (Rohlf and Archie, 1984). This method is also effective in reproducing natural organ shapes from the results of the analysis, i.e. it is possible easily to reconstruct shapes with particular scores in the quantitative variables determined by the analysis. This permits effective creation of artificial flowers with natural shapes using computer graphics based on the results of EF-PCA of the diversity of shapes of real flowers, and makes it possible to use these artificial flowers in conventional behavioural studies.
Primula sieboldii, whose main pollinators are bumblebees, is an appropriate model species because of the diversity of flower shapes in wild populations and the simple structure of its flowers, which consist of five petals that are approximately uniform in shape. Because the petals are arranged radially in a single plane, the variation in petal shape directly affects the flower shape, and it is easy to create artificial flowers that bear a strong resemblance to natural flowers. Yoshioka et al. (2005) analysed the petal shape variation in wild populations of this species by means of EF-PCA, and reported that petal shape varies significantly in terms of the ratio of length to width and in the depth of the head notch. Note, however, that this diversity is defined from a human perspective, and may not be visible to insect pollinators. Whether pollinators can detect variations in these morphological characteristics and whether these characteristics undergo selection based on pollinator behaviour (preferences and ability to discriminate between flowers) in wild populations is a fundamental question in studies of the mechanisms responsible for the formation of intraspecific diversity in flower shape in this species.
The present study demonstrates the effectiveness of combining a traditional behavioural study (the observation of pollinator choice) with image processing methods that are used to create artificial flowers based on the real variation in the characteristics of flowers of P. sieboldii that is observed in nature. In addition, a discussion is provided on whether the diversity in flower corolla shape provides visual cues under natural conditions.
MATERIALS AND METHODS
Plant materials and image analysis
Primula sieboldii E. Morren is a temperate herbaceous species found in Japan, the Korean peninsula, north-eastern China and eastern Siberia (Yamazaki, 1993). Insects, including bees, syrphids and butterflies, are known to visit flowers of this species in Japan (Washitani et al., 1995). Among these species, queens of Bombus diversus diversus Smith and B. diversus tersatus Smith (Hymenoptera: Apidae) are the most important pollinators (Washitani et al., 1995). At flowering time (from April to June) in 2002, 323 fresh flowers were randomly collected from 160 genets of eight Japanese populations of the species. Because these materials were analysed in previous research (Yoshioka et al., 2005), the present report only summarizes the methods and the results of the image analysis.
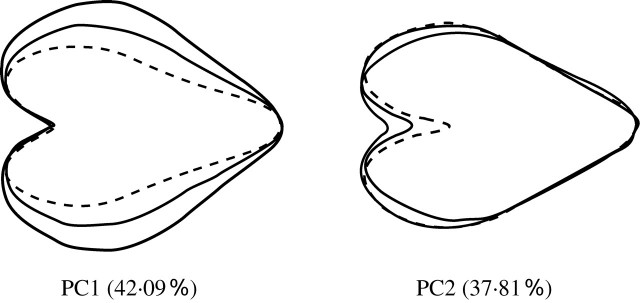
The closed contours of each petal were obtained as chain-coded data from digital images of the petals (Freeman, 1974). The coefficients of the elliptic Fourier descriptors (EFDs), which were normalized to avoid variations related to petal size, rotation and starting point of the contour trace, were then calculated from the chain-coded data using the procedure proposed by Kuhl and Giardina (1982). Using this procedure, the shape of each petal was approximated using the first 20 harmonics, and thus 80 (4 × 20) standardized EFDs were calculated, To summarize the information contained in the coefficients, a PCA was performed based on a variance–covariance matrix using average coefficients for the flowers. As a result, the first two principal components (PCs) provided a good summary of the 80 standardized EFDs, accounting for 42·09 and 37·81 %, respectively, of the petal shape variation. The effect of each PC on petal shape was visualized (Fig. 1) from the coefficients of the EFDs, which were recalculated inversely using an eigenvector matrix, letting the score for a particular PC equal the mean ± 2 standard deviations (s.d.) while leaving the scores of the remaining components equal to the mean. An additional series of trials was performed using the mean ± 4 s.d. to define the flower shapes. The reconstructed contours indicated that the first and second PCs represented the aspect ratio of the petal (i.e. the ratio of its length to its width) and the depth of the petal's head notch, respectively (Fig. 1), and these two PCs were thus used as representative characteristics of petal shape in the present study. Figure 2 shows the range of variation of these two PCs in wild P. sieboldii. The image analysis was described in detail by Yoshioka et al. (2004).
Fig. 1.
The effects of the first (PC1) and second (PC2) principal components on the petal shape of Primula sieboldii. Each shape was reconstructed using elliptic Fourier descriptors calculated by setting the score for the corresponding PC equal to its mean and to its mean plus or minus twice the standard deviation (±2 s.d.), and setting the scores for the remaining principal components to zero. Dashed, solid and thick solid lines represent the mean –2 s.d., the mean, and the mean + 2 s.d., respectively.
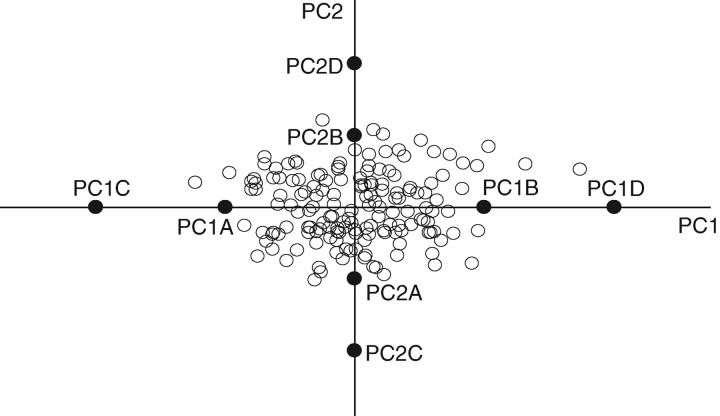
Fig. 2.
Petal shape variations in wild Primula sieboldii and in the artificial flowers used in this study in terms of the first and second principal components (PC).
Artificial flowers
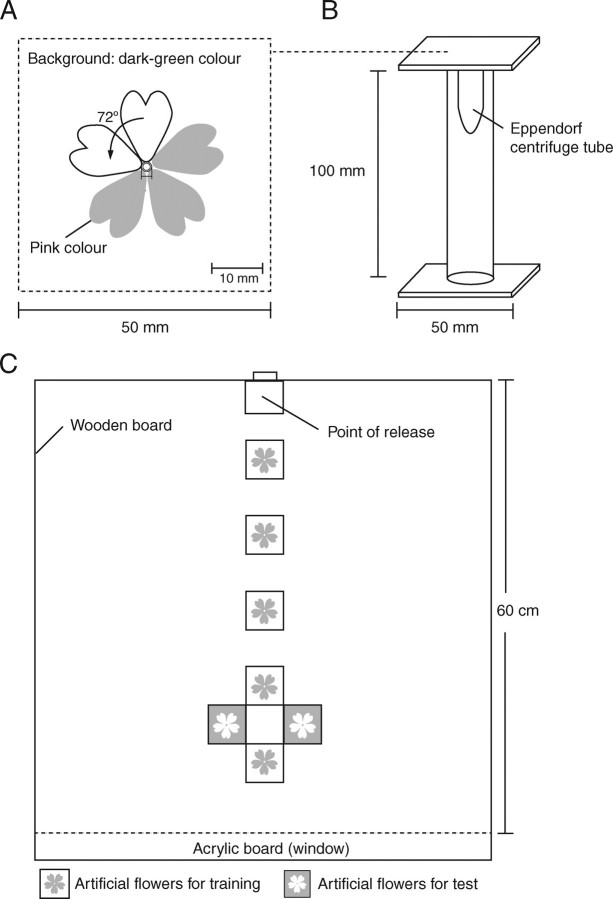
Artificial flowers that fit within a 5 cm square were drawn using the Illustrator 10 software (Adobe Systems, Inc., San Jose, CA, USA). To create the flowers, the contour of a single petal was rotated clockwise at four intervals of 72° around a circle with a radius of 1 mm (Fig. 3A). All petals had the same colour (a shade of pink chosen to match the colour of the real flowers from a human perspective) and were presented on the same dark-green background. Petal length (defined here as the length of the central axis of the petal) was equal for all artificial flowers, thus the diameters of the corolla of the artificial flowers were identical. The pictures of the flowers were printed using a colour inkjet printer (PX-V630, Epson, Tokyo, Japan) on white flock paper, and were attached to the upper surface of a three-dimensional structured platform (Fig. 3B). Four types of artificial flowers were created, with reconstructed contours created using the mean of each PC ± 2 s.d. (PC1B and PC1A, respectively, for PC1, and PC2B and PC2A, respectively, for PC2) and the mean of each PC ± 4 s.d. (PC1D and PC1C, respectively, for PC1, and PC2D and PC2C, respectively, for PC2). The resulting flower shapes are shown in Fig. 2, and the test designs using these flowers are illustrated in Figs 4 and 5.
Fig. 3.
Schematic diagrams of the artificial flowers and flight arena used in this study. (A) The artificial flower was created by rotating a single petal contour four times, at intervals of 72°, to produce a five-petal flower. (B) A three-dimensional illustration of the structured platform used to support the artificial flowers. These platforms were arranged as illustrated in (C) during the experiments. (C) Top view of the flight arena, showing the location of the flower platforms.
Fig. 4.
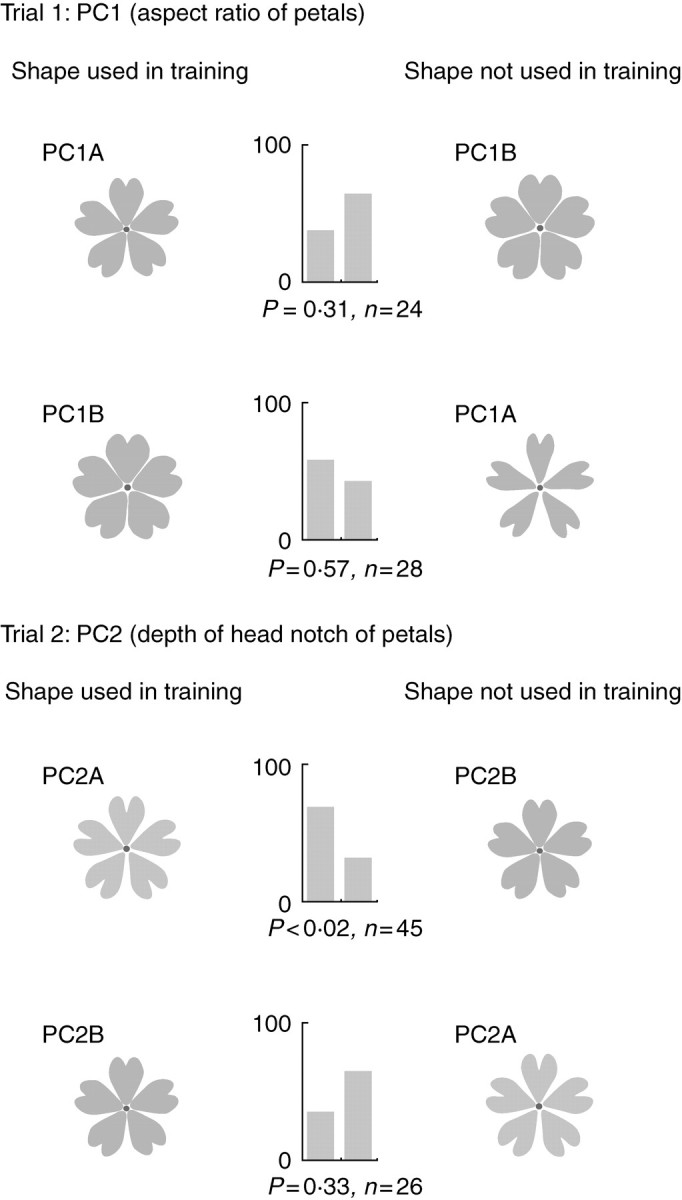
The artificial flowers used in trials 1 and 2, and the results of the choice tests. In each trial, two choice tests were performed by changing the artificial flowers used for training. Bumblebees were trained using the artificial flowers at the left side of the figure. Bar charts show the percentage of the bumblebees that selected the flowers on the left and right, respectively. P, probability (two-tailed binomial test); n, number of bumblebees used in each test.
Fig. 5.

The artificial flowers used in trials 3 and 4, and the results of the choice tests. In each trial, two choice tests were performed by changing the artificial flowers used for training. Bumblebees were trained using the artificial flowers at the left side of the figure. Bar charts show the percentage of the bumblebees that selected the flowers on the left and right, respectively. P, probability (two-tailed binomial test); n, number of bumblebees used in each test.
Although the quantitative variables used to define the petal shape (i.e. PC1 and PC2) contributed the majority of the variation in shape of the artificial flowers, other differences between the artificial flowers resulted from overlapping of the petals (e.g. see PC1B in Fig. 4 and PC1D in Fig. 5). Therefore, although the artificial flowers clearly differed to human eyes, other objective measurements would be required to compare the flower shapes in more detail. To provide this information, the area of the flower corolla (cm2), the contour length (cm) and the contour density (cm–1; the ratio of contour length to the area of the flower corolla) were calculated; these are commonly used measurements in pollination ecology (Dafni and Kevan, 1997; Dafni and Neal, 1997).
Insects
Colonies of the bumblebee Bombus ignitus were obtained from Arysta LifeScience Corporation (Tokyo, Japan). Note that this species is not the primary pollinator of P. sieboldii. Since it is difficult to obtain the queens of B. diversus, commercial colonies of B. ignites were substituted for those of B. diversus. Colonies were provided with pollen daily and with sucrose solution in feeder tubes when they were not being used in experiments. More than 200 workers from four colonies were used throughout the experiments (i.e. 40–60 workers per colony). The bumblebees had no experience foraging on any artificial flower prior to the experiments.
Experimental design
A nest box was connected to a flight arena (60 × 60 × 60 cm) with one wall constructed from translucent acrylic board (Fig. 3C). The floor of the arena was coloured green. Light was provided by two fluorescent lamps and two black-light (UV) lamps. Before the experiments, bumblebees were allowed to familiarize themselves freely with the arena, but were not exposed to the artificial flowers.
During the training phase, bumblebees were trained for 1–2 d using target artificial flowers that contained a reward in the form of 20% sucrose solution in an Eppendorf centrifuge tube (Fig. 3B). During this phase, five artificial flowers were offered arranged in a straight line from the release point in the flight arena (Fig. 3C). Bumblebees that landed and fed on the artificial flowers many times were marked with coloured ink. On the day after this initial training phase, the bumblebees were again allowed to land and feed on the artificial flowers for 30 min to 1 h, but this time the reward was a 30% sucrose solution. In this second phase, bumblebees painted with the first colour were marked on their thorax or abdomen using a different colour. This approach was used to increase the foraging motivation by using high rewards, and to reconfirm that the bumblebees had learned to recognize the artificial flowers.
In the subsequent test phase, bumblebees painted with two different colours were used to test whether the insects could correctly choose the target artificial flower when offered the choice of a different artificial flower. During the test phase, only one bumblebee at a time was allowed to enter the arena. To avoid any effect resulting from the positions of the artificial flowers during the training phase, two artificial flowers were arranged on opposite sides of the line of five artificial flowers that were used during the training phase (Fig. 3C). The bumblebee was allowed to fly freely in the flight arena and choose between the learned artificial flower and an artificial flower with a different shape. The first artificial flower on which the bumblebee landed was recorded. After each test, the bumblebee and the two artificial flowers were removed from the flight arena and replaced with new flowers and a new bumblebee for the next test. Thus, each bumblebee and each flower was used only once.
The choice tests were performed using pairs of artificial flowers for PC1 (PC1A vs. PC1B, referred to as trial 1) and PC2 (PC2A vs. PC2B, referred to as trial 2) to determine whether the bumblebees could discriminate differences in flower shape based on these characteristics. In each trial, two choice tests were performed by changing the target artificial flowers. Thus, a total of four tests were performed. In each test, each artificial flower was assigned alternately to either the right or the left position to determine whether flower position affected the results. During these tests, a choice test using artificial flowers with and without pink petals was also performed to determine whether the bumblebees responded to the pink flower colour, because the spectrum visible to bumblebees differs from that visible to humans. Frequency of choice between the right and left artificial flowers in the first experiments was compared using a binomial test (H0, right: left = 1 : 1). If the null hypothesis was not rejected, it was concluded that the bumblebees had no preference for artificial flowers based on their position. In that case, the frequency of choice between the two artificial flowers in each of the remaining tests was compared using a two-tailed binomial test. The same procedure was followed to test the ability of the bumblebees to discriminate between flowers that differed from the mean by ± 4 s.d.; these are referred to as trials 3 and 4, respectively (Fig. 5).
RESULTS
The artificial flowers differed greatly to the human eye, as well as quantitatively (Table 1). The distances between two artificial flowers in terms of their morphological characteristics in trial 1 were larger than those in trial 2 for all measurements (Table 1), although the proportion of variance in the PCA did not differ greatly between PC1 (42·09 %) and PC2 (37·81%).
Table 1.
Quantitative measurements of the artificial flowers and the morphological distance between the two artificial flowers used in each trial
| Artificial flower | Area (cm2) | Contour length (cm) | Contour density (cm−1) | |
|---|---|---|---|---|
| Trial 1 | ||||
| PC1A | 3·760 | 20·608 | 5·480 | |
| PC1B | 6·174 | 13·260 | 2·148 | |
| Distance | 2·414 | 7·348 | 3·333 | |
| Trial 2 | ||||
| PC2A | 4·753 | 23·477 | 4·940 | |
| PC2B | 4·696 | 20·030 | 4·265 | |
| Distance | 0·057 | 3·447 | 0·674 | |
| Trial 3 | ||||
| PC1C | 2·691 | 20·096 | 7·468 | |
| PC1D | 6·131 | 11·502 | 1·876 | |
| Distance | 3·440 | 8·594 | 5·592 | |
| Trial 4 | ||||
| PC2C | 4·761 | 25·707 | 5·400 | |
| PC2D | 4·362 | 18·999 | 4·355 | |
| Distance | 0·399 | 6·708 | 1·044 | |
The bumblebees showed no preference for the right or left artificial flowers (right: left = 17 : 13, P = 0·58), and showed a strong and highly significant preference for the pink flowers (pink flower: drawing only = 25 : 5, P < 0·001). These results indicated that the bumblebees responded strongly to the pink colour of the artificial flower, and that the position of the flowers did not affect the results of the choice tests.
In trial 1 (PC1, aspect ratio of petals), it was found that the bumblebees showed no preference for the artificial flowers used in training for flowers with narrow petals (PC1A) and flowers with wide petals (PC1B; Fig. 4). In trial 2 (PC2, depth of the head notch of the petals), it was found that the bumblebees showed a significant preference for the artificial flowers used in training when they were trained with flowers that had a deep head notch (PC2A; Fig. 4). However, they showed no preference for the artificial flowers used in training when they were trained using petals with a shallow head notch (PC2B; Fig. 4).
When the choice tests were performed again using a greater morphological distance between the flowers (mean ± 4 s.d.), the resulting shape variations were never observed in the wild populations (Fig. 2). The morphological distances between two artificial flowers in trial 3 were approximately 1·4, 1·2 and 1·7 times larger than those in the trial 1 for the area of the corolla, the contour length and the contour density, respectively (Table 1). The morphological distances between two artificial flowers in trial 4 were approximately 7·0, 1·9 and 1·5 times those in trial 2 for the area of the corolla, the contour length and the contour density, respectively (Table 1). The distances between the artificial flowers in trial 3 were larger than those in trial 4 for all measurements (Table 1). Because the choice tests were performed similarly in all trials, the results suggest that the bumblebees showed significant preferences for the artificial flowers used in training when they were trained with flowers with extremely narrow petals (PC1C) in trial 3 (Fig. 5). Interestingly, the bumblebees also showed significant preference for flowers with extremely narrow petals (PC1C) even when they were trained using flowers that had extremely wide petals (PC1D). However, the bumblebees showed no preference for the artificial flowers used in training when they were trained using flowers with extremely deep head notches (PC2C) and flowers with extremely shallow head notches (PC2D) in trial 4 (Fig. 5).
DISCUSSION
Artificial flowers were successfully created based on the EFDs and PCA that strongly resembled real flowers, and these artificial flowers were used to investigate the ability of bumblebees to discriminate between flowers based on the differences in two shape components of the flower corolla (i.e. the petal aspect ratio and the depth of the petal's head notch). Several studies have reported that insects can discriminate between artificial flowers based on their shape or pattern (Lehrer et al., 1995; Dafni et al., 1997; Johnson and Dafni, 1998). However, these studies have not used artificial flowers that fall within the range of natural variation in shape of the flower corolla. In the present study, this problem was addressed for intraspecific variation in the shape of the flower corolla of P. sieboldii.
The new method described here can be applied to other species whose flower corollas have a simple structure like that of P. sieboldii. Although only two PCs were used separately to create the artificial flowers, future behavioural research could use artificial flowers whose shapes are determined using additional PCs (e.g. PC3, PC4) or using simultaneous variations in two or more PCs. In addition, if the goal is to investigate the differences between flower corollas of two related species, artificial flowers created using the mean PC scores for each species (i.e. the mean corolla shape) could be effectively used in behavioural experiments.
Because it appears that the two artificial flowers in trial 1 (which compared two aspect ratios of the petals, PC1A and PC1B) differed greatly to the human eye, and it was thus expected that the bumblebees could discriminate between flowers based on these differences, it was surprising that the bumblebees showed no significant discrimination (Fig. 4). However, in trial 3 (which compared PC1C and PC1D, with unnaturally exaggerated aspect ratios), the bumblebees showed a significant ability to discriminate between flowers, suggesting that a perception threshold lying between the morphological distances of the artificial flowers used in trials 1 and 3 (i.e. between 2 and 4 s.d. from the mean) determines the point at which the bumblebees can discriminate between flowers. Interestingly, the bumblebees showed a significant preference for flowers with extremely narrow petals (PC1C) even when they were trained using flowers with extremely broad petals (PC1D) in trial 3. This result suggested that bumblebees may have an innate preference for flowers with very narrow petals.
Based on the other measurements of flower corolla shape, the main differences in the morphological distances between artificial flowers in trials 1 and 3 included the area of the flower corolla and the contour density. For the area of the flower corolla, PC1D was clearly larger than PC1C (Table 1), but the bumblebees preferentially visited PC1C (Fig. 4). This suggests that flowers with a large area do not have an advantage in attracting the bumblebees for flowers with equal diameter. Contour density has long been regarded as an important parameter in the attraction of bees, and bees prefer highly dissected shapes with a high contour density (Dafni and Neal, 1997; Dafni et al., 1997; Johnson and Dafni, 1998). In the present study, the artificial flower PC1C had the highest contour density (Table 1) and the narrow pink petals seemed to indicate strongly the exact location of the centre of the flower's corolla. This morphological feature could be responsible for the preference of the bumblebees for PC1C, in agreement with findings of previous reports.
For PC2 (the depth of the head notch of the petals), the bumblebees showed a significant ability to discriminate between artificial flowers only when they were trained with flowers that had a deep head notch (PC2A; Fig. 4). If bumblebees have an innate preference for artificial flowers with deep head notches (a high contour density; Table 1), this result would be reasonable. However, in trial 4 (which compared PC2C and PC2D), bumblebees showed no ability to discriminate between flowers based on head notch depth, irrespective of which artificial flowers were used in training, even though the morphological distances between the two artificial flowers in their PC scores and other quantitative measurements increased (Table 1). Although it cannot be stated, based on the present data, whether this discrepancy between the results of trials 2 and 4 was caused by artificial errors or by chance, two important considerations that may partially explain this discrepancy are mentioned here.
First, the continuous variation detected by means of EF-PCA does not necessarily correspond to the visual perception of bumblebees. Secondly, although the main morphological features of PC2 certainly relate to differences in the depth of the head notch of the petal, differences in the curvature of the sides of the petal also arise from changes in PC2 (Fig. 2), and these differences may be an important feature in visual perception by bumblebees. If these observations are significant, then even if the differences in PC2 of the two artificial flowers is enhanced from 2 to 4 s.d., this enhancement is not important for the bumblebees and the 2 s.d. difference in the artificial flowers would affect the discrimination capability of the bumblebees more than the 4 s.d. difference. To determine the factors that explain this discrepancy, it will be important for future studies to examine the method used to create the artificial flowers and the design of the behavioural experiment.
When the shape of the flower corolla provides visual cues in wild populations of P. sieboldii, there are two possible scenarios in which the shape of the corolla will directly or indirectly affect pollinator behaviour. First, if the shape of the corolla is related to an innate preference of the pollinators, genotypes with a particular corolla shape may be preferentially selected under natural conditions. Secondly, even when the shape of the corolla does not relate to an innate preference of the pollinators, genotypes with a particular corolla shape may be preferentially selected as a result of learned preferences if the bumblebees find that these genotypes offer a much greater reward (nectar or pollen). Although the ability to discriminate between flower shapes of P. sieboldii would differ between bumblebee species, and even between queen and worker, these senarios were discussed under the assumption that the queens of B. diversus and workers of B. ignitus have equivalent ability to discriminate between flower shapes. The morphological ranges of the two artificial flowers used in trials 1 and 2 (±2 s.d.) cover approx. 95 % of the variation among genotypes in wild populations of P. sieboldii. In these trials, many bumblebees visited the artificial flower that they did not experience during training for both PCs, and exhibited no ability to discriminate between two flowers except when they were trained with PC2A (the flowers with deeper head notches, but with the notch depth within the natural range of variation of the species). These results suggest that a behaviour of bumblebees based on innate or learned preferences might not be a strong selective force under current natural conditions. However, if the ranges in PC1 (the aspect ratio of the petals) expand to the extent used in trial 3 (±4 s.d.), possibly as a result of artificial breeding or natural selection based on a factor related to PC1, the bumblebees might exhibit the observed selective behaviour even under natural conditions.
In conclusion, the effectiveness of a new method of behavioural experiment using actual variation in the shape of the flower corolla of P. sieboldii (used here as a model flower) to create realistic artificial flowers was successfully demonstrated. Whether pollinating insects can discriminate among flowers based on variation in corolla shape and whether the variation affects pollinator behaviour are fundamental questions regarding the mechanisms responsible for the formation and maintenance of intraspecific diversity in the shapes of flower corollas in entomophilous plants. The method described herein could be used to answer these questions for many other plants.
ACKNOWLEDGEMENTS
We thank Mr H. Yoichi and Mr T. Fukatsu of the National Agricultural Research Center for their support during the construction of the equipment used in this study, and Dr I. Washitani and Dr M. Honjo of the University of Tokyo for sampling flowers from wild populations. Financial support was provided by the Environmental Research and Technology Development Fund of the Ministry of the Environment, Japan.
LITERATURE CITED
- Bradshaw HD, Jr, Schemske DW. Allele substitution at a flower colour locus produces a pollinator shift in monkeyflowers. Nature. 2003;426:176–178. doi: 10.1038/nature02106. [DOI] [PubMed] [Google Scholar]
- Dafni A, Kevan PG. Flower size and shape: implications in pollination. Israel Journal of Plant Sciences. 1997;45:201–211. [Google Scholar]
- Dafni A, Neal PR. Size and shape in floral advertisement: measurement, concepts and implications. Acta Horticulturae. 1997;437:121–140. [Google Scholar]
- Dafni A, Lehrer M, Kevan PG. Spatial flower parameters and insect spatial vision. Biological Reviews. 1997;72:239–282. [Google Scholar]
- Freeman H. Computer processing of line drawing images. Computing Surveys. 1974;6:57–97. [Google Scholar]
- Furuta N, Ninomiya S, Takahashi S, Ohmori H, Ukai Y. Quantitative evaluation of soybean (Glycine max L. Merr.) leaflet shape by principal component scores based on elliptic Fourier descriptor. Breeding Science. 1995;45:315–320. [Google Scholar]
- Giurfa M, Núñez J, Chittka L, Menzel R. Colour preferences of flower-native honeybees. Journal of Comparative Physiology A. 1995;177:247–259. [Google Scholar]
- Giurfa M, Lehrer M. Honeybee vision and floral displays: from detection to close-up recognition. In: Chittka L., Thomson JD, editors. Cognitive ecology of pollination. Cambridge: Cambridge University Press; 2001. pp. 61–82. [Google Scholar]
- Gould JL. How bees remember flower shapes. Science. 1985;227:1492–1494. doi: 10.1126/science.227.4693.1492. [DOI] [PubMed] [Google Scholar]
- Gumbert A. Color choices by bumble bees (Bombus terrestris): innate preference and generalization after learning. Behavioral Ecology and Sociobiology. 2004;48:36–43. [Google Scholar]
- Hempel de Ibarra N, Giurfa M. Discrimination of closed coloured shapes by honeybees requires only contrast to the long wavelength receptor type. Animal Behaviour. 2003;66:903–910. [Google Scholar]
- Horgan GW. The statistical analysis of plant part appearance – a review. Computers and Electronics in Agriculture. 1998;31:169–190. [Google Scholar]
- Iwata H, Nesumi H, Ninomiya S, Takano Y, Ukai Y. The evaluation of genotype × environment interactions of citrus leaf morphology using image analysis and elliptic Fourier descriptors. Breeding Science. 2002;52:243–251. [Google Scholar]
- Johnson SD, Dafni A. Response of bee-flies to the shape and pattern of model flowers: implications for floral evolution in a Mediterranean herb. Functional Ecology. 1998;12:289–297. [Google Scholar]
- Kuhl FP, Giardina CR. Elliptic Fourier features of a closed contour. Computer Graphics and Image Processing. 1982;18:236–258. [Google Scholar]
- Langlade NB, Feng X, Dransfield T, Copsey L, Hanna AI, Thébaud C, et al. Evolution through genetically controlled allometry space. Proceedings of the National Academy of Sciences of the USA. 2005;102:10221–10226. doi: 10.1073/pnas.0504210102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lehrer M, Horridge GA, Zhang SW, Gadagkar R. Shape vision in bees: innate preference for flower-like patterns. Philosophical Transactions of the Royal Society B: Biological Sciences. 1995;347:123–137. [Google Scholar]
- Lunau K. Colour saturation triggers innate reactions to flower signals: flower dummy experiments with bumblebees. Journal of Comparative Physiology A. 1990;166:827–834. [Google Scholar]
- McLellan T. The roles of heterochrony and heteroblasty in the diversification of leaf shapes in Begonia dregei (Begoniaceae) American Journal of Botany. 1993;80:796–804. [Google Scholar]
- McLellan T, Endler JA. The relative success of some methods for measuring and describing the shape of complex objects. Systematic Biology. 1998;47:264–281. [Google Scholar]
- Rohlf FJ, Archie JW. A comparison of Fourier methods for the description of wing shape in mosquitoes (Ritera culicidae) Systematic Zoology. 1984;33:302–317. [Google Scholar]
- Theobald CM, Glasbey CA, Horgan GW, Robinson CD. Principal component analysis of landmarks from reversible images. Journal of the Royal Statistical Society Series C. 2004;53:163–175. [Google Scholar]
- Washitani I, Kato M, Nishihiro J, Suzuki K. Importance of queen bumble bees as pollinatiors facilitating inter-morph crossing in Primula sieboldii. Plant Species Biology. 1995;9:169–176. [Google Scholar]
- Yamanaka N, Ninomiya S, Hoshi M, Tsubokura Y, Yano M, Nagamura Y, et al. An informative linkage map of soybean reveals QTLs for flowering time, leaflet morphology and regions of segregation distortion. DNA Research. 2001;8:61–72. doi: 10.1093/dnares/8.2.61. [DOI] [PubMed] [Google Scholar]
- Yamazaki T. Primula. In: Iwatsuki K, Yamazaki T, Boufford DE, Ohba H, editors. Flora of Japan 3a. Tokyo: Kodansha; 1993. pp. 87–94. [in Japanese] [Google Scholar]
- Yoshioka Y, Iwata H, Ohsawa R, Ninomiya S. Analysis of petal shape variation of Primula sieboldii by elliptic Fourier descriptors and principal component analysis. Annals of Botany. 2004;94:657–664. doi: 10.1093/aob/mch190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yoshioka Y, Iwata H, Ohsawa R, Ninomiya S. Quantitative evaluation of the petal shape variation in Primula sieboldii caused by breeding process in the last 300 years. Heredity. 2005;94:657–663. doi: 10.1038/sj.hdy.6800678. [DOI] [PubMed] [Google Scholar]
- Yoshioka Y, Iwata H, Hase N, Matsuura S, Ohsawa R, Ninomiya S. Genetic combining ability of petal shape in garden pansy (Viola × wittrockiana Gams) based on image analysis. Euphytica. 2006;151:311–319. [Google Scholar]