Nucleation and Decay Initiation Are the Stiffness-Sensitive Phases of Focal Adhesion Maturation

Abstract

A cell plated on a two-dimensional substrate forms adhesions with that surface. These adhesions, which consist of aggregates of various proteins, are thought to be important in mechanosensation, the process by which the cell senses and responds to the mechanical properties of the substrate (e.g., stiffness). On the basis of experimental measurements, we model these proteins as idealized molecules that can bind to the substrate in a strain-dependent manner and can undergo a force-dependent state transition. The model forms molecular aggregates that are similar to adhesions. Substrate stiffness affects whether a simulated adhesion is initially formed and how long it grows, but not how that adhesion grows or shrinks. Our own experimental tests support these predictions, suggesting that the mechanosensitivity of adhesions is an emergent property of a simple molecular-mechanical system.

Introduction

Cells sense and respond to the mechanical properties of their environment. A striking example of this mechanosensation is that undifferentiated mesenchymal stem cells that adhere to soft two-dimensional (2D) surfaces primarily become neural cell precursors, whereas on stiff surfaces they become bone cell precursors (1). Other adherent cell types also react differently to surfaces of different stiffness, forming large, long-lasting adhesions to the extracellular matrix (ECM) on stiff surfaces, and small, transient adhesions on soft surfaces (2). These cell-ECM adhesions are initially formed at the cell edge in a force- and ECM-stiffness-independent fashion (3). A fraction of these adhesions then increase in size and migrate toward the cell interior, where they eventually decay and disappear (4). The details about how force and ECM stiffness affect maturation probability, adhesion lifetime, and growth/decay processes are unclear. It is important to understand this mechanism so that we can understand how cells sense their mechanical environment (5) and how cancer metastasis is initiated (6).

For adhesions to be mechanosensitive, molecules in the adhesions must sense and respond to mechanical cues. Such molecular mechanosensitivity has been directly observed in several adhesion proteins that undergo force-dependent configuration changes (7–11). Furthermore, because chemical bonds are strain-sensitive, bonds between the cell and the ECM form most readily when molecules are in close proximity to surface binding sites and break most readily when the bond is highly strained. (Consider a binding-unbinding reaction. Over small strains, the bond may be approximated as linear-elastic, with stiffness κ_B. Then the Helmholtz free-energy difference (ΔA) between the bound and unbound states is ΔA = ΔV − TΔS, where V is the potential energy, S is the entropy, and T is the absolute temperature. The potential energy change ΔV includes the potential energy stored in the strained bond: κ_Bx²/2, where x is the bond stretch. Assuming a negligible volume change in the reaction, the equilibrium constant for the reaction K may be written as K = exp(−ΔA). It then follows that K(x) = K(0) exp(−κ_Bx²/2k_BT), implying that bonds form less frequently and/or are broken more frequently when the bond stretch, x, is large.) How does molecular mechanosensitivity translate to adhesion and cell mechanosensitivity? What factors determine how the size of an adhesion varies with time? Why are more numerous and longer-lasting cell-ECM adhesions formed on stiff surfaces than on soft surfaces? Here, we use stochastic simulations, experimental measurements, and theoretical calculations to answer these questions.

In this work, we develop an experimentally based molecular-mechanical model for cell-ECM adhesions and generate a series of predictions for adhesion behavior. These model predictions are shown to agree with our own experimental measurements. Finally, using a simplified model, we develop a theoretical framework to understand the model behaviors. We demonstrate that ECM stiffness affects whether an adhesion is initially formed and how long it grows, but not the growth or decay processes. These results support the view that adhesion dynamics and mechanosensitivity are emergent properties of generic molecular systems with load- and strain-dependent chemical reactions.

Model

To examine how cell-ECM adhesions grow and decay, and how this process depends on ECM stiffness, we introduce a molecular-mechanical model of adhesions. Our aim is to correctly model, at least qualitatively, the behavior of individual molecules in an adhesion, simulate the behavior of ensembles of these molecules, and make testable predictions. The predictions of the model, which we experimentally verify, depend on our model being 2D, forces having a vertical component, and adhesion molecules undergoing both constant force and constant distance reactions. Thus, these behaviors are not predicted by 1D models of adhesion growth (14–17), models that consider only the horizontal component of forces (14–16), or models that consider only constant force reactions (17). We now discuss the details of our molecular-mechanical model.

Cell-ECM adhesions are too complex to model exactly. Therefore, we simplify some aspects of the adhesions while retaining the aspects of adhesion mechanochemistry that are relevant to adhesion growth, decay, and ECM-stiffness dependence. These relevant adhesion properties occur at both the whole-adhesion level and the molecular level. We first consider the whole-adhesion level.

We define four relevant whole-adhesion properties. Cell-ECM adhesions contain hundreds of different protein types that form a dynamic plaque that is sensitive to force and ECM stiffness and is connected to the cytoskeleton through a force-generating, bundled cable of actin filaments (see Fig. 1 A). In this plaque, the proteins are precisely arranged (13,18). ECM-binding integrins spanning the cell membrane are laterally interconnected (18). Various force-sensitive proteins (e.g., talin and vinculin) connect to the integrins on the cell interior. Filamentous actin molecules form a large bundle called a stress fiber and connect a subset of molecules in the adhesion to the cytoskeleton via these force-sensitive proteins (13). Myosin associated with the stress fiber applies force to the adhesion. Thus, a model of a cell-ECM adhesion must include laterally interconnected ECM-binding molecules and force-sensitive molecules, and apply an external force to a subset of molecules in the adhesion.

Figure 1.

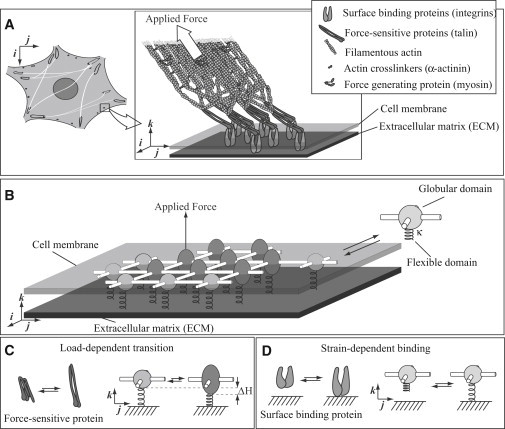
Molecular-mechanical adhesion model. (A) A schematic diagram of a small focal adhesion (adapted in part from Kanchanawong et al. (13)). (B) A schematic diagram of a modeled adhesion. Each molecule may form four lateral bonds to its neighbors, may bind to the surface through a flexible domain, and may exist in two states. (C) The globular domain undergoes a load-dependent extension of length $\Delta H$ from a circle state to an ellipse state, mimicking the load-dependent extension of proteins in the adhesion. (D) The flexible domain may reversibly bind to the surface, mimicking the surface-binding properties of proteins in the adhesion.

We propose a molecular adhesion model that shares these properties. Rather than representing each of the protein types in the adhesion, we lump these various proteins together into a single generic molecule. These generic molecules are arranged in a rectangular lattice (Fig. 1 B). These molecules may bind reversibly to four neighbors and may also bind to the surface, thereby satisfying the first property. Note that in analogy to lattice models for liquid systems, although our model assumes an ordered array of adhesion proteins, it nevertheless captures the basic physics of a disordered molecular arrangement (19). Allowing each molecule to undergo a force-dependent state transition simulates the action of force-sensitive proteins, satisfying the second property. Motivated by the fact that stiffness-sensitive nucleation, stability, growth, and decay in modeled adhesions depend only on the component of force normal to the surface, and wishing to avoid complexities associated with adhesion sliding, we assume that an external normal force is applied to a single molecule in the adhesion. Thus, the action of a stress fiber is modeled (see the Supporting Material for a discussion about the effects of tangential forces), satisfying the third and final property.

In addition to these overall adhesion properties, we must specify the properties of the adhesion molecules. In particular, we must specify which chemical reactions may occur in a growing adhesion and how fast these reactions occur. Additionally, we must specify precisely how external force and/or ECM stiffness will affect the rates of these reactions (20). By creating a simplified mechanical model of a molecule, we may predict these relations.

Molecular model

To specify which chemical reactions to include in our model, we first consider how adhesions in living cells behave. Three general classes of reactions can occur in an adhesion. Each of these reactions is reversible. First, free molecules may bind to or unbind from the adhesion. In our model, because molecules are arranged in a rectangular lattice, each generic molecule must therefore have a domain that binds to four other molecules. Second, force-sensitive molecules in the adhesion may undergo or reverse their force-dependent state transition. Generic molecules in our model must therefore exist in two internal states. Third, molecules in the adhesion may bind to or unbind from the ECM. Thus, molecules in our model must have an ECM-binding domain. Molecules in our model undergo these three reaction types via a rigid, globular domain connected to a flexible domain that acts as a linear spring of stiffness κ (Fig. 1 B).

The globular domain forms up to four lateral bonds, thereby allowing molecules to bind to and unbind from the adhesion. Free molecules bind to unoccupied sites of molecules in the adhesion at a constant rate. Thus, the unbinding rate of molecules in the adhesion can be determined from their free energy and the law of detailed balance. Note that these molecule-molecule bonds represent both the associative nature of adhesion molecules and lateral binding that presumably occurs through actin (18).

To satisfy the constraint that the molecule must exist in two states, we allow the globular domain to transition from a spherical (circle) state to an ellipsoidal (ellipse) state (see Fig. 1 C; a similar picture was previously proposed by Besser and Safran (16)). Because this state transition incorporates a shape change in the direction of force, force tends to favor the transition to the ellipse state. In particular, the transition rate from circle to ellipse increases exponentially with force, according to the simple Bell model (21) (neglecting effects that are important only at large forces, such as force-induced internal energy and entropy changes (22–25)). This force dependence has only a single free parameter: the vertical change in shape between the circle- and ellipse-state $\Delta H$. This force-dependent change has been experimentally measured in focal adhesion proteins such as talin (9), with $\Delta H\approx 15\text{nm}$. In our model, we purposefully chose a small $\Delta H=3\text{nm}$ to demonstrate that mechanosensitive adhesions form with even modest force dependence (see discussion in Supporting Material).

This force-dependent state transition affects the rate at which molecules unbind from the adhesion by changing the free energy of molecule-molecule bonds (recall that binding occurs at a constant rate). To define the model, we must therefore determine how the free energy of intermolecular bonds depends on the molecular state. Because external force is required for adhesion maturation (3, 26), we infer that force stabilizes intermolecular bonds. We incorporate this observation into our model by requiring that the circle state, which is favored at low force, forms lateral bonds less favorably than the ellipse state, which is favored at high force. In particular, the formation of a circle-circle bond results in a large free-energy increase $\left(\Delta G=4k_{\mathrm{B}}T\right)$, circle-ellipse bond formation results in a small free-energy increase $\left(\Delta G=1.5k_{\mathrm{B}}T\right)$, and the formation of an ellipse-ellipse bond results in a small free-energy drop $\left(\Delta G=-0.9k_{\mathrm{B}}T\right)$. Note that because we are more interested in qualitative than quantitative results, these free energies are somewhat arbitrary; it is the overall trend of a free-energy decrease from circle-circle to ellipse-ellipse that is important (see Supporting Material for a discussion of parameters). One potential biological interpretation of this force-dependent stability is that when force-sensitive molecules (such as talin) exist in their extended conformation, binding sites are exposed that reinforce bonds to neighboring molecules in the adhesion (26).

To satisfy the constraint that molecules in the adhesion may bind to and unbind from the ECM, the end of each molecule's flexible domain can bind to the ECM. As we now show, this binding rate depends on the separation between the molecules and the surface, the stiffness of the flexible domain, and the stiffness of the ECM. This ECM-stiffness dependence of surface binding underlies the adhesion mechanosensitivity in the model. Because this mechanosensitivity is a focus of this work, we consider surface binding in some detail below.

Effect of ECM stiffness

When molecules in an adhesion bind to the ECM, they are held a constant distance away from the ECM. Like constant force reactions, constant distance reactions, also called strain-dependent reactions, can be modeled with only a few parameters (27–29). We use a model in which strain-dependent reactions are defined with three parameters (27, 28), the most important of which is k, the assumed linear stiffness of the bond (the other two—the assumed constant width of the binding site and the minimum separation between the ECM and the globular domain—are discussed in the Supporting Material). The bond stiffness k incorporates the elasticity of the ECM in series with the molecule's elasticity, κ. Therefore, in conjunction with our mechanical model for the molecules, a mechanical model of the ECM allows us to predict the effect of separation distance on the molecule-ECM bonds (see Fig. 1 D).

ECM mechanics are likely complex and nonlinear. However, we expect that the qualitative behavior of the ECM is independent of its mechanical details. In particular, when the ECM is stiff, we expect that force applied to an ECM-bound molecule deforms the ECM much less than the molecule, giving an effective stiffness of $k\approx \kappa$. Conversely, when it is soft, the ECM deforms much more than the molecule, implying that ECM stiffness dominates the apparent stiffness of the molecule-surface bond (see Fig. 2). We can achieve this qualitative result by assuming that the ECM is semi-infinite, linear elastic, homogeneous, and isotropic, and that each molecule-surface bond acts in isolation of other molecule-surface bonds. With these assumptions, the stiffness of the ECM (as measured by its Young's modulus E) affects k through the relation

$$k=\frac{2\pi RE}{2\pi RE+3\kappa }\kappa ,$$ (1)

where R is the radius of the assumed circular area over which a molecule applies force to the ECM (28).

Figure 2.

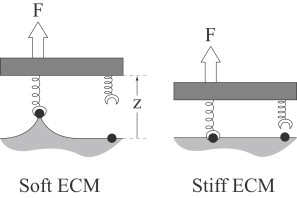
Thought experiment demonstrating how ECM stiffness affects bond formation. Under applied force, the ECM deforms more on a soft surface (left) than on a stiff surface (right). Bond formation is then slower on softer ECMs as described by Eq. 2.

Given this relation between ECM stiffness and bond stiffness, along with the bond-stiffness dependence of strain-dependent reactions, varying the ECM stiffness will change the probability of forming molecule-ECM bonds. This important result can be understood intuitively by means of the following simple thought experiment (see Fig. 2; a more detailed analysis is described in the Supporting Material): Consider a two-molecule system under force F. One of the two molecules is bound to the ECM, and we consider the rate at which the second molecule binds as a function of ECM stiffness, $r_b\left(E\right)$. For simplicity, we assume that the unbinding rate is independent of ECM stiffness r_u (note that although this value is likely a function of the force F, the force on the attached molecule is independent of ECM stiffness). By detailed balance, we may write

$$r_b\left(E\right)=r_u\exp \left(-\frac{k{z}^2}{2}\right),$$

where k is described by Eq. 1 above, and z is the distance between the equilibrium positions of the second molecule and its binding site (see Fig. 2). We recognize that kz is the force F, so that

$$r_b\left(E\right)=r_u\exp \left(-\frac{F^2}{2k}\right)=r_u\exp \left(-\frac{F^2\left(2\pi RE+3\kappa \right)}{4\pi RE\kappa }\right).$$ (2)

This equation shows that the binding rate reaches a maximum of $\max \left(r_b\right)\to r_u\exp \left(-F^2/2\kappa \right)$ on very stiff surfaces, and approaches a minimum of $\min \left(r_b\right)\to 0$ on very soft surfaces. Thus, although we use a more sophisticated treatment of these strain-dependent rate constants in the model, this simple model provides an intuitive explanation for why and how ECM stiffness affects binding rate.

Although the underlying molecular model is simple, the interaction of these various reactions is complex. For example, the force on a given molecule, which affects its transition rate between the circle and ellipse states, depends on whether the molecule is attached to the surface, the force on its neighbors, whether these neighbors are in the circle or ellipse state, and whether the molecule itself is in the circle or ellipse state. Similarly, the distance between the molecule and the ECM, which affects its binding probability, depends on the force on its neighbors, whether they are in the circle or ellipse state, whether the molecule itself is in the circle or ellipse state, and the stiffness of the ECM (these interactions and mathematical expressions that describe them are presented in the Supporting Material). Importantly, however, these complex interactions depend on a small number of mechanical and chemical parameters that we specify before performing simulations.

Both external force applied normally to the adhesion $\left(F\left(t\right)\right)$ and ECM stiffness (E) affect the chemical kinetics of molecules in this experimentally motivated mechanochemical model. Therefore, given expressions for $F\left(t\right)$ and E, and defining the parameters of the molecular model, we may observe when and how aggregates of these molecules tend to form (see Supporting Material for more simulation details). These simulations make specific predictions that are consistent with our own experimental tests, lending support to the assumptions of the model.

Simulations

After the parameters are estimated, simulations of the molecules show load- and ECM-stiffness-dependent aggregates that we identify as adhesions (see Fig. 3 A for still frames from a simulation, and Supporting Material for simulation details and a movie of a simulation). These adhesions increase in size and eventually decay and disappear. Adhesion formation requires the presence of external force and occurs preferentially on stiff ECMs. To compare the model with whole-cell measurements, we incorporate the model into a cell simulation in which nascent adhesions are formed at the cell edge in a time- and stiffness-independent fashion, and then move toward the cell interior with a time-dependent sliding rate (30) (see Supporting Material for simulation details and a movie of a simulation). We identify five specific properties of simulated adhesions:

• 1.Adhesion growth occurs, at least initially, as time squared (see Fig. 3 C).
• 2.Adhesion decay occurs either catastrophically or as time squared (see Fig. 3 D).
• 3.Both adhesion growth and decay are independent of ECM stiffness (see Fig. 3, C and D).
• 4.Adhesion nucleation occurs more easily on stiff than on soft ECMs (see Fig. 3 E).
• 5.Adhesion decay is initiated sooner on soft than on stiff ECMs (see Fig. 3 F).

Figure 3.

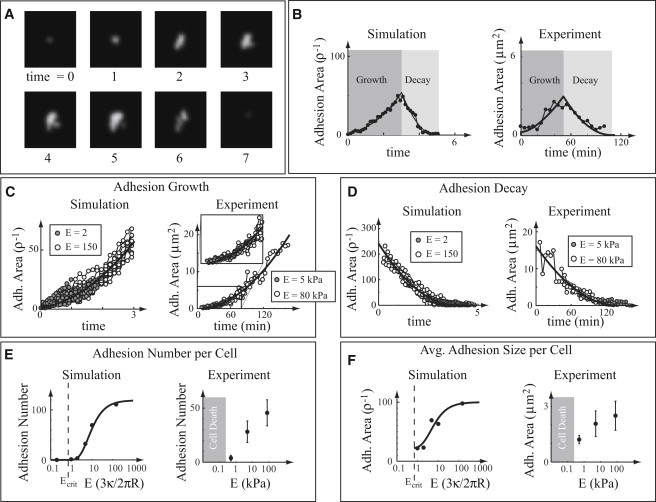
Comparison between simulations and experimental measurements of cultured cells. In plots B–F, simulations are shown on the left and experimental measurements are shown on the right. Time is measured in arbitrary units, and stiffness is measured in units of $3\kappa /2\pi R$ in the simulations. (A) Still shots of a simulation, showing adhesion growth and subsequent decay. (B) Adhesion size as a function of time, showing growth and decay. Fits are the best-fit quadratic. (C) Adhesion growth as a function of time for two different ECM stiffnesses. The best-fit quadratic is shown as a black line. (D) Adhesion decay as a function of time for two different ECM stiffnesses. The best-fit quadratic is shown as a black line. (E) Steady-state adhesion number per cell, as a function of ECM stiffness (note log scale). The solid curve is a guide for the eye. In simulations, an adhesion is defined as an aggregate > 20 molecules. (F) Steady-state average adhesion size per cell, as a function of ECM stiffness (note log scale). The solid curve is a guide for the eye.

We tested these specific predictions with a series of experimental measurements.

Experiments

To test the five predictions of the model, we performed a series of experiments with mouse embryonic fibroblast cells on collagen I-coated substrates of three different stiffnesses (see Supporting Material). We measured the total number of adhesions in these cells and the average size of these adhesions. Additionally, we measured the area of selected adhesions on the two stiffer ECM surfaces as a function of time.

Our measurements of individual adhesions and whole cells support the following model predictions (see Supporting Material for details):

• 1.Adhesion area growth as a function of time is well described by a single quadratic curve but not by a linear (p < 0.001) or exponential (p < 0.001) curve (see Fig. 3 C and Supporting Material for details of the statistics).
• 2.When adhesions do not catastrophically detach, they decay quadratically with time (see Fig. 3 D).
• 3.Adhesion growth and decay are independent of ECM stiffness, and thus adhesion size measurements on ECMs of different stiffness can be fit by a single curve (see Fig. 3, C and D).
• 4.Adhesions mature from nascent adhesions to adhesion complexes more frequently on stiff surfaces, leading to a greater number of adhesions on cells plated on stiffer ECMs (see Fig. 3 E).
• 5.Decay is initiated sooner on softer ECMs, leading on average to smaller adhesions in cells on softer ECMs (see Fig. 3 F).

We used simple calculations to investigate why the simulated adhesions display these five qualities. Given the agreement between simulation and experiment, we expect that this analysis will in turn provide insight into cell-ECM adhesion maturation in vivo under both normal and pathological conditions.

Theory

The full model of adhesion formation is complex. Here, to elucidate the behavior of this complex model, we introduce some simplifications. These simplifications allow us to obtain an intuitive explanation for why the complex model exhibits the five aspects of adhesion maturation enumerated above in the “Simulations” section.

Simplified model

To derive a simplified model for adhesion dynamics, we assume that adhesion growth occurs through three basic steps in the model:

• 1.A molecule in the adhesion that is attached to the ECM experiences sufficient load to transition to the ellipse state.
• 2.That ellipse-state molecule binds a circle-state molecule from outside the adhesion, forming a slightly unstable circle-ellipse bond.
• 3.The newly attached molecule binds to the ECM, thereby sharing some of the load on the adhesion.

The successful growth and maturation of an adhesion requires multiple cycles through these three steps (Fig. 4 A).

Figure 4.

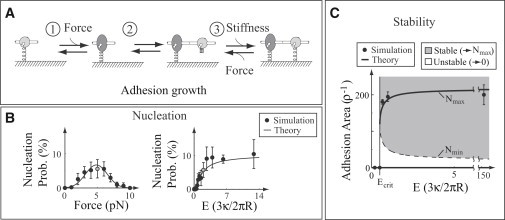
Comparison between simulations and simplified theory. Simulation details and theoretical expressions are presented in the Supporting Material. (A) The simple model, based on a three-step adhesion growth process. (B) Nucleation, the formation of a small molecular aggregate (10 molecules, in these simulations) from a single molecule as a function of force (left) and substrate stiffness (right). The gray point represents the same conditions in both plots. (C) Phase plot of stability as a function of adhesion size and surface stiffness. Here, stability is defined as an adhesion with a nonzero steady-state size.

The three-step growth process determines adhesion maturation and stability. By assuming that binding to and unbinding from the surface (step 3 in Fig. 4 A) occurs more slowly than the other steps (steps 1 and 2 in Fig. 4 A), we can further simplify the model. We can then understand the initial growth of adhesions (a process we call nucleation) through a master equation formalism. Then, using a mean-field approximation, we can analyze the system's steady state to understand adhesion stability, and the system's nonsteady state to understand growth and decay (a more detailed analysis is provided in the Supporting Material).

Master equation (nucleation)

Adhesion nucleation (i.e., the formation of a small molecular aggregate from one or a few molecules attached to the ECM) requires rapid adhesion growth before the few initially attached molecules detach from the ECM. Here, using the simple model, we provide an intuitive explanation for how force and ECM stiffness affect nucleation. Then, using a master equation analysis of the simple model, we justify this explanation by means of an analytic relationship. This analytic relationship is consistent with simulations of the full model and qualitatively consistent with experimental measurements.

The simple model intuitively explains how external force affects nucleation. In particular, the simple model predicts that external force applied to the adhesion affects growth in two places. First, applied force on the adhesion increases the force felt by attached molecules, thereby making the completion of step 1 (the transition from the circle to ellipse state) more likely; however, force increases the strain on a given molecule, thereby making completion of step 3 (surface binding) less likely (see Eq. 2). The balance of these two effects results in the existence of an optimal force, where a given adhesion has the highest growth rate.

Similarly, the simple model provides an intuitive explanation for the mechanosensitivity of nucleation. ECM stiffness affects the stability of adhesion-ECM bonds. On soft surfaces where adhesion-ECM bonds are most compliant (Eq. 1), the strain is large, and thus adhesion-ECM bonds are more easily broken and/or are less likely to be formed than on stiff surfaces, where strain is smaller (see Eq. 2). Therefore, as the ECM stiffness increases, molecules are more likely to be bound to the ECM, causing step 3 to occur more frequently and thereby increasing adhesion growth. Intuitively, then, we expect that adhesion nucleation occurs optimally at intermediate forces on stiff ECMs.

We may use a master equation approach to support this intuition. The general master equation formulation of even this simple model is rather difficult and has no readily found analytic solution. However, we may derive an expression for a simplified situation that we expect to be qualitatively similar to the more-complex case. In particular, we can find an analytic solution for the nucleation probability if we start with an ensemble of nascent adhesions of size N = 1 and define any nascent adhesion that reaches size N = 2 to be successfully nucleated. In this simplified situation, the probability of an adhesion becoming nucleated is the long-time limit of the solution to the differential equations

$$\begin{array}{l}\frac{d{P}_1}{dt}=-\left[r_d\left(F,E,1\right)+r_a\left(F,E,1\right)\right]P_1\hfill \\ \frac{d{P}_2}{dt}=r_a\left(F,E,1\right)P_1,\hfill \end{array}$$

where $r_a\left(F,E,N\right)$ and $r_d\left(F,E,N\right)$ are the rates of molecular attachment and detachment from the adhesion, respectively. Using the expressions for these rates derived in the Supporting Material, the nucleation probability (P_n) is

$$P_n\approx \frac{\exp \left(-F^2/2k{k}_{\text{B}}T\right)}{a_0+a_1\exp \left(-F\Delta H/k_{\text{B}}T\right)+\exp \left(-F^2/2k{k}_{\text{B}}T\right)}$$ (3)

where the nondimensional parameters a₀ and a₁ respectively depend on the rate and equilibrium constants of the simple model in Fig. 4 B, and $\Delta H$ is the height change that occurs when molecules change state (see Fig. 4 C). Equation 3 explains why nucleation occurs more easily on stiff ECMs than on soft ones (prediction 4 above): the attachment rate is greater on a stiffer ECM through Eq. 2.

Equation 3 is consistent with our intuitive picture of adhesion maturation (i.e., there is an optimal nucleation force, and increased ECM stiffness increases the nucleation probability) and also qualitatively consistent with detailed Monte Carlo simulations of adhesion formation (Fig. 4 B). Comparing these results with experimental measurements, we identify nucleation with the development of nascent adhesions into focal complexes or their precursors. The model behaviors are then consistent with our own and others' experimental observations that adhesions are preferentially nucleated on stiff surfaces (2), inhibition of force decreases adhesion nucleation (3), and increased vertical force leads to a loss of cellular adhesion (31). Forces that optimize adhesion have also been directly observed on some engineered surfaces (31).

Mean-field approximation (stability, growth, and decay)

Although the master equation formulation is helpful for small adhesions, it quickly becomes intractable as adhesion size increases. We may, however, simulate large adhesions if we assume that the adhesion grows uniformly, all molecules are attached to the ECM, and growth occurs exclusively at the adhesion edge. With these assumptions, the kinetic equation for adhesion growth is (see Supporting Material for a more complete derivation)

$$\frac{dN}{dt}=\frac{1}{\mathcal{T}}2\sqrt{N}\left(e^{-F^2/2k{N}^2{k}_{\mathrm{B}}T}-\left(1+B\right)e^{-F\Delta H/N{k}_{\mathrm{B}}T}\right).$$ (4)

Here, 𝒯 is a timescale and B is a nondimensional parameter, and both depend on the rate and equilibrium constants of the simple model in Fig. 4 A. We now examine the predictions of Eq. 4 and how these predictions relate to adhesion stability, growth, and decay.

Stability

Perhaps the simplest way to understand Eq. 4, a nonlinear ordinary differential equation, is to find its equilibrium points and their stability. These are the points into which, given enough time, the system settles. To find these points, we set the left-hand size to zero and solve for N = N^eq. In general, there are three such solutions: the trivial solution $\left(N_1^{eq}=0\right)$ and

$$N_{2,3}^{eq}=\left(\frac{\Delta H}{2k_{\text{B}}T\ln \left(1+B\right)}\right)\left(1\pm \sqrt{1-\frac{2k_{\mathrm{B}}T\ln \left(1+B\right)}{k\Delta H^2}}\right)F,$$

where $N_2^{eq}$ and $N_3^{eq}$ correspond to the negative and positive signs, respectively.

Below a critical bond stiffness,

$$k_{crit}=\frac{\Delta H^2}{2k_{\text{B}}T\ln \left(1+B\right)},$$

the roots $N_{2,3}^{eq}$ are imaginary, whereas above this value they are real. Thus, for bond stiffnesses below k_crit, the system has only the trivial equilibrium, $N_1^{eq}=0$. For bond stiffnesses above k_crit, three equilibria exist. We may linearize about these equilibria to determine their stability. We find that the trivial equilibrium is always stable. The intermediate equilibrium $\left(N_2^{eq}=N_{min}\right)$, when it exists, is unstable. The largest equilibrium $\left(N_3^{eq}=N_{max}\right)$, when it exists, is stable. In the language of nonlinear dynamics, a saddle-node bifurcation occurs at k_crit (see Supporting Material).

Using Eq. 1, we can relate the critical bond stiffness k_crit to a critical ECM stiffness E_crit, giving

$$E_{crit}=\frac{3\kappa \log \left(1+B\right)k_{\mathrm{B}}T}{\pi R\left(\Delta H^2\kappa -2k_{\text{B}}T\log \left(1+B\right)\right)}$$

a value that is independent of external force on the adhesion. Thus, on soft ECMs with stiffnesses below E_crit, all nucleated adhesions are unstable and decay. On stiff surfaces with stiffnesses above E_crit, sufficiently large adhesions (i.e., adhesions larger than N_min) grow toward N_max, whereas smaller adhesions abruptly decay to N = 0 (we have more to say about this mode of decay below, in the “Growth” and “Decay” sections). Monte Carlo simulations of adhesions on surfaces of various stiffnesses support these predictions (see Fig. 4 C), as does the observation that below a critical ECM stiffness, cells form few, if any, adhesions leading to cell death (3). This analysis provides some insight into why adhesions are formed less frequently and decay more readily on soft surfaces than on stiff ones (predictions 4 and 5): the range of unstable adhesion sizes increases on soft surfaces (see Fig. 4 C).

Growth

The equilibrium analysis of Eq. 4 shows that for a given force, adhesions grow only if their size is between N_min and N_max. If the adhesion is smaller than N_min, it will rapidly decay. In this case, the force on the adhesion becomes large and each molecule-ECM bond is highly strained. Newly bound molecules cannot attach to the surface, and the adhesion size begins to decrease. As this decay begins, the remaining bound molecules share more of the load, leading to increasing strain of molecule-ECM bonds and initiating a vicious cycle. Thus, if the force becomes too large, all molecules in the adhesion will detach rapidly.

If the adhesion becomes larger than N_max, it will decay toward N_max. In this case, the force on the adhesion is small and each molecule-ECM bond has little strain. Newly bound molecules are able to bind to the surface, but, experiencing little force, they do not transition to the ellipse state. Thus, the adhesion cannot grow and will decay until the strain on the molecule-ECM bonds increases, allowing newly bound molecules to transition to the ellipse state. For large adhesions, this situation can result in a steady state. For small adhesions, however, random fluctuations can either cause rapid detachment if the adhesion becomes smaller than N_min, or cause the force on the adhesion to disappear via detachment of adhesion molecules that directly experience external force (we have more to say about this mode of decay in the “Decay” section). Thus, if the force becomes too small, the adhesion will decay and complete adhesion detachment will become probable for small adhesions. For a given adhesion size, there is therefore a narrow range of forces at which adhesion growth is possible.

A growing adhesion is subject to an increasing external force as force-generating structures associated with the adhesion mature. Most nascent adhesions decay before they become a focal adhesion. We therefore expect that the few adhesions that survive to maturity fortuitously managed to grow in size as the adhesion force increased, keeping a roughly constant force per molecule (see Supporting Material for a more detailed discussion of this point). If, as we expect, the force per molecule remains roughly constant, Eq. 4 may be solved analytically.

Given that the growth rate is constant with time (let us say it is c₀), Eq. 4 becomes

$$\frac{dN}{dt}=2\sqrt{N}{c}_0/\mathcal{T}.$$

Defining the size of the adhesion at time t = 0 as N₀, the solution of this equation is $N={\left(c_{0}t/\mathcal{T}+\sqrt{N_0}\right)}^2$. The growth rate c₀ is largely independent of ECM stiffness (see Supporting Material), implying that, independently of surface stiffness, adhesions grow quadratically with time (predictions 1 and 3 in “Simulations”). Note that any model that assumes 1D growth, such as addition at the leading and/or trailing edge of the adhesion, would predict that adhesions grow linearly with time (14–17). Also note that the independence of growth on ECM stiffness is surprising, given that many aspects of adhesion maturation are dependent on ECM stiffness.

Decay

In our model and experiments, adhesions eventually decay and disappear. In the model, there are two primary mechanisms by which decay is initiated. In the first mechanism (described in detail above), an adhesion becomes smaller than N_min and rapidly detaches. We refer to this mechanism as catastrophic detachment, and observe it in both simulations and experiments (see Supporting Material). In the second mechanism, the molecule in our model that directly experiences external force detaches from the adhesion. Thus, the force on the adhesion drops to zero and the adhesion gradually decays. We expect that this form of adhesion decay in the model is qualitatively similar to the biologically relevant case in which a stress fiber (or other force-producing structure) detaches from a focal adhesion. We focus on the second, more gradual form of decay because it occurred more frequently in our simulations and experimental measurements (Fig. 3, B–D).

For a molecule under external force to detach from the adhesion, the molecule must simultaneously detach from both the ECM and its neighbors. Because molecule-ECM bonds are less stable on soft ECMs (see Eq. 2), this mechanism of detachment occurs more frequently on soft surfaces (prediction 5). As force on the adhesion disappears, Eq. 4 is

$$\frac{dN}{dt}=-2\sqrt{N}\frac{B}{\mathcal{T}}.$$

We can solve this equation analytically. Defining the size of the adhesion at the moment force drops to zero as N_D, the solution of this equation is $N={\left(\sqrt{N_D}-Bt/\mathcal{T}\right)}^2$. This solution predicts quadratic decay independently of ECM stiffness (predictions 2 and 3).

Discussion

Understanding how cells sense the stiffness of the ECM is an important issue from both a basic science and a clinical perspective. Although it is clear that adhesions between the cell and the surface are critical in this process, how and why ECM stiffness affects these adhesions is less clear. Here, we introduce a model that is 2D, is both explicit and physically consistent at the molecular level, and considers force normal to the surface. Using a combination of theory, simulation, and experiment, we provide insight into both how and why adhesion maturation depends on ECM stiffness. We first consider how adhesion maturation is stiffness-sensitive.

In cells, nascent adhesions are formed at the cell edge as actin filaments extend and integrins embedded in the cell membrane bind to the ECM. After this initial ECM-stiffness-independent formation of nascent adhesions, most of the adhesions disappear. However, a small fraction of nascent adhesions increase in size, forming adhesion complexes (4). It is this initial growth that we identify with adhesion nucleation in the model. Based on model simulations and simple theoretical calculations, we predict that this process should be ECM-stiffness-dependent. We find support for this prediction from our observation that more adhesions are formed on stiffer surfaces.

Once an adhesion begins to grow, either from a nascent adhesion to an adhesion complex or from an adhesion complex to an elongated focal adhesion, simulation of the model and theory both predict that its size should increase as time squared and should be stiffness-independent. Both of these predictions were unexpected. Our experimental tests provide support for both predictions, demonstrating that ECM stiffness does not affect how adhesions grow.

Focal adhesions do not last indefinitely; rather, they eventually decay and disappear. The model predicts that this transition from growth to decay occurs faster on soft surfaces than on stiff ones. In our model and experimental measurements, this transition occurs without reaching a steady-state size. Consistent with these predictions, our measurements show that adhesion size increases with surface stiffness. Subsequent adhesion shrinkage is ECM-stiffness-independent. A comprehensive picture of how ECM stiffness affects focal adhesion maturation then emerges in which only adhesion nucleation and decay initiation are stiffness-sensitive. Note that these results depend critically on both the 2D nature of the adhesions and the component of force normal to the surface.

Besides providing insight into how ECM stiffness affects focal adhesion maturation, our model suggests an explanation for why ECM stiffness affects focal adhesion maturation. In particular, we show that molecules with a force-dependent state transition and strain-dependent binding exhibit the force- and ECM-stiffness-dependent aggregation seen in adhesion maturation in live cells. The force-dependent state transition makes aggregation occur only in the presence of force (a process that may be common to many different forms of cell adhesion (32)). Strain-dependent binding to the surface, however, occurs less frequently under large forces. These opposing effects lead to an optimal force for adhesion formation. Varying ECM stiffness affects strain-dependent surface binding, with stiffer surfaces leading to a higher likelihood of binding, but has no effect on the force-dependent transition. Thus, stiffer surfaces result in a higher probability of adhesion maturation. Additionally, because decay may be initiated by force-bearing molecules detaching from both their neighbors and the surface, decay initiation occurs faster on softer surfaces where surface detachment is more likely. Thus, we argue that many aspects of focal adhesion maturation emerge naturally from the molecular properties of the proteins in the adhesions.

Conclusions

The simple molecular model presented here is qualitatively consistent with a broad set of experimental measurements, some of which were performed explicitly to test the model. The model predicts and our experiments demonstrate that ECM stiffness affects whether an adhesion is initially formed and how long it grows, but not how it grows or decays. Therefore, much of the mechanosensitivity of adhesions, and perhaps cell mechanosensitivity as a whole, is an emergent property of a simple molecular-mechanical system. Combined with previous results on adhesion sliding (28,30,33,34), this work may serve as the basis for understanding how cells transduce the mechanical properties of the ECM into variable adhesion formation, and further into cell motility and differentiation under both normal and pathological conditions.