Cardiac Bidomain Bath-Loading Effects during Arrhythmias: Interaction with Anatomical Heterogeneity

Abstract

Cardiac tissue is always surrounded by conducting fluid, both in vivo (blood) and in experimental preparations (Tyrode's solution), which acts to increase conduction velocity (CV) close to the tissue-fluid interface, inducing transmural wavefront curvature. Despite its potential importance, computer modeling studies focused on arrhythmia mechanisms have previously not accounted for these bath-loading effects. Here, we investigate the increase in CV and concomitant change in transmural wavefront profiles upon both propagation and arrhythmia dynamics within models of differing anatomical complexity. In simplified slab models, in absence of transmural fiber rotation, bath-loading induced transmural wavefront curvature dominates, significantly increasing arrhythmia complexity compared to no bath. In the presence of fiber rotation, bath-loading effects are less striking and depend upon propagation direction: the bath accentuates natural concave curvature caused by transmurally rotating fibers, but attenuates convex curvature, which negates overall impact upon arrhythmia complexity. Finally, we demonstrate that the high degree of anatomical complexity within whole ventricular models modulates bath-loading induced transmural wavefront curvature. However, key is the increased surface CV that dramatically reduces both arrhythmia inducibility and resulting complexity by increasing wavelength and reducing the available excitable gap. Our findings highlight the importance of including bath-loading effects during arrhythmia mechanism investigations, which could have implications for interpreting and comparing simulation results with experimental data where such effects are inherently present.

Introduction

Since the first studies using the cardiac bidomain model, it has been well known that the presence of an extracellular conducting medium induces a bath-loading effect on propagating wavefronts within the myocardial tissue with which it interfaces. Close to the tissue surface, the bath provides a low-resistance pathway through which extracellular current can flow. The resulting shunting effect increases conduction velocity (CV) at the tissue edges, causing a curvature in the transmural profile of the electrical wavefront, with surface wavefronts leading those in the bulk (1–3). Such a layer of conducting fluid in contact with the epi-/endocardial tissue surface is present both in vivo (blood in cavities and pericardial fluid layer) as well as in saline-perfused in vitro experiments (4).

However, early bidomain studies suggested the bath-loading induced wavefront curvature to be a relatively minor effect, and instead focused attention upon the effect of the bath on action potential morphology (1,3,5,6), providing important insight into previous experimental data (7). Recently, however, we have demonstrated that a conducting bath can have a potentially significant impact on wavefront morphology, depending strongly upon the specific conductivity parameters used in the model, with surface CV being up to 40% faster with a bath (8).

Previous studies have shown how transmural heterogeneity in fiber rotation can have profound implications upon the complexity and dynamics of arrhythmias through its effect on transmural wavefront morphology. Such transmural heterogeneity has been shown to induce bending and torsion within filaments (the organizing centers of reentrant circuits) that leads to wavebreak (9–11). It is also well established that CV, as a determinant of the wavelength of a propagating impulse, plays a very important role in determining arrhythmia stability and dynamics (12). So far, however, despite the potential importance of bath-loading effects, virtually all simulation-based studies of cardiac electrical activity during propagation and investigations into cardiac arrhythmia mechanisms (9–11,13,14) have fully ignored the impact of bath loading upon locally altered CV and concomitant wavefront curvature.

Using the bidomain model imposes significant computational demands compared to the monodomain model (15), limiting it almost exclusively to studies of defibrillation and shock-induced arrhythmogenesis, in which an extracellular bath is essential for external shock application (4,16). As monodomain approaches are typically ∼10 times faster than bidomain approaches (15), they are widely preferred when activity is simulated for longer durations (>1 s). However, as standard monodomain approaches cannot explicitly represent a bath, they are unsuitable for studying bath-loading induced heterogeneity in CV and wavefront morphology throughout the myocardial wall. Thus, the role played by the bath in governing arrhythmia mechanisms, and the potential need to represent it (either through a full bidomain approach or a recently developed augmented monodomain equivalent model (8)) is as yet unknown.

In this study, to our knowledge for the first time, we investigate the role of the bidomain bath-loading effects during both propagation and episodes of arrhythmias within models of differing anatomical complexity. Specifically, we examine how the bath-loading-induced increases in CV close to the tissue surface affect wavefront morphology, as well as the dynamics and stability of filaments during arrhythmias, and how these effects interact with anatomical and structural heterogeneity within the different models. To achieve our objectives, electrical activity is simulated during both pacing and arrhythmogenic protocols within cardiac tissue slab models in the absence and presence of transmural fiber rotation, and within a recently published anatomically complex rabbit whole ventricular model (17). All protocols are performed for bidomain representations including, as well as in the absence of, a surrounding conducting bath. By examining wavefront morphologies and performing statistical analysis of filament dynamics during arrhythmia episodes for both scenarios, we have found that the presence of the bath always has a significant impact on the three-dimensional (3D) wavefront morphology. How this affects the complexity and sustainability of the resulting arrhythmia, however, is seen to depend strongly upon the degree of anatomical complexity of the model.

Methods

Computational models

A cuboid, tetrahedral finite element model, of dimensions 3.0 cm × 3.0 cm × 0.5 cm and a spatial discretization step h = 200 μm, was used to represent a 3D slab of myocardial tissue, similar to those used in previous arrhythmia mechanism studies (9,14). A perfusing bath, of thickness 0.1 cm in the z direction, was included representing conducting medium in contact with the epi-/endocardial surfaces, as shown in Fig. S1 a of the Supporting Material. Anisotropic conduction was assigned through a locally prevailing cardiac fiber architecture that either varied transmurally between ±60 degrees (relative to the x axis) from epi- to endocardium or a constant fiber orientation of 0 degrees was assigned throughout the myocardium, i.e., fibers parallel to the x axis. In addition, a high-resolution finite element model of the rabbit ventricles (17) was also used, containing a high degree of anatomical complexity, shown in Fig. S1 b. The myocardial ventricular mesh sits within a perfusing bath, filling the ventricular and all intramural cavities.

Simulating electrical activation

Electrical activation throughout the ventricular model was simulated using the bidomain equations (18). Cell membrane dynamics were represented by a recent rabbit ventricular cell model (19). Intra- and extracellular conductivities were based on those of Roberts and Scher (20). Conductivity of the extracellular bath (g_b) was 1.0 S/m (isotropic). The bidomain equations were solved with the Cardiac Arrhythmia Research Package (21). Specific details of the implementation of the bidomain model and conductivity values are given in the Supporting Material, section 2.1.

Stimulation protocols

Pacing

In the slab, two pacing stimuli were separately applied at 1), the x = 0 cm plane and 2), y = 3 cm plane to induce propagation both along and across the midwall fiber direction, respectively. In the whole ventricular model, the midmyocardial fibers lie approximately within the circumferential direction. Thus, a transmural plane stimulus through the left ventricular (LV) wall was used to induce global wavefront propagation approximately along the direction of midwall myofibers and an apical stimulus used to induce propagation across the midwall fiber direction.

Induction of arrhythmia

Episodes of arrhythmias were induced using a standard S1-S2 protocol, described in the Supporting Material. All preconditioning phases were simulated using a monodomain approach (except delivery of the extracellular S2 shock to the ventricular model) and checkpointed 5 ms following S2 stimulus (which involved saving all state variables and V_m values at that instance in time). This procedure eliminated any bath-loading related differences before the onset of arrhythmias. Simulations were then restarted using two separate protocols whereby electrical activation was simulated using the bidomain equations in both the presence and absence of a surrounding conducting bath, termed the full bidomain (BDM) and bidomain no bath (BDMNB) cases, respectively. Such a protocol facilitated the analysis of the presence of a surrounding extracellular bath upon the progression of an arrhythmic episode, where both BDM and BDMNB simulations were begun from exactly the same initial state. Arrhythmia lifetimes were defined as the time from the start of the S2 stimulus until V_m levels of all tissue had returned to rest (< – 80mV).

Filament detection and analysis

The algorithm used for filament detection was based on the approach of Fenton and Karma (9), adapted for use within an unstructured finite element regime. Full details of the method are given in the Supporting Material, section 1.3.

Results

Slab model without transmural fiber rotation

Effects of bath-loading during pacing

Fig. 1 shows V_m distributions within the slab model without fiber rotation 50 ms following pacing in both BDMNB (left) and BDM (right) cases. Top panel shows stimulus along the x = 0 cm plane, inducing wavefront propagation along the fiber direction; bottom panel shows stimulus along the y = 3 cm plane, inducing propagation perpendicular to fibers. Here, the presence of surrounding conducting bath in the BDM case induces a significant curvature of the wavefront, relative to the planar wavefront seen in the BDMNB case, for both propagation directions. However, curvature is more pronounced for propagation along, than across, the fiber direction, as witnessed previously (8). Epicardial conduction velocities are also seen to be significantly higher in the BDM case for both propagation directions, being 47.8 and 20.6 cm/s for the BDM and 28.5 and 13.6 cm/s for the BDMNB case, for propagation along and across the fiber direction, respectively. Consequently, less excitable tissue remains at 50 ms in the BDM case, being 50.1% and 77.3%, compared to 63.2% and 82.6% in the BDMNB case for two respective propagation directions.

Figure 1.

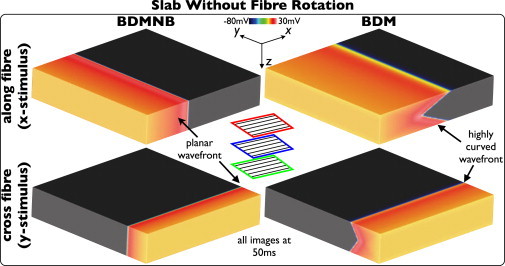
Effects of bath-loading during pacing in the slab model without transmural fiber rotation. V_m distributions for BDMNB (left) and BDM (right), 50 ms following pacing stimulus along the x = 0 (top) and y = 3 cm (bottom) planes.

Effects of bath-loading during arrhythmias

Fig. 2 a shows V_m distributions (top row) and filament locations (bottom row) within the slab model at different times following arrhythmia induction for the BDM (top) and BDMNB (bottom) cases during its early stages. Comparing individual time instances between BDM and BDMNB cases, we see how the increased CV in the BDM case leads to a lengthening of the wavelength, reducing the amount of excitable tissue within the domain as the spiral wave rotates. For example, at 150 ms 29.9% of the slab is excitable in the BDM case, compared to 35.1% for the BDMNB case. Furthermore, evident in all V_m distributions in the BDM case is a pronounced wavefront curvature, compared to the BDMNB case, which all show a planar wavefront morphology (in z); such a difference was also present during pacing (Fig. 1). This induces a bending and twisting of the filament in the BDM case as the arrhythmia progresses, clearly evident in images 150–350 ms; in contrast, the planar wavefront in the BDMNB case leads to entirely straight filaments in all time instances. Such differences in filament dynamics lead to the BDM arrhythmia episode being more complex than the BDMNB, having more frequent episodes of wavebreak. Fig. 2 a (right) shows examples of wavebreak in both models; in the BDM case, the bent nature of the filaments leads to the existence of an U-filament located on the x = 0 cm plane of the slab, in addition to the bent I-filaments. In the BDMNB case, the induced arrhythmia self-terminated following 1854 ms, as the single filament moved out of the domain of the slab model; in the BDM case, the arrhythmia continued beyond the duration of the simulation >2750 ms.

Figure 2.

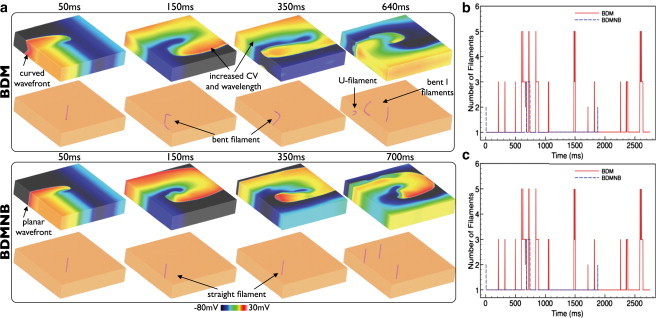
Effects of bath-loading during arrhythmias in the slab model without transmural fiber rotation. (a) V_m distributions (top row) and filaments shown (bottom row) for the BDM (top panel) and BDMNB (bottom panel) cases for time instances 50–350 ms following arrhythmia induction. Right panel shows an example of wavebreak in both models. Variation in total number of individual filaments present in each ms of the simulation (b) and total mean filament length (c) over the duration of the arrhythmia episodes for the BDM (red) and BDMNB (blue) cases.

Fig. 2, b and c, plot the number of individual filaments present at each ms of the simulation and the mean filament length per ms in the BDM (solid line) and BDMNB (dashed line) episodes, respectively. Fig. 2 clearly shows the increased complexity of the BDM arrhythmia episode, having many more filaments throughout its duration: the mean number of filaments was 1.23 with a maximum of 7, compared to 1.07 (maximum 3) for the BDMNB case. Furthermore, we see from Fig. 2 c that the mean filament length per ms is also consistently higher in the BDM (mean 186 elements) compared to the BDMNB case (146). Finally, the increased complexity of the BDM arrhythmia episode is further quantified by the filament interaction statistics. For example, the BDM episode has a higher total filament interaction rate compared to BDMNB (0.061/ms vs. 0.010/ms), shorter mean filament lifetime (38 ms vs. 199 ms), and a larger number of individual filaments produced (87 (0.032/ms) vs. 10 (0.005/ms)) for the episode durations; see also accompanying movies.

Slab model with transmural fiber rotation

Effects of bath-loading during pacing

Fig. 3 shows V_m distributions within the slab model with fiber rotation 50 ms following pacing in both BDMNB (left) and BDM (right) cases. Top panel shows stimulus along the x = 0 cm plane, inducing wavefront propagation along the direction of the midmyocardial fibers; bottom panel shows stimulus along the y = 3 cm plane, inducing propagation perpendicular to the midmyocardial fiber direction. In contrast to the case without fiber rotation in Fig. 1, here the BDMNB model exhibits a curved wavefront for both propagation directions, having convex curvature when midmyocardial fibers are aligned with the global propagation direction and concave curvature when perpendicular to it. However, as witnessed in Fig. 1, the presence of the bath in the BDM case increases CV close to the surface, significantly affecting wavefront curvature. This increased CV is seen to accentuate the concave curvature in the BDMNB model, but attenuate the convex curvature. On the epicardium, CV is seen to increase in the presence of the bath for both propagation directions, being 24.4/44.5 cm/s for BDM and 21.9/25.6 cm/s for the BDMNB case, for propagation along/across the midmyocardial fiber direction, respectively. Consequently, less excitable tissue again remains at 50 ms in the BDM case (63.5/57.6%) compared to the BDMNB case (66.1% and 70.9%) for the two respective propagation directions. Nonetheless, bulk CV is largely unaffected for propagation along the midmyocardial fiber direction as in this case bulk leads surface.

Figure 3.

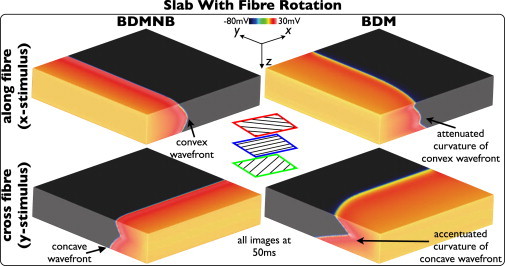
Effects of bath-loading during pacing in the slab model with transmural fiber rotation. V_m distributions for BDMNB (left) and BDM (right), 50 ms following pacing stimulus along the x = 0 (top) and y = 3 cm (bottom) planes.

Effects of bath-loading during arrhythmias

Fig. 4 shows V_m distributions (top row) and filament locations (bottom row) within the slab model with transmural fiber rotation at different times following arrhythmia induction for BDM (top) and BDMNB (bottom) cases during its early stages. Throughout the V_m images of Fig. 4, the important differences in wavefront dynamics seen during pacing are again evident: increased surface CV, accentuated concave curvature, and attenuated convex curvature in the BDM model. After 50 ms, for example, 43.4% of the slab is excitable in the BDM case, compared to 48.1% for the BDMNB case. However, as both models produce transmurally curved wavefronts, the resulting filaments during arrhythmias are seen to be elongated, bent, and twisted in both models (compared to Fig. 2 when the BDMNB filaments were straight). In the BDM case the bending and twisting of the filament appears more severe than in the case without fiber rotation. In both cases, the severe filament torsion causes frequent wavebreak to occur in both models, as the disorganized filament interacts with the tissue boundaries (and, at times, other filaments), an example of which is shown in the 300 ms images.

Figure 4.

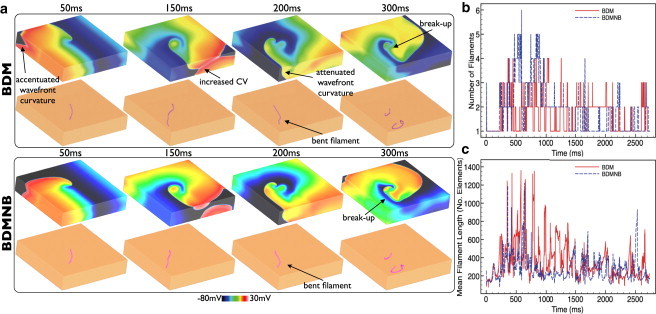
Effects of bath-loading during arrhythmias in the slab model with fiber rotation. (a) V_m distributions (top row) and filaments shown (bottom row) for BDM (top panel) and BDMNB (bottom panel) cases for time instances 50–300 ms following arrhythmia induction. Variation in total number of individual filaments present in each ms of the simulation (a) and total mean filament length (b) over the duration of the arrhythmia episodes for the BDM (solid) and BDMNB (dashed) cases.

Both arrhythmia episodes were sustained over the duration of the simulation time (>2730 ms). Fig. 4, b and c, quantifies the complexity of both arrhythmic episodes by plotting the variation in total filament numbers and mean filament length over time for BDM (solid line) and BDMNB (dashed line) episodes, respectively. Both arrhythmia episodes appear to have very similar degrees of complexity, although are significantly more complex relative to the slab model episodes in absence of fiber rotation (Fig. 2). However, noticeable differences do exist between the BDM and BDMNB episodes. Specifically, in Fig. 4 b we see that the BDMNB episode appears to have a slightly higher number of filaments than the BDM case throughout the arrhythmia episode, with a mean respective value of 1.83 (maximum 6) vs. 1.65 (maximum 5). However, Fig. 4 c shows that the BDM episode has consistently longer filaments than the BDMNB case, with mean respective filament lengths of 358 and 280. Finally, filament interaction statistics appear similar between the BDM and BDMNB episodes exhibiting similar interaction rates (0.87/ms vs. 0.81/ms), mean filament lifetimes (36 ms vs. 45 ms), and a number of individual filaments produced (121 (0.044/ms) vs. 109 (0.040/ms)) for the arrhythmia durations; see also accompanying movies.

Whole-ventricular model

Effects of bath-loading during pacing

Fig. 5 shows V_m distributions throughout the 3D volume of the anatomically complex ventricular model following transmural (top) and apical (bottom) stimuli for BDMNB (left) and BDM (right) cases. The presence of the bath has a similar effect on wavefront morphology as seen within the slab model with fiber rotation: concave wavefront curvature for propagation across the direction of midmyocardial fiber orientation (apex-base direction) is accentuated, whereas convex curvature for propagation along the direction of midmyocardial fiber orientation (circumferential direction) is attenuated. However, it is noted that additional anatomical details (endocardial structures, intramural blood vessels, curved ventricular geometry), also affect wavefront propagation, meaning the effect is less noticeable in the slab model.

Figure 5.

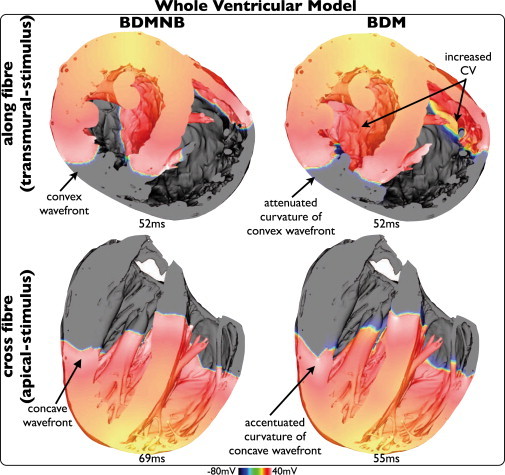
Effects of bath-loading during pacing in the whole-ventricular model. V_m distributions following pacing shown for BDMNB (left) and BDM (right) cases, for apical (top) and transmural (bottom) stimulation.

Fig. 5 also shows that during apical stimulus (apex-base propagation), the BDM model produces a significantly increased CV throughout the entire model, relative to the BDMNB case; the wavefront reaches approximately the same locations after 55 ms in BDM, compared to 69 ms in BDMNB case. At 69 ms in both models, 20.2% of tissue remains excitable in the BDM case, compared to 50.2% in the BDMNB case. During circumferential propagation (transmural stimulus) in the thick LV and septal walls, global CV of the tissue bulk is relatively similar between BDM and BDMNB cases (wavefronts reach similar locations at 52 ms in each case), although a slight increase in CV on the endocardium is noticeable, as here we have a large surface area due to the endocardial structures over which the tissue bath effect can act. However, in the thinner right ventricular (RV) wall, both surface and bulk are affected by the bath. Thus, CV is significantly increased throughout the RV-wall meaning that activation reaches further around the wall in the BDM than BDMNB case after 52 ms. This is further quantified by comparing the amount of excitable tissue remaining at 52 ms, being 29.7% in the BDM case, compared to 42.6% in the BDMNB case.

Effects of bath-loading during arrhythmias

Arrhythmia inducibility. The S1-S2 shock protocol described in the Stimulation protocols section was used to induce arrhythmias within the whole ventricular model. Thirteen separate CIs were used in 5 ms increments from 180 to 240 ms following the S1 pacing stimulus, along with a SS of 10 V. Post-shock activity was simulated for 2500 ms with both BDM and BDMNB approaches. Fig. 6 a shows histograms of the resulting arrhythmia durations for all 13 episodes in BDM (top) and BDMNB (bottom) cases. Arrhythmia episodes simulated with the BDM approach are sustained for significantly less time than the BDMNB: 8 episodes are sustained for < 500 ms, with just 2 being sustained >1000 ms, in the BDM, compared to 0 and 8, respectively, in the BDMNB case.

Figure 6.

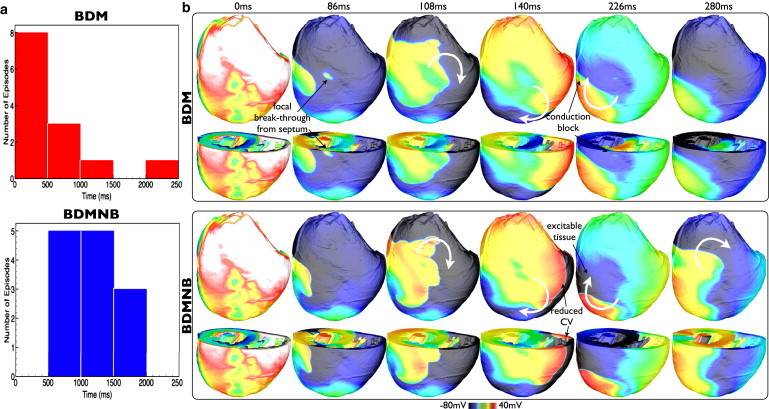
(a) Histograms showing durations of arrhythmias within the whole ventricular model where post-shock behavior is computed using the BDM (top) and BDMNB (bottom) approaches. (b) Premature termination of arrhythmia in whole-ventricular model with BDM approach. V_m distributions within the volume of the ventricles at certain instances in time following the attempted induction of an arrhythmia with CI = 195 ms in the BDM (top panel) and BDMNB (bottom panel) cases. For each panel, posterior epicardial views (top row), as well as views taken with an axial slice to expose anterior endocardial surfaces and septum (bottom row), are shown. White curved arrows show rotation direction of induced arrhythmia.

To explain why, in contrast to the BDMNB episodes, the majority of the BDM episodes terminate before an arrhythmia can be fully established (<500 ms), Fig. 6 b shows the evolution of post-shock V_m activity within the ventricular model for the episode with CI = 195 ms in which the BDM episode was sustained for just 394 ms, compared to 1568 ms for the BDMNB. Following shock-end (0 ms), the induced arrhythmias initially progress in a very similar manner in both models, as the tissue recovers from the shock and the arrhythmia is established. For example, in both models, the initial reentrant wave proceeds from the LV wall (86 ms), across the posterior toward the RV (108, 140 ms), before beginning its rotation in a clockwise fashion on the posterior epicardial surface (140 ms). However, noticeable differences exist between the BDM and BDMNB cases: CV is noticeably faster in the BDM model as the wavefront propagates across the RV wall, enveloping the excitable tissue faster than the BDMNB case (140 ms); and, faster CV along the septum is seen, witnessed by an earlier focal depolarization on the epicardial surface as the septum depolarizes in the BDM model (86 ms, as shown), compared to a similar event witnessed at 91 ms in the BDMNB case (image not shown).

The faster CV across the epicardial surface in the BDM model means that, as the reentry approaches one complete cycle, the leading wavefront encounters tissue in the LV free wall that is still refractory (226 ms) at the spiral wave tail. This is quantified by examining the proportion of excitable tissue remaining at 226 ms, being just 18.4% in the BDM case, compared to 28.9 in the BDMNB case. Consequently, conduction block occurs both in the LV wall and at the septum free-wall junction (226 ms), and the arrhythmia dies-out (280 ms). Conversely, the slower speed of rotation of the BDMNB case means that, as the reentrant wave completes its first cycle, the tissue in the LV free wall has sufficiently recovered to allow conduction, and the reentrant wavefront continues to propagate unhindered. Similar post-shock activity patterns were seen to be responsible for the failure of arrhythmia induction in the majority of the BDM episodes. However, in the particular cases where reentry is sustained for longer than 1 initial cycle (5 cases, from Fig. 6 a), although the main wavefront is still blocked by refractory tissue in the LV free wall, in these instances a small excitable gap is seen to exist within the endocardial structures on the thick LV wall in which propagation can continue, keeping the arrhythmia alive. An example of such a mechanism is shown in Fig. S5. However, due to these different activation pathways taken by the wavefronts after the first reentrant cycle, the BDM and BDMNB arrhythmia patterns diverge rapidly at this point.

Sustained arrhythmia dynamics. All sustained arrhythmia episodes with durations >900 ms (including 3 BDM and 9 BDMNB episodes) had their filament dynamics and V_m patterns analyzed. The BDM episodes were seen to have, on average, a smaller number of total filaments compared to the BDMNB cases (∼4, max ∼13 vs.∼5, max ∼16), as well as longer mean filament lengths (165 vs. 100 elements, respectively). Furthermore, filament interaction statistics appeared marginally smaller in the BDM case than the BDMNB, exhibiting smaller mean filament interaction rates (0.93 vs. 1.11) and a smaller mean number of individual filaments produced (582 or 0.47/ms vs. 619 or 0.56/ms) for the duration of the arrhythmic episodes. The individual statistics concerning the filament dynamics within each episode of sustained arrhythmias are shown in Fig. S6 (see also accompanying movies).

To demonstrate these observations in a particular case, Fig. 7 shows V_m distribution and filament locations during an example of an episode of shock-induced arrhythmogenesis (CI = 180 ms) that was sustained in both BDM (923 ms duration) and BDMNB (1488 ms duration) cases. As shown above for the average case, the BDM episode tends to be characterized by a larger wavelength, less complex V_m distributions, and fewer filaments than the BDMNB episode. In addition, of the filaments present, those in the BDM case appear consistently longer than the BDMNB filaments. Such differences in filament dynamics between BDM and BDMNB cases are quantified in Fig. 7, b and c, which shows the variation in total number of individual filaments and the mean filament length through the duration of the episodes, respectively. The BDM episode consistently has a lower number of filaments (mean 3.66, max 11) than the BDMNB case (mean 5.57, max 17) throughout the arrhythmia duration, although Fig. 7 c confirms that the BDM filaments are consistently longer than those of the BDMNB case (mean respective lengths 178 vs. 106 elements).

Figure 7.

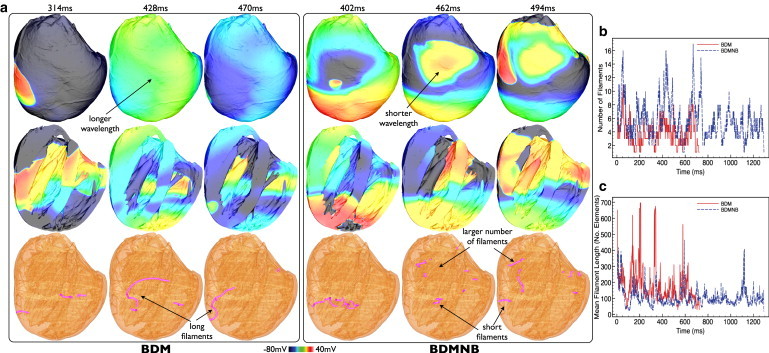
(a) Comparison of sustained episodes of arrhythmia in ventricular model with BDM and BDMNB approaches. V_m distributions and filament locations within the ventricular volume at certain times following arrhythmia induction with CI = 180 ms in the BDM (left panel) and BDMNB (right panel) cases. For each panel, posterior epicardial views (top row), and longitudinal slices to expose anterior endocardial surfaces/septum (center row), are shown, with filament locations identified (bottom row). Variation in total number of filaments present in each ms of the simulation (b) and total mean filament length (c) over the duration of arrhythmia episodes for BDM (solid) and BDMNB (dashed) cases within the ventricular model for CI = 180.

Discussion

Cardiac tissue is always surrounded by some thickness of conducting medium, whether in vivo or in experimental preparations, which is known to affect electrical properties to induce wavefront curvature and increase surface CV along the tissue-bath interface (1–3, 8). Despite this, bath-loading effects are rarely represented in computational cardiac models. Due to the computational costs involved, particularly during investigations of arrhythmia mechanisms that require prolonged simulation times, most studies resort to using the computationally cheaper monodomain approach, which is incapable of representing such a feature. Here, we have demonstrated that the bath can significantly affect the complexity and dynamics of arrhythmias, to an extent that depends strongly upon the degree of inherent structural and anatomical complexity of the model.

The effect of bath-loading during pacing

Through our previously acquired knowledge of the sensitivity of the bath-loading effect to the specific values of bidomain conductivities (8), we intentionally chose a set of experimentally measured parameters (20) that maximized this effect. Consequently, this allowed us to provide an upper limit on the effects of bath-loading during arrhythmias.

During pacing, in the absence of fiber rotation, the bath-loading effect was seen to induce significant 3D wavefront curvature due to the presence of the bath, to a much greater degree than witnessed previously (1–3). In the presence of fiber rotation, curvature in the wavefront profile occurs naturally in the slab model, causing a convex (concave) wavefront when activation propagates parallel (perpendicular) to the direction of midmyocardial fibers. Here, the effect of the bath on wavefront morphology was highly dependent upon the direction of propagation with respect to the fiber arrangement: the bath accentuated natural concave curvature caused by transmurally rotating fibers, but attenuated convex curvature. However, in both cases, surface CV was increased by the bath.

A similar scenario was also seen in the whole ventricular model, whereby wavefront curvature was accentuated during propagation in the apex-base direction, but attenuated for circumferential propagation. In this case, however, the presence of anatomical features, such as endocardial structures and blood vessels, as well as varying myocardial wall thickness and the circular propagation path, were seen to modulate these effects relative to those witnessed in the anatomically simplified slab model. Such knowledge regarding bath-loading induced transmural wavefront curvature (particularly in the LV) could have important implications in the inference of wavefront shapes within the tissue bulk from the corresponding surface activation recordings. Within the much thinner RV wall (only ∼1–2 mm thick in places), however, almost the entire wall is directly affected by the presence of the bath, reducing transmural wavefront curvature, and increasing bulk CV within the whole wall. Although interventricular CV differences are thought to be caused by heterogeneities in RV/LV ion channel expression, this phenomena is not completely understood, and many interrelated mechanisms are thought to be at play (22). Thus, we suggest that differences in RV/LV CV, resulting from bath-loading effects combined with ventricular wall thickness demonstrated in this study, could present an important additional mechanism requiring careful consideration in the experimental measurement of such phenomena. Finally, these insights have highlighted potential variability in wavefront CV and morphology during pacing in the presence of the bath, which could have important implications in the use of models for faithful comparison with experiments where accurate representation of activation times is imperative (for example in cardiac resynchronization therapy studies (23)).

The effect of bath-loading during arrhythmias

The vast majority of previous modeling studies investigating arrhythmia mechanisms have been monodomain, thus excluding the presence of a surrounding conducting bath (9–11,13,14). Here, we have conclusively demonstrated the potentially significant difference that the inclusion of a bath within a bidomain formulation can have upon arrhythmia dynamics and complexity; a difference that is seen to depend strongly on the degree of anatomical complexity of the model.

In a simple slab model with no fiber rotation, the bath-induced wavefront curvature can, on its own, cause filament lengthening, torsion, and instability, thereby significantly increasing arrhythmia complexity relative to the case without a surrounding bath. Differences in filament dynamics with the presence or absence of a bath were also seen in a previous study with a simplified isotropic slab model, in which the authors reported seeing repulsion of the filament from the tissue-bath interfaces (24). Such an effect was not evident in our study, which we believe could be due to the more complete representation of the perfusing bath used here and the fact that we represent bath on both the epi- and endocardial surfaces. The inclusion of transmurally rotating fiber architecture was seen to increase the complexity of the arrhythmic episodes both with/without a bath, agreeing with previous studies using monodomain approaches (9,10). However, in this case, the complexity of the arrhythmias in the presence and absence of the bath were similar (as quantified by metrics such as filament numbers, interaction rates, etc.). We postulate that the effects of accentuated and attenuated wavefront curvature induced by the bath (discussed previously) on filament stability, approximately act to cancel each other out, causing negligible statistical difference in arrhythmia complexity compared to the BDMNB case. However, the model did show a consistently longer mean filament length in the presence of a bath due to the increased surface CV.

With the whole ventricular model, which had greater anatomical complexity, a much more marked bath effect on arrhythmia episodes was seen, both in terms of arrhythmia inducibility and resulting dynamics. Our analysis revealed that both changes are due to the significant differences in wavefront CV between BDM and BDMNB cases. Although, parts of the LV free wall and septum are ≳ 5 mm, much of the other regions (particularly the RV wall) are considerably thinner, and, thus, the presence of the bath around these thinner walls acts to significantly increase CV throughout the whole wall. This large increase in overall CV throughout large parts of the ventricles, coupled with the effects of wavefront curvature within the ventricles discussed previously, has a significant effect on the resulting arrhythmias and filament dynamics.

First, we showed how an increase in CV of the reentrant wavefront due to the bath increased activation wavelength sufficiently to cause premature termination of the arrhythmia before completion of one reentrant cycle, occurring in eight of the BDM cases (compared to none of the BDMNB cases). The importance of a bath in the induction of arrhythmias following shocks, elucidated here, has implications for previous studies of shock-induced arrhythmogenesis and calculations of vulnerability grids (4,16). Although many such studies did use bidomain representations for the entire simulations, some only used bidomain during external shock application, switching to the faster monodomain both before and after shock delivery (25). Furthermore, almost all used conductivity parameters obtained from Clerc (26), which have been recently demonstrated to cause very minor bath-loading effects (8) (i.e., BDM is very similar to BDMNB). We therefore believe that the use of different conductivity sets within such studies would cause more significant bath-loading effects within the ventricles, increasing CV and reducing arrhythmia inducibility at each shock-strength, which could affect the comparison with experiments. A thorough investigation into the effect of different bidomain conductivity parameters upon shock-induced arrhythmogenesis, and how they may affect vulnerability grids and the limits of vulnerability, could now be required.

Of the arrhythmias that were induced within the ventricular model, a further effect of the increased CV in the presence of the bath was the witnessed reduction in complexity of the arrhythmias, in terms of number of filaments, interaction rates, etc. Panfilov (12) quantitatively related the maximum number of rotors that a domain can sustain to the effective size of the tissue, defined as the ratio of its physical dimension to the wavelength (a function of APD and CV). Furthermore, a previous study by Ten Tusscher et al. (13) demonstrated how an increase in wavelength (in this case due to increased minimum APD) dramatically reduced the number of filaments present during an episode of simulated ventricular fibrillation in the human heart, by reducing its effective size (12), thus restricting the number of rotors that could fit within a given volume of tissue. We believe that the same mechanism is responsible in our study for the decreased arrhythmia complexity in the BDM case: the increased wavelength, through a bath induced increase in CV, acts to reduce the number of filaments that can be sustained within the model and their resulting complexity.

Such a phenomenon was witnessed in the whole ventricles, but not in the slab model, as the slab represents a larger volume of myocardial tissue coupled with reduced anatomical and topological complexity relative to the ventricular model. Specifically, noncontinuous boundaries within the slab limit the full degree of reentrant behavior of wavefronts possible within the circular pathways provided by the ventricles and septum, which affects filament interactions, lifetimes, and numbers. The arrhythmias induced within the slab had mean filament numbers of <2 in both BDM and BDMNB (compared to generally >4 in the ventricles) and are thus well within the upper limit of the mean number of rotors it can feasibly sustain, which we would expect to be >5. Therefore, CV and wavelength are not limiting factors in the slab, and, thus, a small increase in CV due to the bath did not limit arrhythmia complexity. However, in the ventricles, the number of rotors sustained without the bath was close to a natural limit of the model, due to its smaller physical size, along with the increased complexity of the arrhythmias. Thus, the change in CV upon addition of the bath (which was greater in the bulk due to the thinner walls than in the slab) was responsible for reducing the complexity of the induced arrhythmia. Finally, the increased CV in the presence of the bath did, similar to the slab; result in longer mean filament lengths in the BDM case. Although in the present study this did not appear to significantly affect arrhythmia dynamics, we believe such an effect could become increasingly important in models of larger physical size, such as in humans, which we leave open as a line of further future investigation.

Role of anatomical complexity

The differences witnessed in the bath-loading effect within models of differing anatomical complexity represents an important finding because different computational models are designed to replicate different experimental preparations; for example, slab models can be compared with cardiac tissue slices, monolayer preparations, or isolated ventricular wall samples, whereas whole ventricular models are designed to be compared with whole-heart optical mapping or electrode recordings. In addition, a wealth of previous simulation studies have been performed with a monodomain approach on models ranging from simplified slabs (9,10) to realistic ventricular models (13), as well as combinations (11,14); thus, our analysis here plays an important role in placing the findings from previous studies in context, and how they may be potentially affected by faithfully representing the conducting fluid layer present in experimental and in vivo situations.

We have demonstrated that the presence of transmurally rotating fibers within the slab model interacts with the bath-loading effect to produce similar overall filament dynamics in the presence and absence of the bath. Consequently, the witnessed arrhythmia dynamics within the slab were similar, both qualitatively and quantitatively, to those seen in previous studies employing the monodomain approach (9,10,14). In addition, at the whole ventricle level the filament dynamics predicted in both BDM and BDMNB cases were again overall similar to those shown previously in whole ventricle arrhythmia studies employing a monodomain approach (13,14), suggesting the overall conclusions from these monodomain studies would not differ significantly by the addition of a perfusing bath in a bidomain setting. However, to facilitate a direct comparison with previous monodomain studies at both the slab and whole-ventricle level, exact matching of anatomical geometries and electrophysiological parameters (action potential durations, CVs, etc.) between models would have to be achieved, which is left as an avenue of future investigation.

We believe that knowledge of how the bath-loading effect impacts pacing and arrhythmia studies, and to what extent in differing complex models, represents an important parameter to modelers in the consideration of whether to employ a full bidomain approach (or an augmented monodomain equivalent (8)) to their model, and potentially the difference it may make when attempting to compare with experimental recordings.

Study limitations

Due to the immense computational demands of the simulations performed in this study, it was unfortunately not possible to assess a range of different bidomain conductivity parameters, giving a range of bath-loading effects, over all protocols performed in this study. For example, simulation of ∼3 s of reentrant activity within the slab model (∼2 m degrees of freedom) took ∼20 h on 32 cores. However, we did perform such analysis during pacing on the slab model, as shown in the Supporting Material (see Computational models section, Figs. S2 and S3). This analysis showed that the bath-loading effects, although present with different conductivity sets, are most significant for those of Robert and Scher (20), and are largely independent of overall CV. We believe that this justifies the focus of this study on using the Robert and Scher values providing a realistic upper limit of the effects of bath-loading on wavefront and arrhythmia dynamics.

Finally, it has been shown previously that the complexity of arrhythmias is sensitive to specific electrophysiological properties that control action potential duration and restitution (13,14), and the effective electrical size of the ventricular model in different species, etc (12,14). Although in this study, we have considered only a single ionic model (rabbit) with standard parameter set within a single rabbit ventricular geometry, at all times we have specifically focused our analysis on the relative differences between the cases with the presence, and absence, of a bath. We thus suggest an interesting avenue of future work to examine how the bath-loading effects highlighted in this study interacts with variations in both electrophysiological parameters and physical ventricular geometries.

Conclusions

In this study, we have performed an in-depth investigation into the presence of a perfusing bath during propagation and arrhythmias within models of differing anatomical complexity. We have demonstrated that the bath can significantly affect 3D wavefront morphology, impacting the complexity and dynamics of arrhythmias, to an extent that depends strongly upon the degree of inherent anatomical complexity of the model. Moreover, due to the omnipresence of a conducting fluid layer in contact with cardiac tissue, the findings from this study also represent an imperative consideration in future modeling studies.