Optimized Torsion-Angle Normal Modes Reproduce Conformational Changes More Accurately Than Cartesian Modes

Abstract

We present what to our knowledge is a new method of optimized torsion-angle normal-mode analysis, in which the normal modes move along curved paths in Cartesian space. We show that optimized torsion-angle normal modes reproduce protein conformational changes more accurately than Cartesian normal modes. We also show that orthogonalizing the displacement vectors from torsion-angle normal-mode analysis and projecting them as straight lines in Cartesian space does not lead to better performance than Cartesian normal modes. Clearly, protein motion is more naturally described by curved paths in Cartesian space.

Introduction

Normal-mode analysis can be a powerful tool for modeling conformational changes in proteins (1–5). Traditionally, normal-mode analysis is done in Cartesian space, where it is easy to formulate and solve the eigenvalue equations. However, the propagation of Cartesian modes can lead to the nonphysical deformation of bond length and angles because atoms move along straight lines and there is no way to describe rotation. This nonphysical deformation can be avoided by performing normal-mode analysis in torsion (dihedral) angle space (6–11). By fixing the bond lengths and angles, and performing the analysis in internal coordinates, all the predicted motions are physical and the number of degrees of freedom is reduced ∼10-fold. This decrease in degrees of freedom leads to a substantial speed up in the calculation and the ability to treat larger systems.

Despite these apparent advantages, a systematic comparison of the lowest frequency displacement vectors arising from torsion-angle normal modes and those arising from Cartesian normal modes has never been carried out. Some studies that have used torsional modes have orthogonalized the linear displacement vectors (8,9,11,12), but we will show that orthogonalized torsional modes do no better than Cartesian modes in describing conformational changes. This has been shown to be the case for individual proteins (13), but not on an entire test set. Other studies (10,14) have derived a nonlinear second-order relationship between changes in torsion-angle space and curved motion in Cartesian space, which works better than the linear first-order treatment, but still only applies to small changes. The method we have developed changes the torsion angles along the normal modes to give the exact curved paths in Cartesian space; it is called optimized torsional normal-mode analysis.

The results on a set of 13 proteins with two conformational states show that with the same number of low-frequency modes, optimized torsional normal-mode analysis reproduces conformational changes more accurately than do either Cartesian or orthogonalized torsional modes. Optimized torsional normal-mode analysis is able to reproduce conformational changes by varying a small number of degrees of freedom. This leads to a dramatic reduction in dimensionality that is crucial if a conformational change is to be analyzed in detail.

Computational Methods

To compare the displacement vectors, we perform Cartesian and torsion-angle normal-mode analysis on a test set of proteins. The test set is made up of 13 pairs of proteins that have two conformations (A and B) with the same sequence, selected from the Protein DataBank (PDB). These proteins were chosen to represent a large range both in size (123–1079 amino acids) and in size of conformational change (root mean-square deviation, RMSD, from 1.7 to 27.6 Å). The test set also contains two complexes comprising more than one chain. See Table 1 for the protein names and the references to their structures.

Table 1.

Fractional RMS for Cartesian, orthogonalized torsional, and optimized torsional modes

Protein	PDB ID A	PDB ID B	No. AA	No. of chains	RMS A to B (Å)	fRMS						Min. num. modes
						A to B			B to A
						Cart.	Orth. tors.	Opt. tors.	Cart.	Orth. tors.	Opt. tors.	A to B	B to A
Ribose-binding protein	1BA2_A	2DRI	271	1	6.2	0.244	0.221	0.136	0.440	0.466	0.480	2	10
Calmodulin	1CLL	1CTR	144	1	14.8	0.561	0.580	0.194	0.655	0.709	0.133	2	1
LAO binding protein	2LAO	1LST	238	1	4.7	0.227	0.244	0.225	0.809	0.867	0.833	10	10
Ribonuclease III	1YZ9_AB	1YYO_AB	436	2	7.3	0.287	0.462	0.273	0.876	0.792	0.376	10	3
Diphtheria toxin	1DDT	1MDT_A	535	1	15.6	0.653	0.637	0.383	0.781	0.826	0.729	3	8
Lactoferrin	1LFH	1LFG	691	1	6.4	0.358	0.415	0.441	0.510	0.642	0.538	10	10
Aspartate transcarbamoylase	8ATC	5AT1	912	4	4.9	0.447	0.451	0.461	0.703	0.444	0.425	10	4
Aspartate aminotransferase	9AAT_A	1AMA	401	1	1.7	0.502	0.495	0.470	0.519	0.496	0.519	8	10
Skeletal muscle Ca2+ ATPase	1SU4_A	1IWO_A	994	1	14	0.546	0.544	0.472	0.778	0.861	0.732	8	5
5′-Nucleotidase	1HPU_D	1OID_A	525	1	9.3	0.663	0.661	0.529	0.676	0.758	0.615	9	9
Scallop myosin II	1QVI_AYZ	1KK8_ABC	1079	3	27.6	0.709	0.719	0.567	0.774	0.810	0.612	4	4
T7 RNA polymerase	1MSW_D	1QLN_A	883	1	18.3	0.808	0.783	0.779	0.982	0.980	0.970	5	9
Nitrogen regulatory protein C	1DC8_A	1DC7_A	123	1	3.2	0.963	0.956	0.892	0.944	0.938	0.939	2	10
Average values						0.536	0.551	0.448	0.727	0.738	0.608	6.4	7.2

Fractional RMS (fRMS) values of Cartesian normal modes (Cart.), orthogonalized torsional normal modes (Orth. tors.), and optimized torsional normal modes (Opt. tors.). The fRMS values are calculated using the 10 lowest frequency modes. The A and B conformations are named so that the average value of the three methods of calculating normal modes describes A to B better than B to A. The lowest fRMS for each conformational change is highlighted. The minimum number of modes (Min. num. modes) is the number of optimized torsional normal modes required to give a value for fRMS that equals the value for 10 Cartesian normal modes; values ≤5 are highlighted. PDB file names for conformations A and B are as follows: Ribose-binding protein (1BA2 (16), 2DRI (17)), Calmodulin (1CLL (18), 1CTR (19)), LAO binding protein (2LAO (20), 1LST (20)), Ribonuclease III (1YZ9 (21), 1YYO (21)), Diphtheria toxin (1DDT (22), 1MDT (23)), Lactoferrin (1LFH (24), 1LFG (24)), Aspartate transcarbamoylase (8ATC (25), 5AT1 (26)), Aspartate aminotransferase (9AAT (27), 1AMA (28)), Skeletal muscle Ca²⁺ ATPase (1SU4 (29), 1IWO (30)), 5′-Nucleotidase (1HPU (31), 1OID (32)), Scallop myosin II (1QVI (33), 1KK8 (34)), T7 RNA polymerase (1MSW (35), 1QLN (36)), Nitrogen regulatory protein C (1DC8 (37), 1DC7 (37)).

To determine how well modes do at describing the conformational change from A to B, we use a metric called the fractional RMSD (fRMS), shown in Fig. 1. The fRMS is the RMS between the predicted conformation X reached by normal modes and the desired final conformation B, |R_XB|, normalized by the original RMS between A and B, |R_AB|, i.e., fRMS = |R_XB|/|R_AB|. An fRMS value of 0 represents the ideal description of A to B, whereas an fRMS of 1 means that the normal modes cannot predict a conformation X any closer to B than the original conformation A. We use the fRMS instead of the dot product defined as the cosine of the angle XAB. Although this dot product (termed dot in Fig. 1) has been used by most other studies (3), it is much less sensitive than the fRMS value. When conformations are defined in a linear, Euclidian space (like Cartesian coordinates), there is a simple relationship between fRMS and dot, with $fRMS=\sqrt{1-do{t}^2}$. This shows that dot seems favorable (close to 1) for a wide range of fRMS values that look much less favorable. For example, an fRMS value of 0.5 (1/2), gives a dot product of 0.87, whereas an fRMS of 0.33 (1/3) gives a dot product of 0.94. In neither case is conformation X particularly close to conformation B: the initial RMSD has just been halved and reduced by two-thirds, respectively.

Figure 1.

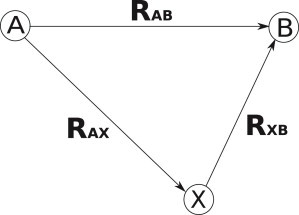
Definition of fractional RMS (fRMS). The fRMS is the metric used to assess how well normal modes describe the change from conformation A to B. When the modes are applied to A, they give the conformation X. The distance, in RMS space, between X and B is |R_XB|, which is then normalized by the original distance between A and B, |R_AB|, to give $fRMS=\left|{\mathbf{R}}_{\mathbf{X}\mathbf{B}}\right|/\left|{\mathbf{R}}_{\mathbf{A}\mathbf{B}}\right|$. If the normal modes describe the conformational change perfectly, conformation X will equal conformation B, and the fRMS value will be 0. The dot product, which is commonly used to assess normal mode performance, is the cosine of the angle BXA. It can be calculated as $dot={\left|{\mathbf{R}}_{\mathbf{A}\mathbf{B}}\right|}^2+{\left|{\mathbf{R}}_{\mathbf{A}\mathbf{X}}\right|}^2-{\left|{\mathbf{R}}_{\mathbf{X}\mathbf{B}}\right|}^2/2\left|{\mathbf{R}}_{\mathbf{A}\mathbf{B}}\right|\left|{\mathbf{R}}_{\mathbf{A}\mathbf{X}}\right|$. If the angle AXB is a right angle, then $dot=\sqrt{1-fRM{S}^2}$.

All-atom Cartesian normal modes (no hydrogen atoms) were calculated for both the A and the B conformations of each protein pair using the program NOMAD-Ref (15). A linear combination of the displacement vectors v_i with the coefficients a_i moves conformation A to conformation X, with ${\mathbf{R}}_{\mathbf{A}\mathbf{X}}={\sum }_i^N{a}_i{\mathbf{v}}_i$ for a given number N of lowest frequency modes. We want to find the coefficients a_i such that the distance between X and B, |R_XB|, is minimized. This also minimizes fRMS. Using least-squares optimization to minimize

$${\mathbf{R}}_{\mathbf{X}\mathbf{B}}^2={\left|{\mathbf{R}}_{\mathbf{A}\mathbf{X}}-{\mathbf{R}}_{\mathbf{A}\mathbf{B}}\right|}^2={\left|\sum _i^N{a}_i{\mathbf{v}}_i-{\mathbf{R}}_{\mathbf{A}\mathbf{B}}\right|}^2$$

gives $a_i={\mathbf{v}}_i{\mathbf{R}}_{\mathbf{A}\mathbf{B}}$. We use this procedure to find the optimum a_i values that best describe the conformational change from A to B and also the reverse change from B to A. The normal modes of conformation A are not the same as those for conformation B, so we calculate both directions, from A to B and from B to A.

In the same way, all-atom torsion-angle normal modes were calculated for both the A and the B conformations of each protein using the program STAND ((9) and M. Levitt, unpublished). For the torsional modes, the determination of the optimal combination of displacement vectors is not straightforward because the Cartesian coordinate displacement vectors derived from torsional-angle normal modes are not orthogonal, so that the formula for the coefficient a_i requires matrix inversion. Instead, the Cartesian coordinate displacement vectors derived from torsion-angle normal modes can be orthogonalized by Gram-Schmidt orthogonalization (as illustrated in Fig. 2) and then the coefficients a_i calculated as described above for Cartesian normal modes.

Figure 2.

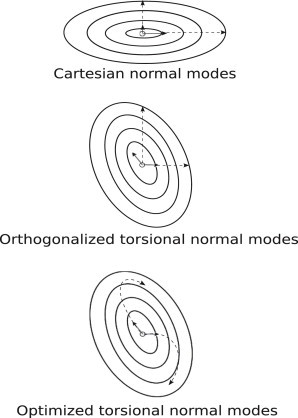
Energy surfaces and normal-mode projections. In this simple illustration, the energy surfaces and normal modes are shown projected into two-dimensional Cartesian space. The elliptical contour lines represent the energy surfaces, the solid arrows the normal mode displacement vectors, and the dashed lines the normal mode movement. Whereas displacement vectors at the origin are always straight lines in Cartesian space, movement along the torsion angle modes follows curved lines in Cartesian space. The displacement vectors at the origin are orthogonal in Cartesian modes but not in torsion-angle modes. The change of conformation between state A and state B is the optimal combination of movements along the dashed lines. This optimum is easily found when the lines are straight in Cartesian space but requires nonlinear optimization when the lines are curved.

Whereas Cartesian coordinate modes move atoms along straight lines in Cartesian space, torsion-angle normal modes move atoms along curved paths (see Fig. 2). Instead of orthogonalizing the torsional modes, the modes can be treated as curved paths in Cartesian space. In this case, there is no simple analytical way to find the optimal combination of torsion-angle modes to minimize the RMSD between conformation X and B. Instead, nonlinear optimization is used to find the optimal coefficients for N modes in torsional space, the starting coefficients are randomly chosen for the N modes, and the torsional modes are physically applied in space. The simplex minimization method, which does not need analytical derivatives, is used to find a set of coefficients a_i that minimizes the fRMS value. Starting coefficients are chosen for the N modes used; the torsional modes are applied as changes in the torsion angles and the value of fRMS is calculated after rigid body superposition. This process is thus iterated until it converges on the minimum value of fRMS. The entire minimization procedure is repeated 10 times with different random initial values for the coefficients, then the values from the minimization run that gives the lowest fRMS are used. This optimization process is nonlinear: changing a torsion angle does not move A along a straight line toward B so that the simple relationship between fRMS and dot does not hold exactly.

Results and Discussion

Although the torsion-angle normal modes are very different from Cartesian normal modes, the displacement vectors are very similar for the low-frequency motion. When these two different sets of displacement vectors are used to reproduce the experimentally observed conformational change using the 10 lowest frequency modes, the results shown in Table 1 are similar for the fRMS values of the Cartesian (Cart.) or orthogonalized torsion angle (Orth. tors.) displacement vectors. The average fRMS values for all the test cases for A to B are very similar for Cartesian modes and orthogonalized torsional modes (0.536 and 0.551, respectively). The same holds for the B-to-A test cases (0.727 and 0.738, respectively). For both the A to B and the B to A, the Cartesian modes are better than the orthogonalized torsional modes in half the cases (6 of 13 cases). Clearly, there is little difference between the Cartesian displacement vectors and the orthogonalized torsional displacement vectors.

In Table 1, we show these fRMS values for all protein pairs in the test set for Cartesian modes, orthogonalized torsional modes, and optimized torsional modes calculated using the 10 lowest frequency modes. We chose 10 modes because this is the average number of modes for which the improvement in fRMS from additional modes is negligible. Optimized torsional modes describe conformational changes significantly better than Cartesian modes or orthogonalized torsional modes. For the A-to-B conformational change, the average fRMS for the entire test set is 0.448 for the optimized torsional modes, as compared to 0.536 for Cartesian modes and 0.551 for orthogonalized torsional modes. An fRMS of 0.431 corresponds to a dot product of 0.894, whereas an fRMS of 0.536 corresponds to a dot product of 0.844. For the A-to-B cases, the optimized torsional modes better describe the conformational change in 11 out of 13 pairs. For the B-to-A conformational changes, the difference in fRMS is even more striking. The optimized torsional modes give an average fRMS of 0.608 in comparison to fRMS values of 0.727 and 0.738 for Cartesian and orthogonalized torsional modes, respectively.

In some cases, most noticeably for both directions of calmodulin, optimized torsional modes do a markedly better job than the Cartesian or orthogonalized torsional modes. For the A-to-B conformational change of calmodulin, the fRMS of the optimized torsional modes is 0.194, whereas it is 0.561 and 0.580 for the Cartesian and orthogonalized torsional modes, respectively. An fRMS of 0.194 corresponds to a dot product of 0.981, whereas an fRMS of 0.561 corresponds to a dot product of 0.828. There is no case in the test set where the Cartesian or orthogonalized torsional modes perform significantly better than the optimized torsional modes. If we repeat the analysis with fewer optimized torsional modes we find that in many cases the dimensionality (number of normal modes) needed to reproduce the conformational change is significantly smaller for optimized torsional modes (see Table 1). With optimized torsional modes, the conformational changes in at least one direction (A to B or B to A) for five of 13 cases are as well described in three or fewer dimensions as in 10 dimensions for Cartesian modes (Ribose-binding protein, Calmodulin, Ribonuclease III, Diphtheria toxin, and Nitrogen regulatory protein C). This is a dramatic reduction in the dimensionality of the problem! Based on these results, optimized torsional mode analysis is clearly the best method for modeling protein conformational changes.

Conclusion

Our finding that the Cartesian and orthogonalized torsional modes perform similarly, and significantly worse than the optimized torsional modes, shows that protein motion is more naturally described by curved paths than by displacement vectors in Cartesian space. Optimized torsional normal mode analysis is a powerful, potentially new way to represent protein conformational changes.