Regulation of Cell Adhesion Strength by Peripheral Focal Adhesion Distribution

Abstract

Cell adhesion to extracellular matrices is a tightly regulated process that involves the complex interplay between biochemical and mechanical events at the cell-adhesive interface. Previous work established the spatiotemporal contributions of adhesive components to adhesion strength and identified a nonlinear dependence on cell spreading. This study was designed to investigate the regulation of cell-adhesion strength by the size and position of focal adhesions (FA). The cell-adhesive interface was engineered to direct FA assembly to the periphery of the cell-spreading area to delineate the cell-adhesive area from the cell-spreading area. It was observed that redistributing the same adhesive area over a larger cell-spreading area significantly enhanced cell-adhesion strength, but only up to a threshold area. Moreover, the size of the peripheral FAs, which was interpreted as an adhesive patch, did not directly govern the adhesion strength. Interestingly, this is in contrast to the previously reported functional role of FAs in regulating cellular traction where sizes of the peripheral FAs play a critical role. These findings demonstrate, to our knowledge for the first time, that two spatial regimes in cell-spreading area exist that uniquely govern the structure-function role of FAs in regulating cell-adhesion strength.

Introduction

Cell adhesion to the extracellular matrix (ECM) plays a central role in mediating and regulating important cellular processes including but not limited to cell migration, bidirectional signaling during morphogenesis, tissue homeostasis, and wound healing (1). Adhesion of cells to ECM components, including fibronectin and laminin, is primarily mediated by transmembrane heterodimeric receptors that belong to the integrin family (2). Receptor-mediated adhesion is a complex process involving integrin recruitment to the interface, activation, and mechanical coupling to extracellular ligands (3). These bound receptors rapidly interact with the actin cytoskeleton and cluster together to form focal adhesions (FA), large supramolecular complexes that contain structural proteins like talin, vinculin, and α-actinin and signaling proteins, such as FAK, Src, and paxillin (4).

FAs are reinforced and stabilized by actin-myosin contractility that enhances adhesion strength (5,6) and generates cellular traction that leads to cell spreading and cell migration by applying mechanical force on the underlying substrate (7). Because the interactions between integrins and actin stress fibers are known to be mediated by FA assembly, cell shape (cell spreading) has been characterized as a main regulator for FA assembly by transmitting force from the ECM to cytoskeletal components (8–10). Moreover, extensive studies during the past decade indicate that mechanical tension generated within the cytoskeleton of living cells is a critical regulator of various cellular functions (11,12). Further probing into the mechanical interactions between the cell and the substrate demonstrated the existence of an inside-out mechanism whereby changes in cell shape by global cell distortion increase the cytoskeletal tension and drive FA assembly (10). As a complementary approach, changing the elasticity of the underlying substrate regulates the level of tension that a cell can exert on the substrate that, in turn, directly affects FA assembly (13).

To elucidate the structure-function relationships between the adhesive components, micropatterned surfaces complemented by a hydrodynamic shear assay have been successfully employed by Gallant et al. (14). That work on the spatiotemporal evolution of cell adhesion strength on micropatterned surfaces dissected the contributions of adhesive area, integrin binding, and FA assembly toward cell adhesion strengthening (5). It was established that steady-state adhesion strength varied nonlinearly with adhesive area and reached a plateau at an adhesive area of 78 μm², beyond which further rises in adhesive area did not enhance the steady-state adhesion strength (5). This is in contrast to studies of cellular traction that demonstrated linear increases in mean traction with increases in cell-spreading area (15,16). The nonlinearity in the adhesion strength was attributed to peripheral clustering of integrins and subsequent formation of FAs (5) in line with the previous analysis by Ward and Hammer (17). Mathematical models that simulate the clustering of integrins and subsequent formation of FAs have been developed to examine the nonlinearity in the adhesion strength with respect to the adhesive area (18,19). However, as the adhesive area is manipulated, the cell-spreading area and the distribution of FAs are inherently affected. Hence, it is unclear whether the extent of cell spreading modulated by the spatial distribution of adhesive complexes or the total available adhesive area is responsible for the enhancement in the adhesion strength. Moreover, it is also unclear whether the set-point area of ∼78 μm²—beyond which there is no significant enhancement in the adhesion strength—is dictated by the total cell adhesive area or by the extent of cell spreading due to the peripheral distribution of adhesive complexes.

Based on our previous observations of the formation of distinct peripheral adhesion complexes (5,6), we hypothesized that the spatial distribution of adhesive complexes plays a significant role in regulating the cell-substrate adhesion strength. To test this hypothesis, cell-adhesive areas were engineered to delineate the cell-spreading area from total cell-adhesive area, thereby enabling us to modulate the position of FAs. In the design of the peripheral adhesion complexes, the adhesive-patch size was limited to 1 μm, which is consistent with our earlier experimental and theoretical adhesion models. We made use of soft lithographic techniques and well-defined surface chemistries to fabricate these adhesive surfaces and control cell shape and adhesive complex position. Specifically, adhesive islands of constant outer diameter or constant area were engineered to dissect the regulatory roles of total adhesive area and adhesive complex distribution (Fig. 1). A hydrodynamic shear assay was used to quantify the adhesion strength of cells cultured on these micropatterned substrates coated with adhesive proteins, thus enabling us to analyze the effect of adhesive complex position on the overall adhesion strength independently of the total cell adhesive area. In light of the recently published observations that cellular traction depends on FA assembly and cell-spreading extent, an attempt has been made to contrast the functional role of these events in cell adhesion and traction. Such a mechanistic insight into the key biophysical regulators of cell adhesion would be indispensible in understanding mechanotransduction to manipulate cell-adhesive interfaces on biomaterials that are critical to applications including tissue engineering and in vitro organ models.

Figure 1.

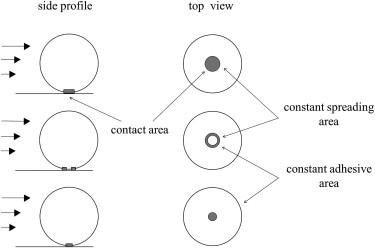
Schematic diagram of cells adhered to micropatterned islands that delineate cell adhesive area and cell spreading area.

Materials and Methods

Reagents

Dulbecco's modified Eagle's medium (Invitrogen, Carlsbad, CA) supplemented with 10% newborn calf serum (Invitrogen) and 1% penicillin-streptomycin (Invitrogen) was used as complete growth media (CGM). Cell culture reagents, including human plasma fibronectin and Dulbecco's phosphate-buffered saline (DPBS), and AlexaFluor 488-conjugated secondary antibodies, Hoechst-33242, and rhodamine-conjugated phalloidin were purchased from Invitrogen. Chemical reagents, including 1-hexadecanethiol [H₃C(CH₂)₁₅SH] and tri(ethylene glycol)-terminated alkanethiol [HO(CH₂CH₂O)₃(CH₂)₁₁SH], and anti-fibronectin polyclonal and anti-vinculin antibodies were purchased from Sigma-Aldrich (St. Louis, MO).

Micropatterned surfaces

Elastomeric stamps

Master templates of required patterns were fabricated on silicon wafers using standard photolithography techniques. Briefly, positive photoresist (Shipley 1813) was spun onto a precleaned silicon wafer to a thickness of ∼2 μm. Sequential ultraviolet exposure of the resist was required to produce features of two size scales (10⁻⁶ and 10⁻⁴ m) with a single development on the template. The wafer was subjected to a primary exposure through an optical mask containing the required low-fill factor stamp features in the pattern zone followed by a secondary exposure through an optical mask containing the annular peripheral zone. This feature was necessary to prevent the parasitic roof collapse inherent to low-fill factor, large-structural-aspect-ratio stamp designs. The exposed areas were developed, leaving behind a template of recessed features. Templates were then exposed to (tridecafluoro-1, 1, 2, 2-tetrahydrooctyl)-1-trichlorosilane (Sigma-Aldrich) in a dessicator under vacuum to prevent the polydimethylsiloxane (PDMS) elastomer from adhering to the exposed silicon. The PDMS precursors and curing agent (Sylgard 184; Dow Corning, Midland, MI) were mixed in the recommended ratio (10:1), degassed under vacuum, poured over the template in a 100-mm-diameter flat dish to a thickness of 5 mm, and cured at 65°C for 2 h. The cured PDMS stamp containing the desired features was then peeled from the template and cut into a 25-mm square, ensuring the annular region was at the periphery.

Substrates

Glass coverslips (25 mm in diameter) were sonicated in 50% ethanol, dried under a stream of compressed N₂, and then oxygen-plasma-cleaned for 5 min (PE50; Plasma Etch, Carson City, NV). These coverslips were sequentially coated with 10 nm of titanium and 20 nm of gold at a deposition rate of 0.5 Å/s in an electron beam evaporator.

Microcontact printing

For microcontact printing (μCP), the flat back of the stamp was allowed to self-seal to a glass slide to provide a rigid backing. The stamp was inked with 2 mM 1-hexadecanethiol (Sigma-Aldrich) and then gently blown dry with compressed N₂. The stamp was gently placed on the substrate to ensure conformal contact of the features over the entire area of substrate. The stamp was kept in contact for 10 s to produce an array of CH₃-teminated monolayer islands, to which proteins readily adsorbed. The stamp was then carefully separated from the substrate with the help of tweezers. The patterned substrates were incubated in 2 mM ethanolic solution of tri(ethylene glycol)-terminated alkanethiol for 2 h to create a nonadhesive background around the CH₃-terminated islands. The substrates were rinsed in 95% ethanol and gently dried under a stream of N₂.

Protein patterning

The substrates were incubated with fibronectin (20 μg/ml in DPBS; Invitrogen) for 30 min and then blocked with denatured (65°C, 2 h) 1% bovine serum albumin (Fisher Scientific, Fair Lawn, NJ) for 30 min to avoid nonspecific protein adsorption.

Cell patterning

NIH3T3 fibroblasts (American Type Culture Collection, Manassas, VA) were cultured in CGM on tissue culture polystyrene. Cells were passaged every other day and used between passages of 5 and 20. For experiments, cells were enzymatically lifted from the culture dish using trypsin/EDTA (Invitrogen) and then seeded onto these micropatterned substrates at a density of 225 cell/mm² in CGM.

Cell adhesion assay

Cell counts at various radial positions on the substrate were used to quantify the adhesion strength after exposure to a hydrodynamic flow created by rotation in a solution of known viscosity and density using a spinning disk device (20). Briefly, a micropatterned substrate with the cells seeded on it was mounted on a spinning platform and spun in 2 mM dextrose in DPBS to apply well-defined hydrodynamic forces to adherent cells. The applied shear stress τ (force/area) varies linearly from the center of the disk to the periphery according to

$$\tau =0.8r{\left(\rho \mu {\omega }^3\right)}^{0.5},$$ (1)

where r is the radial position along the substrate, μ is the viscosity, ρ is the density of the solution, and ω is the angular velocity. After spinning for 5 min, the remaining adherent cells were fixed in 3.7% formaldehyde, permeabilized with 0.1% Triton X-100, and stained with Hoechst dye to identify the nucleus. The number of adherent cells was counted at specific radial positions using an Eclipse Ti-U fluorescent microscope (Nikon Instruments, Melville, NY) fitted with a motorized stage and NIS-Elements Advanced Research software (Nikon Instruments). Sixty-one fields were analyzed per substrate and the number of cells at specific radial locations was then normalized to the number of cells at the center of the substrate where negligible shear stress was applied to calculate the fraction of adherent cells f. The detachment profile (f versus τ) was then fit with a sigmoid curve

$$f=\frac{1}{\left(1+e^{\left[b\left(\tau -{\tau }_{50}\right)\right]}\right)}.$$ (2)

The shear stress for 50% detachment (τ₅₀) was used as the mean cell-adhesion strength.

Statistical analysis

Experiments were performed in triplicate in at least three independent experiments. Data are reported as mean ± SD of the mean, and statistical comparisons using SigmaPlot 11 (Systat Software, San Jose, CA) were based on analysis of variance and the Holm-Sidak test for pairwise comparisons, with a p value < 0.01 considered significant. Curve fits of experimental data to specified functions were conducted in SigmaPlot.

Results

Spatial organization of FAs

NIH3T3 fibroblasts stained for vinculin (a structural FA protein) along with actin filaments and nuclei indicated preferential recruitment of vinculin toward the periphery of the cell-substrate interface (Fig. 2). Using an intensity threshold algorithm provided by the image analysis software to detect intensity peaks in the green channel of the image further reinforces the observation of the distinct peripheral preference of FA organization in a spread cell at 16 h of incubation in CGM. Similar FA enrichment at the adhesive perimeter was observed previously on fully spread unconstrained and micropatterned cells (5). Image analysis was used to quantify the spatial organization of FAs in the radial direction for micropatterned cells (see Fig. S1 in the Supporting Material) indicating a highly nonuniform distribution with consistent enrichment at the periphery. In light of the established dependence of cell adhesion strength on available adhesive area and the correlation between cell spreading and cell traction, this result motivated a thorough investigation of the spatial organization of FAs as a critical regulator of cell adhesion strength.

Figure 2.

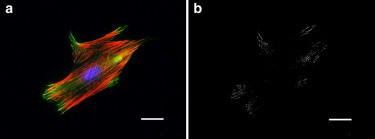
Immunostained image of a (a) spread cell (color online: blue, nucleus; red, f-actin; and green, vinculin). (b) Same cell thresholded for peak intensities of vinculin staining (bars = 10 μm).

Micropatterned substrates to manipulate the cell-adhesive interface

Micropatterned surfaces consisting of adhesive and nonadhesive domains were used to control the cell-substrate adhesive area and restrict the cell shape by modulating spreading. This was necessary to investigate the regulation of cell adhesion strength by cell spreading independently of total adhesive area. μCP (21,22) was employed to pattern self-assembled monolayer domains of alkanethiols onto which fibronectin was adsorbed within a nonfouling, nonadhesive background. However, the standard μCP technique resulted in irreversible roof collapse and propagation due to stamp instability for the small and sparse features and prevented their replication on the substrates (see Fig. S2) as has been observed previously (23). To overcome this parasitic roof collapse, the peripheral stamp stability was enhanced by embedding an annular column circumscribing the pattern zone in the stamp design (see Fig. S2).

The μCP technique was previously applied to pattern surfaces to investigate the effects of cell spreading on cell survival (8), the contributions of cell adhesive area toward cell adhesion strength (5,14), and cytoskeletal interactions with the ECM (10,11). We applied μCP in this study to engineer the adhesive domains to investigate the effect of adhesive complex position on cell-adhesion strength while maintaining similar cell shapes among treatments. Arrays of circular- and annulus-shaped islands were engineered to discern the contribution of cell-spreading area and total cell-adhesive area toward cell-adhesion strength (Fig. 3). The island dimensions were engineered specifically to allow for the delineation of total cell-adhesive area from cell-spreading area as summarized in Table 1. Spacing between the adhesive islands was maintained at 75 μm to avoid any cell-to-cell contact and ensure that each cell would interact with a single adhesive island. Fibronectin preferentially adsorbed onto the stamped islands, whereas the surrounding tri(ethylene glycol)-terminated regions remained devoid of fibronectin.

Figure 3.

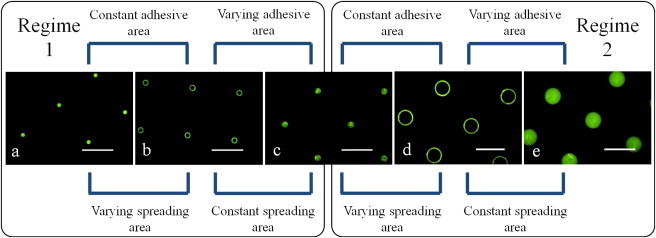
Immunostaining indicates fibronectin adsorbed only to micropatterned islands: (a) 6-μm-diameter circular islands; (b) 10-μm-outer, 8-μm-inner-diameter annulus islands; (c) 10-μm-diameter circular islands; (d) 25-μm-outer, 23-μm-inner-diameter annulus islands; and (e) 25-μm-diameter circular islands (bars = 50 μm).

Table 1.

Micropattern dimensions and corresponding areas

Micropattern	Cell adhesive area	Cell spreading area
6-μm-diameter circular island	28 μm2	28 μm2
10-μm-outer, 8-μm-inner-diameter annulus island	28 μm2	78 μm2
10-μm-diameter circular island	78 μm2	78 μm2
25-μm-outer, 23-μm-inner-diameter annulus island	78 μm2	490 μm2
25-μm-diameter circular island	490 μm2	490 μm2

We previously reported that NIH3T3 fibroblasts remained viable for several days when adhering to fibronectin-coated micropatterned circular islands with dimensions ranging from 2 to 20 μm and remained constrained to the FN area (5,14). Similarly, in this study NIH3T3 cells adhered to fibronectin-coated islands of similar dimensions and remained constrained to the patterned areas. Moreover, the adhesive structures containing vinculin localized to, and remained confined to the micropatterned domains, and cells maintained a nearly spherical or hemispherical morphology (Fig. 4). Taken together, these results demonstrate control of cell-adhesive area to engineer FA size and position, which can be used to decouple the effect of cell-spreading area and total cell-adhesive area on adhesion strength.

Figure 4.

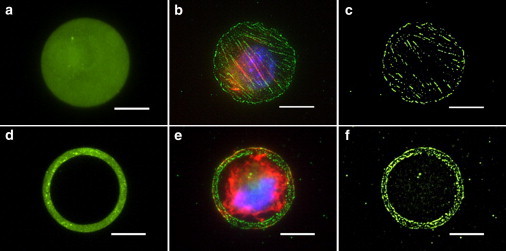
(a–c) Solid circular and (d–f) annular islands were coated with (a and d) fibronectin to regulate cell spreading and focal adhesion assembly. (b and e) Adherent cells were immunostained to identify adhesive structures (color online: blue, nucleus; red, f-actin; and green, vinculin). (c and f) Images were thresholded for the peak intensities of vinculin staining (bars = 10 μm).

Analysis of cell-adhesion strength

Cell-adhesion strength was quantified using a well-characterized spinning disk hydrodynamic shear assay that has been used extensively for investigating structure-function relationships among adhesive components (5,14,20,24). This system applies a well-defined range of hydrodynamic forces to a population of cells adhered to micropatterned islands and provides sensitive measurements of adhesion strength. It was previously established that the wall shear stress (τ) increases linearly with radial position (r) on the disk surface as given by Eq. 1. The shear stress for 50% detachment (τ₅₀) was established as the adhesion strength to allow for quantitative comparisons between experimental conditions.

In our previous work, it was established that an area of 78 μm², which supports half-maximal integrin binding, was a set-point for the segregation of discrete receptor clusters and that the adhesive strength reaches a plateau at this adhesive area (5). However, it is unclear whether this set-point area refers to total-adhesive area or the extent of cell spreading as it was observed that integrin clustering and FA assembly were observed to be enriched at the periphery. Therefore, two distinct regimes are considered for analysis in this study. Regime 1 consists of micropatterned islands with dimensions that support cell-spreading areas up to 78 μm² and regime 2 consists of island dimensions that supported cell-spreading areas >78 μm² (Fig. 3). The results for adherent cells on adhesive islands in regime 1 (Fig. 5 a) indicate that the redistribution of similar adhesive areas to annular shapes with larger diameters to allow for greater cell spreading enhances adhesion strength by 40% (comparing 6-μm-diameter circular island and 10-μm-outer, 8-μm-inner-diameter annulus island). Moreover, adhesion strength increased 35% when the adhesive area was enhanced for islands of similar spreading area (comparing 10-μm-outer, 8-μm-inner-diameter annulus island and 10-μm-diameter circular island).

Figure 5.

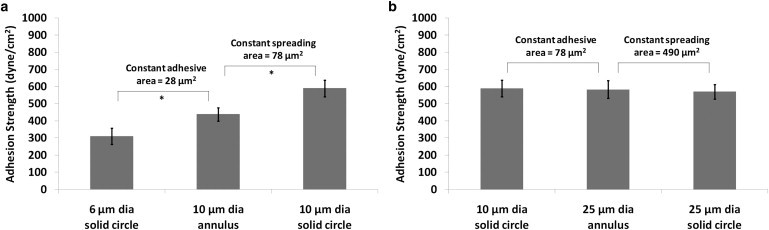
Mean adhesion strength (τ₅₀) at steady state for cells patterned on micropatterned domains in (a) regime 1 up to 78 μm² adhesive area and (b) regime 2 from 78 μm² to 490 μm² adhesive area (asterisk indicates significant difference P < 0.001).

The results for adherent cells on adhesive islands in regime 2 (Fig. 5 b) indicate that redistribution of similar adhesive areas to annular shapes with larger diameters to allow for greater cell spreading with the same adhesive area did not enhance adhesion strength (comparing 10-μm-diameter circular island and 25-μm-outer, 23-μm-inner-diameter annulus island). Furthermore, comparing cells with similar spreading areas but different adhesive areas in regime 2 also clearly indicates that for constant cell spreading area, peripheral FAs accounted for 100% of the adhesion strength (comparing 25-μm-outer, 23-μm-inner-diameter annulus island and 25-μm-diameter circular island). These results indicate that rises in adhesion strength are limited to regime 1 and further reinforce the concept of a set-point total adhesive area of ∼78 μm² to support maximum cell-adhesion strength.

Discussion

Spatial distribution of FAs in regulating cell adhesion strength

It has been observed that FAs tend to accumulate at the periphery of the adhesive contact area. We have demonstrated that the peripheral distribution of adhesive complexes occurs in cells that are constrained to micropatterned islands (Fig. 4 and see Fig. S1) as well as in cells spreading on uniform surfaces (Fig. 2). In both cases, this arrangement of FAs allows large changes in cell shape and results in the cell spreading area exceeding the actual adhesive area. Although this enrichment at the leading edge of migrating cells and its influence on cell traction have been studied extensively, the contribution of this phenomenon to adhesion strength has not yet been investigated.

To understand the roles of cell-spreading area and total cell-adhesive area in modulating adhesion strength, experimentally obtained adhesion-strength data were fitted as functions of spreading area 1), when cell adhesive area was equal to cell spreading area and 2), when those same cell adhesive areas allowed for greater cell spreading by redistributing over annular shapes with larger diameters (Fig. 6). It was observed that an exponential curve explained the rises in adhesion strength in both cases. However, when the adhesive areas were distributed to the periphery to allow for a greater extent of cell spreading, the nonlinearity in the exponential curve is more pronounced. This implies that the nonlinearity in the adhesion strength with respect to area as observed in earlier studies (5) is predominantly due to the peripheral distribution of FAs.

Figure 6.

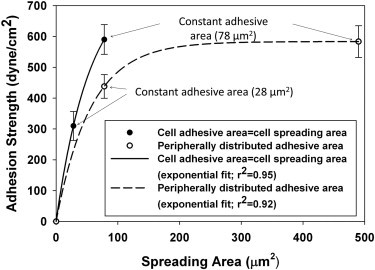
Cell-spreading area and cell-adhesive area each regulates steady-state adhesion strength. Data are plotted separately for circular and annular islands of two corresponding adhesive areas. Exponential curves describe the relationships between adhesion strength and spreading for the different focal adhesion distribution conditions. Symbols represent mean values, but the curves were fit to all data points.

In regime 1, an enhancement in spreading area (independently of total adhesive area) by the peripheral distribution of FAs enhanced adhesion strength by 40% when the outer radius was increased by ∼65%. It can be inferred from this observation that below a set-point area of 78 μm², the total adhesive area alone cannot be used as a parameter for explaining adhesion strength but it can be used in conjunction with cell-spreading area. The regulation of cellular processes by the extent of cell spreading and cell shape was first identified over three decades ago in primary investigations by Folkman and Moscona (25). In addition to modulating adhesion strength, peripheral distribution of FAs has been shown to regulate several important processes during cell-matrix interactions such as transducing cell shape signals in human tendon fibroblasts to regulate expression of collagen type I (26). Cellular traction generated at the periphery of the cell by the FAs was reported to direct fibronectin matrix assembly in NIH3T3 fibroblasts during early phases of cell spreading (27). Investigations by Reinhart-King et al. (16) also reinforce the fact that traction in bovine aortic endothelial cells increases linearly with cell spreading area and was observed to be maximum at the cell periphery, implying that peripheral distribution of FAs not only regulates cell adhesion strength but regulates cellular traction as well.

A second significant observation from this analysis is that in regime 1, adhesion strength increased only 35% when adhesive area was enhanced approximately threefold for islands of similar spreading area (comparing a 10-μm-outer, 8-μm-inner-diameter annulus island and a 10-μm-diameter circular island). This could be explained by increases in integrin binding and FA assembly that both continue to increase with adhesive area even beyond the 78 μm² set-point (5). However, an alternative explanation remains to be explored. It is possible that the spatial distribution of FAs results in a more complex organization of the cell's cytoskeleton, and thus the way applied hydrodynamic forces are transmitted through the cell is altered. This idea of cytoskeletal reorganization to modulate cell adhesion strength has been previously explored in terms of the cytoskeletal prestress (28) and also by the nanoscale-adhesive interface when the spacing between the integrin ligands was varied (29,30).

Validation of the adhesive-patch model

Significant efforts toward understanding the mechanisms of cell adhesion have been made since the identification of adhesive components including adhesion receptors and FA complexes. We previously proposed a model to explain the experimental observations of adhesion strengthening (18), which captures important points of the conceptual model originally developed by Ward and Hammer (17) and Ward et al. (31). The model was based on the concept of a 1-μm adhesive patch providing a tensional force of 200 nN that resists the peeling detachment force. The nonlinear increase in adhesion strength with adhesive area was explained in terms of a moment arm that increases with adhesive area that enhanced the ability of the adhesive patch to withstand the peeling force.

Because we hypothesized that the FAs at the periphery rather than the total adhesive area regulated the adhesion strength, the micropatterned islands employed in this study provided for further experimental testing of the adhesive patch model for cell adhesion strengthening. Moreover, it also provides for the validation of the exponential bond loading condition by comparing the adhesion strength values from the model to the experimentally obtained values from the annular island patterns. We employed the formulation derived by Gallant and Garcia (18) for evaluating adhesive patch bond strength F_T given by

$$F_T=\sum _{i=1}^{i=5}f{B}_i\left[\chi +\left(1-\chi \right)\kappa e^{\left(1-i\right)}\right],$$ (3)

where f is the individual bond strength, B_i is the number of bonds per patch segment, κ modulates the exponential dependence of segment loading, and χ is the fraction of bonds associated with cytoskeletal FA elements. In our earlier work, we varied each model parameter individually to investigate the effect of adhesive area on cell adhesion strength and the dependence on parameter values (18). It was observed that using the previously published values for FA-associated integrin bonds (χ = 0.33) and bond strength (f = 100 pN) (32,33) and an unscaled (κ = 1) exponential loading, the model fit closely to the experimentally obtained adhesion strength values for a range of bond numbers including B_i = 600 (18). Therefore, these parameter values were used for our simulations.

To obtain adhesion strength predictions from the model, mechanical equilibrium was applied to the macroscopic model and the resulting critical shear stress (adhesion strength) was obtained for the engineered adhesive geometries. The cell is assumed to have an approximately spherical shape when the adhesive island diameter was lower than the diameter of the cell in suspended state, whereas for the conditions when the adhesive island diameter is greater, the cell is assumed to take a nearly hemispherical shape (see Fig. S3). The shear-stress equations for spherical and hemispherical protrusions from a surface were previously developed and are given by Eq. 4 and Eq. 5, respectively (18,34), as

$$\tau =\frac{F_T}{\left\{32R^2{\left[1+{\left(0.8R/a\right)}^2\right]}^{0.5}\right\}},$$ (4)

$$\tau =\frac{F_T}{\left(5\pi a^2\right)}.$$ (5)

To understand how the observed rises in the adhesion strength are related to the peripheral distribution of adhesive complexes independently of total adhesive area, the experimentally obtained adhesion strength was plotted against cell spreading area and compared to the simulated values of adhesion strength (Fig. 7). It was observed that in regime 1, our model was able to strongly predict the adhesion strength for cells on islands with peripherally distributed FAs. However, the observation of enhanced adhesion strength for the solid circular island over the annulus with similar outer diameters indicates that either 1), this simple model does not fully capture the effects of spatial distribution of adhesive complexes throughout the adhesive area; or 2), the adhesion strength rises are not solely governed by events at the adhesive interface but rather by the cumulative contributions from other biophysical parameters such as the cell's cytoskeletal organization that might affect adhesion strength by regulating the cell's internal force balance.

Figure 7.

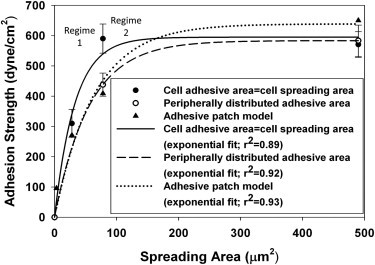
Experimental cell adhesion strength-spreading relationship for peripherally distributed focal adhesions agrees well with theoretical predictions of the adhesive patch model. Data are plotted separately for circular and annular islands. Exponential curves describe the relationships between adhesion strength and spreading for the different focal-adhesion distribution conditions. Symbols represent mean values but the curves were fit to all data points.

FA size in regulating cell adhesion strength

FA size has been established as a putative mechanotransducer that provides for a direct correlation to cellular traction (13). Moreover, FA size has consistently been reported to transduce cell shape (i.e., extent of spreading) signals into contractility that is externally expressed as cellular traction and has been established to play a major role in cell survival for several cell types (8–10,15). A recent report by Rape et al. (35) demonstrated that cell shape affects traction and, more importantly, that FA size regulates local as well as global control of cellular traction. Moreover, cellular traction and FA size increased linearly as the distance of the FAs increased from the cell's moment center. When the peripheral FA size was restricted to 2 μm, no increases in local or global cellular traction was observed at increased distance (35). However, from this study, it can be concluded that individual FA size (above a minimum patch size of 1 μm in the radial direction) does not directly regulate adhesion strength on a global scale. This stark contrast is exemplified by the fact that adhesion strength for 10-μm-outer, 8-μm-inner-diameter annulus islands and 25-μm-outer, 23-μm-inner-diameter annulus islands is significantly different even though the effective FA size is limited to 1 μm at the periphery.

Mechanistic role of FAs in the two spatial regimes

A primary role of FAs is to enhance the structural integrity of the integrin clusters, thus leading to enhancement in the adhesion strength (5,6,36). Consistent with previously reported observations, we found that adhesion strength is enhanced by increasing total cell adhesive area (5,6). A surprising finding is that adhesion strength rises by either enhancing the total available area or the cell spreading area, but the saturation value is governed by the total adhesive area of ∼78 μm² irrespective of the spatial distribution of adhesive complexes. The possibility that the adhesion strength reaches saturation due to limiting receptor or ligand availability has been ruled out in earlier investigations that indicate that the set-point area of ∼78 μm² is only the half-maximal binding value of integrins and FA proteins (talin and vinculin) (5). However, alternative explanations remain to be explored. A possible biophysical explanation for the total adhesive area to govern the saturation of adhesion strength could be the fact that the shape of a cell in vivo where spreading is minimal might only require a total contact area of ∼78 μm² to effectively adhere and perform various cellular functions as opposed to the larger spreading areas that are observed in vitro.

In addition, these results further reinforce that the nonlinearity in the adhesion strength is predominantly due to the adhesive complex position because only a relatively small increase in the radius (65%) was required to achieve an enhancement in adhesion strength similar to that which required a threefold increase in the adhesive area. This analysis demonstrates that the distribution of adhesive patches away from the cell center is more efficient for stabilizing cell attachment than uniformly dispersing the adhesive complexes over greater areas.

Contrasting to the observations of adhesion strengthening, investigations of cellular traction indicate that as the cell spreading area is increased from 500 μm² to 3000 μm², the magnitude of traction increases linearly (15,16). It has also been observed that inhibition of contractility drastically reduces the cellular traction with dissolution of vinculin containing FAs (37). However, inhibiting the formation of FAs reduced adhesion strength only by 30% irrespective of the cell spreading area (5,6). These observations collectively suggest that the functional role of FAs is different in governing the cell adhesion strength and ability to apply cellular traction. To explain the structure-function role of FAs in the two regimes of adhesion strengthening, we hypothesize that FAs in regime 1 primarily enhance adhesion strength and provide anchorage to the underlying substrate, whereas in regime 2, their mechanistic function might be to transduce signals so as to provide traction stresses that are critical to the regulation of important cellular functions including mechanosensation and migration. In other words, a threshold spread area and quantity of FA-reinforced integrin bonds is required for maximal adhesion strength, but additional FA enhancement and redistribution provides additional mechanical functions without altering cell adhesion strength.

Conclusions

A systematic study of the effect of the spatial distribution of FAs on cell adhesion strength was conducted by modulating cell adhesive area independently of spreading area via micropatterning. This approach enabled the identification of what we consider novel biophysical properties of FAs that contribute to adhesion strength, but which contrast sharply with established FA-cellular traction structure-function relationships. Directing FA assembly to the cell periphery demonstrated that the distribution of adhesive patches away from the cell center is more efficient for stabilizing cell attachment than uniformly dispersing the adhesive complexes over greater areas, and results in nonlinear increases in adhesion strength. However, the maximum cell adhesion strength is governed by the total adhesive area. In addition, individual FA size does not directly regulate global adhesion strength. In contrast, cellular traction increases linearly with FA size and its distance from the cell's moment center. This work establishes, to our knowledge for the first time, that the functional role of FAs is different in governing the cell adhesion strength and applying cellular traction.