Effects of Macromolecular Crowding on Genetic Networks

Abstract

The intracellular environment is crowded with proteins, DNA, and other macromolecules. Under physiological conditions, macromolecular crowding can alter both molecular diffusion and the equilibria of bimolecular reactions and therefore is likely to have a significant effect on the function of biochemical networks. We propose a simple way to model the effects of macromolecular crowding on biochemical networks via an appropriate scaling of bimolecular association and dissociation rates. We use this approach, in combination with kinetic Monte Carlo simulations, to analyze the effects of crowding on a constitutively expressed gene, a repressed gene, and a model for the bacteriophage λ genetic switch, in the presence and absence of nonspecific binding of transcription factors to genomic DNA. Our results show that the effects of crowding are mainly caused by the shift of association-dissociation equilibria rather than the slowing down of protein diffusion, and that macromolecular crowding can have relevant and counterintuitive effects on biochemical network performance.

Introduction

The interior of biological cells is a crowded environment, in which the networks of biochemical interactions controlling cellular function may perform very differently compared to the dilute environment of a typical test tube (1). Biochemical reaction networks involve a complex interplay between protein-protein and protein-DNA binding, protein-ligand binding, transcription, translation, protein folding, membrane interactions, and changes in DNA configuration. Macromolecular crowding is expected to have a strong effect on many of these interactions (2–11), yet it is rarely taken into account in computer simulations of biochemical reaction networks. In this work, we propose a simple scheme for rescaling reaction rates, to include the effects of macromolecular crowding in stochastic or deterministic simulations of biochemical networks. This approach avoids the need for computationally expensive, spatially resolved simulations of the crowded intracellular environment. We use this approach to show that crowding can have interesting and counterintuitive effects both on simple genetic modules (a constitutive gene and a repressed gene) and on more complex genetic circuits such as the lysogeny-lysis switch of bacteriophage λ. These effects arise due to crowding-induced changes in the relative affinities of RNA polymerase (RNAp) and transcription factors (TFs) for the promoter, as well as the interplay between crowding and nonspecific binding (NSB) interactions.

The concentration of macromolecules inside a prokaryotic cell is typically 200–400 g/l (12,13), implying that macromolecules occupy a significant fraction (up to 20–30%) of the cellular volume (13). Biochemical kinetic parameters such as equilibrium constants, association and dissociation rates, however, are usually measured in vitro, at much lower macromolecular concentrations. A plethora of observations, reviewed in (1,14), show that the kinetic parameters of many key biochemical processes (including protein-protein (8,9,15,16) and protein-DNA (7) binding, protein folding, and aggregation (10,11,17), and TF searching for DNA target sites (18)) are different at higher macromolecular concentrations, typical of the in vivo environment. Because the performance of biochemical networks often depends strongly on the kinetic parameters of their constituent reactions, we expect crowding to have a significant influence on network function.

In particular, we expect crowding to affect biochemical network dynamics in two principal ways (1,19). First, crowding shifts the equilibrium constant of association-dissociation equilibria toward the associated state. This is largely because the associated state occupies less volume than the dissociated molecules. In the associated state, more volume is therefore available for the surrounding crowder molecules and the total entropy of the system is greater (20). Second, crowding decreases the rate at which components of the biochemical network diffuse, because the presence of crowders tends to obstruct molecular motion. This decreases the association rate of diffusion-limited bimolecular reactions; motivated by the observation that TFs typically diffuse slowly (21), we assume all association reactions to be diffusion limited. In experiments, it is very difficult, if not impossible, to separate these two effects of crowding—adding crowding agents to a solution will, in general, change both the rate of diffusion of the molecules and the chemical equilibria. Computer simulations, however, can be used to separate these two effects. For all three biochemical networks studied in this work, we find that crowding-induced changes in the equilibrium constant play a much more important role; the effect of the absolute rate constant values is minor.

A natural approach to study the effect of crowding by computer simulations is to use a particle-based algorithm such as Brownian dynamics (22–25) or Green's function reaction dynamics (26–28). This approach is, however, computationally demanding because the concentration of crowders in the cellular environment is large. A much more computationally efficient way to simulate biochemical networks is to assume spatial mixing and use deterministic or stochastic algorithms to propagate the dynamics of the numbers of molecules of each chemical species. The approach described in this work allows us to capture the effects of macromolecular crowding in such simulations.

Our approach is based on the assumption that the effects of crowding can be captured simply by renormalizing the association and dissociation rates of biochemical reactions. This assumption is motivated by consideration of the likely effects of crowding on molecular motion on both long and short distance and timescales. On long distance and timescales, recent theoretical (29) and experimental (21) work shows that molecules still move by normal diffusion in the presence of crowders, but the diffusion constant is decreased by the presence of the crowders. We therefore expect that diffusion-limited association reactions will be slowed down by macromolecular crowding, but the distribution of association times will remain exponential for a long time (28,30), even in the crowded environment of the cell. On short length and timescales, crowding will enhance the probability of rebinding (31). Such rapid rebindings lead to an algebraic distribution of association times for short timescales (28,30)—whereas well-mixed biochemical network models assume exponential waiting time distributions on all timescales. For some biochemical networks, the nonexponential distribution of association times can qualitatively change the macroscopic behavior of the network (e.g., in the MAPK pathway where a single rebinding event can cause irreversible modification of a reactant) (28). However, in many biochemical networks, slower downstream processes (such as protein removal) tend to integrate out the effects of the rapid rebindings, so that the details of the association time distribution at short timescales are not important. In these cases the effect of the rebindings can be taken into account simply by renormalizing the association and dissociation rates in a well-mixed biochemical network model (30). In previous work, we found that for a simple gene regulatory module, a model that explicitly describes the diffusive motion of a TF in space gave essentially identical results to a well-stirred model with renormalized TF-DNA association and dissociation rates (30). For the gene networks studied in this work, we assume that complicated rebinding dynamics at short timescales can indeed be integrated out, so that the effects of crowding can be represented by a simple rescaling of the rate constants in a well-mixed model.

In this work, we also consider the interplay between macromolecular crowding and another global factor that can influence network dynamics: NSB of proteins to genomic DNA. DNA-binding proteins have been found to spend a large fraction of their time bound nonspecifically to genomic DNA (21); this is likely to be important for gene regulatory network function, because the large number of NSB sites can compensate for the low affinity of NSB. Crowding is expected to increase both specific binding of proteins to their DNA target sites, and NSB to genomic DNA—in this work, we show that interesting effects can arise from the interplay between these two effects. For example, for a constitutive gene, we find that NSB causes the relation between gene expression and crowder concentration to become nonmonotonic.

Background and Methodology

To provide a simple way to include the effects of macromolecular crowding in well-mixed models of biochemical networks, we incorporate the effects of crowding into a single parameter Γ, which is related to the concentration of crowders. This parameter is then used to rescale all bimolecular association and dissociation rates to represent in a coarse-grained way the thermodynamic and dynamic effects of crowding.

Effect of crowding on molecular binding equilibria

Under dilute, ideal, conditions, the chemical potential ${\mu }_i^{\mathrm{id}}$ of a chemical species i is related to its molar concentration c_i by ${\mu }_i^{\mathrm{id}}={\mu }_i^0+RT\ln c_i$, where ${\mu }_i^0$ defines a standard chemical potential for that species (32,33). In the crowded cellular environment, however, nonspecific intermolecular interactions shift the chemical potential by an amount ${\mu }_i^{\text{non}-\text{id}}=RT\ln {\gamma }_i$ where γ_i is known as the activity coefficient of species i (32,33). A value of ${\gamma }_i=1$ corresponds to the dilute case. If the nonspecific interactions are on average attractive, then ${\gamma }_i<1$. In this work, we will consider nonspecific repulsive interactions, which are inevitably present; in this case the chemical potential is increased compared to the dilute case and ${\gamma }_i>1$ (1). We will also make the simplifying assumption that all reactants in the network experience the same shift of chemical potential: γ_i is the same for all species i (although this assumption could be lifted in future work).

These crowding-induced changes in the chemical potential have important implications for reaction equilibria of bimolecular reactions (although not for unimolecular reactions, whose reactants and products, following our model assumptions, experience equal shifts in chemical potential). For a bimolecular reaction equilibrium $A+B\rightleftharpoons C$, the molar free energy change $\Delta G$ will be shifted by an amount $-RT\ln \Gamma$, where $\Gamma ={\gamma }_A{\gamma }_B/{\gamma }_C$, so that the association equilibrium constant $K_{\mathrm{eq}}$ under crowded conditions is related to the ideal equilibrium constant $K_{\mathrm{eq}}^{\left(0\right)}$ (measured under dilute conditions) by

$$K_{\mathrm{eq}}=\Gamma K_{\mathrm{eq}}^{\left(0\right)}.$$ (1)

The dimensionless parameter Γ is related to the difference between the free energy of nonspecific interactions for the products compared to the reactants (33). For example, $\Gamma =100$ corresponds to an increase in binding energy of ∼2.8 kcal/mol. Under our assumption that γ is the same for all species, $\Gamma =\gamma$, but this could easily be generalized. For repulsive steric interactions with the crowders, $\gamma >1$ and hence $\Gamma >1$, indicating that crowding favors the formation of the bound complex. This arises because formation of the bound complex increases the total volume available to the crowders, thus decreasing the total free energy of the system. In this work, we will assume that equilibrium constants measured in vitro correspond to $K_{\mathrm{eq}}^{\left(0\right)}$ in Eq. 1, and we will model changes in the concentration of macromolecular crowders by varying systematically the value of Γ in the range $\Gamma \ge 1$.

Minton (33) has mapped the activity coefficient γ for hemoglobin to macromolecular concentration by analyzing data on the osmotic pressure of hemoglobin solutions at different concentrations (34). This allows us to relate the values of the parameter Γ used in our work to approximate intracellular concentrations (using the assumption $\Gamma \approx \gamma$), because we expect the crowders in the intracellular environment to be of similar size to hemoglobin ($\approx 70$ kDa) and of roughly spherical shape. Table 1 presents data obtained from (33). These data shows that Γ is a monotonically increasing, highly nonlinear function of crowder concentration, increasing sharply at concentrations where the crowding agents occupy a significant fraction of the total volume. Under physiological conditions inside the cell (i.e., solute concentrations of 200–300 g/l), $\Gamma =10-100$, showing that physiological concentrations of crowders are likely to cause significant changes to the equilibria of bimolecular reactions.

Table 1.

Approximate mapping of Γ to crowder concentration, using the data of (33,34), obtained for hemoglobin and assuming $\Gamma =\gamma$ for bimolecular reactions

Γ	1	2	3	5	7	10	15	25	50	100
Concentration (g/l)	0	75	110	150	175	200	220	250	278	300
$D/D_0$	1	0.78	0.67	0.56	0.50	0.44	0.38	0.31	0.25	0.19

Also shown is the expected change in the diffusion constant as a function of Γ, calculated from Eq. 2.

Effect of crowding on molecular diffusion and reaction rates

In addition to shifting chemical equilibria, macromolecular crowding also slows down diffusion. Specifically, measurements of the diffusion of the protein carbon monoxide hemoglobin in the presence of several different crowding agents suggest that the diffusion constant can be related to the value of Γ by a power law (35):

$$\frac{D}{D_0}={\Gamma }^{-k},$$ (2)

where D is the measured diffusion coefficient, D₀ is the diffusion coefficient under ideal conditions, and $k=0.36$ is a constant obtained by fitting the experimental data. Table 1 shows values of $D/D_0$ corresponding to the range of Γ values used in this work. At the estimated macromolecular concentration inside a bacterial cell (200–300 g/l), the diffusion constant of a typical protein molecule is expected to be reduced by a factor 2–5 compared to its value in a dilute solution.

The association rate for a bimolecular reaction, $k_{\text{f}}$, is given by $k_{\text{f}}^{-1}=k_{\text{a}}^{-1}+k_{\text{diff}}^{-1}$, where $k_{\text{a}}$ is the intrinsic association rate for molecules that are in contact, and $k_{\text{diff}}$ is the rate at which the molecules move into contact by diffusion. Motivated by the observation that in vivo TFs diffuse slowly, with diffusion constants that can be as low as $1\mu {\text{m}}^2{\text{s}}^{-1}$ (21), we assume that the association rate is limited by diffusion: $k_{\text{a}}\gg k_{\text{diff}}$, leading to $k_{\text{f}}\approx k_{\text{diff}}$. The association rate is then given by

$$k_{\text{f}}\approx k_{diff}=4\pi \sigma D,$$ (3)

where σ is the interaction radius of the interacting molecules and D the sum of their diffusion constants. We therefore expect molecular association rates to decrease as the concentration of crowders increases; we model this effect by combining Eq. 2 with Eq. 3 to obtain

$$k_{\text{f}}=k_{\text{f}}^{\left(0\right)}{\Gamma }^{-k},$$ (4)

where $k_{\text{f}}^{\left(0\right)}$ is the association rate in the absence of crowders. We note that an alternative rescaling of rate constants, which includes in the association rate constant the effects of both crowding-induced slower diffusion of reactants and shifting of chemical of equilibria, is described in (16,17).

Incorporating crowding into well-mixed biochemical network models

In this work, we use the crowding parameter Γ to rescale the association and dissociation rates of all bimolecular reactions to represent the effects of crowding on biochemical networks. We study three scenarios. In the Full Crowding scenario, intended to represent both the shift in equilibria and the slowing of diffusion, all bimolecular association rates are scaled by a factor $\Gamma {}^{-k}$ (where $k=0.36$ as in Eq. 2), whereas all dissociation rates are scaled by a factor $\Gamma {}^{-k-1}$. This ensures that the diffusion-limited association rate varies as prescribed by Eq. 4, whereas the equilibrium constant $K_{\text{eq}}=k_{\text{f}}/k_{\text{b}}$ is shifted toward the bound state by a factor Γ as prescribed by Eq. 1. In this model, crowding thus leads to a (stronger) attraction between the reactants because the dissociation rate decreases more strongly with increasing Γ than the association rate.

Although this scenario should provide a full description of the effects of crowding, we are also interested in how the equilibrium shift and the slowing of the dynamics separately influence network performance. In addition to Full Crowding therefore, we also study the Equilibrium Shift scenario, in which bimolecular equilibria are shifted toward the bound state by crowding but the association rates remain unchanged, and the Slower Dynamics scenario, in which the association rates are decreased by crowding but the equilibria are unchanged (this necessitates also a decrease of the dissociation rates). The Equilibrium Shift scenario thus accounts for the thermodynamic, but not the dynamical, effects of crowding, whereas the Slower Dynamics scenario is intended to investigate the dynamical effects of changing the reaction timescale, without changing the thermodynamics. In summary, the three prescriptions used in this work are i), Full Crowding: scale association rates by $\Gamma {}^{-k}$; scale dissociation rates by $\Gamma {}^{-k-1}$; ii), Slower Dynamics: scale both association and dissociation rates by $\Gamma {}^{-k}$; and iii), Equilibrium Shift: scale dissociation rates by $1/\Gamma$ without changing the association rates.

Simple Cases

To determine the consequences of macromolecular crowding for biochemical network function, we begin with two simple, yet ubiquitous examples: a constitutively expressed gene, which experiences no regulatory interactions, and a gene whose transcription is repressed by a TF.

Constitutive gene

The constitutive gene is represented by the reaction scheme in the first five lines of Table 2. The promoter O is bound by RNAp (${\text{R}}_{\text{p}}$) at rate $k_{\text{f}}$, to form a closed complex $O{\text{R}}_{\text{p}}$. Once bound, ${\text{R}}_{\text{p}}$ can then either detach from the promoter (at rate $k_{\text{b}}$) or initiate transcription. The latter process (including open complex formation, promoter clearance, and gene transcription) is represented by a single reaction (with rate $k_{\text{M}}$) in which an mRNA molecule (M) is produced and ${\text{R}}_{\text{p}}$ detaches from O. The mRNA transcripts are translated to produce protein P at rate $k_{\text{P}}$ (ribosomes are assumed to be abundant and therefore are not included in the model explicitly). Finally, both mRNA molecules and protein products are removed from the system with rates ${\mu }_{\text{M}},{\mu }_{\text{P}}$, respectively: these reactions model dilution and active degradation. We set our reaction rates by defining all times in units of $k_{\text{M}}^{-1}$.

Table 2.

Reaction scheme for the constitutively expressed gene and for the repressed gene

	Reaction	Rates
RNAp binding	$O+{\text{R}}_{\text{p}}\rightleftharpoons O{\text{R}}_{\text{p}}$	$k_{\text{f}},k_{\text{b}}$
mRNA production	$O{\text{R}}_{\text{p}}\to O+{\text{R}}_{\text{p}}+\text{M}$	$k_{\text{M}}$
Protein production	$\text{M}\to \text{M}+\text{P}$	$k_{\text{P}}$
mRNA decay	$\text{M}\to \varnothing$	${\mu }_{\text{M}}$
Protein decay	$\text{P}\to \varnothing$	${\mu }_{\text{P}}$
Nonspecific RNAp binding	$D+{\text{R}}_{\text{p}}\rightleftharpoons D{\text{R}}_{\text{p}}$	$k_{\text{f},NS},k_{\text{b},NS}$
Repressor binding	$O+\text{R}\rightleftharpoons O\text{R}$	$k_{on},k_{off}$
Nonspecific repressor binding	$D+\text{R}\rightleftharpoons D\text{R}$	$k_{on,NS},k_{off,NS}$

Our baseline parameter set, for $\Gamma =1$, is $k_{\text{f}}=100k_{\text{M}}V$, $k_{\text{b}}=2000k_{\text{M}}$, $k_{\text{P}}=60k_{\text{M}}$, ${\mu }_{\text{M}}=3k_{\text{M}}$, and ${\mu }_{\text{P}}=0.15k_{\text{M}}$. These values have been chosen to approximately match the binding free energies measured for the bacteriophage λ genetic switch (see A model for the phage λ switch section). We set $V=1$ for the cell volume and fix the total number of ${\text{R}}_{\text{p}}$ molecules to 20. For this system, mean-field results can be obtained analytically for the average copy numbers in steady state: $\langle \text{P}\rangle =k_{\text{P}}/{\mu }_{\text{P}}\langle \text{M}\rangle =k_{\text{P}}{k}_{\text{M}}/\left({\mu }_{\text{P}}{\mu }_{\text{M}}\right)\langle O{\text{R}}_{\text{p}}\rangle$, whereas $\langle O{\text{R}}_{\text{p}}\rangle ={\text{K}}_{{\text{R}}_{\text{p}}}\left[{\text{R}}_{\text{p}}\right]/\left(1+{\text{K}}_{{\text{R}}_{\text{p}}}\left[{\text{R}}_{\text{p}}\right]\right)$, where $\left[{\text{R}}_{\text{p}}\right]=20/V$ is the total RNAp concentration and ${\text{K}}_{{\text{R}}_{\text{p}}}=k_{\text{f}}/\left(k_{\text{b}}+k_{\text{M}}\right)$.

To model the effects of crowding on the constitutive gene, we scale $k_{\text{f}}$ and $k_{\text{b}}$—i.e., the rates of association and dissociation of ${\text{R}}_{\text{p}}$ from the promoter, as described in Background and Methodology. We assume that the rates of open complex formation, promoter clearance, and transcript elongation are crowding independent, so that $k_{\text{M}}$ does not change with the crowder concentration, and likewise the translation and degradation rates are unaffected by crowding.

Fig. 1 (top panels) shows the average protein copy number, as a function of the crowding parameter Γ. Focusing on the Full Crowding scenario (panel C), we see that the mean protein expression level increases with crowding. This can be easily understood, because crowding increases the probability that RNAp is bound to the promoter; the saturation of expression at high Γ reflects saturation of the promoter by ${\text{R}}_{\text{p}}$. Comparing the Slower Dynamics, Equilibrium Shift, and Full Crowding scenarios (panels A–C, respectively), we see that changing the timescale of the ${\text{R}}_{\text{p}}$ association and dissociation rates (panel A) has little effect on the protein expression level, which might be expected because these rates are faster than that of gene expression; the shift of binding equilibria (panel B) accounts for almost all the effects that are observed in the Full Crowding scenario (panel C).

Figure 1.

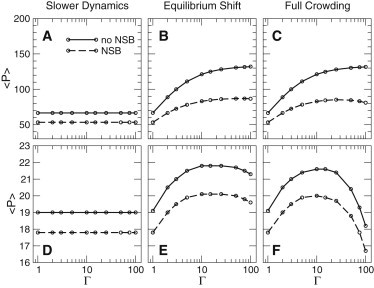
Average protein copy numbers for a constitutively expressed gene (top panels) and for a gene under the control of a repressor (bottom panels). The concentration of the constitutively expressed protein increases with the crowding parameter Γ as RNAp binds tighter to the promoter. This effect is due to a shift of the RNAp binding equilibrium (panel B). The expression level of a gene under the control of a repressor shows a nonmonotonic dependence on the degree of crowding, as the binding affinity of the repressor increases more strongly with Γ than that of the RNAp. NSB (dashed lines) depletes the amount of RNAp available for binding to the promoter and therefore lowers the gene expression level.

To account for the effects of NSB interactions between RNAp and genomic DNA, we add an extra reaction, in which ${\text{R}}_{\text{p}}$ binds reversibly to a species D, representing a generic nonspecific DNA binding site (line 6 of Table 2). On the basis of arguments made previously for the phage λ regulatory circuit embedded in the Escherichia coli chromosome (36), we assumed 10⁷ NSB sites that can bind ${\text{R}}_{\text{p}}$ with binding free energy $\Delta G_{\text{N}SB}=-2.1$ kcal/mol. Because of the large number of NSB sites, standard brute-force kinetic Monte Carlo simulations of the nonspecific association and dissociation reactions are not feasible; instead, we coarse-grain these reactions using the method described in (22,36). This coarse-graining procedure preserves information on the absolute association and dissociation rates (22) and is therefore compatible with the rescaling of these rates, which we use to model crowding. The dashed lines in the top panels of Fig. 1 show the steady-state protein expression levels in the presence of NSB. As one might expect, NSB lowers the concentration of RNAp, which is available to bind to the promoter, hence decreasing the expression level. Interestingly, NSB causes the protein copy number to go through a maximum with crowding, at $\Gamma \approx 20$, whereas in the absence of NSB a monotonic increase with Γ was observed (in the physiological range). This maximum occurs because, for very high values of Γ, the dominant mechanism by which ${\text{R}}_{\text{p}}$ leaves the promoter is transcription (at crowding-independent rate $k_{\text{M}}$) rather than dissociation—thus promoter occupancy becomes limited by the (crowding independent) transcription rate $k_{\text{M}}$. In contrast, NSB of ${\text{R}}_{\text{p}}$ continues to increase with Γ. The effect of NSB on promoter occupancy therefore becomes more important as the degree of crowding increases.

Repressed gene

The repressed gene is represented by reactions 1–5 and 7 in Table 2. In addition to the reactions detailed previously for the constitutive gene, a repressor protein molecule can now bind reversibly to the promoter region with association and dissociation rates $k_{\mathrm{on}}$ and $k_{\text{off}}$; we suppose that when the repressor is bound, it physically prevents the binding of ${\text{R}}_{\text{p}}$ to the promoter. We fix the number of repressor proteins at 100 and we choose as baseline parameters $k_{\text{on}}=k_{\text{f}}$ and $k_{\text{off}}=k_{\text{b}}$. Once again, analytical results can be derived for the mean steady-state copy numbers (in the absence of NSB); in particular, $\langle O{\text{R}}_{\text{p}}\rangle ={\text{K}}_{{\text{R}}_{\text{p}}}\left[{\text{R}}_{\text{p}}\right]/\left(1+{\text{K}}_{\text{R}}\left[\text{R}\right]+{\text{K}}_{{\text{R}}_{\text{p}}}\left[{\text{R}}_{\text{p}}\right]\right)$, where $\left[\text{R}\right]=100/V$ and ${\text{K}}_{\text{R}}=k_{\text{on}}/k_{\text{off}}$.

Fig. 1 (bottom panels) shows the average protein copy number as a function of the crowding parameter Γ, for the repressed gene. In contrast to the constitutive gene, the repressed gene shows a striking nonmonotonic dependence of gene expression level on the degree of crowding: for small crowder concentration, expression increases with crowding, while it decreases markedly at higher crowder concentrations ($\Gamma >20$). This behavior arises because the repressor-bound promoter state $\langle O\text{R}\rangle$ and the ${\text{R}}_{\text{p}}$-bound promoter state $\langle O{\text{R}}_{\text{p}}\rangle$ are quite differently affected by crowding. Although the occupancy of the repressor-bound state always increases with crowding, the occupancy of the ${\text{R}}_{\text{p}}$ bound state increases at low values of Γ but decreases for large Γ, because the dominant mechanism for removal of ${\text{R}}_{\text{p}}$ from the promoter becomes crowding-independent transcription rather than crowding-dependent dissociation. Thus, the repressor can compete more effectively with ${\text{R}}_{\text{p}}$ for promoter occupancy at high crowder concentrations. Analytical calculations show that the protein copy number peaks at $\Gamma \approx 11$.

The results for the Equilibrium Shift scenario (panel E) are in close agreement with those of the Full Crowding scenario, although the results for the Slower Dynamics scenario (panel D) confirm that P is essentially unchanged when the association and dissociation reactions are slowed down. We therefore conclude that the peak in protein production with increasing crowding, for the parameters and the range of Γ considered, is entirely due to a crowding-induced shift of chemical equilibria.

To investigate the effects of nonspecific DNA binding, we included also reversible binding of both repressor and RNAp to genomic DNA sites (D), via the reactions in lines 6 and 8 in Table 2, with $k_{\text{on},\text{NS}}=k_{\text{f},\text{NS}}$, and $k_{\text{off},\text{NS}}=k_{\text{b},\text{NS}}$. NSB depletes both R_P and repressor from the promoter, lowering the occupancy of both the $\langle O\text{R}\rangle$ and $\langle O{\text{R}}_{\text{p}}\rangle$ states: the result is an approximately uniform decrease of the mean protein number compared to the results in the absence of NSB.

To summarize, these simple cases not only constitute an interesting benchmark to study the effects of crowding, but also provide us with general principles, which we can use to understand how the behavior of more complex networks is affected by the presence of crowding agents. For a constitutive gene, crowding increases protein expression due to tighter binding of RNAp. However, when a gene is controlled by a repressor, the tighter binding of the repressor decreases protein expression for high, but physiologically realistic, values of Γ, leading to a peak in expression levels as a function of the crowder concentration. Finally, we have established that, in the parameter range we considered, the effects on protein production due to the slowing down of diffusion proteins are much weaker than those related to the crowding-induced equilibrium shifts.

A Model for the Phage λ Switch

We now study the effects of crowding on a more complex genetic network: a simplified representation of the lysogeny-lysis switch of bacteriophage λ. Phage λ is a virus that infects the bacterium E. coli ((37) and references therein). This phage can enter a lysogenic state, in which its genome is integrated into the chromosome of the host cell and the phage remains dormant. It remains stably in the lysogenic state until a stimulus (involving activation of the host's SOS DNA damage response) triggers the induction of the lytic pathway, upon which the phage DNA is excised from the host chromosome and the host biochemical machinery is used to make progeny phages, eventually killing the host. In lysogens lacking the SOS response, spontaneous transitions from lysogeny to lysis are extremely rare (38). In previous work, we have shown that a detailed stochastic model of the underlying gene regulatory network can reproduce this extremely low spontaneous switching rate (36); here, we investigate the effects of macromolecular crowding on the performance of a pared-down version of this model, which neglects DNA looping.

The genetic network controlling the switch between lysogeny and lysis consists of two genes, cI and cro, transcribed in divergent directions under the control of an operator region (O_R); the operator has three binding sites O_R1, O_R2, and O_R3, each of which can bind either CI or Cro dimers. Gene cI is transcribed from the P_RM promoter, which overlaps with O_R3, whereas gene cro is transcribed from the P_R promoter, overlapping with O_R1 and O_R2 (see Fig. 2). The production of Cro protein triggers the transition to lysis, whereas the CI protein acts to maintain the lysogenic state. This genetic switch is bistable: if the downstream pathway leading to lysis is deactivated, switching out of the lysogenic state produces a state with a high concentration of Cro, which is stable for several cell generations. This is known as the anti-immune state (39).

Figure 2.

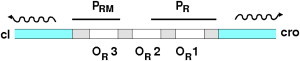
Schematic diagram of the O_R region of the bacteriophage λ genome.

The genes cI and cro are regulated as follows. CI dimers bind most strongly to O_R1, the occupancy of which blocks the transcription of cro. A cooperative interaction causes CI dimers also to be recruited to O_R2, and binding of a CI dimer at this site greatly enhances the transcription of cI. At high CI concentrations, O_R3 also becomes occupied by a CI dimer; this blocks transcription of cI. Thus, the gene cI is positively autoregulated at low CI concentrations and negatively autoregulated at high CI concentrations. In contrast, the Cro protein binds (also as a dimer) most strongly at O_R3, where it represses cI. The cro gene is negatively autoregulated at very high Cro concentrations via binding of Cro dimers at O_R1, but for cro there is no positive autoregulation. When the P_RM promoter is upregulated by binding of CI at O_R2, the two promoters are of about the same strength. If P_RM is not upregulated, however, the P_R promoter controlling cro is ∼10 times stronger. CI and Cro are also asymmetric in their propensities to dimerize: Cro dimerizes weakly while CI is found mostly in the dimer form. Recent work has shown that there is also an important DNA looping interaction between O_R and another, distant, operator site called O_L (40,41); however, for simplicity we neglect the looping interaction in this work.

Our model has 194 reactions. These represent dimerization of CI and Cro proteins, degradation of mRNA transcripts, and of CI and Cro monomers and dimers, binding of CI and Cro dimers to specific DNA binding sites O_R1, O_R2, O_R3 and nonspecific DNA binding sites, binding of RNAp to promoters P_RM and P_R, transcription of cI and cro, and translation of the corresponding mRNA transcripts. Details and parameters can be found in (36); the reaction set used here is identical except for the absence of DNA looping. As in the section Simple Cases, we assume 10⁷ genomic DNA sites and set the free energy of NSB of TF dimers and RNAp to these sites at $\Delta G_{\text{N}SB}=-2.1$ kcal/mol.

We carry out stochastic simulations of this model (42,43), rescaling all protein-protein and protein-DNA association and dissociation rates to represent macromolecular crowding, as described in Background and Methodology, and we compute how the steady states and the switch stability depend on the crowding parameter Γ, in the presence and absence of NSB. Because these simulations are computationally intensive, we coarse-grain monomer-dimer association-dissociation reactions and NSB reactions according to the procedure described in (22,36). We have previously shown for a simple model genetic switch that this coarse-graining procedure does not affect the steady states or the switching rate (22,36). For this system, we limit our analysis to the range $1\le \Gamma \le 15$, as this model does not predict a stable lysogenic state for stronger crowding (our previous work suggests, however, that DNA looping may keep the system bistable for higher values of Γ (36)).

We first consider the effects of crowding on the concentrations of CI and Cro in the lysogenic and anti-immune steady states in the absence of NSB interactions (Fig. 3, solid lines). Interestingly, the lysogenic state (panel A) is very robust: its steady-state CI concentration is hardly affected by crowding over the full range of Γ values tested here. This is probably because, in the lysogenic state, the O_R1 and O_R2 sites are almost always occupied by CI, and almost all the CI is in the dimer form. Because the P_RM promoter is already fully activated almost all the time, there is little scope for crowding to increase its level of activation. For very strong crowding, one might expect increased negative autoregulation by CI binding at O_R3; analysis of the operator occupancy as a function of Γ does show a slight increase in autorepression of P_RM, but this is not very significant: P_RM is overwhelmingly occupied by RNAp even when the environment is highly crowded.

Figure 3.

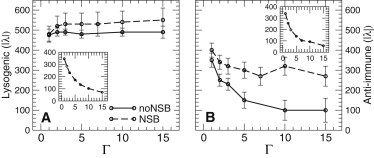
Phage λ model: effects of crowding on the total number of molecules of CI (panel A) and Cro (panel B) in the two steady states of the switch (Full Crowding scenario). The amount of CI in the lysogenic state is not much affected by crowding, whereas the amount of Cro in the anti-immune state is very sensitive to crowding, and decreases for high values of Γ. The introduction of NSB interactions does not change the amount of CI in the lysogenic state, but tends to buffer the decrease of Cro in the anti-immune state.

In contrast, the anti-immune state (panel D) is strongly affected by crowding: the steady-state Cro concentration shows a sharp decrease for increasing Γ. In comparison to CI, Cro is much more likely to be found in the monomer form, so that crowding is expected to shift the Cro population significantly toward the dimer state. An increased number of Cro dimers leads to a higher probability of occupying the operator sites O_R1 or O_R2, thus decreasing the transcription of cro, leading to a reduced concentration of Cro in the anti-immune state, as Γ increases. An analysis of operator occupancy in the anti-immune stable state, as a function of Γ, indeed shows that as crowding increases, P_R is less likely to be occupied by RNAp and more likely to be blocked by Cro binding at O_R1. Comparing the Slower Dynamics and Equilibrium Shift scenarios confirms that the patterns we observe for both steady states are entirely due to the crowding-induced shift of binding equilibrium constants (data not shown).

The introduction of NSB interactions (Fig. 3, dashed lines) has little effect on the lysogenic steady state (panel A), but tends to buffer the drop in the concentration of Cro for increasing Γ in the anti-immune steady state (panel B). Although crowding stabilizes the dimeric form of Cro, leading to enhanced autorepression of Cro expression and thus to a decrease of Cro levels, NSB tends to weaken this effect, because the NSB sites sequester the Cro dimers, thereby depleting the number of Cro dimers that are available for autorepression via binding to the O_R1 and O_R2.

We next consider how the dynamical stability of the lysogenic and anti-immune states is affected by crowding. Fig. 4 shows the spontaneous switch flipping rates out of the lysogenic (panel A) and anti-immune (panel B) states, computed using forward flux sampling (44–47) (with 40–50 interfaces and 500–2000 points per interface), as a function of the crowding parameter Γ. The stability of the lysogenic state shows an intriguing nonmonotonic dependence on the degree of crowding (panel A): for low Γ, crowding increases the stability of the lysogen (decreases the flipping rate) by several orders of magnitude, although for high Γ, it has the opposite effect. Maximal stability is obtained for $\Gamma \approx 3$, corresponding to an intracellular concentration of $\approx 100$ g/l. Because the steady-state CI concentration is virtually independent of Γ (Fig. 3), the effects of crowding on the switching rate must be attributable to the molecular binding events that occur during the switch flipping trajectory. Two different types of molecular binding events are likely to be involved in the flip of this switch: CI dimers dissociate from O_R1 and O_R2 (deactivating P_RM and releasing the repression of P_R), and a Cro dimer binds to O_R3, repressing P_RM. The relative importance of these events in the switching mechanism has been the subject of some debate (48,49). By shifting all protein-DNA binding equilibria toward the bound state, crowding strengthens the binding of CI to O_R1 and O_R2, an effect that is expected to decrease the switching rate. However, the likelihood that Cro binds to O_R3 is also increased by crowding, an effect that should increase the switching rate. We speculate that the nonmonotonic dependence of the switching rate on Γ observed here reflects a crossover in the importance of these two effects. For small Γ, the release of CI from O_R1 and O_R2 dominates, so that crowding stabilizes the switch. However, for $\Gamma >3$, Cro dimer binding to O_R3 becomes dominant, so that crowding destabilizes the lysogen.

Figure 4.

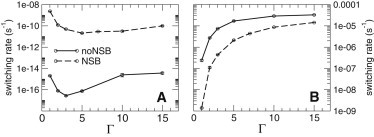
Phage λ model: spontaneous switching rate from the lysogenic to anti-immune state (panel A) and vice versa (panel B) (Full Crowding scenario). The lysogenic-to-anti-immune switching rate is extremely low, as reported experimentally (38). This rate shows a nonmonotonic dependence on Γ, with a minimum switching rate (maximum in lysogen stability) for $\Gamma \approx 3$. The switching rate from the anti-immune to the lysogenic state, in contrast, increases with Γ and eventually approaches a plateau. The introduction of NSB interactions destabilizes strongly the lysogenic state but stabilizes mildly the anti-immune state.

The effects of crowding on the stability of the anti-immune state (panel B of Fig. 4) are more straightforward to interpret: the observed decrease in stability of the anti-immune state with crowding is likely to be a simple consequence of the crowding-induced decrease in the steady-state concentration of Cro shown in Fig. 3.

The introduction of NSB interactions (dashed lines in Fig. 4) destabilizes the lysogenic state, yet stabilizes the anti-immune state, in agreement with (36). We believe this is related to the different strengths of P_R and P_RM: in the absence of CI bound to O_R2, P_RM is very weak, and the lysogenic state cannot be maintained. NSB interactions reduce the number of TFs available for specific binding, and thereby reduce the probability that P_RM is in the autoactivated state at the moment when the switch commits to flipping (transition state). This makes it more likely that the switch will successfully flip into the anti-immune (lytic) state. This result is confirmed by simulations initiated with neither CI nor Cro molecules present: these invariably proceed toward the anti-immune state.

Finally, we note that a comparison of the Slower Dynamics and Equilibrium Shift scenarios with the results for Full Crowding (data not shown) shows that the Equilibrium Shift can account for almost all the effects of crowding on the phage λ switch. Thus, even for a dynamical quantity such as the switching rate the effects of crowding are dominated by the shift in binding equilibria, rather than by changes in the absolute values of the association and dissociation rates.

Discussion

In this work, we have used a simple scaling of bimolecular association and dissociation rates to mimic the effects of crowding on biochemical networks. This approach allows us to model crowding in biochemical network simulations without the need for computationally expensive explicit spatial models, by varying a single nonideality parameter Γ. The simulation framework described here is not restricted to genetic networks and could equally well be applied to other types of biochemical reaction networks. Using this approach, we tested the relative importance of crowding-induced changes in the association-dissociation equilibrium constant, versus changes in the absolute values of the rate constants, due to a change in the diffusion constant. Our results show that for the genetic networks studied here, the effect of the equilibrium shift is dominant.

An analysis of the effects of crowding on a simple model for a constitutively expressed (unregulated) gene shows that the tighter binding of RNAp to the promoter, induced by the presence of crowding agents, leads to enhanced gene expression. However, the average activity of a gene under the control of a repressor shows nonmonotonic behavior for increasing crowding: it first increases due to enhanced binding of ${\text{R}}_{\text{p}}$, but eventually decreases when the repressor-bound state becomes dominant; this is because at high Γ the occupation of the promoter by ${\text{R}}_{\text{p}}$ is limited by the rate of transcription rather than ${\text{R}}_{\text{p}}$ dissociation. Our minimal model for the phage λ switch has a number of more complex regulatory features, including mutual repressive interactions between the cI and cro, cooperative binding of both CI and Cro dimers at the promoter, autoactivation of the cI gene and autorepression of both the cI and cro genes. Our results show an intricate interplay between these regulatory features and macromolecular crowding. In the lysogenic state, the P_RM operator, which controls the cI gene, is strongly autoactivated; moreover, CI dimerizes very strongly. Consequently, crowding has little effect on the lysogenic CI concentration, because even in the absence of crowding P_RM is more or less fully activated. In the anti-immune state, on the other hand, the P_R promoter, which controls the cro gene, is more easily autorepressed by Cro, which dimerizes only weakly. Crowding pushes the Cro dimerization equilibrium toward the dimer, and strengthens its binding to the operator, greatly destabilizing the anti-immune state. The complexity of the regulation in this model also leads to an intriguing nonmonotonic dependence of the lysogenic →lytic switching rate on the crowder concentration, which we attribute to a crossover between CI-dominated and Cro-dominated switching mechanisms.

Our results also underscore the importance of NSB of proteins to genomic DNA (36,50,51). These interactions are enhanced by crowding and deplete the number of TFs and RNAp molecules available for specific binding; in simple single-gene networks they reduce protein production, although in the model of the phage λ switch they lead to a stabilization of the anti-immune state and a destabilization of the lysogenic state. Taken together, our results suggest that the effects of crowding on genetic networks can be very significant, but the nature of these effects depends both on the detailed gene regulatory feedback structure and on the intrinsic strength of the protein-protein and protein-DNA binding interactions.

It would be very interesting to measure experimentally the effects of macromolecular crowding on biochemical network performance. The most direct way to do this might be via in vitro protein expression systems designed de novo (52), in which the macromolecular concentration could be varied by adding inert polymers such as polyethylene glycol or dextran. Alternatively, one might take a diluted cytoplasmic cell extract and study the importance of crowding under physiological conditions by adding polyethylene glycol; recently, this approach has been used successfully to study the effect of crowding on protein signaling (53). In vivo measurements would require control of the intracellular crowder concentration by manipulating conditions external to the cell; one possible way to achieve this might be via changes in osmotic pressure, for example by adding glycerol (54).

In summary: macromolecular crowding is a feature of the intracellular environment that is often neglected when modeling biochemical networks. The simple approach described here provides a way to include the effects of crowding in dynamical simulations of biochemical networks. Our results suggest that the effects of macromolecular crowding on gene regulatory networks are interesting, significant, and deserving of further experimental and theoretical investigation.