Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2012 Nov 22.
Published in final edited form as: Curr Biol. 2011 Nov 10;21(22):1931–1936. doi: 10.1016/j.cub.2011.10.013

The Dynamic Range of Human Lightness Perception

Ana Radonjić 1, Sarah R Allred 2, Alan L Gilchrist 3, David H Brainard 1
PMCID: PMC3244211  NIHMSID: NIHMS332453  PMID: 22079116

Summary

Natural viewing challenges the visual system with images that have a dynamic range of light intensity (luminance) that can approach 1,000,000:1 and that often exceeds 10,000:1 [1, 2]. The range of perceived surface reflectance (lightness), however, can be well-approximated by the Munsell matte neutral scale (N 2.0/ to N 9.5/), consisting of surfaces whose reflectance varies by about 30:1. Thus, the visual system, must map a large range of surface luminance onto a much smaller range of surface lightness. We measured this mapping in images with a dynamic range close to that of natural images. We studied simple images that lacked segmentation cues that would indicate multiple regions of illumination. We found a remarkable degree of compression: at a single image location, a stimulus luminance range of 5905:1 can be mapped onto an extended lightness scale that has a reflectance range of 100:1. We characterized how the luminance-to-lightness mapping changes with stimulus context. Our data rule out theories that predict perceived lightness from luminance ratios or Weber contrast. A mechanistic model connects our data to theories of adaptation and provides insight about how the underlying visual response varies with context.

Results

At the core of any theory of surface lightness perception is a characterization of how luminances in the retinal image are mapped onto percepts that range from black through gray to white. Because the dynamic range of natural images (which can approach 1,000,000:1) vastly exceeds the dynamic range of reflectance scales that describe perceptual lightness (e.g., fresh snow reflects about 80% of the incident light across the visible spectrum, while black shingles or black rich soil reflect approximately 4% [3] for a reflectance ratio of 20:1), the mapping cannot be accomplished by a multiplicative scaling of luminance onto lightness. Theories of lightness account for this observation by noting that image luminance is affected both by object surface reflectance and by the intensity of the illuminant, and that the visual system contains mechanisms that discount the variation introduced by the illuminant [4-7]. Such theories divide the research program of understanding lightness into two parts. First, how is luminance mapped to lightness within an image region that is uniformly illuminated? Second, how does the visual system parse the image into regions that share common illumination, and how does information from multiple such regions interact (if at all)? Here we report fundamental measurements that address the first part of this program: our data characterize the luminance-to-lightness mapping in high-dynamic range images that lack cues indicating the presence of multiple regions of illumination. Our measurements probe the limits of the mechanisms that underlie lightness perception and address key questions about their function.

In Experiment 1, observers viewed a 5 × 5 grayscale checkerboard, consisting of homogeneous squares that varied in luminance over the range that we estimate to be greater than 10,000:1 and presented on the high-dynamic range display (Figure 1). The center square of the 5×5 checkerboard served as a test stimulus. The remaining 24 squares varied in luminance over the stimulus range in equal log steps. On each trial, the test square took on the luminance value of one of the surrounding contextual squares. Observers matched lightness of the test by selecting a sample from an extended Munsell neutral palette (N 0.5/ to N 9.5/ in 0.5 value steps). Observers also had the option of responding with three out-of-range judgments: “Darker than 0.5”, “Lighter than 9.5, but still a surface” or “Glowing”. Experimental protocols were approved by the institutional review board at the University of Pennsylvania.

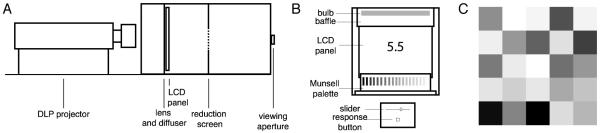
Figure 1. Apparatus.

Figure 1

Open in a new tab

A) Schematic view of the high-dynamic range display. A DLP projector projects an image onto an LCD display panel through a Fresnel lens and diffuser, placed directly against the backside of the panel. Because the LCD panel is a transmissive display, it provides a multiplicative attenuation of the projector image, resulting in an overall dynamic range that is nominally the product of the native dynamic ranges of the projector and panel. The observer viewed the resulting image monocularly through an aperture and a reduction screen. The dotted portion of the reduction screen in diagram shows the vertical extent of a square aperture in that screen. The display is built following the design by Seetzen et al. [9]; details on its calibration are available in a technical report by Radonjić et al. [10]. B) The matching chamber was diffusely illuminated by a fluorescent bulb and contained a matching palette. The palette consisted 19 glossy papers ranging from Munsell N 0.5/ to N 9.5/. A baffle prevented light from the bulb from reaching the observer directly. Observers matched the test square, presented in the center of a checkerboard, to one of the palette papers. They indicated their response using a slider on a custom response box (shown below chamber in diagram). The slider varied a number displayed on an LCD panel mounted at the back of the viewing chamber. Out of range response options were displayed as text on the same monitor. C) The stimulus was a 5 × 5 checkerboard. The checker squares had CIE chromaticity x = 0.309, y = 0.338 and varied in luminance. The test, which was the center square of the checkerboard, took on 24 different luminances during each block of trials. Additional detail on the experimental procedures is provided in the supplement.

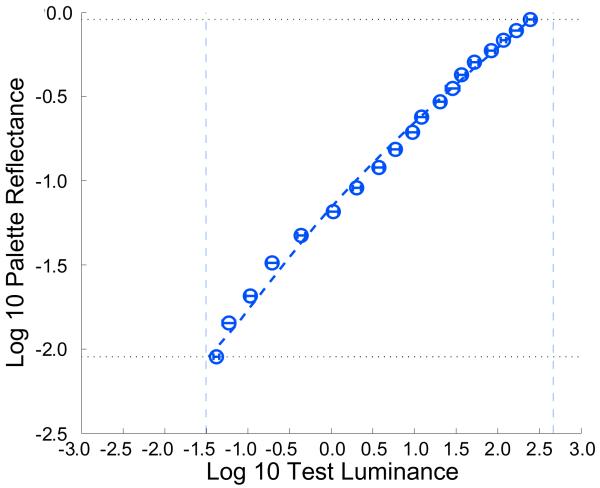
The measured luminance-to-lightness matching function, shown in Figure 2, exhibits remarkable compression. When viewed in the unsegmented high-dynamic-range context, a luminance range of 5905:1 was mapped onto a reflectance range of 100:1. Our data falsify a key implication of Wallach’s ratio principle [8] and of theories that base perceived lightness on Weber contrast, namely that to match any pair of test patches in a region of uniform illumination, a human observer will select two chips from the palette that stand in the same luminance ratio to each other as the tests.

Figure 2. Luminance-to-lightness mapping shows high compression.

Figure 2

Open in a new tab

Palette log 10 reflectance plotted against test log 10 luminance (cd/m2) for Experiment 1. Open circles plot the average test luminance for which that paper was chosen as a match, averaged across observers (N=8), error bars indicate +/− 1 between-observers standard error of the mean (SEM). Dashed vertical lines show upper and lower limits of contextual/test luminances. Dotted horizontal lines show the minimum and maximum palette paper reflectance. The line through the data shows the fit of the model described in the text. Figure S1 shows that similar results are obtained when a standard Munsell palette (N2.0/ to N 9.5/) is used.

In Experiment 2 we measured the luminance-to-lightness matching function for contextual checkerboards that varied in their photometric properties: the contextual luminance range (that is, luminance ratio between the lowest and the highest contextual square), the overall contextual luminance, and the distribution of contextual luminances when the highest and lowest luminances were held fixed.

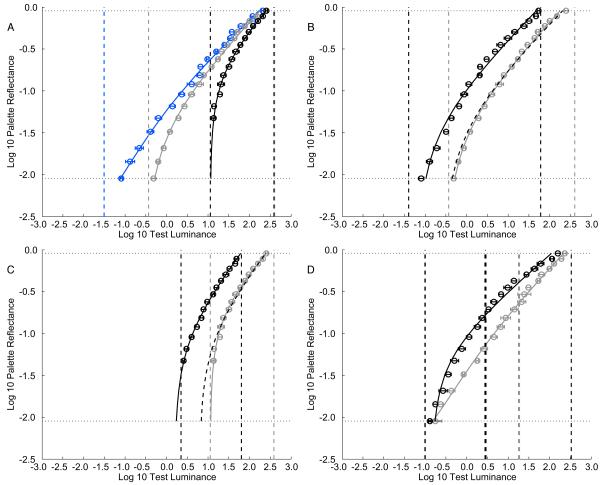
Figure 3A plots the matching function for three dynamic range conditions (~10,000:1, ~1,000:1 and ~30:1) across which the highest contextual luminance was held approximately constant. The data for the 10,000:1 checkerboard replicate the results of Experiment 1, for different observers and a different spatial arrangement of the checkerboard. The data for the other two checkerboards show that the luminance-to-lightness mapping depends strongly on the contextual range. For example, the luminance range mapped onto the reflectance scale between N 2.5/ and N 9.5/ (the palette range used in common by observers across all three contexts) varied by 1.3 log units across the three dynamic range conditions (see Table S1). Across this large variation, however, the white point (i.e., the luminance matched to N 9.5/) was approximately constant. In addition, the white point was close to the highest contextual luminance (Table S1) in all conditions, broadly consistent with a “highest luminance appears white” anchoring rule [4, 11]. The agreement is not perfect, however. For example, analysis of the out of range judgments (Table S2) shows that the highest luminance test, which matched the highest contextual luminance, was judged glowing on most trials in the 10,000:1 and 1,000:1 contexts. It may be that the minor deviations from the “highest luminance appears white” anchoring resulted from the fact that our stimuli were presented on an emissive display, and thus that the perceptual interpretation of the stimuli as surfaces was imperfect.

Figure 3. Luminance-to-Lightness Mapping Varies with Context in Experiment 2.

Figure 3

Open in a new tab

All panels have same basic format as Figure 2 (N = 5). Error bars indicate +/− 1 SEM computed across observers. (A) Luminance-to-lightness matching functions for three contextual luminance ranges from 10,000:1 (blue), 1,000:1 (gray), and 30:1 (black). (B) Luminance-to-lightness matching functions for 1,000:1 luminance range context. Solid lines plot the model fits to each overall luminance condition. The dashed line through the high-luminance-condition data shows a shifted version of the fit for the low-luminance condition. The overall contextual luminance change was 0.8 log units. The shift in model fit from high to low overall contextual luminance condition is 0.64 log units. In (B) and (C), the gray points and fit are replotted from (A). (C) Data for the 30:1 range condition, same format as (B). The overall contextual luminance change was 0.72 log units. The shift in model fit from high to low overall contextual luminance condition is 0.6 log units. (D) Luminance-to-lightness matching functions for two contexts that had the same lowest two and highest two luminances but a different luminance distribution. Low mean luminance is plotted in black and high mean luminance in gray. Thick dashed vertical lines in corresponding colors represent the contextual mean luminance level for the two contextual configurations (center square excluded). Figure S2 connects our measurements to classic results obtained with uniform surrounds.

We also measured the effect of varying the overall contextual luminance for the 1,000:1 and 30:1 range conditions. In essence, we scaled all contextual and test luminances by a common multiplicative factor (see supplement for luminance values). Figure 3B,C shows that this manipulation has a simple effect: the luminance-to-lightness matching function shifted by close to the same factor as the stimuli. In particular, perceptual white remained anchored close to the highest contextual luminance, and the shape of the matching functions on the log-log plots was invariant. Subtle effects of overall luminance variation are reflected in the distribution of out-of-range judgments (Table S2).

The final measurements of Experiment 2 studied the effect of varying the distribution of contextual luminances while holding the two lowest and highest two contextual luminances constant. The results (Figure 3D) show that this manipulation has little effect on the white point or the luminance range of the matching function, but substantially affects the matching function’s shape.

We developed a mechanistic model that describes our measured luminance-to-lightness matching functions. We built on models developed in the literature on visual adaptation, which are formulated primarily to account for measurements of visual thresholds [12]. The key idea is that the visual system has a limited response range, described by a saturating response function. The response function varies with context through the action of a small set of adaptation parameters. We combined this idea with the Fechnerian notion that perceived lightness is related to the response by a fixed context-independent transformation, with higher responses corresponding to greater perceived lightness [13-16]. Thus two tests, each seen in its own context, are predicted to match in lightness if they both produce the same response. The model captures contextual effects on the luminance-to-lightness mapping entirely through changes in the adaptation parameters with context.

We characterized the relation between stimulus luminance L and visual response R using a modified Naka-Rushton function [17]

R=(g(L−c))n(g(L−c))n+1.

Three adaptation parameters control the behavior of this function: a multiplicative gain parameter g and a subtractive offset parameter c (which both modify the input to the standard Naka-Rushton function) and an exponent n (which controls the shape of the function). For any choice of adaptation parameters, the response increases from 0 to 1 as a function of luminance. The supplemental methods describe how the model was fit to the data.

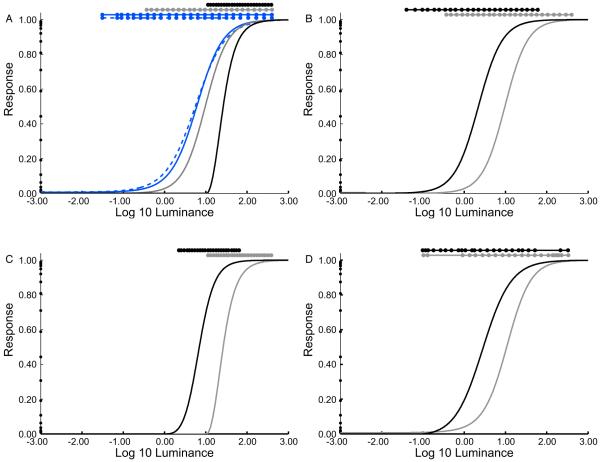
The lines through the data shown in Figures 2 and 3 show the model predictions. Clearly, the model fits the data well for all experiments and contexts. Figure 4 shows the visual response functions derived from the model. These provide additional insight. First, for all contexts, the upper end of the response functions is located near the highest luminance of the surrounding checkerboard. This is the response function manifestation of the “highest luminance appears white” anchoring rule. Second, as the range of the contextual stimuli increases, the slope of the response function becomes shallower, so that the available response range is allocated to approximately match the luminances in the checkerboard context (Figure 4A). Third, scaling the overall contextual luminance while keeping its range constant simply shifts the response function, so that the response range remains matched to the contextual luminance (Figure 4B, C). Finally, when the range of the contextual stimuli is held constant, the visual response function changes so that a larger portion of the response range is allocated to stimulus luminances that occur most often in the checkerboard (Figure 4D). The latter three behaviors are consistent with the general notion that adaptation serves to optimize the use of available response range [18-21].

Figures 4. Inferred response functions shift to match contextual luminance distributions.

Figures 4

Open in a new tab

A) Response functions inferred from data shown in Figure 2 and 3A. Response is plotted against log test luminance (cd/m2). The solid dots on the y-axis indicate the response corresponding to each palette paper. The bars above the plots indicate the contextual stimulus range for each condition, and the solid dots on these bars indicate the 24 contextual luminances. Dashed blue line: Experiment 1. Solid lines: Experiment 2, same color code as Figure 3. B) Response functions inferred from data in Figure 3B. C) Response functions inferred from data in Figure 3C. D) Response functions inferred from data in Figure 3D.

Discussion

Our measurements provide a foundation for future work that considers more natural contextual images in which segmentation cues cause the luminance-to-lightness mapping to vary from one image region to another. For example, a luminance value that is perceived as black in a region of high illumination might be perceived as white in a region of low illumination [22, 23]. This is consistent with theories of lightness [7, 24, 25] that suggest that the visual system relies on segmentation cues in (e.g., depth boundaries, penumbrae) to stabilize the mapping between object reflectance and perceived lightness. Although our measurements do not speak to directly to the effect of such cues, we can now proceed to ask questions such as i) whether variation in adaptation parameters we identified can describe luminance-to-lightness mapping functions in high-dynamic-range images that are segmented into differentially illuminated regions and ii) if so, whether the parameters are set by the local within-illuminant context, by the global context, or by some combination of both [for theoretical overviews, see 6, 7, 11]. We have conducted initial experiments along these lines, where photometric cues are available for segmentation [26].

It may seem surprising that the visual system can maintain a lightness scale over a luminance range that exceeds 5000:1 at a single image location, since this is much larger than is necessary to perceive variation in surface reflectance. Perhaps the excess operating range serves to preserve useful representations of surface lightness in the face of failures in image segmentation according to illuminant or to handle bright specular highlights on glossy objects. Or perhaps it is a side effect of the early visual system’s need not only to represent surface lightness but also to preserve discriminability of image luminances [see 21]. It will be of interest to understand how the effects we report come into play in high-dynamic range images that can be segmented into separate regions, each of which has a low-dynamic range.

The adaptation model we developed to describes contextual variation in the luminance-to-lightness mapping function, provides a connection between two traditions, one that studies the functional characteristics of lightness perception and whose goal is to relate perceived lightness to the visual stimulus and a second that uses threshold psychophysics and physiological measurements to identify and characterize mechanisms that mediate visual processing. We are not the first to develop adaptation models to account for judgments of appearance, however, and our model incorporates ideas available in the literature. There is ample evidence of the need for an adaptation parameter to describe some form of multiplicative gain control [12]. Our data clearly require additional adaptation parameters: if the only effect of context were to change a multiplicative gain, then the luminance-to-lightness matching functions would all have the same shape on the log-log plots and differ only in their horizontal positions.

The need for an additional adaptation parameter has been noted previously by numerous authors using a variety of experimental stimuli, methods, and terminologies [7, 27-39]. Our second adaptation parameter, the subtractive offset c, is an instantiation of this second parameter. In addition, we found that a third adaptation parameter, the exponent n, was required to fit our data. When this parameter was held fixed, there were systematic deviations between the model predictions and the data.

Our model allows lightness measurements to generate mechanistic hypotheses that can be explicitly tested. For example, if early mechanisms of adaption mediate our results, the model predicts the way in which the corresponding physiologically measured luminance-response functions should vary with high-dynamic range contexts. In addition, understanding the parametric form of the luminance-to-lightness matching functions should be useful for refining algorithms designed to render high-dynamic range images on low-dynamic range displays [40, 41].

The model in its current form does not provide a complete theory of lightness, as it does not specify how context sets the adaptation parameters. To understand context effects, our strategy was to first determine the parameters that vary with context, as we have done here, and then proceed towards understanding how those parameters are set [42-45]. The regularities in our data suggest that simple rules may suffice for this purpose. Testing the generality of these rules, both for simple checkerboards and for more complex stimuli, will be of considerable interest.

We measured the mapping of stimulus luminance onto perceptual lightness in high-dynamic range images. We find the visual system can maintain a lightness scale over more than 3 log units of luminance, considerably larger than is necessary to represent variation in natural surface reflectance. The large degree of compression revealed by our data rules out theories that predict perceived lightness from luminance ratios or Weber contrast. In addition, the luminance-to-lightness mapping depends on the image context. For our experimental images, which contained no cues that would allow segmentation of the image into separate regions of illumination, we found three regularities that described this dependence. First, perceptual white is anchored near the highest luminance in the contextual image, across variations of highest luminance and contextual image luminance range. Second, varying the contextual image luminance range while holding the highest luminance fixed has its primary effect on the range of luminances mapped between perceptual white and perceptual black. Third, changing the distribution of contextual image luminances while holding the highest luminance and luminance range fixed left the luminances mapped to white and black unchanged, but affected the shape of the matching function in a manner broadly consistent with theories of optimal image coding. We accounted for the contextual effects using a model based on the adaptation of an underlying visual response function, and used the model to derive the response function for each of our experimental contexts.

Supplementary Material

Supplement, new version

Highlights.

  • The dynamic range of lightness perception exceeds 5,000:1 in a single image context

  • Ratio-based models fail to account for the measured luminance-to-lightness mappings

  • Simple regularities describe how luminance-to-lightness mapping varies with context

  • Luminance-to-lightness mappings are described by inferred visual response functions

Acknowledgments

Supported by NIH RO1 EY10016, RO1 EY10016S1, NIH P30 EY1001583 (DHB) and NSF BCS 1027093 and NIH 1R25GM096161-01 (ALG). We thank Christopher Broussard for technical assistance.

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

References

  • 1.Heckaman RL, Fairchild MD. Jones and Condit redux in high dynamic range color; Seventeenth Color Imaging Conference: Color Science and Engineering Systems, Technologies, and Applications; Albuquerque, New Mexico. 2009.pp. 8–14. [Google Scholar]
  • 2.Xiao F, DiCarlo J, Catrysse P, Wandell B. High dynamic range imaging of natural scenes; Tenth Color Imaging Conference: Color Science, Systems, and Applications; Scottsdale, AZ. 2002. [Google Scholar]
  • 3.Wyszecki G, Stiles WS. Color Science - Concepts and Methods, Quantitative Data and Formulae. 2nd Edition John Wiley & Sons; New York: 1982. [Google Scholar]
  • 4.Land EH, McCann JJ. Lightness and retinex theory. Journal of the Optical Society of America. 1971;61:1–11. doi: 10.1364/josa.61.000001. [DOI] [PubMed] [Google Scholar]
  • 5.Arend LE, Goldstein R. Simultaneous constancy, lightness, and brightness. Journal of the Optical Society of America A. 1987;4:2281–2286. doi: 10.1364/josaa.4.002281. [DOI] [PubMed] [Google Scholar]
  • 6.Adelson EH. Lightness perception and lightness illusions. In: Gazzaniga M, editor. The New Cognitive Neurosciences. 2nd ed. MIT Press; Cambridge, MA: 2000. pp. 339–351. [Google Scholar]
  • 7.Gilchrist A. Seeing Black and White. Oxford University Press; Oxford: 2006. [Google Scholar]
  • 8.Wallach H. Brightness constancy and the nature of achromatic colors. Journal of Experimental Psychology. 1948;38:310–324. doi: 10.1037/h0053804. [DOI] [PubMed] [Google Scholar]
  • 9.Seetzen H, Heidrich W, Stuezlinger W, Ward G, Whitehead L, Trentacost M, Ghosh A, Vorozcovs A. High dynamic range display systems. ACM Transactions on Graphics. 2004;23:760–768. [Google Scholar]
  • 10.Radonjić A, Broussard C, Brainard DH. Characterizing and controlling the spectral output of an HDR display. Department of Psychology, University of Pennsylvania; Philadelphia, PA: 2011. Brainard Lab Technical Report 2011-1. http://color.psych.upenn.edu/brainard/papers/hdrcharacterize.pdf. [Google Scholar]
  • 11.Gilchrist A, Kossyfidis C, Bonato F, Agostini T, Cataliotti J, Li X, Spehar B, Annan V, Economou E. An anchoring theory of lightness perception. Psychological Review. 1999;106:795–834. doi: 10.1037/0033-295x.106.4.795. [DOI] [PubMed] [Google Scholar]
  • 12.Walraven J, Enroth-Cugell C, Hood DC, MacLeod DIA, Schnapf JL. Visual Perception: the neurophysiological foundations. Academic Press; San Diego: 1990. The control of visual sensitivity. Receptoral and postreceptoral processes; pp. 53–101. [Google Scholar]
  • 13.Fechner GT. Elemente der Psychophysik. Breitkopf and Hartel; Leipzig: 1860. [Google Scholar]
  • 14.Nachmias J, Steinman RM. Brightness and discriminability of light flashes. Vision Research. 1965;5:545–557. doi: 10.1016/0042-6989(65)90087-8. [DOI] [PubMed] [Google Scholar]
  • 15.Hillis JM, Brainard DH. Do common mechanisms of adaptation mediate color discrimination and appearance? Contrast adaptation. Journal of the Optical Society America A. 2007;24:2122–2133. doi: 10.1364/josaa.24.002122. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Hillis JM, Brainard DH. Distinct mechanisms mediate visual detection and identification. Current Biology. 2007;17:1714–1719. doi: 10.1016/j.cub.2007.09.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17.Naka KI, Rushton WA. S-potentials from colour units in the retina of fish (Cyprinidae) Journal of Physiology (London) 1966;185:536–555. doi: 10.1113/jphysiol.1966.sp008001. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Brenner N, Bialek W, de Ruyter van Steveninck R. Adaptive rescaling maximizes information transmission. Neuron. 2000;26:695–702. doi: 10.1016/s0896-6273(00)81205-2. [DOI] [PubMed] [Google Scholar]
  • 19.Grzywacz NM, Balboa RM. A Bayesian framework for sensory adaptation. Neural Computation. 2002;14:543–559. doi: 10.1162/089976602317250898. [DOI] [PubMed] [Google Scholar]
  • 20.von der Twer T, MacLeod DIA. Optimal nonlinear codes for the perception of natural colors. Network: Computation in Neural Systems. 2001;12:395–407. [PubMed] [Google Scholar]
  • 21.Abrams AB, Hillis JM, Brainard DH. The relation between color discrimination and color constancy: when is optimal adaptation task dependent? Neural Computation. 2007;19:2610–2637. doi: 10.1162/neco.2007.19.10.2610. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Gilchrist AL. When does perceived lightness depend on perceived spatial arrangement? Perception and Psychophysics. 1980;28:527–538. doi: 10.3758/bf03198821. [DOI] [PubMed] [Google Scholar]
  • 23.Radonjić A, Todorović D, Gilchrist A. Adjacency and surroundedness in the depth effect on lightness. Journal of Vision. 2010;10(9:12):1–16. doi: 10.1167/10.9.12. [DOI] [PubMed] [Google Scholar]
  • 24.Koffka K. Principles of Gestalt Psychology. Harcourt, Brace and Company; New York: 1935. [Google Scholar]
  • 25.Kardos L. Ding und Schatten: Eine experimentelle Untersuchung über die Grundlagen des Fabensehens. Zeitschrift für Psychologie. 1934;23 [Google Scholar]
  • 26.Allred SR, Radonjić A, Gilchrist AL, Brainard DH. Context transfer functions in high-dynamic range images. Submitted for review. 2011 [Google Scholar]
  • 27.Jameson D, Hurvich LM. Visual Psychophysics, Handbook of Sensory Physiology. Springer-Verlag; Berlin: 1972. Sensitivity, contrast, and afterimages; pp. 568–581. [Google Scholar]
  • 28.Geisler WS. Adaptation, afterimage and cone saturation. Vision Research. 1978;18:279–289. doi: 10.1016/0042-6989(78)90162-1. [DOI] [PubMed] [Google Scholar]
  • 29.Adelson EH. Saturation and adaptation in the rod system. Vision Research. 1982;22:1299–1312. doi: 10.1016/0042-6989(82)90143-2. [DOI] [PubMed] [Google Scholar]
  • 30.Walraven J. Discounting the background: The missing link in the explanation of chromatic induction. Vision Research. 1976;16(3):289–295. doi: 10.1016/0042-6989(76)90112-7. [DOI] [PubMed] [Google Scholar]
  • 31.Shevell SK. The dual role of chromatic backgrounds in color perception. Vision Research. 1978;18:1649–1661. doi: 10.1016/0042-6989(78)90257-2. [DOI] [PubMed] [Google Scholar]
  • 32.Chubb C, Sperling G, Solomon JA. Texture interactions determine perceived contrast. PNAS. 1989;86:9631–9635. doi: 10.1073/pnas.86.23.9631. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 33.Victor JD, Conte MM, Purpura KP. Dynamic shifts of the contrast-response function. Visual Neuroscience. 1997;14:577–587. doi: 10.1017/s0952523800012232. [DOI] [PubMed] [Google Scholar]
  • 34.Chander D, Chichilnisky EJ. Adaptation to temporal contrast in primate and salamander retina. Journal of Neuroscience. 2001;21:9904–9916. doi: 10.1523/JNEUROSCI.21-24-09904.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 35.Solomon SG, Peirce JW, Drhruv NT, Lennie P. Profound contrast adaptation early in the visual pathway. Neuron. 2004;42:155–162. doi: 10.1016/s0896-6273(04)00178-3. [DOI] [PubMed] [Google Scholar]
  • 36.Manookin MB, Demb JB. Presynaptic mechanism for slow contrast adaptation in Mammalian retinal ganglion cells. Neuron. 2006;50:453–464. doi: 10.1016/j.neuron.2006.03.039. [DOI] [PubMed] [Google Scholar]
  • 37.Heeger DJ. Normalization of cell responses in cat striate cortex. Visual Neuroscience. 1992;9:181–197. doi: 10.1017/s0952523800009640. [DOI] [PubMed] [Google Scholar]
  • 38.Foley JM. Human luminance pattern-vision mechanisms: masking experiments require a new model. Journal of the Optical Society of America A. 1994;11:1710–1719. doi: 10.1364/josaa.11.001710. [DOI] [PubMed] [Google Scholar]
  • 39.Blakeslee B, McCourt ME. A unified theory of brightness contrast and assimilation incorporating oriented multiscale filtering and contrast normalization. Vision Research. 2004;44:2483–2503. doi: 10.1016/j.visres.2004.05.015. [DOI] [PubMed] [Google Scholar]
  • 40.DiCarlo JM, Wandell BA. Rendering high dynamic range scenes; Proceedings of the SPIE, Image Sensors; (San Jose, CA. 2000.pp. 392–401. [Google Scholar]
  • 41.Reinhard E, Ward G, Pattanaik S, Debevec P. High Dynamic Range Imaging. Elsevier; San Francisco: 2006. [Google Scholar]
  • 42.Stiles WS. Mechanism concepts in colour theory. Journal of the Colour Group. 1967;11:106–123. [Google Scholar]
  • 43.Krantz D. A theory of context effects based on cross-context matching. Journal of Mathematical Psychology. 1968;5:1–48. [Google Scholar]
  • 44.Brainard DH, Wandell BA. Asymmetric color-matching: how color appearance depends on the illuminant. Journal of the Optical Society of America A. 1992;9(9):1433–1448. doi: 10.1364/josaa.9.001433. [DOI] [PubMed] [Google Scholar]
  • 45.Brainard DH, Maloney LT. Surface color perception and equivalent illumination models. Journal of Vision. 2011;11(5:1):1–18. doi: 10.1167/11.5.1. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplement, new version
NIHMS332453-supplement-Supplement__new_version.doc (568KB, doc)

RESOURCES