Cerebral Microbleeds: Burden Assessment by Using Quantitative Susceptibility Mapping

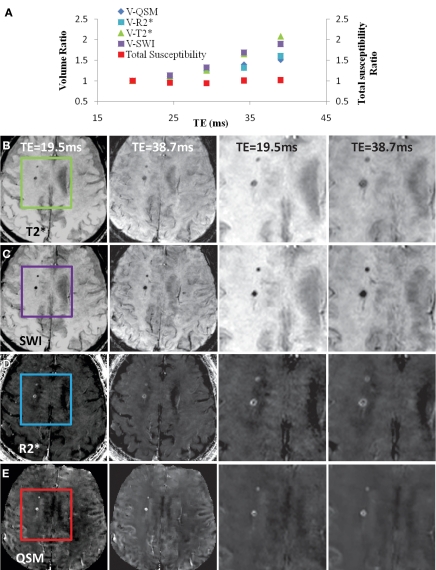
A cerebral microbleed has much improved consistency compared with its size measurements over a large range of echo times on gradient-echo MR images.

Abstract

Purpose:

To assess quantitative susceptibility mapping (QSM) for reducing the inconsistency of standard magnetic resonance (MR) imaging sequences in measurements of cerebral microbleed burden.

Materials and Methods:

This retrospective study was HIPAA compliant and institutional review board approved. Ten patients (5.6%) were selected from among 178 consecutive patients suspected of having experienced a stroke who were imaged with a multiecho gradient-echo sequence at 3.0 T and who had cerebral microbleeds on T2*-weighted images. QSM was performed for various ranges of echo time by using both the magnitude and phase components in the morphology-enabled dipole inversion method. Cerebral microbleed size was measured by two neuroradiologists on QSM images, T2*-weighted images, susceptibility-weighted (SW) images, and R2* maps calculated by using different echo times. The sum of susceptibility over a region containing a cerebral microbleed was also estimated on QSM images as its total susceptibility. Measurement differences were assessed by using the Student t test and the F test; P < .05 was considered to indicate a statistically significant difference.

Results:

When echo time was increased from approximately 20 to 40 msec, the measured cerebral microbleed volume increased by mean factors of 1.49 ± 0.86 (standard deviation), 1.64 ± 0.84, 2.30 ± 1.20, and 2.30 ± 1.19 for QSM, R2*, T2*-weighted, and SW images, respectively (P < .01). However, the measured total susceptibility with QSM did not show significant change over echo time (P = .31), and the variation was significantly smaller than any of the volume increases (P < .01 for each).

Conclusion:

The total susceptibility of a cerebral microbleed measured by using QSM is a physical property that is independent of echo time.

© RSNA, 2011

Introduction

The potential causes of cerebral microbleeds and/or iron deposition in the brain are broad, including those most commonly associated with systemic hypertension and cerebral amyloid angiopathy. Additional causes include diffuse axonal injury secondary to trauma (1,2), cavernous malformations, demyelinating disease, vasculitis, neurodegenerative diseases, hemorrhagic micrometastases, primary arterial diseases such as cerebral autosomal dominant arteriopathy with subcortical infarcts and leukoencephalopathy, and secondary arterial diseases like radiation vasculopathy. Cerebral microbleeds indicate prior extravasation of blood from rupture of cerebral arterioles damaged by hyaline degeneration and microaneurysm formation caused by longstanding hypertension or aging and signify the presence of an underlying hemorrhage-prone microangiopathy (3–6).

There is a substantial research interest in the predictive value of determining cerebral microbleed severity regarding the incidence or recurrence of primary intracerebral hemorrhage (7–10). Additionally, results of recent studies (11,12) indicate that cerebral microbleed burden is strongly and independently related to the incidence of intracerebral hemorrhage in patients receiving anticoagulant therapy. Thus, there is a pressing need to further assess the diagnostic and prognostic utility of calculating cerebral microbleed burden and its impact on treatment decisions.

T2*-weighted gradient-echo magnetic resonance (MR) imaging is the method of choice for detecting cerebral microbleeds because of its sensitivity to the field inhomogeneity caused by hemosiderin deposits (5). The presence, number, distribution, and especially the size of round parenchymal signal voids have traditionally been used to characterize cerebral microbleed burden (5,13). However, the size of cerebral microbleeds may vary substantially with field strength, flip angle, section gap, and section thickness. Furthermore, previous studies (5) have shown inconsistencies in defining cerebral microbleed size, and the measured size is very sensitive to the choice of echo time, mainly because the intravoxel dephasing effect accumulates over time, leading to a progressively enlarging signal void as the echo time increases (14). Owing to these variables, a good correlation between microbleeds and other clinical measures has not yet been clearly established. According to Greenberg and Vernooij (5), there is an ongoing need to establish “a shared set of standards for the detection of microbleeds that will enable informative cross-study comparisons and robust longitudinal data collection” (15).

Hence, in the current study, we assessed quantitative susceptibility mapping (QSM) for reducing the inconsistency of standard MR imaging sequences in cerebral microbleed burden measurements.

Materials and Methods

Data Acquisition

This retrospective analysis was approved by our institutional review boards and was in compliance with the Health Insurance Portability and Accountability Act. We reviewed data in 178 consecutive patients who underwent an MR imaging protocol for stroke in a 1-week period (from September 20, 2010, to September 27, 2010) at our institutions (Weill Cornell Medical College, Columbia University, the Second Affiliated Hospital of Zhejiang University School of Medicine, and Chinese PLA General Hospital). Inclusion criteria were age greater than 40 years and the presence of one or more cerebral microbleed in the brain parenchyma that measured 2–10 mm on T2*-weighted MR images. Fifty-six patients (31.5%) met these criteria. Patients imaged at 1.5 T were excluded (n = 43, 24.2%). Additional exclusion criteria included excessive motion artifacts on T2*-weighted images as determined by a neuroradiologist (K.S., with 7 years of experience), because this limits the accuracy of the measurement of cerebral microbleed size (n = 3, 1.7%). Ten patients (5.6%) met all study criteria. The mean age was 72 years ± 18 (standard deviation) for the cohort, 76 years ± 9 for the five male patients (50% of the cohort), and 68 years ± 24 for the five female patients (50% of the cohort). Imaging was performed with 3.0-T MR imaging units (HDx; GE Healthcare, Waukesha, Wis) and an eight-channel phased-array head coil. The stroke protocol included T2*-weighted angiography enabled with three-dimensional multiecho spoiled gradient-echo sampling. Imaging parameters of the T2*-weighted angiography sequence were as follows: axial planes that covered the brain; number of echo times, seven to 10; first echo time, 4.9–13 msec; uniform echo time spacing, 3.8–5.2 msec; repetition time, 39.8–67.6 msec; flip angle, 15°–25°; bandwidth per pixel, 244 Hz; field of view, 24 × 19.2–24.0 × 7.2–18 cm; and acquisition matrices, 240–448 × 180–384 × 36–60. A parallel imaging method (array spatial sensitivity encoding technique) was used with a reduction factor of two.

Data Reconstruction

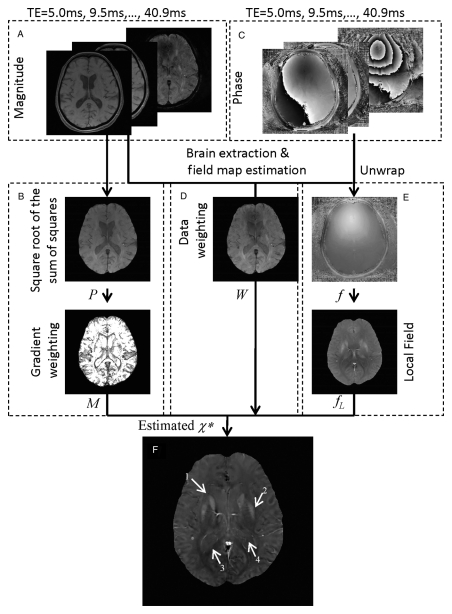
The reconstruction of QSM images from the measured complex phase data is an ill-posed inverse problem, in the sense that many solutions can generate a field that is virtually identical to that derived from the phase data (16). Here, we formulate this inverse problem as a weighted L1 minimization problem (17,18). Among all the candidate solutions, the estimated susceptibility distribution χ* (Fig 1f) is the one with the sparsest difference between its edges and those from the anatomic (magnitude) image. This spatial prior helps to eliminate solutions with spurious edges resulting from the streaking artifacts often seen in QSM (22) and determines a solution that is physically meaningful. A schematic view of this morphology-enabled dipole inversion (MEDI) approach is shown in Figure 1. The gradient weighting, which represents the edge information (Fig 1b), is calculated by applying a threshold to the gradient of the magnitude images (Fig 1a and 1b). The phase images (Fig 1c) are used to derive the field map (Fig 1e) and estimate its noise (Fig 1d). The field map (Fig 1e) was further processed by using a projection onto dipole fields method (23) for the background field removal. The gradient weighting, data weighting, and the local field images are subsequently input into the MEDI algorithm for calculating the quantitative susceptibility map (Fig 1f). For each patient and for each echo time equal to t_e, a QSM image was calculated by using all echo times up to t_e.

Figure 1:

(a–f) Schematic view of QSM reconstruction method in 70-year-old woman. A, The square root of the sum of squares of the axial magnitude images from multiple echo times forms, B, an anatomic image P. An automatic brain extraction algorithm (19) was used to mask out the nonbrain region. A simple threshold method was used to set the nonnegligible gradients on P to zero while setting others to one to generate the gradient weighting term M. Both the, A, magnitude and, C, phase images were used to estimate, D, the data weighting term W and, E, the field map f (20). The spatial unwrapping of the field map was accomplished by using a quality map–guided region-growing algorithm (21). The projection onto dipole fields method was subsequently used to estimate the local magnetic field f_L. F, Finally, the QSM was reconstructed by using the MEDI method. Arrows 1–4 show the caudate nucleus, putamen, splenium of corpus callosum, and atrium of the lateral ventricle, respectively. TE = echo time.

Data Analysis

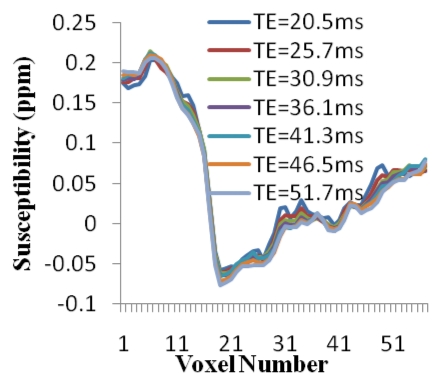
Evaluation of QSM profile.—To analyze the variations of both the contrast and noise of the QSM profiles over a range of echo times, the reconstructed QSM profiles were plotted over echo time for visual inspection to assess the echo time dependence. For each patient, one section of the globus pallidus was manually segmented on the QSM profile at an echo time of approximately 40 msec, and the segmented template was applied to other echo times. The contrast of the QSM profile was defined as the mean susceptibility value of the globus pallidus, and the noise of the QSM profile at echo time t_e was defined as the standard deviation of the difference between the QSM at echo time t_e – Δt_e and the QSM at echo time t_e. For each patient, contrast measured at an echo time of approximately 40 msec was divided by the contrast measured at an echo time of approximately 20 msec to obtain a measure of contrast ratio dependence on echo time; a similar measure of noise ratio dependence on echo time was also obtained.

Cerebral microbleeds were identified by two radiologists (K.S. and another radiologist with 6 years of experience) on the magnitude image obtained at an echo time of approximately 40 msec. A round or ovoid hypointense lesion whose diameter was greater than 2 but smaller than 10 mm and that was clearly not a vessel was considered to be a microbleed. The two radiologists performed independent quantification of the microbleeds on QSM profiles. The second radiologist repeated the QSM analysis 6 weeks later to assess intraobserver variability. For each cerebral microbleed, a 1 × 1 × 1-cm³ cubic region of interest (ROI) was placed at the center of the microbleed to enable calculation of its total susceptibility. Although susceptibility itself is dimensionless, tissue susceptibility is usually on the order of 10⁻⁶, so parts per million is commonly used as its unit. The susceptibility of brain parenchyma is less than 0.05 ppm, as found in a previous study in healthy volunteers (17). Therefore, voxels inside the cube whose susceptibility values were greater than 0.05 ppm were considered as part of the microbleed, and the susceptibility of all selected voxels was summed to calculate the total susceptibility with the following equation: m = ∑_Rχ · Δv, where m denotes the total susceptibility of a cerebral microbleed, R denotes the region of selected voxels, and Δv is the voxel size. The total susceptibility was further used as an indicator of cerebral microbleed burden and was compared with the size measurement as described below.

Line segments traversing the globus pallidus, the internal capsule, and the thalamus on QSM profiles were examined for the influence of echo time on the susceptibility variation. A linear regression was performed between the total susceptibility and echo time. The noise on the QSM profile was fitted to a power function.

Comparison with R2* map, susceptibility-weighted images, and T2*-weighted images.—Similar to the QSM profile, a R2* map with a monoexponential fit was obtained for each echo time t_e by selecting all echo times up to this echo time. For each echo time, a susceptibility-weighted (SW) image was generated by multiplying the magnitude image with a corrected phase image raised to the fourth power (24), and a T2*-weighted image was retained. The diameter d_M of each microbleed was measured by the two radiologists (once by K.S. and twice by the second radiologist) on the QSM profiles, R2* images, SW images, and T2*-weighted images for each echo time to assess echo time dependence. For a consistent comparison with the total susceptibility over a volume, the microbleed diameters were further converted into microbleed volumes, assuming a spherical shape: V = 1/6πd_M³. To quantitatively assess the volume of a microbleed for each echo time, the volume ratio of a microbleed at echo time t_e was calculated as the ratio of volumes measured at echo time t_e and at an echo time of approximately 20 msec, which has been suggested to be the minimal echo time for cerebral microbleed examination (5). Similarly, total susceptibility ratio was calculated as the ratio of total susceptibilities estimated at echo time t_e and an echo time of approximately 20 msec. Linear regression was performed between the total susceptibility of each cerebral microbleed and its volume on the T2*-weighted image obtained at an echo time of approximately 40 msec. A histogram of the total susceptibility of each cerebral microbleed over all the patients was generated to analyze its distribution.

It has been shown that R2* has high correlation with iron concentration (25). Therefore, we compared total susceptibility with total R2*, which also indicates the total amount of iron in a cerebral microbleed. The total R2* for each microbleed was calculated by summing the R2* values inside the 1 × 1 × 1-cm³ cubic ROI used for calculating the total susceptibility value. Linear regression was performed between the total R2* of each cerebral microbleed and its total susceptibility at an echo time of approximately 40 msec.

Statistical Analysis

For all ratio measurements, the results are reported as means ± standard deviations. Inter- and intraobserver variabilities of the total susceptibility and size measurements were assessed by using the intraclass correlation coefficient (26). The following criteria for clinically relevant agreement were used to assess the calculated intraclass correlation coefficient: agreement of less than 0.40 was considered poor; agreement of 0.40–0.59, fair; agreement of 0.60–0.74, good; and agreement greater than 0.74, excellent (27). One-way analysis of variance was used to test the difference among the QSM profiles measured at different echo times. One-tailed Student t tests were performed to assess whether the total susceptibility ratio was smaller than each of the volume ratios. Additional Student t tests were performed to evaluate the significance level of the difference between these ratios and 1. A retrospective power analysis was performed to assess the chance of detecting a 20% increase in total susceptibility when echo time approximately doubled. For the linear regressions, the F test was performed to assess significance. All statistical evaluations were performed with software (SPSS, release 16; SPSS, Chicago, Ill), and α = .05 was considered to indicate a significant difference.

Results

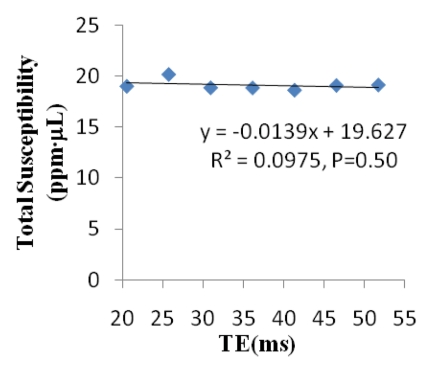
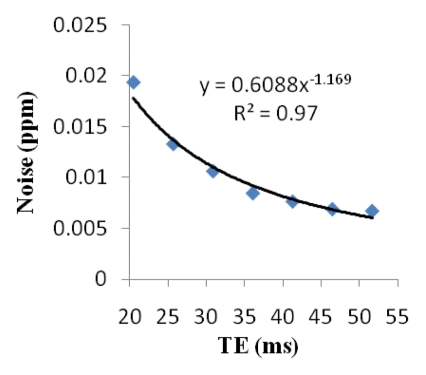
Cerebral microbleed findings are summarized in Table 1. The measured contrast of the QSM profile was independent of the number of echo times used (mean contrast ratio, 1.04 ± 0.12; P = .31), but the noise decreased when an increasing number of echo times were included in the QSM reconstruction (mean noise ratio, 0.29 ± 0.08; P < .01) (Fig 2). There was no significant variation in the line segments on QSM profiles between the different echo times (P = .997) (Fig 2d). The microbleed total susceptibility did not show a significant linear dependence on the choice of echo time (slope, −0.032; P = .50) (Fig 2e). QSM noise decayed monotonically with increasing echo time (exponent, −1.169) (Fig 2f).

Table 1.

Cerebral Microbleed Finding Summary

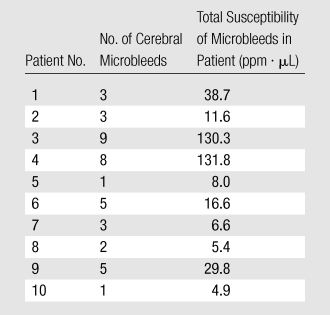
Figure 2a:

Qualitative and quantitative analysis of the QSM profile in a 40-year-old woman at different echo times. (a–c) Axial QSM profiles reconstructed at the various echo times (a) 20.5 msec, (b) 41.3 msec, and (c) and 51.7 msec do not show echo time dependence at visual inspection. The window/level of the QSM is adjusted from −0.2 to 0.4 ppm. White line in b = mark of line segment, white square in b = area of total susceptibility measurement. (d, e) Graphs show echo time (TE) independency of the QSM profile, which is quantitatively confirmed by the susceptibility measured along (d) a line segment and by (e) the total susceptibility of the microbleed at various echo times. (f) Graph shows that the noise of the QSM decays monotonically with increasing echo time (TE).

Figure 2d:

Qualitative and quantitative analysis of the QSM profile in a 40-year-old woman at different echo times. (a–c) Axial QSM profiles reconstructed at the various echo times (a) 20.5 msec, (b) 41.3 msec, and (c) and 51.7 msec do not show echo time dependence at visual inspection. The window/level of the QSM is adjusted from −0.2 to 0.4 ppm. White line in b = mark of line segment, white square in b = area of total susceptibility measurement. (d, e) Graphs show echo time (TE) independency of the QSM profile, which is quantitatively confirmed by the susceptibility measured along (d) a line segment and by (e) the total susceptibility of the microbleed at various echo times. (f) Graph shows that the noise of the QSM decays monotonically with increasing echo time (TE).

Figure 2e:

Qualitative and quantitative analysis of the QSM profile in a 40-year-old woman at different echo times. (a–c) Axial QSM profiles reconstructed at the various echo times (a) 20.5 msec, (b) 41.3 msec, and (c) and 51.7 msec do not show echo time dependence at visual inspection. The window/level of the QSM is adjusted from −0.2 to 0.4 ppm. White line in b = mark of line segment, white square in b = area of total susceptibility measurement. (d, e) Graphs show echo time (TE) independency of the QSM profile, which is quantitatively confirmed by the susceptibility measured along (d) a line segment and by (e) the total susceptibility of the microbleed at various echo times. (f) Graph shows that the noise of the QSM decays monotonically with increasing echo time (TE).

Figure 2f:

Qualitative and quantitative analysis of the QSM profile in a 40-year-old woman at different echo times. (a–c) Axial QSM profiles reconstructed at the various echo times (a) 20.5 msec, (b) 41.3 msec, and (c) and 51.7 msec do not show echo time dependence at visual inspection. The window/level of the QSM is adjusted from −0.2 to 0.4 ppm. White line in b = mark of line segment, white square in b = area of total susceptibility measurement. (d, e) Graphs show echo time (TE) independency of the QSM profile, which is quantitatively confirmed by the susceptibility measured along (d) a line segment and by (e) the total susceptibility of the microbleed at various echo times. (f) Graph shows that the noise of the QSM decays monotonically with increasing echo time (TE).

Figure 2b:

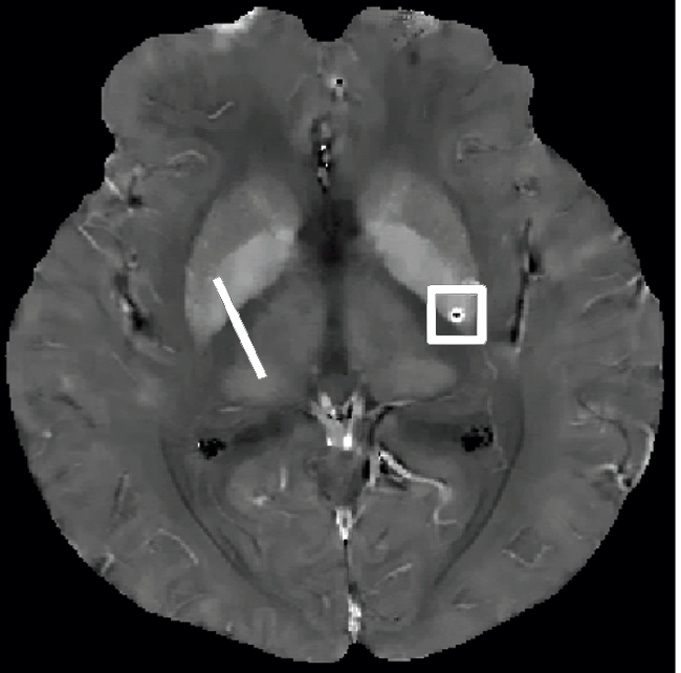
Qualitative and quantitative analysis of the QSM profile in a 40-year-old woman at different echo times. (a–c) Axial QSM profiles reconstructed at the various echo times (a) 20.5 msec, (b) 41.3 msec, and (c) and 51.7 msec do not show echo time dependence at visual inspection. The window/level of the QSM is adjusted from −0.2 to 0.4 ppm. White line in b = mark of line segment, white square in b = area of total susceptibility measurement. (d, e) Graphs show echo time (TE) independency of the QSM profile, which is quantitatively confirmed by the susceptibility measured along (d) a line segment and by (e) the total susceptibility of the microbleed at various echo times. (f) Graph shows that the noise of the QSM decays monotonically with increasing echo time (TE).

Figure 2c:

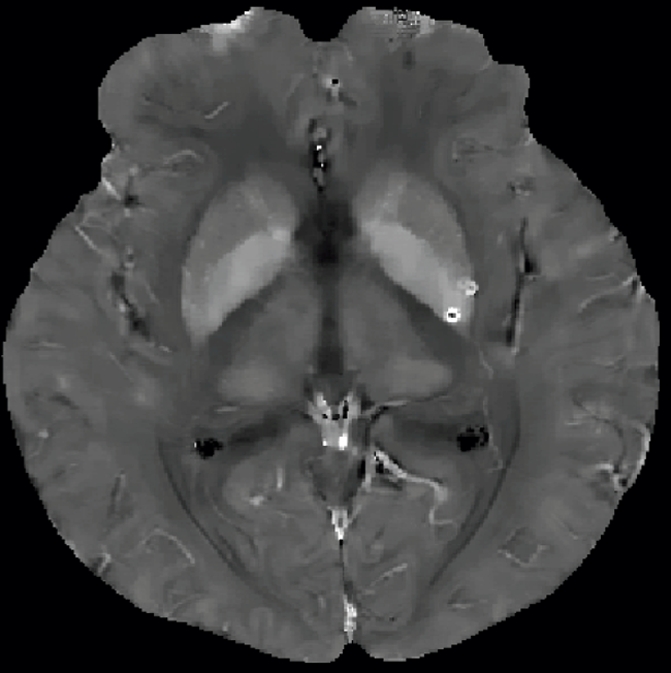
Qualitative and quantitative analysis of the QSM profile in a 40-year-old woman at different echo times. (a–c) Axial QSM profiles reconstructed at the various echo times (a) 20.5 msec, (b) 41.3 msec, and (c) and 51.7 msec do not show echo time dependence at visual inspection. The window/level of the QSM is adjusted from −0.2 to 0.4 ppm. White line in b = mark of line segment, white square in b = area of total susceptibility measurement. (d, e) Graphs show echo time (TE) independency of the QSM profile, which is quantitatively confirmed by the susceptibility measured along (d) a line segment and by (e) the total susceptibility of the microbleed at various echo times. (f) Graph shows that the noise of the QSM decays monotonically with increasing echo time (TE).

The reduced variation of the total susceptibility of cerebral microbleeds over a wide spectrum of echo times is further illustrated in another example (Fig 3), which also includes volume measurements and a comparison of a QSM profile with T2*-weighted, SW, and R2* images. The susceptibility ratio did not change substantially, while the volume ratio increased with echo time (Fig 3a). All the microbleeds identified on T2*-weighted images were also detected on SW images, R2* maps, and QSM profiles at the same echo time (approximately 40 msec). The diameter of the microbleed exhibited substantial enlargement with increasing echo time on T2*-weighted (Fig 3b) and SW (Fig 3c) images. The enlargement was moderate on R2* images (Fig 3d) and was substantially reduced on QSM profiles (Fig 3e).

Figure 3:

A, Comparison of QSM profile with R2* map, T2*-weighted image, and SW image (SWI) in representative case in 84-year-old man. A, The volume (V) of the microbleed monotonically increased with increasing echo time (TE) on all the images, as indicated by the volume ratios. However, the total susceptibility ratio, defined as the total susceptibility measured at a certain echo time normalized by the total susceptibility measured at an echo time of 20 msec, did not demonstrate significant echo time dependence (P = .47). B–E, Axial T2*-weighted images, SW images (SWI), R2* maps, and QSM profiles, respectively, of the same microbleed are shown at echo times (TE) of 19.5 (first column) and 38.7 (second column) msec. The third and fourth columns show zoomed-in areas in the box in the first column at the two echo times in the first and second columns. The boxes in the first column show the measured microbleeds. The window/level of the QSM profile is adjusted from −0.1 to 0.2 ppm.

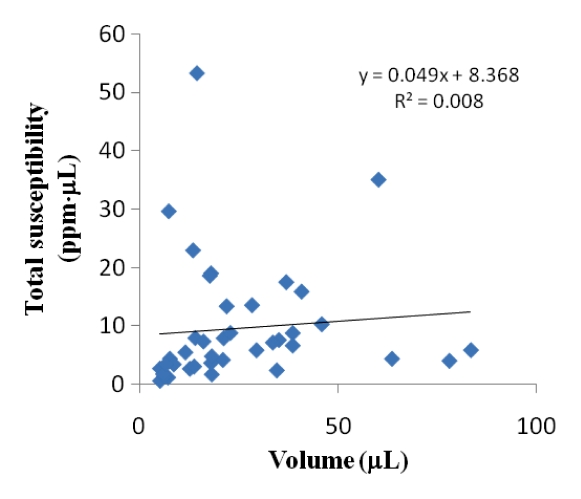
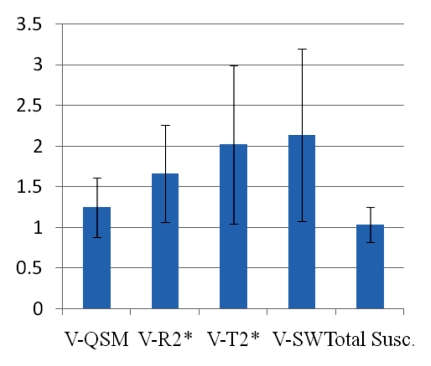
Inter- and intraobserver results are listed in Table 2. Intraclass correlation coefficients ranged between good (0.60–0.74) and excellent (>0.74). Averaging the three readings (one by K.S, and two by the other radiologist), the mean volume ratios at an echo time of approximately 40 msec were 1.49 ± 0.86, 1.64 ± 0.84, 2.30 ± 1.20, and 2.30 ± 1.19 for QSM profiles, R2* maps, T2*-weighted images, and SW images—all significantly larger than 1 (P < .01). The total susceptibility ratio at an echo time of approximately 40 msec was 1.03 ± 0.30, significantly smaller than any of the volume ratios (P < .01 for each) and not significantly different from 1 (P = .31). This finding was unanimously confirmed in each of the three readings. With a one-sample t test and an α of .05, the retrospective power analysis confirmed that the sample size was sufficient to achieve 94% power to detect a 20% increase in total susceptibility when echo time approximately doubled. There was no correlation between the total susceptibility of a cerebral microbleed and its volume (measured at an echo time of approximately 40 msec) (P = .47) (Fig 4b). The total susceptibility in 37 (92%) of 40 microbleeds was less than 25 ppm · μL (Fig 4c).

Table 2.

Inter- and Intraobserver Variability

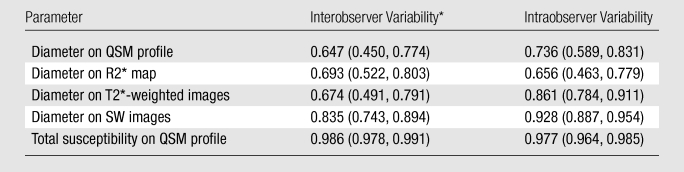
Note.—Data are intraclass correlation coefficients, with 95% confidence intervals in parentheses.

^*Data are from the first reading of observer 2.

Figure 4b:

(a) Graph shows comparison of QSM profiles with R2* maps, T2*-weighted images, and SW images across all patients. All the volume (V) ratios at an echo time of approximately 40 msec substantially deviated from 1. However, the total susceptibility ratio did not show a significant difference from 1 (P = .31). Error bars = standard deviations. (b) There was also no significant correlation between total susceptibility and volume (P = .47). (c) Histogram of total susceptibility of all cerebral microbleeds. Count = number of cerebral microbleeds.

Figure 4c:

(a) Graph shows comparison of QSM profiles with R2* maps, T2*-weighted images, and SW images across all patients. All the volume (V) ratios at an echo time of approximately 40 msec substantially deviated from 1. However, the total susceptibility ratio did not show a significant difference from 1 (P = .31). Error bars = standard deviations. (b) There was also no significant correlation between total susceptibility and volume (P = .47). (c) Histogram of total susceptibility of all cerebral microbleeds. Count = number of cerebral microbleeds.

Figure 4a:

(a) Graph shows comparison of QSM profiles with R2* maps, T2*-weighted images, and SW images across all patients. All the volume (V) ratios at an echo time of approximately 40 msec substantially deviated from 1. However, the total susceptibility ratio did not show a significant difference from 1 (P = .31). Error bars = standard deviations. (b) There was also no significant correlation between total susceptibility and volume (P = .47). (c) Histogram of total susceptibility of all cerebral microbleeds. Count = number of cerebral microbleeds.

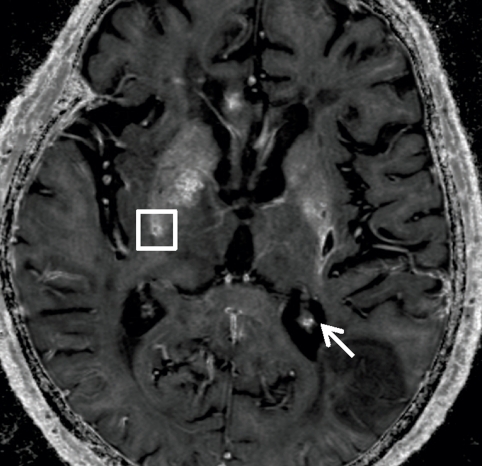
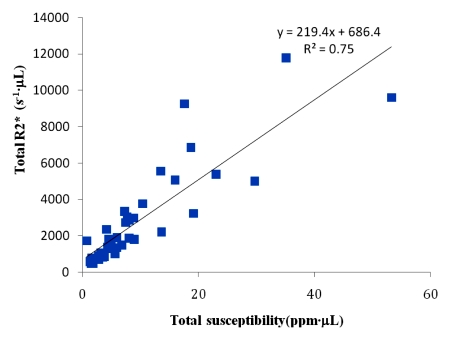
The linear regression between the total R2* and the total susceptibility showed a slope of 219.4 (P < .01), with a coefficient of determination of R² = 0.75 (Fig 5).

Figure 5a:

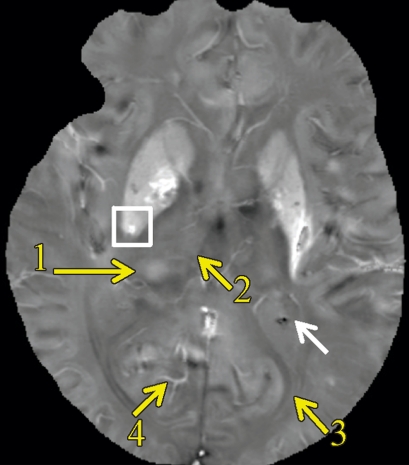
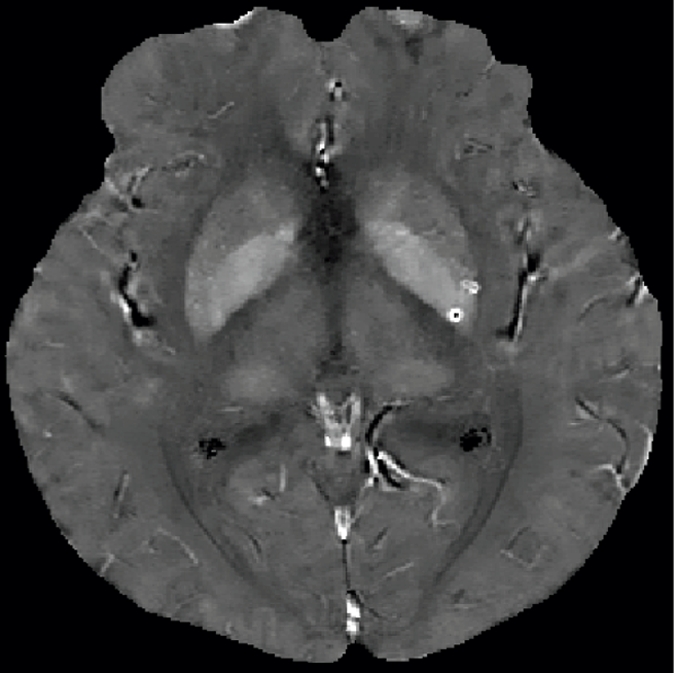
Axial (a) R2* map and (b) QSM profile in 75-year-old man show iron and calcium deposits. The same cube ROI used for measuring total susceptibility was translated to the R2* map for measuring the total R2* of each microbleed. Note that calcification in the choroid plexus (white arrow) has a similar hyperintense appearance as a microbleed on a. This ambiguity is removed on b. There is a contrast between the pulvinar nucleus (yellow arrow 1) and the rest of the thalamus (yellow arrow 2). Myelin-rich structures such as the optic radiations (yellow arrow 3) show negative susceptibility. Deoxyhemoglobin in venous blood, such as in the internal occipital vein (yellow arrow 4), is paramagnetic. (c) Graph shows the positive linear relationship observed between the total R2* and total susceptibility of the 40 cerebral microbleeds. The window/level is adjusted to from 0 to 100 sec⁻¹ for the R2* map and from −0.1 to 0.2 ppm for the QSM.

Figure 5b:

Axial (a) R2* map and (b) QSM profile in 75-year-old man show iron and calcium deposits. The same cube ROI used for measuring total susceptibility was translated to the R2* map for measuring the total R2* of each microbleed. Note that calcification in the choroid plexus (white arrow) has a similar hyperintense appearance as a microbleed on a. This ambiguity is removed on b. There is a contrast between the pulvinar nucleus (yellow arrow 1) and the rest of the thalamus (yellow arrow 2). Myelin-rich structures such as the optic radiations (yellow arrow 3) show negative susceptibility. Deoxyhemoglobin in venous blood, such as in the internal occipital vein (yellow arrow 4), is paramagnetic. (c) Graph shows the positive linear relationship observed between the total R2* and total susceptibility of the 40 cerebral microbleeds. The window/level is adjusted to from 0 to 100 sec⁻¹ for the R2* map and from −0.1 to 0.2 ppm for the QSM.

Figure 5c:

Axial (a) R2* map and (b) QSM profile in 75-year-old man show iron and calcium deposits. The same cube ROI used for measuring total susceptibility was translated to the R2* map for measuring the total R2* of each microbleed. Note that calcification in the choroid plexus (white arrow) has a similar hyperintense appearance as a microbleed on a. This ambiguity is removed on b. There is a contrast between the pulvinar nucleus (yellow arrow 1) and the rest of the thalamus (yellow arrow 2). Myelin-rich structures such as the optic radiations (yellow arrow 3) show negative susceptibility. Deoxyhemoglobin in venous blood, such as in the internal occipital vein (yellow arrow 4), is paramagnetic. (c) Graph shows the positive linear relationship observed between the total R2* and total susceptibility of the 40 cerebral microbleeds. The window/level is adjusted to from 0 to 100 sec⁻¹ for the R2* map and from −0.1 to 0.2 ppm for the QSM.

Discussion

Our data demonstrated that cerebral microbleeds can be quantified by their magnetic susceptibility properties determined by using QSM. The total susceptibility measurement of a cerebral microbleed has much improved consistency compared with its size measurements over a large range of echo times on gradient-echo MR images.

Geometric measurements in gradient-echo MR imaging and its derivatives (including T2*-weighted, SW, and R2* imaging) fundamentally suffer from inherent blooming artifacts (28); hypointensity at a voxel indicates only the local field variation, not the precise location of the paramagnetic source responsible for that local field disturbance. The deconvolution with the magnetic field of the unit dipole in QSM can theoretically eliminate these blooming artifacts when proper prior information is used such as morphology derived from images with no or few blooming artifacts. Our current QSM method uses a composite T2*-weighted magnitude in which a small microbleed may still experience moderate blooming artifacts. Consequently, there is a minor volume increase with echo time on the calculated QSM profile or a decrease with echo time in the estimated volume susceptibility of the cerebral microbleed. It is shown here that even in the current MEDI implementation, the integration of susceptibility over volume quantifying the magnetic moment of a microbleed is more invariant against changes of echo time compared with size measurements; these findings are in accordance with results of previous phantom and ex vivo validations (29), where QSM has been shown to be able to accurately quantify the amount of iron. Assuming that magnetization of iron in hemosiderin is not saturated (nonferromagnetic), then the total susceptibility measurement should be independent of field strength (30).

The susceptibility changes within cerebral microbleeds are primarily due to hemosiderin deposits and reflect the amount of iron that is recognized as an important factor for brain injury in intracerebral hemorrhage (31,32). Accordingly, there is increasing interest in the magnetism of hemorrhages (33,34). Because total susceptibility has a much improved consistency over a wide range of echo times, it may be a more useful measurement for microbleed burden than volume as measured on T2*-weighted images. The lack of correlation between volume and total susceptibility in our data indicates that there is marked variation in volume susceptibility. Further study is needed to investigate the relation between total susceptibility, volume susceptibility, neurologic damage, and risk in disease and pharmacologic therapy. For example, cerebral microbleed burden at QSM may be a valuable indicator for prognosis in children with acute nonaccidental head trauma (2) and for assessing the hemorrhage risk in patients receiving chronic treatment with anticoagulants (11,12).

The noise at QSM decreases with increasing echo time because a longer echo time allows for more dephasing and thus a more accurate field map estimation, as long as the signal intensity on the magnitude image has not decayed to below the noise level (35). The contrast of QSM, which is determined by tissue susceptibility, does not depend on echo time. This physical principle supports the use of QSM to characterize cerebral microbleed burden. It is preferable to have a short echo time to capture the morphology and field information before the signal in a voxel decays to the noise level because of surrounding strong susceptibility sources and a long echo time to reduce the noise on the QSM profile to improve sensitivity for weak susceptibility sources. This multiecho gradient-echo sequence offers the benefit of simultaneous acquisition of all echo times in one excitation. The total number of echo times for a fixed repetition time increases linearly with the receiver bandwidth. A low receiver bandwidth may be used to acquire a single echo of high signal-to-noise ratio. However, a single echo with a desired echo time may not make use of the whole available sampling time in a repetition time, leading to a lower signal-to-noise ratio than that of the sum of all echo times in the multiecho approach. Furthermore, the temporal evolution information in the multiecho approach enhances the robustness of the unwrapping algorithm on the estimated field map. Most modern clinical imaging units are conveniently equipped with a multiecho gradient-echo sequence.

In this study, we did not measure the total hypointensities of cerebral microbleeds on T2*-weighted and SW images. These hypointense regions mostly contain noise. Consequently, the total hypointensities would be just volume times noise level, which does not provide useful information in addition to the volume of a cerebral microbleed. Although there was a linear relationship between total R2* and total susceptibility (R² = 0.75), it should be pointed out that the fitting used only cerebral microbleeds, which were all paramagnetic. Compared with iron, calcium deposits have an opposite sign at QSM because they are diamagnetic (29,34,36). On R2* maps, however, they have a similar appearance. Additionally, the measured R2* is subject to the T2 quench effect (37). Therefore, total R2* measurement of a cerebral microbleed may not be an optimal method for detecting cerebral microbleeds or characterizing their burden.

Limitations of this study included the retrospective nature of the analysis. Another limitation was that data acquisition parameters were not homogeneous across all subjects. From results of earlier preliminary investigations (not shown here), it was found that high spatial resolution is beneficial for the QSM reconstruction because it reduces digitization error in determining the phase. Additionally, a larger range of echo times will improve the accuracy of the estimated field map. These findings are useful for designing a proper prospective study in the future. Improved data acquisition will reduce the noise at QSM, increase the magnitude of the standardized effect size, and lead to greater statistical power if the same sample size is used.

In summary, the total susceptibility of a cerebral microbleed is an intrinsic physical property independent of echo time. Measurement of cerebral microbleeds by using total susceptibility have much reduced variations associated with changes in echo time on gradient-echo MR images compared with their size measurements, offering a more consistent means to characterize the cerebral microbleed burden.

Advances in Knowledge.

• • Cerebral microbleeds can be quantified by their magnetic susceptibility properties determined by using quantitative susceptibility mapping (QSM).

• • The total susceptibility of cerebral microbleeds measured by using QSM is more consistent compared with size measurements over a large range of echo times.

• • The contrast-to-noise ratio of QSM increases with echo time.

Implication for Patient Care.

• • Quantitative assessments of cerebral microbleeds according to their physical magnetic susceptibilities may offer consistent characterization over a wide spectrum of imaging parameters that will enhance the confidence in disease stratification.

Disclosures of Potential Conflicts of Interest: T.L. No potential conflicts of interest to disclose. K.S. No potential conflicts of interest to disclose. M.L. No potential conflicts of interest to disclose. L.Q. No potential conflicts of interest to disclose. P.S. No potential conflicts of interest to disclose. Y.W. Financial activities related to the present article: none to disclose. Financial activities not related to the present article: listed as an inventor on patent that institution has applied for. Other relationships: none to disclose.