Skip to main content
PMC home page
Journal of Computational Biology logoLink to Journal of Computational Biology
. 2012 Jan;19(1):42–54. doi: 10.1089/cmb.2010.0188

An Overview of Population Genetic Data Simulation

Xiguo Yuan 1,*, David J Miller 3,*, Junying Zhang 1, David Herrington 4, Yue Wang 2,✉
PMCID: PMC3244809  PMID: 22149682

Abstract

Simulation studies in population genetics play an important role in helping to better understand the impact of various evolutionary and demographic scenarios on sequence variation and sequence patterns, and they also permit investigators to better assess and design analytical methods in the study of disease-associated genetic factors. To facilitate these studies, it is imperative to develop simulators with the capability to accurately generate complex genomic data under various genetic models. Currently, a number of efficient simulation software packages for large-scale genomic data are available, and new simulation programs with more sophisticated capabilities and features continue to emerge. In this article, we review the three basic simulation frameworks—coalescent, forward, and resampling—and some of the existing simulators that fall under these frameworks, comparing them with respect to their evolutionary and demographic scenarios, their computational complexity, and their specific applications. Additionally, we address some limitations in current simulation algorithms and discuss future challenges in the development of more powerful simulation tools.

Key words: backward simulators, disease association study, forward simulators, genome simulation, resampling

1. Introduction

In evolutionary biology, population simulation plays an increasingly important role in helping researchers to investigate the effects of various genetic models on genetic diversity and DNA sequence patterns (Calafell et al., 2001), and to study hypotheses on how genomic variation affects diseases, for example, the Common Disease–Common Variant hypothesis (Peng and Kimmel, 2007). Simulation is also used to evaluate the performance of statistical techniques, for example, those designed to partition haplotype blocks and to select tag single-nucleotide polymorphisms (SNPs) (Zhang et al., 2004; Kimmel and Shamir, 2005) and those developed to identify disease-associated SNP interactions in genetic studies (Hahn et al., 2003; Miller et al., 2009). Thus, along with the rapid development of genotyping and resequencing technologies, it is crucial, for the aforementioned performance assessments, to design tools for simulating large-scale genomic data under realistic scenarios that include the effects of natural selection, recombination, gene conversion, and complex demographic and environmental factors.

One of the central research directions in genetic analysis is the identification and characterization of SNPs that confer increased susceptibility to complex human diseases such as Type 2 diabetes and breast cancer. Genome-wide association studies (GWAS) is an example of a commonly applied methodology in this field (Hirschhorn and Daly, 2005; Marchini et al., 2005; Saxena et al., 2007). Generally, GWAS uses linkage disequilibrium (LD) patterns as a foundation for SNP selection and data interpretation. When real data are used to test novel GWAS designs, it is impossible to verify their performance because there is no ground-truth knowledge of which SNPs are actual disease markers. Simulation of case-control populations with realistic patterns of LD and allele frequencies for SNP markers has great potential both for the assessment and improvement of GWAS designs, because simulated data (for which ground-truth is known) can provide clear answers to users about whether contemplated designs are able to detect causal or correlated SNPs with acceptable error rates and cost. In real data, complex traits are usually produced by multiple factors, including gene-gene interactions and gene-environment interactions (e.g., in the case of essential hypertension) (Kardia, 2000; Moore and Williams, 2002). Therefore, to support the design and validation of powerful GWAS methods for detecting multiple effects, simulation of various genetic disease models is needed, especially epistatic SNP interactions involving multiple susceptibility markers, each with rather small effect.

Currently, a variety of software packages exist for performing population genetic data simulations. These packages have each been designed with different modeling emphases, and thus have distinct applicable goals for users in the study of population genetics. Each of the existing simulators covers just a subset of evolutionary and demographic scenarios. Computational complexity, which is also an important performance dimension, varies for the different simulators and also depends on the chosen parameter settings. In this article, we make an overview of population genetic data simulation and introduce some currently popular simulators. We also describe their specific applications and compare their computational complexities. Finally, we discuss some challenging problems and future work in the simulation field.

2. Simulation Methods

Three main categories of genetic data simulation algorithms are currently available: backward-time, forward-time, and resampling approaches. The backward-time approach, also known as coalescent simulation (Kingman 1982), starts from the observed sample in the present generation and works backward— that is, starting from a population of individuals, this approach first traces all alleles to a single ancestor, dubbed the most recent common ancestor (MRCA), and then works forward up to the current generation, introducing mutations or other genetic information into the generated genealogy. The forward-time approach is designed to start from an initial population and track its evolution under various genetic models, over multiple generations, with samples usually drawn from either the final or one of the last several generations. The resampling approach works from existing genomic data sets such as the HapMap data (http://www.hapmap.org/). A simple version of this approach generates samples by bootstrap resampling from the existing data. In the following subsections, we demonstrate the principles for each of these three simulation categories, discussing the primary features of each of these simulator types, as well as their differences.

2.1. Coalescent approach

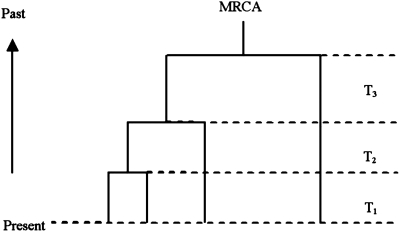
The coalescent theory was originally developed in the 1980s (Kingman, 2000) and was then extended by many researchers to allow recombination, selection, and other complex evolutionary models. Coalescent simulation in population genetics can be generally divided into two processes. The first is the coalescent process, describing the ancestral history of a sample of individuals originating from the MRCA. Figure 1 shows Kingman's n-coalescent process, where four individuals in the present day are coalesced to the MRCA in the past under three coalescent events, and where the expected time interval is

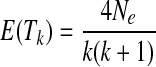graphic file with name M1.gif (1)

FIG. 1.

FIG. 1.

Open in a new tab

Kingman's n-coalescent process.

Here Ne is the effective population size, k = (1, 2, 3), and Tk is the time interval between the (k-1)st and kth coalescent events. The second process is the permutation process, which describes when and how alleles mutate over time across the genealogy. After these two processes are run, each sample is output as a sequence, with each allele represented by the ancestral state or the derived state.

The coalescent process is usually implemented based on the Wright-Fisher (W-F) model (named after Sewell Wright and R.F. Fisher). The W-F model is simply described as follows. Assume that we have a population of N diploid individuals and that initially there are i copies of allele a and (2N – i) copies of allele A at a particular locus. Thus, the probability of getting j copies of allele a in the next generation by randomly sampling from the current population is given by Equation (2) below. Using this equation, we can calculate distributions of allele frequencies in successive generations.

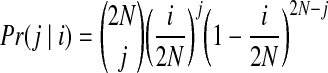graphic file with name M2.gif (2)

In the backwards (coalescence) process beginning from the current generation T, supposing that the sequence of population sizes is NT, NT-1, NT-2, NT-3,…, the (Markovian) transition probability from generation t to t – 1 is as follows (Slatkin, 2001):

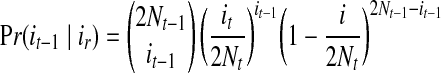graphic file with name M3.gif (3)

where it denotes the copies of allele a at generation t.

Since the coalescent process traces individuals to their MRCA, it is designed to simulate the trajectory (path) H = {iT, iT-1, iT-2, iT-3, … , i2, i1, i0}, where iT = i, … , i1 = 1, and i0 = 0 (Slatkin, 2001). This trajectory reflects that the simulation starts from the current generation and goes backward in time until the generation where allele a is lost. At this point, the individuals in the current generation have been coalesced to a single ancestor (i.e., MRCA), exclusively composed of alleles A. The probability of the sample trajectory H is given by:

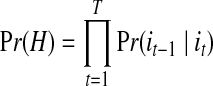graphic file with name M4.gif (4)

In the coalescent process, recombination can be flexibly simulated and it is usually implemented under a finite-site model (Hudson, 2002), in which the number of sites (markers) between which recombination can occur is finite. Recombination events can split chromosomes being simulated into a number of segments. Each segment will be modeled by a genealogy tree (i.e., ancestral history) through the coalescent process. Consider a population of n chromosomes, with population recombination rate 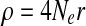Inline graphic, where r is the recombination rate between the ends of the chromosome. Let R denote the number of recombination events in the history of the population. The expectation of R can be expressed as follows (Hudson and Kaplan, 1985):

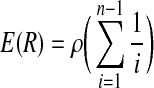graphic file with name M6.gif (5)

In the permutation process, mutations are usually simulated according to a Poisson process. Each mutation is assumed to occur uniformly and independently on the genealogy tree. Assume the population mutation parameter is θ = 4Neμ, where μ is the mutation rate for the chromosome being simulated. The expected number of mutations on the ith branch of the genealogy tree is expressed as (Hudson and Kaplan, 1985):

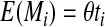graphic file with name M7.gif (6)

where ti is the length of the ith branch.

Theoretically, this simulation scheme gives an excellent framework for population genetics studies in terms of sampling properties and sample statistics. Moreover, this approach is computationally efficient since it only traces the history of the observed sample backward in time. Thus, the coalescent approach is very widely used, with a number of powerful simulators developed under this framework.

In order to provide a clear overview of the current development situation of coalescent methods, we list a number of simulators in Table 1. Each is able to simulate various evolutionary or demographic scenarios at a large sequence level. To get a complementary perspective, interested readers should read Carvajal-Rodriguez (2008). One early simulator, ms (Hudson, 2002), is a Monte Carlo program generating samples under a variety of neutral models. It allows recombination, gene conversion, migration, and various demographic histories. This program also provides a very flexible interface for users to efficiently generate many independent replicant samples and trees under different parameter settings. However, it simulates only infinite-site mutation models and does not manage hotspot events such as recombination and gene conversion hotspots (i.e., small genome regions where recombination or gene conversion rates are much higher than those of the surrounding regions). Modified versions of ms have been developed: msHot (Hellenthal and Stephens, 2007) and Mlcoalsim (Ramos-Onsins and Mitchell-Olds, 2007). msHot allows multiple recombination and gene conversion hotspots in the simulated genome regions, while Mlcoalsim allows selection events and analysis of multi-locus data in linked and independent regions. These three simulators are very suitable for investigating statistical properties of simulated samples, evaluating the performance of statistical tests, assisting in interpreting polymorphism data, and studying the molecular evolution process.

Table 1.

Coalescent Simulators for Genomic Data Under Different Evolutionary and Demographic Scenarios

Simulator Vrec Sel Vmu GConv Mig HS Vdm Phen Reference
ms No No No Yes Yes No Yes No (Hudson, 2002)
SNPsim Yes No Yes No No Yes Yes No (Posada and Wiuf, 2003)
SIMCOAL2 Yes No Yes No Yes No Yes No (Laval and Excoffier, 2004)
Coasim Yes No Yes Yes Yes Yes Yes Yes (Mailund et al., 2005)
Cosi Yes No Yes Yes Yes Yes Yes No (Schaffner et al., 2005)
GeneArtisan Yes Yes No No No Yes No Yes (Wang and Rannale, 2005)
FastCoal Yes No No No Yes Yes Yes No (Marjoram and Wall, 2006)
Recodon Yes Yes No No Yes No No No (Arenas and Posada, 2007)
msHot Yes No No Yes Yes Yes Yes No (Hellenthal and Stephens, 2007)
GENOME Yes No No No Yes Yes No No (Liang et al., 2007)
Mlcoalsim Yes Yes Yes No Yes Yes Yes No (Ramos-Onsins and Mitchell-Olds, 2007)
MaCS Yes No No Yes Yes Yes Yes Yes (Chen et al., 2009)
Open in a new tab

Note that all of the above listed simulators allow for recombination. “Yes” or “No” indicates whether a simulator incorporates a given modeling capability. Vrec, variable recombination rates; Sel, selection; Vmu, various mutation models; GConv, gene conversion; Mig, migration; HS, recombination, mutation, or gene conversion hotspots; Vdm, various demographic models; Phen, generates phenotypes (i.e., quantitative or binary [case-control] traits).

From Table 1, we can see that almost all of the simulators handle variable recombination rates, but few handle selection pressures and few produce samples with phenotypes; none of them can deal with all the listed scenarios of interest. Generally, different simulators emphasize different scenarios of evolution or demography and thus may have distinct applications. For instance, GeneArtisan (Wang and Rannale, 2005) pays more attention to the evolution of the disease-mutation frequency by assigning selection pressures on disease alleles, and produces case-control samples under penetrance functions so that these samples can be used to study the expected performance of disease-association mapping strategies; on the other hand, SIMCOAL2 (Laval and Excoffier, 2004), an extended version of SimCoal (Excoffier et al. 2000), is able to manage arbitrary patterns of recombination and migration and handle multiple coalescent events in each generation, and its simulated genomic diversity of samples can be used to estimate demographic parameters, migration, or recombination rates. However, even simulators which do not implement many evolutionary or demographic scenarios may have significant utility. For example, Recodon (Arenas and Posada, 2007) is a (currently) unique program that can simulate codon sequences under the interactions of recombination, migration, and demography, even though it only handles certain scenarios. In addition, due to the required large sequence simulations in genetic analysis, computational efficiency is another challenging aspect. An example here is GENOME (Liang et al., 2007), which is well known for its efficiency in simulating large-scale sequences under various scenarios.

In order to assess computational complexity of coalescent methods, we performed an experimental comparison of running times for four classic simulators (Table 2). All experiments were run using modest computational resources, available to all researchers. Specifically, our platform was Linux OS, 2.16-GHz CPU, and 1.99-GB RAM. We used the publicly available codes for each of the methods. The setting for these experiments was as follows. Each simulation was structured as two subpopulations, each with effective population size of 10,000 diploid individuals; both mutation and recombination rates were set to 10−8 per site per generation, and the migration rate was set to 2.5 × 10−4 per generation. The resulting samples were equally drawn from the two subpopulations. This simulation scenario is the default setting for most of the coalescent methods' software. From Table 2, we can see that GENOME is obviously faster than other simulators under each scenario; there is no obvious difference between ms and msHot; MaCS (Chen et al., 2009) is fast, especially when the population size and genome size are not very large. These results should not be strongly platform-dependent since the machine memory is sufficient for the four algorithms to simulate the scenarios that we considered. However, as indicated by the big-Oh memory requirements given in Table 3, if simulating much larger scale scenarios, ms, msHot, and GENOME are likely to perform worse than MaCS on some platforms due to memory issues. Here, as given in the table, n is the population size, l is the genome length, and m is the number of fragments for the genome.

Table 2.

Comparison of Execution Times for Four Coalescent Simulators

 
 Time (minute)
Simulator (1000, 10) (1000, 50) (1000, 100) (1600, 10) (1600, 50) (1600, 100)
ms 15.80 22.55 30.55 16.10 26.76 36.22
msHot 15.97 22.02 30.70 17.08 23.02 31.35
GENOME 1.62 8.03 15.85 1.85 8.50 17.33
MaCS 2.52 13.03 26.80 4.22 24.05 49.85
Open in a new tab

(K, L) represents a simulation of K sequences of length L Mb. These sequences are equally drawn from the two subpopulations.

Table 3.

Comparison of big-Oh Complexities Between Four Coalescent Simulators

Simulator ms msHot GENOME MaCS
Big-Oh time complexity O(nl + w1n + w2l) O(nl + w1n + w2l) O(f (n)l) O(nl)
Big-Oh memory complexity O(nl) O(nl) O(nm + l/m) O(l)
Open in a new tab

From inspection of the simulation algorithms, the run-time can be affected by multiple factors, including population size (n), genome length (l), evolutionary scenarios, demographic models, and other parameters. For a general comparison of the efficiency of the four methods, we give big-Oh computational complexities for the methods in Table 3, where for ms and msHot w1 and w2 are the weighting parameters (greater than one) that mainly incorporate the effects of recombination and mutation, and where for GENOME f is a function used to scale the population size. This function is not given explicitly in the GENOME paper, but it clearly underlies the algorithm's complexity, since under GENOME multiple (more than two) samples can coalesce to a common ancestor simultaneously, whereas in standard coalescent methods only two samples can coalesce to a common ancestor at one time. Comparing Tables 2 and 3, we find that the big-Oh computational complexities are roughly consistent with the simulation run-time results.

Other simulators such as SNPsim (Posada and Wiuf, 2003), SelSim (Spencer and Coop, 2004), GeneArtisan (Wang and Rannale, 2005), and Cosi (Schaffner et al., 2005) can also simulate sequences within acceptable time running on our platform, but likely have platform-sensitive performance. For example, SNPsim and SelSim use about 45 and 446 seconds, respectively, to finish a simulation of 500 sequences of length 20 kb on our platform, but SNPsim is likely to be limited by its memory usage when simulating relatively large-scale sequences, and SelSim is limited to a sample size of 500 and sequence length of 100 kb; GeneArtisan uses about 23 minutes on our platform to simulate 500 individuals (250 cases and 250 controls) of length 200 kb, but becomes very slow when simulating lengths greater than 2 Mb; and Cosi needs about 16 minutes to simulate a population of size 1000 and length 3 Mb under mutation and recombination rates of 10−8 per site per generation, but it crashes on our platform when simulating more than 1000 sequences of length 15 Mb or greater.

Coalescent simulators have advanced rapidly and have been extended to model more and more realistic scenarios of evolution and demography. Moreover, most of them are extremely efficient in simulating large DNA regions under complex scenarios. Consequently, coalescent simulation is widely used by researchers to investigate sampling properties and evaluate statistical tests and other genetic study strategies. However, coalescent-based simulators only focus on modeling the genealogy of the observed sample, ignoring other members of the population. Thus, they are not suitable for researchers who want to track complete ancestral information. Furthermore, some selection scenarios such as multi-locus selection and purifying selection models are difficult to simulate under the coalescent framework. For example, SelSim does not incorporate multi-locus selection and GeneArtisan is not good at controlling the frequency of disease alleles under purifying selection when the age of the disease allele is large. Finally, coalescent simulators usually focus on simulating haploid sequences, so diploid-specific effects such as complex selection scenarios and complex disease models cannot be incorporated.

2.2. Forward-time approach

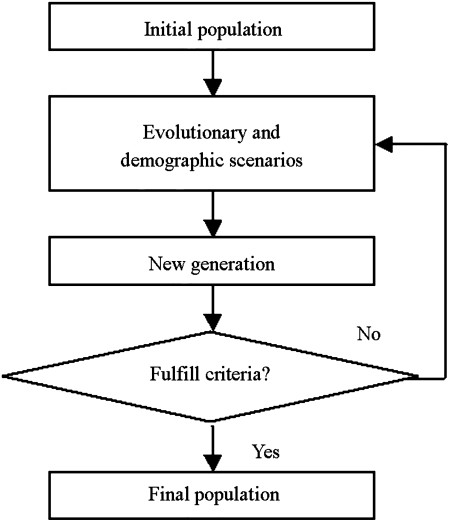
Unlike coalescent simulators, the forward-time approach usually starts from an initial, ancestral population and then follows its evolution over a number of generations under various evolutionary and demographic scenarios. The general architecture of forward simulation is given in Figure 2. The final population is achieved when the stopping criterion (e.g., a specified number of generations) is fulfilled. Under this simulation strategy, entire ancestral information can be tracked and population properties can be observed at any generation. Unrelated individual samples or family-based samples can be drawn partly or wholly from either the final or last several generations. Theoretically, this approach is flexible in being able to simulate any evolutionary and demographic scenario, as well as complex disease models.

FIG. 2.

FIG. 2.

Open in a new tab

The general architecture of forward-time simulation.

Next we discuss the implementation of some of the evolutionary scenarios and their effects on allele frequency and allele correlation under the forward approach. Let us consider a population of diploid individuals of size Nt at generation t, and focus on a locus with major allele A and minor allele a. The relative fitnesses (selection pressures) of the three genotypes AA, Aa (we assume there is no difference between Aa and aA), and aa are 1 + s1, 1 + s2, and 1, respectively, where s1 and s2 can take any values greater than − 1. Assuming the minor allele frequency (MAF) of the locus is pt at generation t and that the population follows the Hardy-Weinberg principle (HWP), the frequencies of genotypes AA, Aa, and aa are (1- pt)(1- pt), 2pt(1- pt), and pt pt, respectively. The frequency of allele a at the next generation t + 1 can then be estimated by

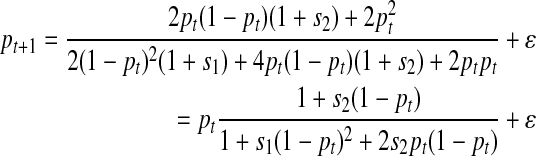graphic file with name M8.gif (7)

This equation is an extension of that proposed in Slatkin (2001). The variable ɛ is a deviation value, which is directly related to the population size Nt+1. If Nt+1 → 0, then ɛ → 0. In this equation, we have only taken selection into account. If mutation events randomly occur in the locus at generation t + 1 and the mutation rate is μ, then the minor allele frequency can be expressed as below in Equation (8). Here, the mutation events are based on a two-allele mutation model, in which both forward mutation and backward mutation are allowed at the same mutation rate.

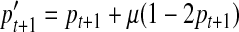graphic file with name M9.gif (8)

Regarding allele correlation, the forward approach usually obtains LD patterns through mating and recombination over generations, and uses mean LD over genome distance to characterize LD features:

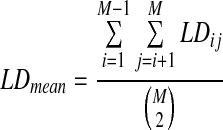graphic file with name M10.gif (9)

where M is the genome distance (i.e., the number of markers) and LDij denotes the LD coefficient between marker i and marker j. The mean LD usually decreases as distance increases and generations proceed, since the correlation between long-distant markers is weakened by recombination events.

Under the forward framework, recombination occurs within a pair of parental individuals in the current generation to produce children for the next generation. The recombination probability between two adjacent markers can be designed to be uniform or non-uniform over the chromosome, and the probabilities between any two markers are generally calculated by Haldane's (1919) or Kosambi's (1994) mapping functions. The total number of recombination events within a pair of chromosomes usually follows a Poisson distribution, and its expectation value is

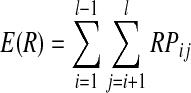graphic file with name M11.gif (10)

where l is the length of the chromosome, and RPij is the recombination probability between marker i and marker j.

In order to provide an overview of the development situation of forward simulators, we list a number of standard ones proposed within the latest several years in Table 4. Compared with coalescent simulators, the maturation of forward-time ones is relatively recent, with most of these simulators developed around 2008. From Table 4, we can see that most of the listed simulators can implement heterogeneous recombination, selection, and migration models, but few of them allow gene conversion. The most classic forward simulator, simuPOP (Peng and Kimmel, 2005), is extremely flexible in simulating various chromosome types such as autosome, chromosome X and Y, and arbitrary mating schemes such as non-random mating (Peng and Amos, 2008). simuPOP was extended by the same authors in 2007 to develop a new framework, simuComplexDisease.py (Peng et al., 2007), which focuses on controlling the disease allele frequencies and simulating large multi-generation populations with complex diseases. Hence, simuPOP can generate various types of samples such as case-control, sibpair, pedigree samples, and others. These samples can be used to design various kinds of genetic disease studies. However, when modeling genetic diseases, simuPOP only handles one or several diallelic disease susceptibility loci (DSL) under selection, and cannot handle linked DSL. Addressing this problem, Hoggart et al. et al. (2007) developed a new algorithm, FREGENE, to manage the effects of interactions among multiple sites under selection. However, FREGENE cannot control the frequency of a selected variant in the final generation. Nevertheless, another attractive feature of FREGENE is its reduced computational complexity, based on its use of rescaling techniques. GenomePop (Carvajal-Rodriguez, 2008) also adopts the same techniques for improving simulation efficiency. For example, if a scaling factor of 10 is used, the population size and the number of generations are divided by 10, and the mutation rate is multiplied by the same factor.

Table 4.

Forward Simulators for Genomic Data Under Different Evolutionary and Demographic Scenarios

Simulator Vrec Sel Vmu Gconv Mig HS Vdm DisM GD EF Phen Reference
simuPOP Yes Yes Yes No Yes No Yes Yes Yes No Yes (Peng and Kimmel, 2005)
genomeSIM Yes No No No No No No Yes No No Yes (Dudek et al., 2006)
Nemo Yes Yes Yes No Yes No Yes No No Yes Yes (Guillaume and Rougemont, 2006)
FREGENE Yes Yes No Yes Yes Yes Yes Yes No No Yes (Hoggart et al., 2007)
GenomePop Yes Yes Yes No Yes Yes Yes No Yes No No (Carvajal-Rodriguez, 2008)
genomeSIMLA Yes No No No Yes Yes No Yes Yes Yes Yes (Edward et al., 2008)
SFS_CODE No Yes Yes Yes Yes Yes Yes No No No No (Hernandez, 2008)
ForSim No Yes No No Yes No Yes Yes Yes Yes Yes (Lambert et al., 2008)
QuantiNEMO Yes Yes No No Yes No Yes Yes Yes Yes Yes (Neuenschwander et al., 2008)
ForwSim Yes Yes No No No No No No Yes No No (Padhukasahasram et al., 2008)
Open in a new tab

Note that all the above listed simulators allow for recombination. “Yes” or “No” indicates whether the simulator incorporates a given modeling capability. Vrec, variable recombination rates; Sel, selection; Vmu, various mutation models; GConv, gene conversion; Mig, migration; HS, recombination, mutation, or gene conversion hotspots; Vdm, various demographic models; DisM, various disease models; GD, genetic drift; EF, environmental factors; Phen, generates phenotypes (i.e., quantitative or binary [case-control] traits).

In reality, the development of the human genome is an extremely complicated process, not only involving complex genetic factors but also environmental effects. Several simulators have sought to model these effects. For example, Nemo (Guillaume and Rougemont, 2006), QuantiNEMO (Neuenschwander et al., 2008), GenomeSIMLA (Edward et al., 2008), and ForSim (Lambert et al., 2008) incorporate joint effects of genetic and environmental factors into the development of individual phenotypes. Particularly, GenomeSIMLA is able to simulate realistic patterns of LD in human populations. This is a very important feature for developing powerful GWAS on complex diseases since LD is a universal feature among SNP markers across the genome. Apart from SNPs, some other forms of mutations such as amplifications and deletions are also frequent genomic events. Recently, a software package named SFS_CODE (Hernandez, 2008) was proposed to incorporate various kinds of mutations. It provides a flexible interface for managing various mutation models and forms such as insertions and deletions. Thus, the simulated samples can be used to investigate chromosomal instability resulting from various genetic polymorphisms, including copy number changes and chromosome rearrangement.

As far as computational complexity is concerned, we analyzed several forward simulators that are easy to implement for simulating different population sizes and genome lengths. A comparison between three simulators is shown in Table 5. Again, we used publicly available source code for all three methods. We set both mutation and recombination rates to 10−4 per site per generation, and the migration rate to 2.5 × 10−4 per generation. For Nemo and QuantiNEMO we set the number of generations to 200, while for GenomePop we set the number to 50,000 since it employs scaling techniques to reduce the number of required generations. This is a modest benchmarking setting, and under this setting there are no memory problems when the simulators run on our platform. From Table 5, GenomePop is obviously faster than the other two simulators, and there are no obvious differences between Nemo and QuantiNEMO. Considering other forward simulators, genomeSIMLA (Edward et al., 2008) takes about 6 hours to finish the simulation of 100,000 chromosomes and 500k SNP markers in simulation of desired LD patterns; and SFS_CODE takes about 4 minutes on our platform to finish simulation of 1000 diploid individuals of sequence length 1 Mb over 10,000 generations.

Table 5.

Comparison of Execution Times for Three Forward Simulators

 
 Time (minute)
Simulator (1000, 10) (1000, 20) (1000, 30) (1600, 10) (1600, 20) (1600, 30)
Nemo 3.35 6.87 13.20 6.53 10.45 18.20
QuantiNEMO 3.62 7.27 10.90 5.78 11.57 22.80
GenomePop 2.60 2.60 2.62 2.50 2.67 2.68
Open in a new tab

(K, L) represents a simulation of K sequences of length L kb, equally drawn from two subpopulations.

From inspection of the simulation algorithms, the big-Oh time complexities for Nemo, QuantiNEMO, and GenomePop appear to be O(nlg), O(nlg), and O(s(nlg)), respectively, where n is population size, l is genome length, g is the number of generations, and s is a scaling function to save computation time. The execution times in Table 5 are consistent with this analysis. For Nemo and QuantiNEMO, run-time grows ∼linearly with n and l, and for GenomePop run-time is weakly affected by n and l due to its scaling option.

Inevitably, some bias might be introduced in the run-time comparisons in Table 5. For one thing, since these algorithms simulate different evolutionary or demographic scenarios, it is difficult to make parameter settings for each of the methods that allow a truly fair comparison. Moreover, since forward simulations usually track whole ancestral information, many of the methods may have performance that is platform-dependent, i.e., they may become memory-intensive when simulating large-scale populations. In particular, the big-Oh memory complexities for Nemo, QuantiNEMO, and GenomePop are estimated as O(nlg), O(nlg), and O(nls(g)), respectively.

Compared with coalescent simulators, most forward simulators are computationally heavier and the practically feasible simulated sequence lengths are shorter. This is due to the fact that forward simulations track complete ancestral information while coalescent simulations preserve only partial information. Thus, simulating large-scale sequences such as 10 Mb tends to make forward simulators crash due to memory usage. However, when one needs to fully investigate the evolution of the whole population, forward simulators should be preferred. Moreover, forward simulators in principle are able to handle extremely flexible scenarios such as various selection schemes under multiple sites and evolution of complex diseases. This is hard to achieve through coalescent simulations. However, there are still many challenging problems for the forward-time framework. First, how to create an initial population with moderate size and suitable phasing state is a difficult question. Second, the control of disease allele frequency is not an easy task, especially when correlations between multiple disease susceptibility loci (DSL) need to be considered. Finally, when tracking and preserving whole ancestral information, computation time and memory usage are crucial issues, especially when the required number of generations is large. Some existing methods have well considered these problems; for example, simuPOP (Peng and Kimmel, 2005) uses a burn-in process to control the properties of the initial population and a backward approach to simulate trajectories of allele frequencies at each DSL for the control of disease allele frequencies, while FREGENE (Hoggart et al., 2007) and GenomePop (Carvajal-Rodriguez, 2008) use rescaling techniques to improve computational efficiency. Still, some more sophisticated simulation frameworks that deal with all of these problems can be expected in the future.

2.3. Resampling approach

Another genome simulation strategy is resampling, which is usually based on existing data sets such as HapMap data. Unlike coalescent and forward approaches, which need to manage complex scenarios of evolution and demography, resampling usually does not require such modeling; instead, it directly generates samples by random selection (e.g., bootstrapping) from existing data sets. The sample size is theoretically unlimited, just depending on the user's specification and memory usage, while the length of the simulated genome is usually limited to that of the existing genome.

Under this approach, the simulated data usually follows the allele frequency and linkage disequilibrium patterns in the observed chromosome population. However, some deviations between the simulated data and the observed data with respect to allele frequency and LD will still exist. The amount of deviation clearly greatly depends on the simulated population size (n). Assuming that in the observed population the frequency of allele a at one locus is p, a one-standard deviation interval around the expected frequency (p′) of allele a in the simulated population is

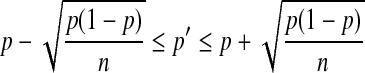graphic file with name M12.gif (11)

Here, we assume that the number of individuals with allele a follows a binomial distribution a ∼ B (n, p). Similarly, for two SNP markers with minor alleles a and b respectively, a one-standard deviation interval around the expected frequency (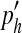Inline graphic) of haplotype 'ab' in the simulated population is

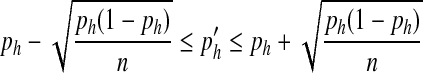graphic file with name M14.gif (12)

where ph is the haplotype frequency of ‘ab’ in the observed population. Subsequently, the LD (measured by r2) between the two SNPs in the simulated population can be expressed as

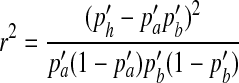graphic file with name M15.gif (13)

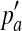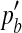where Inline graphic and Inline graphic are the frequencies of allele a and b in the simulated population.

Currently, some resampling algorithms have been developed to simulate case-control or affected child trio datasets, which can be used for power analyses and investigations of competing genotype-phenotype association methods. For example, HAP-SAMPLE (Wright et al., 2007) is a web-based tool that simulates SNP data with realistic patterns of LD and allele frequencies for disease association studies by resampling chromosome-length haplotypes from three populations of Phase I/II HapMap data. HAP-SAMPLE implements crossovers based on the pool formed by the sampled individuals and permits considerable flexibility in disease models, potentially involving a number of interacting loci. However, it cannot simultaneously embed multiple disease models into the generated genome data, and its simulated length of sequences is limited to a maximum of 125 k SNP markers. Another example is a simulation program introduced by Miller et al. (2009) and Chen et al. (2009), where the program can simulate case-control data of any sample size but with the length of sequences limited to 317 K. This program can also handle flexible disease models such as various epistatic SNP interactions. One advantage of this program over HAP-SAMPLE is that it is able to simultaneously manage multiple disease SNP-interactions, where each interaction is independently affecting individual phenotypes.

Regarding computational complexity, resampling is usually faster than coalescent and forward approaches. This is mainly due to the fact that resampling does not require modelling a complex evolutionary process, which is often computationally heavy. For example, HAP-SAMPLE takes less than 5 minutes to finish the simulation of 1,000 cases and 1,000 controls of length 50-k SNP markers on our platform, and needs less than 5 minutes to finish the simulation of 1,500 trios of length 50-k SNP markers.

Although there are few resampling software packages that have been disseminated to the research community, the use of such approaches has some clear advantages. On the one hand, this approach can preserve LD structure and allele frequencies at actual SNP markers, reflecting the real population. On the other hand, the memory and CPU usage are light compared to both coalescent and forward simulations. Thus, if one focuses on study design and analysis on real genome data, resampling should be preferred. However, unlike coalescent and forward simulation, resampling is not good at generating genomic diversity; as a result, the applicability of this approach is not as wide as the other two simulator types. For example, populations produced by resampling are not suitable for observing the evolutionary process or for estimating recombination or mutation parameters.

3. Conclusion

Simulation is a powerful tool for researchers involved in evolutionary and statistical biology. Numerous programs belonging to the three kinds of approaches (coalescent, forward-time, and resampling) have been proposed for the simulation of genomic data. These programs support exploration of evolutionary processes and evaluation of statistical analysis methods. In general, the three approaches emphasize different aspects of human genomic data. Coalescent simulations focus on construction of genealogies rooted in the MRCA under various scenarios of evolution and demography, ignoring individuals not linked with the MRCA. One appealing feature of coalescent simulators is their high computational efficiency in simulating extremely long sequences. However, they do not possess flexibility to handle complicated scenarios such as natural selection under multiple sites, and they are not suitable for simulating diploid individuals. Forward-time simulations manage the evolutionary process of the entire initial population and track its complete ancestral information across generations. This simulation framework is able to simulate almost any population genetic model (e.g., directional and balancing selections). However, speed and memory usage may become critical issues when simulating large-scale whole genome samples for a large number of generations. Resampling approaches generate a simulated population by sampling from existing genomic data sets. They can simulate case-control or affected child trio data under various disease models, including single-locus marginal effects and epistatic SNP interactions. Theoretically, resampling approaches can preserve the LD patterns and allele frequencies found in the real population. Accordingly, this approach is very useful for validating genotype-phenotype association studies and for evaluating methods for epistatic interaction detection; however, it is not suitable for the study of evolutionary processes and demographical structures since resampling does not carry or generate much ancestral information.

Overall, the three simulation approaches have distinct strengths and weaknesses. In real applications, these methods complement each other. Thus, further development of all three approaches should make substantial contribution to genomic and evolutionary biology research. Meanwhile, designing more sophisticated frameworks by combining coalescent and forward-time techniques is a promising strategy to improve the efficiency and quality of simulations. Currently, some existing programs have attempted this. For example, the forward-time simulator, simuPOP (Peng and Kimmel, 2005; Peng et al., 2007) uses a backward approach to simulate trajectories of allele frequencies at each DSL, and ForwSim (Padhukasahasram et al., 2008) uses a backward approach to calculate the probability that a pair of lineages resulting from a recombination event will eventually find two different ancestors.

It appears that there are many future challenges for further advancing population genetic simulation. First, real population evolution is an extremely complicated process which itself is not fully understood; also, the development of genomic sequences involves both genetic pressures and complex environmental factors, which can only be approximated and which have not been accounted for in most simulations. Exploring various evolutionary models that include both genetic and epigenetic interactions will improve modeling accuracy. Second, it is also necessary and useful to simulate heterogeneous sequences containing neutral loci, SNP markers, intersections, and copy number amplifications and deletions. Such data will be of great help for researchers to further investigate chromosomal instability and genetic disease associations (Redon et al., 2006). Finally, improvement in computational efficiency and memory usage should be a focus of future work. Distributed computing platforms will be helpful in this effort.

Acknowledgments

We would like to thank Carl Langefeld of Wake Forest University for sharing his SNP simulation software with us. This work was supported in part by the U.S. National Institutes of Health (grants HL090567 and GM085665) and by the National Science Fund of China (grants 61070137; 60933009).

Disclosure Statement

No competing financial interests exist.

References

  1. Arenas M. Posada D. Recodon: coalescent simulation of coding DNA sequences with recombination, migration and demography. BMC Bioinform. 2007;8:458. doi: 10.1186/1471-2105-8-458. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Calafell F. Grigorenko E.L. Chikanian A.A., et al. Haplotype evolution and linkage disequilibrium: a simulation study. Hum. Hered. 2001;51:85–96. doi: 10.1159/000022963. [DOI] [PubMed] [Google Scholar]
  3. Carvajal-Rodriguez A. GENOMEPOP: a program to simulate genomes in populations. BMC Bioinform. 2008;9:223. doi: 10.1186/1471-2105-9-223. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Carvajal-Rodriguez A. Simulation of genomes: a review. Curr. Genomics. 2008;9:155–159. doi: 10.2174/138920208784340759. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Chen G.K. Marjoram P. Wall J.D. Fast and flexible simulation of DNA sequence data. Genome Res. 2009;19:136–142. doi: 10.1101/gr.083634.108. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Chen L. Yu G. Miller D., et al. A ground truth based comparative study on detecting epistatic SNPs. Proc. IEEE Int. Conf. Bioinform. Biomed. 2009 doi: 10.1109/BIBMW.2009.5332132. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Dudek S.M. Motsinger A.A. Velez D.R., et al. Data simulation software for whole-genome association and other studies in human genetics. Pac. Symp. Biocomput. 2006:499–510. [PubMed] [Google Scholar]
  8. Edward T.L. Bush W.S. Turner S.M., et al. Evolutionary Computation, Machine Learning and Data Mining in Bioinformatics. Springer; Berlin: 2008. Generating linkage disequilibrium patterns in data simulations using genomeSIMLA, 24–35. [Google Scholar]
  9. Excoffier L. Novembre J. Schneider S. SIMCOAL: a general coalescent program for the simulation of molecular data in interconnected populations with arbitrary demography. J. Hered. 2000;91:506–509. doi: 10.1093/jhered/91.6.506. [DOI] [PubMed] [Google Scholar]
  10. Guillaume F. Rougemont J. Nemo: an evolutionary and population genetics programming framework. Bioinformatics. 2006;22:2556–2557. doi: 10.1093/bioinformatics/btl415. [DOI] [PubMed] [Google Scholar]
  11. Hahn L.W. Ritchie M.D. Moore J.H. Multifactor dimensionality reduction software for detecting gene-gene and gene-environment interactions. Bioinformatics. 2003;19:376–382. doi: 10.1093/bioinformatics/btf869. [DOI] [PubMed] [Google Scholar]
  12. Hellenthal G. Stephens M. msHOT: modifying Hudson's ms simulator to incorporate crossover and gene conversion hotspots. Bioinformatics. 2007;23:520–521. doi: 10.1093/bioinformatics/btl622. [DOI] [PubMed] [Google Scholar]
  13. Hernandez R.D. A flexible forward simulator for populations subject to selection and demography. Bioinformatics. 2008;24:2786–2787. doi: 10.1093/bioinformatics/btn522. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Hirschhorn J.N. Daly M.J. Genome-wide association studies for common diseases and complex traits. Nat. Rev. Genet. 2005;6:95–108. doi: 10.1038/nrg1521. [DOI] [PubMed] [Google Scholar]
  15. Hoggart C.J. Chadeau-Hyam M. Clark T.G., et al. Sequence-level population simulations over large genomic regions. Genetics. 2007;177:1725–1731. doi: 10.1534/genetics.106.069088. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Hudson R.R. Generating samples under a Wright-Fisher neutral model of genetic variation. Bioinformatics. 2002;18:337–338. doi: 10.1093/bioinformatics/18.2.337. [DOI] [PubMed] [Google Scholar]
  17. Hudson R.R. Kaplan N.L. Statistical properties of the number of recombination events in the history of a sample of DNA sequences. Genetics. 1985;111:147–164. doi: 10.1093/genetics/111.1.147. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Kardia S.L. Context-dependent genetic effects in hypertension. Curr. Hypertens. Rep. 2000;2:32–38. doi: 10.1007/s11906-000-0055-6. [DOI] [PubMed] [Google Scholar]
  19. Kimmel G. Shamir R. GERBIL: genotype resolution and block identification using likelihood. Proc. Natl. Acad. Sci. USA. 2005;102:158–162. doi: 10.1073/pnas.0404730102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Kingman J.F. Origins of the coalescent: 1974–1982. Genetics. 2000;156:1461–1463. doi: 10.1093/genetics/156.4.1461. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Kingman J.F.C. The coalescent. Stochastic Process. Appl. 1982;13:235–248. [Google Scholar]
  22. Lambert B.W. Terwilliger J.D. Weiss K.M. ForSim: a tool for exploring the genetic architecture of complex traits with controlled truth. Bioinformatics. 2008;24:1821–1822. doi: 10.1093/bioinformatics/btn317. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Laval G. Excoffier L. SIMCOAL 2.0: a program to simulate genomic diversity over large recombining regions in a subdivided population with a complex history. Bioinformatics. 2004;20:2485–2487. doi: 10.1093/bioinformatics/bth264. [DOI] [PubMed] [Google Scholar]
  24. Liang L. Zollner S. Abecasis G.R. GENOME: a rapid coalescent-based whole genome simulator. Bioinformatics. 2007;23:1565–1567. doi: 10.1093/bioinformatics/btm138. [DOI] [PubMed] [Google Scholar]
  25. Mailund T. Schierup M.H. Pedersen C.N., et al. CoaSim: a flexible environment for simulating genetic data under coalescent models. BMC Bioinform. 2005;6:252. doi: 10.1186/1471-2105-6-252. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Marchini J. Donnelly P. Cardon L.R. Genome-wide strategies for detecting multiple loci that influence complex diseases. Nat. Genet. 2005;37:413–417. doi: 10.1038/ng1537. [DOI] [PubMed] [Google Scholar]
  27. Marjoram P. Wall J.D. Fast “coalescent” simulation. BMC Genet. 2006;7:16. doi: 10.1186/1471-2156-7-16. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Miller D.J. Zhang Y. Yu G., et al. An algorithm for learning maximum entropy probability models of disease risk that efficiently searches and sparingly encodes multilocus genomic interactions. Bioinformatics. 2009;25:2478–2485. doi: 10.1093/bioinformatics/btp435. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Moore J.H. Williams S.M. New strategies for identifying gene-gene interactions in hypertension. Ann. Med. 2002;34:88–95. doi: 10.1080/07853890252953473. [DOI] [PubMed] [Google Scholar]
  30. Neuenschwander S. Hospital F. Guillaume F., et al. quantiNemo: an individual-based program to simulate quantitative traits with explicit genetic architecture in a dynamic metapopulation. Bioinformatics. 2008;24:1552–1553. doi: 10.1093/bioinformatics/btn219. [DOI] [PubMed] [Google Scholar]
  31. Padhukasahasram B. Marjoram P. Wall J.D., et al. Exploring population genetic models with recombination using efficient forward-time simulations. Genetics. 2008;178:2417–2427. doi: 10.1534/genetics.107.085332. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Peng B. Amos C. Forward-time simulations of non-random mating populations using simuPOP. Bioinformatics. 2008;24:1408–1409. doi: 10.1093/bioinformatics/btn179. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Peng B. Amos C.I. Kimmel M. Forward-time simulations of human populations with complex diseases. PLoS Genet. 2007;3:e47. doi: 10.1371/journal.pgen.0030047. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Peng B. Kimmel M. simuPOP: a forward-time population genetics simulation environment. Bioinformatics. 2005;21:3686–3687. doi: 10.1093/bioinformatics/bti584. [DOI] [PubMed] [Google Scholar]
  35. Peng B. Kimmel M. Simulations provide support for the common disease–common variant hypothesis. Genetics. 2007;175:763–776. doi: 10.1534/genetics.106.058164. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Posada D. Wiuf C. Simulating haplotypes blocks in the human genome. Bioinformatics. 2003;19:289–290. doi: 10.1093/bioinformatics/19.2.289. [DOI] [PubMed] [Google Scholar]
  37. Ramos-Onsins S.E. Mitchell-Olds T. Mlcoalsim: multilocus coalescent simulations. Evol. Bioinform. Online. 2007;3:41–44. [PMC free article] [PubMed] [Google Scholar]
  38. Redon R. Ishikawa S. Fitch K.R., et al. Global variation in copy number in the human genome. Nature. 2006;444:444–454. doi: 10.1038/nature05329. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Saxena R. Voight B.F. Lyssenko V., et al. Genome-wide association analysis identifies loci for type 2 diabetes and triglyceride levels. Science. 2007;316:1331–1336. doi: 10.1126/science.1142358. [DOI] [PubMed] [Google Scholar]
  40. Schaffner S.F. Foo C. Gabriel S., et al. Calibrating a coalescent simulation of human genome sequence variation. Genome Res. 2005;15:1576–1583. doi: 10.1101/gr.3709305. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Slatkin M. Simulating genealogies of selected alleles in a population of variable size. Genet. Res. 2001;78:49–57. doi: 10.1017/s0016672301005183. [DOI] [PubMed] [Google Scholar]
  42. Spencer C.C. Coop G. SelSim: a program to simulate population genetic data with natural selection and recombination. Bioinformatics. 2004;20:3673–3675. doi: 10.1093/bioinformatics/bth417. [DOI] [PubMed] [Google Scholar]
  43. Wang Y. Rannale B. In silico analysis of disease-association mapping strategies using the coalescent process and incorporating ascertainment and selection. Am. J. Hum. Genet. 2005;76:1066–1073. doi: 10.1086/430472. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Wright F.A. Huang H. Guan X., et al. Simulating association studies: a data-based resampling method for candidate regions or whole genome scans. Bioinformatics. 2007;23:2581–2588. doi: 10.1093/bioinformatics/btm386. [DOI] [PubMed] [Google Scholar]
  45. Zhang K. Qin Z.S. Liu J.S., et al. Haplotype block partitioning and tap SNP selection using genotype data and their applications to association studies. Genome Res. 2004;14:908–916. doi: 10.1101/gr.1837404. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Journal of Computational Biology are provided here courtesy of Mary Ann Liebert, Inc.

RESOURCES