Automating the design of informative sequences of sensory stimuli

Abstract

Adaptive stimulus design methods can potentially improve the efficiency of sensory neurophysiology experiments significantly; however, designing optimal stimulus sequences in real time remains a serious technical challenge. Here we describe two approximate methods for generating informative stimulus sequences: the first approach provides a fast method for scoring the informativeness of a batch of specific potential stimulus sequences, while the second method attempts to compute an optimal stimulus distribution from which the experimenter may easily sample. We apply these methods to single-neuron spike train data recorded from the auditory midbrain of zebra finches, and demonstrate that the resulting stimulus sequences do in fact provide more information about neuronal tuning in a shorter amount of time than do more standard experimental designs.

1 Introduction

Adaptive stimulus optimization methods hold a great deal of promise for improving the efficiency of sensory neurophysiology experiments (Tzanakou et al. 1979; Mackay 1992; deCharms et al. 1998; Anderson and Micheli-Tzanakou 1998; Foldiak 2001; Machens 2002; Edin et al. 2004; Machens et al. 2005; O’Connor et al. 2005; Chen et al. 2005; Paninski 2005; Benda et al. 2007; Yamane et al. 2008). We previously developed methods for efficiently computing the stimulus that will provide the most information about a neuron’s tuning properties (Lewi et al. 2007, 2009). These methods were tested in a variety of simulated examples, and demonstrated the potential to speed convergence in our parameter estimates (and therefore reduce the total experimental time needed to characterize neural tuning) by an order of magnitude.

However, we face two major problems when applying these methods directly in real experimental settings. First, often stimuli need to be presented in “batches,” instead of one stimulus frame at a time. In auditory experiments, for example, we typically do not present a single 10 ms “frame” of an auditory stimulus; instead, we usually present longer stimuli (e.g., bird song, or other naturalistic sequences) with strong temporal correlations, since auditory neurons integrate information over longer timescales to detect acoustic features. Thus, we need a method to optimize temporally-coherent sequences of stimuli, instead of choosing the best stimulus on a frame-by-frame basis, since the latter approach will typically lead to choppy, temporally-incoherent, highly non-naturalistic stimuli.

Second, the methods described in Lewi et al. (2007, 2009) require the development of highly-optimized, real-time software; in particular, for the real-time adaptive stimulus design approach to be feasible, the stimulus generation and spike detection software necessarily need to be tightly integrated. This may be quite challenging, depending on the recording setup available in a given sensory neurophysiology lab. Thus, it would be very helpful to relax our goals somewhat: instead of computing the optimal stimulus one presentation frame at a time, we would like to develop related methods to compute a highly-informative “batch” of stimuli that can be presented over the next (possibly large) set of presentation frames. This greatly reduces the requirement for real-time integration of stimulus generation and spike detection, since the necessary processing can be done over large batches of presentation frames instead of single frames (which will typically require processing on a time scale of milliseconds).

In this paper we present methods for solving both of these problems and demonstrate their applicability to single-neuron spike train data recorded from the auditory midbrain of songbirds.

2 Overview and review

Our setting is as follows. We are recording from a neuron which responds to a vector input s_t presented at time t according to some conditional distribution p(r_t|θ, s_t), where r_t is the response at time t and θ denotes the vector of parameters that control the neuron’s response properties. As in Paninski et al. (2007), Lewi et al. (2009), we will focus our attention on a generalized linear model (GLM) for the neural responses:

$$r_t|\theta ,s_t~\text{Poiss}[f({\theta }^T{s}_t)\mathit{\text{dt}}],$$ (1)

with the rectifying function f(.) chosen to be convex and log-concave; as discussed in more detail in Paninski (2004), these constraints ensure that the loglikelihood in this model will be a concave function of the parameter θ. We will describe an example implementation of the GLM in much more detail in Section 3.1.1 below.

Given the t previously-observed input-response pairs (s_1:t, r_1:t), our knowledge about θ is summarized by the posterior distribution p(θ|s_1:t, r_1:t). Our main goal when choosing the next sequence of b inputs s_t+1:t+b is to reduce the entropy (uncertainty) of this conditional distribution as much as possible; more precisely, we want to choose s_t+1:t+b to optimize the conditional mutual information (Cover and Thomas 1991) between the parameter θ and the response sequence r_t+1:t+b given the input sequence s_t+1:t+b,

$$I\left(\theta ;r_{t+1:t+b}|\{s_{1:t+b},r_{1:t}\}\right)=H[p(\theta |s_{1:t},r_{1:t})]-H[p(\theta |s_{1:t+b},r_{1:t+b})],$$ (2)

where H[p] denotes the entropy of the distribution p. The conditional mutual information is the difference between our parameter uncertainty at time t, H[p(θ|s_1:t, r_1:t)], and our expected uncertainty at time t + b, H[p(θ|s_t+1:t+b, r_t+1:t+b)], and therefore this quantity measures the amount of information we expect an experiment to provide about θ.

As discussed at length in Lewi et al. (2009), it is quite difficult to compute and optimize this mutual information exactly. However, good approximations are available. In particular, we approximate the posterior distribution p(θ|s_1:t, r_1:t) as a Gaussian density with respect to the parameter θ,

$$p(\theta |s_{1:t},r_{1:t})\approx {𝒩}_{{\mu }_t,C_t}(\theta ),$$ (3)

where μ_t and C_t denote the posterior mean and covariance of θ given (s_1:t, r_1:t); intuitively, μ_t represents our “best guess” about θ given the data observed in the first t responses, and C_t summarizes our posterior uncertainty about θ. This Gaussian approximation turns out to be asymptotically precise in the large-sample limit t → ∞ (Paninski 2005), and is also fairly accurate even for finite t for the log-concave neural response models we consider here (Paninski et al. 2007; Lewi et al. 2009). Using this Gaussian approximation, we can simplify the posterior entropy:

$$I(\theta ;r_{t+1:t+b}|s_{1:t+b},r_{1:t})\approx H[p(\theta |s_{1:t},r_{1:t})]+\frac{1}{2}{E}_{\theta }{E}_{r_{t+1:t+b}|s_{1:t+b},r_{1:t},\theta }\text{log}\left|C_t^{-1}+{\displaystyle \sum _{i=1}^b}{J}_{\text{obs}}(r_{t+i},s_{t+i})\right|+\text{const}.,$$ (4)

where E_x f(x) denotes the expectation of f(x) under the distribution of the random variable x. Since the first term on the right hand side is constant with respect to the input sequence s_t+1:t+b, we will focus our attention on the second term. We have already discussed the posterior covariance C_t; J_obs(r_t+i, s_t+i) denotes the observed Fisher information matrix about θ in the response r_t+i, given the input s_t+i:

$$J_{\text{obs}}(r_{t+i},s_{t+i})=-\nabla {\nabla }_{\theta }\text{log}p(r_{t+i}|\theta ,s_{t+i}),$$ (5)

where ∇∇_θ denotes the Hessian matrix with respect to θ.

Now, with these preliminaries out of the way, we consider three different cases:

1. The single-stimulus case, b = 1;

2. The finite-sequence case, 1 < b < ∞;

3. The long-sequence limit, b → ∞.

Note that case 1, b = 1, which was considered in depth in Lewi et al. (2009), is essentially a special case of case 2. We will discuss case 2 in Section 3 and case 3 in Section 4 below. In neither case are we able to solve the information-maximization problem exactly with the full desired generality. Instead, for case 2, we develop a useful lower bound for the information in a sequence of stimuli which is easier to optimize than the original expression. This lower bound turns out to be closely related to the b = 1 case. We will see that optimizing this lower bound leads to significantly more efficient experiments. Similarly, we will show that we can simplify the problem by letting b → ∞. Unfortunately, even in this limiting case it appears that optimizing the information is in general still quite difficult. Therefore we focus our attention on a useful special case; again, we find that the resulting optimized experimental designs are more efficient. Before moving on to the details of these latter two cases, we briefly review our approach to case 1.

2.1 Case 1: the single-frame case, b = 1

The special structure of the GLM (Eq. (1)) allows us to compute the Gaussian information (Eq. (4)) fairly explictly. In particular, since the firing rate in the GLM at time t + 1 depends only on the one-dimensional projection ρ_t+1 = θ^T s_t+1 of the input onto the parameter vector θ, the Fisher information matrix J_obs(r_t+1, s_t+1) is guaranteed to have rank one. Thus, by applying the Woodbury matrix lemma to $C_t^{-1}+J_{\text{obs}}(r_{t+1},s_{t+1})$ we can derive an expression for the mutual information which depends on just two scalar variables, ${\mu }_{\rho }=s_{t+1}^T{\mu }_t\text{and}{\sigma }_{\rho }^2=s_{t+1}^T{C}_t{s}_{t+1}$:

$$I(\theta ;r_{t+1}|s_{1:t+1},r_{1:t})\approx \frac{1}{2}{E}_{\theta |{\mu }_t,C_t}{E}_{r_{t+1}|S_{t+1},\theta }\text{log}(1+D(r_{t+1},{\rho }_{t+1}){\sigma }_{\rho }^2)+\text{const}.$$ (6)

$$=\frac{1}{2}{E}_{{\rho }_{t+1}|{\mu }_{\rho },{\sigma }_{\rho }^2}{E}_{r_{t+1}|{\rho }_{t+1}}\text{log}(1+D(r_{t+1},{\rho }_{t+1}){\sigma }_{\rho }^2)+\text{const}.,$$ (7)

where ρ_t+1 is a linear projection of the Gaussian variable θ and is therefore itself Gaussian with mean μ_ρ and variance ${\sigma }_{\rho }^2$, and we have abbreviated the Fisher information along the projection ρ_t,

$$D(r_t,{\rho }_t)=-\frac{{\partial }^2\text{log}p(r_t|\rho )}{\partial {\rho }^2}{|}_{\rho ={\rho }_t}.$$ (8)

In the special case that f(.) = exp(.) (in the GLM literature, this is referred to as the “canonical” link function for Poisson responses, so we will refer to this as the “canonical Poisson” case), the Fisher information does not depend on the observed response r_t+1, and we can compute the above quantities directly to obtain

$$I(\theta ;r_{t+1}|s_{1:t+1},r_{1:t})=\frac{1}{2}{E}_{{\rho }_{t+1}|{\mu }_{\rho },{\sigma }_{\rho }^2}\text{log}(1+\text{exp}({\rho }_{t+1}){\sigma }_{\rho }^2)+\text{const}.,$$ (9)

which can be further reduced and computed analytically, via standard Gaussian formulae, when the approximation log(1 + x) ≈ x (for x small) is valid for $x=\text{exp}({\rho }_{t+1}){\sigma }_{\rho }^2$. Given this relatively simple formula for the stimulus informativeness, we can choose a good stimulus, present this stimulus to the neuron and record the response r_t, update our approximate mean μ_t and covariance C_t using the online maximum a posteriori methods described in Lewi et al. (2009), and then choose a new stimulus according to our now-updated objective function, in a closed loop. Again, see Lewi et al. (2009) for further details.

3 Case 2: constructing a tractable lower bound for the informativeness of stimulus sequences of finite length b

Now we turn to the question of computing the second term on the right-hand side of Eq. (4) for b > 1. We have not been able to develop efficient algorithms for computing this term directly. However, we can easily derive a tractable lower bound on this term: we use Jensen’s inequality applied to the concave log-determinant function (Cover and Thomas 1991) to move the summation over stimuli outside the determinant:

$$\text{log}\left|C_t^{-1}+{\displaystyle \sum _{i=1}^b}{J}_{\text{obs}}(r_{t+i},s_{t+i})\right|=\text{log}\left|C_t^{-1}+{\displaystyle \sum _{i=1}^b}D(r_{t+i},{\rho }_{t+i})s_{t+i}{s}_{t+i}^T\right|$$ (10)

$$=\text{log}\left|{\displaystyle \sum _{i=1}^b}\frac{1}{b}{C}_t^{-1}+\frac{b}{b}D(r_{t+i},{\rho }_{t+i})s_{t+i}{s}_{t+i}^T\right|$$ (11)

$$\ge {\displaystyle \sum _{i=1}^b}\frac{1}{b}\text{log}|C_t^{-1}+bD(r_{t+i},{\rho }_{t+i})s_{t+i}{s}_{t+i}^T|$$ (12)

$$={\displaystyle \sum _{i=1}^b}\frac{1}{b}\left(\text{log}|C_t^{-1}|+\text{log}(1+bD(r_{t+i},{\rho }_{t+i})s_{t+i}^T{C}_t{s}_{t+i})\right)$$ (13)

$$=\text{log}|C_t^{-1}|+\frac{1}{b}{\displaystyle \sum _{i=1}^b}\text{log}\left(1+bD(r_{t+i},{\rho }_{t+i})s_{t+i}^T{C}_t{s}_{t+i})\right)$$ (14)

$$=\text{log}|C_t^{-1}|+\frac{1}{b}{\displaystyle \sum _{i=1}^b}\text{log}(1+bD(r_{t+i},{\rho }_{t+i}){\sigma }_{\rho ,t+i}^2)),$$ (15)

where we have applied the Woodbury lemma and in the last line defined

$${\sigma }_{\rho ,t+i}^2=s_{t+i}^T{C}_t{s}_{t+i},$$ (16)

with the projected Fisher information D(r_t+i, ρ_t+i) defined as in the last section. When b = 1 this inequality is an equality and is exactly the same expression we discussed above (c.f. the term inside the expectation in Eq. (7); the $\text{log}|C_t^{-1}|$ term is cancelled when we subtract this conditional entropy from the prior entropy to form the mutual information). When b > 1 this expression may be plugged into the expectation in Eq. (4) to obtain a sum of terms which are essentially similar to the objective function in the b = 1 case. As a result, we may use the methods in Lewi et al. (2009) to efficiently compute the terms in the summation. As before, the key insight is that for the GLM under consideration here, each term in the resulting summation is simply a function of the two scalar variables $({\mu }_{\rho ,t+i},{\sigma }_{\rho ,t+i}^2)$, so to efficiently evaluate the bound we can simply precompute this function on some suitable range of $({\mu }_{\rho ,t+i},{\sigma }_{\rho ,t+i}^2)$; alternatively, in the canonical Poisson case, as discussed above, these formulas may be simplified even further and in some cases computed analytically.¹ Again, see Lewi et al. (2009) for full details.

We can use this result to optimize our experiments in a straightforward manner. Suppose we are given n stimulus sequences, each of length b, and we want to choose the best sequence from among these n examples. Using the above expression, we compute the lower bound evaluated for each of these sequences, and then we select the sequence which maximizes this lower bound,² present the sequence, and update our posterior parameters μ_t and C_t based on the observed responses, as in Lewi et al. (2009). See Fig. 1 for an illustration, and the following section for further details. This lower bound can also be applied in more elaborate receding-horizon settings (Kwon and Han 2005), where we update our chosen stimulus sequence every time step (instead of every b time steps), but we will stick to the simpler case (update every b steps) below for clarity.

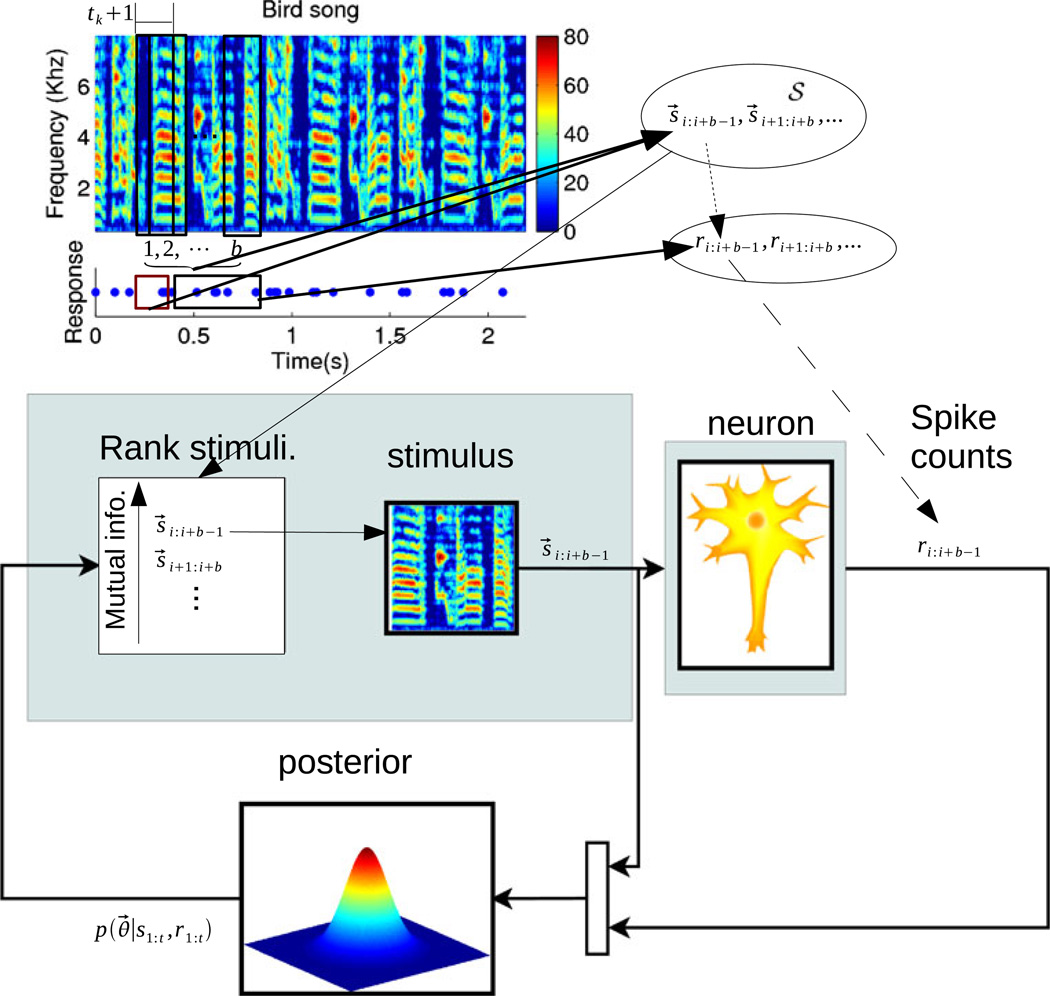
Fig. 1.

A schematic of the online experimental design approach. Top: an illustration of how stimulus sequences and the associated responses are obtained from the actual data. Each input, s⃗_t, consists of t_k + 1 columns of the spectrogram (with each column of width dt = 2.5 ms here) as indicated by the black boxes on the spectrogram (note the boxes are not drawn to scale, for improved visibility). Each input also consists of the recent spike history as indicated by the red box on the raster plot. On each iteration we pick a sequence of b consecutive inputs. Taken together these b inputs yield one possible stimulus sequence s⃗_i:i+b−1 in the set of possible input sequences, 𝒮. The responses to these stimuli, indicated by the black box in the raster plot, are the responses that we will observe when this stimulus sequence is chosen. Bottom: the iterative loop that describes our experiment. At each timestep we rank all remaining sequences in 𝒮 that have not been selected yet. The sequences are ranked according to the lower bound of the mutual information (plugging Eq. (15) into Eq. (4) using our current posterior p(θ|s_t:t, r_t:t). The sequence which optimizes this objective function is chosen and the neuron’s response to this sequence is used to update our Gaussian approximation of the posterior (Eq. (3)). Using our updated posterior we then re-rank the remaining stimuli in 𝒮, having removed the stimulus sequence we just presented, and continue the process

3.1 Application to zebra finch auditory data

One key question left unanswered by our previous work (Lewi et al. 2009) was how well our techniques will work with real data. We can use the methods presented above to begin to address this question. The idea is to take the set of stimulus-response pairs obtained during an actual experiment and check whether the infomax approach leads to a more informative ordering of the data. A more informative ordering of the data is one for which our parameter estimates converge faster (as a function of the number of stimulus sequences presented) to the final estimate of the model trained using all the data. Here we will not choose stimuli arbitrarily, from the space of all possible auditory stimuli, but rather we will restrict our attention to stimuli which were actually presented, i.e., to simple reorderings of the trials, because we want to use the actual neural response observed with each presented stimulus.

We begin by describing the physiological experiments and data collected. Experimental details have been previously described in Woolley and Casseday (2004, 2005). We played auditory stimuli to adult male zebra finches while recording the responses of neurons in the mesencephalicus lateralis pars dorsalis (MLd) using extracellular electrodes; for further details, see Woolley et al. (2006). MLd is a midbrain auditory nucleus which is the avian homolog of the mammalian inferior colliculus. The set of stimuli consisted of samples of the songs of 20 different adult zebra finches and 10 modulation-limited noise stimuli (ml-noise), which is described below. Each stimulus had a duration of approximately 2 s and was repeated 10 different times to the bird in a random order. Before and after each stimulus was played there was a randomized period of silence of 1,200–1,600 ms. This period of silence allowed the neuron to return to its resting state before the next stimulus was played, thereby minimizing the effects of adaptation.

Examples of each stimulus type and an accompanying raster plot for one neuron are shown in Fig. 2. For comparison, ml-noise stimuli were also presented to the birds; this is a form of broadband noise which is designed to have the same power and maximum spectral and temporal modulations that occur in the songs of adult zebra finches (Hsu et al. 2004; Woolley et al. 2006) Thus, ml-noise can be used to contrast the responses to conspecific vocalizations compared to noise stimuli with a similar spectral range.

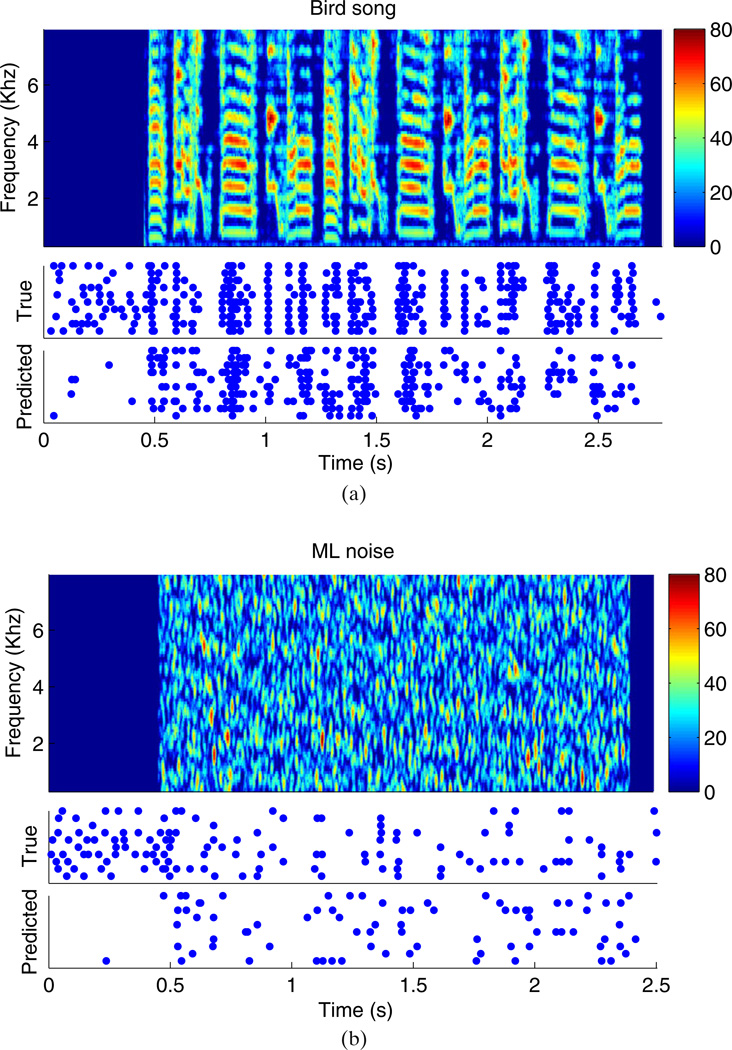
Fig. 2.

(a) The top plot shows the spectrogram of one of the bird songs used during the experiments (color scale is in units of sound intensity). The middle plot shows the raster plot of the recorded neuron’s spiking in response to this stimulus, over ten identical repetitions. The bottom plot shows the predicted raster plot computed using a GLM fitted to the training set. Each row of the raster plots shows the firing of the neuron on independent presentations of the input. (Note that these responses to repeated stimuli are useful for validating any model we fit to the observed data, but repeated responses are not necessary for the stimulus-design procedures developed here.) The training set did not include this song or the ml-noise stimulus shown in (b). (b) The same as panel (a), except the stimulus is ml-noise instead of birdsong. When fitting a GLM, the stimulus, x⃗_t, corresponds to one column of the spectrogram matrix; the “input” s_t corresponds to t_k + 1 adjacent columns, as illustrated in Fig. 1

3.1.1 Fitting the GLM to birdsong data

In this section we describe our efforts to estimate the receptive field of MLd neurons using GLM methods. We used the canonical Poisson model (f(.) = exp(.)) for simplicity; in this case, as discussed above, the expected Fisher information is exponential and independent of the response r_t. This property makes the computations required to optimize the design much more tractable, and the results in Paninski (2004), Lewi et al. (2009) indicate that the results should be fairly robust with respect to the choice of the rectifying nonlinearity f(.) here. Finally, we have found in Calabrese et al. (2010) that the canonical Poisson model provides good predictions of spike train responses in this system.

The canonical Poisson model assigns a probability to the number of spikes we expect to observe in some window of time, as a function of the stimulus, past responses, and background firing rate. The log-likelihood of the response at time t is

$$\begin{array}{cc}\hfill \text{log}p(r_t|s_t,\theta )& =-\text{log}{r}_t!+r_t{s}_t^T\theta -\text{exp}(s_t^T\theta )\mathit{\text{dt}}\hfill \\ \hfill s_t^T& =\{{\overrightarrow{x}}_{t-t_k}^T,\dots ,{\overrightarrow{x}}_t^T,r_{t-t_a},\dots ,r_{t-1},1\}.\hfill \end{array}$$ (17)

The response, r_t, is the number of spikes observed in a single trial in some small time window of length dt. The input, s_t, consists of the most recent t_k + 1 stimuli, {x⃗_t−tk, …, x⃗_t}, the most recent t_a responses of the neuron, and a constant term that allows us to include a bias which sets the background firing rate of the neuron. The stimulus x⃗_t is defined more explicitly below.

For auditory neurons, the receptive field of the neuron is typically represented in the spectrotemporal domain because the early auditory system is known to perform a frequency decomposition. Furthermore, transforming the input into the power spectral domain is a nonlinear transformation which generally improves the accuracy of the linear model for auditory data (Gill et al. 2006). The spectro-temporal receptive field (STRF) of the neuron, θ_x(τ, ω), is a two-dimensional filter which relates the firing rate at time t to the amount of energy at frequency ω and time t − τ in the stimulus. The subscript on θ is used to distinguish the elements of θ which measure the dependence of the response on the stimulus, spike-history, and bias terms respectively.

The stimuli and responses were computed from the experimental data by dividing the recordings into time bins of 2.5 ms. The time bin was small enough that more than one spike was almost never observed in any bins. To construct the corresponding stimulus, x⃗_t, we computed the power spectrum over a small interval of time centered on t (Gill et al. 2006). The power was computed for frequencies in the range 300–8,000 Hz, in intervals of approximately 100 Hz; previous work has suggested that this frequency spacing is suitable for computing the STRF in this context (Singh and Theunissen 2003; Gill et al. 2006).

We initially estimated a GLM with a STRF that had a duration of 50 ms (t_k + 1 = 20 time bins) and had t_a = 8 spike history terms as well as a bias term, for a total of 1,589 unknown parameters.³ The durations of the STRF and spike history dependence were chosen based on prior knowledge that these durations were long enough to capture most of the salient features of the STRF and spike history dependence (Woolley et al. 2006). Examples of the estimated STRF, spikehistory, and bias terms are shown in Fig. 3. The STRFs have similar temporal and frequency tuning to the STRFs trained on ml-noise using reverse-correlation methods presented in previous work (Woolley et al. 2006); see Calabrese et al. (2010) for further details. Also plotted is the estimated spike history filter. The largest coefficients are negative and occur for delays close to zero; thus the effect of the spike-history terms is to inhibit spiking immediately after the neuron fires (i.e., a relative refractory effect). The bias terms were also significantly negative, corresponding to low background firing rates; for the neurons shown in Fig. 3 the background firing rates are ≈ 3–5 Hz.

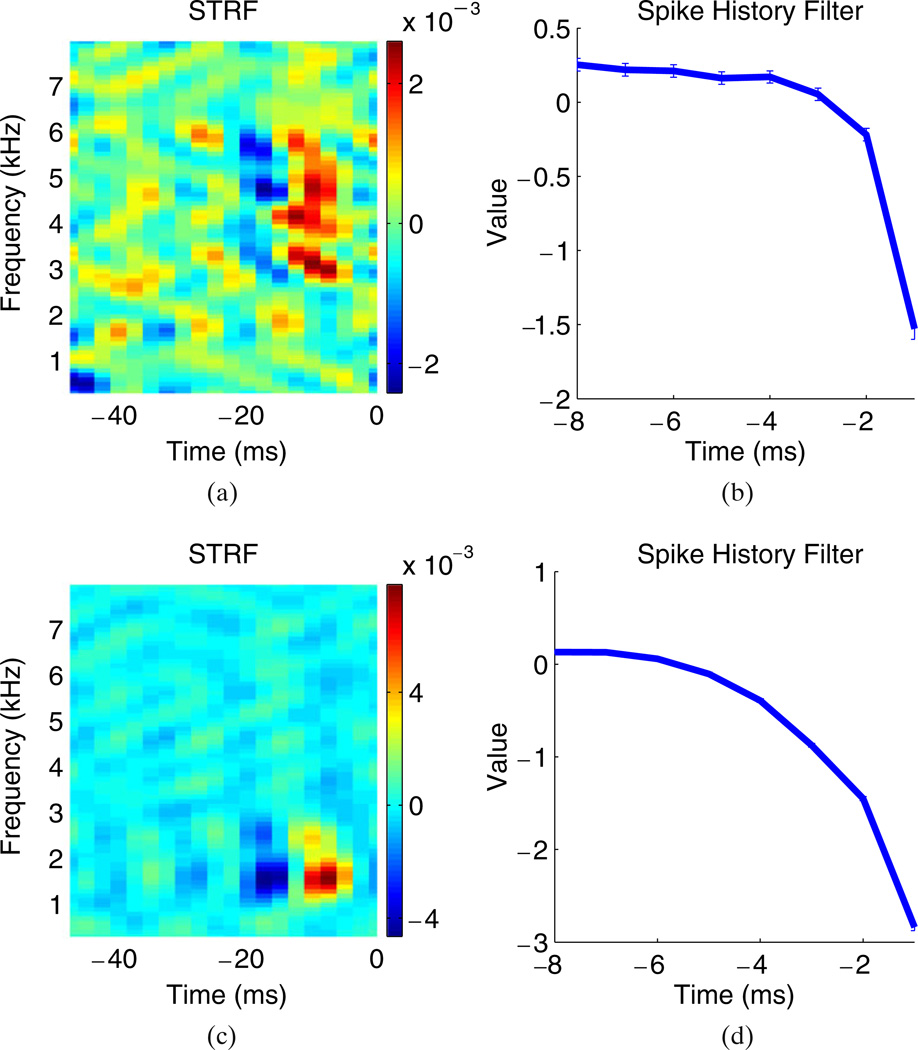
Fig. 3.

The receptive fields for two different neurons estimated with cutoff frequencies n_fc = 10 and n_tc = 4; see Appendix A for details. (a) The STRF for the first neuron. (b) The spike history coefficients (the curve shows the values of the filter coefficients at different delays). The bias in this case was −4.3. The error bars indicate plus and minus one standard deviation for each coefficient. (c) The STRF for the second neuron. (d) The spike history for the second neuron. The bias in this case was −4.6

To produce the STRFs shown in Fig. 3 we incorporated a regularizer in the fitting procedure to remove high-frequency noise (Theunissen et al. 2000, 2001; Machens et al. 2003; Smyth et al. 2003; Theunissen et al. 2004). Our preliminary results (data not shown) indicated that removing this regularization led to overfitting, which is unavoidable given the dimensionality of the STRF and the size of the dataset: the 30 stimuli, each ≈ 2 s in duration, translate into ≈ 20,000 distinct inputs when using a 50 ms STRF. Furthermore, most of these inputs are highly correlated due to the temporal structure of birdsong and the fact that we generate the inputs s⃗_t by sliding a window over the spectrogram. To deal with this issue efficiently, we represent the STRF in the frequency domain and incorporate a prior on the amplitudes of the frequency coefficients; fitting the STRF by maximum penalized likelihood (instead of maximum likelihood) biases the STRF towards smoother features when the available data are limited. This regularization procedure is discussed in detail in Appendix A.

3.1.2 Quantifying the improvement due to infomax stimulus design

Our goal now is to measure how many fewer trials an infomax design would require to accurately estimate these neurons’ receptive fields. We simulated a closed-loop infomax experiment by iterating the following steps. First, we initialized our Gaussian prior given no observed stimulus-response data; this Gaussian corresponds to the exponent of the quadratic low-pass regularizing penalty term described in Appendix A. Next, we considered all sequences of b consecutive stimuli and computed the lower bound on the informativeness of each sequence, given all of the previously-presented stimuli and corresponding responses, using Eq. (15). In these experiments we chose b = 20, so that each subsequence had a duration of roughly 50 ms, the approximate length of most relevant auditory features in the zebra finch song. We then selected the stimulus sequence which maximized this lower bound on the informativeness. To update our posterior mean μ_t and covariance matrix C_t we used the actual responses recorded given this sequence of inputs; using this data (s_t+1:t+b, r_t+1:t+b), we updated the posterior (Eq. (3)) via the methods described in Lewi et al. (2009). We then recomputed the informativeness of the remaining stimulus segments (excluding all previously chosen inputs), using the new, updated posterior mean μ_t+b and covariance C_t+b. We repeated these steps until all of the stimulus-response segments were processed. Below we will compare the performance of this procedure against a “shuffled” procedure in which stimulus-response pairs were drawn without replacement from the true data set at each time step; i.e., the same data are presented, just in a shuffled order.

We used 28 different training stimulus files to generate input/response pairs (s_t, r_t). Each stimulus was presented 10 times to the bird. The total number of spikes in the training sets ranged from roughly 300–4,000 per neuron. For each neuron, we trained a single model on all the training data (including both ml-noise and bird song stimuli), as opposed to fitting separate GLMs on the bird song and ml-noise training sets, so that the training set would span the input space as much as possible. For each neuron, the responses to one bird song and one ml-noise stimuli were held out as test stimuli to evaluate the fitted models. The expected log-likelihood (averaged over our posterior uncertainty about the model parameters, p(θ|μ_t, C_t)) provides a measure of how well the model predicts the responses to novel stimuli:

$$Q(t)=\frac{1}{T}{\displaystyle \sum _{i=1}^T}{E}_{\theta |{\overrightarrow{\mu }}_t,C_t}\text{log}p(r_i|s_i,\theta ),$$ (18)

where the summation over i is over each stimulus-response pair in the test set and T is the number of stimuli in the test set. Note that if the neuron’s response is perfectly predictable, and the GLM achieves a perfect level of prediction, then Q(t) = 0 (since in this case the conditional entropy of the response r_t will be zero). In practice, Q(t) will converge to some value less than 0, since neural responses are noisy and the GLM is an imperfect model. The results of this analysis are shown in Fig. 4 for two different neurons. In each case, the infomax design reduces the number of trials needed to accurately estimate the neuron’s receptive field.

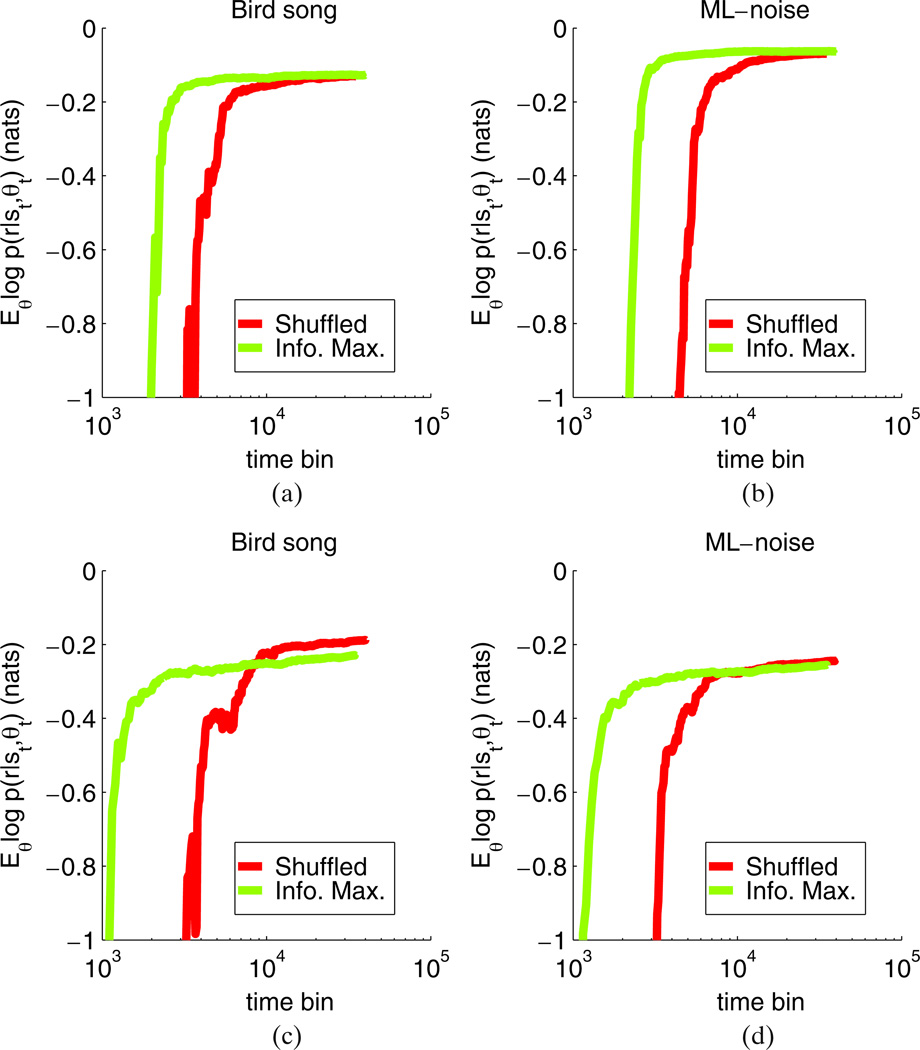
Fig. 4.

Quantifying the relative performance of the info. max. vs. the shuffled experimental design. Each panel shows the expected log-likelihood, up to a normalization constant, computed on the test sets for a different neuron. The test set for each neuron consisted of one bird song and one ml-noise stimulus. The expected log-likelihood is plotted as a function of the number of time bins used to train a model using inputs chosen by either an info. max. or shuffled design as described in the text. The results clearly show that the info. max. design achieves a higher level of prediction accuracy using fewer trials. We quantify the improvement as the “speedup” factor defined in the main text; see Fig. 5(b) and Table 1 for details and quantitative comparisons. As noted in the text, the expected log-likelihood is proportional to the amount of variability of the observations that can be explained by knowing θ and s. In this case, a larger number means more of the variability can be explained by knowing θ and s. The units are nats

To quantify the improvement in efficiency over a larger neural population, we exponentiated the expected log-likeliood Q(t) to obtain a quantity bounded between 0 and 1. We then examined the ratio of the number of trials needed to achieve a given level of accuracy (as measured by exp(Q(t)), normalized by its asymptotic maximum value computed using the full dataset) for each neuron, comparing the infomax approach to the original (random) order in which the stimuli were presented. This ratio (measured in units of % improvement) is summarized in Fig. 5(b), which plots the average and standard deviation of the speedup over all of the neurons in our dataset. The results show that on average the shuffled design required three times as many trials to produce a model that fit the data as well as a model trained using the information maximizing design. Table 1 lists the median as well as maximum and minimum speedup for all 11 neurons examined here.

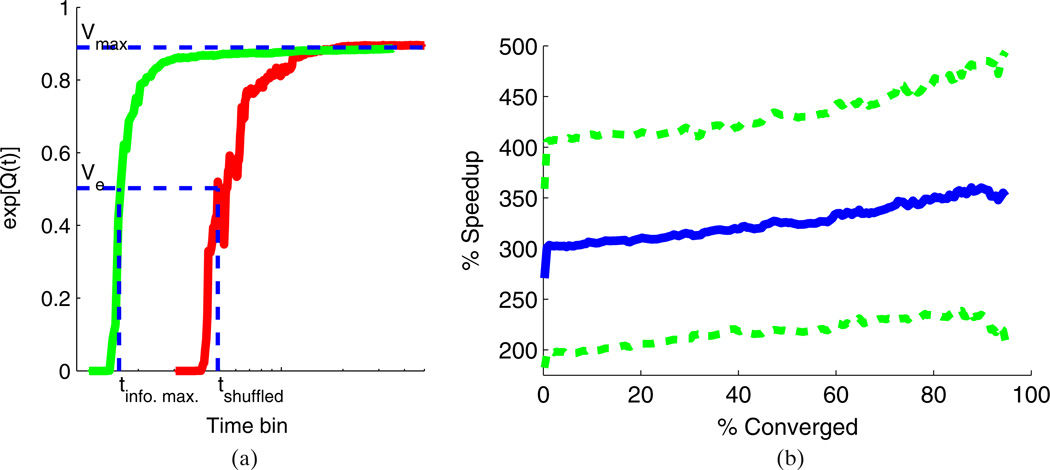
Fig. 5.

(a) A plot illustrating the quantities used to compute the speedup due to the infomax approach. For each design, we make a plot of exp[Q(t)] (as defined in Eq. (18)) vs. t. The maximum value, V_max, is the horizontal asymptote that both traces converge to. V_max measures how well we can predict the neuron’s responses using a GLM if we train on all the data. For any value, V_e, we can read off the number of stimuli, t_{info. max.} and t_shuffled, required by each design to train a GLM that can account for V_e percent of the response variability. The ratio $\frac{t_{\text{shuffled}}}{t_{\text{info. max.}}}$ is the Speedup as a function of V_e. b) A plot of the speedup achieved by using the info. max. design instead of a shuffled design. The speedup is plotted as a function of % Converged, as described in the text following Eq. (18). The solid blue line shows the average speedup across all 11 neurons and the dashed green lines show plus and minus one standard deviation. The results show that using a shuffled design would require roughly 3 times as many trials to achieve the same level of prediction accuracy as the info. max. design

Table 1.

A table listing the median as well as minimum and maximum values of the speedup evaluated over all 11 neurons

	Bird song	ml-noise
Median	330%	310%
Min	160%	200%
Max	630%	480%

The statistics are computed separately on the bird song and ml-noise stimuli in the test set. The statistics were computed at 50% converged (c.f. Fig. 5(b))

It is also worth noting that we expect the results in Fig. 5(b) to underestimate the potential improvement in actual experiments, because in our simulations the infomax design could only pick inputs which were actually presented to the birds. We know from Lewi et al. (2009) that restricting the input to a poorly chosen set of stimuli can dramatically reduce the relative advantage of the infomax design. Therefore, we would expect an infomax design which is allowed to choose stimuli from a much larger stimulus space than the relatively small set of songs and ml-noise stimuli considered in these experiments to perform significantly better.

4 Case 3: constructing informative random sequences in the long-sequence limit, b → ∞

In the previous section we chose informative stimuli with complex temporal features by optimizing sequences of b inputs. However, even for values of b for which the stimulus segment is reoptimized just once every 50 ms or so, a good deal of real-time computation is required. Thus it is natural to ask whether the computations may be simplified if we let b become even larger. In particular, can we form some convenient approximation of our objective function as b → ∞? This would correspond to a situation in which we re-optimize our stimuli only occasionally during an experiment, and would greatly reduce the required computational overhead. In addition, once we pick an arbitrarily long sequence of inputs, we can continue the experiment indefinitely. Thus, while we are computing an updated, optimized sequence using the most recent data, we can continue our experiment using the previously chosen sequence, further reducing any real-time computational requirements.

How can we evaluate this b → ∞ limit? If we look at the form of Eq. (4) once again, we see that the log-determinant term involves the inverse prior covariance $C_t^{-1}$ plus a sum of Fisher information matrices J_obs over b responses. Thus we might hope that we can neglect the prior term $C_t^{-1}$ and apply the law of large numbers to more easily evaluate the summed information matrices J_obs in the large-b limit. This idea is well-known in the experimental design literature (Fedorov 1972); see also Paninski (2005) for some concrete results related to the setting discussed here.

Unfortunately, the resulting limiting objective function (Eq. (19) below) is still not very tractable. Thus we relax our problem further, in three steps:

1. We restrict our consideration to stimulus sequences with a Gaussian distribution. Thus, instead of searching over infinitely long stimulus sequences, we just need to optimize our objective function over the much more tractable space of mean vectors and covariance functions.

2. We restrict our attention to the canonical Poisson GLM, which allows us to compute the objective function explicitly.

3. We construct a lower bound on this objective function to arrive at a function we can optimize tractably.

4.1 Deriving a tractable objective function in the large-b limit

We begin by showing that as b → ∞ maximizing the mutual information is equivalent to maximizing the average information per trial. If we think of the mutual information as measuring the total information acquired from b trials then the average information per trial (or the information rate) is just the mutual information normalized by the number of trials. More concretely, let’s rewrite Eq. (4) slightly:

$$E_{\theta }{E}_{r_{t+1:t+b}|s_{t+1:t+b},\theta }\text{log}\left|C_t^{-1}+{\displaystyle \sum _{i=t+1}^{t+b}}{J}_{\text{obs}}(r_i,s_i)\right|=E_{\theta }{E}_{r_{t+1:t+b}|s_{t+1:t+b},\theta }\text{log}\left|\frac{C_t^{-1}}{b}+\frac{1}{b}{\displaystyle \sum _{i=t+1}^{t+b}}{J}_{\text{obs}}(r_i,s_i)\right|+\text{dim}(\theta )\text{log}b.$$

The dim(θ) log b term does not depend on the input sequence, and may therefore be ignored. If C_t is invertible and the average Fisher information $\frac{1}{b}{\displaystyle {\sum }_{i=t+1}^{t+b}}{j}_{\text{obs}}(r_i,s_i)$ is of full rank,⁴ then $(1/b)C_t^{-1}$ will be negligible as b → ∞, and

$$\underset{b\to \mathrm{\infty }}{\text{lim}}{E}_{\theta }{E}_{r_{t+1:t+b}|s_{t+1:t+b},\theta }\text{log}\left|\frac{C_t^{-1}}{b}+\frac{1}{b}{\displaystyle \sum _{i=t+1}^{t+b}}{J}_{\text{obs}}(r_i,s_i)\right|=\underset{b\to \mathrm{\infty }}{\text{lim}}{E}_{\theta }{E}_{r_{t+1:t+b}|s_{t+1:t+b},\theta }\text{log}\left|\frac{1}{b}+{\displaystyle \sum _{i=t+1}^{t+b}}{J}_{\text{obs}}(r_i,s_i)\right|.$$ (19)

The result is that maximizing the average Fisher information per trial is asymptotically equivalent to maximizing the total information. See e.g. Chaloner and Verdinelli (1995) for background on the resulting “Bayesian D-optimal” design criterion. As discussed in Paninski (2005), this log-determinant of the average Fisher information is a concave function of the input distribution, p(s_t), and therefore in principle we can optimize this function by ascent methods over the convex space of all possible input distributions p(s_t). Unfortunately, since we are considering very high-dimensional inputs s_t here (e.g., bird songs), this optimization over p(s_t) will not be tractable in general, and we have to search for a simpler relaxation of our problem.

4.1.1 Restricting our attention to Gaussian stimulus sequences

The first simplification is to restrict our attention to Gaussian stimulus distributions p(s_t). The advantage here is obvious: Gaussian distributions are easy to sample from, and are specified completely by their mean vector μ_s and covariance matrix C_s. Thus, if s_t is d-dimensional, we can reduce our original infinite-dimensional problem (search over all possible distributions p(s_t)) to a much simpler O(d²)-dimensional problem (search over the space of allowable (μ_s, C_s)). So our optimization problem is reduced from maximizing Eq. (19) over all input distributions p(s_t) to

$$\underset{{\mu }_s,C_s}{\text{max}}{E}_{\theta }\text{log}\left|E_{s|{\mu }_s,C_s}{E}_{r|s,\theta }\frac{1}{b}{\displaystyle \sum _{i=1}^b}{J}_{\text{obs}}(r_i,s_i)\right|.$$ (20)

4.1.2 Specializing to the canonical Poisson case

As emphasized above, computations involving Fisher information simplify dramatically in the canonical Poisson model, since the observed Fisher information does not depend on the response r_t. In fact, the Fisher information has a particularly simple form here:

$$J_{\text{exp}}(s^T\theta )=E_{r|s,\theta }{J}_{\text{obs}}(r,s)=\text{exp}(s^T\theta ){\mathit{\text{ss}}}^T.$$ (21)

Note that Eq. (20) involves a Gaussian integral over the Fisher information; the simple exponential form of J_exp allows us to evaluate this expectation analytically here:

$$E_{\theta }\text{log}\left|E_{s|{\mu }_s,C_s}{E}_{r|s,\theta }{J}_{\text{obs}}(r,s)\right|=E_{\theta }\text{log}\left|E_{s|{\mu }_s,C_s}\text{exp}(s^T\theta )\mathit{\text{ss}}\right|$$ (22)

$$=E_{\theta }\text{log}\left|\text{exp}\left({\theta }^T{\mu }_s+\frac{1}{2}{\theta }^T{C}_s\theta \right)\times \left(({\mu }_s+C_s\theta ){({\mu }_s+C_s\theta )}^T+C_s\right)\right|$$ (23)

$$=E_{\theta }\left(d{\theta }^T{\mu }_s+\frac{d}{2}{\theta }^T{C}_s\theta +\text{log}|C_s|+\text{log}(1+{({\mu }_s+C_s\theta )}^T{C}_s^{-1}({\mu }_s+C_s\theta ))\right)$$ (24)

$$=d{\overrightarrow{\mu }}_t^T{\mu }_s+\frac{d}{2}\mathit{\text{Tr}}(C_s{\overrightarrow{\mu }}_t{\overrightarrow{\mu }}_t^T+C_s{C}_t)+\text{log}|C_s|+E_{\theta }\text{log}(1+{({\mu }_s+C_s\theta )}^T{C}_s^{-1}({\mu }_s+C_s\theta ))$$ (25)

(Note that we have incorporated the sum over s_i in Eq. (20) into the expectation over s in the first line here.) More generally, for other GLMs, the expected Fisher information E_p(s) J_exp(s^Tθ) may be computed in terms of a rank-2 perturbation of the stimulus covariance matrix C_s (see Appendix B). This is still tractable in principle, but we have not explored this direction systematically.

4.1.3 Computing a tractable lower bound

Computing the last term in Eq. (25) is difficult. However, it is easy to see that this term must be nonnegative, since

$${({\mu }_s+C_s\theta )}^T{C}_s^{-1}({\mu }_s+C_s\theta )\ge 0\Rightarrow \text{log}(1+{({\mu }_s+C_s\theta )}^T{C}_s^{-1}({\mu }_s+C_s\theta ))\ge 0.$$ (26)

Thus, by dropping the log term⁵ we obtain a rather simple lower bound:

$$E_{\theta }\text{log}|E_s\text{exp}(s^T\theta )\mathit{\text{ss}}|\ge d{\overrightarrow{\mu }}_t^T{\mu }_s+\frac{d}{2}\mathit{\text{Tr}}(C_s{\overrightarrow{\mu }}_t{\overrightarrow{\mu }}_t^T+C_s{C}_t)+\text{log}|C_s|.$$ (27)

Qualitatively, this lower bound leads to a reasonable objective function for optimizing the design. Our goal is to pick inputs which maximize the amount of new information provided by the experiment. The utility of an input is thus a function of 1) the informativeness of the experiment as measured by the Fisher information, which is independent of what we already know, and 2) our posterior covariance, which quantifies what we already know. We can interpret each of the terms in Eq. (27) as reflecting these goals. For example, in the canonical Poisson model the Fisher information increases with $\text{exp}(s_t^T\theta )$. Thus, to increase the Fisher information of the inputs we want to maximize the projection of the inputs on θ. Clearly, maximizing $\mathit{\text{Tr}}(C_s{\overrightarrow{\mu }}_t{\overrightarrow{\mu }}_t^T)={\overrightarrow{\mu }}_t^T{C}_s{\overrightarrow{\mu }}_t\text{and}{\overrightarrow{\mu }}_t^T{\mu }_s$ entails placing as much stimulus power as we can in the direction of μ⃗_t, which is our best estimate of θ at time t. As a result, the first two terms quantify the extent to which the design picks inputs with large Fisher information.

In contrast, the effect of the log |C_s| term is to whiten the design, since this term is maximized (given a bound on Tr(C_s), i.e., a bound on the total mean square power of C_s) when all the eigenvalues of C_s are equal. Similarly, the Tr(C_sC_t) term is directly related to our prior uncertainty and the Fisher information. The Tr(C_sC_t) term forces us to explore areas of uncertainty: maximizing Tr(C_sC_t) subject to a constraint on Tr(C_s) entails putting all stimulus power along the largest eigenvector of C_t. Thus, maximizing Tr(C_sC_t) favors designs which explore regions of θ space where our uncertainty is high.

All of these terms may be increased trivially by increasing the magnitude of the stimuli. Therefore, we must constrain the stimuli in order to get a well defined optimization problem. A reasonable constraint is the average power of the stimuli,

$$E(s^{T}s)=\mathit{\text{Tr}}(C_s)+{\mu }_s^T{\mu }_s.$$ (28)

Thus, finally, we arrive at our desired optimization problem:

$$\underset{({\mu }_s,C_s):\mathit{\text{Tr}}(C_s)+{\mu }_s^T{\mu }_s<m}{\text{max}}\left(d{\overrightarrow{\mu }}_t^T{\mu }_s+\frac{d}{2}\mathit{\text{Tr}}(C_s{\overrightarrow{\mu }}_t{\overrightarrow{\mu }}_t^T+C_s{C}_t)+\text{log}|C_s|\right),$$ (29)

over the space of semi-positive definite stimulus covariance matrices C_s. It turns out to be fairly straightforward to solve this optimization problem semianalytically; only a one-dimensional numerical search over a Lagrange multiplier is required. See Appendix C for the details.

4.2 Results

We tested our methods using simulated experiments in which we generated synthetic responses from a GLM whose parameters were estimated directly from the data described in Section 3.1.1 above. In particular, for the simulations shown here, we used the STRF and bias term fit to the neuron shown in Fig. 3(a); similar results were observed with parameters estimated from other neurons (data not shown). We chose stimuli either by sampling from an optimized Gaussian process using the methods discussed above, or by sampling i.i.d. stimuli from a Gaussian distribution with mean zero and covariance proportional to the identity matrix; the proportionality constant was chosen so that both Gaussian processes were subject to the same average power constraint. The prior p(θ) was chosen as discussed in the previous section.

In Fig. 6 we compare the posterior mean estimate of the parameters using the two designs as a function of t. In Fig. 7 we compute the expected error

$$E_{\theta |{\mu }_t,C_t}{\Vert \theta -{\theta }_o\Vert }_2,$$

where the expectation is computed using our posterior on θ and θ_o is the true parameter vector. While the posterior mean parameter estimates μ_t qualitatively seem to converge at a similar rate in Fig. 6, it is clear that the uncertainty in our estimates converges to zero faster when we use the optimized Gaussian stimulus distribution.

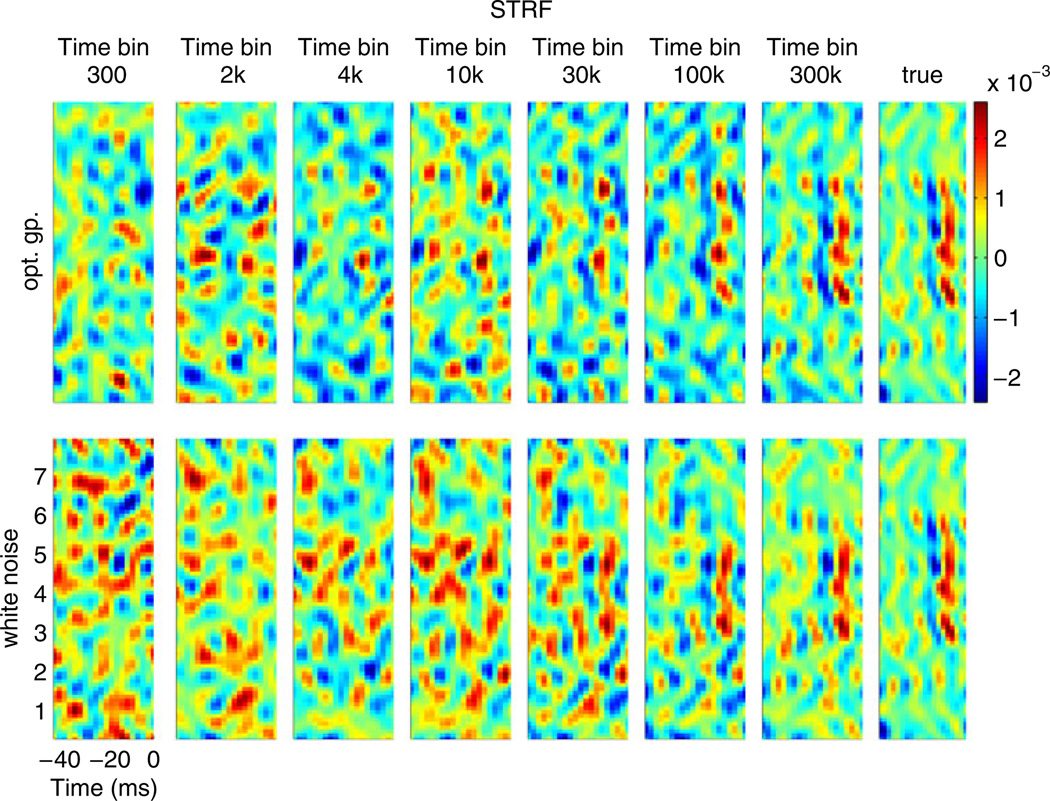
Fig. 6.

Simulation results comparing the posterior mean estimates of the STRF estimated using a white vs. optimized Gaussian process. The STRF used to generate the data was the STRF fitted to the neuron in Fig. 3(a). In this case the posterior mean estimates seem to converge to the true STRF at the same qualitative rate; however, as shown in Fig. 7 below, the uncertainty of our estimate shrinks more rapidly under the optimized Gaussian process design

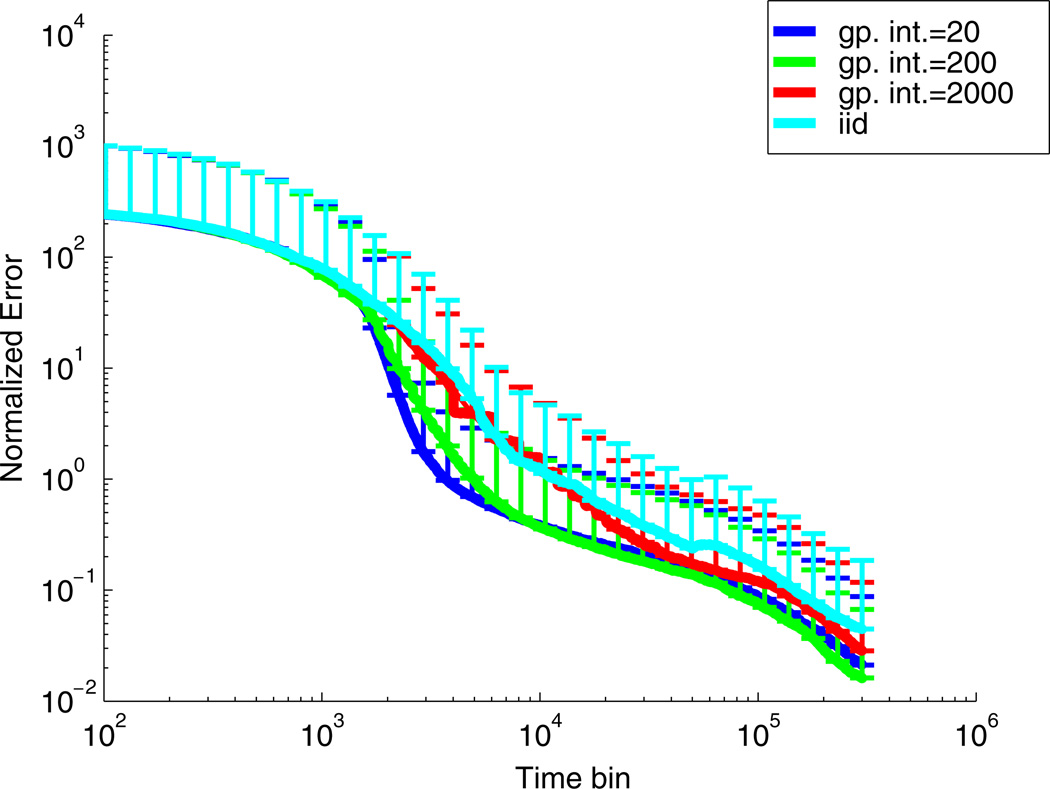
Fig. 7.

Plots of the expected squared error between the posterior mean and the corresponding true value of θ. The error is only computed for the stimulus coefficients (i.e the spike history and bias terms were not included). The expected error is normalized by the square of the magnitude of the STRF. For the optimal design, we tried several different designs in which we varied the interval over which we updated our Gaussian stimulus distribution. The interval corresponding to each trace is shown in the legend. The results show that we can achieve an improvement over an i.i.d. design even if we only update the Gaussian process every 200 timesteps (≈ 500 ms in this case); no major improvement is seen (relative to the i.i.d. design) if we only update every 2,000 timesteps. For each design, we repeated the simulation 10 times, using the same real STRF each time (shown in Fig. 3(a)), and computed the mean and standard deviation of the expected squared error. The results did not depend strongly on the STRF used to simulate the data. The plot shows the mean of the error and the errorbars show plus one standard deviation

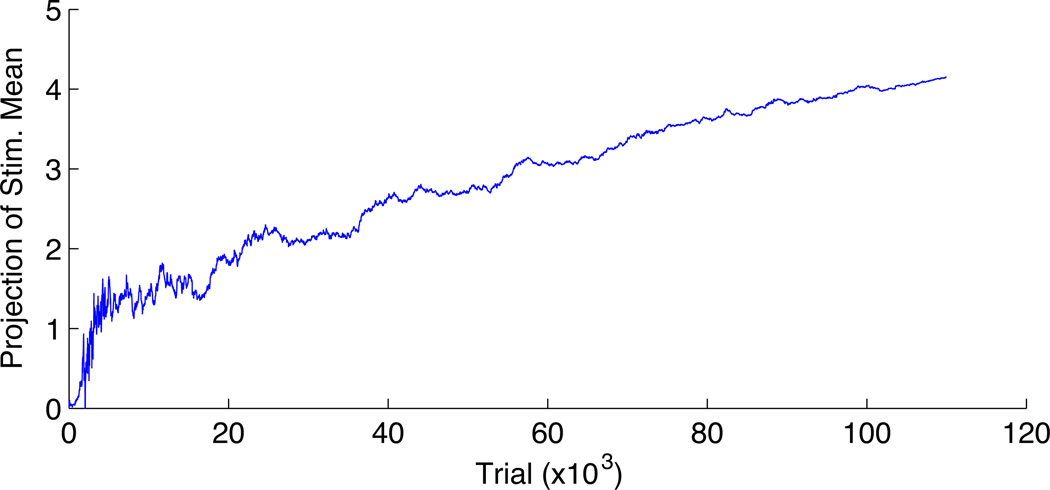
In Fig. 8 we plot the observed firing rate as a function of time for the synthetic neuron. This plot shows that the optimized design ends up picking inputs which drive the neuron to fire at a higher rate; recall that for the canonical Poisson the Fisher information increases with the firing rate.

Fig. 8.

A plot of the projection of the stimulus mean onto the posterior mean estimate μ_t, for the design using the optimized Gaussian process. The projection tends to increase with t, which corresponds to an increase in the expected firing rate and in the informativeness of each stimulus

5 Conclusion

In this work we have developed two methods for choosing informative stimulus sequences for use in on-line, adaptive sensory neurophysiology experiments. Our primary goal was to extend the methods introduced in Lewi et al. (2007, 2009), which focused on the problem of choosing a stimulus for which the corresponding response (measured as the spike count in a single short time bin) will provide as much information as possible about the observed neuron’s response properties. The extension pursued here—to the problem of choosing a sequence of stimuli whose corresponding sequence of responses will be as informative as possible—turns out to be computationally quite challenging, and so we have taken a more modest approximate approach instead. In Sections 3 and 4 we developed two lower bounds on our original information-theoretic objective function; these bounds provide rather natural extensions of the single-stimulus objective function to the stimulus-sequence case, and are much more computationally tractable than the full stimulus-sequence informativeness. The first method (described in Section 3) leads to efficient scoring of sequences of stimuli, so we can quickly pick the most informative stimulus sequence out of a large batch of candidate sequences. The second method (Section 4) finds a good distribution over sequences, from which we may then draw sample stimuli quite easily. In each case, despite a number of approximations and simplifications to ensure the tractability of the resulting algorithm, the chosen stimulus sequences decreased the error significantly faster than did standard experimental designs when tested on real and simulated birdsong auditory responses. We emphasize that the methods described here are simple enough to be implemented in on-line experiments without extraordinary effort, as compared to the single-stimulus methods discussed in Lewi et al. (2009), which require implementation of rather sophisticated real-time spike train processing and stimulus generation methods.

We close by noting a few attractive directions for future work. First, as emphasized in Section 4.1 and in the Appendix, it should be possible to develop tighter lower bounds and better approximations for the informativeness, perhaps at the expense of some computational tractability. By maximizing better approximations to the original information-theoretic objective function, we would hope to obtain even better performance. Second, it would be very useful to extend these methods to compute informative stimulus sequences in the context of multiple-neuron recordings, which have proven especially powerful in studying the early visual system (Segev et al. 2004; Ohki et al. 2005; Pillow et al. 2008) and which hold great promise in other sensory modalities (Luczak et al. 2007). Third, higher-level neurons often show nonlinear selectivity for specific feature conjunctions, which makes discovering optimal stimuli difficult, but ripe for efficient stimulus optimization methods. While the simple GLM approach we have pursued here is poorly suited for such neurons, it may be possible to adapt the nonlinear methods described in our previous work (Lewi et al. 2008, 2009) to handle these cases. Similarly, central neurons frequently exhibit strong response adaptation, which is often partially stimulus-specific. The method discussed in Section 4 tends to drive sampling toward stimuli that have a strong projection onto the cell’s receptive field, leading to an increasingly strongly-driving and homogeneous subset of stimuli (cf. Fig. 8). Incorporating more profoundly stimulus-dependent adaptation terms into our approach remains an important open challenge. Finally, we are currently pursuing applications to real online experiments, in order to better understand the role of plasticity and spectral filtering in the songbird auditory system.

Appendix A: Using a frequency representation to smooth the STRF

To represent the STRF in the Fourier domain, we applied the Fourier transform separately to the spectral and temporal dimensions of the STRF. Applying the separable Fourier transform to the STRF is just a linear transformation. This transformation maps the STRF into a coordinate system in which the basis functions are rank one matrices. Each of these matrices is the product of 1-dimensional sine-waves in the spectral and temporal directions of the STRF. Using these basis functions we can write the STRF such that each row and column of the STRF is a linear combination of 1-d sine-waves,

$$\theta (i,j)={\displaystyle \sum _{\alpha =1}^{m_f}}{\displaystyle \sum _{\beta =1}^{m_t}}{\gamma }_{\alpha ,\beta }^1\text{sin}(2\pi ·f_{o,f}·\alpha ·i)\times \text{sin}(2\pi ·f_{o,t}·\beta ·j)$$ (30)

$$+{\displaystyle \sum _{\alpha =1}^{m_f}}{\displaystyle \sum _{\beta =0}^{m_t}}{\gamma }_{\alpha ,\beta }^2\text{sin}(2\pi ·f_{o,f}·\alpha ·i)\times \text{cos}(2\pi ·f_{o,t}·\beta ·j)$$ (31)

$$+{\displaystyle \sum _{\alpha =0}^{m_f}}{\displaystyle \sum _{\beta =1}^{m_t}}{\gamma }_{\alpha ,\beta }^3\text{cos}(2\pi ·f_{o,f}·\alpha ·i)\times \text{sin}(2\pi ·f_{o,t}·\beta ·j)$$ (32)

$$+{\displaystyle \sum _{\alpha =0}^{m_f}}{\displaystyle \sum _{\beta =0}^{m_t}}{\gamma }_{\alpha ,\beta }^4\text{cos}(2\pi ·f_{o,f}·\alpha ·i)\times \text{cos}(2\pi ·f_{o,t}·\beta ·j).$$ (33)

The functions sin(2π · f_{o, f} · α · i) and cos(2π · f_{o, f} · α · i) determine how each basis function varies across the spectral dimension of the STRF while the functions sin(2π · f_o,t · β · j) and cos(2π · f_o,t · β · j) determine how the basis functions vary across time in the STRF. Each pair of sine-waves measures the amount of energy at particular frequencies in the spectral and temporal dimensions. The amplitude of each frequency is determined by the coefficients ${\gamma }_{\alpha ,\beta }^i$. To form an orthogonal basis for the STRF we need to project the STRF onto sinusoids with frequencies

$$\{0,f_{o,f},2f_{o,f},\dots m_f{f}_{o,f}\}\{0,f_{o,t},2f_{o,t},\dots ,m_t{f}_{o,t}\}$$ (34)

$$f_{o,f}=\frac{1}{n_f}{f}_{o,t}=\frac{1}{n_t}$$ (35)

$$m_f=\lceil \frac{1}{2f_{o,f}}-1\rceil m_t=\lceil \frac{1}{2f_{o,t}}-1\rceil ;$$ (36)

f_{o, f} and f_o,t are the fundamental frequencies and are set so that one period corresponds to the dimensions of the STRF (n_t and n _f denote the dimensions of the STRF in the time and frequency dimensions, respectively), and m_f and m_t are the largest integers such that m_f f_{o, f} and m_t f_o,t are less than the Nyquist frequency. We subtract 1 and take the ceiling to make sure the frequencies of our basis functions are less than the Nyquist frequency. The unknown parameters in this new coordinate system are the amplitudes, $\overrightarrow{\gamma }=\{{\gamma }_{\alpha ,\beta }^1,{\gamma }_{\alpha ,\beta }^2,{\gamma }_{\alpha ,\beta }^3,{\gamma }_{\alpha ,\beta }^4\}$. For simplicity, we will continue to refer to the unknown parameters as θ, realizing that the STRF is represented using this new basis. Since this transformation is linear we can continue to apply our methods for fitting theGLMand optimizing the stimuli.

To low pass filter the STRF we can simply force the coefficients of θ corresponding to high frequencies to zero; i.e we pick cutoffs n_tc and n _{f c} for the time and spectral directions respectively and set

$${\gamma }_{\alpha ,\beta }^i=0\mathrm{i}f\alpha >n_{f_c}\text{ or }\beta >n_{\mathit{\text{tc}}}.$$ (37)

Decreasing the cutoff frequencies not only makes the estimated STRFs smoother, it also reduces the dimensionality of the model. Reducing the dimensionality makes it easier to fit the GLM and optimize the stimuli, but the risk is that the lower-dimensional model may be too simple to adequately model auditory neurons. We can mitigate this risk by using a soft cutoff. Rather than force all high-frequency components to zero, we can adjust our prior to reflect our strong belief that high frequencies should have little energy; we simply set the prior mean of these coefficients to zero and decrease their prior variance. If we now estimate the STRF using the maximum of the posterior then the amplitudes at high frequencies will be biased by our prior towards zero. However, given sufficient evidence the posterior mean will yield non-zero estimates for the amplitudes of high frequencies. See Theunissen et al. (2001) for details and David et al. (2007), Calabrese et al. (2010) for further discussion.

We chose to impose a hard cutoff because we wanted to reduce the dimensionality to make online estimation of the model and online optimization of the stimuli more tractable. To pick the cutoff frequencies, we picked a single neuron and estimated the STRF using maximum-likelihood for a variety of cutoff frequencies. We evaluated the quality of each model by computing the log-likelihood of the bird’s responses to inputs in a test set. The test set consisted of one bird song and one ml-noise stimulus which were not used to train the models. We chose the cutoff frequencies to be n _{f c} = 10 and n_tc = 4 because these values provided good predictive performance for both the bird song and ml-noise while keeping the number of unknown parameters tractable (in this case the STRF has 189 unknown parameters).

Appendix B: Computing the average information for a Gaussian process

In this section we show how the average information per stimulus,

$$E_{\theta }\text{log}\left|E_s\text{exp}(s^T\theta ){\mathit{\text{ss}}}^T\right|,$$

can be computed when the input distribution is a Gaussian process. For the GLM the expected Fisher information matrix E_s J_exp(s, θ) has a simple 1-dimensional dependence on θ,

$$J_{\text{exp}}(s,\theta )=J_{\text{exp}}(s^T\theta ){\mathit{\text{ss}}}^T$$ (38)

$$J_{\text{exp}}(s^T\theta )=-E_r\frac{{\partial }^2\text{log}p(r|\rho =s^T\theta )}{\partial {\rho }^2}{\mathit{\text{ss}}}^T$$ (39)

$$=J_{\text{exp}}(\rho =s^T\theta ){\mathit{\text{ss}}}^T.$$ (40)

This 1-dimensional structure along with the fact that p(s) is Gaussian makes computing the expectations tractable. We start by defining a new coordinate system in which the first axis is aligned with θ. This coordinate system is defined by the orthonormal matrix, ℛ_θ. The first column of ${ℛ}_{\theta }\text{is}\frac{\theta }{{\Vert \theta \Vert }_2}$ and the remaining columns are a suitable set of orthonormal vectors. We can thus define the transformation of s and θ into this new coordinate system,

$$\theta \prime ={ℛ}_{\theta }^T\theta$$ (41)

$$\overrightarrow{w}={ℛ}_{\theta }^{T}s.$$ (42)

This coordinate system has the convenient properties

$${\theta }_i^{\prime }=0\forall i\ne 1$$ (43)

$$\Rightarrow {\overrightarrow{w}}^T\theta \prime =w_1{\theta }_1^{\prime }.$$ (44)

We can now rewrite our objective function

$$ℱ(p(s))=E_{\theta }\text{log}|E_{p(s)}{J}_{\text{exp}}(\rho ){\mathit{\text{ss}}}^T|$$ (45)

$$=E_{\theta }\text{log}|E_{p(\overrightarrow{w})}{J}_{\text{exp}}(w_1{\theta }_1^{\prime })\overrightarrow{w}{\overrightarrow{w}}^T|$$ (46)

$$=E_{\theta }\text{log}|E_{w_1}{J}_{\text{exp}}(w_1{\theta }_1^{\prime })E_{w_2,\dots ,w_{\text{dim}(s)}|w_1}\overrightarrow{w}{\overrightarrow{w}}^T|.$$ (47)

Since p(s) is Gaussian and $\overrightarrow{w}={ℛ}_{\theta }^{T}s,p(\overrightarrow{w})$ is Gaussian with mean ${ℛ}_{\theta }^T{\mu }_s$ and covariance matrix ${ℛ}_{\theta }^T{C}_s{ℛ}_{\theta }^T$. Consequently, p(w⃗|w₁) is also Gaussian and can be computed using the standard Gaussian conditioning formulas,

$$p(\overrightarrow{w}|w_1)=𝒩({ℛ}_{\theta }^T{\mu }_s+\frac{1}{{\sigma }_{{\omega }_1}^2}{ℛ}_{\theta }^T\mathit{\gamma }(w_1-{\mu }_{{\omega }_1}),{ℛ}_{\theta }^T{C}_s{ℛ}_{\theta }-\frac{1}{{\sigma }_{{\omega }_1}^2}{ℛ}_{\theta }^T\mathit{\gamma }{\mathit{\gamma }}^T{ℛ}_{\theta })$$ (48)

$${\mu }_{{\omega }_1}=\frac{{\theta }^T}{{\Vert \theta \Vert }_2}{\mu }_s$$ (49)

$${\sigma }_{{\omega }_1}^2=\frac{{\theta }^T}{{\Vert \theta \Vert }_2}{C}_s\frac{\theta }{{\Vert \theta \Vert }_2}$$ (50)

$$\mathit{\gamma }=C_s\frac{\theta }{{\Vert \theta \Vert }_2}.$$ (51)

Using this distribution we can easily compute the conditional expectation,

$$E_{\overrightarrow{w}|w_1}\overrightarrow{w}{\overrightarrow{w}}^T={ℛ}_{\theta }^T\left(C_s-\frac{1}{{\sigma }_{{\omega }_1}^2}\mathit{\gamma }{\mathit{\gamma }}^T+\left({\mu }_s+\frac{1}{{\sigma }_{{\omega }_1}^2}\mathit{\gamma }(w_1-{\mu }_{{\omega }_1})\right)\times {\left({\mu }_s+\frac{1}{{\sigma }_{{\omega }_1}^2}\mathit{\gamma }(w_1-{\mu }_{{\omega }_1})\right)}^T\right){ℛ}_{\theta }$$ (52)

$$={ℛ}_{\theta }^T\left(C_s+\left({\mu }_s+\frac{1}{{\sigma }_{{\omega }_1}^2}\mathit{\gamma }(w_1-{\mu }_{{\omega }_1})-\frac{1}{\sqrt{{\sigma }_{{\omega }_1}^2}}\mathit{\gamma }\right)\times {\left({\mu }_s+\frac{1}{{\sigma }_{{\omega }_1}^2}\mathit{\gamma }(w_1-{\mu }_{{\omega }_1})+\frac{1}{\sqrt{{\sigma }_{{\omega }_1}^2}}\mathit{\gamma }\right)}^T\right){ℛ}_{\theta }$$ (53)

$$={ℛ}_{\theta }^T\left(C_s+\left(\overrightarrow{\kappa }{w}_1+\overrightarrow{\delta }\right){(\overrightarrow{\kappa }{w}_1+\overrightarrow{\eta })}^T\right){ℛ}_{\theta }$$ (54)

$$\overrightarrow{\kappa }=\frac{\mathit{\gamma }}{{\sigma }_{{\omega }_1}^2}$$ (55)

$$\overrightarrow{\delta }={\mu }_s-\frac{\mathit{\gamma }}{{\sigma }_{{\omega }_1}^2}{\mu }_{{\omega }_1}-\frac{\mathit{\gamma }}{\sqrt{{\sigma }_{{\omega }_1}^2}}$$ (56)

$$\overrightarrow{\eta }={\mu }_s-\frac{\mathit{\gamma }}{{\sigma }_{{\omega }_1}^2}{\mu }_{{\omega }_1}+\frac{\mathit{\gamma }}{\sqrt{{\sigma }_{{\omega }_1}^2}}$$ (57)

The key point is that the expected value is just a rank-1 perturbation of a rotated C_s. We can now evaluate the expectation over w₁,

$$E_{w_1}{J}_{\text{exp}}(w_1{\theta }_1^{\prime })E_{\overrightarrow{w}|w_1}\overrightarrow{w}{\overrightarrow{w}}^T={ℛ}_{\theta }^T\left(C_s{\varpi }_1+{\varpi }_3\left[\left(\overrightarrow{\kappa }+\frac{{\varpi }_2}{{\varpi }_3}\overrightarrow{\delta }\right){\left(\overrightarrow{\kappa }+\frac{{\varpi }_2}{{\varpi }_3}\overrightarrow{\eta }\right)}^T+\left(\frac{{\varpi }_1}{{\varpi }_3}-{\left(\frac{{\varpi }_2}{{\varpi }_3}\right)}^2\right)\overrightarrow{\delta }{\overrightarrow{\eta }}^T\right]\right){ℛ}_{\theta }$$ (58)

$${\varpi }_1=E_{w_1}{J}_{\text{exp}}(w_1{\theta }_1^{\prime })$$ (59)

$${\varpi }_2=E_{w_1}{J}_{\text{exp}}(w_1{\theta }_1^{\prime })w_1$$ (60)

$${\varpi }_2=E_{w_1}{J}_{\text{exp}}(w_1{\theta }_1^{\prime })w_1^2;$$ (61)

$w_1=\frac{{\theta }^T}{{\Vert \theta \Vert }_2}s$, and p(w₁) is Gaussian with mean and variance $({\mu }_{{\omega }_1},{\sigma }_{{\omega }_1}^2)$. The above are just 1-dimensional expectations so for any value of θ we could compute them numerically.

Equation (58) is a rank 2 update of C_s. Therefore we can use the matrix determinant lemma to compute |E_w1 E_w⃗|w1 J_exp w⃗w⃗^T|,

$$\text{log}|E_{w_1}{E}_{\overrightarrow{w}|w_1}{J}_{\text{exp}}(w_1{\theta }_1^{\prime })\overrightarrow{w}{\overrightarrow{w}}^T|=\text{dim}(C_s)\text{log}{\varpi }_1+\text{log}|I+V^T{({\varpi }_1{C}_s)}^{-1}U|+\text{log}|C_s|$$ (62)

$$U={\varpi }_3\left[\left(\overrightarrow{\kappa }+\frac{{\varpi }_2}{{\varpi }_3}\overrightarrow{\delta }\right),\left(\frac{{\varpi }_1}{{\varpi }_3}-{\left(\frac{{\varpi }_2}{{\varpi }_3}\right)}^2\right)\overrightarrow{\delta }\right]$$ (63)

$$V=\left[\left(\overrightarrow{\kappa }+\frac{{\varpi }_2}{{\varpi }_3}\overrightarrow{\eta }\right),\overrightarrow{\eta }\right].$$ (64)

Since I + V^T (ϖ₁ C_s)⁻¹ U is a 2-d matrix, we can compute its determinant analytically. Taking the expectation with respect to θ yields,

$$E_{\theta }\text{log}|E_{w_1}{E}_{\overrightarrow{w}|w_1}{J}_{\text{exp}}(w_1{\theta }_1^{\prime })\overrightarrow{w}{\overrightarrow{w}}^T|=\text{dim}(C_s)E_{\theta }\text{log}{\varpi }_1+E_{\theta }\text{log}|I+V^T{({\varpi }_1{C}_s)}^{-1}U|+\text{log}|C_s|.$$ (65)

Appendix C: Solving the optimization problem described in Section 4.1.3

Our goal is to solve the optimization problem

$$\text{arg }\underset{{\mu }_s,C_s}{\text{max }}d{\overrightarrow{\mu }}_t^T{\mu }_s+\frac{d}{2}\mathit{\text{Tr}}(C_{s}R)+\text{log}|C_s|,$$ (66)

where we have abbreviated

$$R={\overrightarrow{\mu }}_t{\overrightarrow{\mu }}_t^T+C_t,$$ (67)

over all (μ_s, C_s) subject to the constraints

$$s^T{C}_{s}s>0\forall s\ne 0$$ (68)

$$\mathit{\text{Tr}}(C_s)<m-{\Vert {\mu }_s\Vert }^2,$$ (69)

where m is the maximum allowed average stimulus power. Clearly the optimal μ_s will be parallel to μ⃗_t. Therefore, only the magnitude of the optimal μ_s is unknown. We can therefore rewrite the objective function as

$$\text{arg }\underset{\Vert {\mu }_s\Vert }{\text{max }}\left[d\Vert {\overrightarrow{\mu }}_t\Vert \Vert {\mu }_s\Vert +\text{arg }\underset{C_s}{\text{max }}\left(\frac{d}{2}\mathit{\text{Tr}}(C_{s}R)+\text{log}|C_s|\right)\right]$$ (70)

We rewrite the inner problem to make the dependence on ||μ_s|| (through the power constraint) more explicit:

$$\text{arg }\underset{C_s}{\text{max}}\frac{d}{2}\mathit{\text{Tr}}(C_{s}R)+\text{log}|C_s|$$ (71)

$$s.t{s}^T{C}_{s}s>0\forall s\ne 0$$ (72)

$$\mathit{\text{Tr}}(C_s)<m-{\Vert {\mu }_s\Vert }^2.$$ (73)

We solve this optimization problem by introducing a Lagrange multiplier,

$$L=\frac{d}{2}\mathit{\text{Tr}}(C_{s}R)+\text{log}|C_s|-\lambda \mathit{\text{Tr}}(C_s)$$ (74)

$$=\mathit{\text{Tr}}\left[C_s\left(\frac{d}{2}(R-\lambda I)\right)\right]+\text{log}|C_s|.$$ (75)

This Lagrangian is exactly isomorphic to twice the loglikelihood in a multivariate Gaussian model with zero mean, if we interpret C_s as the inverse covariance matrix in the Gaussian model and $-\frac{d}{2}(R-\lambda I)$ as the observed sample covariance matrix. Standard arguments involving a change of basis now imply that the optimal C_s is given by

$$C_s=-{\left(\frac{d}{2}(R-\lambda I)\right)}^{-1},$$ (76)

for any λ > max_i{r_i}, where r_i denotes the i-th eigenvalue of R. This condition on λ is required to ensure that the resulting C_s maximizes the Lagrangian L, and guarantees that C_s is positive definite.

We now solve for λ by plugging this C_s into our power constraint:

$$\mathit{\text{Tr}}(C_s)=\frac{2}{d}{\displaystyle \sum _i}\frac{1}{\lambda -r_i}=m-{\Vert {\mu }_s\Vert }^2$$ (77)

We can easily solve this equation numerically on the allowed range λ > max_i r_i to compute λ as a function of ||μ_s||. We can then in principle do a search over all ||μ_s|| to find the optimal value (μ_s, C_s). In fact, a more efficient method is to instead just compute the optimal (||μ_s||, C_s) for each value of λ; thus, a single 1-d search over λ is guaranteed to find the optimal (μ_s, C_s). Also note that we can compute the inverse in Eq. (76) efficiently for any value of λ by computing the eigendecomposition of R once and then using the fact that eig(R − λI) = eig(R) − λ; we used this formula already in Eq. (77).

Enforcing stationarity by incorporating Toeplitz constraints

It is worth noting, in the case of stimulus filters θ that extend over more than one time bin (i.e., n_t as defined in Appendix A is greater than one), that the stimulus sequence drawn from the Gaussian distribution defined above will not be temporally stationary. Instead, the stimulus sequence will consist of a series of appended n_t-long segments of draws from a Gaussian distribution, and therefore the marginal distribution of the inputs s_t will in general be an n_t-mixture of Gaussians, instead of a single Gaussian distribution. We recover a single Gaussian only in the special stationary case that the stimulus covariance C_s is constrained to have a Toeplitz structure and the mean vector μ_s is constrained to be constant with respect to time-shifts.

Since we are observing the neural responses r_t given the input s_t presented at each time point t, we should arguably optimize our information over this marginal mixture distribution, instead of the single Gaussian distribution optimized in this appendix. Alternately, we could enforce stationarity in our optimized Gaussian process by including Toeplitz constraints on C_s in our derivation above. We have had limited success deriving a computationally efficient optimization strategy in either of these cases, but this remains an attractive direction for future research. Meanwhile, the results described in Section 4.2 (with a non-stationary optimized Gaussian stimulus ensemble) remain encouraging.