eQuilibrator—the biochemical thermodynamics calculator

Abstract

The laws of thermodynamics constrain the action of biochemical systems. However, thermodynamic data on biochemical compounds can be difficult to find and is cumbersome to perform calculations with manually. Even simple thermodynamic questions like ‘how much Gibbs energy is released by ATP hydrolysis at pH 5?’ are complicated excessively by the search for accurate data. To address this problem, eQuilibrator couples a comprehensive and accurate database of thermodynamic properties of biochemical compounds and reactions with a simple and powerful online search and calculation interface. The web interface to eQuilibrator (http://equilibrator.weizmann.ac.il) enables easy calculation of Gibbs energies of compounds and reactions given arbitrary pH, ionic strength and metabolite concentrations. The eQuilibrator code is open-source and all thermodynamic source data are freely downloadable in standard formats. Here we describe the database characteristics and implementation and demonstrate its use.

INTRODUCTION

The structure and function of cellular metabolism has been a central area of biological inquiry for over a century. The metabolic networks of numerous organisms have been studied in detail as well as their responses to changes in internal and external conditions (1–4). More recently, metabolic models have succeeded in accurately predicting bacterial growth modes and biologists have succeeded in designing and implementing novel biosynthetic pathways for the production of fuels and other valuable chemicals (5–9). In these metabolic research and engineering efforts it is essential to account for thermodynamic constraints: chemical reactions can sustain flux in a given direction only if they lead to a reduction in the Gibbs energy (G). That is, the change in Gibbs energy due to a reaction (Δ_rG) must be negative.

Biochemical reactions have context: they take place inside cells. The cellular conditions—temperature, pH, ionic strength, concentrations of metabolites and ions, etc.—can significantly affect the thermodynamic feasibility of a particular reaction direction. Therefore, a metabolic reaction or pathway can be subjected to thermodynamic analysis to determine whether it is feasible under physiological conditions and which conditions enable it to produce the desired outputs (6,10). For example, recent work engineering Escherichia coli for 1,4-butanediol production leveraged thermodynamic analysis to highlight the most promising candidate pathways and to eliminate those unlikely to flow to 1,4-butanediol (7).

It can be quite time-consuming to apply thermodynamic analyses to a pathway or reaction of interest. For example, consider a simple thermodynamic question: in which direction does the fructose bisphosphate aldolase reaction in glycolysis proceed when all reactants are present in 1 mM concentrations at pH 7.5 and ionic strength 0.2? To answer this question, thermodynamic parameters must be retrieved from the literature. Care must be taken to ensure that the various data sources used are compatible with each other and that all reactions analyzed are properly balanced. Reaction energies must be transformed to physiological conditions by applying metabolite concentrations, pH and ionic strength values from the literature. This work is straightforward, but also arduous and error-prone.

The most reliable way to perform these calculations is by using a well-tested computer program with access to a comprehensive and accurate database of thermodynamic data. Indeed, that is exactly what eQuilibrator is. eQuilibrator houses a collection of measured and approximated thermodynamic data. The database is coupled to a web interface that enables users to perform thermodynamic calculations with ease. All thermodynamic source data is available for download in standard formats. eQuilibrator was motivated by the notion that thermodynamic analysis is a powerful way to develop and check hypotheses about biochemical systems, but that such analyses are underused because of the amount of effort involved.

ESSENTIALS OF BIOCHEMICAL THERMODYNAMICS

Hydrogen atoms are not balanced in biochemical reactions as the pH is held constant. Rather, the aqueous environment is treated as a reservoir of protons and the pH determines their Gibbs energy. The assumption of constant pH is quite reasonable since many organisms use buffers to maintain the intracellular pH (11,12). Therefore, we use Δ_rG′—the change in Gibbs energy at a fixed pH—rather than Δ_rG when discussing biochemical reactions.

If a biochemical reaction carries net forward flux, the second law of thermodynamics demands that Δ_rG′< 0. Δ_rG′ is a function of the standard transformed Gibbs energy (Δ_rG′°) as well as reactant concentrations. The effect of concentrations on Δ_rG′ is given by the apparent reaction quotient Q′, the stoichiometric ratio of product concentrations to substrate concentrations. Δ_rG′° = Δ_rG′° + RTln(Q′), where R is the gas constant (8.31446 J mol⁻¹K⁻¹) and T is the temperature in kelvin (at 25°C RT = 2.47896 kJ/mol). At equilibrium, Δ_rG′ = 0 and Q' assumes a characteristic value K′ = exp(−Δ_rG′°/RT) called the apparent equilibrium constant (11,13,14).

Δ_rG′° is defined in standard conditions where all reactants aside from protons have unit (1 M) concentrations. However, in E. coli, for instance, metabolite concentrations range from ∼0.1 μM to ∼100 mM, spanning about six orders of magnitude (15). A 10-fold increase in the concentration of a single reaction product will add RT ln(10) = 5.708 kJ/mol to Δ_rG′ (13). For example, the citrate dehydratase reaction in the TCA cycle (citrate ⇌ H2O + cis-aconitate) has a positive Δ_rG′° of 8.5 kJ/mol (where pH = 7.0, ionic strength = 0.1 and T = 298.15 K), but when concentrations measured in E. coli are applied ([citrate] = 610 μM, [cis-aconitate] = 16 μM) Δ_rG′ is reduced to −0.5 kJ/mol (15). Furthermore, changes in multiple reactant concentrations could potentially change Δ_rG′ by tens of kJ/mol.

Similarly, changes in pH, ionic strength and the concentrations of ions like Mg²⁺ and Ca²⁺ can have a significant effect on Δ_rG′ by way of altering Δ_rG′°. Indeed, the Δ_rG′° of ATP hydrolysis is quite dependent on pH: it is roughly −33 kJ/mol at pH 5 and −41 kJ/mol at pH 8, implying more than an order-of-magnitude change in K′. As such, it is crucial to account for metabolite concentrations, pH and ionic strength in thermodynamic analyses (11,13).

ESTIMATING STANDARD REACTION ENERGIES

Δ_rG′° must be measured or estimated in order to calculate Δ_rG′. Measuring K′ is equivalent to measuring Δ_rG′° and K′ has been measured for roughly 400 unique biochemical reactions (16). Alternatively, Δ_rG′° can be calculated from the Gibbs energies of formation (Δ_fG′°) of the reactants participating in the reaction. Indeed, the decades-long efforts of Robert Alberty and colleagues have produced accurate Δ_fG′° values for approximately 200 biochemical compounds (11). However, even this approach is somewhat limited as there are thousands more metabolically-interesting compounds and reactions that remain thermodynamically uncharacterized (11,17,18).

Unknown Δ_fG′° values can be estimated accurately using group-contribution approximation methods. These methods assume that compounds are composed of chemical groups that each have characteristic contributions to Δ_fG′° independent of all other groups present in the compound (19,20). Applying the group-contribution method yields formation energies for a large fraction of metabolites, enabling thermodynamic analysis of pathways and genome-scale metabolic models (21,18). Moreover, recent work has integrated acid dissociation constants into the group-contribution framework to accurately account for the effect of pH and ionic strength on compound and reaction Gibbs energies (Noor, E. et al., Submitted for publication).

THE DATABASE

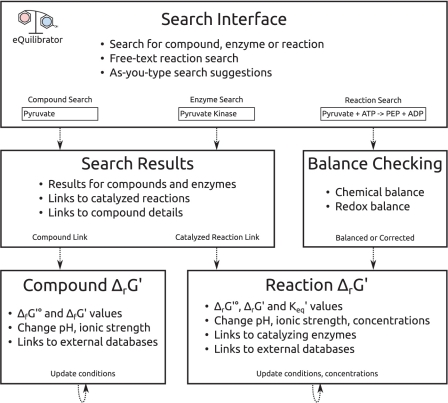
The eQuilibrator web interface is designed to guide users to Δ_rG′° values as quickly as possible, detecting and correcting mistakes along the way (Figure 1). Users can search for biochemical reactions in free text or by the name of a catalyzing enzyme. For example, the aldolase reaction can be written as ‘fructose 1,6 bisphosphate ⇌ glyceraldehyde 3-phosphate + dihydroxyacetone phosphate‘. The same reaction can also be found by searching for ‘aldolase’ or ‘fructose bisphosphate aldolase.’ As you type, the search interface suggests matching compound and enzyme names, helping to avoid errors.

Figure 1.

Summary of the flow and features of usage of the eQuilibrator web interface. Users arrive at the main page and may search for a compound (‘pyruvate’), an enzyme (‘pyruvate kinase’) or a reaction (‘PEP + ADP ⇌ pyruvate + ATP’). Users who enter a reaction formula are taken directly to a reaction page where the chemical and redox balance of the reaction is checked and the Δ_rG′° is given. The reaction can be transformed easily to different cellular conditions and reactant concentrations to yield Δ_rG′. Users who search for a compound or enzyme are taken to a search results page. Search results offer links to catalyzed reactions for enzymes and links to a summary page with chemical and thermodynamic data for compounds.

eQuilibrator detects chemical and charge imbalance and can automatically correct it in some cases. In the case of the putative reaction ‘glucose ⇌ gluconate’, eQuilibrator recognizes that this hydration is missing a water molecule and offers to automatically balance the reaction. Once the water is added, eQuilibrator detects that ‘glucose + H2O ⇌ gluconate’ is not redox balanced: glucose and water have two more electrons than gluconate. eQuilibrator offers to balance the half-reaction with NAD and NADH. In our experience balance checking prevents common errors in analyzing reactions.

If a reaction query is properly balanced then eQuilibrator shows a reaction page including Δ_rG′° and K′, the formation energies of all reactants and any known catalyzing enzymes (Figure 2). In calculating Δ_rG′°, eQuilibrator ensures that formation energies are from consistent sources, avoiding errors stemming from contradictory assumptions. The reaction page also allows users to transform Δ_rG′° into Δ_rG′ by applying arbitrary pH, ionic strength and reactant concentrations and to plot Δ_rG′° as a function of pH and ionic strength (Figure 2).

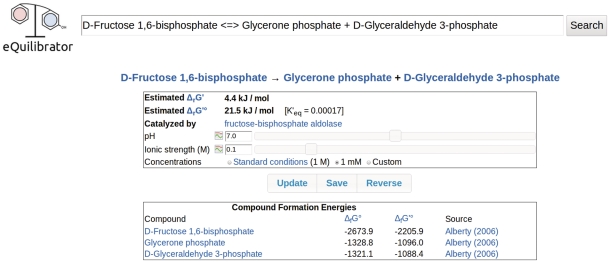
Figure 2.

A reaction page for the fructose bisphophate aldolase reaction showing Δ_rG′°, K′ and Δ_rG′ for 1 mM reactant concentrations at pH 7 and ionic strength 0.1.

From the reaction page it is simple to explore the properties of reactants and catalyzing enzymes. Each compound and enzyme in the database has a dedicated page that can be reached from a reaction page (or via the search interface). Enzyme pages list all known catalyzed reactions and provide links to KEGG and BRENDA (17,22). eQuilibrator's compound page shows the compound formula, mass, structure and formation energy and enables transformation of Δ_fG′° to different pH and ionic strength (Figure 1).

The structure of the eQuilibrator database is summarized in Table 1. General biochemical data like compound structures and molecular weights are drawn from the KEGG database (17). In all, eQuilibrator draws data on approximately 13 500 compounds, ∼6400 reactions and ∼2800 enzymes from KEGG. eQuilibrator catalogues formation energies for the various protonation states of ∼11 700 of the compounds. As discussed above, these formation energies are of two general types: those inferred from measurements (11,23,24) and those approximated according to the group-contribution assumption (Noor, E. et al. Submitted for publication). Source references are given for all formation energies (Figure 2).

Table 1.

Summary of eQuilibrator database structure

Entity	Description
CommonName	The name of a compound or enzyme.
Species	A protonation state of a biochemical compound. Contains the number of hydrogens, net charge and formation energy.
SpeciesGroup	A consistent group of Species for a specific compound from a single data source. Contains a source reference.
Compound	A biochemical compound. Contains a list of CommonNames, links to external databases, the chemical formula, mass, compound structure, and a list of SpeciesGroups for computing formation energies.
StoredReaction	A known biochemical reaction. Contains a list of compounds and their stoichiometric coefficients and a list of references to any catalyzing enzymes.
Enzyme	An enzyme. Contains a list of CommonNames and a list of StoredReactions catalyzed by this enzyme.

eQuilibrator also serves an important pedagogical role, providing detailed explanations of essential matters including the appropriate handling of pH, redox reactions and dissolved CO₂. Links to these explanations are provided during use. For example, if a reaction query is not redox balanced, we link to a discussion of redox reactions and a description of how eQuilibrator handles them. In this way, users are exposed to the basics of biochemical thermodynamic analysis through repeated use of eQuilibrator.

EXAMPLES OF USE

Evaluating reaction reversibility

Many metabolic models rely on tagging the reversibility of reactions to constrain the space of possible solutions (25–27,21). eQuilibrator greatly simplifies this process. For example, the fructose bisphosphate aldolase reaction mentioned above has a Δ_rG′° of ∼21 kJ/mol (pH = 7.0, ionic strength = 0.1 and T = 298.15 K here and throughout). Using eQuilibrator it is trivial to adjust all concentrations to 100 μM and see that the reaction is easily reversed at physiological concentrations (Δ_rG′° = −1.5 kJ/mol). Though the aldolase reaction is reversible, the reaction direction is sensitive to cellular pH and ionic strength. By using eQuilibrator to plot Δ_rG′ as a function of pH at 1 mM concentrations we find that acidic pH and high ionic strength favor the reverse reaction direction and the formation of fructose 1,6 bisphophate.

Some reactions are in fact irreversible given biological constraints. PEP phosphatase catalyzes the reaction PEP + H₂O ⇌ pyruvate + Pi which has a Δ_rG′° of −65 kJ/mol. Even if we set the concentration of PEP to 1 nM—about one molecule per E. coli cell (28)—and the concentrations of Pyruvate and Pi to 1 M Δ_rG′ is still negative (∼−14 kJ/mol). Indeed, the phosphate moiety of PEP is particularly energetic: some organisms couple the hydrolysis of PEP to the production of two ATP equivalents (29,30). Thus, the PEP phosphatase reaction always flows in the direction of pyruvate and Pi formation. Using eQuilibrator it is also simple to verify that changes in pH and ionic strength don't alter the reaction direction.

Thermodynamic feasibility of pathways

Using eQuilibrator we can analyze the net feasibility of a pathway and examine its sensitivity to pH. Here we analyze the fermentation of glucose to lactate as an example. Without accounting for ATP production, the net reaction of lactic acid fermentation is glucose ⇌ 2 lactate (12). Assuming 1 mM concentrations, pH 7 and ionic strength of 0.1, the Δ_rG′ of this reaction is −217 kJ/mol (31,21,15). In glycolysis this energy is coupled to ATP production from ADP and inorganic phosphate, which requires roughly 50–60 kJ/mol at physiological concentrations (12,13).

Most organisms produce two ATP during glucose fermentation (12). The net energetics imply that this is quite feasible: there is an excess of 120 kJ/mol of glucose. So why not make three or even four ATP? We can plot the pH dependence of Δ_rG′ for a fermentation strategy producing four ATP at 1 mM reactant concentrations. It is clear from the graph that this strategy is only favorable in a very narrow pH range (∼pH 6–7.25), suggesting that it is perhaps too fragile for biological use.

METHODS

eQuilibrator source code is freely available on Google Code (http://code.google.com/p/milo-lab/). The eQuilibrator web interface is composed of a back-end implemented in Python and a user interface implemented with HTML, CSS and JavaScript. A wide range of open software and databases significantly aid the development and maintenance of eQuilibrator. Non-thermodynamic data including compound names, masses and formulae, enzyme names, EC classes and catalyzed reactions are drawn from KEGG (17) and stored in a MySQL database. Thermodynamic data is drawn from several sources (11,23,24) and is stored in the same database. The Django framework is used to simplify database setup and querying, HTML generation, and web serving. Search queries are parsed via the pyparsing library and search results are ranked according to the degree to which they match the search query, where the degree of matching is computed using the edit-distance algorithm. The user interface is implemented using standard HTML and CSS. The dynamic portions of the interface, including real-time search suggestions, are implemented in JavaScript using the jQuery framework.

Thermodynamic data is available for download in standard formats—JavaScript Object Notation (JSON) and Comma-Separated Values (CSV)—and is provided at several levels of granularity. Files containing compound Δ_fG′° and reaction Δ_rG′° values at various combinations of pH and ionic strength are available. For those interested in detailed analyses involving varying cellular pH and ionic strength, files containing Δ_fG° values for the various protonation states of KEGG compounds are also available.

FUTURE PLANS AND CONCLUSIONS

Though thermodynamic data is available for download, the eQuilibrator interface performs many calculations that users may not want to re-implement. Accordingly, we plan to create a programmatic interface to eQuilibrator that allows client software to perform thermodynamic calculations regardless of their programming language of choice.

We are especially proud that eQuilibrator is fully open source and that our data is freely available in standard formats. We have experienced firsthand how open-source software and data simplifies our work, and we are happy to contribute to the community. We believe that eQuilibrator facilitates the development and testing of novel hypotheses about metabolism and is the appropriate resource for those interested in biochemical thermodynamics.

FUNDING

European Research Council (grant 260392 - SYMPAC); Azrieli Foundation (to E.N.). Adams Fellowship Program of the Israel Academy of Sciences and Humanities (to A.B.E.); ERC (260392 - SYMPAC) (to R.M.); Anna and Maurice Boukstein career development chair (to R.M.). Funding for open access charge: ERC.

Conflict of interest statement. None declared.