Compensation of Slice Profile Mismatch in Combined Spin- And Gradient-Echo EPI Pulse Sequences

Abstract

Combined acquisition of gradient-echo and spin-echo signals in MRI time series reveals additional information for perfusion-weighted imaging and functional magnetic resonance imaging due to differences in the sensitivity of gradient-echo and spin-echo measurements to the properties of the underlying vascular architecture. The acquisition of multiple echo trains within one time frame facilitates the simultaneous estimation of the transversal relaxation parameters R₂ and R₂*. However, the simultaneous estimation of these parameters tends to be incorrect in presence of slice profile mismatches between signal excitation and subsequent refocusing pulses. It is shown here that improvements in pulse design reduced R₂ and R₂* estimation errors. Further improvements were achieved by augmented parameter estimation through the introduction of an additional parameter δ to correct for discordances in slice profiles to facilitate more quantitative measurements. Moreover, the analysis of time-resolved acquisitions revealed that the temporal stability of R₂ estimates could be increased with improved pulse design, counteracting low contrast-to-noise ratios in spin-echo-based perfusion and functional MRI.

INTRODUCTION

A combined acquisition of gradient-echo (GE) and spin-echo (SE) signals offers considerable benefits in dynamic susceptibility-contrast perfusion-weighted imaging (DSC-PWI) and functional MRI (fMRI). GE and SE signals experience different sensitivities to the underlying vasculature. Specifically, GEs have a higher overall sensitivity to susceptibility-modulating mechanisms such as Gadolinium-based contrast agents in DSC-PWI or deoxyhemoglobin in fMRI. The sensitivity of GEs is highest for medium and large vessels, while SEs are mostly sensitive to the small vessel range, as shown in (1). Thus, simultaneous measurements of SE and GE signals (2) enhance PWI and fMRI experiments and allow vessel size imaging (3–8). The information obtained from R₂ and R₂* maps is of particular interest for quantitative approaches in PWI and fMRI. Measurements of absolute R₂(t) and R₂*(t) instead of their relative changes to baseline, i.e. ΔR₂(t) and ΔR₂*(t), reduce confounding T₁-effects during contrast agent passage, as shown in several studies using multi-GE acquisitions (9–13). Also, the blood oxygen saturation can be quantified with knowledge of absolute R₂ and R₂* (14,15).

PWI and fMRI require fast imaging to achieve high temporal resolution, a goal that is most often accomplished by echo-planar imaging (EPI) techniques (16). A problem with combined GE/SE acquisitions in EPI sequences are poor slice profiles, specifically caused by short radiofrequency (RF) pulse durations required for fast imaging, including spectral-spatial (SPSP) RF pulses. Longer RF pulses with better slice profiles are seldom feasible due to sequence timing constraints, and SPSP pulses are limited by the maximum gradient strength and slew rate of the MRI system.

In combined GE/SE imaging, the combination of two RF pulses with non-ideal slice profile characteristics leads to a slice profile-induced mismatch between gradient-echoes prior and gradient- and spin-echoes after the 180° refocusing pulse. This mismatch can cause considerable differences between signal magnitude before and after the refocusing pulse. These differences increase as the slice profile mismatch becomes more pronounced. In previous studies with combined GE and SE signal readouts, either this effect has not been considered (8,17), readouts prior to the 180° pulse were not acquired (15,18), or too few echo trains prevented the absolute quantification of R₂ and R₂* (3,4,6,7).

In this study, we describe the problem of mismatched slice profiles in combined GE/SE EPI sequences, demonstrate its consequences for quantification of R₂ and R₂*, and propose an augmented parameter estimation to address the signal disparity caused by the mismatched profiles. In the proposed solution, the slice profile mismatch was simultaneously estimated with the transversal relaxation parameters to better fit the MR signal decay. A central aim of this study was to show that a correction for slice profile mismatches mitigated errors in the estimation of R₂ and R₂*. This approach was tested with two different sets of RF pulses: a) RF pulses provided by the vendor of our MRI systems, in the following referred to as product pulses, and b) RF pulses optimized for simultaneous GE and SE EPI acquisitions designed at our institute, referred to as optimized pulses.

THEORY

A multi-echo combined gradient- and spin-echo EPI pulse sequence (8,19) facilitates simultaneous measurements of R₂ and R₂*. Repeated dynamically, such a sequence offers added quantitative features in DSC-PWI and fMRI through measurements of the time-dependent signals R₂(t) and R₂*(t). All echo trains experience different R₂*- and R₂-weighting as a result of intrinsic and extrinsic susceptibility sources (see Fig. 1). For each time point t, R₂ and R₂* can be directly observed with such a multi-echo pulse sequence by least-squares (LSQ) fitting of the following MR signal equations (17):

$$S(\tau )=\{\begin{array}{cc}{S}_0^I·e^{-\tau ·(R_2+R_2\text{'})}=S_0^I·e^{-\tau ·R_2^{*}}\hfill & ,0<\tau <\frac{\mathit{\text{TE}}}{2}\hfill \\ S_0^{\mathit{\text{II}}}·e^{-\mathit{\text{TE}}·R_2\text{'}}·e^{-\tau ·(R_2-R_2\text{'})}=S_0^{\mathit{\text{II}}}·e^{-\mathit{\text{TE}}·(R_2-R_2^{*})}·e^{-\tau ·(2·R_2-{R_2}^{*})}\hfill & ,\frac{\mathit{\text{TE}}}{2}<\tau \le \mathit{\text{TE}}\hfill \end{array},$$ (1)

with S₀ the equilibrium signal for each signal excitation and R₂* = R₂ + R₂’. In practice, the assumption that the equilibrium signals S₀^I and S₀^II are identical does not hold for combined GE/SE EPI measurements. This can be attributed to differences between radiofrequency (RF) excitation and refocusing pulse profiles, as both are tradeoffs between optimal pulse shape and pulse duration. The slice profiles of the short duration RF pulses needed for fast imaging deviate substantially from the ideal rectangular shape (cf. Fig. 2).

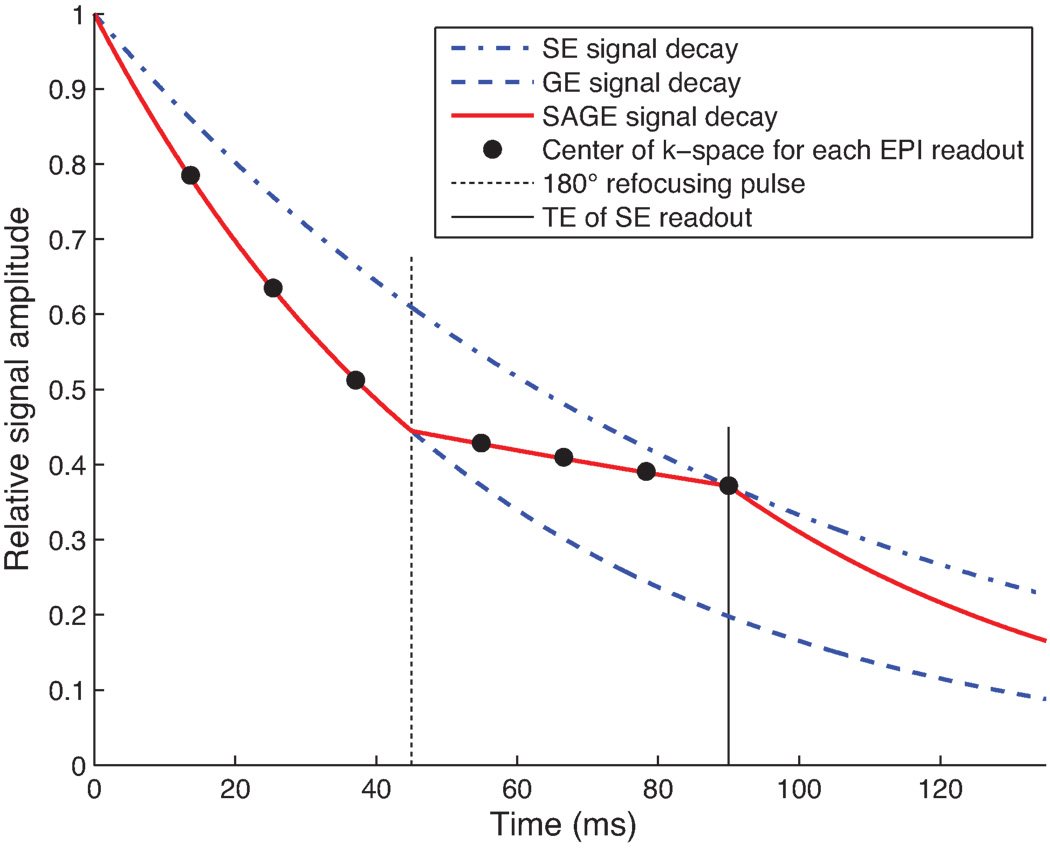
Fig. 1.

Theoretical signal decay in a uniform voxel within brain tissue using a 7-echo Spin- And Gradient-Echo (SAGE) pulse sequence with perfectly matched excitation and refocusing pulses, and the transversal relaxation parameters R₂ = 11 s⁻¹ and R₂* = 18 s⁻¹.

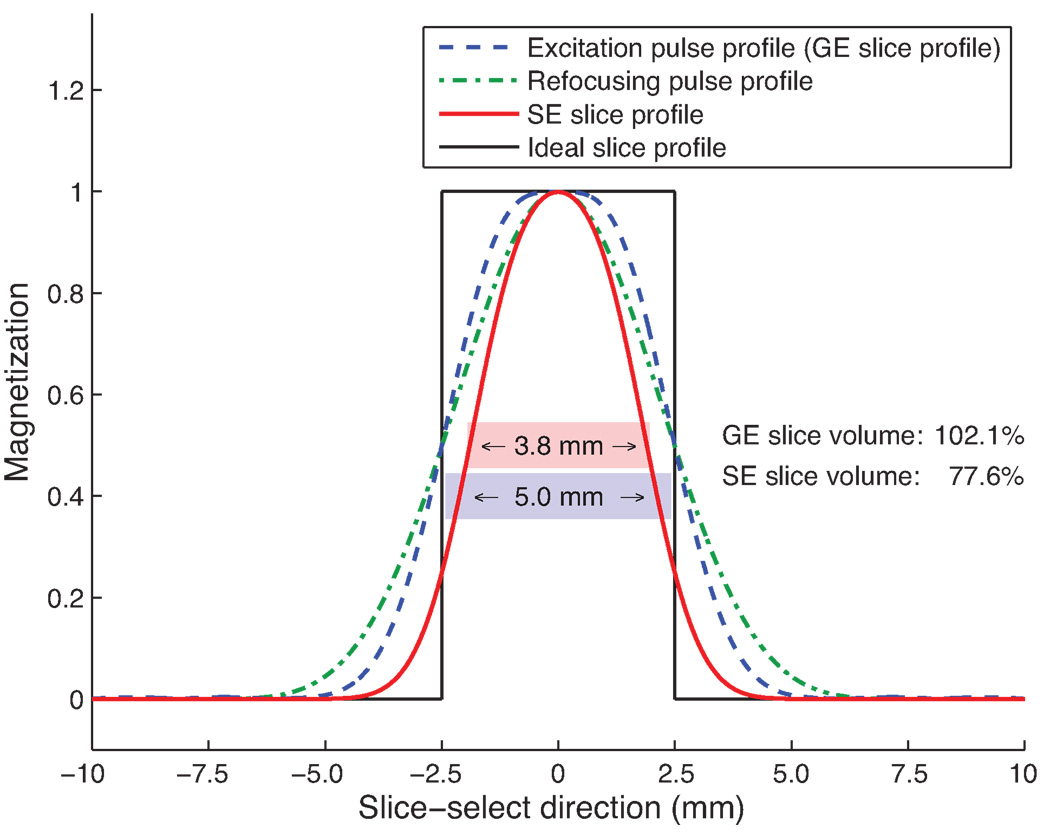
Fig. 2.

Slice profiles in acquisitions with regular pulses. The ideal slice profile is shown in black. 90° excitation pulse (blue) was followed by 180° refocusing pulse (green), resulting in a narrowed effective slice profile (red). In this particular case, both pulses were designed to affect all spins within a 5.0 mm thick slice. However, due to rounded edges in the slice profiles of both the excitation and the refocusing pulses, the resulting SE profile had a full-width-half-maximum (FWHM) slice thickness of only 3.8 mm, and a slice volume (area under red curve) of 77.6% relative to the size of the ideal pulse profile shown in black, whereas the GE slice volume covered an area that was 102.1% as large as the size of the area covered by the ideal box-shaped slice profile, producing a SE slice volume that was 24% smaller than the GE slice volume.

Slice profiles in spin-echo sequences are generated by the multiplication of the pulse profile of the excitation pulse with the profile of the refocusing pulse, as long as a pair of well-designed crusher gradients is present to suppress the free induction decay (FID) signal produced by the transition regions of the pulse profiles (20). Consequently, mismatched excitation and refocusing pulse profiles lead to incomplete signal refocusing and an altered spin-echo slice profile. In this case, the initial signals S₀^I and S₀^II used to model the exponential signal decay before and after the refocusing pulse are not identical, thus S₀^I ≠ S₀^II.

In Ref. (17), multiple echoes were sampled both before and after the refocusing pulse with a pulse sequence named GESFIDE (gradient-echo sampling of FID and echo). The first and second lines in Equation 1 were treated separately. Thus, extensive issues with slice profile imperfections could be avoided. However, to achieve high temporal resolution, only a limited number of echo trains can be acquired with an EPI sequence. Thus, the separate treatment of lines 1 and 2 in Equation 1 renders R₂ and R₂* estimates using EPI-based acquisition methods more susceptible to measurement errors in any individual echo train, a limiting factor that also applies to the MESSER (multi-gradient-echo single-shot sampling of spin-echo refocusing) sequence used in (8). Moreover, the exponential signal decay constants before (R₂*) and after (R₂⁻ = 2·R₂ – R₂*) the refocusing pulse are affected by differences in the underlying slice volumes with implications for the estimation of R₂.

To eliminate the effects of a mismatch between the excitation and the refocusing pulse, Yablonskiy et al. (18) proposed a pulse sequence termed GESSE (gradient-echo sampling of the spin-echo), in which GEs and SEs were sampled after the refocusing pulse only, distributed about the echo time for a Hahn spin-echo. However, due to rapid signal drop-off associated with the length of each EPI echo train as well as temporal constraints in DSC-PWI and fMRI, the acquisition of additional echo trains following a spin-echo is feasible only to a limited extent. Instead, sampling gradient-echo signals prior to the refocusing pulse, i.e. between signal excitation and refocusing, allows better utilization of otherwise unused scan time and it improves the signal-to-noise ratio (SNR) of the EPI images used for the parameter estimation.

To achieve immunity against slice profile differences, one potential remedy to these limitations is the introduction of an additional correction term δ that relates the equilibrium signal S₀^I prior to the refocusing pulse to the equilibrium signal S_O^II after the refocusing pulse to account for pulse profile differences. Here, δ can be estimated from the ratio of S₀^I and S₀^II in Equation 1, i.e.

$$S_0^I=\delta ·S_0^{\mathit{\text{II}}}.$$ (2)

Thus, S₀^I and S₀^II can be treated as independent variables, and both can be estimated through LSQ fitting of Equation 1, given a large enough number of echoes M ≥ 4. Then, δ can be calculated using Equation 2.

Alternatively, δ can be derived from the ratio of the integrals of the transversal magnetization along the slice-select dimension before and after the refocusing pulse using

$$\delta =\frac{S_0^I}{S_0^{\mathit{\text{II}}}}=\frac{{\displaystyle \underset{-\epsilon }{\overset{\epsilon }{\int }}}{M}_{\mathit{\text{xy}}}^I(z)\mathit{\text{dz}}}{{\displaystyle \underset{-\epsilon }{\overset{\epsilon }{\int }}}{M}_{\mathit{\text{xy}}}^{\mathit{\text{II}}}(z)\mathit{\text{dz}}},$$ (3)

with ε equal to the spatial extent of the transversal magnetization M_xy^I,II in slice-select dimension. Due to limitations in the MRI hardware, such as imperfect RF amplifiers and gradient delays, the slice profiles in an MRI experiment deviate from the slice profiles determined by computer simulations. Hence, the exact slice profiles in a given experiment are unknown. However, δ can be determined in RF pulse simulation using Equation 3 and then compared to the results of an MRI experiment and subsequent determination of δ according to Equations 1 and 2. In the present study, Equation 3 was used to determine δ in RF pulse simulations, and Equations 1 and 2 were used to estimate δ in a given MRI experiment.

METHODS

MRI experiments

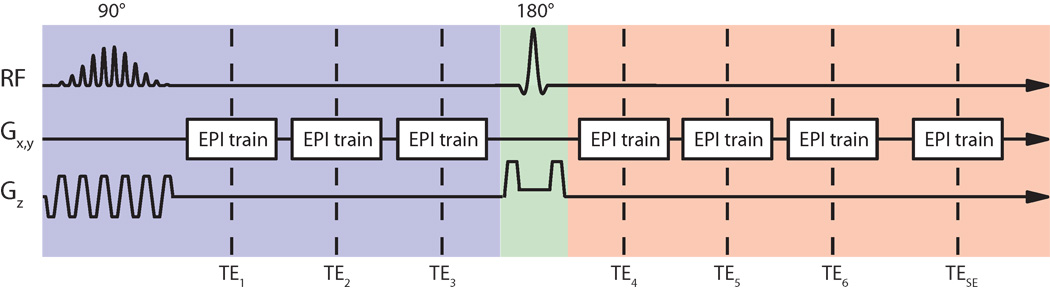
Images were acquired with a GE/SE EPI sequence with EPI echo trains both before and after the refocusing pulse (Fig. 3, Ref. (19)). In the remainder of this work, we refer to this pulse sequence as SAGE EPI (Spin- And Gradient-Echo Echo-Planar Imaging). Multi-echo acquisition with SAGE EPI was facilitated by parallel imaging acceleration using GRAPPA (Generalized Autocalibrating Partially Parallel Acquisitions (21)) with a 2D kernel size of 2 × 5 (k_y, k_x) k-space points (22).

Fig. 3.

SAGE EPI sequence (19) with 7 echo trains distributed about the refocusing pulse. Parallel imaging acceleration was used to increase the number of echo trains that could be acquired. The first 3 echo trains (TE_1–3) in this sequence were R₂*-weighted and experienced the excitation pulse profile (blue background), whereas the subsequent 3 echo trains (TE_4–6) were R₂- and R₂*-weighted, while the last echo train (TE_SE) was R₂-weighted. All echo trains acquired after the 180° refocusing pulse experienced the spin echo slice profile (red background).

Our experiments were carried out in an agar nickel-chloride phantom and a human brain. Informed consent was obtained for all human volunteers scanned as part of this study. MRI experiments were conducted on a 1.5T Signa Excite 14.0 MRI scanner (General Electric Healthcare, Waukesha, WI, USA) with gradient strength = 50 mT/m and gradient slew rate = 150 T/m/s, using an 8-channel head array (Invivo Corporation, Orlando, FL, USA) and the following acquisition parameters: 7 echo trains with parallel imaging reduction factor R = 3, matrix size = 66 × 66, number of slices = 15, slice thickness = 5 mm, spacing = 2 mm, field of view = 24 cm, repetition time (TR) = 1800 ms, flip angles: 90° SPSP excitation pulse and 180° refocusing pulse, echo times (TEs): TE₁ = 11.5 ms, TE₂ = 22.8 ms, TE₃ = 34.2 ms, TE₄ = 58.2 ms, TE₅ = 69.6 ms, TE₆ = 80.9 ms, and TE_SE = 95.0 ms.

Experiments were carried out with product pulses provided by the vendor of our MRI systems and optimized pulses. RF pulses were designed and analyzed in MATLAB (The MathWorks, Natick, MA, USA) using rf_tools (Radiological Sciences Laboratory, Stanford University, Stanford, CA, USA). The following two paragraphs briefly describe the properties of the RF pulses used in this study.

Product pulses provided by the vendor

The excitation pulse used in the product EPI sequence on our 1.5T unit was an SPSP pulse developed for a maximum gradient slew rate of 150 T/m/s. It was designed with the Shinnar-Le Roux (SLR) algorithm (20,23–27) using a true-null design. A total of 12 sub-pulses formed an SPSP pulse with an overall pulse width of 14.4 ms, spatial time-bandwidth product (TBW) of approximately 3.1, and RF power deposition of 1.63·10⁻⁶ G²·s. The spin-echo refocusing pulse in the product sequence was also designed using the SLR algorithm; its pulse width was set to 3.2 ms and TBW was 2.9, with RF power deposition of 17.99·10⁻⁶ G²·s.

Optimized pulses for SAGE EPI

We re-developed both the SPSP pulse as well as the spin-echo pulse with the goal of achieving a better match between the two pulse profiles, while keeping the RF pulse lengths reasonably short. A new SPSP pulse was designed with a 2D SLR algorithm using true-null design, with 15 side lobes of 1.088 ms duration each, resulting in a pulse width of 16.32 ms. Both spatial as well as spectral TBW were set to 4.0. The gradients were designed with a slew rate limit of 150 T/m/s. Peak B₁ of this pulse was 0.074 G for a nominal flip angle of 90°, resulting in an RF power deposition of 3.12·10⁻⁶ G²·s. A 180° spin-echo refocusing pulse was designed with minimal transition width, reasonably small ripples in the pulse profile, and an RF pulse amplitude below 0.164 G (700 Hz). The SLR refocusing pulse was designed with TBW = 4.9, pulse width = 6.4 ms, RF power deposition = 17.93·10⁻⁶ G²·s. Due to small changes in the pulse durations, echo times were adjusted accordingly, such that TE₁ = 15.0 ms, TE₂ = 26.4 ms, TE₃ = 37.7 ms, TE₄ = 57.7 ms, TE₅ = 69.1 ms, TE₆ = 80.4 ms, and TE_SE = 95.0 ms.

Verification of augmented parameter estimation

In the first experiment, we acquired phantom and in-vivo data with the SAGE EPI pulse sequence and solved the MR signal equation with and without consideration of the correction factor δ. In the following, the method that corrects for mismatched slice profiles is referred to as 4-parameter estimation model and the method without mismatch correction is referred to as 3-parameter estimation model. Equation 1 was solved with a LSQ approach, with average MR signals of each echo train within a specified region of interest (ROI) as the measured variables.

In the second experiment, we replaced the product pulses with the optimized pulses to minimize the slice profile mismatches and to determine if slice profile mismatches indeed are the main cause for estimation errors of the transversal relaxation parameters in combined GE/SE EPI measurements.

The goodness of fit to the signal decay model was assessed by calculating the root mean square percentage error (RMSPE):

$$\mathit{\text{RMSPE}}=\sqrt{\frac{1}{n}·{\displaystyle \sum _{i=1}^n}{\left(100·\frac{\tilde{S}(t)-S(t)}{\tilde{S}(t)}\right)}^2}.$$ (4)

Here, S̃(t) represents the measured signal at time t, and n is the number of acquired echo trains. RMSPE was calculated for both pulse pairs and for the 3-parameter as well as the 4-parameter estimation.

In addition, estimated R₂ and R₂* were compared to reference values obtained in separate acquisitions. A reference value for R₂* was determined with a 7-echo GE EPI sequence (13,28) with equidistant echo times ranging from 11.5 ms to 75.6 ms, using the SPSP product pulse provided by the vendor, which was described earlier. The reference acquisitions immediately followed the SAGE EPI acquisitions, using the same imaging parameters and geometrical setup, except for TR = 5000 ms. R₂ was determined through the combination of 7 single-echo SE EPI datasets, acquired with varying echo times ranging from 35 ms to 95 ms and a repetition time of 5000 ms. These measurements were acquired following the two product pulses described earlier. All other parameters were identical to those used in SAGE EPI. The pre-scan values were kept constant for all 7 SE EPI acquisitions. The patients’ heads were padded to prevent them from moving between acquisitions. R₂ and R₂* were calculated using LSQ fitting of the mono-exponential functions

$$S_{\mathit{\text{GE}}}(t)=S_{0,\mathit{\text{GE}}}·{\mathrm{e}}^{-t·{R_2}^{*}},$$ (5)

and

$$S_{\mathit{\text{SE}}}(t)=S_{0,\mathit{\text{SE}}}·{\mathrm{e}}^{-t·R_2}.$$ (6)

Temporal signal stability of EPI trains acquired with product pulses and optimized pulse design

In fMRI and PWI experiments, the temporal signal stability (signal precision) is of highest importance. Therefore, the experiments with both pulse pairs were repeated in an agar phantom for a total of 60 time frames, similar in duration to a PWI or short fMRI experiment. For each pulse pair, voxel-wise relative standard deviation (RSD) of the signal of each echo train over all time points was determined. To assess the temporal stability of R₂ and R₂* estimates, all 7 echo trains per time point were used for data fitting. Then, the RSDs of R₂ and R₂* over time were calculated.

RESULTS

Slice profile simulations with product pulses

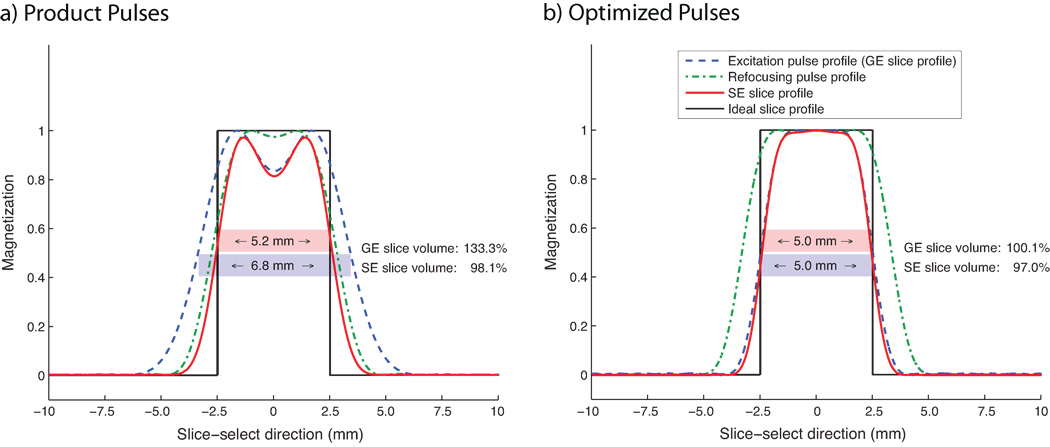
The standard 90° SPSP excitation product pulse produced a FWHM (full width at half maximum) slice thickness of 6.8 mm, as opposed to a prescribed slice thickness of 5.0 mm. This value was determined through pulse profile simulations using MATLAB. Thus, the slice thickness of the excitation pulse was 36% too wide. The slice volume, i.e. the integral of the transversal magnetization along z (see Equation 3), was 33.3% larger than prescribed. The ratio of the widths between passband and transition band in spatial domain was equal to 1.45. For simulations showing the slice profile of this excitation pulse, refer to Fig. 4a.

Fig. 4.

Slice profile shapes determined through MATLAB simulations. (a) Slice profiles of pulses in product EPI sequence (product pulses). The excitation pulse profile using a 90° SPSP excitation pulse provided by the vendor resulted in a FWHM slice thickness of 6.8 mm for a prescribed slice thickness of 5.0 mm. The SE pulse profile had a FWHM slice thickness of 5.2 mm. This error led to a GE slice volume that covered an area that was 133.3% as large as the size of the area covered by an ideal box-shaped slice profile, whereas the SE slice volume covered an area that was 98.1% relative to the size of the area covered by an ideal volume. From these simulations follows that this pulse combination was likely designed for pure spin-echo EPI acquisitions. (b) Optimized pulses for better match between gradient-echo slice profile (blue) and spin-echo profile (red). The slice-selective gradient that was played out during the refocusing pulse was reduced to 75% of its original value to achieve a good match between the pulses without sacrificing multi-slice acquisition capability. Simulations revealed that the resulting spin-echo (gradient-echo) slice profile covered an area that was 97.0% (100.1%) as large as the size of the area covered by an ideal box-shaped slice profile.

The effective FWHM of the 180° refocusing product pulse was 5.6 mm in simulations, given a nominal slice thickness of 5.0 mm. The design constraints of a short pulse duration (3.2 ms) and small TBW (2.9) resulted in a ratio of the spatial passband to the transition band of 1.38, which is relatively low for a spin-echo pulse. See Fig. 4a for the pulse profile of the refocusing pulse.

The slice profile of the SPSP excitation product pulse was larger than the nominal slice thickness (Fig. 4a, blue dashed), while the slice profile of the vendor’s 180° refocusing product pulse was considerably narrower (Fig. 4a, green dashed). The slice profile resulting from the application of both pulses had a FWHM slice thickness of 5.2 mm, slightly larger than the prescribed 5.0 mm (Fig. 4a, red). Compared to the volume of a box-shaped slice profile with 5.0 mm thickness, the volume of the resulting slice was 98.1% as large, while the slice volume excited by the 90° SPSP pulse was 133.3% as large. This difference exists because the product pulses were likely optimized for the refocused spin-echo pulse profile. In SAGE EPI, however, a good 90° SPSP pulse profile is desired because gradient-echo readouts are used in addition to spin-echo readouts.

Slice profile simulations with optimized pulses

The optimized SPSP pulse had a simulated slice thickness equal to the prescribed thickness of 5.0 mm, and a slice volume that covered an area that was 100.1% as large as the size of an area covered by a 5.0 mm wide box-shaped product pulse. The ratio of the spatial passband to the transition band was 1.75, an increase compared with the product pulse mainly due to a larger TBW in conjunction with higher peak B₁, resulting in a better-defined pulse profile (see Fig. 4b).

The 180° refocusing pulse also resulted in the same slice thickness as prescribed. The passband to transition band ratio, 2.25, was considerably higher than that of the product pulse; this increase was achieved with larger pulse width.

The spin-echo profile resulting from the application of the optimized 90° SPSP excitation and 180° refocusing pulse is illustrated in red in Fig. 4b. To match the slice profiles of the 90° pulse and the combined 90°–180° pair, the slice-selective gradient strength applied during signal refocusing was decreased by 33.3% compared to its nominal value, a technique commonly applied in spin-echo imaging to widen the refocusing pulse. The resulting slice volume after signal refocusing was 97.0% as large as the size of an area covered by an ideal box-shaped slice, with a resulting slice thickness of 4.9 mm. Thus, we achieved a good match between GE slice profile and SE slice profile by optimized pulse design and adjustments in slice-selective gradient strength.

Signal behavior in phantom experiment

The fit to the case of product pulses using 3-parameter estimation (without δ) provided large overestimations of R₂ and R₂* and a large fitting error (RMSPE = 5.97, cf. Table 1a). By incorporating S₀^II = S₀^I/δ into the fitting function, thus using 4-parameter estimation, the fit was much better (RMSPE = 0.37). δ was estimated at 1.38, indicating that the GE slice volume was 38% larger than the SE slice volume. According to the simulations shown in Fig. 4a, the GE (SE) slice volume mismatch resulted in δ = 1.36 and a simulated GE slice volume that was 36% larger than the SE slice volume.

Table 1.

a: Estimated parameters R2, R2*, S0I, S0II, in phantom measurements.
		RF Pulses	Model	R2 [s−1]	R2* [s−1]	S0I	S0II	δ	RMSPE
Phantom	(a)	Product pulses	3-parameter estimation	24.49 (+24.9%)1	27.08 (+35.7%)	9280	9280	1.00	5.97
	(b)	Product pulses	4-parameter estimation	19.18 (−2.1%)	19.49 (−2.3%)	8012	5819	1.38	0.37
	(c)	Optimized pulses	3-parameter estimation	20.69 (+5.6%)	21.60 (+8.3%)	9281	9281	1.00	1.84
	(d)	Optimized pulses	4-parameter estimation	19.15 (−2.2%)	19.48 (−2.2%)	8852	8117	1.09	0.42
	Reference data			19.60	19.95	-	-	-	-

b: In-vivo measurements within ROIs comprising gray matter or white matter.
		RF Pulses	Model	R2 [s−1]	R2* [s−1]	S0I	S0II	δ	RMSPE
Human GM	(a)	Product pulses	3-parameter estimation	15.97 (+55.2%)1	21.05 (+67.2%)	16671	16671	1.00	6.88
	(b)	Product pulses	4-parameter estimation	9.83 (−4.5%)	12.28 (−2.5%)	14067	9720	1.45	0.45
	(c)	Optimized pulses	3-parameter estimation	11.54 (+12.1%)	14.98 (+18.9%)	11448	11448	1.00	1.90
	(d)	Optimized pulses	4-parameter estimation	9.99 (−2.9%)	12.84 (+2.0%)	10916	10005	1.09	0.64
	Reference data			10.29	12.59	-	-	-	-
Human WM	(a)	Product pulses	3-parameter estimation	17.99 (+39.2%)	21.25 (+45.3%)	13068	13068	1.00	5.58
	(b)	Product pulses	4-parameter estimation	13.03 (+0.9%)	14.17 (−3.2%)	11393	8453	1.35	0.48
	(c)	Optimized pulses	3-parameter estimation	14.07 (+8.9%)	16.15 (+8.9%)	9210	9210	1.00	1.80
	(d)	Optimized pulses	4-parameter estimation	12.63 (−2.3%)	14.15 (−3.2%)	8810	8122	1.08	0.66
	Reference data			12.92	14.63	-	-	-	-

¹Shown in parentheses are deviations from the reference data listed at the bottom.

With optimized pulses, slice profile mismatches were greatly reduced, resulting in a smaller RMSPE = 1.87 using 3-parameter estimation, compared to the same model with product pulses (RMSPE = 5.97). However, the pulse profiles could not be matched perfectly. A fit to the 4-parameter estimation model of the data collected using optimized pulses gave δ = 1.09, indicating a slice volume mismatch of 9% according to Equation 3. This is larger than the 3% volume mismatch obtained in pulse simulations using Equation 3. The RMSPE of the fit of the data collected using optimized pulses to the 4-parameter estimation model was 0.42, similar to the value (0.37) achieved with the same model using product pulses.

Estimations of R₂ and R₂* were close to the reference values with both pulse designs using 4-parameter estimation (less than 2.5% deviation from the reference values), whereas the relaxation coefficients obtained from fits to the 3-parameter model were overestimated by 24.9% for R₂ and 35.7% for R₂* using product pulses, and by 5.6% and 8.3% for R₂ and R₂* respectively using optimized pulses. A summary of the phantom experiments is given in Table 1a. Fig. 5 shows parameter estimates of δ, R₂, and R₂* for the 3-parameter as well as the 4-parameter estimation using both optimized and product pulses.

Fig. 5.

Parameter estimations of δ, R₂*, and R₂ for a selected slice in a phantom experiment. Shown are parameters estimated in measurements with (a) product pulses using 3-parameter estimation, (b) product pulses using 4-parameter estimation, (c) experiments with optimized pulses using 3-parameter estimation, and (d) optimized pulses using 4-parameter estimation. δ_Avg is the average of δ within the slice shown in this figure using 4-parameter estimation.

Signal behavior in in-vivo experiment of the human brain

The relaxation parameters measured in ROIs in gray matter (GM) and white matter (WM) in the human brain are summarized in Table 1b. Both ROIs were manually outlined with a size of 24 voxels each. The 4-parameter estimation model provided a good fit to the measured data in acquisitions with both pulse pairs.

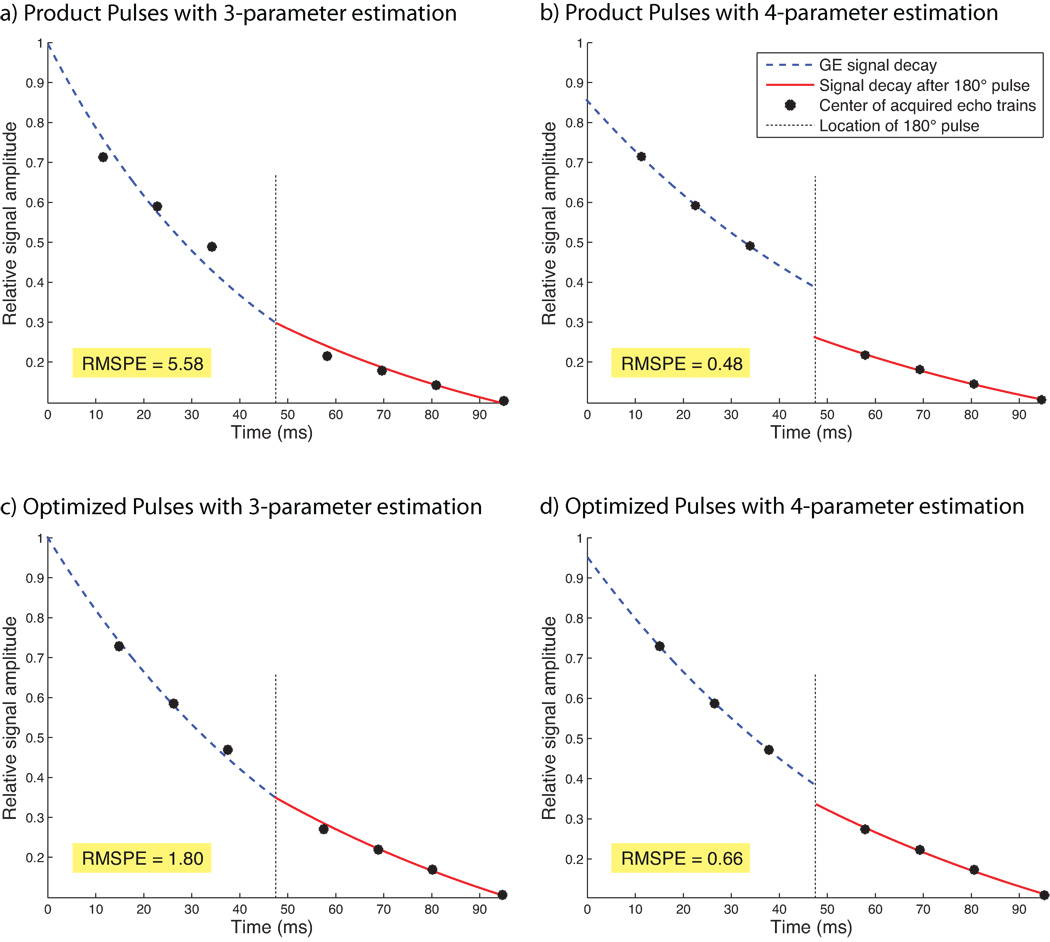
The RMSPEs of fits to experimental data collected with the product pulses in GM and WM were 0.45 and 0.48 with the 4-parameter model, while the RMSPEs in GM and WM were 6.88 and 5.58 respectively using the 3-parameter estimation. For fits to data obtained with product pulses, δ was 1.45 in GM and 1.35 in WM. For fits to data obtained with optimized pulses, δ was 1.09 in GM and 1.08 in WM, similar to the estimate of δ = 1.09 determined in the selected ROI in the phantom experiment. RMSPE using the 4-parameter estimation and optimized pulse design was 0.64 in GM and 0.66 in WM; with the 3-parameter estimation, RMSPE was determined at 1.90 in GM and 1.80 in WM respectively. See Fig. 6 for a comparison of the measured data and the estimated signal behavior between all four methods, including the corresponding RMSPE values. This figure shows the average signal of each echo train (black dots) in an ROI within gray matter, and the lines of best fit to Equation 1 (blue, red).

Fig. 6.

Estimations of R₂ and R₂* in an ROI within gray matter in the human brain using product pulses (a,b) and optimized pulses (c,d). The left column (a,c) shows results using 3-parameter estimation without correction for slice profile mismatches, whereas the right column (b,d) shows results using the 4-parameter estimation with correction for slice profiles mismatches. Shown in blue is the gradient-echo signal decay prior to the refocusing pulse, and shown in red is the signal decay after signal refocusing. The corrected MR signal decay (4-parameter estimation) experienced a sudden step at the location of the 180° pulse. This step accounts for mismatched slice profiles; its size is characterized by the parameter δ. With optimized pulses (cf. d), the step is much smaller, indicating a better match between RF pulses.

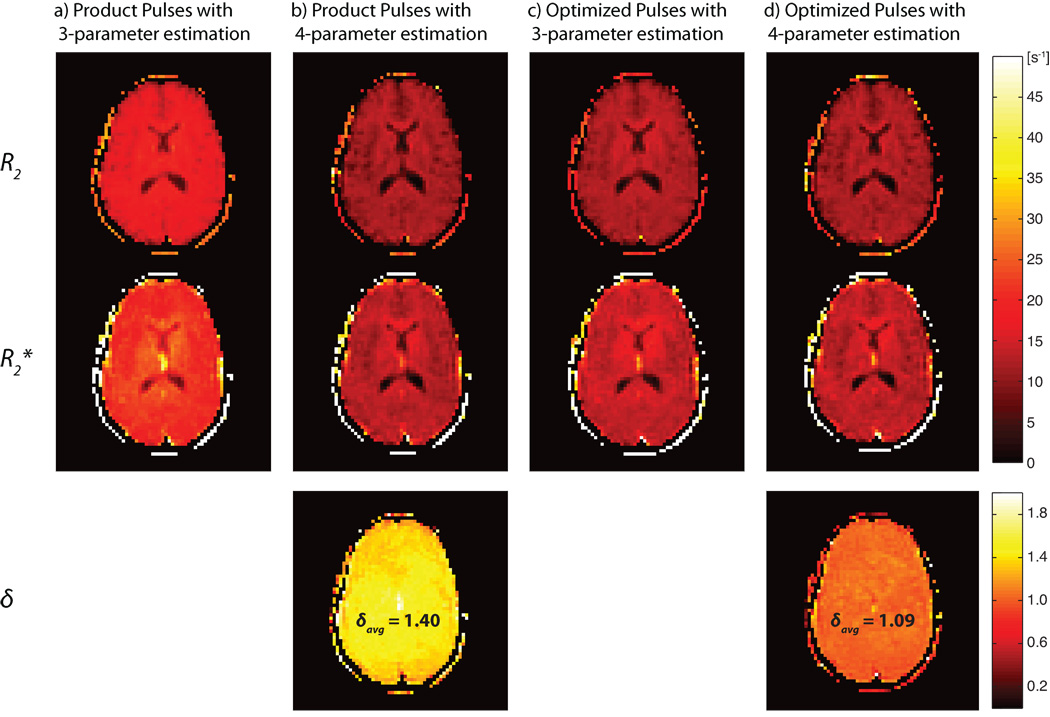
Compared to reference values of R₂ and R₂*, experiments with the optimized pulse design and 4-parameter estimation resulted in deviations of 2.0–3.2% in GM and WM, and experiments with the product pulses resulted in estimation errors of 0.9–4.5% (see Table 1b). With the 3-parameter model, large overestimation of the relaxation parameters R₂ and R₂* of at least 39.2% occurred in both ROIs when using product pulses (see Table 1b). With the optimized pulse design, the 3-parameter estimation improved, but even in the best case, within WM, relaxation parameters were 8.9% and 10.4% higher than the reference values. Fig. 7 shows estimations of δ, R₂, and R₂* in a selected slice within the brain.

Fig. 7.

Parameter estimations of δ, R₂*, and R₂ for a selected slice within the human brain. Shown are parameters estimated in measurements with (a) product pulses using 3-parameter estimation, (b) product pulses using 4-parameter estimation, (c) experiments with optimized pulses using 3-parameter estimation, and (d) optimized pulses using 4-parameter estimation. δ_Avg is the average of δ within the slice shown in this figure using 4-parameter estimation.

Temporal stability of R₂ and R₂* estimation

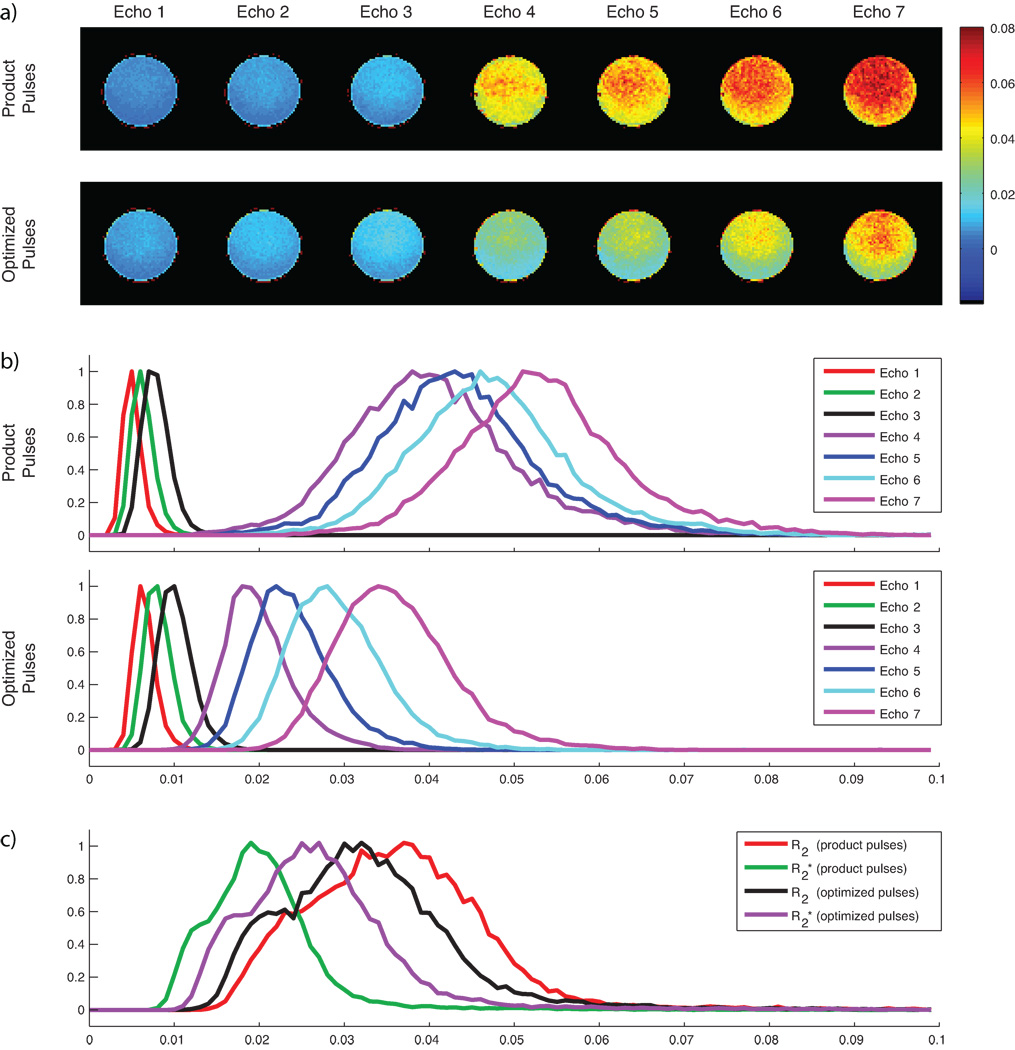
The analysis of temporal signal stability by means of the relative standard deviation over time of individual echo trains is shown in Fig. 8. Using product pulses, this analysis resulted in lower RSDs within images acquired prior to the 180° pulse when compared with measurements using optimized pulses. In contrast, optimized pulse design resulted in reduced RSDs in images acquired after the 180° pulse. The combined estimation of R₂ and R₂* using Equation 1 resulted in lower temporal R₂*-fluctuations when using product pulses, whereas with optimized pulses the estimation resulted in lower temporal R₂-fluctuations.

Fig. 8.

Analysis of the temporal signal stability in an agar phantom by means of the relative standard deviation (RSD) of the signal acquired over 60 time points. (a) RSD images in a selected slice for each acquired echo train, using product pulses (top row) and optimized pulses (bottom row). (b) Histograms showing the normalized distribution of RSDs within the total imaging volume for each echo train. It is shown that acquisitions using product pulses resulted in slightly reduced average RSDs in images acquired prior to the refocusing pulse, whereas acquisitions using optimized pulses resulted in considerably reduced RSDs in images acquired after the refocusing pulse. (c) Histogram showing the normalized distribution of RSDs within the total imaging volume for estimated R₂ and R₂* using both pulse pairs. While acquisitions using product pulses resulted in lower RSDs of R₂*, acquisitions using optimized pulses resulted in lower RSDs of R₂.

DISCUSSION

With product pulses, the mismatch between GE and SE slice profiles was 36% in simulations, and 35–45% in phantom and in-vivo measurements. This caused large overestimations of R₂ and R₂* compared to reference values. The above results motivated the development of optimized pulses with better slice profile properties to evaluate the effect of mismatched slice profiles on the estimation of the transversal relaxation parameters. With optimized pulses, R₂ and R₂* estimation errors using 3-parameter estimation were greatly reduced, thus verifying our claims that mismatched slice profiles are considerable confounders for the accurate estimation of R₂ and R₂* using any combined multi-echo GE and SE sequence.

However, the goal of perfectly matching slice profiles before and after a 180° refocusing pulse could not be achieved due to non-zero transition bands in the pulse profiles, even though the development of better pulses with larger time-bandwidth products helped decrease the extents of the transition bands and produced sharper slice profiles. In fact, simulations of the slice volumes using optimized pulses still showed a 3% discrepancy, and measurements even resulted in 8–9% larger volumes before application of the refocusing pulse. Likely, this discrepancy is a result of maximizing the slice-selective gradients with the consequences that nonlinear gradients, eddy-currents, and susceptibility effects produced slightly increased slice profile mismatches compared to pulse simulations. Moreover, the accuracy of the B₁ amplitudes played out on the MRI system may be limited.

Consequently, the introduction of an additional correction factor that relates the equilibrium signals S₀^I and S₀^II to each other is necessary for the combined estimation of the transversal relaxation parameters. This correction effectively reduced errors in the estimation of R₂ and R₂*. However, small overestimation of R₂ might remain, caused by the negligence of diffusion effects that have their origin in the properties of the vascular network (29,30). These diffusion effects may cause superimposed non-linear signal-drops that increase with increasing echo time (30). Such effects do not exist in an agar phantom, resulting in a slightly better fit to the signal decay model when compared to an experiment in the human head (cf. RMSPE in Table 1). Ideally, further analysis of diffusion should be taken into account, however, despite considerable effort using simulations, cf. (29–32), so far no analytical formula for the MR signal decay that accounts for diffusion effects within the full range of physiological parameters has been presented.

As shown by our results, there were hardly any differences between optimized pulses and product pulses when using the 4-parameter estimation model. In the phantom and within human WM, the estimation accuracy using product pulses was even slightly better than with optimized pulses. It is questionable though if the reference values indeed resulted in the best estimation of the transversal relaxation parameters; the reference values in this study were obtained using product pulses, i.e. the underlying slice volumes for the determination of R₂* (Fig. 4a, blue dashed) and R₂ (Fig. 4a, red) were quite different: additional information from the slice gaps was included in the estimation of R₂* using the reference method and SAGE EPI with product pulses, whereas SAGE EPI with optimized pulses excited spins that matched the geometric slice prescription better. Thus, measurements with product pulses lead to unwanted incorporation of signal originating from outside of the prescribed volumes (cf. Fig. 4), possibly inducing R₂ and R₂* estimation errors in inhomogeneous tissue due to the presence of susceptibility gradients. Ideally, R₂* estimates should be determined in slice volumes as close to the geometric prescription as possible. This was only the case for SAGE EPI with optimized pulses, but not for the reference method. As a result, reference values for R₂* might be slightly biased towards product pulses.

Although the use of product pulses resulted in slightly lower temporal signal fluctuations and thus higher SNR in readouts prior to the refocusing pulse (cf. Fig. 8), the additional SNR, as mentioned before, did not originate from the proper geometric locations. In contrast, optimized pulses were more confined to the prescribed slice locations (see Fig. 4), reducing the excited volume and thus SNR in signal readouts prior to the 180° pulse. However, the optimized 180° pulse refocused a larger portion of the initially excited spins compared to the product pulse, effectively reducing signal fluctuations in echo trains acquired after the refocusing pulse (see Fig. 8). Overall, product pulse design resulted in temporally more stable R₂* estimation with the drawbacks discussed earlier, whereas optimized pulses resulted in more stable R₂ estimation. However, contrast agent-induced changes in R₂ are smaller than corresponding changes in R₂* (1). Thus, to achieve similar CNR in R₂- and R₂*-based perfusion and functional MRI data, R₂ estimation needs to be temporally more robust than R₂* estimation, revealing important advantages of an optimized pulse pair.

All experiments were carried out with interleaved slice acquisition, a prescribed slice thickness of 5.0 mm, and a slice gap of 2.0 mm to facilitate multi-slice acquisition with minimal cross-talk between slices. Acquisitions using product pulses excited a FWHM slice thickness of 6.8 mm and a full signal extent of approximately 10 mm (cf. Fig. 4). As a consequence, these acquisitions required slice gaps to prevent substantial signal saturation within adjacent slices. In contrast, the optimized refocusing pulse would result in residual signal refocusing within adjacent slices in absence of slice gaps.

In this study, we considered spectral-spatial excitation pulses only, due to their superior suppression of lipid signals compared to spatial-only excitation pulses preceded by additional spectral pre-saturation pulses (33). Although spatial excitation pulses allow earlier signal readouts than SPSP pulses, the gain of additional readout time would not allow us to fit another full echo train with the current imaging parameters. Furthermore, other studies have shown that the MR signal decay for the first few milliseconds following signal excitation is not strictly mono-exponential (14), potentially inducing errors in the estimation of the transversal relaxation parameters.

In conclusion, there is added benefit of using a multi-echo spin- and gradient-echo EPI pulse sequence (facilitated by parallel imaging) over dual-echo spin- and gradient-echo EPI approaches in PWI and fMRI to facilitate R₂ and R₂* quantification. However, mismatches between excitation and refocusing slice profiles cause errors in the combined estimation of R₂ and R₂*. While optimized pulses can provide better-matched profiles, thus improve the estimation of the transversal relaxation parameters, it is nearly impossible to match slice profiles perfectly in multi-slice acquisitions. The introduction of an additional parameter δ into the signal equation model to correct for slice profile mismatches mitigates remaining fitting errors in R₂ and R₂*. The introduction of the 4-parameter signal estimation model improves fMRI and PWI through the simultaneous determination of R₂(t) and R₂*(t) instead of their relative changes to baseline and it reflects a next step towards quantitative MRI methods.