Continuous distribution model for the investigation of complex molecular architectures near interfaces with scattering techniques

Abstract

Biological membranes are composed of a thermally disordered lipid matrix and therefore require non-crystallographic scattering approaches for structural characterization with x-rays or neutrons. Here we develop a continuous distribution (CD) model to refine neutron or x-ray reflectivity data from complex architectures of organic molecules. The new model is a flexible implementation of the composition-space refinement of interfacial structures to constrain the resulting scattering length density profiles. We show this model increases the precision with which molecular components may be localized within a sample, with a minimal use of free model parameters. We validate the new model by parameterizing all-atom molecular dynamics (MD) simulations of bilayers and by evaluating the neutron reflectivity of a phospholipid bilayer physisorbed to a solid support. The determination of the structural arrangement of a sparsely-tethered bilayer lipid membrane (stBLM) comprised of a multi-component phospholipid bilayer anchored to a gold substrate by a thiolated oligo(ethylene oxide) linker is also demonstrated. From the model we extract the bilayer composition and density of tether points, information which was previously inaccessible for stBLM systems. The new modeling strategy has been implemented into the ga_refl reflectivity data evaluation suite, available through the National Institute of Standards and Technology (NIST) Center for Neutron Research (NCNR).

INTRODUCTION

Lipid bilayers in biological membranes are thermally disordered leaflets of fluid aliphatic molecules, assembled by hydrophobic interactions that expose a chemically diverse interface to their aqueous environment. They form the plasma membranes facing the intercellular space and the internal membranes that confine cell organelles. In both cases, the bilayer acts as a tightly controlled permeation barrier that interacts with proteins in a multitude of ways and mediates responses of the cell to external and internal cues. If these responses follow predefined patterns, the cell goes about its complex business plan using well-orchestrated, feedback-controlled reactions. However, this complexity of choreographed transcription and signaling events also holds the prospect for a wide range of pathologies, if something goes wrong.

X-ray and neutron scattering have been essential for characterization of the basic bilayer structure through small-angle scattering from vesicles, one-dimensional (1D) diffraction from aligned multi-bilayer stacks, and reflection from single planar bilayers. As explored extensively by many laboratories,^{1, 2, 3, 4, 5, 6} scattering techniques are well suited to unravel the disordered nature of fluid membranes where crystallography fails due to the lack of long-range order. With the basic bilayer structure firmly established, it has now become possible to ask detailed questions as to how membrane-specific proteins interact with bilayers and if protein-lipid interactions differ for proteins in their active and mutated forms. Within the family of scattering techniques, such questions are arguably best investigated with x-ray or neutron reflectometry (XR and NR, respectively) on single bilayers supported by solid substrates, a methodology that allows for the investigation of the membranes without and with protein in subsequent scans of the same physical sample.

In recent years, we developed the technology to perform such studies with NR.^{7, 8, 9} Here we describe a flexible and modular modeling technique, based on earlier work in our lab and others,^{10, 11, 12, 13} to maximize the information extracted from reflectivity measurements of substrate-supported bilayers. While simple slab models (“box” models)¹¹ are still widely used in the evaluation of reflectometry data of membrane structures, such models cannot describe partial overlap of molecular fragments along the membrane normal. However, such a coexistence of distinct molecular components within the same cross-sectional area of the bilayer occurs generally in membranes. The new model developed here overcomes this limitation, thereby providing a logical step toward more realistic descriptions of membrane structures.

In this paper, we describe the use of NR isotopic contrast variation to unravel details of bilayer structures. However, the procedures we developed are equally applicable to XR data interpretation, or to the joint refinement of XR and NR data. We discuss the model implementation and application to solid-supported bilayers, specifically, a sparsely-tethered bilayer lipid membrane (stBLM). A software implementation of the model has been integrated into the reflectometry data evaluation program ga_refl by the NIST Center for Neutron Research (NCNR).¹⁴

Composition-space refinement of interfacial structures

In the analysis of reflectivity or multilayer diffraction data of membranes, modeling of the underlying structure in terms of chemical composition is often advantageous.¹³ Modeling techniques for reflectivity data evaluation were initially developed to bypass the phase problem, i.e., phase information lost in the measurement of scattering intensity. These approaches were refined to parameterize molecular components and their configurations within a sample, an approach termed composition-space refinement.^{10, 11} In reflectometry, even if scattering length density (SLD) profiles can be worked out from first principles or can be determined by direct inversion,^{15, 16} composition-space refinement has advantages in that it allows intuitive models to be implemented that constrain the full range of SLD profiles by retaining only those relevant for plausible chemical structures. This is particularly important in neutron scattering when using isotopic variation of selected chemical species, typically by ¹H/²H substitution in biological samples. Data evaluation can be very effectively dealt with in the composition-space refinement approach if volumetric information is available for the sample components because the parameterized molecular structures can be directly mapped to reflect the isotopic constitutions of the sample. Finally, this approach also permits the consistent evaluation of x-ray and neutron measurements of identically prepared samples.^{10, 11}

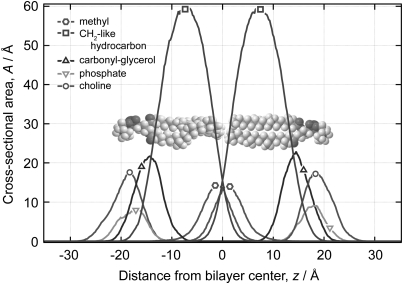
In more detail, a composition-space refinement approach for NR represents sub-molecular components of the sample as cross-sectional area profiles A(z) along an axis of orientation z, which for membrane studies usually is the bilayer normal. Figure 1 shows the space-filling structures of two molecules of a membrane-forming lipid, DMPC,¹⁷ arranged in opposite leaflets of a bilayer and the out-of-plane distributions of its sub-molecular components as obtained from a molecular dynamics (MD) simulation. Absolute component volumes can be computed by integration of the area profile A(z): $V_c={\int }_{\mathit{bilayer}}{A}_c(z)\mathit{dz}$.

Figure 1.

(Color online) Distribution of sub-molecular components along the membrane normal in a DMPC bilayer, as obtained from a MD simulation (Ref. ⁵²). The overlaid DMPC molecules are drawn to scale.

A variety of real-space models that approximate the area profiles of sub-molecular components, such as those shown in Fig. 1, have been developed for neutron scattering from membrane structures. These include “box” models (slab models or strip-function models^{18, 19}), models that use Gaussian distributions of sub-molecular components,^{12, 20, 21} hybrids of strip-function and Gaussian models,²² and disordered crystalline models.²³ Thermal and conformational disorder is generally described as a Gaussian broadening of the out-of-plane positions of the atoms of the film-forming molecules. This can be implemented in real space, for example, by convoluting the intrinsic (i.e., unbroadened) profile of an “average” molecule within the bilayer with a Gaussian function of appropriate width σ, or by multiplying the scattered intensity computed for the intrinsic SLD distribution with a Debye-Waller term in reciprocal space.²⁴ The assumption of Gaussian broadening is also the basis for the model developed here, which implements thermal disorder by using error functions.

An approach that has been most widely used for organic interface structures in XR and NR data analysis is the box model,^{25, 26, 27} in which the 1D SLD profile is parameterized in terms of stratified slabs of certain average chemical compositions. At the boundaries, the average SLDs jump according to the different sub-molecular contents of the neighboring slabs, rather than changing smoothly as the spatial distributions of sub-molecular groups change along z.²⁸ A composition-space refinement with box models is thereby achieved by appropriately subdividing the overall SLD profile with regard to (abrupt) changes in the chemical composition of the slabs along the surface normal. Also widely used are models employing Gaussian functions,²⁹ or direct inversion techniques.^{16, 30}

In this paper, we implement a general modeling strategy for NR or XR, which we will call ”continuous distribution” (CD) modeling, that takes advantage of the self-consistency intrinsic to the composition-space refinement approach. The CD model addresses efficiently the requirement of complete space-filling within the sample. Although we discuss its features in terms of modeling phospholipid bilayers supported by a solid substrate, it is a general approach that may also benefit investigations of more complex structures.

DISTRIBUTION OF MOLECULAR COMPONENTS ACROSS AN INTERFACE: MODEL IMPLEMENTATION

Design of an error function-based model and comparison to Gaussian distributions

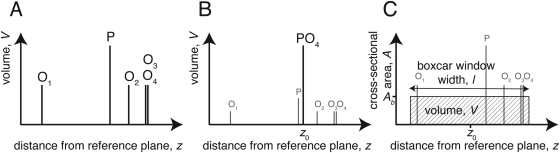
Figure 2A shows a hypothetical example of the projected positions of a subset of atoms in a lipid on the interface normal. This subset may define a sub-molecular component of a molecule, such as the lipid’s phosphate group. An ensemble of such molecules, e.g., lipids, detergents, peptides or proteins, or polymers is self-assembled at the interface to form an extended, in-plane homogeneous surface architecture, such as a lipid bilayer in contact with buffer or a self-assembled monolayer (SAM) in contact with air or organic solvent. Under the assumption that each atomic position within the ensemble can be approximated by a normalized Gaussian function G(z,σ), the area profile A(z) takes on the form of Eq. 1 where V_i is the volume of an individual atom i, and z_i is its position,

$$A(z)=G(z,\sigma )*{\int }_{-\infty }^{\infty }\sum _i{V}_i{\delta }_i(z-z_i)\mathrm{d}z=\sum _i{V}_{i}G(z-z_i,\sigma )$$ (1)

Equation 1 is usually impractical to use because it accounts for all individual atoms, A(z) = A(z,σ, V_1…i, z_1…i). For reflectometry, the experimental resolution is also generally too low to determine positions of individual atoms. An appropriate grouping of atoms into sub-molecular components is therefore required. Figure 2B illustrates an approach,¹⁰ in which the atomic positions z_i of a sub-molecular component are combined into a single average position z₀ and the individual atomic volumes V_i are lumped into the component volume V. Thus, the area profile becomes a single Gaussian function,

$$A_{\mathrm{Gauss}}(z)=G(z,\sigma )*{\int }_{-\infty }^{\infty }{V}_i{\delta }_i(z-z_0)\mathit{dz}=\mathit{VG}(z-z_0,\sigma ).$$ (2)

Although this simplification reduces the number of parameters drastically, it may cause complications for XR/NR data analysis. First, the information about the projected extension of the component along the z direction, previously contained in the values z_i, is now convoluted with the width of the Gaussian function, σ. Second, combining area profiles of distinct sub-molecular components will result in an uneven filling of the available space along z, even if the integral in Eq. 2 matches exactly the total molecular volume, because Gaussian area profiles of neighboring components will not add to a constant area A. Instead, A(z) will vary as a function of z, such that overfilling will occur for some positions z, compensated for by underfilling elsewhere along the bilayer normal.

Figure 2.

Possibilities of accounting for atomic positions along the normal direction z at an interface for reflectivity modeling. (A) Average positions of the five atoms of a lipid phosphate group. (B) Lumping together atomic positions into one average position as a basis of describing the phosphate distribution by a Gaussian function. (C) Approximating the associated volume V of the component atoms by a boxcar function of width l and height A_b = V/l that represents the cross-sectional area of the component. This approximation is the basis of the model developed in this work.

A different approach [Fig. 2C] avoids these problems: The positions of individual atoms are approximated by a boxcar function, b(z₀,l,A) with A = V/l, where V is the volume of the sub-molecular component, l is the projected extension along z, and z₀ the center position. The functional form of the area profile then becomes the sum of two error functions,

$$A_{\mathrm{Erf}}(z)=G(z,\sigma )*b(z,z_0,l,A)={\int }_{-\infty }^{\infty }G(z\text{'},\sigma )b(z-z\text{'},z_0,l,A)\mathit{dz}\text{'}={\int }_{-\infty }^{\infty }G(z\text{'},\sigma )\frac{V}{l}[H(z-z_0+\frac{1}{2}l-z\text{'})\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}-H(z-z_0-\frac{1}{2}l-z\text{'})]\mathit{dz}\text{'}=\frac{V}{2l}(\mathrm{erf}\left(\frac{{\mathrm{z}\mathrm{-}\mathrm{z}}_0\mathrm{+}\frac{1}{2}l}{\sqrt{2}\sigma }\right)-\mathrm{erf}\left(\frac{z-z_0-\frac{1}{2}l}{\sqrt{2}\sigma }\right)).$$ (3)

H(z) is the Heaviside function. The functional form of this area profile conserves the parameter l as the intrinsic (i.e., the unbroadened) value of the projected length of the molecular component. The Gaussian model is included in this model implementation as a special case for $A_{\mathrm{Gauss}}(z)=\underset{l\to 0}{\lim }{A}_{\mathrm{Erf}}(z)$. The functional form in Eq. 3 accommodates two occurrences of the width parameter σ which may be assigned distinct values. A(z) is then parametrized by the component volume V, the projected length l on z, the center position z₀, and σ₁ and σ₂,

$$A(z)=\frac{V}{2l}(\mathrm{erf}\left(\frac{z-z_0+\frac{1}{2}l}{\sqrt{2}{\sigma }_1}\right)-\mathrm{erf}\left(\frac{z-z_0-\frac{1}{2}l}{\sqrt{2}{\sigma }_2}\right)).$$ (4)

Using distinct σ values is one way to extend the model beyond Eq. 3. Intrinsic volume distributions may differ from a boxcar function or variations in disorder along z may arise from different conformational degrees of freedom within a molecular component. However, σ₁ ≠ σ₂ may result in A(z) < 0 at large values of |z| for that particular component. We show in the Supplemental Information that moderate constraints on σ_i ensure that A(z) remains positive in a computationally relevant interval and that the error in the integrated area profile along z, i.e., the volume, remains sufficiently small due to the limitation of the computation to this interval.

The integral of the area profile equals V, independent of l and σ,

$${\int }_{-\infty }^{\infty }A(z)\mathrm{d}z={\int }_{-\infty }^{\infty }\frac{V}{2l}[\mathrm{erf}\left(\frac{z-z_0+\frac{1}{2}l}{\sqrt{2}{\sigma }_1}\right)-\mathrm{erf}\left(\frac{z-z_0-\frac{1}{2}l}{\sqrt{2}{\sigma }_2}\right)]\mathrm{d}z=\frac{V}{2l}(\sqrt{2}{\sigma }_1{[\frac{z-z_0+\frac{1}{2}}{\sqrt{2}{\sigma }_1}\mathrm{erf}\left(\frac{z-z_0+\frac{1}{2}}{\sqrt{2}{\sigma }_1}\right)+\frac{e^{-{\left(\frac{z-z_0+\frac{1}{2}}{\sqrt{2}{\sigma }_1}\right)}^2}}{\sqrt{\pi }}]}_{-\infty }^{\infty }\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}-\sqrt{2}{\sigma }_2{[\frac{z-z_0-\frac{1}{2}}{\sqrt{2}{\sigma }_2}\mathrm{erf}\left(\frac{z-z_0-\frac{1}{2}}{\sqrt{2}{\sigma }_2}\right)+\frac{e^{-{\left(\frac{z-z_0-\frac{1}{2}}{\sqrt{2}{\sigma }_2}\right)}^2}}{\sqrt{\pi }}]}_{-\infty }^{\infty })=\frac{V}{2l}([-2z_0+l]-[-2z_0-l])=V.$$ (5)

For the purpose of XR/NR data analysis, each molecular component c is assigned its scattering length, i.e., the neutron scattering length, b_c, or the total electron number for x-rays, $n_c^{\mathrm{e}}\mathrm{x}{r}_{\mathrm{e}}$ (where r_e = 2.82 × 10⁻⁵ Å is the Thomson electron radius).

Error functions ensure volume filling intrinsically

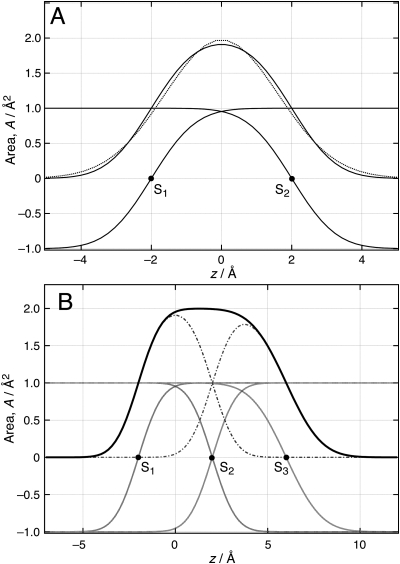
Figure 3 shows how the sum of two error functions, expressed by Eq. 4, forms a spatially confined distribution. This distribution approximates a Gaussian, i.e., the functional form often used to represent the thermal or conformational spread [Fig. 3A] for the case when the distance between the two roots, S₁ and S₂, vanishes. It also shows [Fig. 3B] how the sum of four error functions, in which the second set is characterized by distinct σ parameters, create an asymmetric distribution that satisfies volume filling as long as the values of σ are identical at the common interface between the two sub-molecular distributions. In fact, any number, n, of sub-molecular components, described by two error functions each, can be combined and will fill the area profile A(z) homogeneously along the z axis, thus achieving an ideal volume filling, under the following conditions:

• 1.The maximum value, max(A(z)) = V/l, of each component area profile equals the global area per molecule.
• 2.The roots of two error functions, with a positive and with a negative slope, of adjacent molecular components coincide at the same position z.
• 3.The values σ_i,2 and σ_i + 1,1 of the overlapping error functions are identical for 1 ≤ i < n.

Figure 3.

(Color online) (A) The sum of two error functions represents an area profile A(z) of a sub-molecular component within a layered interface structure with the following parameters: l = 4 Å, V = 8 ų, σ₁ = σ₂ = 1 Å. The overlaid Gaussian function has the same volume V and a width parameter σ_Gauss ≈ 1.63 σ₁. (B) Adding a second sub-molecular component with the same l, V/l, and σ₁ at the common interface results in ideal volume filling, even if σ₁ ≠ σ₂ for the second component. For details, see text.

Generally, any odd function symmetric about its root z_S, A(z_S − z) = −A(z_S + z), will lead to ideal volume filling under the above conditions. In this respect, the choice of the error function is arbitrary. Figure 3B shows an exemplary representation of two area profiles A₁(z) and A₂(z) that satisfy the above conditions. Ensuring that the area per molecule V/l is equal for both area profiles fulfills condition 1. Conditions 2 and 3 are fulfilled, as σ₂ of the area profile A₁(z) equals σ₁ of A₂(z) and the roots of the overlapping error functions coincide in S₂. Because conditions 2 and 3 are satisfied, these two error functions cancel all along z. The total sum of the two area profiles then equals the sum of the two remaining error functions with half-maxima through points S₁ and S₃. Since the values of V/l of the two profiles are the same, the two error functions add up to a new area profile of the form of Eq. 4. The extension of this line of arguments to any number of component area profiles is straightforward.

If the area per molecule V/l of any one of the component profiles is smaller than the global area per molecule, this will lead to underfilling of the available volume. This is indeed a realistic situation that may often occur, e.g., for hydrated lipid head groups where the solvent fills the remaining volume.

The second condition stated above may not be strictly satisfied in all situations. Rather, a distance, leading to a depletion of film-forming species, may separate two adjacent sub-molecular components. This situation is not necessarily unphysical, as the solvent may fill the voids. An unphysical situation might only arise if the two sub-molecular components are chemically bonded to each other in which case a depletion zone would not be consistent with a physically valid model. In any case, a spatial separation of two sub-molecular components increases the number of model parameters. For joined components, the parameters l and z₀ of all components are linked by the constraint that the roots of adjacent error functions coincide. This link is broken for separated components, leading to a larger number of independent parameters.

In some cases it is necessary to mirror an area profile on a given interface at a position z_M because of physical constraints. An example is an impermeable solid substrate, such as a gold film that supports a SAM. Volume overfilling is avoided if both roots of the error functions associated with the terminal component are located on one side of z_M. Ideal volume filling occurs if the root of the error function closest to the substrate is located at z_M.

Negative areas

For σ₁ ≠ σ₂, the area profile of a given component described by Eq. 4 is negative for some values of z. For computational purposes, however, we truncate the calculation of the area profile at distances mσ on either side of the half-maximum points of the distribution, where the constant m controls the precision of the approximation. We show in the Supplemental Information that the area profile remains positive within the interval [z₀ – l/2 – mσ₁, z₀ + l/2 + mσ₂] if the difference between the largest and smallest σ does not exceed l/m. The maximum difference l/m between the two σ is independent of their actual values, and it is large enough for the modeling of typical molecular architectures considered in this application to remain realistic. The relative error between the integral of the truncated profile and the parameter V in Eq. 5, i.e., the volume of the sub-molecular group, is smaller for σ₁ ≠ σ₂ than for σ₁ = σ₂. For m = 3, this relative error is below 0.3% for all l. It is thereby smaller than the precision with which an SLD profile can be experimentally determined in a typical XR or NR measurement.

VALIDATION OF THE CD MODEL WITH MD SIMULATIONS OF DMPC AND DOPC BILAYERS

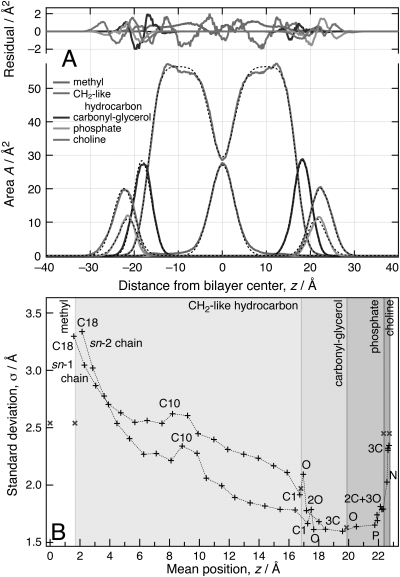
To explore how well the error function approach is capable of describing realistic spatial distributions of sub-molecular components in planar molecular aggregates, the output of atomistic MD simulations of single-component phospholipid bilayers were modeled. Because of the small system sizes and the imposed periodic boundary conditions, the simulated bilayers are essentially planar. To facilitate a comparison, area profiles were computed from number density profiles of the lipid components obtained from the simulations. Individual atoms were assigned to lipid components using established definitions,⁴ thus parsing the phospholipid molecules as follows: chain-terminal methyls (m), hydrocarbon (hc) methylenes, carbonyl-glycerol (cg) backbone, phosphate (p), and choline (c). The methyl and polymethylene groups of the two chains were assigned to one single component each. An algorithm³¹ implemented in the SIMtoEXP software³² was used to determine component area profiles from atomistic number densities in the MD simulations. Literature values⁴ were used for head group component volumes because the low hydration of the bilayer in the simulations prohibited a determination directly from the MD output. The obtained model parameters, i.e., projected component extensions, volumes, and interfacial roughness values, were compared with average values in the simulation thus providing a quantitative validation of the model. Furthermore, this procedure let us explore how well the projected component lengths and interfacial roughness parameters are separated in the CD model, and what is the accuracy of the modeled component volumes.

Constraints to the model were applied as discussed in the previous section. The values of the projected component extensions l along z and the volumes V of the methyls and methylenes were constrained to yield the cross-sectional area per lipid, A^lipid, according to A = V/l. l was chosen to be a fit parameter, thus deriving the component volumes V from the fit since A^lipid = 59.4 Ų for DMPC and A^lipid = 57.1 Ų for DOPC were globally determined from the simulations. In the DOPC simulation, carried out at low hydration,³³A^lipid is significantly smaller than 72 Ų, the value for DOPC at full hydration. The z positions of all components were calculated from their values of l under the constraint that the roots of the overlapping error functions of adjacent molecular components coincide. Similarly, the σ values of the overlapping error functions of neighboring components were constrained to be equal. Therefore, there is effectively only one free parameter σ per component. The methyl and the choline components each have two identical σ associated with their error functions because of the lack of a second neighboring component. All sub-molecular components were simultaneously fitted using a global minimizer.³⁴

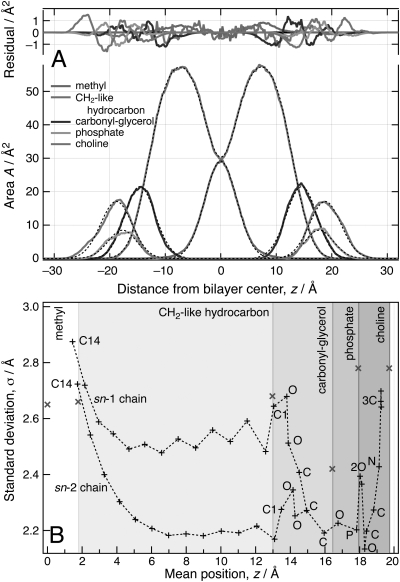
Figures 4A, 5A show best-fits of the continuous distribution model to the area profiles of sub-molecular components in the DMPC and the DOPC simulations, with unweighted χ² values of 0.06 Ų and 0.11 Ų, respectively. Figures 4B, 5B compare the model-derived extensions of the molecular components along z (shades of gray) with averaged atomic positions (abscissae in the plots) obtained from 1000 frames of the simulations. The standard deviations of these positions from the simulation and the roughness parameters σ are shown on the ordinate axes. Tables TABLE I. and TABLE II. list the model parameters and compare them with related values from the simulation. Projected extensions in the simulations were derived from mean atomic positions by defining the location of the interfaces between two sub-molecular components as the halfway points between the mean atomic positions of the peripheral atoms. The lowest and the highest possible values are displayed where ambiguities arose because of the staggering of lipid sn-1 and sn-2 chains or due to spatial overlap of adjacent components. Interfacial roughness parameters from simulation are reported as the lowest and the highest standard deviation of any atom within one σ (interfacial roughness) of the interface as found in the model fit.

Figure 4.

(Color online) Validation of the model by fitting to an NAMD simulation (Ref. ⁵¹) of a DMPC bilayer (72 lipids, 6 waters/lipid; T = 315 K, initial configurations from Ref. 55) that used the CHARMM27 force field (Refs. ⁵², ⁵³, ⁵⁴). For details, see Supplemental Information. (A) Best-fit of the error-function based continuous distribution model with constraints (see text) to component distributions obtained from an average of 1000 configuration snapshots of the MD simulation. The overall space filling of the lipid molecules is broken down into the area profiles of individual lipid components, as indicated, for both the model (dashed black lines) and the simulation (continuous lines). Residuals shown at the top of the panel quantify the agreement between the model and the simulation data. (B) Comparison of the interfacial positions of molecular components, defined in the text, and their interfacial roughness with mean atomic positions and standard deviations from the mean obtained in the simulation. Different background gray levels indicate the projected extensions of sub-molecular lipid components. Crosses (x) on the interfaces between two sub-molecular components indicate the interfacial roughness σ of adjacent error functions determined by the fit. These parameters describe the thermally disordered distributions of neighboring molecular components. Upright crosses (+) provide the averaged locations and standard deviations from the mean of non-hydrogen atomic positions observed in the MD snapshot. For the methyl, carboxyl-glycerol, phosphate and choline components, non-hydrogen atoms are labeled. Dashed lines are guides for the eye.

Figure 5.

(Color online) Validation of the model by fitting to an NAMD simulation of a DOPC bilayer (72 lipids, 5.4 waters/lipid, T = 296 K; initial configuration from Ref. 33). Other details as given in Fig. 4 and the Supplemental Information. (A) Best-fit of the error-function based continuous distribution model with constraints to a simulation snapshot. (B) Comparison of the interfacial positions of molecular components and their interfacial roughness with mean atomic positions and standard deviations from the mean obtained in the simulation.

TABLE I.

Parameters of the continuous distribution model fitted to the area profiles obtained from MD simulation of a DMPC bilayer (6 waters per lipid, Fig. 4) and equivalent quantities directly determined from the MD snapshot (see text). The parameters σ refer to the interface of the respective sub-molecular component with that on the preceding row. A^lipid determined from the fit was (59.50 ± 0.04) Ų and 59.43 Ų in the simulation.

	l / Å		σ / Å		V / Å3
Lipid component	Model fit	Simulation	Model fit	Simulation	Model fit	Simulation
two methyls, m	1.77 ± 0.01	12.81 … 13.29	n/a	n/a	105.3 ± 0.6	108.4
methylenes, hc	11.20 ± 0.01	2.68 ± 0.01	2.72 … 2.87	666.4 ± 0.8	665.7
carbonyl-glyc, cg	3.45 ± 0.02	3.07 … 3.54	2.69 ± 0.01	2.17 … 2.68	150.7 ± 0.3	145.3
phosphate, p	1.50 ± 0.08	1.99	2.42 ± 0.01	2.13 … 2.41	54.5 ± 0.3	53.7
choline, c	1.78 ± 0.15	0.90 … 1.20	2.78 ± 0.01	2.13 … 2.70	121.0 ± 0.4	120.4

TABLE II.

Parameters of the continuous distribution model fitted to the area profiles obtained from MD simulation of a DOPC bilayer (5.4 water per lipid, Fig. 5) and equivalent quantities directly determined from the MD snapshot. A^lipid determined from the fit was (56.53 ± 0.04) Ų and 57.06 Ų in the simulation.

	l / Å		σ / Å		V / Å3
Lipid component	Model fit	Simulation	Model fit	Simulation	Model fit	Simulation
two methyls, m	1.66 ± 0.01	16.31 … 16.84	n/a	n/a	93.8 ± 0.6	101.4
methylenes, hc	15.14 ± 0.01	2.52 ± 0.01	2.70 … 3.34	855.9 ± 0.9	856.3
carbonyl-glyc, cg	3.06 ± 0.02	3.22 … 3.75	1.97 ± 0.01	1.61 … 2.23	142.9 ± 0.4	143.9
phosphate, p	2.48 ± 0.07	1.77 … 2.21	1.63 ± 0.01	1.60 … 1.62	56.2 ± 0.4	53.7
choline, c	0.39 ± 0.12	0.43 … 1.18	2.41 ± 0.01	1.65 … 2.35	121.1 ± 0.4	120.4

The continuous distribution model with constraints is in excellent agreement with the area profiles derived from the simulation data. The average number of parameters per lipid component is 3. This is comparable to established composition-space models in neutron diffraction.²² The standard deviation between the volume parameters V determined from the model and from simulation is 3.43 ų, and that between the projected component extensions l is 0.33 Å. The standard deviation of the interfacial roughness parameters σ from the intervals given by the simulation is 0.08 Å. Methyl groups contribute significantly to the observed standard deviations.

Figures 4A, 5A demonstrate visually that the model parameterization describes the MD simulation output realistically by accurately determining molecular component positions and interfacial roughness parameters. Generally, the σ parameters derived from the model resemble closely the maximum standard deviations from mean positions of atoms in the vicinity of the interface (± σ), as observed in the MD simulations. For DOPC, the interface between the methyl and methylene components is less well defined in terms of mean atomic positions because of the staggering of the two hydrocarbon chains. In addition, the shape of the methyl area profile and the high standard deviations from mean positions observed there are less accurately captured in the model. For both lipids, the enforced compliance with a predefined functional form results in underestimating the interfacial roughness between these components. The phosphate and choline groups in the DOPC bilayer show significant spatial overlap in terms of mean atomic positions. Consequently, the interface between those two groups is ill-defined. Because of this overlap, the model determines an interfacial position, which is to some extent arbitrary.

DISCUSSION OF THE CD MODEL

In the previous sections a versatile model for the composition-space refinement of neutron or x-ray scattering data from stratified samples has been developed and validated against MD simulations of lipid membranes. The close correspondence between model fit parameters and equivalent quantities obtained from the simulations demonstrates that the model is well suited in realistically describing the distributions of molecular lipid components across an interface. In particular, the intrinsic area profiles of sub-molecular components (i.e., the profiles as they would appear without thermal roughening) are well disentangled from the effects of broadening due to conformational or dynamic disorder.

Discrepancies between model fits and MD simulations were, however, observed for the distributions of methyl groups. X-ray and neutron diffraction showed earlier that the distributions of terminal methyl groups in the bilayer leaflets are asymmetric and are therefore not well described by Gaussians.³⁵ Here we find that it is impossible to describe these methyl groups by a single profile that consists of two error functions. For both bilayers, Figs. 4B, 5B show an increasing flexibility of the methylene carbons toward the terminal methyls. It has been reported that lipid chains may even turn back within the hydrophobic interior of the bilayer toward the lipid head groups.^{36, 37} Indeed, a better description of the m/hc interface was achieved by using distinct roughness parameters on two error functions defining the methyls distribution. An even better description was afforded by a superposition of two area profiles, one symmetric (σ₂ ≈ σ₁) and one asymmetric (σ₂ > σ₁; results not shown). It might be speculated that this separation into two sub-molecular components is warranted due to different populations of methyl groups. One of these populations might be associated with fairly extended lipid hydrocarbon chains; a second would then be related to highly disordered chains on which the methyl groups have a measurable probability of locating as far as away from the bilayer center as the lipid head groups. While the superposition of two area profiles for a particular molecular component lies well within the capabilities of the model, such degree of accuracy is most probably not needed for the purpose of modeling NR data at this point. We therefore did not explore this possibility any further.

Figures 4B, 5B demonstrate the difficulty of determining some of the interfaces between sub-molecular components within a bilayer with certainty. For example, the polymethylene to carbonyl-glycerol (hc/gc) interface is intrinsically ill-defined because of the staggering of the two lipid chains. Similarly, the intrinsic area profiles of the phosphate and the choline groups in the DOPC bilayer overlap significantly in their projections on the z axis. This is due to a significant head group tilt from the normal. The CD model is sufficiently flexible to describe this structural feature by introducing a parameter that quantifies this overlap. Again, as such detail is outside the resolution of a typical NR experiment we will not further investigate this conformational freedom of the lipid head groups here.

Superficially viewed, the close mathematical relationship between error functions and boxcar functions suggests a close relation between the conventional box model and the model described here. However, there are significant differences: Foremost, the new model implements an intuitive way of accounting for spatial overlap of two or more molecular fragments that will frequently occur in multi-component systems. Figure 6 (below) gives an example where the smaller PS head group in a two-component bilayer overlaps the location of the larger PC head group only partially. Such situations cannot be realistically modeled within the more limited framework of a box model.

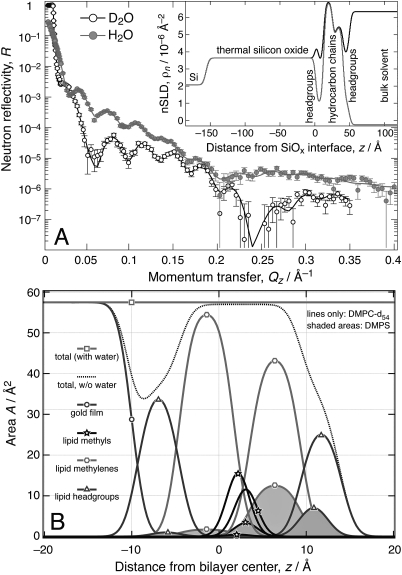
Figure 6.

(Color online) NR at two different solvent contrasts and structural analysis of a bilayer, deposited from floating surface monolayers with a composition, DMPS:DMPC-d₅₄ 30:70, on a thermally oxidized Si wafer. (A) Experimental data. Error bars represent 66% confidence intervals. Inset: Neutron SLD determined from the fit using the molecular distribution model. (B) Decomposition of the area profile into sub-molecular components. The PS:PC compositions in the two bilayer leaflets is distinctly different from that of the parent monolayer, particularly in the leaflet proximal to the solid substrate. Note the slight displacement of the PS with respect to the PC head groups toward the bilayer center, which illustrates the capabilities of the new model, as such shifts of molecular fragments against each other cannot be described within the conventional box model.

Moreover, while the new model shares the advantage of the box and strip-function models with their intrinsic mechanism that ensures ideal volume filling, it overcomes a major disadvantage of the smoothed strip function model by realistically taking into account thermal and conformational disorder. This is achieved by assigning distinct interfacial roughness parameters to each interface, thus accounting for the standard deviations in the z positions from the mean of atoms close to the interface. In contrast to common implementations of box models, interfacial roughness parameters can be significantly larger than the intrinsic, unbroadened width of sub-molecular components. This allows us to account for individual, small sub-molecular components that might be more broadly distributed within the overall structure. Furthermore, the new model shares the realistic parameterization of sub-molecular groups within molecular architectures with Gauss-function based models, but is does so without requiring additional parameters – a significant advantage over the existing modeling techniques. With approximately the same number of parameters as a Gauss-function based model, the new approach is capable of disentangling the width of an intrinsic (unbroadened) sub-molecular component distribution due to thermal and conformational disorder from conformal roughness. These two quantities are combined in one parameter, the standard deviation σ, in the Gaussian model, and hence difficult to separate.

APPLICATIONS OF THE CD MODEL IN NR MEASUREMENTS (REF. ³⁸)

Typical NR measurements reach momentum transfer values up to Q_z = 0.3 Å⁻¹, depending on the design of the spectrometer and – equally important – the sample environment, where a careful minimization of material intersecting the neutron beam can help minimize incoherent scattering background. Indeed, it has been shown that minimizing both the amount of material associated with the sample cell and the volume of the bulk buffer adjacent to a supported lipid membrane can suppress the scattering background to such low levels that Q_z can reach values around 0.6 Å⁻¹ in NR.³⁹ XR measurements typically reach even further, although without very limited options of contrast manipulation, due to a much higher photon density and may achieve data sets that may approach Q_z = 0.8 Å⁻¹ and more.¹³ However, even at such high momentum transfer, the canonical spatial resolution²¹ given by the sampling theorem, $\Delta z=\pi /Q_z^{\max }$, where $Q_z^{\max }$ is the maximum momentum transfer achieved in a single measurement (i.e., no contrast variation),¹³ is rather limited. For example, the canonical resolution is limited to > 3 Å, even for Q_z = 1.0 Å⁻¹. It has been shown that the use of isotopically varied isomorphous samples in neutron scattering or the co-refinement of x-ray and neutron scattering data from identically prepared samples may increase the measurement precision significantly beyond the canonical spatial resolution, in particular with composition-space refinement.^{10, 11} In what follows, we demonstrate that the newly developed CD modeling procedure leads to a significant gain in the precision of the model parameters determined from the NR measurements of isotopically varied samples that is due to the intrinsic use of chemical constraints in the model parameterization.

Neutron reflection from a solid-supported lipid bilayer

A dual-component phospholipid bilayer was deposited onto a thermally oxidized silicon wafer in two successive Langmuir–Blodgett transfers from a 70:30 mixture of chain-deuterated DMPC-d₅₄ and fully hydrogenated DMPS. Its neutron reflection under buffer (two isotopic contrasts using buffers based on pure D₂O and pure H₂O, see Fig. 6A) was determined on the NG1 reflectometer at the NCNR. The inset in Fig. 6A shows the nSLD profiles obtained from the model fit. Area profiles of the sub-molecular groups are shown in Fig. 6B. Volume that is not filled by either the substrate or the lipid components are filled with buffer. The distinct nSL of water molecules creates the observed difference in the nSLD profiles [inset in Fig. 6A], and hence in the model reflectivities (continuous red and black lines in Fig. 6A). Fitted model parameters and constants used in to describe the structure are listed in Table TABLE III..

TABLE III.

Fit parameters for a solid supported bilayer derived using the continuous distribution model. 95.4% confidence intervals were computed using a Monte Carlo resampling technique (Ref. ⁹).

Fit parameter	Value ± 2σ
thickness SiOx	137.6 ± 0.9
thickness of water gap / Å	1.4 ± 0.4
thickness of proximal hydrocarbon chains / Å	14.4 ± 0.8
thickness of distal hydrocarbon chains / Å	13.4 ± 0.5
bilayer completeness	0.99 ± 0.02
fraction of PS in proximal leaflet	0.03 ± 0.02
fraction of PS in distal leaflet	0.22 ± 0.02
bilayer roughness / Å	2.6 ± 0.3
substrate roughness / Å	3.6 ± 1.3

The continuous distribution model was significantly simplified in comparison to the possibilities discussed in the previous sections for the evaluation of the NR data. Lipid head groups were modeled as one component that combines the phosphate and carbonyl-glycerol groups with the choline or serine, respectively. The projected length of the head groups were assumed to be 9.0 Å for phosphocholine (PC) (Ref. ⁴) and 6.5 Å for phosphoserine (PS).⁴⁰ The methyl groups were modeled separately from the polymethylene chains in order to account for their relatively large effective volume and its impact on the SLD profile. However, the methyl groups did not require any free fit parameter because their cross-sectional area is identical to that of the two polymethylene chains. Volumes of sub-molecular components were used as constants fixed to literature values.^{4, 40}

The data analysis shows that the lipid bilayer is complete. It also suggests that the distribution of DMPS is asymmetric across the bilayer leaflets, despite the fact that both monolayers were deposited from the same Langmuir film. The lipid leaflet proximal to the substrate holds only (3 ± 2) vol% of PS. The distal leaflet contains (22 ± 2) vol% of PS, still significantly less than expected from the molar ratio of the two phospholipids in the spreading solution for the Langmuir film. A recent report of MD simulations of solid-supported bilayers showed a dramatic asymmetry of the pressure profile across the membrane in the two monolayer leaflets in which the proximal leaflet showed pressure values that were at least a factor of 3 larger than those in the distal leaflet.⁴¹ Translating these results to our experimental system, one would expect that charged phospholipids, which experience long-range electrostatic repulsion between their head groups, should in fact be disproportionally less represented in the proximal leaflet. The leaflet thicknesses determined as (14.4 ± 0.8) Å for the proximal and (13.4 ± 0.5) Å for the distal leaflets correspond to average areas per lipid of (53 ± 3) Ų and (58 ± 3) Ų, respectively. These results appear realistic in view of the values reported for DMPC membranes in the gel phase, (47.2 ± 0.5) Ų (Ref. ⁴²) and in the fluid phase, 59.6 Ų (Ref. ⁴). This observed imbalance between the molecular areas across the bilayer is consistent with the in-plane pressure difference predicted by the MD simulation. Moreover, a higher density of lipids close to the substrate than in the distal leaflet is directly observed in both coarse-grained⁴³ and in atomistic simulations.⁴⁴ In our experimentally derived model, the hydration layer between the proximal head groups and the substrate has a thickness of only (1.4 ± 0.4) Å. However, this conclusion depends on the choice of the thickness of the head group layer, which was not a free parameter in the fit. A smaller head group thickness would most likely result in a compensation by a thicker hydration layer within the model.

Neutron reflection from a sparsely tethered bilayer lipid membrane

We also investigated a stBLM formed on a Si-supported gold film by co-adsorption of a tether lipid, WC14,^{8, 45} with β-mercaptoethanol (βME), followed by the precipitation of DMPC-d₅₄ through rapid solvent exchange.⁸ WC14, used in a 3:7 mol:mol ratio with βME in the incubation solution for the precursor SAM, consists of a thiolated hexa(ethylene oxide) tether ligated to two myristyl chains. The NR of this stBLM was measured at the NCNR’s AND/R instrument (for details, see Supplemental Information) and is shown in Fig. 7.

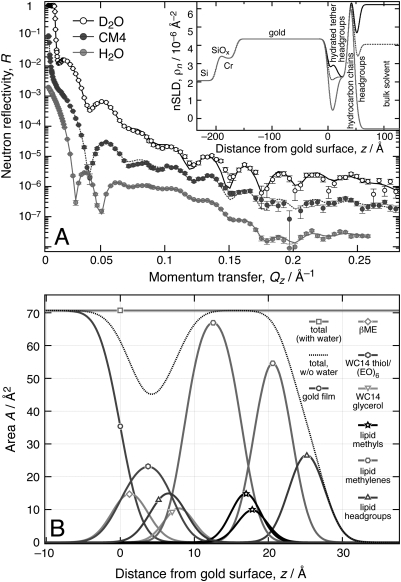
Figure 7.

(Color online) NR at three different solvent contrasts and structural analysis of a stBLM based upon WC14:βME 3:7 completed with DMPC-d₅₄ (Ref. ⁸; details, see Supplemental Information). (A) Experimental data. Error bars represent 66% confidence intervals. Inset: Neutron SLD determined from the fit using the molecular distribution model. (B) Decomposition of the area profile into sub-molecular components. Note the high density of hydrocarbons in the proximal bilayer leaflet compared to the distal leaflet which comes about by the large content (≈ 63%) of myristyl chains associated with WC14 that pack more densely than the myristoyl chains of DMPC. The decomposition of the sub-membrane space between the bilayer and the substrate into its components, βME, oligo(ethyleneoxide) of the WC14 and water, is a unique capability of the new model and has not been possible within the limitations of conventional box models. This allows, for the first time, quantitative estimates of the area density ratio between βME and WC14 at the interface and of WC14 and free DMPC in the proximal bilayer leaflet within the self-organized tBLM structure.

For data modeling, the stBLM structure was parsed into 9 different sub-molecular components: (1) the βME backfiller, (2) the ethylene oxide (EO) spacer with thiol, (3) the glycerol group of the tether lipid, (4, 5) phospholipid head groups of the proximal and distal monolayers within the bilayer, (6) the proximal hydrocarbon chains of DMPC and WC14, (7, 8) the proximal and distal terminal methyl groups, and (9) the phospholipid hydrocarbon chains of the distal monolayer.⁴⁵ Again, phospholipid head groups were modeled as a combination of the carbonyl-glycerol backbone and the phosphate and choline groups. Parameters describing the volumes and relative arrangement of those constituents were obtained from the DOPC MD simulation discussed earlier. Although nine individual components were modeled, the number of parameters describing the stBLM is only 7, as summarized in Table TABLE IV.. This reduction in the number of free parameters is a result of constraints that restrict the model. These are mainly due to the chemical connectivity, but also reflect assumptions on the supramolecular organization of the interface structure. For example, it is assumed that the distal monolayer of the stBLM consists entirely of phospholipid molecules. For a more detailed description of the model implementation for the stBLM, see the Supplemental Information.

TABLE IV.

Fit parameters for the sparsely tethered lipid bilayer membrane derived using the continuous distribution model. 95.4% confidence intervals were computed using a Monte Carlo resampling technique (Ref. ⁹).

Fit parameter	Value ± 2σ
thickness of gold film / Å	144.9 ± 0.7
thickness of spacer/ sub-membrane space / Å	17.6 ± 0.4
thickness of proximal hydrocarbon chains / Å	17.5 ± 0.5
thickness of distal hydrocarbon chains / Å	10.9 ± 0.3
bilayer completeness	1.00 ± 0.02
molar fraction of DMPC in proximal leaflet	0.37 ± 0.01
molar fraction of DMPC in distal leaflet	1.00 (fixed)
number of βME per WC14	1.6 ± 0.8
bilayer roughness / Å	4.0 ± 0.1
substrate roughness / Å	4.5 ± 1.2

The sub-membrane space contains the surface-ligated βME, (EO)₆ plus thiol and the tether glycerol. Phospholipid head groups protrude into this space. Its thickness is d = (17.6 ± 0.4) Å, consistent with the thickness of the sub-membrane space for the same system as determined earlier with a box model approach, d = (16.7 ± 1.0) Å.⁸

The hydrocarbon thickness within the bilayer is d = (28.4 ± 0.5) Å, as seen by the new model, which is about 4 Å thinner than reported from box model fits, d = (32.6 ± 4.0) Å.⁸ This discrepancy may be due to differences in modeling lipid head groups next to the substrate. The continuous distribution model of the head groups from the MD simulation yields a projected length of the lipid head groups of about 9 Å, used as a constant to describe the NR data, a value that may slightly overestimate the actual head group size. In contrast, the box model of stBLMs used earlier assumed d = 7 Å for the distal phospholipid head groups and did not explicitly account for the head groups near the substrate at all.

In the error-function based continuous distribution modeling, the inner bilayer leaflet, composed of 63% tether chains and 37% DMPC chains, is characterized by a high average leaflet thicknesses of (17.6 ± 0.4) Å, comparable to the extended length of a myristyl group (17.9 Å). The cross-sectional area in this monolayer amounts to ≈ 19 Ų per chain, which would constitute an extremely small value for phospholipids.⁴⁶ However, the WC14 tether has its hydrocarbon chains attached by an ether linkage that lacks the carboxyl oxygens at the C₁ carbon and is therefore structurally related to diether lipids. A structural study of a comparable diether lipid, 1,2-dihexadecyl-sn-glycero-3-phosphocholine (DHPC),^{47, 48} determined a hydrocarbon thickness of 20.3 Å for the interdigitated, non-tilted, gel phase and an area per lipid molecule of 38.6 Ų. The tilted gel phase of DHCP has a hydrocarbon thickness of 17.3 Å and an area per lipid molecule of 46.9 Ų. This comparison suggests that the hydrocarbon chains of WC14 may form a tilted gel phase at high tether surface densities. Properties of the possibly phase-separated DMPC minority component cannot be discerned.

The surface density of WC14 can be calculated from the model parameters and is (1.4 ± 0.1) molecules/100 Ų. There are (1.6 ± 0.8) βME molecules per tether on the surface. The large uncertainty of this fitting parameter shows the insensitivity of the model to the backfiller:tether ratio. The SAM was prepared from a 70:30 βME:WC14 solution. The value of βME:WC14 = 1.6 corresponds to a 62:38 ratio of backfiller and tether and therefore appears to be a reasonable estimate of the actual surface composition.

CONCLUSIONS

A new continuous distribution modeling strategy based on a flexible error-function description of molecular distributions within layered interface architectures has been presented. While rooted in earlier work, this approach overcomes limitations of established models in the description of membrane structures and, most significantly, is particularly economical in the use of independent model parameters. Chemical constraints, e.g., in the form of the connectivity between components within a molecule can be naturally implemented by controlling the relative positions of the constituent error functions that form the overall area profiles. It has been previously shown^{9, 21} that such approaches may significantly increase the precision by which structural parameters can be determined from scattering experiments, in particular if isotopic contrast variation is used in neutron experiments. However, the described approach lends itself equally well to the evaluation of x-ray scattering data or to the joint refinement of x-ray and neutron experiments on similarly prepared samples.^{10, 11}

Using this new data modeling technique, we demonstrated the refinement of NR data sets for solid-supported bilayers. While both compositionally simple lipid membranes could be examined with the conventional box model, the novel approach unveiled properties of interest that bear physical meaning which would otherwise not have been directly accessible. Previously, the compositions of the proximal bilayer leaflets in terms of tether lipid and phospholipids and of the thiolated compounds, tether lipid and backfiller, on the surface of the gold films in stBLMs could not be determined. The new approach yields precise and physically reasonable estimates of these quantities from NR data. We also demonstrated that areas per molecule, molecular composition of the lipid leaflets, and thickness of the sub-membrane space can be determined with high precision.

The versatility of the model developed here will in future be exploited in investigations of complex biological architectures such as tethered lipid bilayer membrane systems interacting with peptides or proteins.^{27, 49, 50} The robust framework with which we implemented the constraints between sub-molecular groups of complex molecular architectures makes such investigations feasible. In particular, it will also be possible to define hybrid models that combine the layered surface architecture described here with atomic-scale models for proteins derived from x-ray crystallography or NMR.

The algorithms described here have been implemented into publicly accessible modeling software, the NCNR’s ga_refl reflectometry data evaluation suite.¹⁴