Abstract
Exon–intron architecture is one of the major features directing the splicing machinery to the short exons that are located within long flanking introns. However, the evolutionary dynamics of exon–intron architecture and its impact on splicing is largely unknown. Using a comparative genomic approach, we analyzed 17 vertebrate genomes and reconstructed the ancestral motifs of both 3′ and 5′ splice sites, as also the ancestral length of exons and introns. Our analyses suggest that vertebrate introns increased in length from the shortest ancestral introns to the longest primate introns. An evolutionary analysis of splice sites revealed that weak splice sites act as a restrictive force keeping introns short. In contrast, strong splice sites allow recognition of exons flanked by long introns. Reconstruction of the ancestral state suggests these phenomena were not prevalent in the vertebrate ancestor, but appeared during vertebrate evolution. By calculating evolutionary rate shifts in exons, we identified cis-acting regulatory sequences that became fixed during the transition from early vertebrates to mammals. Experimental validations performed on a selection of these hexamers confirmed their regulatory function. We additionally revealed many features of exons that can discriminate alternative from constitutive exons. These features were integrated into a machine-learning approach to predict whether an exon is alternative. Our algorithm obtains very high predictive power (AUC of 0.91), and using these predictions we have identified and successfully validated novel alternatively spliced exons. Overall, we provide novel insights regarding the evolutionary constraints acting upon exons and their recognition by the splicing machinery.
In the process of splicing, introns are removed from an mRNA precursor (pre-mRNA), and exons are ligated to form a mature mRNA (Black 2003). Exons and introns are recognized in the splicing process by many different signals and interactions along the exon–intron structure. Several signals along the pre-mRNA help the splicing machinery to recognize exon–intron junctions: The 3′ and 5′ splice sites (3′ss and 5′ss) located on both exon–intron junctions, and the branch site and polypyrimidine tract (PPT) located upstream of the 3′ss (Black 2003). In alternative splicing, the splicing mechanism produces more than one mRNA from a single pre-mRNA (Graveley 2001). This is done by the splicing of different sets of exons from a single pre-mRNA, resulting in an increased number of protein isoforms that can be synthesized from one gene. Previous studies revealed that the percentage of exons undergoing alternative splicing is higher in vertebrates compared with invertebrates, and in human compared with other vertebrates (Kim et al. 2007). This suggests that alternative splicing has a major role in the production of higher levels of biological complexity.
Exon–intron structure plays a major role in the recognition of exons by the splicing machinery. It was previously demonstrated in Drosophila (Fox-Walsh et al. 2005) and in vertebrates that intron length affects the inclusion of exons (Bell et al. 1998; Yeo et al. 2005; Kim et al. 2007). Long introns were found to flank alternative exons while short introns maintain efficient exon recognition (Fox-Walsh et al. 2005; Kim et al. 2007). The suggested mechanism for this phenomenon is that long introns hinder the activity of the spliceosome through interference with the proper positioning of the spliceosome upon exon–intron junctions. Long introns were also found to correlate with splice site strength, where short introns tend to flank weak splice sites and long introns tend to flank exons with strong splice sites (Fields 1990; Clark and Thanaraj 2002; Weir and Rice 2004; Dewey et al. 2006). A more recent study reveals that novel alternative exons tend to appear within long introns (Roy et al. 2008), suggesting that the association of alternative splicing with long introns is a consequence of the higher likelihood of new exons to originate in long introns.
There is much debate over the mechanism by which the splicing machinery recognizes exons from within the vast intronic oceans. Two main models are frequently used to explain this issue: the intron definition and exon definition pathways (Robberson et al. 1990; Berget 1995; Ast 2004; Ram and Ast 2007; Keren et al. 2010). Intron definition is when the splicing machinery recognizes the intronic unit and places the basal splicing machinery across introns, thereby constraining intron length. This mechanism is proposed to be widespread in early diverging eukaryotes and is also thought to be the ancestral mechanism (Berget 1995; Romfo et al. 2000). Exon definition occurs when the basal machinery is placed across exons that have a pair of closely spaced splice sites, thus constraining the length of the exons. This mechanism is thought to occur in vertebrate species (Collins and Penny 2006). Since both the exon definition and intron definition pathways are highly influenced by the exon–intron structure, it is interesting to examine whether the structural changes of exons and introns throughout evolution can back up or refute these two models.
Despite the accumulation of knowledge concerning exon–intron architecture and splicing signal strength, there are still many open questions: (1) What is the nature of the association between intron lengths and alternative splicing? Do these structures co-evolve? (2) Does the fact that long introns and alternative splicing are both characteristics of higher organisms indicate that long introns are the evolutionary driving force for the transition from constitutive to alternative exons observed in higher organisms? (3) Which other genomic factors determine evolutionary shifts from constitutive to alternative, and do we understand these factors well enough as to allow us to accurately predict if an exon is constitutively or alternatively spliced?
In this study, we explore evolutionary changes in exon–intron architecture, and examine their influence on alternative splicing. We analyze 17 vertebrate species, employing a genome-wide, comparative genomic approach. We reconstruct ancestral exon and intron lengths, and show that introns expanded and exons shortened in the lineage leading to mammals. By also reconstructing the ancestral splice site motifs, we can indicate that splice site composition plays a major role maneuvering intron length. Based on these results, we provide a novel evolutionary theory for the formation of alternative cassette exons (exon skipping) through a transition from constitutive exons, during the evolution of vertebrates. In addition, by analyzing evolutionary rate shifts, we identify cis-acting regulatory sequences and prove their functionality through experimental validations. Finally, we apply a machine-learning approach to classify exons as either alternative or constitutive and use this classification to identify and experimentally validate the splicing of novel alternative cassette exons. Overall, our findings shed light on the driving forces that have shaped exon–intron architecture throughout vertebrate evolution.
Results
Constitutive and alternative conservation analysis
To study evolutionary dynamics of exon–intron structure during vertebrate evolution, we calculated per base level of identity with respect to human for alternative and constitutive exons and for the flanking introns. We retrieved a total of 4433 human alternative cassette exons and 111,617 constitutive exons based on the RefSeq tracks from the UCSC Genome Browser (http://genome.ucsc.edu/; Karolchik et al. 2003) as was previously published (Schwartz et al. 2009a). Classifications of exons into alternative and constitutive were based on human genome EST support alone (see Methods). Thus, the mode of splicing was determined only in the human genome, not in any other vertebrates. Using the retrieved exon coordinates, and the UCSC Galaxy engine tools, we constructed multiple sequence alignment (MSA) data sets for the exons and flanking intronic sequences (200 nt from each side). MSAs were constructed for 17 vertebrate organisms that diverged ∼400 million years ago, including early diverging vertebrates (three fish species, frog, and chicken), marsupials (opossum), and 11 mammalians including rodents and primates (see Supplemental Fig. S1).
Each orthologous sequence in all exonic MSAs was verified to reside within an exon in an annotated RefSeq (Pruitt et al. 2005) of that species. Sequences orthologous to human exonic sequences that were not within exons in other species were omitted from any further analyses. Next, we separated the exons into three age groups as was done by Corvelo and Eyras (2008): vertebrate and older (VO), mammalian specific (MS), and primate specific (PS) (see Methods). This was done in order to ensure that only ancient exons that emerged during early vertebrate evolution (the VO exons), and not younger exons, were analyzed.
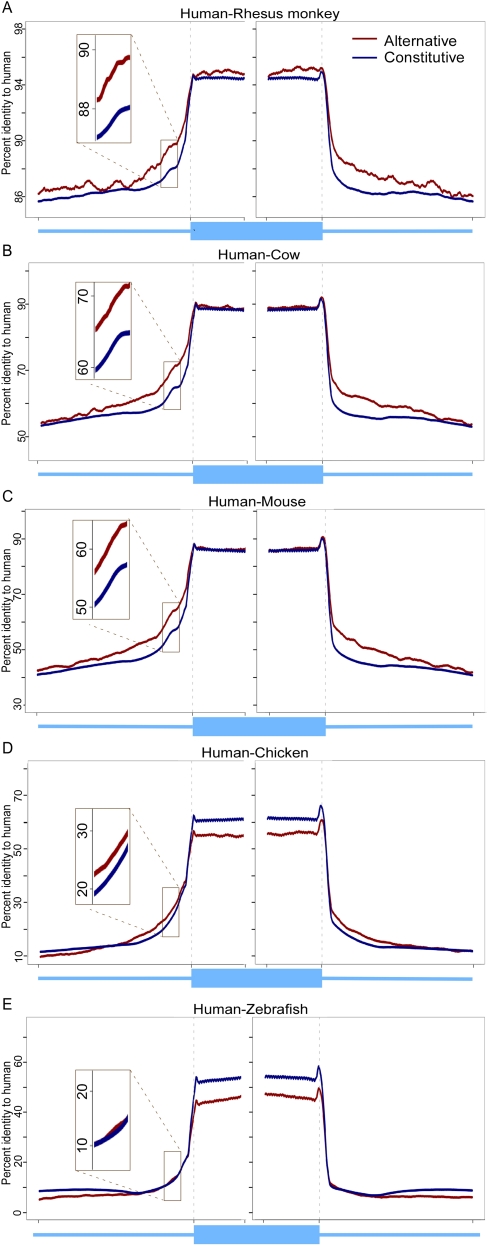
Approximately 87% of the constitutive exons and 68.5% of the alternative exons were found to be VO exons that were created prior to the transition from vertebrates to mammals. The higher portion of younger alternative exons (31.5% MS and PS exons) compared to constitutive exons (13%) was previously noted (Alekseyenko et al. 2007). The identity plots presented in Figure 1 for VO exons in five vertebrate species are representative (all 16 plots are presented in Supplemental Fig. S2). As expected, there was a clear distinction between exons and introns for all vertebrates tested with higher identities in coding than noncoding sequences. This distinction was also observed in primates even though the level of sequence identity is very high for both exons and introns as a result of a very short evolutionary distance.
Figure 1.
Percent identity-to-human of vertebrates or older (VO) exons and flanking introns of five vertebrate genomes. (A–E) Identity was calculated per base for alternative (red) and constitutive (blue) exons (75 nt from each splice site) and flanking intronic regions (200 nt).
There is a general decrease in both exons and introns identity when evolutionary distance from human is increased, with rat and mouse exons being less conserved to human compared with dog and cow exons (P-value < 2.2 × 10−16, multiple t-tests for all corresponding species). Furthermore, the rat and mouse intronic sequences have very low conservation with respect to human. These two results are likely due to the accelerated evolutionary rate of Rodentia (Thomas et al. 2003). The general decrease in identity-to-human with increased evolutionary distance may also be a result of a decrease in alignment coverage as the species distance from human increases, particularly in noncoding regions (Chen and Tompa 2010).
The results do not exhibit a significant difference in the sequence identity of the mammalian group between alternative and constitutive exons. However, the identity-to-human of the alternative exon orthologs in the early vertebrate species (chicken, frog, fugu fish, zebrafish, and tetraodon) was lower than that of constitutive exon orthologs (multiple t-tests, P-value < 2.2 × 10−16). Previous studies have reported that there are fewer evolutionary constraints on alternative exons compared with constitutive exons in fruit flies and mosquito (Malko et al. 2006) and in human and mouse (Chen et al. 2006). Here we observed this phenomenon only in early vertebrates and not in the mammalian group.
For flanking intronic sequences (Fig. 1; Supplemental Fig. S2), there was a higher level of conservation in mammals for the regions flanking alternative exons compared to the regions flanking constitutive exons (multiple t-tests, P-value < 2 × 10−5). This observation includes also primates, where the identity is very high in general. We observed that in early vertebrates there was no significant difference in conservation level between alternative and constitutive flanking introns. These results are in line with previous works that showed increased conservation within intronic sequences flanking alternative exons relative to intronic sequences flanking constitutive exons (Sorek et al. 2004b; Chen and Zheng 2008). This is presumably due to the presence of intronic splicing enhancers in the vicinity of the 3′ and 5′ss (Yeo et al. 2004).
Length analysis of constitutive and alternative orthologous exons/introns and ancestor length reconstruction
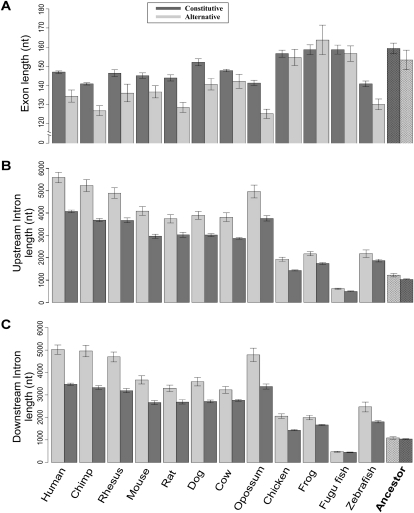
We next examined the evolutionary dynamics of exon–intron length changes throughout the vertebrate tree. Our null hypothesis was that the sequences of alternative and constitutive exons are subjected to the same dynamics throughout the evolutionary tree. To test this hypothesis, we reconstructed the ancestral exon and intron lengths using a maximum-parsimony based algorithm. The algorithm receives a set of exon or intron lengths and an evolutionary tree as input, and reconstructs the most parsimonious ancestral length at the node that corresponds to the vertebrate root (see Methods). Reconstruction of the ancestral exon and intron lengths revealed two major observations: In exons, there was a shift to reduce length from ∼157 nt in the vertebrate ancestor, with no significant difference between alternative exons and constitutive exons, to a mean of 147 nt for constitutive exons in human, with alternative exons having a significantly shorter mean length of 134.5 nt (Fig. 2A) (t-test, P-value < 1 × 10−4). This finding reinforces recent reports connecting nucleosome occupancy to exon–intron architecture, revealing that the length of DNA wrapped around a mononucleosome is approximately the mean exon length found in human (Schwartz et al. 2009b). This observation leads to the realization that constitutive exons length was reduced by the evolutionary process to approximately the same length as the DNA wrapped around nucleosomes in human. Though early diverging vertebrates do not show significant difference between the length of alternative and constitutive orthologous exons, a major change is observed between early diverging vertebrates and mammals, resulting in shorter alternative exons orthologs in mammals. The shorter length of alternative exons was previously reported for human-mouse conserved alternative exons (Sorek et al. 2004a), and is shown here as a larger phenomenon embracing all mammalian orthologous exonic sequences. The lack of difference between alternative and constitutive exons length in the vertebrate ancestor and early diverging vertebrates indicates a shift in mammals toward a possible discrimination of the alternative exons via length property.
Figure 2.
Length of constitutive and alternative exons and their flanking introns in 12 vertebrate genomes and reconstruction of ancestral length. (A) Mean lengths of alternative (light gray) and constitutive (dark gray) exons. The reconstructed most parsimonious ancestral length is plotted in the right-most column. Error bars represent the standard error of the mean. (B,C) As in A, for the intronic regions upstream of and downstream from alternative and constitutive exons, respectively.
In introns, reconstruction of length revealed that the last common ancestor of vertebrates contained introns of ∼1100 nt and, as in the exons, there were no length differences between the reconstructed ancestral length of introns flanking constitutive exons and those flanking alternative exons. However, the results in all vertebrates tested show that both upstream and downstream introns are characterized by longer introns flanking alternative exons while shorter introns flank constitutive exons (Fig. 2B,C). The introns extended in human to a mean length of ∼4070 and ∼3470 nt for upstream and downstream introns flanking constitutive exons. This trend is even more pronounced for introns flanking alternative exons: mean length of ∼5580 and ∼5020 nt for upstream and downstream introns, respectively. The length differences between human alternative and constitutive exons/introns and their vertebrate orthologs are drawn in Supplemental Figure S3. To prevent a bias that might be caused by the sample of species, we repeated the reconstruction analysis with different subsets of species; results were in agreement with the analysis of the full set of species (see Methods).
These results indicate that human introns are longer than other vertebrates such as mouse, dog, and chicken, as well as invertebrates (Schwartz et al. 2008). It appears that there is a much larger difference between introns flanking alternative exons and introns flanking constitutive exons in mammals (+30%–42%) than the difference in early vertebrates (+15%–25%) (multiple t-tests, P-value < 0.003). This result suggests an extensive lengthening of some introns, most likely due to insertions of transposable elements (Sela et al. 2010). Such a lengthening may contribute to exon skipping (see Discussion).
After the examination of the major differences between alternative and constitutive data proposed by the length analysis, we next verified that the observed changes in mean intron length are not caused by the first intron of the transcripts, which is known to be significantly longer than the following introns (Kalari et al. 2006). For that purpose, we extended our analysis further to regard intron length data with respect to position from transcription start site (TSS). We observed that the mean length of the first intron in the transcript is always the longest of all introns in all 12 vertebrates tested. We then used it as the upper marker to create a relative ratio based on intron length divided by the first intron length. This resulted in a maximal value of 1 for the first intron and smaller values for the remaining sequential introns, ranging between 0 and 1. Next, we plotted the mean length of the first 20 introns for 12 vertebrates (Supplemental Fig. S4). The results indicate the extended length of the first introns for all vertebrates tested. Furthermore, we observe a gradient of shortening length in the first introns, i.e., we see an inverse correlation between intron length and distance from the TSS. This suggests that the lengthening of the intronic sequences is most pronounced in the first intron from the TSS, and it continues along the sequential internal introns of the transcript. Furthermore, the lengthening of the introns, starting from the TSS, is much stronger in mammals than in early diverging vertebrates, excluding zebrafish (Supplemental Fig. S4B). The lengthening of the first introns might be explained by enhanced density of transcription factors binding sites in first introns (Majewski and Ott 2002). We suggest that mammals gained regulatory intronic elements in a biased manner, so that first introns gained the highest number of such elements, and the trend continues downstream from the sequential introns (see Discussion).
The link between splice site strength and intron lengthening
Since the 3′ss and 5′ss play a major role in introducing introns (or exons) to the splicing machinery, we were interested in examining how the splice site motifs have changed through vertebrate evolution and how these changes affected the length of the flanking introns. In order to achieve that goal, we reconstructed the ancestral motifs of both 3′ and 5′ss using a maximum-likelihood based algorithm (Pupko et al. 2000). The algorithm receives a set of 3′ or 5′ signals and an evolutionary tree as input, and reconstructs the most likely ancestral signal at the node that corresponds to the vertebrate root (see Methods). Reconstruction of the ancestral splice site motifs of orthologous sequences (Supplemental Fig. S5) revealed a high overall similarity of both 3′ and 5′ss motifs to the mammalian signals (Pearson's correlation coefficient 0.973 and 0.93 for 3′ss and and 5′ss, respectively). When comparing the consensus nucleotides of each of the splice sites, between the vertebrate ancestor and mammalian motifs, three minor fluctuations were observed: (1) In the 3′ss, at the −4 intronic position there is a switch from a preferred thymidine in the ancestor to a minor preference of cytosine in the mammalian group. (2) In the 5′ss motif, at exonic position −3, there is a shift from adenine in the ancestor to thymidine in the mammalian signal, and (3) in the mammalian group, there is a lessening of guanine and thymidine preference at intronic positions +5 and +6, respectively. These results are in line with previously published results (Schwartz et al. 2008), suggesting that the 5′ss and the 3′ss signals are subject to minor phylogenetic fluctuations along the phylogenetic tree.
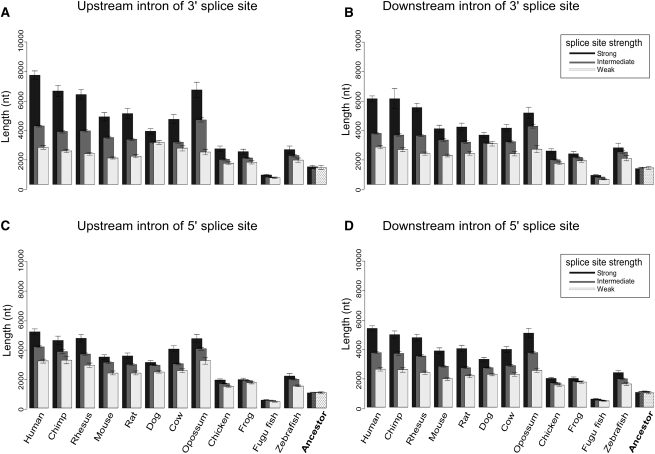
We next analyzed changes in the splice site strength with respect to the flanking introns length through the vertebrate phylogenetic tree. For that purpose, we retrieved the human and orthologous 3′ss and 5′ss MSAs and scored all splice sites, for each organism and ancestor separately, based on the algorithm of Shapiro and Senapathy (1987). Splice site strength tables were thus built for each organism tested. Only canonical splice sites (i.e., AG in positions −2 and −1 for 3′ss and GT or GC in positions +1 and +2 for 5′ss) were considered. We omitted the first intron of all transcripts from this analysis since they are longer in all vertebrates tested (see Supplemental Fig. S4). Next, we correlated splice site strength with intron length data for all the sequences tested, alternative or constitutive. By doing so, we were able to examine the changes in intron length with respect to the changes in splice site strength, while taking into account the evolutionary perspective. In Figure 3 we display the length of introns flanking constitutive exons as a function of splice site strength, for 3′ss (Fig. 3A,B) and 5′ss (Fig. 3C,D) across 12 vertebrate species and ancestor tested. We divided all the splice sites into 10 bins, each bin containing 10% of the sites, based on their strength. The top 10% of the values represent the strongest splice sites, the bottom 10% of the values represent the weakest splice sites, and the values in between are the medium-strength splice sites. Overall, our results indicate that, most strikingly, introns flanked by weak 3′ss or weak 5′ss are short for all the genomes tested. Moreover, the intron length of those flanked by weak splice sites does not present the same evolutionary lengthening seen on Figure 2B, but remains short throughout vertebrate evolution, with no significant difference between the organisms (P-value = 0.35 and 0.12, one-way ANOVA test for upstream and downstream introns, respectively), excluding fugu fish and vertebrate ancestor, where overall intron length is extremely short (480 and 1000 nt for fugu fish and ancestor, respectively). This suggests a purifying selection pressure against the lengthening of introns when the splice sites are weak. This result was replicated for all the organisms in our data, showing that it is a strong and comprehensive attribute of vertebrate evolution. We also found that introns flanked by strong 5′ss or 3′ss (marked as black columns) are significantly longer than their counterparts flanked by weaker splice sites (marked as white columns). Following that line, we find upstream introns flanking strong 3′ss to be much longer (P-value 1.386 × 10−11, t-test) on average than upstream introns flanking strong 5′ss, exhibiting an average length of 7614 nt in human when 3′ss is strong and 5202 nt when 5′ss is strong. This effect, albeit significant (P-value 0.005, t-test) is weaker in the downstream intron (length of the downstream introns flanking strong 3′ss is 5960 nt vs. length of downstream introns flanking strong 5′ss, which is 5246 nt). The same results are observed for all tested organisms, suggesting a major role for the 3′ss in binding the spliceosome when it comes to compensating for long upstream introns.
Figure 3.
Constitutive flanking introns’ length with relation to splice site strength for 12 species. Upstream (A) and downstream (B) introns that flank constitutive exons were divided into three groups based on 3′ss strength: strong splice site (black), intermediate splice site (gray), and weak splice site (white). Same as for A and B, but for upstream (C) and downstream (D) introns based on 5′ss strength. The reconstructed ancestral lengths are plotted in the right-most column.
The effect of splice site strength on introns flanking constitutive exons was not observed for the reconstructed ancestor introns and splice site signals. No significant difference was found between the three splice site strength groups, for neither upstream nor downstream introns, for both splice sites (P-value > 0.14, one-way ANOVA test). When comparing nonmammalian vertebrates to mammals, the effect of splice site strength on intron length appeared to be stronger in the latter (Fig. 3). Together, these results suggest that splice site effect on intron length originates in early diverging vertebrates and yet intensifies in later divergences through vertebrate evolution.
This analysis was also repeated for introns flanking alternative exons (Supplemental Fig. S6), and overall, the results were in agreement with the constitutive introns analysis, with two exceptions: (1) There were not enough data to allow a founded reconstruction of splicing signals for alternative exons, thus the ancestor was omitted from this analysis. (2) The average length of the introns flanking alternative exons is much longer than that of constitutive exons (consistent with Fig. 2B,C).
To confirm our results, we performed the same analysis based on a splice site scoring algorithm developed by Yeo and Burge (2004) for modeling sequence motifs based on the Maximum Entropy principle. The results using this method supported the same findings as the Senapathy scoring system (see Supplemental Fig. S7). Integrating the results concerning intron length and splice site strength (Figs. 2, 3), we conclude that there is a general tendency for intron lengthening through vertebrate evolution, but this tendency is restricted to the introns flanked by strong splice sites. In addition, this phenomenon is not restricted to first introns, but rather holds for internal introns as well.
Evolution rate of alternative and constitutive exons
Changes in splicing are the source for proteomic diversification and susceptibility to different diseases (Wang and Cooper 2007). Alternative splicing is also an important mechanism to generate gene function novelties. Therefore, shifts from alternative splicing to constitutive splicing (or vice versa) may be an evolutionary force shaping protein evolution. We have previously demonstrated that exons can change their mode of splicing during evolution from constitutive to alternative. For a specific case it was shown that such a change is associated with mutations leading to fixation of splicing regulatory sequences that are important for the regulation of the exon inclusion level (Lev-Maor et al. 2007). This observation suggests that selection forces on motifs regulating inclusion levels may change during the transition between one form of splicing and another. It follows that evolutionary rate changes (a conserved position became variable and vice versa) are expected at those points in evolution where shifts between splicing forms have occurred. Specifically, a shift from variability to conservation implies a gain of function (e.g., for alternative exons, such evolutionary rate shift in a certain evolutionary lineage may indicate that a sequence has acquired the skipping mode in that lineage).
We searched for changes in evolutionary rates at the single base pair resolution using a maximum-likelihood based approach (Pupko and Galtier 2002). In this approach we search for evolutionary rate shifts between two sub-trees. We split the vertebrate tree several times, each time in a different edge, looking for rate shifting sites between the two extracted sub-trees. Specifically, we search for sites in which the rate of evolution in one sub-tree is significantly different (higher or lower) than that of the second sub-tree. Highly different rates in the two sub-trees suggest a change in the functional constraints (Pupko and Galtier 2002).
Applying this method to the exon data sets, only in the branch point between the mammalian and the nonmammalian sub-trees we detected an amount of significant “rate shifts to conservation” that was sufficient for our analyses (maximum-likelihood test, P-value < 0.05, see Methods). We next analyzed the rate shifting sites that were detected. We identified two types of rate shifting sites by the direction of their shift: (a) “rate shifts to variability,” which are highly conserved sites in nonmammalian vertebrates that became variable in mammals, and (b) “rate shifts to conservation,” which are variable sites in nonmammalian vertebrates that became highly conserved in mammals.
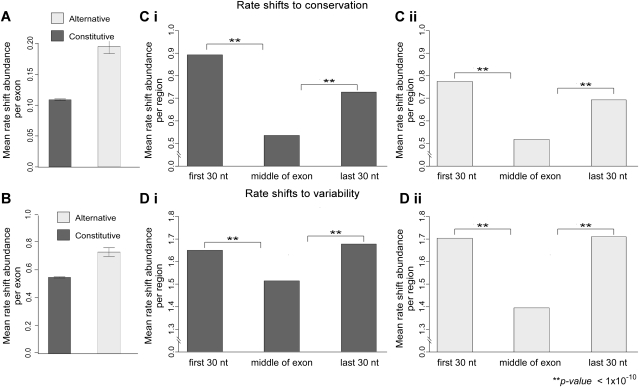
Our analysis detected 0.195 “rate shifts to conservation” per 100 nt for all alternative exons in our data set compared to 0.108 “rate shifts to conservation” per 100 nt in constitutive exons (Fig. 4A). This 81% increase in rate shift score in alternative exons is highly significant (P-value 8.6 × 10−14, two-sample t-test). These results suggest that more sites became conserved in alternative exons compared to constitutive exons in the lineage leading to mammals. We also observed more sites (+33%) that became variable in mammals in alternative exons compared with constitutive exons (Fig. 4B), although the difference was less but still highly significant (P-value 1 × 10−09, two-sample t-test). The high number of both types of rate shifts in alternatively spliced exons compared to constitutive exons suggests that regulation of alternative splicing has changed during the emergence of mammals, more so compared to changes in the regulation of constitutive exons (see Discussion).
Figure 4.
Distribution of rate shifting sites per exon and along the exon. Mean rate shift abundance of “rate shifts to conservation” (A) and “rate shifts to variability” (B) are plotted for all examined constitutive (dark gray) and alternative (white) exons. Rate shift abundance was calculated as the mean number of rate shifting sites normalized per length. Constitutive exons have a lower conserved rate shift score and a lower variable rate shift score than alternative exons. Abundance of “rate shifts to conservation” (C) and “rate shifts to variability” (D) along exons are plotted for constitutive (Ci, Di) and alternative (Cii, Dii) exons. Each exon was divided into three regions (x-axis): 30 nt downstream from the 3′ss, middle of the exon, and 30 nt upstream of the 5′ss. Abundance of rate shifting sites in each of the regions are indicated (y-axis). Error bars represent the standard error of the mean.
Several groups including ours have previously demonstrated that exonic splicing regulatory sequences tend to cluster near the splice sites (Fairbrother et al. 2004; Goren et al. 2006). We, therefore, tested whether rate shifting sites reside preferentially in certain regions along exons. We compared the number of rate shifting sites among three exonic regions: downstream from the 3′ss (30 nt), middle of the exon, and upstream of the 5′ss (30 nt). While in the previous analysis the abundance of rate shifting sites was calculated for all exons that were examined, here it was calculated only for exons that were found to contain rate shifts. The results of this analysis show that the abundance of both types of rate shifting sites is significantly higher (P-value < 1 × 10−10) in close proximity to the splice sites (Fig. 4C,D), for constitutive (left panel) as well as alternative (right panel) exons. These results suggest that the differences between alternative and constitutive exons, with regard to “rate shifts to conservation” and “rate shifts to variability” mentioned above, are mainly due to changes in selection intensity around the splice sites.
Prediction of cis-acting splicing regulatory elements
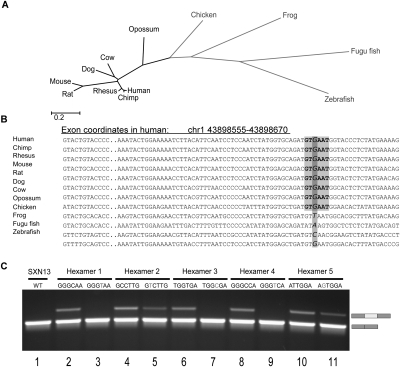
To identify splicing motifs that act as major regulators of alternative splicing, we analyzed the exons on the nucleotide level using the rate shifts data we have obtained. Regions along constitutive and alternative exons that have a fast evolutionary rate in the nonmammalian group and are highly conserved in mammals might point to regulatory sequences that are important for splicing regulation in mammals. We looked for sequence words composed of six nucleotides (hexamers) that have a tendency to overlap sites that became more conserved in mammals. These hexamers were formed in mammals through the fixation of point mutations that were variable in nonmammalian vertebrates. An example for a hexamer found using this method is shown in Figure 5A,B.
Figure 5.
Prediction and validation of splicing regulatory hexamers by rate shift analysis. (A) Twelve vertebrate species divided in two sub-trees: mammals (black) vs. nonmammalian vertebrates (light gray). (B) An example of motif identified using rate shift analysis. The position is variable among nonmammalian vertebrates (two species of fish, frog, and chicken) and is highly conserved among mammals. Marked in light gray is one of six possible hexamers that are formed by the rate shifting substitution. (C) The effect of putative enhancing hexamers and their mutants in SXN13 reporter system. Each tested hexamer was inserted into the second exon of a reporting minigene comprised of four exons. Splicing patterns of each hexamer and its mutant are demonstrated in lanes 2, 4, 6, 8, and 10 and 3, 5, 7, 9, and 11, respectively. (Lane 1) SXN13 wild type. The upper bands indicate exon inclusion while the lower bands indicate exon skipping.
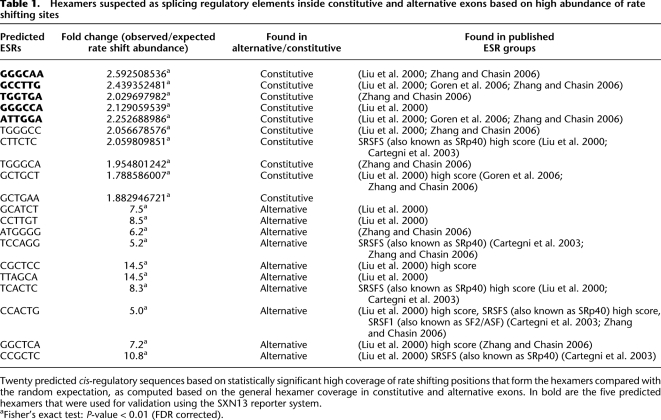
We developed a method that enabled us to locate these hexamers by analyzing all possible 4096 hexamers and identifying those that have an overabundance of sites in which the evolutionary rate shifted to conservation in mammals, compared with the random expectations given by their relative frequency. The constructed tables of rate shift expected vs. observed fold change in hexamers (for both constitutive and alternative exons) are presented in Supplemental Table S1. Using statistical tests (Fisher's exact test) to score the hexamers based on P-value after applying a false discovery rate (FDR), we identified 141 hexamers (α < 0.01) as possible cis-acting regulatory elements in constitutive exons and 23 in alternative exons. Table 1 lists the 10 hexamers for each exon type that were most significantly enriched with rate shifting sites. We searched for these hexamers in putative exonic splicing regulatory elements (ESRs) and found that 98 out of 141 constitutive hexamers (70%) and 18 out of 23 of the alternative hexamers (78%) are responsive to the human SR proteins SRSF1, SRSF5 (Cartegni et al. 2003), and mostly SC35 (Liu et al. 2000). These results imply that these SR proteins are important for the regulation of alternative splicing—especially for exons that became alternative in human.
Table 1.
Hexamers suspected as splicing regulatory elements inside constitutive and alternative exons based on high abundance of rate shifting sites
We next validated the assumed regulative role of the highly rated hexamers. In order to examine the role these hexamers have in splicing regulation, we used the SXN13 minigene reporter system (Coulter et al. 1997), which is well characterized and widely used (Goren et al. 2006; Didiot et al. 2008; Bensaid et al. 2009). The middle exon of SXN13 minigene is predominantly skipped and can be used to identify splicing enhancers. We introduced each of the five highest rated hexamers identified using constitutive exons (Table 1, rows 1–5), assumed to be splicing enhancers, into the middle exon of the SXN13 in their human form and in the form found in early vertebrates (before the evolutionary rate shift occurred). Figure 5C exhibits the splicing pattern of SXN13 with the SXN13 WT (lane 1), the human hexamers (lanes 2, 4, 6, 8, and 10), and the early vertebrate hexamers (lanes 3, 5, 7, 9, and 11). The introduction of all five hexamers increased the inclusion of the middle exon, validating the enhancer role of the predicted ESRs. Furthermore, with the introduction of the mutated hexamers, the exon was fully skipped in three of the cases (lanes 3, 7, and 9), and in the other two cases the inclusion level decreased (lanes 5 and 11), indicating that the hexamers affected the recognition of the entire exon. Through this analysis of evolutionary rate shifting sites within hexamers, we were able to locate sequences in exons that are highly conserved in mammals. We found that these conserved hexamers matched highly scored SR protein binding sites and confirmed the regulatory function of certain hexamers experimentally. This verification of the splicing regulation function of the predicted ESRs also validates the evolutionary rate shifts abundance method.
Distinguishing alternative from constitutive exons using machine-learning algorithms
In the process of splicing, the spliceosome uses many splicing signals. The output of such signals determines the mode of splicing—constitutive or alternative—and the level of inclusion in alternative splicing. We decided to use the features obtained in this work, in order to classify alternative exons using machine-learning algorithms. The output of the machine-learning algorithm is a score that represents the confidence of the classifier in predicting whether a given exon is constitutively or alternatively spliced. In a sense, this provides a measure of our current understanding of how the mode of splicing is determined.
Toward this aim, we used three different classification algorithms: Naïve Bayes (Morrison 1990; Langley et al. 1992), Bayesian networks (Heckerman et al. 1995), and Support Vector Machine (SVM) (Burges 1998; Vapnik 2000). For each classification algorithm, a phase of feature selection was applied to identify the subset of features that performs best with the classifier. Receiver operating characteristics graphs (ROC curves) were constructed in order to test the classification performance. The Area Under the ROC Curve (AUC) of a classifier is equivalent to the probability that the classifier will rank a randomly chosen positive instance higher than a randomly chosen negative instance (Green and Swets 1966; Fawcett 2006). Thus, a yielded AUC value of 0.5 represents a random classification and a yielded AUC value of 1 is a perfect classifier (see Methods for machine-learning protocols).
We used 93 features to distinguish between alternative and constitutive exons that are human-mouse conserved by class, namely exons that are alternatively spliced in both species, and the same for constitutive exons. Fifteen features are exon structure properties such as sequence length and GC content. Two features represent the evolutionary rate analysis of the exon, and eight features measure length, conservation, and rate shift abundance for both flanking introns of the exon. The other 68 features represent hexamers with the highest rating that were obtained from the evolutionary rate shift analysis of alternative and constitutive exonic data (see Methods). The individual performance of each individual feature is listed in Supplemental Table S2.
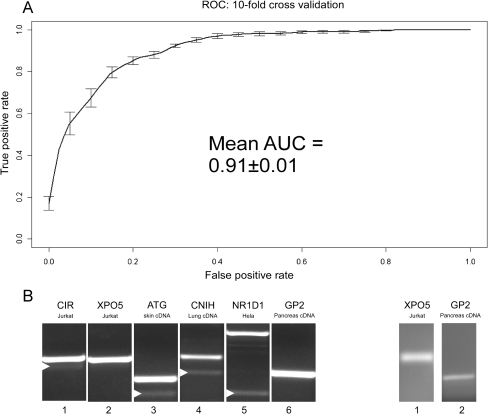
Based on the combination of these features, the machine-learning scheme was able to obtain very accurate classification. The best performing classifier achieved an AUC value of 0.91 (Fig. 6A) on a training set composed of all 414 alternative exons that are human-mouse conserved and 414 constitutive exons, chosen randomly from the 3396 constitutive exons that are human-mouse conserved. In order to verify that this is not an overestimation, we have also tested the performances of the whole machine-learning scheme using cross-validation, achieving the same AUC of 0.91 (see Methods). This substantiates our ability to distinguish between human and mouse conserved alternative exons and constitutive exons based on the features we have obtained.
Figure 6.
Accuracy of the machine-learning algorithm trained to classify exons as either constitutive or alternative and identification of novel alternatively spliced exons. (A) Average ROC and AUC values based on 10 cross-validation runs. (B) Identification of the skipping forms of six constitutive exons (100% inclusion, based on ESTs) that were identified as alternative using machine-learning algorithms. Splicing pattern validation using primers for flanking exons identified four exons (left panel, lanes 1,3,4,5). Validation using primers to junctions of flanking exons revealed skipped forms for two more exons (right panel).
The above analysis measures our ability to correctly classify exons that maintain the same pattern of splicing in both human and mouse (i.e., discrimination between human and mouse conserved exons). This classification was based also on features that rely on the sequence conservation among these two species (Sorek and Ast 2003), and so it is possible that the high accuracy of such classification is limited to this type of exons and the accuracy does not reflect our ability to classify exons that are not conserved in their mode of splicing between human and mouse. We thus tested our ability to correctly classify exons without limiting ourselves to conserved exons. Specifically, we used the entire human alternative exon data set and a same number of randomly selected constitutive exons as the data set for analysis. We obtained an AUC score of 0.85, which is, to some extent, a less accurate classification than for the data set of exons that have the same pattern of splicing in both human and mouse. However, since the classification accuracy was performed in a genome-wide manner, without putting any conservation restrictions on the examined exons, this high score still suggests that combining features that differentiate one type of exon from another has a strong predictive power.
Quite unexpectedly, we found that the chromosome property of the exon (i.e., in which chromosome the exon resides) is an informative feature in the distinction between alternative and constitutive exons. This result may imply that the properties of alternative and constitutive exons, which we examine in this study, may differ between the chromosomes, i.e., the properties of the two groups vary among chromosomes. Further investigation is required to understand this observation.
We next wanted to determine whether results of the machine learning can be used to identify novel alternative exons. For that purpose, we constructed experiments to search for the skipped form of 10 exons that were predicted to be alternatively spliced with high confidence by the machine-learning algorithm, although they are completely constitutive by EST standards (100% inclusion). We used primers designed to the flanking exons to evaluate the splicing pattern of the exons in various human cell lines as well as normal cDNA from different human tissues (see Methods). The results confirmed that four of the 10 examined exons were alternatively spliced in certain tissues (Fig. 6B, left panel, lanes 1,3–5). Next, in order to detect extremely low levels of skipping, we designed primers to predicted junction sequences to allow detection of the skipped forms. Using this method, we validated the skipping pattern of two more of the exons (Fig. 6B, right panel). Thus, six of the 10 predicted exons were found to be alternatively spliced. Since alternative splicing is often tissue specific, it may be that, by enlarging the number of cell lines and tissues examined, additional exons will prove to be alternatively spliced.
Discussion
In this study, we analyzed evolutionary dynamics of alternative and constitutive exons and their flanking introns both in their sequence and structure. Our analyses have provided several major findings that shed light on the evolutionary processes that influence alternative splicing, and we identify some of the evolutionary changes associated with the acquisition of the skipping mode of exons. Our first finding relates to length changes in the exon–intron structure in vertebrate evolution. We reconstructed vertebrate ancestor length of exons and introns, revealing the trend of change through the evolutionary process. Constitutive exons tend to decrease in length in the transition from non mammalian vertebrates to mammals, with a greater decrease observed for alternative exons. Introns tend to lengthen in mammals compared with nonmammalian vertebrates, resulting with longest introns in humans, while introns flanking alternative exons are longer still. Second, by reconstructing the vertebrate ancestor splice site signals, we were able to perform splice site score correlations with intron length changes from an evolutionary perspective. We reveal a negative selection pressure against the lengthening of the introns when flanked by a weak 3′ss or 5′ss. Along the same lines, we observed that in vertebrate evolution a strong 3′ss and 5′ss is associated with longer flanking introns, with a much stronger influence of a strong 3′ss. Third, we were able to identify site-specific evolutionary rate changes in alternative exons, following the point of divergence from nonmammalian vertebrates to mammals, and used these sites to identify a list of predicted cis-acting splicing regulatory sequences. We also successfully validated the regulatory function of a selection of those predicted regulatory sequences. Fourth, we applied machine-learning algorithms that use the exon and intron properties obtained in this work to demonstrate accurate classification of exons as either alternative or constitutive and to identify novel alternative cassette exons.
Evolution of the exon–intron structure and ancestral reconstruction
The study of exon–intron structure from the evolutionary perspective helps explain what causes a constitutive exon to acquire the skipping mode. By using comparative genomics to analyze conservation and structural changes in both kinds of exons, we were able to ask how these changes affect the recognition of the exon by the splicing machinery. Sequence identity of exons, with regard to human, was found to be higher in constitutive compared with alternative exons only in early vertebrate species, but not in mammals. However, in the flanking intronic sequences in mammals, the opposite was observed: The identity was higher in alternative than constitutive flanking regions. Alternative exons are known to be under less restriction, and so they tend to evolve faster than constitutive exons (Ermakova et al. 2006). However, an increased density of intronic sequences that serves as cis-acting splicing regulators, near both the 3′ss and 5′ss of alternative exons, results in higher conservation of intronic regions flanking alternative exons (Sorek and Ast 2003).
Reconstruction of ancestral constitutive exon lengths suggests longer vertebrate ancestor exons than the current length in mammals. One possibility is that the average length of 147 nt found in mammals results in better splicing site recognition by the splicing machinery. This may be linked with recent findings that nucleosome densities are higher along exons, and that keeping exon lengths in a range compatible with mono-nucleosome lengths has a role in splicing, as we previously proposed (Schwartz et al. 2009b). We find alternative exons and their orthologs to be somewhat shorter in mammals (∼135 nt), which may suggest that shorter exons may result in a less accurate wrapping around nucleosomes that, in turn, might disrupt exon recognition in co-transcriptional splicing. However, we are not aware of any studies up to date that have managed to back this hypothesis. Notably, the restriction of exon length is also compatible with the exon definition pathway hypothesis for detection of exons in the vast intronic sequences, assumed to take place in higher eukaryotes, where exon length is believed to be restricted (Berget 1995; Keren et al. 2010).
Reconstruction of ancestral length for introns flanking both human constitutive and alternative exons and their orthologs reveals short introns of ∼1100 nt in the vertebrate ancestor. The introns are significantly longer in mammals and longest in primates. Introns flanking alternative exons are longer than those flanking constitutive exons in all vertebrates tested (+15%–+40%). This lengthening of the introns, specifically regarding the primate genomes, strengthens the exon definition pathway hypothesis that restricts exon length, but allows the lengthening of the introns (Berget 1995; Ast 2004; Ram and Ast 2007).
The longer length of introns found in mammals might be explained by the length of the first intron, which was reported to be extremely long (Kalari et al. 2006). Analysis of the first 20 introns for the 12 vertebrates tested revealed that indeed the first intron is longest for all vertebrates tested. However, this increase in length is not specific to the first intron but embraces the internal introns as well. There is a gradual decrease in intron length along all mammalian genes, which stabilizes around the eighth intron. This pattern is not consistent in nonmammalian vertebrate genes. The explanation for this inconsistency might be that the mean number of introns in an average human gene is ∼7.8, compared with the 5.2 in fugu fish, for example, where the genes have a smaller number of introns (Lynch 2006). We suggest that introns lengthen from the TSS downstream, starting with the first intron and on to the sequential introns. Transposable elements (TEs) insertions are commonly observed in first and internal introns and may have lengthened introns during vertebrate evolution (Sela et al. 2010). However, in the first introns, TEs are usually not found in proximity to the TSS and that region is thought to be responsible for the regulation of transcription (Majewski and Ott 2002; Kalari et al. 2006). In internal introns, TEs may contain potential splicing sites and can lead to formation of alternative transcripts (Nekrutenko and Li 2001). In summary, longer internal introns may influence splicing in a number of ways: (1) causing suboptimal recognition of the exon by the splicing machinery (Kim et al. 2007), as is also indicated by our findings that longer introns accompany alternative exons; (2) harboring inserted transposable elements that contain potential splicing sites; (3) enabling better chances for the existence of splicing regulatory binding sites, thus enhancing the complexity of the organism via a more intricate transcriptome.
Splice sites restrictions on intron length
Due to the substantial number of exons analyzed in this study, we were able to reconstruct the splice site motifs of both 3′ss and 5′ss of the vertebrate ancestor. The reconstruction of splice sites revealed that there were only minor changes in both splice sites during vertebrate evolution, and the overall correlation between the human splice site motifs and the vertebrate ancestor motifs is very high, suggesting that splice site composition did not alter significantly in mammalians compared with earlier diverging vertebrates. We correlated intron lengths with splice site scores for all orthologous exons, as well as the vertebrate ancestor, revealing dependencies between the two properties. Strong splice sites are flanked by relatively longer introns, this trend embraces all vertebrate species analyzed and is in line with previous reports for various vertebrates and invertebrates (Fields 1990; Clark and Thanaraj 2002; Weir and Rice 2004; Dewey et al. 2006). In addition, strong 3′ss are accompanied by extremely longer upstream introns than strong 5′ss, expressing the importance of the binding to the 3′ss in the splicing process. Moreover, when either splice site is weak, the tendency to increase intron length via evolution is not observed, and the introns remain short in mammals.
It was previously shown, for the human and mouse genomes, that when an intron lengthens between two vertebrate species usually the splice site strengthens as well (Dewey et al. 2006). Here we present an overall vertebrate phenomenon: In each of the 12 genomes examined, longer introns are flanked by stronger splice sites, but not so in the vertebrate ancestor. We hypothesize that the splice sites, as major splicing signals, can cover up for long introns, enabling recognition of exons even when flanking introns are long. Thus, a strong splice site reduces the intensity of purifying selection against intron lengthening via insertions of new sequences. However, when a splice site is weak and there is a major risk for the recognition of the exon, purifying selection acts against the fixations of such insertions. We suggest a way for the formation of alternative cassette exons during vertebrate evolution: A constitutive exon with strong splice sites allows stochastic increase in the length of its flanking introns. The introns increase in length above a certain length (averaging ∼5000 nt in the human genome). Only then, if, by chance, a single-base substitution weakens either the 3′ss or the 5′ss, the exon recognition will falter, and the exon will be skipped.
Evolution rate changes predict cis-acting regulatory elements
Site-specific inference of evolutionary rates is often used to predict functionally important residues (Mayrose et al. 2004). Deceleration of the evolutionary rate suggests a gain of function while acceleration of the evolutionary rate most often points to relaxation of constraints. Using in silico methods, we identified all single-base substitutions in constitutive and alternative exons that were variable in nonmammalian vertebrates and became highly conserved in mammals (“rate shifts to conservation”).
Interestingly, we observed higher amounts of both types of rate shifts (to conservation and to variability) in alternative exons, indicating both increased and decreased selection pressure in alternative exons. The evolutionary constraints acting upon alternative exons were previously reported in several studies using analyses of Ka and Ks (representing the non-synonymous and synonymous substitution rates, respectively) upon different pairs of species (human vs. mouse, human vs. chimp, and mouse vs. rat). Alternative exons have higher Ka values and Ka/Ks ratios compared to constitutive exons, indicating faster amino acid evolution in alternative exons, whereas the Ks values were found to be lower, indicating a slower evolutionary rate at the DNA level (Baek and Green 2005; Xing and Lee 2005; Chen et al. 2006). Baek and Green (2005) and Xing and Lee (2005) suggested that lower Ks values in alternative exons indicate that synonymous sites are important carriers of splicing regulation information. In addition, we found that “rate shifts to conservation” reside at higher density in exonic regions near the splice sites. Others and we have previously shown that ESRs also tend to cluster near the splice sites (Fairbrother et al. 2004; Goren et al. 2006) and are highly conserved in alternative exons (Sorek and Ast 2003). Taken together, this suggests that “rate shifts to conservation” reside within ESRs and may be related to gain of functionality. Therefore, we used these sites in search for sequences that might function as ESRs.
We searched inside constitutive and alternative exons for the overabundance of “rate shifts to conservation” in all possible 6-nt combinations or hexamers, and yielded a list of 141 and 23 highly significant hexamers as possible cis-acting regulatory elements in constitutive and alternative exons, respectively. These hexamers were also found in putative ESR groups that specifically bind to the human SR proteins SRSF1 and SRSF5 (Cartegni et al. 2003), and mostly to SC35 (Liu et al. 2000). We conducted experiments that provide strong evidence for the predicted function of a selection of the hexamers identified in this research. Our results suggest that analyzing evolutionary rate in constitutive and alternative exonic sequences can help identify the elements that take an active role in the regulation of alternative splicing.
Machine-learning prediction of the mode of splicing
In this study, we identified several new features that discriminate alternative from constitutive exons and used these features to predict the mode of exon splicing. We were able to achieve an AUC score of 0.91 for exons that maintain their skipping mode in human and mouse, in a data set comprising a 1:1 ratio of alternative and constitutive exons. While others have achieved similar AUC values for human-mouse conserved exons (Dror et al. 2005), here we show that the new features obtained in this work not only discriminate well between human-mouse conserved alternative and constitutive exons, but can also distinguish between exons with no restrictions applied, embracing the whole human exome (AUC score of 0.85 when discriminating between all the alternative exons in our data and randomly selected constitutive exons).
Experiments were used to validate the predicted exon classifications. These experiments indicated that exons that are predicted to be alternatively spliced by the machine learning and that were previously labeled as constitutive exons are genuine alternatively spliced exons with a low level of skipping. These misidentified alternatively spliced exons probably reflect the fact that the splicing pattern varies depending on specific conditions or tissue types. They were likely to be misidentified because they were inferred from EST data that originate from conditions in which they are not spliced. Our machine-learning predictions classified numerous constitutive exons as highly likely to be alternatively spliced. Taken together with the experimental results above, our study suggests that the total number of exons that are currently labeled as alternatively spliced in the human genome is underestimated.
In conclusion, our findings enable better understanding of the complex network of signals that influence the recognition of exons by the splicing machinery. We provide a novel evolutionary theory for the formation of the skipping mode in exons, and finally, we were able to use the features obtained here for a highly accurate identification of the mode of exon splicing within the human genome.
Methods
Constitutive and alternative exon data set construction
Data sets for human constitutive and alternative exons were obtained as in Schwartz et al. (2009a), based on the RefSeq and the spliced EST tracks of the human genome from the UCSC Genome Browser (http://genome.ucsc.edu/; Karolchik et al. 2003). Constitutive exons were defined as those having 100% inclusion supported by at least five ESTs, yielding a total of 111,617 constitutive exons. For alternative cassette exons, we required a minimum of five ESTs overlapping the exon, with a minimum of three ESTs supporting skipping, and a total inclusion level of 30%–98%. This yielded 4433 human alternative exons; no information regarding their skipping mode in more remote species was gathered.
Compilation of 17 vertebrate genome multiple sequence alignments and identity calculation of “vertebrate and older” exons
For the construction of the MSA data set, we used the coordinates of the exons excluding the first and last exons of a gene (which are not designated to be alternative cassette exons) and 200 nt from their flanking introns. Using the alternative and constitutive data, we extracted sequence alignments for 17 vertebrate organisms: human, chimp, rhesus monkey, mouse, rat, cow, dog, armadillo, elephant, tenrec, opossum, rabbit, chicken, frog, and three fish species: fugu fish, zebrafish, and tetraodon. MSAs are based on the University of California at Santa Cruz (UCSC) multi-species alignments (17-way conservation track) and were downloaded from the Galaxy platform (http://galaxy.psu.edu/; Giardine et al. 2005) using exonic coordinates of the human genome (hg18). The UCSC alignments are produced using the MULTIZ aligning method (Blanchette et al. 2004), which is well-characterized and widely used (Washietl et al. 2005; Zhang and Chasin 2006; Alekseyenko et al. 2007). We used the “Fetch Alignments–Extract MAF blocks” tool of the Galaxy platform. This tool superimposes genomic coordinates on multiple alignments and excises alignment blocks corresponding to each set of coordinates. A single genomic interval may correspond to two or more alignment blocks, and therefore a Perl script was used to concatenate alignment blocks based on exon–intron boundaries, which provided us with MSA data sets for all 17 vertebrates, of alternative and constitutive exons and 200 nt of their flanking intronic sequences. Next, we used the following rules to ensure the nature (exonic/intronic) of the alignments: (a) We verified for each species that every two sequences that were concatenated originated from the same genomic location. Alignments that did not match to the same locations were omitted, resulting in the removal of the whole exon from the analysis. (b) Each exonic alignment of every species was verified to originate from an exon in an annotated RefSeq (Pruitt et al. 2005) of that species in order to prevent using intronic or intergenic sequences as exonic. (c) We calculated exon age (as explained below) and verified that all exons used for percent identity calculations were of the same VO group so that younger exons did not bias the identity calculations in primates and mammals.
The exons were separated into three age groups as in Corvelo and Eyras (2008). An ortholog to a human exonic sequence that originates from an exon and was found in at least one of the early vertebrate species and at least in one of the mammalian species was considered to belong to the VO group. A sequence that was found in at least one of the mammalian species, and not in any of the early vertebrate species was considered as MS, and a sequence that was found only in human and any of the other primates was considered PS.
Per base identity was calculated between each species and human. The identity was calculated for each human exon and flanking introns (200 nt). Identity was given a value of 1 for a perfect nucleotide match or 0 for any mismatch or nonhuman gaps. Human gaps were omitted. Next, an average identity of each base was calculated.
Splice site scoring
In order to score the splice sites across the various organisms, it was necessary to obtain Position Specific Scoring Matrices (PSSMs) of the 3′ss and 5′ss in those organisms. For this purpose, we extracted these two signals from splice site MSAs that had sequences of 12 vertebrate species, thus excluding the following species: armadillo, elephant, tenrec, rabbit, and tetraodon. The 3′ss was defined as the 20 intronic nucleotides upstream of exons concatenated with the first three exonic nucleotides, whereas the 5′ss was defined as the three terminal exonic nucleotides concatenated with the first six intronic nucleotides. Only G[T/C]-AG exons were used for this analysis. Subsequently, every 3′ss and 5′ss was scored based on its adherence to the species-specific PSSM (Schwartz et al. 2008), as follows:
where A is the sequence motif to be scored, K is the motif length, and fi,Ai is the PSSM frequency at character Ai that is found in the ith nucleotide in the motif, as in Shapiro and Senapathy (1987). Next, the score was normalized between 0 and 100 as follows:
where Min and Max are the minimum and maximum splice site scores over all motifs in that genome. As controls, we also scored the sequences based on the Maximum Entropy Model of Short Sequence Motifs according to Yeo and Burge (2004).
Orthologous exon identification and properties
Based on the exon alignment data sets, we retrieved the data concerning the orthologous exons coordinates, their splicing pattern in human, length, and flanking introns data (length, position, and sequence). We used those data sets to examine the relationship between splice site scores, sequence conservations, and length. Dependencies between the different factors were analyzed using the R statistical computing program (R Development Core Team 2006), which was also used for the statistical tests.
Reconstruction of exon and intron ancestral length
To reconstruct the length of ancestral exons and introns, we used the maximum parsimony paradigm. The reconstruction was performed using only MSAs with a taxon sampling of 12 species and using sequences that originate from exons according to RefSeq annotation (Pruitt et al. 2005), thus verifying that all exons selected for this process are of the same VO aged exons group. Exon and intron lengths were retrieved using the RefSeq tracks of each species from the UCSC Genome Browser (http://genome.ucsc.edu/; Karolchik et al. 2003). Ancestral sequence length was reconstructed at each internal node of the tree using Sankoff's maximum parsimony algorithm (David 1975). The size of the alphabet used is determined according to the size of the longest sequences present in the leaves, and the cost of transition between two different sequence lengths is assumed to be the squared difference between these two lengths.
The small differences in exon length between mammalians and vertebrate ancestor might be biased by the sample of species. Thus, the reconstruction analysis for exons and flanking introns was performed three times using three different phylogenetic trees, each excluding a different species (human, mouse, or zebrafish). The re-analyzed reconstruction produced similar results of the ancestral exon length with no significant differences among the three cases and the original 12-species data. Intron length reconstruction exhibited a small but significant difference among the three cases and the reconstruction of the original 12-species data. However, the reconstructed lengths in the cases excluding human (upstream intron: 1173, downstream intron: 1145) or mouse (upstream: 1170, downstream: 1144) were very close in intronic measures (<100 nt) to the original 12-species data (upstream: 1107, downstream: 1097). In the case of ancestor length reconstruction excluding zebrafish, the results show the ancestral introns (flanking either alternative or constitutive exons) were of shorter length than reported for the 12-species data (ranging between 756 and 909). These outcomes verify that the reconstructions that were made for the 12-species sample set are suitable for use in the length analyses.
Reconstruction of splice site motifs
The ancestral reconstruction of the 3′ss and 5′ss was performed with the FASTML program for computing maximum-likelihood ancestral sequence reconstruction (Pupko et al. 2000), using the Jukes and Cantor (1969) substitution model. The reconstruction was performed using the same MSA selection restrictions as the length reconstruction, thus verifying a taxon sampling of at least 12 species, sequence exonic origin in an annotated RefSeq (Pruitt et al. 2005) of the species, and VO age exon group. Splice sites were retrieved only for introns that had their length reconstructed, so that for each pair of reconstructed intron length (upstream and downstream) we reconstructed both splice sites of their middle exon. We next used the FASTML program to reconstruct the ancestor motifs. The program receives a set of sequences and an evolutionary tree as input and reconstructs the ancestral maximum-likelihood sequence. We then retrieved, for each pair of introns, the sequence at the ancestral node.
Pictograms
Graphical representations of PSSMs were composed using a BioPerl (Stajich et al. 2002) module for generating Scalable Vector Graphics (SVG) output of Pictogram display for consensus motifs, as was described by Burge et al. (1999). The height of each letter is proportional to the frequency of the corresponding base at the given position, and bases are listed in descending order of frequency from top to bottom. Pictograms were constructed for all orthologous splice sites (Supplemental Fig. S5), and also in a genome-wide manner, to include all splice sites of each of the 12 species examined (Supplemental Fig. S8).
Detection of site-specific variation in evolutionary rate
For the detection of evolutionary rate shifts in the exonic and intronic sequences, we used “Covarion” (Pupko and Galtier 2002). The “Covarion” program is based on maximum-likelihood site-specific evolutionary rate estimates at every site of a given MSA. Given a specific branch point the program estimates for each site the rate for one sub-tree and the rate for the other sub-tree, both extracted from a phylogenetic tree consisting of 12 vertebrate species. The underlying assumed substitution model was of Jukes and Cantor (1969). For a given site, statistically different rates for the two sub-trees reveal a change in functional constraints. The significance of the difference between the two groups was assessed using a likelihood-ratio test. This approach allowed the detection of sites that had highly different rates in two subgroups, and so reveals a change in the selection pressure of the site.
We distinguished rate shift positions by the direction of their shift: “Rate shifts to conservation” are sites where the rate of the sub-tree containing human was significantly lower than the rate of the sub-tree of the evolutionary remote species, i.e., the examined position became conserved. “Rate shifts to variability” are sites where the rate of the sub-tree containing human was significantly higher than the rate of the sub-tree of the evolutionary remote species, namely a conserved position that became variable. We split the vertebrate tree at several branch points to identify rate shifting sites between the two extracted sub-trees. We detected significant rate shifting sites (maximum-likelihood test, P-value < 0.05) at several branch points along the phylogenetic tree. However, only when comparing the evolutionary rates between the mammalian and the nonmammalian sub-trees did we receive an amount of “rate shifts to conservation” that was sufficient for the analyses. Since the phylogenetic tree used for these analyses is virtually small (four nonmammalian and eight mammals), the relatively small size of the sub-trees might explain this outcome. We therefore chose to examine only rate shifts found in the transition from vertebrates to mammals.
Next, each sequence was given two rate shift scores normalized to sequence length. For both types of rate shifts, the score was calculated as follows:
where RS is the sum of rate shifts in the sequence (rate shifts to conservation or variability), and L is the sequence length. Hence, the final score was calculated as the average rate shift abundance in exons (normalized per length) and was repeated for the entire alternative or constitutive exon data (exons with no rate shifts received a value of 0).
To test the distribution of rate shifting sites along the exons, we focused only on exons that contain rate shifts. The abundance of rate shifting sites was calculated per exon position in three regions along constitutive and alternative exons: the first 30 nt of the exon downstream from the 3′ss, the middle of the exon, and the last 30 nt of the exon upstream of the 5′ss. The rate shift score represents the density of shifting sites in each of these regions (normalized per length).
Prediction of splicing cis-regulatory elements
The prediction of regulatory sequences was done for all possible 4096 hexamers, for alternative and constitutive exons. The number of sites that were shifted to conservation was counted for each hexamer, for both kinds of exons. We then compared this number to the expected number assuming rate shifting sites are randomly distributed. P-values were calculated using Fisher's exact test and corrected for multiple testing (FDR, α < 0.01). Hexamers with P-values < 0.01 were considered functionally important (separate tests were performed for each type of exon, alternative and constitutive). For alternative exons, when a hexamer is created by significantly more conserved rate shifts than expected, this hexamer might have functionality as an exonic splicing silencer (ESS) regulatory motif and supports the skipping of the exon. For constitutive exons, hexamers overlapping many conserved rate shifting sites are predicted as ESEs—enhancing the selection of the exon by the splicing mechanism.
Machine-learning algorithms for predicting exons as constitutively or alternatively spliced.
Machine-learning classification algorithms were trained on a data set of exons that maintain their splicing pattern in both human and mouse. The data set consists of 414 alternative exons and 414 constitutive exons randomly selected out of a total of 33,197 constitutive exons. Ninety-three features were used for the classification algorithm. Nine features capture exon structure properties: chromosome, length, serial position in the transcript, human-mouse conservation, 3′ss and 5′ss score (for two different scoring methods), and division of exon length by 3 (yes/no). Two features represent the evolutionary rate analysis of the exon: abundance of “rate shifts to conservation” and abundance of “rate shifts to variability.” Since the GC content of the sequence is a major structural property, we added six features that represent the GC content and DNA methylation level: GC content of the exon, GC content of 15 nt upstream of and downstream from the exon, difference of GC content between exon and upstream and downstream introns, and CpG DNA methylation level of the exon as obtained from genome-wide data generated by Lister et al. (2009). Eight features are computed for the flanking introns of the exon: length, human-mouse conservation, abundance of rate shifting sites to conservation, and abundance of rate shifting sites to variability. The other 68 features represent the hexamers with the highest rating that were obtained by performing “rate shifts to conservation” abundance tests: 39 hexamers that were found to be significantly enriched (P-value < 0.005) in “rate shifts to conservation” in constitutive exons, and 29 hexamers that were found to be significantly enriched (P-value < 0.02) in “rate shifts to conservation” in alternative exons (one hexamer existed in both lists and was therefore removed).
The machine-learning schemes were written in Java using algorithms implemented in the WEKA library (Witten and Frank 2005). The classification algorithms tested were naïve Bayes, Bayesian networks, and SVM (SMO). For the Bayesian networks, two different search algorithms were used to estimate the dependencies between the features: K2 search algorithm (Cooper and Herskovits 1991, 1992) and the tree augmented Bayes network (TAN) search algorithm (Friedman et al. 1997). The SVM classifier was used with two different kernels: polynomial and radial basis function (RBF). For the Bayesian classifiers, a preprocess of discretization of the continuous data into 10 equal-frequency bins was tested in addition to the default discretization of WEKA. Feature selection was performed by applying a “wrapper” (John et al. 1994; Kohavi and John 1997) to find the best performing features for each one of the algorithms, using BestFirst hill-climbing search algorithms (Dechter and Pearl 1985). The classification performances were measured twice: first for the model selection, i.e., to select the best classifier, and second to assess the accuracy of the classification scheme. The evaluation was done using 10-fold cross validation, i.e., 90% of the training data were randomly chosen and used to train a classifier, and the remaining 10% were used to evaluate the classifier performance (Witten and Frank 2005). For each fold, ROC curves were constructed to test the performance in classifying exons to either alternative or constitutive. From the ROC curves, the AUC of the classifier was computed, a score which is equivalent to the probability that the classifier will rank a randomly chosen positive instance higher than a randomly chosen negative instance (Green and Swets 1966; Fawcett 2006). A yielded AUC value of 0.5 represents a random classification and a yielded AUC value of 1 is a perfect classifier. Since the performance depends on the division of the training data, the procedure is repeated 10 times, so that each 10% is used once to evaluate performance. The reported AUC of each classifier is the average AUC of the 10 iterations of the cross-validation procedure. The chosen classifier was the one with the highest average AUC. In order to estimate the classification scheme accuracy while avoiding overestimation, the whole process underwent 10-fold cross-validation: 90% of the training set was used for the model selection (i.e., to select the best performing classifier using an inner 10-fold cross-validation) and the 10% were used as an untouched test set to assess the performances of the best classifier selected. This was repeated 10 times, and the accuracy of the scheme is the mean AUC of the best performing classifiers on the 10 different test sets. Applying the outer 10-fold cross validation on both data sets tested (human-mouse conserved exons and all the human alternative exons) gave virtually the same results. The human-mouse conserved data yielded an AUC lower by 0.0004, and the data including all the alternative exons in human yielded a mean AUC higher by 0.0008 than the one achieved in the model selection phase. The individual performances of each feature were computed using the “One Rule” (Holte 1993) classifier with default parameters.
Construction of the SXN13-derived minigenes
The hexamer-regulatory motifs and their mutants were cloned into SalI and BamHI sites of the SXN13 reporter system using the oligonucleotides depicted in Supplemental Table S3. The SXN13 minigene was a kind gift from Thomas A. Cooper (Coulter et al. 1997). The following primers were used to detect the splicing pattern: 5′-CATTCACCACATTGGTGTGC-3′ and 5′-AGAACCTCTGGGTCCAAGGGTAG-3′.
RNA isolation and RT-PCR amplification
RT-PCR analysis was performed on human RNA from skin, lung, and pancreas tissues, as well as RNA extracted from Jurkat and HeLa cell lines. RNA extraction was done using TRI reagent (Sigma) and then treated with RNase-free DNase (Ambion). cDNA was reverse-transcribed using RT-AMV (Roche) and oligo-dT primers following the manufacturer supplied protocol. The cDNA was amplified by PCR using Red Load Taq Master (Larova).
Amplification of splicing products
For each exon tested, oligonucleotide primers were designed to flanking exons (Supplemental Table 1A) and exon junctions (Supplemental Table 1B). Amplification with primers from flanking exons was performed for 30 cycles, consisting of 94°C for 45 sec, annealing at a primer-specific temperature (4°C below the primer's melting temperature) for 45 sec, and extension at 72°C for 1 min. The program was ended by one stage of gap filling at 72°C for 10 min. The spliced cDNA products were separated in 1% agarose gel and confirmed by sequencing. Amplification with primers that were located on exon junctions was performed for 35 cycles, consisting of 94°C for 45 sec, annealing at a primer-specific temperature (4°C below the primer's melting temperature) for 45 sec, and extension at 72°C for 1 min. The program was ended by one stage of gap filling at 72°C for 10 min. The products were resolved on 2% agarose gel and confirmed by sequencing. To confirm that exon-junction primers aimed at the exclusion isoforms did not accidentally amplify inclusion isoforms, the inclusion isoforms’ cDNAs were cloned into TOPO TA cloning kit (Invitrogen) and verified by sequencing. These clones were then amplified by PCR using exon-junction primers aimed at the exclusion isoforms and were verified to have no PCR product.
Acknowledgments
This work was supported by a grant from the Israel Science Foundation (ISF 61/09); Joint Germany-Israeli Research Program (ca-139); Deutsche-Israel Project (DIP MI-1317); and Israel Cancer Research Foundation. S.G., D.B., and O.P. are fellows of the Edmond J. Safra Bioinformatics Program at Tel-Aviv University. D.B and O.P. are also fellows of the Converging Technologies Program of the Israeli Council for Higher Education. T.P is supported by grants from the Israel Science Foundation (878/09) and by the National Evolutionary Synthesis Center (NESCent), NSF #EF-0905606.
Footnotes
[Supplemental material is available for this article.]
Article published online before print. Article, supplemental material, and publication date are at http://www.genome.org/cgi/doi/10.1101/gr.119834.110.
References
- Alekseyenko AV, Kim N, Lee CJ 2007. Global analysis of exon creation versus loss and the role of alternative splicing in 17 vertebrate genomes. RNA 13: 661–670 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ast G 2004. How did alternative splicing evolve? Nat Rev Genet 5: 773–782 [DOI] [PubMed] [Google Scholar]
- Baek D, Green P 2005. Sequence conservation, relative isoform frequencies, and nonsense-mediated decay in evolutionarily conserved alternative splicing. Proc Natl Acad Sci 102: 12813–12818 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bell MV, Cowper AE, Lefranc MP, Bell JI, Screaton GR 1998. Influence of intron length on alternative splicing of CD44. Mol Cell Biol 18: 5930–5941 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bensaid M, Melko M, Bechara EG, Davidovic L, Berretta A, Catania MV, Gecz J, Lalli E, Bardoni B 2009. FRAXE-associated mental retardation protein (FMR2) is an RNA-binding protein with high affinity for G-quartet RNA forming structure. Nucleic Acids Res 37: 1269–1279 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berget SM 1995. Exon recognition in vertebrate splicing. J Biol Chem 270: 2411–2414 [DOI] [PubMed] [Google Scholar]
- Black DL 2003. Mechanisms of alternative pre-messenger RNA splicing. Annu Rev Biochem 72: 291–336 [DOI] [PubMed] [Google Scholar]
- Blanchette M, Kent WJ, Riemer C, Elnitski L, Smit AF, Roskin KM, Baertsch R, Rosenbloom K, Clawson H, Green ED, et al. 2004. Aligning multiple genomic sequences with the threaded blockset aligner. Genome Res 14: 708–715 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burge CB, Tuschl T, Sharp PA 1999. Splicing of precursors to mRNAs by the spliceosomes. Cold Spring Harb Monogr Ser 37: 525–560 [Google Scholar]
- Burges CJC 1998. A tutorial on support vector machines for pattern recognition. Data Min Knowl Discov 2: 121–167 [Google Scholar]
- Cartegni L, Wang J, Zhu Z, Zhang MQ, Krainer AR 2003. ESEfinder: A web resource to identify exonic splicing enhancers. Nucleic Acids Res 31: 3568–3571 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen X, Tompa M 2010. Comparative assessment of methods for aligning multiple genome sequences. Nat Biotechnol 28: 567–572 [DOI] [PubMed] [Google Scholar]
- Chen L, Zheng S 2008. Identify alternative splicing events based on position-specific evolutionary conservation. PLoS ONE 3: e2806 doi: 10.1371/journal.pone.0002806 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen FC, Wang SS, Chen CJ, Li WH, Chuang TJ 2006. Alternatively and constitutively spliced exons are subject to different evolutionary forces. Mol Biol Evol 23: 675–682 [DOI] [PubMed] [Google Scholar]
- Clark F, Thanaraj TA 2002. Categorization and characterization of transcript-confirmed constitutively and alternatively spliced introns and exons from human. Hum Mol Genet 11: 451–464 [DOI] [PubMed] [Google Scholar]
- Collins L, Penny D 2006. Proceedings of the SMBE Tri-National Young Investigators’ Workshop 2005. Investigating the intron recognition mechanism in eukaryotes. Mol Biol Evol 23: 901–910 [DOI] [PubMed] [Google Scholar]
- Cooper GF, Herskovits E 1991. A Bayesian method for constructing Bayesian belief networks from databases. In The seventh conference on uncertainty in artificial intelligence (ed. D'Ambrosio D et al. ), pp. 86–94 Morgan Kaufmann, Los Angeles, CA [Google Scholar]
- Cooper GF, Herskovits E 1992. A Bayesian method for the induction of probabilistic networks from data. Mach Learn 9: 309–347 [Google Scholar]
- Corvelo A, Eyras E 2008. Exon creation and establishment in human genes. Genome Biol 9: R141 doi: 10.1186/gb-2008-9-9-r141 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coulter LR, Landree MA, Cooper TA 1997. Identification of a new class of exonic splicing enhancers by in vivo selection. Mol Cell Biol 17: 2143–2150 [DOI] [PMC free article] [PubMed] [Google Scholar]
- David S 1975. Minimal mutation trees of sequences. SIAM J Appl Math 28: 35–42 [Google Scholar]
- Dechter R, Pearl J 1985. Generalized best-first search strategies and the optimality of A*. J ACM 32: 505–536 [Google Scholar]
- Dewey CN, Rogozin IB, Koonin EV 2006. Compensatory relationship between splice sites and exonic splicing signals depending on the length of vertebrate introns. BMC Genomics 7: 311 doi: 10.1186/1471-2164-7-311 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Didiot MC, Tian Z, Schaeffer C, Subramanian M, Mandel JL, Moine H 2008. The G-quartet containing FMRP binding site in FMR1 mRNA is a potent exonic splicing enhancer. Nucleic Acids Res 36: 4902–4912 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dror G, Sorek R, Shamir R 2005. Accurate identification of alternatively spliced exons using support vector machine. Bioinformatics 21: 897–901 [DOI] [PubMed] [Google Scholar]
- Ermakova EO, Nurtdinov RN, Gelfand MS 2006. Fast rate of evolution in alternatively spliced coding regions of mammalian genes. BMC Genomics 7: 84 doi: 10.1186/1471-2164-7-84 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fairbrother WG, Holste D, Burge CB, Sharp PA 2004. Single nucleotide polymorphism-based validation of exonic splicing enhancers. PLoS Biol 2: e268 doi: 10.1371/journal.pbio.0020268 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fawcett T 2006. An introduction to ROC analysis. Pattern Recognit Lett 27: 861–874 [Google Scholar]
- Fields C 1990. Information content of Caenorhabditis elegans splice site sequences varies with intron length. Nucleic Acids Res 18: 1509–1512 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fox-Walsh KL, Dou Y, Lam BJ, Hung SP, Baldi PF, Hertel KJ 2005. The architecture of pre-mRNAs affects mechanisms of splice-site pairing. Proc Natl Acad Sci 102: 16176–16181 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friedman N, Geiger D, Goldszmidt M 1997. Bayesian network classifiers. Mach Learn 29: 131–163 [Google Scholar]
- Giardine B, Riemer C, Hardison RC, Burhans R, Elnitski L, Shah P, Zhang Y, Blankenberg D, Albert I, Taylor J, et al. 2005. Galaxy: A platform for interactive large-scale genome analysis. Genome Res 15: 1451–1455 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goren A, Ram O, Amit M, Keren H, Lev-Maor G, Vig I, Pupko T, Ast G 2006. Comparative analysis identifies exonic splicing regulatory sequences—the complex definition of enhancers and silencers. Mol Cell 22: 769–781 [DOI] [PubMed] [Google Scholar]
- Graveley BR 2001. Alternative splicing: Increasing diversity in the proteomic world. Trends Genet 17: 100–107 [DOI] [PubMed] [Google Scholar]
- Green D, Swets J 1966. Signal detection theory and psychophysics. J. Wiley, New York [Google Scholar]
- Heckerman D, Geiger D, Chickering DM 1995. Learning Bayesian networks: The combination of knowledge and statistical data. Mach Learn 20: 197–243 [Google Scholar]
- Holte RC 1993. Very simple classification rules perform well on most commonly used datasets. Mach Learn 11: 63–90 [Google Scholar]
- John GH, Kohavi R, Pfleger K 1994. Irrelevant features and the subset selection problem. In Proceedings of the eleventh international conference on machine learning, pp. 121–129 Morgan Kaufmann, San Mateo, CA/New Brunswick, NJ [Google Scholar]
- Jukes T, Cantor C 1969. Evolution of protein molecules. Mammalian protein metabolism 3: 21–132 [Google Scholar]
- Kalari KR, Casavant M, Bair TB, Keen HL, Comeron JM, Casavant TL, Scheetz TE 2006. First exons and introns—a survey of GC content and gene structure in the human genome. In Silico Biol 6: 237–242 [PubMed] [Google Scholar]
- Karolchik D, Baertsch R, Diekhans M, Furey TS, Hinrichs A, Lu YT, Roskin KM, Schwartz M, Sugnet CW, Thomas DJ, et al. 2003. The UCSC genome browser database. Nucleic Acids Res 31: 51–54 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keren H, Lev-Maor G, Ast G 2010. Alternative splicing and evolution: Diversification, exon definition and function. Nat Rev Genet 11: 345–355 [DOI] [PubMed] [Google Scholar]
- Kim E, Magen A, Ast G 2007. Different levels of alternative splicing among eukaryotes. Nucleic Acids Res 35: 125–131 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kohavi R, John GH 1997. Wrappers for feature subset selection. Artif Intell 97: 273–324 [Google Scholar]
- Langley P, Iba W, Thompson K 1992. An analysis of Bayesian classifiers. In Proceedings of the tenth national conference, The Association for the Advancement of Artificial Intelligence, pp. 223–228 AAAI Press and MIT Press, San Jose, CA [Google Scholar]
- Lev-Maor G, Goren A, Sela N, Kim E, Keren H, Doron-Faigenboim A, Leibman-Barak S, Pupko T, Ast G 2007. The “alternative” choice of constitutive exons throughout evolution. PLoS Genet 3: e203 doi: 10.1371/journal.pgen.0030203 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lister R, Pelizzola M, Dowen RH, Hawkins RD, Hon G, Tonti-Filippini J, Nery JR, Lee L, Ye Z, Ngo QM, et al. 2009. Human DNA methylomes at base resolution show widespread epigenomic differences. Nature 462: 315–322 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu HX, Chew SL, Cartegni L, Zhang MQ, Krainer AR 2000. Exonic splicing enhancer motif recognized by human SC35 under splicing conditions. Mol Cell Biol 20: 1063–1071 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lynch M 2006. The origins of eukaryotic gene structure. Mol Biol Evol 23: 450–468 [DOI] [PubMed] [Google Scholar]
- Majewski J, Ott J 2002. Distribution and characterization of regulatory elements in the human genome. Genome Res 12: 1827–1836 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malko DB, Makeev VJ, Mironov AA, Gelfand MS 2006. Evolution of exon-intron structure and alternative splicing in fruit flies and malarial mosquito genomes. Genome Res 16: 505–509 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mayrose I, Graur D, Ben-Tal N, Pupko T 2004. Comparison of site-specific rate-inference methods for protein sequences: Empirical Bayesian methods are superior. Mol Biol Evol 21: 1781–1791 [DOI] [PubMed] [Google Scholar]
- Morrison DF 1990. Multivariate statistical methods. McGraw-Hill, New York [Google Scholar]
- Nekrutenko A, Li WH 2001. Transposable elements are found in a large number of human protein-coding genes. Trends Genet 17: 619–621 [DOI] [PubMed] [Google Scholar]
- Pruitt KD, Tatusova T, Maglott DR 2005. NCBI Reference Sequence (RefSeq): A curated non-redundant sequence database of genomes, transcripts and proteins. Nucleic Acids Res 33: D501–D504 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pupko T, Galtier N 2002. A covarion-based method for detecting molecular adaptation: Application to the evolution of primate mitochondrial genomes. Proc Biol Sci 269: 1313–1316 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pupko T, Pe'er I, Shamir R, Graur D 2000. A fast algorithm for joint reconstruction of ancestral amino acid sequences. Mol Biol Evol 17: 890–896 [DOI] [PubMed] [Google Scholar]
- R Development Core Team 2006. R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna [Google Scholar]
- Ram O, Ast G 2007. SR proteins: A foot on the exon before the transition from intron to exon definition. Trends Genet 23: 5–7 [DOI] [PubMed] [Google Scholar]
- Robberson BL, Cote GJ, Berget SM 1990. Exon definition may facilitate splice site selection in RNAs with multiple exons. Mol Cell Biol 10: 84–94 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Romfo CM, Alvarez CJ, van Heeckeren WJ, Webb CJ, Wise JA 2000. Evidence for splice site pairing via intron definition in Schizosaccharomyces pombe. Mol Cell Biol 20: 7955–7970 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roy M, Kim N, Xing Y, Lee C 2008. The effect of intron length on exon creation ratios during the evolution of mammalian genomes. RNA 14: 2261–2273 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwartz SH, Silva J, Burstein D, Pupko T, Eyras E, Ast G 2008. Large-scale comparative analysis of splicing signals and their corresponding splicing factors in eukaryotes. Genome Res 18: 88–103 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwartz S, Gal-Mark N, Kfir N, Oren R, Kim E, Ast G 2009a. Alu exonization events reveal features required for precise recognition of exons by the splicing machinery. PLoS Comput Biol 5: e1000300 doi: 10.1371/journal.pcbi.1000300 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwartz S, Meshorer E, Ast G 2009b. Chromatin organization marks exon-intron structure. Nat Struct Mol Biol 16: 990–995 [DOI] [PubMed] [Google Scholar]
- Sela N, Kim E, Ast G 2010. The role of transposable elements in the evolution of non-mammalian vertebrates and invertebrates. Genome Biol 11: R59 doi: 10.1186/gb-2010-11-6-r59 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shapiro MB, Senapathy P 1987. RNA splice junctions of different classes of eukaryotes: Sequence statistics and functional implications in gene expression. Nucleic Acids Res 15: 7155–7174 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sorek R, Ast G 2003. Intronic sequences flanking alternatively spliced exons are conserved between human and mouse. Genome Res 13: 1631–1637 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sorek R, Shamir R, Ast G 2004a. How prevalent is functional alternative splicing in the human genome? Trends Genet 20: 68–71 [DOI] [PubMed] [Google Scholar]
- Sorek R, Shemesh R, Cohen Y, Basechess O, Ast G, Shamir R 2004b. A non-EST-based method for exon-skipping prediction. Genome Res 14: 1617–1623 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stajich JE, Block D, Boulez K, Brenner SE, Chervitz SA, Dagdigian C, Fuellen G, Gilbert JGR, Korf I, Lapp H, et al. 2002. The Bioperl toolkit: Perl modules for the life sciences. Genome Res 12: 1611–1618 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thomas JW, Touchman JW, Blakesley RW, Bouffard GG, Beckstrom-Sternberg SM, Margulies EH, Blanchette M, Siepel AC, Thomas PJ, McDowell JC, et al. 2003. Comparative analyses of multi-species sequences from targeted genomic regions. Nature 424: 788–793 [DOI] [PubMed] [Google Scholar]
- Vapnik VN 2000. The nature of statistical learning theory. Springer-Verlag, New York [Google Scholar]
- Wang GS, Cooper TA 2007. Splicing in disease: Disruption of the splicing code and the decoding machinery. Nat Rev Genet 8: 749–761 [DOI] [PubMed] [Google Scholar]
- Washietl S, Hofacker IL, Lukasser M, Huttenhofer A, Stadler PF 2005. Mapping of conserved RNA secondary structures predicts thousands of functional noncoding RNAs in the human genome. Nat Biotechnol 23: 1383–1390 [DOI] [PubMed] [Google Scholar]
- Weir M, Rice M 2004. Ordered partitioning reveals extended splice-site consensus information. Genome Res 14: 67–78 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Witten IH, Frank E 2005. Data mining: Practical machine learning tools and techniques. Elsevier, Amsterdam [Google Scholar]
- Xing Y, Lee C 2005. Evidence of functional selection pressure for alternative splicing events that accelerate evolution of protein subsequences. Proc Natl Acad Sci 102: 13526–13531 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yeo G, Burge CB 2004. Maximum entropy modeling of short sequence motifs with applications to RNA splicing signals. J Comput Biol 11: 377–394 [DOI] [PubMed] [Google Scholar]
- Yeo G, Hoon S, Venkatesh B, Burge CB 2004. Variation in sequence and organization of splicing regulatory elements in vertebrate genes. Proc Natl Acad Sci 101: 15700–15705 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yeo GW, Van Nostrand E, Holste D, Poggio T, Burge CB 2005. Identification and analysis of alternative splicing events conserved in human and mouse. Proc Natl Acad Sci 102: 2850–2855 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang XH, Chasin LA 2006. Comparison of multiple vertebrate genomes reveals the birth and evolution of human exons. Proc Natl Acad Sci 103: 13427–13432 [DOI] [PMC free article] [PubMed] [Google Scholar]