Death of PRDM9 coincides with stabilization of the recombination landscape in the dog genome

Abstract

Analysis of diverse eukaryotes has revealed that recombination events cluster in discrete genomic locations known as hotspots. In humans, a zinc-finger protein, PRDM9, is believed to initiate recombination in >40% of hotspots by binding to a specific DNA sequence motif. However, the PRDM9 coding sequence is disrupted in the dog genome assembly, raising questions regarding the nature and control of recombination in dogs. By analyzing the sequences of PRDM9 orthologs in a number of dog breeds and several carnivores, we show here that this gene was inactivated early in canid evolution. We next use patterns of linkage disequilibrium using more than 170,000 SNP markers typed in almost 500 dogs to estimate the recombination rates in the dog genome using a coalescent-based approach. Broad-scale recombination rates show good correspondence with an existing linkage-based map. Significant variation in recombination rate is observed on the fine scale, and we are able to detect over 4000 recombination hotspots with high confidence. In contrast to human hotspots, 40% of canine hotspots are characterized by a distinct peak in GC content. A comparative genomic analysis indicates that these peaks are present also as weaker peaks in the panda, suggesting that the hotspots have been continually reinforced by accelerated and strongly GC biased nucleotide substitutions, consistent with the long-term action of biased gene conversion on the dog lineage. These results are consistent with the loss of PRDM9 in canids, resulting in a greater evolutionary stability of recombination hotspots. The genetic determinants of recombination hotspots in the dog genome may thus reflect a fundamental process of relevance to diverse animal species.

In all the eukaryotes studied so far, recombination events are not spaced uniformly along chromosomes but cluster in narrow regions called recombination hotspots (Petes 2001; Paigen and Petkov 2010). In humans, coalescent analysis of fine-scale patterns of linkage disequilibrium (LD) suggests that 80% of all recombination events are concentrated within just 10%–20% of the DNA sequence (Myers et al. 2005). It was recently suggested that a 13-bp sequence motif (CCNCCNTNNCCNC) could account for the recombinogenic activity of up to 41% of all human hotspots (Myers et al. 2008). Several lines of evidence indicate that this motif is bound by a zinc finger array of the PRDM9 protein (Baudat et al. 2010; Myers et al. 2010; Parvanov et al. 2010). When bound to DNA, a methyl transferase domain also present in this protein likely promotes the methylation of histone bound to nearby DNA (Baudat et al. 2010). This in turn attracts the recombination machinery, beginning with the formation of a double-stranded break (DSB).

Although it is likely that the genomic distributions of crossover events in many mammals will resemble that observed in humans, the physical locations of recombination hotspots are not expected to coincide. Hotspot locations are typically not consistent between humans and chimpanzees (Ptak et al. 2005; Winckler et al. 2005), and there is evidence of population-specific hotspots in humans (Graffelman et al. 2007; Berg et al. 2010; Kong et al. 2010). Hotspot locations have also been shown to vary among different mouse strains (Gray et al. 2009; Parvanov et al. 2009; Baudat et al. 2010). These results indicate that there is a rapid turnover of hotspot locations in mammals. Intriguingly, the zinc finger array of PRDM9 has evolved extremely rapidly in mammals, likely under the influence of positive selection (Oliver et al. 2009). In addition, a transmission bias in favor of the nonrecombinogenic allele has been observed in recombination hotspots, a phenomenon known as the “hotspot conversion paradox” (Boulton et al. 1997; Coop and Myers 2007). Rapid evolution of both the recombination initiating protein and its target sequence is predicted to result in a constantly shifting recombination landscape in species with an active PRDM9 gene.

Surprisingly, analysis of the dog genome assembly suggests that its PRDM9 ortholog has accumulated a number of loss-of-function mutations, including a premature stop codon and frame shift mutations, predicted to render it nonfunctional (Oliver et al. 2009). Although a diverse group of organisms, including birds, some fish, frogs, tunicates, diptera, and nematodes (Oliver et al. 2009), appears to lack a functional PRDM9 ortholog, the dog is the only mammal analyzed thus far for which this gene is believed to be nonfunctional. While we now have considerable insight into the control of recombination initiation in humans and the mouse, whose recombination appears to be under at least partial control of PRDM9, we know very little about the control of recombination initiation in animals lacking PRDM9. Do fine-scale recombination rates in species lacking PRDM9 vary to the same extent as in humans and the mouse? Do hotspots of recombination exist in the absence of PRDM9? What signals, other than the PRDM9 target motif, can attract the recombination machinery? In this regard, the absence of a functional PRDM9 gene in the dog genome represents a unique natural experiment that has the potential to shed light on the control of recombination initiation in many other organisms.

A pedigree-based linkage map indicates that the genetic map of the dog genome is similar in length to that of other mammals (Wong et al. 2010). From this analysis, it is evident that recombination rates vary at a megabase scale in the dog and generally increase near telomeres, consistent with studies in many other species (Yu et al. 2001; Kong et al. 2002; Shifman et al. 2006). However, to be able to fully address potential differences and similarities in the control of recombination in the dog and human, a finer-resolution recombination map is needed. Detailed inferences of variation in recombination rates are possible using coalescent-based analysis of LD between tightly spaced SNP markers (McVean et al. 2004). These methods facilitate the analysis of many more recombination events on a much finer scale than linkage-based approaches.

Recombination can have a marked effect on genome evolution via the process of GC-biased gene conversion (gBGC). This process is believed to result in the biased transmission of G or C alleles by AT/GC heterozygotes due to a bias in the repair of heteroduplex molecules formed during meiosis (Duret and Galtier 2009). This transmission bias has been observed experimentally in yeast, and indirect evidence suggests that it occurs in many eukaryotes, including mammals. Observations that the pattern of nucleotide substitution correlates with crossover rates and that highly recombining regions tend to become GC rich are likely to be due to the action of gBGC. In particular, it has been suggested that localized regions in which rates of substitution are strongly accelerated and GC biased can be generated by the presence of recombination hotspots (Dreszer et al. 2007; Galtier and Duret 2007; Berglund et al. 2009). Hence analysis of nucleotide substitutions can indicate the presence of historical recombination hotspots by traces left by gBGC.

In this study, we first characterize the evolution of PRDM9 by sequencing exon 7 in multiple dogs and canids. To further determine when the loss-of-function mutations observed in the dog genome assembly occurred, we examine the cat and panda genomes. This analysis indicates that PRDM9 was inactivated early during canid evolution. We next produce a fine-scale recombination map for dogs using more than 170,000 SNP markers in about 500 dogs, which demonstrates that recombination rates vary significantly in the dog genome. We use these data to identify more than 4000 recombination hotspots. We identify sequence features present in these hotspots and analyze their rates and patterns of molecular evolution since the canid ancestor. These regions bear a molecular signature consistent with long periods of gBGC. This finding supports the hypothesis that the loss of PRDM9 has led to an altered landscape of recombination in dogs, characterized by hotspots that are exceptionally long-lived.

Results

Death of canid PRDM9

We resequenced exon 7 of PRDM9 in representatives from 15 different dog breeds (see Methods) to investigate whether they carry the same two frameshift mutations observed in the publicly available boxer assembly (Supplemental Fig. S1; Oliver et al. 2009). All 15 dogs were observed to have the same mutations, suggesting that the pseudogenized state of PRDM9 is not private to the reference individual but is likely common among all dogs (Supplemental Fig. S2). Further analysis of orthologous exon 7 sequence in two Swedish wolves supports this view as they also carry these frameshift changes (Supplemental Fig. S2).

To understand when PRDM9 may have ceased to function, we first analyzed the orthologs of PRDM9 in the cat and panda, two other carnivores for which genome assemblies are available (Pontius et al. 2007; Li et al. 2010). Alignments of human PRDM9 to panda or cat DNA show no frameshifts or premature stop codons, suggesting that PRDM9 is functional in each of these species (Supplemental Figs. S3, S4). This sets an earliest possible date for the loss of PRDM9 to around the Caniformia diversification (the dog–panda split) at ∼49 Myr ago (MYA) (Eizirik et al. 2010).

Finally, DNA from a set of five diverse canids, representing most of the canidae family: the African wild dog, black backed jackal, and golden jackal, which belong to the wolf-like clade and hence are close relatives of the dog and wolf; the bush dog, which belongs to the South American clade; and the red fox, which belongs to the red fox–like clade (Lindblad-Toh et al. 2005), were resequenced. We found all of these species to carry at least one frameshift in exon 7 (Supplemental Fig. S5), which argues strongly that the nonfunctionalization of PRDM9 is a feature that is shared by most, or all, members of the Canidae family. As we have not sampled the most divergent canidae lineage, the Urocyon genus, it is possible that PRDM9 remains functional there. This suggests a latest possible time point for the PRDM9 pseudogenization at some time shortly after the diversification of the canidae at ∼7.8 MYA (Eizirik et al. 2010).

Recombination rate variation

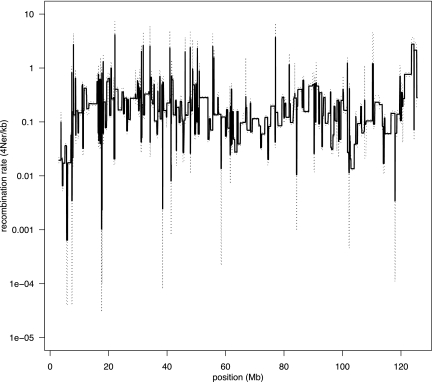
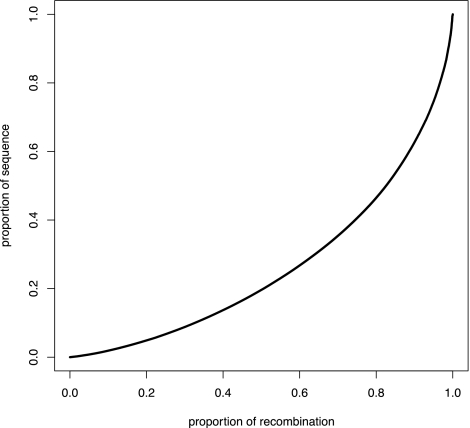
To investigate whether the ancient loss of PRDM9 may have affected the distribution of crossovers in the genome, we next used the interval program, which is distributed in the LDhat package (McVean et al. 2004), to infer historical recombination rates in the domestic dog. Starting with a data set consisting of 173,622 SNPs typed in a total of 471 dogs from 30 different breeds (Supplemental Table S5), we randomly sampled 100 haplotypes per chromosome for analysis. This produced a recombination map with significantly improved resolution compared with previous linkage maps. The difference between the lowest and highest rates estimated across all autosomes and the X-chromosome spans five orders of magnitude in dog (0.00007–9.5 4N_er/kb, where r is the recombination rate per generation) (Fig. 1; Supplemental Fig. S6). By conducting a similar analysis to that previously performed in humans (Myers et al. 2005), we note a weaker relationship between the recombination rate and distance to genes in the dog than in humans, and there is only a weak tendency for recombination rates to be reduced within dog genes (Supplemental Fig. S7). As an alternative way of describing recombination rate variation, we then calculated the proportion of recombination that occurs in a certain fraction of the genome (Myers et al. 2005). For instance, in the dog we see that 80% of all recombination events occur within 46% of the sequence (Fig. 2); alternatively, 50% of all crossovers take place in <20% of the sequence. In humans it was previously estimated that 80% of all recombination is concentrated within 10%–20% of the sequence (or 50% of all recombination events occur in <10% of sequence [McVean et al. 2004]) (Myers et al. 2005). In these terms, it thus may appear that recombination rates are less variable in the dog than in humans. Nevertheless, although this difference may reflect a true biological difference, it is likely that we lack power with the present data to detect rate variation in the dog at the same fine scale as for humans.

Figure 1.

Recombination rate (4N_er/kb) variation across dog chromosome 1, as inferred using interval. (Solid line) Mean posterior estimated rate; (dashed lines) 2.5 and 97.5 percentiles of the posterior.

Figure 2.

Proportion of sequence versus the proportion of recombination. The cumulative proportion of the total length of the dog recombination map is plotted against the proportion of the genome that has been sampled. This analysis suggests that 80% of all recombination events occur in 46% of the dog genome. Due to the relatively sparse marker density in our data set, we believe that this figure represents an underestimate of the true recombination rate variation in dog.

How accurate and detailed is the analysis in the dog?

We next considered two potential reasons why the data analyzed here may fail to accurately detect all recombination rate variation in the dog. First, markers are less densely spaced in the dog data (average of one SNP every 13,046 bp) compared with the human data sets (about one SNP every 2000 bp) previously analyzed using interval (McVean et al. 2004; Myers et al. 2005). Second, the demographic history of the dog clearly deviates from assumptions of the Wright-Fisher model inherent to the interval analyses. To address these issues, we undertook extensive simulations, under a realistic demographic model, to study the ability of interval to detect recombination rate variation using the present data.

Fitting LD decay to extend the dog demographic model

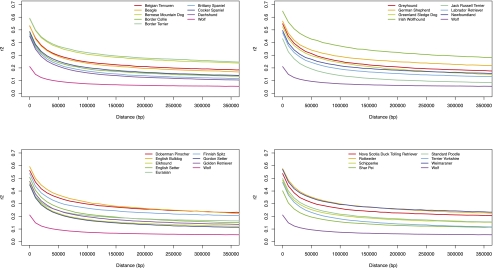
While previous modeling efforts have outlined the general features of the demographic history of the dog (Lindblad-Toh et al. 2005; Gray et al. 2009), each individual breed also has its own unique demographic history. To extend the demographic model, we estimated the effective population size of each breed included in this study by comparing LD decay in real and simulated data sets. In line with previous observations, we first note that LD decay varies considerably among dog breeds (Fig. 3). This variation largely reflects the diverse breed histories of the dogs sampled for this study, which further underlines the potential of using LD to model breed history. For instance, the decay of LD is modest in the Irish wolfhound, which is expected given the severe bottleneck this breed experienced about 200 yr ago (Willes 2003). The Labrador retriever, on the other hand, has maintained a large population size throughout the history of the breed (Lindblad-Toh et al. 2005), which is reflected in a relatively rapid decay of LD. We subsequently set up a demographic model including parameter estimates from previous studies (see Methods) and used MaCS (Chen et al. 2009) to simulate data from the dog breeds using breed-specific effective population sizes ranging from 0.001 × (N_{e wolf}) − 0.03 × (N_{e wolf}), where N_{e wolf} = 22600 (Gray et al. 2009). Finally, to estimate the bottleneck size of each breed (Supplemental Table S1), LD decay of real and simulated data was fitted using the least squares method (Supplemental Fig. S8).

Figure 3.

Decay of linkage disequilibrium (LD-decay) in 30 dog breeds and the wolf. Average LD-decay, measured as r² for markers separated by, at most, 400 kb, is plotted for 10-kb bins.

Simulated recombination rate variation in the dog

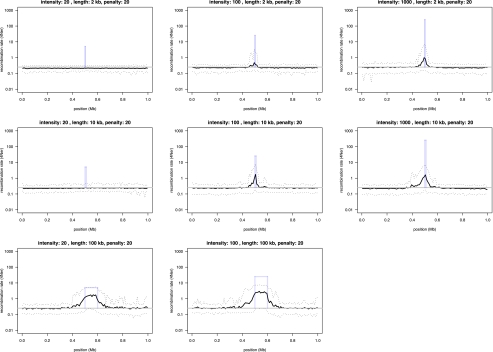
With the resultant extended demographic model, we were then able to simulate recombination rate variation in data that are similar to those used for the original inferences. We simulated eight different scenarios, including narrow, 2-kb hotspots as well as regional rate variation spanning 100 kb in length. The intensity of the “hotspot” varied from weak (20× background rate), to moderate (100× background rate), and to strong (1000× background rate). All scenarios were repeated over 100 iterations, and the average rates estimated using interval were compared to simulated rates. The simulations show that at weak hotspots, interval has no power to detect rate variation in the present data set (Fig. 4). Interval will, however, detect a small fraction of moderate and strong, narrow hotspots. The ability to detect rate variation then clearly improves as the “hotspot” regions increase in size (Fig. 4). Our analysis is thus able to detect a large fraction of all regional recombination rate variation in the dog but will overlook a significant part of the fine-scale variation that resides within the narrow hotspots of recombination. The frequency of rate change along dog chromosomes presented here will therefore represent an underestimate of the true variation. However, based on the low levels of spurious rate variation inferred in regions simulated under a constant recombination rate (see Fig. 4), it is likely that the variation we detect is real.

Figure 4.

Power simulations to test the ability of interval to infer recombination rate variation in the dog. By using a realistic demographic model, we generated genotype data for 1-Mb regions centered around a hotspot of recombination with known intensity and width. Recombination rates outside the hotspot were kept uniform. Nine different scenarios were simulated in which hotspot intensity that varied from weak (20× background rate), to intermediate (100× background rate), to strong (1000× background rate) were combined with three different hotspot widths (2, 10, and 100 kb). We set interval to penalize rate change (bp = 20) and inferred recombination rates in 100 simulated data sets for each scenario, and compared the average inferred rate (solid black line) to the uniform background rate (gray solid line), as well as the hotspot intensity (solid blue bars) used in the simulations. Dotted lines show the 2.5 and 97.5 percentiles of the sampling distribution.

LD-based and linkage maps agree well

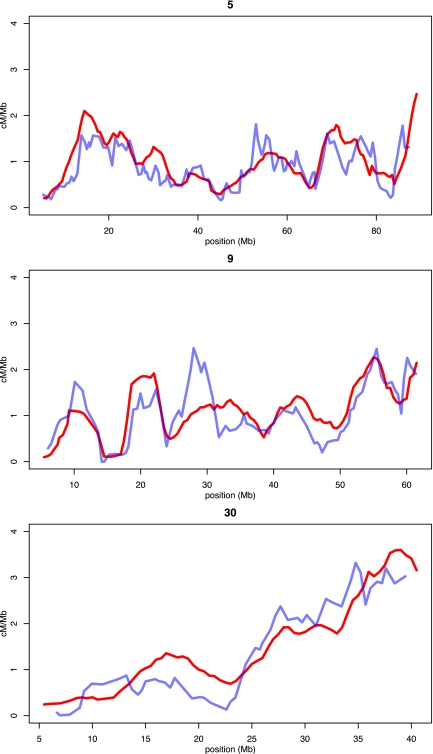
The joint estimation of N_e and r, inherent to the method used here, presents a further possible confound to the recombination map presented here. It is known that N_e can vary considerably across genomes (Tenesa et al. 2007) due to genetic drift and selection, suggesting that the observed fluctuations in rho (4N_er) may not always reflect true recombination rate variation but instead changes in N_e. Therefore, to further validate the recombination rate estimates obtained in this study, we compared the recombination map generated here with that of a previously published linkage map (Wong et al. 2010). To allow comparison of the fine-resolution LD-based map with the more coarse resolution linkage map, we first averaged rates in 5-Mb windows for both maps separately (Fig. 5; Supplemental Fig. S9). Second, in order to convert the LD-based map into units of centimorgans per mega base pair, we estimated the dog effective population size (N_{e dog} = 7752) by comparing the extension of the two maps where they overlap. We find that although there are slight deviations that could possibly be attributed to changes in N_e, overall both maps agree well. A noteworthy difference between the two maps is a general increase in subtelomeric recombination rates in the LD-based map compared with the linkage map. This may be explained in part by the fact that our map extends further into subtelomeric regions than the previous linkage map but also may reflect that LD-based methods enable rate estimation on finer physical scales than do pedigree-based linkage maps.

Figure 5.

Comparing recombination rates in the LD-based recombination map and a previously published linkage map for chromosomes 5, 9, and 30. Recombination rates of the linkage map (blue lines) and our LD-based inference (red lines) have been averaged across 5-Mb windows prior to plotting. We rescaled population genetic estimates by estimating the effective population size (N_e) of the dog from comparing the complete extension of the overlapping portions of the two complete recombination maps.

Sample-to-sample variation

As the recombination map presented here is based on a single random draw of 100 haplotypes (out of 2 × 471), we also sought to understand how variable rate estimates are across independent haplotype samples. To this end we created 10 independent subsamples, each containing 100 haplotypes of chromosome 1. We then used interval to estimate recombination rates in each sample and plotted the mean and standard deviation of the 10 recombination maps for each position within a subsection of chromosome 1 (Supplemental Fig. S10). We note that the sample-to-sample variation generally is modest. However, when two of these maps are compared directly, it is clear that sharp increases in recombination rate across narrow stretches of DNA may go undetected in some samples (Supplemental Fig. S11). This is in line with our simulations, which suggest that we have limited power to detect narrow hotspots of recombination in the present data set.

Detecting hotspots of recombination

To further explore the extent of recombination rate variation, we next used SequenceLDhot (Fearnhead 2006) to detect regions in the dog genome that are likely to contain a recombination hotspot (henceforth we shall refer to these regions as hotspot regions). In order to accurately define a hotspot region, with regards to physical extension and thresholds for statistical significance, we used simulations to train SequenceLDhot on data similar to the dog data but with known recombination rate variation. The resultant tuning of the SequenceLDhot parameters resulted in the power to detect hotspots of 10% at a false-discovery rate (FDR) of 10%. Given the average marker density of one SNP every 13,046 bp, we found that in order to ensure that a 2-kb wide hotspot was included within the physical limits of a significant hotspot region, the minimum size of the region needed to span 18 kb. Applying these settings to the analysis of the dog data, we detected a total of 4373 hotspot regions. Given the low power of our analysis, this translates to an estimated total number of around 40,000 hotspots in the dog genome. On average, the width of a detected hotspot region extended to ∼33 kb in the dog analysis. As expected, we note that the number of hotspots detected in a particular region correlates with marker density (rho = 0.19, P < 2.2 × 10⁻¹⁶, Spearman rank correlation).

Sequence motifs in hotspots

We next sought to define the sequence characteristics of dog hotspots of recombination. We matched 1683 narrow hotspot regions (18-kb wide) to “cold” regions, in which we see no evidence for hotspots of recombination. To identify sequence motifs enriched in hotspot or cold regions, respectively, we utilized RepeatMasker (http://www.repeatmasker.org). We used a Fisher's exact test to compare the frequency of each motif in the two sequence categories and then corrected the resultant P-values for multiple tests using a Bonferroni correction (Supplemental Table S2). Similar to previous observations in humans (Myers et al. 2005), in dog hotspot regions, the L1 family of LINEs (long interspersed nuclear elements) are underrepresented, and MIRb SINEs (short interspersed nuclear elements) are overrepresented. In addition, we further note that a DNA transposon, Charlie1a, is significantly enriched in hotspot versus cold regions. Two complementary runs of triplets, (CCG)_n and (CGG)_n, are also overrepresented in dog hotspot regions. However, the most significant difference between the two sets of regions relates to the overrepresentation of GC-rich repeats in hotspot regions (relative risk ratio; the ratio of the frequency in hotspots regions to the frequency in cold regions, rr = 2.57, P < 1 × 10⁻¹⁶). Such repeats remain significantly overrepresented even when the difference in average base composition between hotspot and cold regions is accounted for (data not shown).

Motivated by this finding, we studied the base composition of narrow (18-kb) hotspots regions in dogs using a sliding window of 500 bp. This revealed that a large fraction of these regions contains a prominent peak in GC content (Fig. 6). By formally defining a GC peak as a 50% increase in GC content (measured in a 500-bp sliding window) compared with the average base composition of the hotspot region, we observe 481 of 1683 hotspot regions to show a narrow (average width, 904 bp) peak in GC content (average base composition in GC peaks, 69%; average base composition of entire narrow hotspot regions, 42%). This compares to 238 such peaks in an equal number of cold regions studied (P < 1 × 10⁻⁴, χ² test). Hence, 29% of the hotspot regions in the dog genome show a distinct peak in GC content. Considering that standard sequencing methods often fail to produce reliable results in regions of high GC content, we also asked whether assembly gaps are enriched within hotspot regions. Indeed, short gaps in the genome assembly are overrepresented in hotspot regions (n = 197), relative to cold regions (n = 107), by a factor of 1.84, similar to the approximately twofold enrichment of GC-rich repeats in hotspot regions. Alternatively, this finding could also indicate that inferred recombination hotspots may cluster around gaps as a result of poor assembly or poor genotyping rather than high GC content. However, we note that the average GC content of 200 bp located immediately upstream of and downstream from gaps is 58%, which is substantially higher than the average GC content of 47% observed for the entire hotspot regions with assembly gaps. This supports the notion that gaps observed in hotspot regions may often represent additional GC peaks. If true, up to 40% of narrow hotspot regions in dog could include a sharp peak in GC content.

Figure 6.

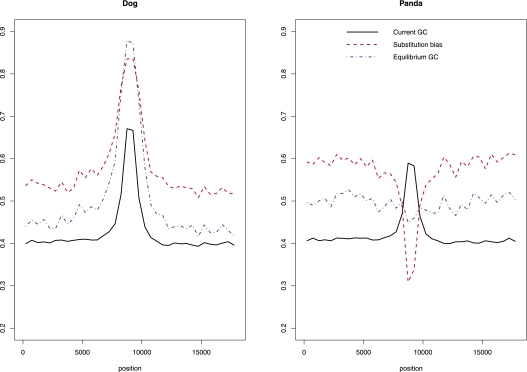
The molecular evolution of GC peaks in the dog and panda. Three hundred nine GC peaks for which we had alignment data for the dog, panda, and cat were centered in 18-kb windows prior to analyses. We used a sliding window of 500 bp to estimate average values of three different parameters related to the evolution of base composition near GC peaks in the dog and panda. First, solid black lines depict the average current GC content. Second, red lines show the nucleotide substitution bias (SB = WS/[WS + SW], where numbers of strong-to-weak [GC-to-AT] and weak-to-strong [AT-to-GC] substitutions are SW and WS, respectively). Third, blue lines show the equilibrium GC content (GC* = u/[u + v], where the rate of strong-to-weak [GC-to-AT] and weak-to-strong [AT-to-GC] substitutions are u and v, respectively).

In contrast to our observations in the dog, the average elevation in GC content for human hotspots has been estimated to be a modest 1%–2% (Spencer et al. 2006). To confirm this difference, we analyzed the base composition of 9405 narrow (5-kb-wide) human hotspot regions identified by Myers et al. (2005). By centering the midpoint of these hotspot regions in 18-kb windows, we scanned the GC content using a sliding window approach, equivalent to that previously applied to dogs. In line with previous observations, this analysis finds only ∼10% (951) of the regions as containing a GC peak, and only a fifth of these (203) are confined within the narrowly defined hotspot region. Moreover, when we repeat this analysis in 9292 human coldspots (that were also identified by Myers et al. 2005), we find a similarly low proportion (13%, n = 1213) of GC peaks.

Substitution patterns in GC peaks are highly GC biased

The process of gBGC tends to resolve heteroduplexes formed during pairing of heterozygous DNA in favor of G and C over A and T nucleotides (Duret and Galtier 2009). Although this bias is relatively weak, it can result in strongly GC-biased substitution patterns in regions of elevated recombination rate. It is possible that locally confined, persistently high crossover rates may have generated the GC peaks observed in the dog due to high levels of gBGC and that these GC peaks demarcate the location of persistent crossover hotspots. Alternatively, GC peaks may be an ancient feature of dog hotspot regions that in some way serve to attract local recombination events.

In order to analyze whether the GC peaks are a cause or a consequence of elevated recombination rates, we constructed alignments of GC peaks in dog hotspots with orthologous sequence in the panda and cat. Orthologous sequence in both the cat and panda could be identified for 309 of the 481 GC peaks. We first observed that the GC peaks, although weaker, are also present in panda (average GC-content of the 309 panda GC-peaks is 59% compared with 67% in dogs for the set analyzed) (Fig. 6), suggesting that dog hotspot regions were somewhat GC rich prior to the split of the dog and panda and, hence, before the loss of PRDM9.

We next compared orthologous positions in the dog, panda, and cat (as an outgroup species) to estimate the nucleotide substitution bias (SB = WS/(WS + SW), where numbers of strong-to-weak [GC-to-AT] and weak-to-strong [AT-to-GC] substitutions are SW and WS, respectively) in GC peaks for both the dog and panda lineages. Substitution rates differed significantly (P < 1 × 10⁻³, by bootstrap) between the two lineages, with substitutions on the dog lineage being strongly GC biased (SB = 0.84) and substitutions on the panda lineage being AT biased (SB = 0.31). Nine hundred sixty of our sample of 1683 “cold regions” had alignments to both the cat and panda. These showed a mild GC bias in the panda (SB = 0.58) and no bias in the dog (SB = 0.50).

It thus appears that there is a strong GC-biased substitution pattern that is restricted to GC peaks in the dog. To verify this, we centered each GC peak in an 18-kb window and plotted the average substitution bias across all GC peak windows using a 500-bp sliding window (Fig. 6). This analysis confirms that the GC-biased substitution bias in the dog lineage is indeed specific to the GC peak. We conclude that this GC-biased substitution pattern, consistent with the action of gBGC, must have been sustained over an extended period of time over the canid lineage. Based on the assumption that the observed substitution patterns persist, we also estimate the equilibrium GC content (GC*; GC* = u/[u + v], where the rate of strong-to-weak [GC-to-AT] and weak-to-strong [AT-to-GC] substitutions are u and v, respectively) (Meunier and Duret 2004) and predict that the GC peaks will be further reinforced in the dog but that they will vanish in the panda (Fig. 6). We therefore find that the hotspot GC peaks were present in the common ancestor of the dog and panda, but while they have been decaying in the panda, they are reinforced in the dog.

Finally, as it has been suggested that accelerated rates of evolution in localized regions may be caused by the presence of recombination hotspots (Dreszer et al. 2007; Galtier and Duret 2007; Berglund et al. 2009), we analyzed total substitution rates (S) in GC peaks. In line with this suggestion, we find that GC peaks have an almost twofold increase in substitution rate in the dog (S = 0.112) relative to the panda (S = 0.066) lineage. This difference is also apparent when the substitution rate of GC peaks is contrasted with that of cold regions (S = 0.046) in the dog lineage. The substitution rate of cold regions in the panda lineage (S = 0.043) is similar to that seen in the dog.

Discussion

Death of PRDM9 predates the canid diversification

In agreement with a previous report (Oliver et al. 2009), we observed five nonsense and missense mutations in the complete PRDM9 sequence in the dog genome assembly. These indicate that the death of PRDM9 may have occurred early on the dog lineage. To date the appearance of these mutations in canid PRDM9, we initially sequenced the zinc finger–encoding exon 7 of PRDM9 in 15 different dog breeds and two wolves (Supplemental Fig. S2). In all 17 samples we noted the presence of the same two frameshift mutations that were observed in the publicly available boxer assembly (Supplemental Fig. S1). This indicates that the loss of PRDM9 function is a feature shared among all dogs. The two frameshift mutations in wolf also suggest that the PRDM9 loss of function predated dog domestication. Sequence from an additional set of five diverse canids, representing most of the canidae diversity (only lacking a representative of the most divergent group, the Urocyon genus), indeed shows that exon 7 carries at least one frameshift mutation in each of the species analyzed (Supplemental Fig. S5). This argues that most, and possibly all, canids lack a complete functional PRDM9 gene and, hence, that disruption of this gene occurred prior to canidae diversification ∼7.8 MYA (Eizirik et al. 2010). The earliest that loss of PRDM9 function occurred is the start of the Caniformia diversification ∼49 MYA (Eizirik et al. 2010). This is because both the cat and panda genome assemblies contain complete PRDM9 open reading frames (Supplemental Figs. S3, S4). Specifying a narrower time span for the pseudogenization of PRDM9 is difficult given the relatively recent divergence of all extant canids.

Recombination rates vary despite absence of PRDM9

In other mammals, PRDM9 has been proposed as a major determinant of recombination hotspot locations (Baudat et al. 2010; Myers et al. 2010; Parvanov et al. 2010). The recombination map presented in this article reveals considerable recombination rate variation across the dog genome. The difference between the most extreme recombination rates estimated here spans five orders of magnitude, which matches the span of rate variation in the human genome (McVean et al. 2004). When represented as a proportion of recombination that occurs in a given fraction of the sequence, rate variation in the dog compared with humans may appear, however, to be reduced (Fig. 2). Nevertheless, our simulations indicate that the map is likely missing a large proportion of true rate variation, because of the low marker density used for the map or because of the complex breed structure in the domestic dog. The estimated total number of hotspots of recombination in the dog (about 40,000) is similar to the number estimated in humans (25,000–50,000) (Myers et al. 2005). In summary, our findings indicate that dogs exhibit a similar spread of recombination rates as do humans despite the lack of a functional PRDM9 protein.

Stable, GC-rich hotspots of recombination in dogs?

By contrasting sequence features of hotspot regions and cold regions, respectively, we sought to understand what defines a hotspot of recombination in the dog. The finding that a repeat class termed “GC rich” is overrepresented in dog hotspot regions (rr = 2.57, P < 1 × 10⁻¹⁶) is surprising given that this term is underrepresented in human hotspot regions (rr = 0.4, P = 0.22) (Myers et al. 2005). Consistent with this observation, sharp peaks in GC content are significantly overrepresented and occur in a large fraction of the dog hotspot regions (Fig. 6). These peaks are considerably more prominent in the dog than in humans. In the dog, within a narrow window (average, ∼904 bp), GC content is elevated by >50% in 29%, and possibly up to 40%, of all hotspot regions. In humans, GC content elevations have been reported of ∼1%–2% (Spencer et al. (2006). Our analysis of base composition around the human hotspot regions finds only ∼10% of regions as containing a GC peak, and only a fifth of these are confined within the narrowly defined hotspot region. Moreover, human coldspots also contain a similarly low proportion (13%) of GC peaks.

How might this difference in base composition between the human and dog hotspot regions be explained? There is now a large body of evidence to suggest that recombination affects GC content through the process of gBGC, in particular resulting in an increase of GC content in highly recombining regions (Duret and Galtier 2009). If the GC peaks were generated at least in part by this process, we would expect to observe GC-biased substitution patterns on the dog lineage. In line with these predictions, we find a marked GC bias and acceleration in evolutionary rates in the GC peak locations in the dog but not the panda lineage since the common ancestor of these two species (Fig. 6). This observation supports the hypothesis that high levels of recombination have occurred in the GC peak locations in the dog (but not in the panda).

In comparison to the dog, gBGC appears to have had only a modest impact on the base composition of human hotspots. This is likely due to the dynamic nature of recombination rate variation in our own species. We share few hotspot locations with the chimpanzee (Ptak et al. 2005; Winckler et al. 2005), and there is evidence of significant differences in hotspot use between human individuals (Coop et al. 2008). Hotspots likely remain in the same position for too short a time to have had a large effect on local GC content in the human genome. The presence of narrow stretches of extremely elevated GC levels in a large fraction of dog hotspot regions indicates that the dynamics of recombination rate variation may differ between the dog and humans. In order for gBGC to have caused the observed bias in substitution patterns within these GC peaks, in the dog, high recombination rates would have to have been sustained over an extended period of time. We thus propose that many dog hotspots have remained in the same location for many millions of years, possibly ever since PRDM9 ceased to function in an early canid, some 7–49 MYA.

Another feature of gBGC is that it appears to be associated more strongly with recombination in males than females (Webster et al. 2005; Dreszer et al. 2007). We are unable to measure sex-specific recombination rates using our population genetic approach. However it is notable that a number of measures that are enriched in GC peaks (GC-rich repeats, CpG dinucleotide sites, and CpG islands) have all been found to be significantly associated with male, but not female, recombination rates in the dog (Wong et al. 2010). This could indicate that hotspots containing GC peaks are more strongly associated with recombination in males. A human recombinogenic motif (CCNCCNTNNCCNC) was also previously found to be associated with elevated male, but not female, recombination rates (Wong et al. 2010). However, we suggest that this is most likely due to its GC richness, as this specific motif is targeted by human PRDM9, which is both highly diverged and inactive in dogs.

Recombination initiation in dogs

The PRDM9 protein contains a SET methyltransferase domain, which induces a histone modification in the vicinity of a sequence motif bound by a zinc finger domain. This modification serves as a mark for the initiation of recombination beginning with a DSB. The rapid evolution of the zinc finger domains and its target sequences across the genome is likely to account for rapidly shifting fine-scale recombination landscapes. The absence of a functional copy of PRDM9, or another similar gene with SET and zinc finger domains, in the dog genome assembly suggests that a different mechanism of recombination initiation predominates in dogs. This mechanism could also be important in species with an active copy of PRMD9, occurring in parallel with PRDM9 initiation.

Several genomic features may be targets for recombination initiation besides PRDM9 binding motifs. In Saccharomyces yeasts (which lack a PRDM9 ortholog), recombination hotspots are also well conserved over evolution (Tsai et al. 2010) and are thought to require open chromatin and may also require accessibility for transcription-factor binding (α-hotspots), nucleosome-excluding sequences (β-hotspots), or high GC content (γ-hotspots) (Petes 2001). An association between promoters and DSBs in yeast provides evidence for the existence of α-hotspots. However, Myers et al. (2005) showed that recombination rates tend to be reduced in the vicinity of genes in humans, which suggests that this mechanism is not important. Additionally, there is evidence for a negative association between recombination and germline transcription in humans (Necsulea et al. 2009). We find a weak association between coding regions and recombination rates in dogs (Supplemental Fig. S7), although we are unable to determine whether there is an association between promoters and high recombination rates due in part to the poor quality of the current gene annotations.

Recombination rates and GC content are correlated in a wide variety of organisms (Eyre-Walker 1993). Although this correlation is seen in human data, local GC is only a poor predictor of recombination rates in humans (McVean et al. 2004). Equilibrium GC content (GC*) predicted by the pattern of substitution exhibits a much better correlation with crossover rate than present GC content (Duret and Arndt 2008). This supports the hypothesis that recombination, via gBGC, causes the correlation between recombination and GC content (Duret and Arndt 2008). It has, however, also been suggested that GC-rich sequences are more recombinogenic (Petes 2001; Spencer et al. 2006), and it is possible that to differing extents, elevated GC content could be both a cause and consequence of recombination.

On average, the GC peaks we observed in dog recombination hotspot regions have a GC content of 67% (note that this relates to GC peaks for which alignment data with the cat and panda are available), compared with a background of ∼40%. Examination of nucleotide substitutions in the dog lineage revealed a strongly GC-biased pattern within these peaks, consistent with persistent gBGC. However, in the panda genome, elevated GC content is also observed in regions orthologous to dog GC peaks. Average GC content in these regions is 59% compared with the background of ∼41% in the panda, and substitution patterns in the panda lineage suggest that these peaks are evolving toward background GC content. It is therefore possible that the GC richness of these regions in the dog–panda ancestor promoted recombination in the dog lineage, leading to an even greater increase in GC content in the dog genome due to gBGC. In the panda, however, there is no evidence for continued action of gBGC in these regions, suggesting that they have not been persistent foci for recombination along the panda lineage.

We also observed that the GC-rich trimers (CCG)_n and (GGC)_n are overrepresented in dog hotspot regions compared with cold regions. Arrays of these trimers match the degenerate motif (C/G)₃NN, which for several reasons may cause DNA to be in a state of open chromatin. First, for theoretical reasons, arrays of the (C/G)₃NN motif are believed to be poor substrates for nucleosome formation (Turner 2001a). It has also been shown experimentally that arrays of 12, 24, or 48 copies of the CCGNN motif exclude nucleosomes in vitro (Wang and Griffith 1996). Additionally, DNase1-sensitive sites (likely reflecting nucleosome-free DNA) (Turner 2001b) tend to be located within and upstream of CCGNN repeats in yeast (Kirkpatrick et al. 1999). Finally, experimental evidence show that nucleosome excluding (CCGNN)₁₂ arrays stimulate recombination in yeast (Kirkpatrick et al. 1999). It is thus possible that open chromatin is a defining characteristic of many recombination hotspots in the dog and that degenerate (C/G)₃NN arrays, rather than simple GC richness, stimulate recombination initiation in these regions. Note that in contrast to the PRDM9 mechanism, this proposed mechanism is sequence nonspecific. However, it is also possible that an additional, sequence-specific factor is responsible for both the high GC content and elevated recombination rate in dog recombination hotspots and that the presence of these motifs is simply a function of the elevated GC content due to gBGC.

Hotspot locations are expected to be rapidly shifting in species where they are controlled by PRDM9, due to rapid evolution of its DNA-binding domain and meiotic drive against the active hotspot motif (Oliver et al. 2009; Myers et al. 2010). However, in species where recombination is not initiated in the same manner, for example, due to the lack of an active PRDM9, hotspot locations may be more stable. In dogs, recombination hotspots do not appear to be associated with a specific sequence motif, which suggests that meiotic drive at hotspots may not occur and thus the “hotspot conversion paradox” (Boulton et al. 1997; Coop and Myers 2007) does not exist. We expect the panda, and all other mammals with the exception of canids, to exhibit evolutionarily unstable recombination hotspots initiated by PRDM9. The dog is one of a large group of organisms, including birds, some fish, frogs, tunicates, diptera, and nematodes (Oliver et al. 2009), that lack a functional, full-length PRDM9 gene. Findings here may thus provide insight into the control of recombination initiation, not only in dogs but for a vast group of organisms. We speculate that the control of recombination in dogs is governed by an ancestral mechanism that is also present in other mammals. However, competition for the recombination machinery from sites targeted by PRDM9 may reduce the importance of this mechanism in species where PRDM9 is active, preventing these sites from being hotspots outside the canid lineage.

Finally we also note that there is evidence suggesting that sites targeted by PRDM9 in the human genome are susceptible to genomic rearrangements (Myers et al. 2008). If we assume that recombination in dogs is targeted more at ancestrally GC-rich sequence then in other lineages, then this would predict that chromosomal rearrangements in dogs would occur preferentially at GC-rich sequence. In support of this prediction, Webber and Ponting (2005) previously reported that the evolution of the canid karyotype has been under the influence of chromosomal rearrangements that showed a tendency to target GC-rich sequence. It is therefore likely that the loss of PRDM9 influenced the distribution of recombination events and the nature of karyotype evolution in canids.

Methods

PRDM9 sequencing

Samples

DNA was extracted from 15 dogs (Canis lupus familiaris) representing 15 breeds (beagle, Portuguese water dog, bearded collie, standard poodle, boxer, Dalmatian, Labrador retriever, German shepherd, rough collie, Eurasier, Polish lowland sheepdog, Rottweiler, Smålandsstövare, Swedish elkhound, and Nova Scotia duck tolling retriever) using standard procedures. We also extracted DNA from two Swedish wolves (Canis lupus; reference identification nos. 21 and 34), one black-backed jackal (Canis mesomelas), one golden jackal (Canis aureus), one African wild dog (Lycaon pictus), one red fox (Vulpes vulpes), and one bush dog (Speothos venaticus).

PCR and sequencing

Two sets of PCR primers were designed to amplify the pseudo-exon 7 (coding, in other species, for the zinc finger array) of canid PRDM9: one set with complete sequence complementarity to the published boxer genome assembly, used for PCR in dogs and wolf, and a second set showing a high degree of sequence conservation across the dog, human, mouse, and rat, used for PCR in the remaining canid species (Supplemental Table S1). PCR was then performed under the following conditions: (1) 5-min activation at 95°C; (2) 30 sec denaturing at 95°C; (3) annealing using specific touchdown scheme; (4) extension at 72°C, steps 2–4 repeated for 10 cycles; (5) denaturing at 95°C; (6) annealing for 30 sec; and (7) extension at 72°C, steps 5–7 repeated for 30 cycles (for details, see Supplemental Table S1).

Nested PCR, using a combination of two primer pairs, was performed for the African wild dog and bush dog on a 1:10 dilution of the PCR product obtained in the initial PCR (for details, see Supplemental Table S2).

Prior to sequencing, PCR products were cleaned using Exo1 and CIAP (Fermentas), according to the manufacturer's instructions. Cleaned products were then sent to the Uppsala Genome Sequencing Center for sequencing. For all samples, sequencing was performed with all possible primers listed in Supplemental Table S2.

Sequence analyses

Sequencing reads were assembled using Codon Code Aligner (CodonCode Corporation). To infer the functional status of the zinc finger array in the analyzed canids, we aligned the sequenced exon 7 to (1) the dog reference sequence using ClustalW2 (Larkin et al. 2007) and (2) human PRDM9 exon 7 using the GeneWise webpage (http://www.ebi.ac.uk/Tools/Wise2/index.html). Similarly, the status of PRDM9 in both the panda (Ailuropoda melanoleuca) (Li et al. 2010) and cat (Felis catus) (Pontius et al. 2007) was probed by collecting orthologous PRDM9 sequence from the publicly available genome assemblies of the two species and comparing them with human PRDM9 using GeneWise.

Recombination rate variation

Data set

To be able to infer recombination rates across the dog genome, we used data produced with the Canine HD array. This is a recently developed high-density SNP array containing 173,622 SNPs that are near to being uniformly distributed across the dog genome (Vaysse et al. 2011). The average SNP spacing is 13 kb, and there are no more than 21 genomic regions >200 kb that lack coverage on the array. For this study, we use a data set referred to as the “reduced” data set (Vaysse et al. 2011), consisting of data from 471 individuals from 30 breeds (for a list of all breeds included, see Supplemental Table S5). In total 157,393 SNPs were found to be polymorphic across these individuals. In addition, data from 15 wolves were also included to be able to compare LD-decay in wolves and dogs. Prior to all subsequent analyses, we phased the genotypes using fastPHASE version 1 with default parameters (Scheet and Stephens 2006).

Decay of LD

The amount of LD, as inferred using r², was calculated for all pairs of SNPs within a distance of 500 kb. These values were subsequently grouped into bins spanning every 10-kb interval from 10–500 kb. Values of each bin were averaged and plotted against distance. This procedure was repeated for each breed and for the wolf.

Recombination rate inference

We used the interval program included in the LDhat package (McVean et al. 2004) to estimate local recombination rates across all autosomes and the X-chromosome in the dog. This program has been argued to produce more reliable rate estimates, compared with, for instance, rhomap (LDhat package), when marker density is low, as in our data set (Auton and McVean 2007). To reduce computational cost we subsampled the original data set and used 100 randomly chosen haplotypes as input to interval. A look-up table downloaded from http://www.stats.ox.ac.uk/∼mcvean/LDhat/instructions.html, which assumes a population mutation rate (θ) of 0.001, was also provided to interval. To further increase computational efficiency, we split each chromosome into windows spanning at most 2000 SNPs and analyzed each window separately in interval. We then merged the results of each window into a coherent map spanning each chromosome. To obtain reliable rate estimates at the ends of windows, we ensured that neighboring windows overlapped by 200 SNPs. Each analysis was run for 1 million iterations, and the initial 100,000 runs were discarded as burn-in. Based on observations from inferences of simulated data sets (see below), we decided to set the rate change penalizing option in interval to 20 (bp = 20). Although setting bp = 0 increased the sensitivity of the inference, it also resulted in considerable rate variation in data sets generated without any recombination rate variation (Supplemental Fig. S12).

Validating the performance of interval on dog data

Interval has been shown to be relatively robust to deviations from the assumptions of the Wright-Fisher model (McVean et al. 2004). However, given that the demographic history of the dog includes both bottlenecks and strong selection, it was important to test whether interval performs well with this type of data. In addition, we sought to understand the effect of the relatively low SNP density of our data set on recombination rate inferences from interval. We used two different approaches to investigate the performance of interval on our dog data: (1) simulations and (2) comparisons to known recombination rates.

Simulations

We used MaCS (Chen et al. 2009) to simulate replicates of the dog data under models with known recombination rate variation. However, to make simulations realistic, we first had to model breed bottlenecks for each breed individually. This modeling was itself based on MaCS simulations. We built on previous dog demographic modeling efforts in setting up a simple simulation scheme to estimate the strength of bottlenecks at breed formation. Our model thus assumed an effective population size of the ancient wolf population (N_{e wolf}) of 22,600 (Gray et al. 2009). It furthermore assumed that dog domestication occurred 5000 generations ago, accompanied by an instantaneous decrease in population size to 5560 (N_{e dog}), and that breed formation took place 100 generations ago (Gray et al. 2009). The mutation rate was set to 1 × 10⁻⁸ (Lindblad-Toh et al. 2005), and the generation time was assumed to be 3 yr. We then used MaCS to simulate genome-wide replicas of our data set according to the model described above, for 59 breed bottleneck sizes, ranging from 0.001 × (N_{e wolf}) − 0.03 × (N_{e wolf}) (this corresponds to an increment in bottleneck size of 0.0005 × (N_{e wolf}) for every new simulation). We repeated these simulations for each of the sample sizes represented in the original data (ranging from 10–52 haplotypes), resulting in 767 simulated data sets. All simulations were run using regional recombination rates as inferred in the real data. We also corrected simulated data for ascertainment bias in the original data by providing MaCS with allele frequency distributions matched with those from the original data. The simulated data were also thinned to match the SNP density of the real data. Next, we estimated LD decay (as r²) in the experimental data, as well as in all simulated data sets. We used least squares to fit LD decay curves of real and simulated data sets (Supplemental Fig. S8). The best-fitting simulation provided an estimation of bottleneck size for each breed individually (Supplemental Table S1).

We subsequently used the model for dog domestication and breed formation described above to simulate realistic data that accounted for known recombination rate variation. Interval was then used to infer recombination rates in these simulated data sets, and comparisons between the rates provided to the simulations and rates estimated using interval could be made. We tested eight different scenarios in this way. For each scenario, we simulated a 1-Mb region, including a “hotspot” of recombination at the center (all scenarios used a background recombination rate as inferred from real chromosome 1 data [4N_er = 0.234] and a hotspot of intensity and width as follows: [1] intensity: 20, width: 2 kb, [2] intensity: 20, width: 10 kb, [3] intensity: 20, width: 100 kb, [4] intensity: 100, width: 2 kb, [5] intensity: 100, width: 10 kb, [6] intensity: 100, width: 100 kb, [7] intensity: 1000, width: 2 kb, [8] intensity: 1000, width: 10 kb). The three simulated hotspot intensities were chosen to, first, reflect observations from sperm typing experiments in humans and mice, where hotspots on average were found to have recombination rates 62 times more intense than the background rate, while the most frequently recombining hotspot exhibited a 811 times higher recombination rate relative to the background rate (Arnheim et al. 2007). Second, by choosing intensities used in previous simulations for human data (McVean et al. 2004), we wanted to facilitate the comparison of recombination maps in humans and dogs. Each scenario was repeated 100 times, and recombination rate estimates were averaged across all replicas and compared with the rate used as input to simulations (Fig. 4; Supplemental Fig. S10). As indicated above, this procedure was repeated using interval option “bp” set to both 0 and 20.

Comparing the LD-based map to a previously published linkage map

To compare the recombination rates estimated here with known recombination rates in the dog, we made use of a previously published linkage map (Wong et al. 2010). To do this, we first had to translate our map, measured in units of population scaled recombination rate (ρ), into a map measured in centimorgans. This in turn requires that we know the effective population size of the dog, which can be estimated by comparing the length of the linkage map with the length of the LD-based map (where they overlap). The effective population size of the dog was in this way estimated to be 7752 individuals. Second, as the resolution of the linkage map is different from that of the LD-based map, it was also necessary to transform the maps to a similar scale. For both maps we therefore averaged rates across 5-Mb windows, before comparing them on a single plot (Fig. 5; Supplemental Fig. S9).

SequenceLDhot to detect hotspots

Although interval can be used to detect hotspots, other programs have been shown to perform better at this task (Fearnhead 2006). In this study we have used SequenceLDhot (Fearnhead 2006) to locate hotspots of recombination in the dog genome. Before analyzing real data, it is important to optimize parameter settings in SequenceLDhot to obtain reliable output at a reasonable computational cost. We again used simulations (data not shown) as a guide to good parameter settings, and decided to use the default values given in the SequenceLDhot instructions (Infile 1), with the following exceptions: The background recombination rate (ρ) varied depending on type of analysis (see below), θ was set to 0.00031 (which we calculated using the above estimated dog N_e and a mutation rate of 1 × 10⁻⁸), and a new hotspot was considered every 10,000 bp. We then simulated 100 sequences of length 1 Mb, using the mean recombination rate of dog chromosome 1 as background rate and including a 2-kb wide hotspot at the center, with a recombination rate 100 times the background rate (detailed simulation parameters are as described above). The simulated data sets were then used to train SequenceLDhot to locate hotspots in the dog data by finding the best tradeoff between power and accuracy. We found that by requiring that the likelihood ratio statistics (lr) must equal or exceed 8 (lr ≥ 8) for a window to contain a hotspot and by simultaneously setting the limit for neighboring windows to be considered as part of an extended hotspot region to lr ≥ 4, we were able to optimize this tradeoff. We also noted that we needed to add 8 kb of sequence to each side of an inferred hotspot region to ensure that the simulated hotspot was contained within the borders of the suggested region. This reflects the fact that the average SNP density in the dog data exceeds the 2-kb definition of a hotspot used in the analyses. By applying the above settings, SequenceLDhot detected 10 out of 100 simulated hotspots. Simultaneously, it also noted the presence of one false hotspot outside of the simulated hotspots. From this we conclude that the power of SequenceLDhot to detect hotspots in our dog data is near 10% at a FDR of ∼10%. To increase computational efficiency when inferring hotspots in the real dog data, we analyzed windows of 100 SNPs separately (on average spanning 1.3 Mb). Neighboring windows overlapped by 20 SNPs to allow us to detect rate variation at ends of windows. The median recombination rate of all marker pairs of a window (inferred using interval) was provided to SequenceLDhot as background rate for a particular window. To test whether the number of detected hotspots depended on the marker density of a particular region, we compared the number of markers and hotspots found in 500-kb windows across the dog genome using a Spearman rank correlation.

Motif search

To characterize the DNA sequence of hotspots, 1683 narrow hotspot regions, all of which contained a putative hotspot embedded within a 18-kb region, were compared to an equal number of cold regions. A cold region was defined as a region in the genomic vicinity of a particular hotspot region (average distance, ∼27 kb) equal in size to but not overlapping any hotspot region. The cold region also had to match a hotspot with regards to whether the hotspot region was within or outside a gene. We scanned the two categories for repeat elements as defined using RepeatMasker (http://www.repeatmasker.org), and counted the number of occurrences of motifs in each group. To find sequence motifs that were either over- or underrepresented in hotspot regions versus “cold” regions, a Fisher's exact test was applied, and P-values were corrected for multiple tests using a Bonferroni correction.

Substitution patterns

To infer, and compare, lineage-specific substitution patterns in hotspot regions, we downloaded chained blastz alignments of dog–panda and dog–cat from the UCSC Genome Browser (http://hgdownload.cse.ucsc.edu). By comparing orthologous positions in the dog, panda, and cat, we determined the direction of substitutions that affect GC content. More specifically, we quantified the number of strong-to-weak (SW, GC→AT) and weak-to-strong substitutions (WS, AT → GC) in a particular lineage. A measure of the relative direction of substitutions, or the substitution bias, was then calculated as follows: SB = WS/(WS + SW). Several analyses involving this substitution bias were performed. First, to contrast the substitution patterns of the dog and panda lineages, we estimated the substitution bias in all GC peaks residing within hotspot regions (for which alignment data were available) and compared values obtained for the dog and panda lineage. Statistical significance was tested by bootstrapping over GC peaks using 1000 iterations. Second, as a control, we tested whether substitution patterns in the dog and panda differ in general by measuring the average substitution bias in the first 1000 bp of the set (n = 1683) of “cold” control regions described above. Finally, to understand if the observed substitution bias in the dog is restricted to GC peaks in hotspot regions, we centered all available hotspot GC peak alignments (n = 309) in 18-kb windows and estimated the average substitution bias in the dog across the entire window using a 500-bp sliding window.

Assuming that historical substitution patterns persist, it is possible to estimate the GC content toward which a sequence is evolving (GC*) (Meunier and Duret 2004). We calculated the average GC* (GC* = u/(u + v), where the rate of strong-to-weak [GC-to-AT] and weak-to-strong [AT-to-GC] substitutions are u and v, respectively) in the dog as well as the panda, across the GC peak–centered, 18-kb windows described above using a 500-bp sliding window. Finally, by dividing the total number of observed lineage-specific substitutions with the total number of aligned base pairs, we also estimated the overall substitution rates (S) for GC peaks and “cold regions” in the dog as well as the panda.

Data access

DNA sequences analyzed in this manuscript have been deposited in GenBank (http://www.ncbi.nlm.nih.gov/genbank) under the following sequential accession numbers: JF750638–JF750659. Genotype data used for recombination rate inferences in this manuscript are available in Supplemental Material and at http://dogs.genouest.org/SWEEP.dir/Supplemental.html.