Compressive Sensing–Based Interior Tomography: Preliminary Clinical Application

Abstract

Compressive sensing (CS)-based interior tomography is a state-of-the-art method for accurate image reconstruction from only locally truncated projections. Here, we report our preliminary interior tomography results reconstructed from raw projections of a patient acquired on a GE Discovery CT750 HD scanner. This is the first clinical application of the CS-based interior reconstruction techniques, and the results show an excellent match with those reconstructed from global projections.

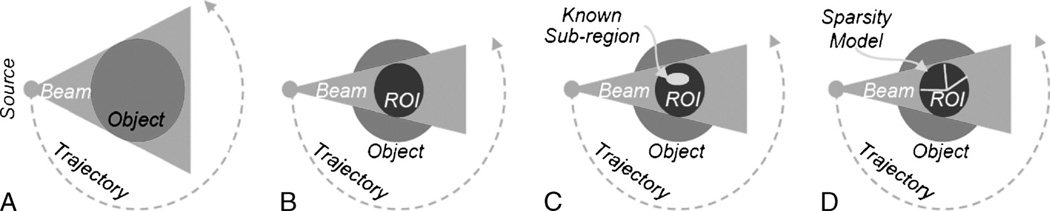
Whereas classic computed tomographic (CT) theory targets the exact reconstruction of a whole cross section from complete projections, biomedical applications often focus on much smaller internal regions-of-interest (ROI) such as cardiac structures in a CT study, which is called the “interior problem.” Because this interior problem does not have a unique solution,¹ the classical CT theory cannot exactly reconstruct an internal ROI only from truncated projections associated with x-rays through the ROI. In 2007, we proved that the interior problem can be exactly and stably solved if a subregion inside the ROI is known.^2–5 This knowledge-based interior reconstruction is called interior tomography. Inspired by the recently developed compressive sensing (CS) theory, in 2009 we proved that exact interior reconstruction is achievable with an interior scan if an ROI is piecewise constant or piecewise polynomial,^6–10 which strongly suggests that the interior tomography can be accurately achieved in the CS framework without precise knowledge of a subregion in the ROI (Fig. 1). Because it requires less projection data sets, the CS-based interior tomography has a great potential to handle large objects, minimize radiation dose, suppress scattering artifacts, enhance temporal resolution, reduce system cost, increase scanner throughput, etc.

FIGURE 1.

Interior tomography. A, Conventional tomography allows exact reconstruction of an object from a half-scan. B, It was considered impossible to uniquely reconstruct an ROI from truncated local data (the interior problem). C, We proved in 2007 that the interior problem can be exactly and stably solved assuming a known subregion. D. We showed in 2009 that for a piecewise or polynomial ROI the interior problem can be uniquely solved.

To evaluate the state-of-the-art CT algorithms developed at Wake Forest University Health Sciences (WFUHS), a research agreement was made between WFUHS and GE Healthcare Technology for potential research collaboration. According to this agreement, clinical CT raw data sets will be preprocessed by GE, reconstructed by WFUHS with WFUHS algorithms, and then evaluated by GE. Here, we report our preliminary results on a preprocessed clinical data set to demonstrate the application of the CS-based interior tomography. To the best of our knowledge, this is the first case of clinical application of the CS-based interior reconstruction techniques.

PRELIMINARY RESULTS

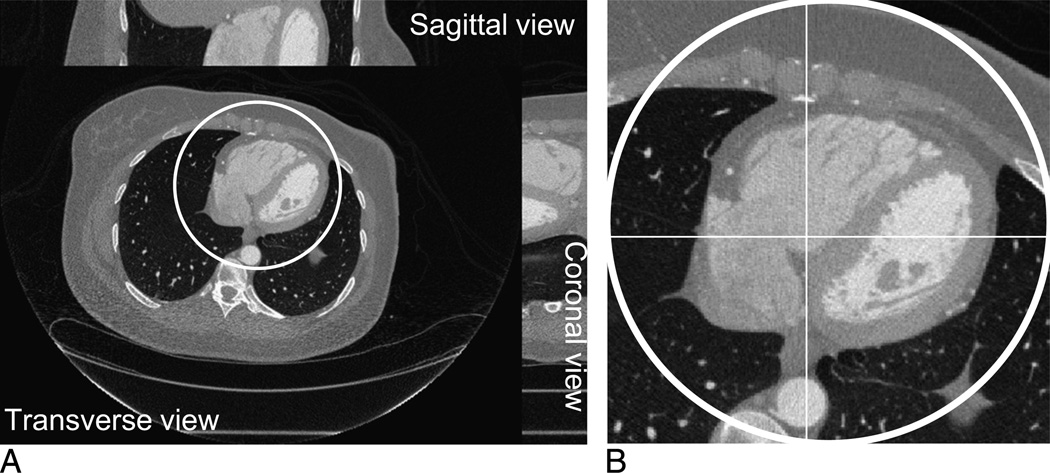
A cardiac-gated CT examination was performed on a GE Discovery CT750 HD scanner at WFUHS to evaluate the coronary arteries in a patient presenting with a history of chest pain. The scanning trajectory was a typical helical geometry. After appropriate preprocessing, we obtained a set of 64-slice fan-beam sinograms. The radius of the scanning trajectory is 53.85 cm. Over a 360-degree range, 2200 projections are uniformly acquired. For each projection, 888 detector elements are equiangularly distributed, which defines a field of view (FOV) of a 24.92-cm radius. For each sinogram, an 800 × 800 image matrix is reconstructed by the conventional filtered back projection (FBP) method covering a region of 44.86 × 44.86 cm, which serves as a benchmark to evaluate our interior reconstruction techniques. The transverse, sagittal, and coronal views of the reconstructed volume are shown in Figure 2A. To evaluate our CS-based interior reconstruction techniques, each projection is truncated by discarding 300 detector elements on each of its 2 sides, which covers a small interior FOV of an 8.70-cm radius. Figure 2B shows a magnified interior part of the transverse slice no. 32.

FIGURE 2.

A volumetric image reconstructed by the conventional filtered back projection algorithm from one helical turn (64 slices) clinical patient data set collected on a GE Discovery CT750 HD scanner. A, Transverse, sagittal, and coronal slices of the image volume. B, The magnified interior cardiac region of the transverse slice no. 32.

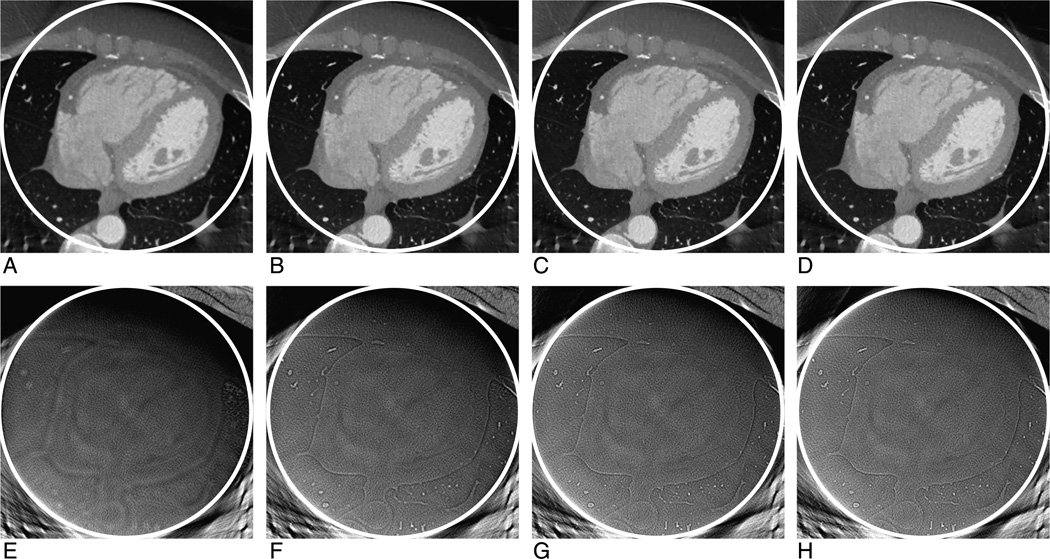
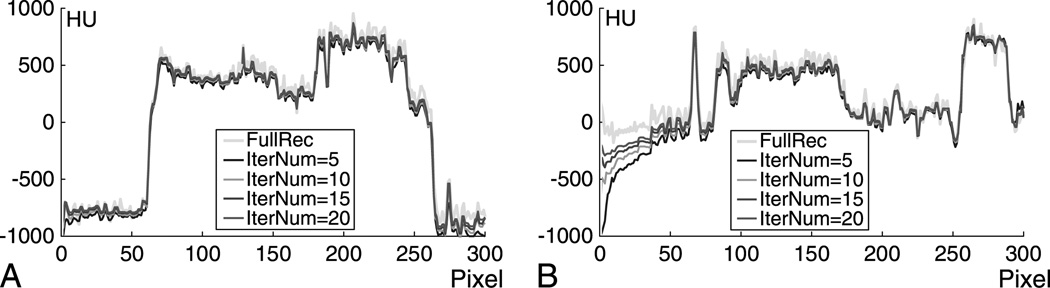
In this study, the interior reconstruction is performed by a soft-threshold filtering-based method¹¹ for each sinogram using the aforementioned fan-beam geometry. The algorithm consists of 2 major steps. In the first step, the ordered-subset simultaneous algebraic reconstruction technique¹² is used to reconstruct a digital image based on all the truncated local projections. In the second step, the L1 norm of the total difference (also bilateral total variation)¹¹ is minimized using the fast iterative shrinkage thresholding algorithm.¹³ To further accelerate the convergence, the projected gradient method¹⁴ is used to determine an optimal threshold for each filtering. The 2 steps are iteratively performed in an alternating manner. In our experiment, the initial image is set to be zero, and the 2200 truncated projections are divided into 88 subsets and each of them includes 25 uniformly distributed projections. In each iteration step, all the subsets are used in a specific order to make the projections of 2 adjacent subsets distributed as uniform as possible. For each sinogram, the reconstructed image is also an 800 × 800 matrix covering a region of 44.86 × 44.86 cm. Figure 3 shows the magnified ROIs of the transverse slice no. 32. Figure 4 shows 2 representative profiles along the white lines indicated in Figure 2B for the images in Figure 3, which shows an excellent match between the FBP reconstruction from global projections and the interior reconstructions from truncated projections. From Figures 3 and 4, we can see that the differences between the interior reconstruction and global reconstruction become smaller and smaller with the increment of the iteration number. This phenomenon is detectable along the profiles for the pixel range 0 to 70 in Figure 4B. This implies that the image can be accurately reconstructed when the iteration number trends to infinity, which is consistent with our theoretical analysis.^6–10 Comparing Figures 2B and 3A to D, the image quality of interior reconstruction is even better than that of global FBP reconstruction. This is because the soft-threshold filtering method has a strong capability of denoising.

FIGURE 3.

Compressive sensing–based interior reconstruction of a cardiac region from a clinical patient data set collected on a GE Discovery CT750 HD scanner. From left to right, the iteration number for the top row images (Window Width, W = 2000 HU; Window Center, C = 0 HU) are 5, 10, 15, and 20, respectively. The bottom row images are the corresponding difference images between the interior reconstruction and global reconstruction (Window Width, W = 200 HU; Window Center, C = 0 HU).

FIGURE 4.

Profiles of the images in Figure 3 along the horizontal (A) and vertical (B) white lines indicated in Figure 2.

DISCUSSION

Because our CS-based interior reconstruction algorithms are iterative, they usually require a more computational cost than other analytic ones. In addition, a finite detector based super-resolution projection model is used,¹⁵ which requires much more time to compute an intersection area between a square pixel and a narrow fan-beam connecting a finite width detector and the x-ray source. Furthermore, our algorithm is implemented in Matlab, whose efficiency is not as high as other scientific computing languages (eg, Fortran). As a result, it takes approximately 20 minutes to complete a single iteration using one core on a PC (32-bit, 2-core, 4.0-G RAM, 3.16-G CPU). To make the interior reconstruction technique practical, we are working to develop a hardware-based acceleration method and implement a parallel computing version for a PC cluster.

Compressive sensing–based interior reconstruction is a promising direction for accurate reconstruction from truncated projections. Extensive theoretical analysis^6–10 has been performed to establish its uniqueness, but its stability is still an open problem. In the implementation of the CS-based algorithm used in this report, several parameters (eg, the subset number and the iteration number) were empirically chosen. Despite the excellent match between the interior tomography result and the traditional global reconstructions in this report, we observed relatively minor profile mismatches with some other data sets. One possible reason is data inconsistency due to the polychromatic nature of diagnostic x-rays. Therefore, we are motivated to perform stability analysis, include additional constraints, and improve algorithms.

In summary, the CS-based interior reconstruction technique was evaluated and demonstrated by raw projections of a patient from a GE Discovery CT750 HD scanner. This is the first time for the CS-based interior reconstruction to be applied for clinical application. Although our initial results are very promising, much additional effort will be required to improve this technique.