Abstract
Small modifications of the molecular structure of a ligand sometimes cause strong gains in binding affinity to a protein target, rendering a weakly active chemical series suddenly attractive for further optimization. Our goal in this study is to better rationalize and predict the occurrence of such interaction hot-spots in receptor binding sites. To this end, we introduce two new concepts into the computational description of molecular recognition. First, we take a broader view of noncovalent interactions and describe protein–ligand binding with a comprehensive set of favorable and unfavorable contact types, including for example halogen bonding and orthogonal multipolar interactions. Second, we go beyond the commonly used pairwise additive treatment of atomic interactions and use a small world network approach to describe how interactions are modulated by their environment. This approach allows us to capture local cooperativity effects and considerably improves the performance of a newly derived empirical scoring function, ScorpionScore. More importantly, however, we demonstrate how an intuitive visualization of key intermolecular interactions, interaction networks, and binding hot-spots supports the identification and rationalization of tight ligand binding.
Introduction
A good understanding of the key determinants for tight protein–ligand binding is a prerequisite for successful structure-based design. The work presented here aims at contributing to this understanding in a 2-fold manner, by providing a more comprehensive description of interacting protein and ligand atoms and by providing a conceptual framework allowing one to move beyond the concept of pairwise interactions.
Neither physics-based nor empirical approaches to computationally assess the strength of protein–ligand binding have significantly advanced over the past decade. Scoring functions are still crude estimates of affinity useful for an enrichment of ligand candidates in virtual screening, but not for the prediction of affinity.(1) More sophisticated free energy calculations may work well for specific systems but cannot be applied with confidence across diverse data sets.2,3 What has advanced, however, is our qualitative understanding of the types of interactions that play a role in protein–ligand binding—through systematic mining of structural data, theoretical calculations, and detailed case studies.(4) Examples are halogen bonds,5,6 orthogonal multipolar interactions,(7) and weak hydrogen bonds.(8) We believe that the knowledge about such interactions could be more broadly and directly applied. Empirical scoring functions may be limited in predictive power but are an ideal vehicle to absorb this additional know-how, as they do not require a strict theoretical framework and, if used in conjunction with graphical methods, foster an intuitive understanding of molecular recognition.
All current scoring methods, whether descriptive, knowledge, or force field based, rely on the concept of pairwise interactions. Contributions of such pairs are treated as independent and additive, whereas in reality all interactions are influenced by neighboring groups. The environment of a functional group can strengthen or weaken the interactions it forms; in other words, interactions can be positively or negatively cooperative. In medicinal chemistry, such effects are frequently manifested in the form of a nonadditive SAR.9−12
Cooperativity may, in turn, have different causes. Interactions such as hydrogen bonds that are accompanied by strong shifts in electron density can reinforce each other through polarization. In crystals, hydroxyl-containing molecules often arrange in particularly stable chains or cycles.(13) Quantum-mechanical calculations suggest significant cooperative enhancement of hydrogen bonding energies in model systems such as long water chains(14) or a water–crownophane complex.(15) The stacking of multiple β strands in amyloid fibrils has been, in part, ascribed to cooperative hydrogen bonding,(16) just as urea molecules stack up in nonpolar solvents.(17)
As opposed to polarization effects, which are already apparent in the ground state of systems, cooperativity can also be caused by dynamic effects. Classical experiments by Williams et al. on glycopeptide antibiotics(18) and on the streptavidin–biotin complex(19) have shown that binding causes these systems to be more rigid and thus enthalpically more favorable. The loss of binding entropy caused by the reduced motion is more than compensated by the gain in enthalpy achieved through tighter interactions. Similar conclusions were drawn recently by the Hangauer and Klebe groups in a series of experiments on thrombin complexes, where the presence of a hydrogen bond reinforces lipophilic interactions in the complex, and vice versa.11,12
In the following, we first propose a comprehensive set of attractive and repulsive noncovalent interactions. We then investigate the hypothesis that useful information about cooperativity can be directly obtained from X-ray structures of protein–ligand complexes. We treat protein–ligand complexes as interaction networks with some of the properties of “small world” networks.(20) The nodes of the network are formed by amino acid reduced graphs, water molecules, and ligand atoms. The edges of the network are formed by covalent bonds and noncovalent interactions. In the network model, the binding of a ligand introduces many new edges in the protein network and thus more closely links protein nodes with each other. From the networks, we can thus extract parameters indicative of local tight binding. To quantify the relevance of the network description, we use these parameters to derive a new empirical scoring function, termed ScorpionScore, and assess its performance against various test sets. In this way, we present a first systematic attempt to account for cooperativity in a scoring function.
A number of groups have described protein 3D structure using the small world network paradigm, with nodes representing amino acids and edges indicating a short distance between α carbons. Such networks have been employed for analyzing the protein folding process,(21) protein flexibility and dynamics,22,23 protein function,(24) and structural features in protein–protein complexes.(25) Also related is a graph theory approach applied to study rigidity in protein structures.26,27 Computational small world network theory has been applied to many different realms of biology, communication systems, and social organizations,(28) but its application to protein–ligand interactions is new.
Optimization of an empirical scoring function requires high quality and consistency in both X-ray complex structures and associated binding affinities. We apply very stringent quality criteria in our complex selection and perform all optimizations against training sets of the same protein with ligand affinities determined with the same assay. We illustrate the utility of the new scoring function and the network concept by means of multiple examples combining structural and SAR data from drug discovery projects, and we show how the visualization of interactions and the network helps to identify contact “hot-spots” as well as poorly interacting functional groups. Finally, we close with a critical discussion of the scope and limitations of the network model and present options of how the model could be further extended.
Methods
Overview
Our approach is based (a) on the identification and classification of different types of favorable and unfavorable close contacts within protein–ligand binding sites and (b) on the subsequent calculation of subgraph network descriptors. We combine all covalent and all favorable noncovalent interactions to create a network and then define a set of descriptors that encode the complexity of the network. In this network, we use a reduced graph representation of the protein structure, in which all side chains and all backbone amides are treated as single groups each. Crystallographic water molecules are assigned a geometric Rank score which enables us to discriminate waters that have a role in binding from waters that can be ignored. Unfavorable close contacts, which include van der Waals clashes, and mismatches between hydrogen bond donors or acceptors and lipophilic atoms, which we refer to as desolvation penalties, are also identified. We generate a scoring function which is a sum of favorable and unfavorable close contacts and the contributions of network terms.
Identification and Classification of Favorable and Unfavorable Interactions
A new software tool, ViewContacts, was created, enabling us to identify not only the classical interaction types (hydrogen bonds, ionic pairs, and van der Waals contacts) but also nonclassical interactions including cation–dipole, cation−π, hydrogen bonding to π systems, halogen bonding, orthogonal dipolar alignment, dipolar antiperiplanar interactions, π-stacking, π edge-to-face contacts, and hydrogen bonding involving polarized CH groups. All geometric thresholds for favorable interaction distances and angles are listed in detail in Table 1.
Table 1. Summary of Favorable Interaction Types, Interaction Partners, and Geometry Definitionsa.
| interaction type | interacting atom types | cutoff distance, dcut [Å] | angle definitions |
|---|---|---|---|
| hydrogen bond | hdon | hacc | 0.2 | sp: 135.0 ≤ (hdon···hacc–X) ≤ 180.0b |
| sp2: 80.0 ≤ (hdon···hacc–X) ≤ 180.0b and | |||
30.0 ≤ (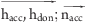 ) ≤ 90.0b ) ≤ 90.0b
|
|||
| sp3: 70.0 ≤ (hdon···hacc–X) ≤ 180.0b | |||
| metal | met | hacc | 0.2 | see hydrogen bond, with hdon replaced by met |
| ionic | cat | ani | 1.0 | |
| cation–dipole | cat | dneg | 0.7 | 120.0 ≤ (cat···dneg–X) ≤ 180.0 |
| cation-π | cat | π | 0.5 | 0.0 ≤ (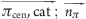 ) ≤ 45.0 ) ≤ 45.0 |
| dipolar | dpos | dneg | 0.4 | 60.0 ≤ (dneg1···dpos2–dneg2) ≤ 120.0 or |
| 150.0 ≤ (dneg1···dpos2–dneg2) ≤ 180.0b | |||
| halogen bond | σpos | σneg | 0.2 | 120.0 ≤ (σneg···σpos–X) ≤ 180.0 |
| 80.0 ≤ (σpos···σneg–X) ≤ 180.0 | |||
| hydrogen bond donor−π | hdon | π | 0.2 | 0.0 ≤ (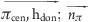 ) ≤ 45.0 ) ≤ 45.0 |
| see also hydrogen bond, with hacc replaced by πcen | |||
| π–π | π | π | 0.5 | (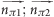 ) ∈ [0.0–35.0; 55.0–125.0; 145.0–180.0] ) ∈ [0.0–35.0; 55.0–125.0; 145.0–180.0] |
| parallel: distance (π1···π2cen) ≥ 2.0 Å and distance (π2···π1cen) ≥ 2.0 Å | |||
| orthogonal: distance (π1···π2cen) ≥ 2.0 Å or distance (π2···π1cen) ≥ 2.0 Å | |||
| vdW | hyd | hyd | 0.5 |
An interaction between two atoms A and B is counted as favorable if (a) their distance is below rvdW,A + rvdW,B + dcut, where rvdW are the van der Waals radii according to Bondi(34) and dcut is an interaction type-specific distance cutoff, and (b) all involved angular thresholds are fulfilled. X denotes a covalently attached non-hydrogen atom and n⃗ stands for the normal vector of the plane. For hydrogen bonds and metal interactions, angle definitions are dependent on the hybridization states of donor and acceptor, respectively.
Analogous terms with exchanged atom types are additionally used.
Apart from favorable interaction types, eight unfavorable types of contacts are encoded (Table 2). These take into account three different classes of unfavorable interactions: (1) close contacts of wrongly matched atom types, e.g., two hydrogen bond donors pointing at each other (unf_hydrogen_bond, unf_metal, unf_ionic, unf_dipolar; in this class, we use the geometry thresholds of the corresponding favorable interaction), (2) clashes of atom pairs, characterized by very short distances (clash_apolar, clash_polar), and (3) contacts to which a desolvation penalty is assigned (desolv_donor, desolv_acceptor). For each hydrogen bond donor or acceptor atom, it is determined whether any of its close apolar contact atoms occupy the region where a matching acceptor or donor would be expected. This is done by placing a water molecule in the position of the apolar contact partner and then applying distance and angle criteria to determine whether a polar atom would be “preferred” at the location of the apolar atom. We consider only strong hydrogen bond donor and acceptor atoms as candidates for desolvation penalties, and we apply a further subdivision into two sets with different distance thresholds. A smaller desolvation penalty is expected in cases in which the donor or acceptor is already engaged in a favorable interaction with another partner or is considerably solvent-exposed. We use a shorter cutoff distance here, resulting in fewer contacts being counted as unfavorable.
Table 2. Summary of Unfavorable Interaction Types, Interaction Partners, and Geometry Definitionsa.
| interaction type | interacting atom types | cutoff distance, dcut [Å] | angle definitions |
|---|---|---|---|
| unf_hydrogen bond | hdon | hdon | 0.2 | sp: 135.0 ≤ (hdon1···hdon2–X) ≤ 180.0 b |
| hacc | hacc | sp2: 80.0 ≤ (hdon1···hdon2–X) ≤ 180.0 b and | ||
30.0 ≤ ( ) ≤ 90.0b ) ≤ 90.0b
|
|||
| sp3: 70.0 ≤ (hdon1···hdon2–X) ≤ 180.0 b | |||
| unf_metal | met | hdon | 0.2 | see hydrogen bond, with hdon2 replaced by met |
| unf_ionic | cat | cat | 1.0 | |
| unf_dipolar | dneg | dneg | 0.4 | 60.0 ≤ (dneg1···dneg2–dpos2) ≤ 120.0 or 150.0 ≤ (dneg1···dneg2–dpos2) ≤ 180.0 b |
| dpos | dpos | |||
| dneg | ani | |||
| clash_apolar (interaction type ∈ [π–π, vdW]) | −0.45 | ||
| clash_polar (interaction type ∉ [π–π, vdW]) | –0.7 | ||
| desolv_donor | hdon | hyd | 0.0c | see hydrogen bond, with hdon2 replaced by hyd |
| 0.8d | |||
| desolv_acceptor | hacc | hyd | 0.0c | see hydrogen bond, with hdon2 replaced by hyd and hdon1 replaced by hacc |
| 0.8d |
An interaction between two atoms A and B is counted as unfavorable if (a) their distance is below rvdW,A + rvdW,B + dcut, where rvdW is the van der Waals radii according to Bondi(34) and dcut is an interaction type-specific distance cutoff, and (b) all involved angular thresholds are fulfilled. For hydrogen bonds, metal interactions, and donor and acceptor desolvation pairs, angle definitions are dependent on the hybridization states of donor and acceptor, respectively.
Analogous terms with exchanged atom types are additionally used.
Cutoff distance if hdon or hacc already form a hydrogen bond with hacc or hdon, respectively.
Cutoff distance if hdon or hacc is not already involved in a hydrogen bond and is not solvent-exposed.
Each non-hydrogen atom in a protein structure is assigned one or more of 11 atom types (hdon, hacc, met, cat, ani, dneg, dpos, σpos, σneg, π, and hyd) that define the interactions it can form with neighboring atoms (Tables 1 and 2). Atom types are assigned according to element, hybridization state, number of protons and/or lone pairs (for acceptors and donors), and the local covalent bond pattern. We use SMARTS matching(29) to encode these properties into SMARTS strings, a line notation that is both convenient to use and easy to modify and extend. A similar approach has been described by others.(30) In some cases, the same atom types are represented by alternative SMARTS strings to handle tautomers and/or different representation of the same group of atoms in different connectivity tables. Our SMARTS strings are stored as an ordered list. Each string in turn is used to identify matching atoms in a ligand from our curated database, Proasis2,(31) until all atoms are assigned. We also use a graph matching algorithm(32) to identify all π systems. For most atoms in a protein, we simply use atom names to assign types according to precalculated results. Exceptions are CYS SG, which exists as part of a thioether or as a free SH group, and SER OG, THR OG1, and TYR OH when phosphorylated. We allow for cases where an atom can be both acceptor and donor, e.g., OG in SER, and allow for cases where an atom can be either acceptor or donor, but not both at the same time, for example, ND1 and NE2 in HIS.
In order to assign interaction types to specific contacts, the starting point is a list of atom–atom contacts sorted by distance and in ascending order. The list of close contacts is pruned. We ignore contact pairs less than or equal to a covalent bond distance, pairs across a bond angle and torsion, and all intramolecular contacts within small molecules. To ensure that only “true” interactions are counted, we apply a line of sight filter, pruning out longer contacts of bystander atoms which arise primarily because they are covalently connected to the main contact atom. In this filter, contacts A and B are removed if both dA,B is longer than the distance from a covalently bonded atom A′ to B and the line connecting A and B intersects the sphere around A′ with a sphere radius of 1.0 Å.(33) For each remaining close contact, a list of allowed favorable and unfavorable interactions is obtained on the basis of the assigned atom types. In some cases, a close pair of atoms may have no favorable interaction type and not be a repulsive pair; these are flagged as candidates for desolvation penalties. If these pairs do not satisfy the rules and geometric constraints required for a desolvation penalty, then they are labeled as unclassified contacts and are not further involved in scoring. For each of the allowed interactions, we first use distance cutoffs, which are simple functions of the sum of the van der Waals radii,(34) to determine whether a contact is close enough for a given type of interaction. For example, for a pair of hydrogen bond partners, the atoms must be no closer than the sum of their van der Waals spheres, −0.7 Å (otherwise classified as a clash), and no further apart from each other than the sum of the van der Waals spheres, +0.2 Å. If an interaction satisfies the distance criteria, we use angle cutoffs to determine whether a contact satisfies the required angular constraints. If any constraint is not fully satisfied for a given interaction type, distance and angle criteria are tested for the next allowed type of the contact pair, and so on, until a match is found. In some cases, a close contact may not satisfy all angle constraints for any interaction type. Such contacts are labeled as poor contacts and treated as candidates for desolvation penalties.
Handling of Water Molecules
Structural water molecules are classified according to their interactions with neighboring protein atoms and water molecules. We use a scoring scheme similar to the geometric Rank score developed by Kellogg and co-workers.(35) For each water, a Rank score is calculated on the basis of the deviation from ideal tetrahedral coordination:
where rn is the distance between the water oxygen and the hydrogen-bonded heavy atom n (n is the number of interacting atoms up to a maximum of 4). This is scaled relative to 2.8 Å, the median hydrogen bonding distance in the Cambridge Structural Database (CSD)(36) for C=O acceptors interacting with OH and NH donors.(4) θTd is the ideal tetrahedral angle (109.5°), and θnm is the angle between contact atoms n and m (m = 1 to n – 1). A maximum of two donors and two acceptors are considered, and any angle less than 60° is rejected from the analysis. Rank scores can range from 0 (no hydrogen bond) to 6 (four hydrogen bonds in ideal tetrahedral coordination). Water molecules with a Rank score < 2.0, which corresponds to waters not involved in two or more good hydrogen bonds, are omitted from the analysis. Water–water contacts are included in the calculation of the Rank score if the contacting oxygen atom itself has a score above the threshold of 2.0.
Subgraph Network Descriptors
In our model, nodes are ligand atoms, protein backbone amide groups, and protein side chains represented as a reduced graph, as well as water, metals, ions, and other HET groups, while edges are favorable noncovalent contacts and covalent bonds. We use the expression “network descriptor” when discussing our overall concept, and we use the following terminology when describing the details of our method:
-
•
network path: a continuous pathway of covalent bonds and favorable noncovalent interactions
-
•
network element: a shorthand notation we use to classify different types of network paths (definitions see below)
-
•
network sum: weighted and normalized sum of the number of network paths for a protein–ligand contact
-
•
interaction term: a scoring function term corresponding to the pairwise contact component of a protein–ligand contact
-
•
network term: a scoring function term corresponding to the network component of a protein–ligand interaction
-
•
network score: the magnitude of the contribution of the network to the total score, that is, the sum of the strong network terms
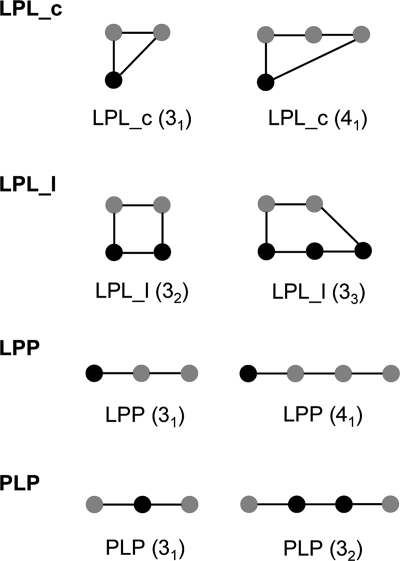
We have extended the concept of protein–ligand (PL) interactions and introduce the concept of protein–ligand network elements, labeled as LPL, PLP, and LPP, where L is a ligand atom and P is a protein atom (Figure 1). Each network path begins and ends with a noncovalent interaction. We further distinguish the network element LPL into two types. If a path begins at a ligand atom, traces through the network, and returns to the same ligand atom, we call that a ligcycle (LPL_c). If a path begins and ends at different ligand atoms, we call that a ligloop (LPL_l). The network element LPP corresponds to a path that starts at a ligand atom but does not return to the ligand within a predefined path distance. We call this network element a ligpath. Ligpaths are in fact truncated ligcycles and ligloops. We also explored incorporating network elements of type PLP but found that these are correlated too closely with molecular weight to be useful (with the exception of combinations of hydrogen bonds, see below). All other network element types that can be constructed, such as LLP, PPL, PLL, LLL, and PPP, are just subsets or a reordering of the network elements already defined.
Figure 1.
Diagrams of network elements used in this study including two representative examples for each type. Black nodes denote ligand atoms, and gray nodes denote backbone amide or side chain groups of the protein reduced graph. An edge stands for a noncovalent favorable or covalent interaction. LPL_c represents ligand–protein–ligand network paths which begin and end at the same atom (ligcycle). LPL_l represents ligand–protein–ligand network paths which begin and end at different ligand atoms (ligloop). LPP represents ligand–protein–protein paths (ligpath), and PLP represents protein–ligand–protein paths. The numbers in parentheses indicate the number of nodes in the network, where connected ligand atoms are counted as one node and, in subscript, the number of connected ligand atoms in the path. Additional special network path types are derived from this collection using the following specific constraints. Privileged pairs of hydrogen bonds (HLH) are PLP elements in which the two protein–ligand contacts are hydrogen bonds with the two ligand atoms being close in space. Pure hydrogen bond networks involving neither covalent bonds nor non-hydrogen bond interactions are derived for LPL_c (LPL_chb), LPP (LPPhb), and PLP (PLPhb) network elements.
Hydrogen bonding networks are particularly important in molecular recognition, and so we augmented the network descriptors with two additional network path types. First, we introduced an additional hydrogen bonding network element involving pairs of protein–ligand hydrogen bonds that are close in space to one another. These are special cases of PLP elements corresponding to an arrangement of correlated hydrogen bonds. We refer to these as a privileged pair of hydrogen bonds and abbreviate them as HLH. The threshold for the Euclidean distance between ligand atoms involved in the hydrogen bonds was set to 2.8 Å, approximately twice the radius of a water molecule. Second, a pure hydrogen bond network was defined, consisting only of acceptor and donor atoms and hydrogen bonding interactions. Three types of subgraph descriptors, marked with the superscript “hb”, are relevant in this hydrogen bonding network: LPL_chb, PLPhb, and LPPhb terms. A ligcycle in the pure hydrogen bonding network is a continuous cycle of hydrogen bonds that starts and ends at the same ligand atom. The PLPhb element involves one ligand atom which is involved in two protein–ligand hydrogen bonds but does not have a closed cycle of protein–protein hydrogen bonds. The ligpaths are all remaining protein–ligand hydrogen bonds that define a path with additional protein–protein hydrogen bonds. Ligloops are not involved, as covalent bonds are excluded.
Reduced Graph Representation of Protein Structure
Another concept we introduce is a reduced graph treatment of the protein. Broadly speaking, two methods dominate the computational treatment of protein structures: (1) treating proteins as a set of atoms and (2) treating proteins as a set of amino acid residues. A scheme better suited to our network approach is an intermediate approach in which a protein structure is treated as a collection of small groups of atoms. We split each amino acid into a side chain and a backbone amide part and treat each as a single network node. Other investigators have mentioned combining protein atoms into groups in their work.(37) The reduced graph concept has also been used in small-molecule chemical similarity analysis.(38)
In our implementation, a reduced graph is conveniently created by separating side chain from main chain, with Cα being part of the side chain. This leaves the amide backbone as separate groups. Proline residues are handled as a special case—the main chain group is just C=O, and N is part of the side chain. In our reduced graph representation of structure, the ligand is counted as a single node. When discussing the length of any network element, we are referring to the reduced graph node path length, that is, the number of reduced graph nodes that make up the path.
Network Counting
Our method identifies network paths in binding sites within a cutoff distance of 10 Å around any ligand atom. We found that larger scoop distances did not have a major effect on results, though they did lead to significantly longer run times. We ignore all water contacts involving Rank scores < 2.0. Breadth First searching is done to find all ligcycles and ligloops. For ligcycles, all network paths with a reduced graph node length of three or greater are counted, while for ligloops, we consider network paths with a reduced graph node length of two or greater. Importantly, for both ligloops and ligcycles, not just shortest paths but all short paths are counted. That is, we check for, and include, multiple paths through the same set of protein groups when they share multiple noncovalent contacts. For ligpaths, all network paths with a reduced graph node length of three or greater are counted. We ignore ligpaths that have already been accounted for in ligcycles and ligloops and only count the unique component of each network ligpath. Furthermore, we require each ligpath to include at least two noncovalent contacts and exclude paths that have long chains of covalent bonds. The maximum number of continuous covalent bonds allowed in a ligpath was set to three in order to (1) prevent redundant paths around rings in side chains and (2) maintain an even balance between covalent and noncovalent contacts in the network. For privileged hydrogen bonding pairs, nearly all network paths have a reduced graph node length of three. Additionally, the ligand path in privileged hydrogen bonding pairs can be up to five ligand atoms. In the pure hydrogen bonding network, all PLPhb terms consist of one ligand atom and have a reduced graph node length of three.
For a given favorable protein–ligand contact A···B, a network sum, nsAB, is calculated, which is a weighted and normalized sum of the number of network paths that include the contact:
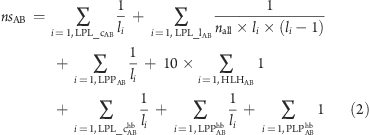 |
The weighted sum is over all ligcycles (LPL_c), ligloops (LPL_l), ligpaths (LPP), and privileged hydrogen bond pairs (HLH) from the total network and all ligcycles (LPL_chb), ligpaths (LPPhb), and PLPhb from the pure hydrogen bonding network. In eq 2, li denotes the length of the short path, i.e., the number of nodes in the reduced graph path, and leads to higher weighting being assigned to shorter network paths. Since the total number of ligloops in a complex is much larger and increases more steeply with ligand size than ligcycles and ligpaths, we scale down the contribution from ligloops more drastically, normalizing also by the total number of protein–ligand contacts, nall. The contribution from the privileged hydrogen bond pairs is multiplied by an empirical factor so that the values are closer in magnitude to those of the other network elements.
Scoring Function: Training and Test Sets
Optimization of an empirical scoring function requires high-quality biostructure information as training input. Several sets of protein–ligand complexes were selected from the Roche structure collection and the Protein Data Bank (PDB), fulfilling the quality criteria listed in Table 3. The majority of these criteria involve local properties of the contact atoms in the binding site, which, in contrast to the often used global Rfree, are more directly relevant for the optimization of a scoring function. Most of the properties of Table 3 are automatically parsed or computed from the PDB file during upload into our biostructure repository, Proasis2/3,(31) and X-ray structures fulfilling the thresholds can be easily retrieved from this database with SQL queries. The calculation of two properties requires further comment. First, ligand strain energy in the X-ray complex was estimated by the energy difference of two ligand minimizations: (1) using a harmonic, 0.2-Å-wide flat-bottomed potential on all atoms and (2) applying no constraints. This estimate of the strain energy with respect to the next local energy minimum is a useful quantity for identifying highly strained conformations which often arise from wrongly refined ligand atoms.(39) An empirical threshold of 8 kcal/mol was used to filter out problematic structures. Calculations were performed with the MMFF94s force field and a dielectric constant of 8.0, as implemented in the Macromodel program.(40) Second, for all protein–ligand contact atoms, we computed real space correlation coefficients (RSCC), which are a measure of how well the fitted X-ray model explains the observed electron density. To this end, electron density from deposited structure factors had to be generated and the experimental map correlated with the calculated electron density from the model. This was performed with different modules from the CCP4 software package.(41) To ensure that all relevant atoms were well-defined by the electron density, structures in which any protein–ligand contact atom had an RSCC < 0.7 were filtered out.
Table 3. Quality Criteria for the Selection of Training Set Structures I–IIIa.
| - X-ray structure with crystallographic resolution ≤2.5 Å |
| - successful match of ligand topology (best Proasis2 ligand quality) |
| - only noncovalent binding between ligand and protein* |
| - no symmetry contacts* |
| - no alternative conformations* |
| - no clashes* |
| - no missing atoms* |
| - no broken residues* |
| - minimum occupancy = 1.0* |
| - minimum real space correlation coefficient ≥ 0.7* |
| - ligand strain energy ≤ 8 kcal/mol |
| - ligands from medicinal chemistry programs |
| - binding data available (Ki, Kd, IC50) and measured with same assay |
Points marked with ∗ apply only to protein–ligand contact atoms within a distance threshold of 5.0 Å.
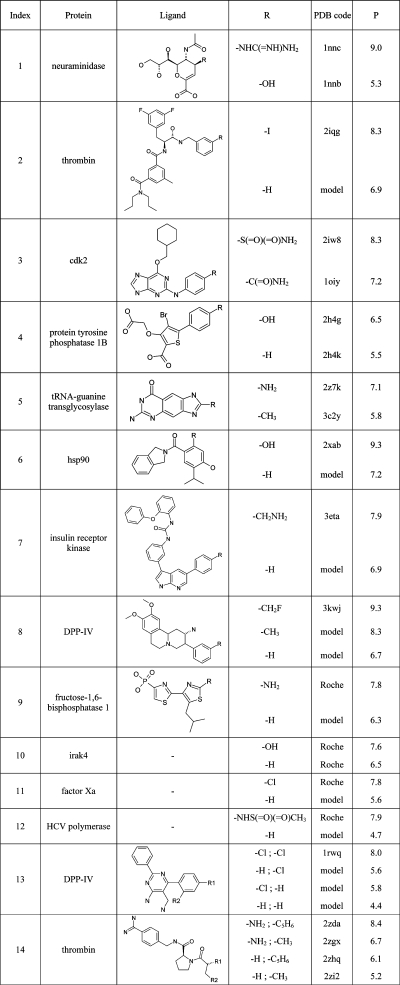
Using the criteria of Table 3, several training sets from past or current medicinal chemistry programs were compiled (Table 4). Since biostructure had to be of high quality and binding affinity had to be measured in a consistent way, we finally had to resort to mostly internal structures. Data set IV is special in that it contains pairs of compounds in which a small structural change in the ligand leads to a drastic change in binding affinity (Table 5). For these “activity cliffs”, sometimes only the X-ray structure of the bigger ligand of the SAR pair was available. We then built a model of the smaller analogue by removing the differing atom. Training set IV was complemented with two examples of nonadditive SAR (four protein–ligand complexes from DPP-IV(9) and thrombin11,12 each). Since we also use modeled structures, the quality criteria of Table 3 do not apply to this set. The neuraminidase data set (Figure S1, Supporting Information) and the public subset of IV (i.e., without structures 9−12 of Table 5) are freely available from http://www.desertsci.com.
Table 4. Summary of Affinity Training Setsa.
| Protein target | No. of complexes | pIC50 range | |
|---|---|---|---|
| I | Neuraminidase | 31 | 6.7–10.0 |
| II | PDE10 | 46 | 5.7-10.0 |
| III | IRAK4 | 10 | 5.1-8.3 |
| BTK | 9 | 4.2-7.9 | |
| HCV polymerase | 9 | 3.9-7.6 | |
| HIV protease | 8 | 6.9-9.7 | |
| DPP-IV | 2 | 6.4-8.0 | |
| PKACA | 2 | 5.5-5.7 | |
| LCK | 2 | 7.7-9.3 | |
| IV | see Table 5 | ||
Protein target abbreviations are PDE10, phosphodiesterase 10; IRAK4, interleukin-1 receptor-associated kinase 4; BTK, Bruton’s tyrosine kinase; DPP-IV, dipeptidyl peptidase 4; PKACA, cAMP dependent protein kinase; LCK, lymphocyte-specific protein kinase.
Table 5. Affinity Training Set IV Containing Pairs with SAR Cliffs (1–12) and Cooperativity Sets (13, 14)a.
Model indicates a model structure which was built using the X-ray complex structure of the analogue with the same index as the template. P denotes the potency values of the compounds and can be pIC50, pKi, or pKd.
Scoring functions derived only from X-ray complex structures will not yield reliable estimates of terms representing unfavorable interactions, as such structures typically show a good fit of the ligand to the protein active site.(42) To provide additional negative data with a good sampling of unfavorable interactions, we also compiled a pose training set, based on 122 X-ray complex structures, with four conformationally distinct binding modes created for each complex. The respective reference complex structures all fulfill the stringent quality criteria of Table 3 and are composed of 93 complexes from the Roche collection and 29 complexes from the PDB (Table S2, Supporting Information). The four docking poses, generated by Glide,(43) differ by a root mean-square deviation (RMSD) ≥ 1.5 Å or have a maximum atomic displacement ≥2.0 Å from each other. All water molecules were removed before docking.
As an external test, we use the HIV protease, thrombin, trypsin, and factor Xa subsets compiled by Englebienne and Moitessier(44) and compare our predicted rank order with the published results of other scoring functions. We excluded the MMP-3/8 data from the list of subsets, as we do not have metalloenzymes in our training collection. As an additional test, we compare the virtual screening performance of our scoring function for eight targets of the Directory of Useful Decoys (DUD) data set(45) with the Glide/SP scoring function.(43) To this end, the top-ranked Glide docking poses were postprocessed with our scoring function. Receiver operating characteristic (ROC) enrichments(46) for several early false positive rates were calculated and used to compare performance.
Optimization of the Scoring Function
In our scoring function approach, we approximate the binding free energy by sums of contributions from individual protein–ligand interactions and network contributions for those interactions that are involved in networks. ScorpionScore, SScorpion, is expressed as
where the summation is over all protein–ligand contact pairs AB which are associated with interaction type i. Coefficients for pairwise interaction (pi) and network (ni) contributions were determined with the semiautomatic Genetic algorithm optimization detailed below, and nsAB denotes the network sum from eq 2. Using scoring function performance as a criterion, we evaluated whether a network contribution should be added for all networked contacts or only a subset of them. Best results were obtained by awarding the additional score ni × nsAB only to protein–ligand interactions that are part of strong networks. This was implemented by defining interaction type-specific thresholds nthres,i and setting network coefficients ni to 0 if the network sums nsAB were below nthres,i. Including a network contribution for only a subset of contacts further ensured that our network terms would not simply correlate with the total number of contacts.
After calculating favorable and unfavorable protein–ligand interactions and corresponding network terms for the training sets, we filtered and clustered these descriptors to remove weakly populated (<10%) as well as highly correlated (Spearman rank correlation ρ > 0.8) terms from the set. For the residual descriptors, initial scoring function models were optimized by a multiobjective genetic algorithm.(47) We maximized the Spearman rank correlation coefficient for affinity data sets I–III and minimized deviations in absolute affinity differences for training set IV in parallel, with each data set being weighted by 25%. The population size was set to 400 chromosomes and the mutation rate to 1.8%; crossover and reproduction were carried out according to roulette wheel selection while ensuring that the highest scoring chromosome was kept in the population (“elitism”).(48) Internal score weights for the training sets were recalculated each generation until the termination criterion of 10 generations without a new highest scoring chromosome was fulfilled. Performing 100 parallel optimizations of the coefficients, a statistical analysis of the pooled set of highest scoring chromosomes was conducted, removing descriptors showing high variance among the individual models from the set. Three stages of iterative refinement with decreasing maximum descriptor variance were performed, yielding a well-defined set of descriptor coefficients for SScorpion. The obtained descriptors were kept constant while adding further descriptors badly determined in these training sets. To this end, we also optimized a separate scoring function on the docking poses only, SScorpion,pose, by maximizing the fraction of X-ray determined binding modes predicted correctly (within an RMSD ≤ 2.0 Å) in the set of decoys. Coefficients for unfavorable interactions were indeed generally much better determined in this training set and manually adjusted values fed into SScorpion.
Visualization
A central goal of this work has been to identify ways of quickly and easily visualizing the details of ligand binding for the widest possible range of protein complexes. The Proasis3 system, which provides easy access to all PDB structures, public domain and in-house, and to curated ligand data, has been linked with the software tools for calculating nonbonded interactions and subgraph network descriptors. Thus, the system is ideally suited to display interactions, networks, and derived parameters in the context of protein structures. PyMol scripts,(49) which are created on-the-fly, highlight the ligand and binding site region, color-code all of the different classifications of favorable and unfavorable close contacts, show water molecules colored and labeled according to the water Rank score, and show additional ligand atom objects enabling the highlighting of atom-based Scorpion scores. We also enable the visualization of network paths, separated by the ligand atom. These network path views are often complex and difficult to interpret, and so atom-based representations were generated. Calculation of all interactions in a binding site is on the order of 0.5 s per complex, while the computation of network descriptors is roughly a factor 10 more demanding.
Results and Discussion
Interaction Definitions and Water Scores
Any structure-based design work relies heavily on visual analysis by means of simple, intuitive models of interactions and their preferred geometric arrangements. While hydrogen bonds and van der Waals contacts belong to the standard repertoire of graphical tools, evidence from SAR studies, crystal structure database statistics, and model calculations suggest that there exist other interaction types with a clear net stabilizing effect if their geometry is within certain boundaries.(4) Examples for more recently characterized favorable recognition motifs are halogen bonding5,6 or orthogonal multipolar interactions.(7) On the basis of CSD distributions of interaction distances and angles, descriptions in published force fields,(50) as well as basic rules for electrostatic interactions, we have compiled geometric thresholds for 10 favorable and eight unfavorable interaction types (Tables 1 and 2).
Water molecules are an important component in receptor binding sites, and their degree of coordination ranges from weakly interacting on the surface of proteins to tightly bound in buried cavities. Buried water molecules often form multiple hydrogen bonds with the protein and are hard to displace, so for purposes of drug design, they are effectively part of the protein. We assess the coordination of structural water to the protein and neighboring water molecules using a geometric scoring scheme similar to the Rank score developed by Kellogg and co-workers.(35) This simple geometric assessment has served as a useful metric, for example when characterizing water molecules in the binding site of PDE10.(4)
User-friendly visualization of the relevant protein–ligand contacts is of great help in quickly identifying strongly interacting ligand atoms and mismatched atom pairs. Figure 2 shows a typical binding site view illustrating different types of protein–ligand contacts, both direct and water-mediated. In the displayed thrombin–inhibitor complex, a strong halogen bond between the ligand chlorine atom and the backbone carbonyl oxygen is detected (1) which might explain the 8-fold drop in thrombin activity when replacing the Cl with an H atom.(51) Further nonstandard interactions that are highlighted include the π-interaction between the benzamidine phenyl and the protein backbone at the rim of the S1 pocket (2) or the orthogonal dipolar interaction of a bridging water molecule with the ligand carbonyl group (3). In this complex, an unfavorable contact is detected between two carbonyl dipoles that point at each other (4) with a short oxygen–oxygen contact (3.1 Å). This is only slightly longer than the adjacent hydrogen bond of the ligand carbonyl (3.0 Å), and such secondary electrostatic interactions have been shown to be important for the energetics of hydrogen-bonded systems.8,52,53 Structural water molecules are color-coded according to the geometric Rank score ranging from green (deemed easily replaceable) to orange (tighter binding). It reveals a poorly bound water deeply buried in the S1 pocket next to the ligand amidino group (5). This water molecule is indeed replaceable, for example by the chlorine substituent of aromatic moieties binding in the S1 pocket, which are hallmarks of second-generation serine protease inhibitors involved in the coagulation cascade.54,55
Figure 2.
Binding site visualization including favorable and unfavorable protein–ligand interactions as well as color-coded water Rank scores in the thrombin–inhibitor complex (PDB code 2cf8). The number labels refer to the description in the text.
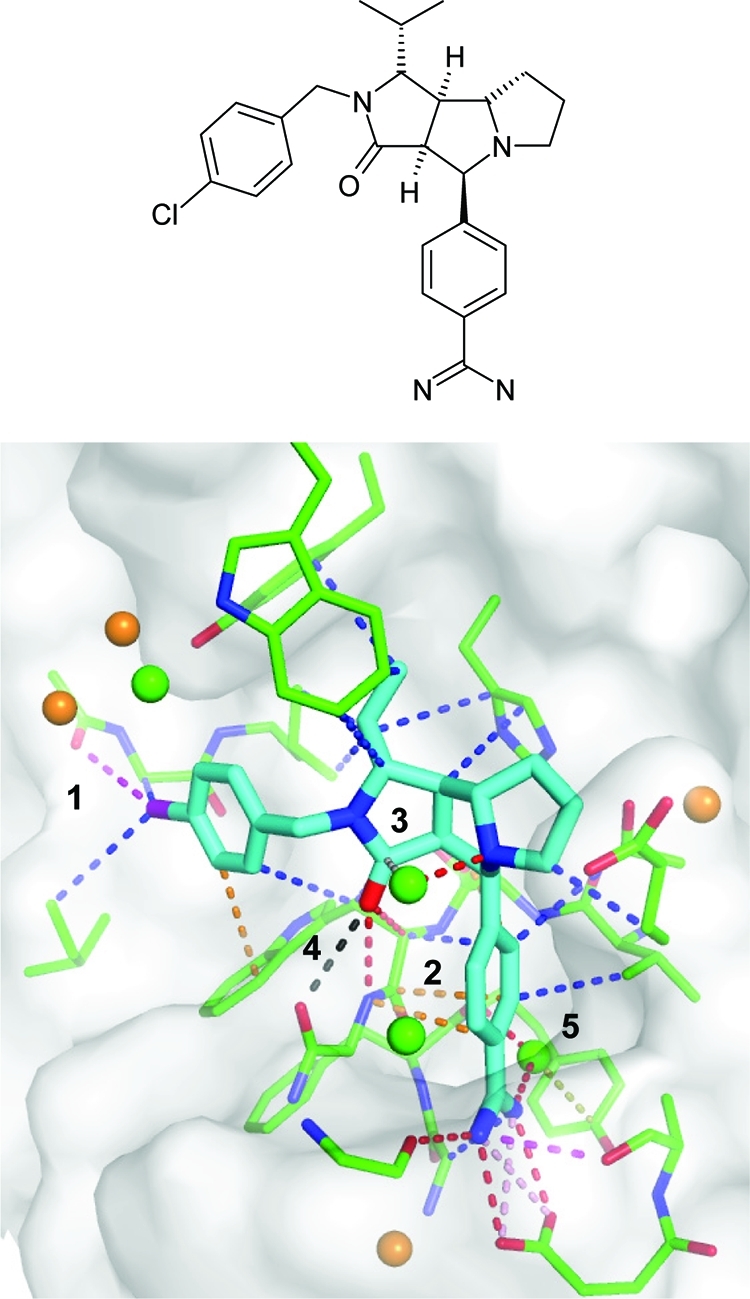
Some protein–ligand contacts are not inherently repulsive but are still strongly avoided because they are associated with desolvation penalties. Database surveys and calculations on model systems suggest that unsatisfied hydrogen bond donors and, to a smaller extent, acceptors in a hydrophobic environment are energetically costly.56,57 We detect such situations by placing virtual water molecules at the positions of apolar atoms in close contact with a strong hydrogen bond donor or acceptor. If the virtual water molecule could form a good hydrogen bond, the respective apolar–polar contact is flagged as unfavorable. Figure 3 shows the example of an aminopyrrolidine inhibitor binding to factor Xa, in which the ligand with a difluoro-ethylamino substituent has a Ki of only 1.1 μM. Most likely, this is due to a poor polar–apolar contact of the amine substituent with the side chain of Gln 192. The analogue with a difluoro-ethoxy substituent, exposing a weak hydrogen bond acceptor to the apolar protein region, binds considerably more strongly with a Ki of 21 nM.(58)
Figure 3.
Illustration of an unfavorable protein–ligand contact with a potential desolvation penalty in factor Xa. With R = NHCH2CHF2 the Ki against factor Xa is 1100 nM, while with R = OCH2CHF2 the Ki is 21 nM. The model is built on the basis of the X-ray structure of the close analogue R = OCH3 by replacing O with NH and H with CHF2, respectively (PDB code 2vvc).(58)
Small World Interaction Network and Scoring Function
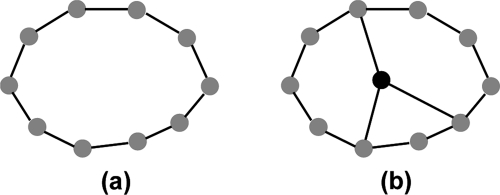
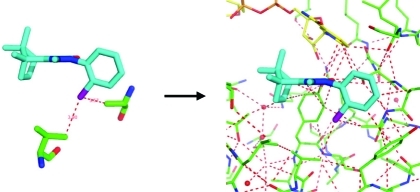
Molecular graphics displays of noncovalent contacts in binding sites suggest the presence of a network of interactions (Figure 2). Furthermore, the observation that binding sites are comprised of residues from very different segments of the protein chain, and that ligand binding typically involves contacts with residues that are separate in space and would not otherwise be functionally related, lead us to consider that the interaction network should be modeled as a small world network. The small world network phenomenon, and how it relates to ligand binding, is illustrated schematically in Figure 4. It shows how the addition of just one node to a network, and a few extra edges, can have a significant impact on the shortest path lengths between many pairs of nodes. Note that in Figure 4 the physical arrangement of the gray nodes ensures that a central node will be in close proximity to multiple other nodes and be optimally placed to have the greatest impact on the average shortest path length. This arrangement is analogous to the way that ligands fit into binding site cavities. According to our small world network model, ligand binding results in an increase in the number of favorable interactions, involving complementary functionality between guest and host, thereby leading to a tighter, more robust network.
Figure 4.
Network diagrams illustrating how ligand binding fits the small world network paradigm. Gray nodes denote protein binding site groups. The black node represents the ligand, and an edge represents a noncovalent favorable or covalent interaction. (a) Schematic representation of an unliganded binding site and (b) an occupied binding site. The network diagrams show how the addition of just one new node and a few extra edges leads to shorter path lengths between many pairs of nodes in the network. The presence of individual nodes with connections that lead to short paths between many pairs of nodes is a key feature of small world networks.
If we restrict ourselves to visual analysis, the network analogy remains only a superficial one. It may be stimulating to discuss interactions in small world network terminology, but the complexity of the systems will make it hard to make comparisons and to derive general insights. We were interested in investigating how protein–ligand interactions could be computationally described as networks and whether we could, from such a description, derive metrics to quantify cooperative aspects of molecular recognition. In this way, we could go beyond the pairwise-additive approach of treating interactions. However, we did not aim at developing a traditional scoring function best suited as a stand-alone “black box” computational tool but at deriving parameters that could again be visualized in a 3D model. In particular, we were interested in whether a network approach enables us to better understand how small changes in a ligand can sometimes provide large contributions to binding affinity. To arrive at this goal, we first created a consistent network description of protein–ligand complexes and then experimented with multiple derived parameters. We then used these parameters in conjunction with the interaction types introduced above to derive a classical empirical scoring function. The scoring function mainly serves the purpose of calibrating network terms relative to standard pairwise interactions. In the following, we introduce the network model, then describe the principles underpinning our new scoring function, and subsequently illustrate its utility, and the benefits of our network approach, by means of multiple examples. More details on the implementation can be found in the Methods section.
Any network model consists of nodes and edges. In our model, nodes are ligand atoms, protein groups (groups are backbone amides and side chains; that is, the protein is represented as a reduced graph), waters, metals, ions, and other HET molecules, while edges are favorable noncovalent contacts and covalent bonds. Initially, we explored the standard concepts of network theory, testing shortest-paths algorithms and computed properties such as clustering coefficients, betweenness centrality, and degree centrality.(59) However, we soon discovered that these global properties were overly sensitive to specific individual close contacts. It is possible that this overall approach is not well suited to our interaction networks simply because of the tight geometric constraints associated with the maximum number of interactions any atom can make.
We focused then on subgraph network descriptors extending the concept of protein–ligand (PL) interactions to protein ligand network elements, such as illustrated in Figure 5, and found them more useful than global descriptors. All networks involve at least one ligand and protein atom and are further classified depending on the atoms at which the network path begins and ends (LPL, LPP, PLP). To account for the importance of hydrogen bonding cooperativity, we introduce two additional network path types. First, we specifically consider an arrangement of correlated hydrogen bonds (HLH, Figure 5b). Second, we separately account for pure hydrogen bonding networks involving only donor and acceptor atoms and containing no covalent bonds or non-hydrogen bonding interactions (PLPhb, Figure 5c). Upper limits on the size of the network paths were imposed to ensure that the results are not biased toward the size of the ligand or the extent of the network within the protein alone. We also explored purely apolar networks, consisting of π–π and van der Waals contacts, and involving atoms which do not form hydrogen bonds. Although very promising for specific targets, apolar networks did not lead to improvements across larger data sets. This was found to be due to the fact that the descriptors were too heavily biased toward the network within the protein, and less dependent on the protein–ligand contacts than other descriptors.
Figure 5.
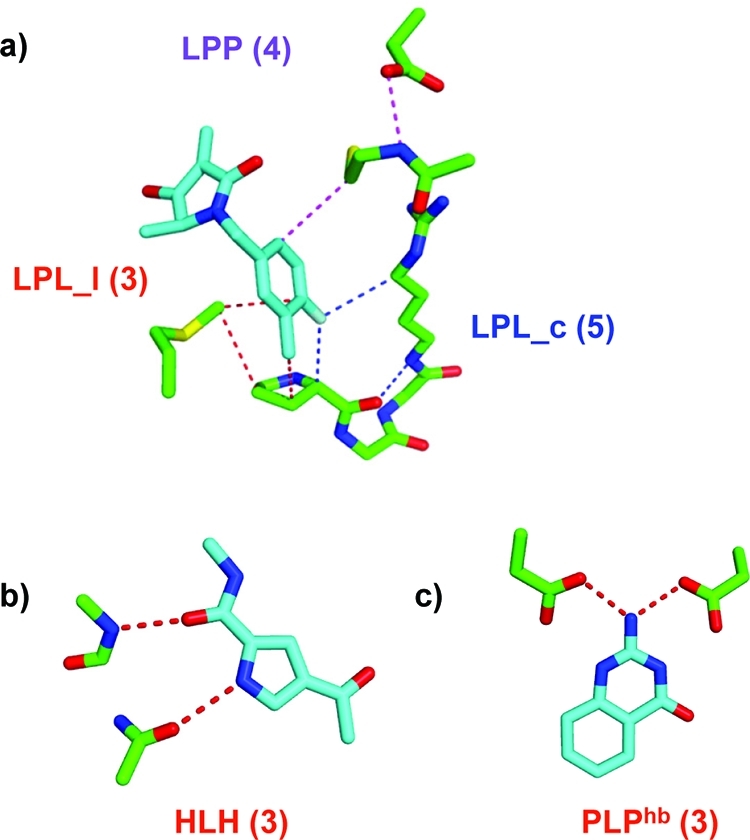
Illustration of subgraph network descriptors used in this study. The number in parentheses indicates the number of nodes in the network. Ligand atoms count as one network node, and protein residues are treated as a reduced graph with backbone amide and side chain groups counting as one node, each. (a) LPL_c is a ligand–protein–ligand network path which begins and ends at the same atom (ligcycle). LPL_l is a ligand–protein–ligand network path which begins and ends at different ligand atoms (ligloop). LPP is a ligand–protein–protein path (ligpath). (b) HLH is a privileged hydrogen bonding network element in which pairs of hydrogen bonds are adjacent to each other, and (c) PLPhb is a representative of a pure hydrogen bonding network element in which the ligand atom bridges two protein groups by hydrogen bonds. See Figure 1 and the Methods section for a complete list of network elements.
To identify a robust network description and optimal model parameters from the many possibilities to count and weight individual network elements, we generate a scoring function against four carefully selected training sets for the ranking of binding affinities (Tables 4 and 5). In contrast to traditional empirical scoring functions, which are a sum of interaction terms and additional factors to account for ligand flexibility etc., the scores we calculate are sums of protein–ligand interaction and network terms, in which the network terms are derived from network paths that contain one or more ligand atoms. Since we were not able to build a robust model in which every protein–ligand contact is assigned a network score, we opted for an approach in which only the contributions from strongly networked interactions are included. Protein–ligand contacts that are part of strong networks thus receive both an interaction score and an additional network score contribution. It needs to be stressed again that the scoring function is primarily derived to learn about the relative importance of network terms for high affinity ligands rather than to provide accurate predictions of binding affinity in all complexes.
A training set for an empirical scoring function must have high quality in both crystallographic structure data and in binding affinity data to be useful. Unfortunately, published data sets that have previously been employed in the optimization of other scoring functions37,60,61 are of limited value, as they fail in at least one of the following quality criteria: good X-ray structure quality with unambiguous identification of protein–ligand contacts, ligand space relevant for medicinal chemistry, and consistent binding data. Often, affinity data from a mix of different assays and proteins are used, which necessarily introduces a large amount of noise into the training set. Since only few public domain complex structures exist that fulfill all three quality criteria, we had to complement public with proprietary X-ray structures and binding affinities. Using a set of very stringent criteria (Table 3), which focus on local properties of the binding site and go far beyond the often used pure X-ray resolution criterion, we selected training sets I–III. Of particular interest to us is training set IV, which contains “activity cliffs”, i.e., pairs of compounds in which a small structural change in the ligand, for example an additional heteroatom, leads to a drastic change in affinity. Training our scoring function with such a “difficult” data set is another unique aspect of our approach. It is important to note that we optimize against a combination of training sets, in which for each set ligand affinities were determined with the same assay and for the same protein.
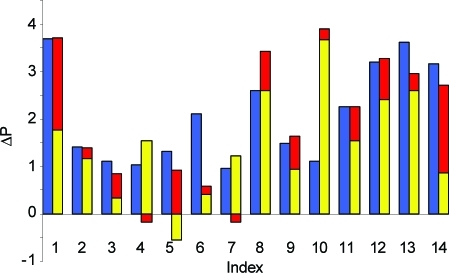
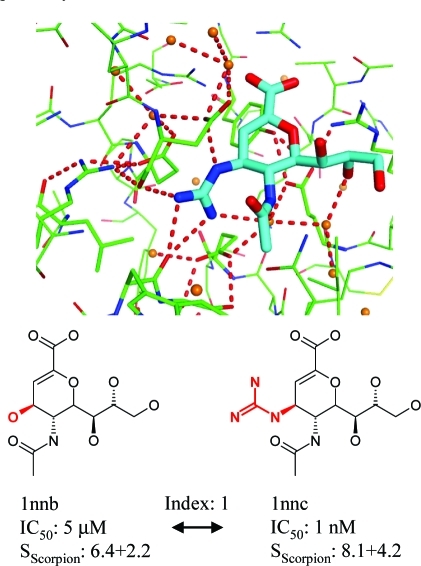
For the hydrogen bond, van der Waals, and π–π interactions, we could identify network terms with reasonable statistical significance, i.e., low variance within the set of 100 genetic algorithm models. As can be seen from eq 3, each interaction of these types first contributes the respective pairwise component to the total score. If the sum of the respective network terms (eq 2) is above its threshold, the score is further augmented by a network contribution, which is the product of the network coefficient and the network sum. Robust statistics for unfavorable contacts cannot be extracted from experimental complex structures alone, as these typically show a good protein–ligand fit. For this reason, we also optimized a scoring function for pose prediction (Tables S3 and S4, Supporting Information) and reused manually adjusted parameters for most unfavorable interaction types from there. We further ensured that the final terms in the scoring function do not correlate with the size of the ligand. The scoring function optimization for ranking ligand affinities yielded parameters as detailed in Table 6, and the performance of SScorpion for the training sets is displayed in Table 7. For data sets I–III, we use Spearman’s rank correlation coefficient, ρ, a nonparametric measure of the correlation between ranked lists of experimental binding affinities and predicted scores (ρ of ±1 indicates perfect ordering, and 0 indicates no correlation), while for the activity cliff data set IV, we are interested in differences in absolute binding free energies. Comparing the results for SScorpion with an optimization of pairwise interactions only, and considering here the same number of descriptors (13) in the final model, shows a clearly improved performance for the neuraminidase and activity cliff data sets when network terms are included. In contrast, no improvement is observed for the PDE10 and diverse data sets. Some correlation of binding affinity with ligand size is often found in the SAR of chemical series active against a given protein, especially when mostly hydrophobic binding sites are targeted, and it is difficult to avoid in training sets. Interestingly, this is pronounced for data sets II and III, where the correlation with the number of non-hydrogen ligand atoms is relatively high (ρ = 0.55–0.60), and for which we do not see an additional benefit in adding network terms. Apparently, the heavy atom count baseline is so high that it is hard to improve by means of additional terms. More detailed results for the activity cliff set are shown in Figures 6 and 7. An example for a steep SAR is found for neuraminidase where the replacement of a hydroxyl by a guanidino substituent improves the IC50 5000 fold, yielding the influenza drug Zanamivir. This gain in binding affinity is nicely reproduced in the Scorpion scores, and the interaction diagram shows that the guanidino group not only forms favorable interactions with contact atoms in the direct environment but also reinforces the network of the entire protein–ligand complex. Accordingly, both non-network and network contributions to the Scorpion score are increased.
Table 6. Optimized Scoring Function Parameters (SScorpion), See Also eq 3.
| interaction type (i) | pairwise interaction coefficient (pi) | network coefficient (ni) | network threshold (nthres,i) |
|---|---|---|---|
| hydrogen bond | 0.47 | 0.13 | 1 |
| vdW | 0.52 | 0.39 | 4 |
| π–π | 0.19 | 0.93 | 4 |
| cation-dipole | 0.29 | ||
| cation-π | 0.61 | ||
| halogen bond | 0.65 | ||
| unf_hydrogen bond | –0.39 | ||
| unf_ionic | –1.50 | ||
| clash_apolar | –1.15 | ||
| clash_polar | –1.15 | ||
| desolv_donor | –0.90 |
Table 7. Performance of Scorpion Scoring Function in Ranking Ligand Affinities of the Training Sets after Optimization with (SScorpion) and without (Spairwise) Network Terms, and in Comparison with Predictions Using the Number of Ligand Heavy Atoms Onlya.
| Neuraminidase (I) | PDE10 (II) | Diverse (III) | Activity cliffs (IV) | |
|---|---|---|---|---|
| ρ | ρ | ρ | ΔP | |
| SScorpion | 0.61 | 0.51 | 0.60 | 0.52 (0.48) |
| Spairwise | 0.49 | 0.54 | 0.54 | 0.74 (0.71) |
| no. of heavy atoms | 0.22 | 0.55 | 0.60 | 1.06 (0.92) |
For data sets I–III, Spearman rank correlation coefficients are given (higher is better). For data set IV, the average absolute error over all pair comparisons is shown (lower is better), where P can be pIC50, pKi, or pKd. Numbers in parentheses are the results for the publicly available subset of IV, i.e., without structures 9−12 of Table 5.
Figure 6.
Comparison of experimental (blue) vs predicted (red, network contribution; yellow, non-network contribution) logarithmic affinity differences ΔP for the activity cliff training set IV (Table 5). Predicted affinity differences are the sum of the respective yellow and red bars.
Figure 7.
Binding affinities and Scorpion scores for the neuraminidase pair (index 1 in data set IV, PDB codes 1nnb, 1nnc), differing in a hydroxyl vs guanidino substituent. Top: hydrogen bonding network up to path length 4 in which the guanidino moiety is involved.
The performance of scoring functions in predicting binding affinities is often assessed by correlating computed and experimental rank order of a large set of diverse proteins and ligands.62,63 Such comparisons are often misleading, as the noise introduced by mixing binding constants from different assays and proteins is substantial. Unfortunately, validation sets with both high quality structural data and consistent binding affinity data are not available. To obtain some standard figures of merit, we compare ScorpionScore with the results of a comparative evaluation by Englebienne and Moitessier(44) on a more focused list of HIV protease, thrombin, trypsin, and factor Xa subsets. The results in Table S5 (Supporting Information) show that ScorpionScore ranks among the best of the tested scoring functions with a clear separation from molecular weight as a simple descriptor. Performance for the trypsin set is rather low, also for other scoring functions, which could be due to the questionable quality of these structures. Only one (1f0u) out of 13 complexes passes our quality criteria of Table 3. Also, the structure 1v2k has an engineered binding site, which effectively looks more like factor Xa than trypsin. Given the quality issues with publicly available test sets and additional factors that affect binding affinity but are not captured here, such as for example different amounts of ligand strain,(64) we do not attach too much weight to this scoring function comparison. Our focus is on identifying protein–ligand interaction networks that promote tight binding.
The DUD data set is a popular reference for benchmarking virtual screening. In Table S6 (Supporting Information), we compare the performance of SScorpion with Glide/SP scoring using ROC enrichments at several early false positive rates (0.5%, 1%, and 2%), which are useful measures to assess the early recovery of actives. We selected Glide/SP as a benchmark because it was one of the two best performing approaches in a previous virtual screening comparison of the DUD set.(65) For the eight DUD targets that we investigated, we find ROC enrichments that are superior for three targets (PR, PDGFrb, P38) and inferior for another three targets (FGFr1, FXa, NA). Although we have not optimized against any virtual screening data set, it is encouraging that our scoring function is able to identify considerably more actives than the Glide/SP reference for a number of different proteins.
Examples of Complexes with High Network Contribution
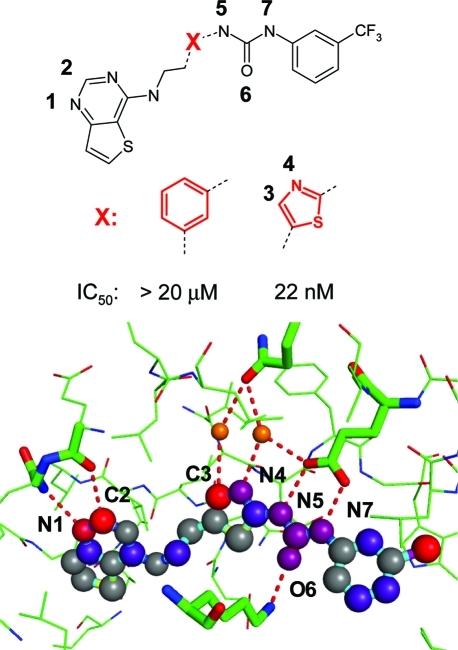
To quickly grasp the relative interaction strengths of ligand atoms in a binding site, we have mapped score contributions onto atoms using a blue to red color scale. Figure 8 illustrates this visualization together with the protein–ligand hydrogen bond network for an Aurora kinase inhibitor series from Sunesis.(66) All labeled ligand atoms have a network contribution to their score, indicating that these are involved in strong interaction networks. Two features of our approach are noteworthy, as they show the importance of comprehensive interaction definitions for the topology of the network. First, two polarized CH groups of the inhibitor form weak hydrogen bonds,(8) one between thienopyrimidine C2 to a hinge carbonyl oxygen and one between the thiazole C3 to a bridging water molecule. Second, our water classification scheme identifies two critical water molecules involved in bridging interactions with Glu and Gln side chains. The network of hydrogen bond interactions around the thiazole unit is likely the reason for the large drop in binding affinity when replacing this motif with a phenyl linker. Also, the urea linker receives extra network stabilization from the two HLH motifs (Glu–carboxylate···ligand urea···amino–Lys), which is reasonable, as the strong urea dipole is perfectly aligned between the two charges. It is not surprising that replacing the urea with an amide or acetamide significantly reduced activity, as did N-methylation.
Figure 8.
Hydrogen bond interaction network of Aurora A kinase inhibitor complex (PDB code 3d15, has −Cl instead of the −CF3 group).(66) Atom-based contributions to the Scorpion scores are translated into a blue to red color scheme, with red indicating interaction hot spots (score contribution > 1.5). Gray indicates no score contribution. Total scores (network contributions) for the atoms with numbers are N1, 1.1 (0.2); C2, 1.6 (0.2); C3, 1.7 (0.3); N4, 0.8 (0.3); N5, 0.9 (0.4); O6, 0.7 (0.3); N7, 0.8 (0.3).
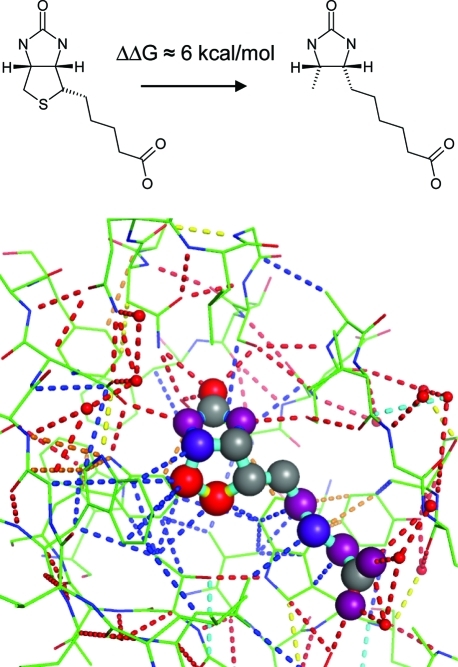
The very strong association of biotin to avidin (Ka ≅ 1015 M–1)(67) and streptavidin (Ka ≅ 1013 M–1)(68) is difficult to rationalize with empirically determined scoring functions and represents an outlier in binding affinity surveys.69,70 The origin of this strong binding is not fully clear; recent mutagenesis(71) and computational(72) studies suggest that hydrogen bond cooperativity of the urea motif plays a major role. Also, reduced hydrogen/deuterium exchange is observed experimentally when biotin binds to streptavidin, suggesting that existing noncovalent interactions within the streptavidin protein are reinforced.(19) As illustrated in Figure 9, we observe for this complex a very dense network of favorable interactions and obtain large score contributions for several ligand atoms. In particular, the sulfur atom stands out with an atom score of 4.9 and an unusually large network contribution of 3.4. While engaging in three vdW interactions with Trp79, Thr90, and Trp92, the most striking feature is the strong network of interactions in which these residues are engaged, connecting distant parts of the protein and ligand with the sulfur atom. In line with the special role of the sulfur atom is the observation that its removal leads to a dramatic loss of binding free energy of approximately 6 kcal/mol, i.e., a more than 104-fold reduction in Ka.(67) Although we do see cooperative hydrogen bonding interactions for the urea motif, our results suggest that the origin of the strong binding affinity lies predominantly in interactions of the tetrahydrothiophene ring.
Figure 9.
Interaction network diagrams, color-coded by interaction type, of biotin bound to streptavidin (PDB code 1stp). Atom-based contributions to the Scorpion scores suggest that the carbonyl oxygen (1.7), sulfur (4.9), and adjacent carbon (2.1) atoms of biotin are interaction hot spots (red ligand atom spheres) with streptavidin.
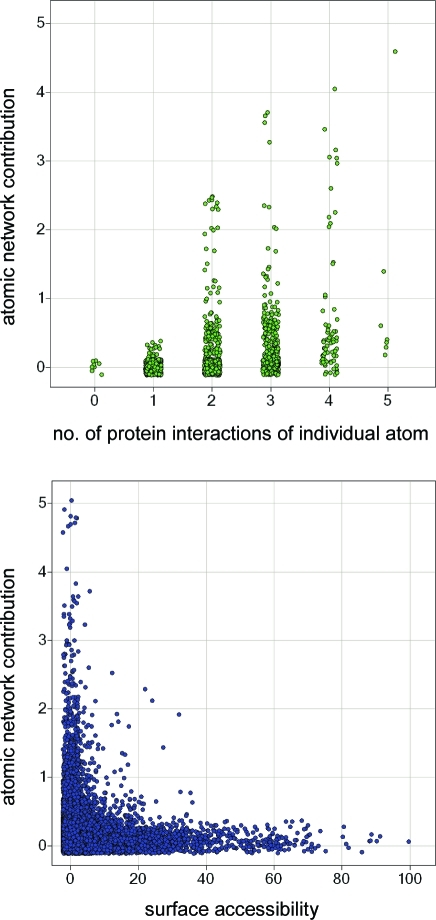
To identify additional examples with strong interaction networks and better understand which molecular environments lead to high network contributions, we calculated atomic Scorpion scores for all X-ray structures with protein–ligand contacts as stored in our Proasis2 database (12 139 complexes). Statistics plots of these results reveal that network contributions show a wide range for a given number of protein interactions of an individual atom (Figure 10, top) and that significant network scores can also be achieved for partially solvent-exposed ligand atoms (Figure 10, bottom). There is a weak correlation between the atomic network contribution and the number of protein contacts as well as surface accessibility. For example, the median network scores for atoms with zero surface accessibility are 0.15, 0.22, and 0.30 for one, two, and three contacts, respectively.
Figure 10.
Atom-based Scorpion scores were calculated for a subset of 12 139 protein–ligand complex structures taken from Proasis2. For this subset, the top graph shows the distribution of network contributions vs the number of protein interactions of individual fluorine atoms (1932 data points). The bottom graph shows the distribution of network contributions vs the solvent surface accessibility of individual nitrogen atoms (21 273 data points). Some jitter is applied to the visualizations to better differentiate overlapping data points.
Many ligand atoms assigned high network scores are deeply buried in hydrophobic pockets and form several favorable interactions with the protein environment. Examples are para-chloro or para-methyl phenyl atoms in thumb binding site inhibitors of HCV polymerase(73) (Figure 11, PDB code 1yvz, total score = 5.3, network contribution = 2.7), small nonpolar substituents in the 3 position of pyrazolopyrimidine CDK2 inhibitors(74) (PDB code 2r3r, total score = 3.5, network contribution = 1.4), or the chloro substituents pointing deeply into the S1 pocket of factor Xa(75) (PDB code 1wu1, total score = 3.7, network contribution = 1.6). In these examples, the gain in binding affinity compared to an unsubstituted inhibitor is a substantial, at least 20-fold, decrease in IC50 values. Further SAR examples exist in which single atom substitutions in buried hydrophobic pockets lead to even more drastic, up to >1000-fold, affinity increases.(76) In contrast to these examples, low network scores for a deeply buried ligand substituent indicate either imperfect shape complementarity or a suboptimal match of contact atom types.
Figure 11.
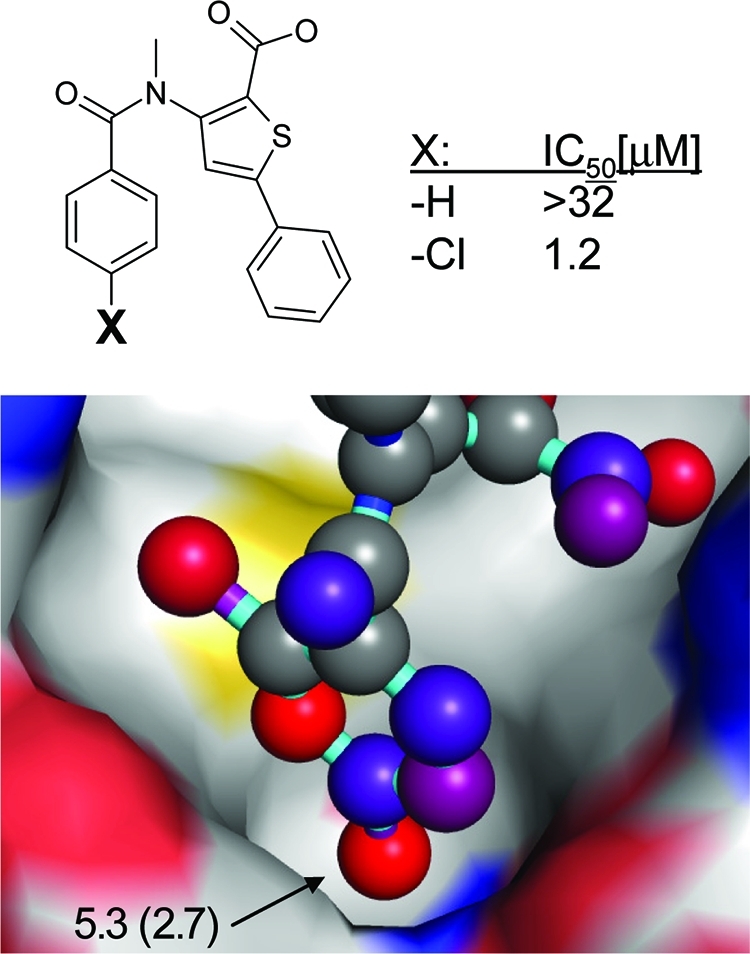
HCV polymerase inhibitor complex (PDB code 1yvz) with an interaction network hot spot originating from a chlorine atom in a buried hydrophobic binding pocket. The numbers in the figure indicate atom-based Scorpion score and network contribution of the para-Cl atom.
Thus, and as evident from the bottom plot of Figure 10, high network scores are more than another measure of the “buriedness”. Ligand atoms can be assigned high Scorpion scores in spite of being highly solvent-exposed. An example is shown in Figure 12. Substitution of a terminal phenyl with an aminomethyl group in an IGF-1R (insulin-like growth factor-1 receptor) tyrosine kinase inhibitor leads to an almost 10-fold gain in binding affinity, although the only additional protein interactions are formed via bridging water molecules on the surface of the protein.(77) This is rather unusual, as such hydrogen bonds typically do not contribute much to binding affinity due to compensating desolvation effects. The Scorpion scores correctly identify the amino group as an interaction hot spot. A network of interactions exists to a chain of three water molecules strongly bound to each other and to the protein (Rank scores > 2.0).
Figure 12.
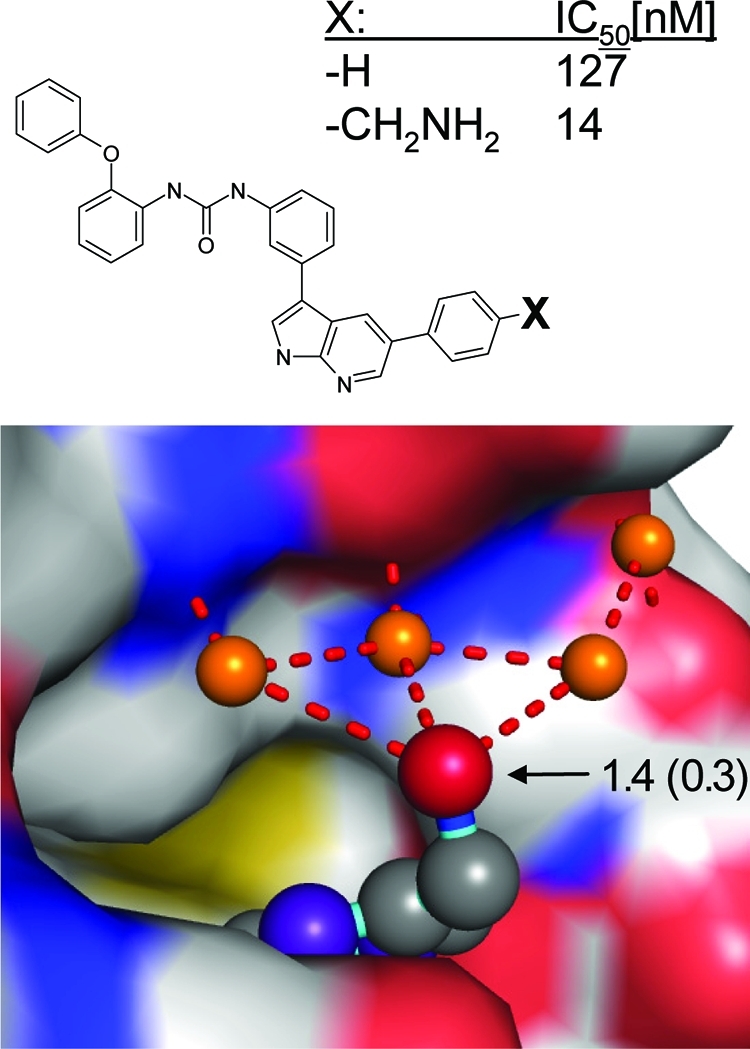
Insulin receptor kinase–pyrrolopyridine complex (PDB code 3eta) with the interaction network hot spot originating from a solvent-exposed amino group. The numbers in the figure indicate the atom-based Scorpion score and network contribution of the terminal amino group. The X-ray crystal structure is with the insulin receptor kinase, while the SAR was obtained from IGF-1R tyrosine kinase. They have a sequence identity of 80% in their kinase domains and have no amino acid differences within 5 Å of the ligand.
Correlated hydrogen bond interactions, in particular within hydrophobic environments, generally receive high network scores. An example is the CDK2/3–aminoindazole complex displayed in Figure 13. An array of three nitrogen hydrogen bond donors and acceptors (N1–N3) interact with the hinge backbone (Glu81–Leu83), resulting in a network contribution in addition to the pairwise hydrogen bond score. The network is further enhanced by a sandwich of van der Waals interactions of the aromatic heterocycle with Leu and Ala side chains of CDK2. In silico mutation of the amino nitrogen (N3) to an oxygen atom, which is not able to form a hydrogen bonding interaction with the backbone carbonyl oxygen, leads to a drop of the network contribution for N2 from 0.9 to 0.6, suggesting cooperative enhancement of interactions. Unfortunately, no published SAR around this hydrogen bonding motif is available for CDK2 to verify this hypothesis. The 3-aminoindazole core is also known to inhibit KDR kinase, albeit with a terminal 3-amino group. In this system, the removal of one of the three intermolecular hydrogen bonds by omitting the amino functionality leads to a considerable reduction (6- to 42-fold) in binding affinity.(78) Correlated protein–ligand hydrogen bonds in hydrophobic environments are known to increase binding affinity. It has been hypothesized that water molecules bound to such protein motifs cannot form a full set of hydrogen bonds, causing a net enthalpy gain when they are replaced by ligand motifs that exactly complement the donor–acceptor pattern of the protein.(37) Our empirical method cannot capture the solvation/desolvation effects but clearly identifies the high degree of protein–ligand complementarity through the refined interactions and network model.
Figure 13.
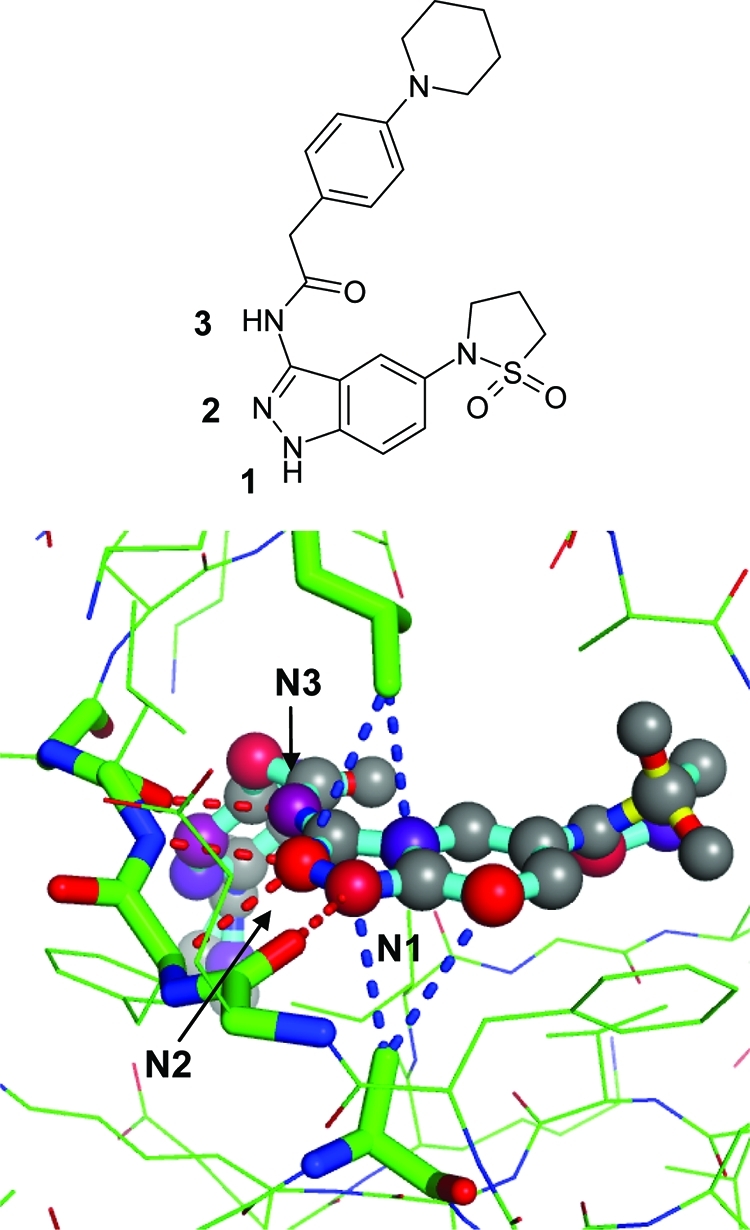
Hydrogen bond and van der Waals interaction network of selected atoms in a CDK2–inhibitor complex (PDB code 2r64). Atom scores (network contributions) for the atoms with numbers are N1, 1.3 (0.3); N2, 2.3 (0.9); N3, 0.9 (0.4).
In unliganded polar binding sites, water molecules interact with exposed protein residues and with each other, forming intricate interaction networks (though these are both weak and transient). To effectively desolvate such environments, ligands have to present their hydrogen bond acceptor and donor functionalities in such a way that similarly extended contact networks are created. This requires a number of geometric constraints to be fulfilled, and consequently few chemical variations are typically allowed to maintain good binding. With our network scores it is straightforward to identify complexes in which extended polar networks are present. The complex of dihydropterate synthase (DHPS) with the substrate analogue 6-hydroxymethyl-pterine-pyrophosphate is shown in Figure 14, illustrating how several ligand donor and acceptor atoms are engaged in strong hydrogen bonds with DHPS residues and tightly bound water molecules. The large interaction network leads to substantial score contributions, and a number of ligand atoms are highlighted as interaction hot spots. Further examples of extended polar networks are the complexes of isothiazolidinedione-containing inhibitors with protein tyrosine phosphatase 1B (PDB code 2cnf), 2-aminotriazines with HSP90 (PDB code 2wi2), or aminotetrazole ligands with β-lactamase (PDB code 3g2z).
Figure 14.
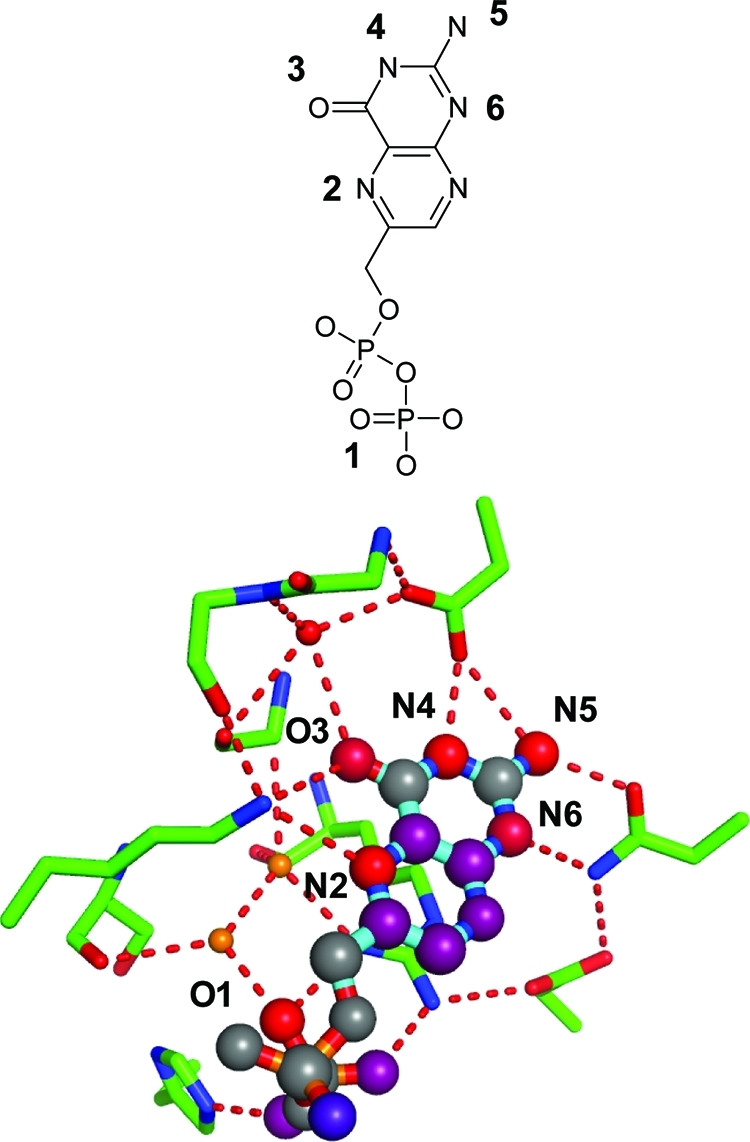
Hydrogen bond interaction network of DHPS inhibitor complex (PDB code 1tww). Atom scores (network contributions) for the atoms with numbers are O1, 1.9 (0.9); N2, 1.5 (0.3); O3, 1.9 (0.6); N4, 1.9 (0.9); N5, 1.5 (0.6); N6, 1.4 (0.4).
Ligand Atom Cooperativity
The network descriptors that turned out to be generally applicable in this study are primarily suited to capture highly local effects of cooperative binding. They visualize and to some extent quantify the tight embedding of specific functional groups within the protein binding site; i.e., they describe cooperativity to a large extent from a protein perspective. In medicinal chemistry, this type of cooperativity manifests itself in the form of specific recognition elements or “privileged motifs”. Cooperativity, however, means much more than local complementarity. The term also covers synergies between parts of a ligand that independently form good interactions with the protein and, when present together, lead to affinity gains larger than the individual contributions. Such ligand parts can be quite distant in space. We believe the main reason why network descriptors that capture nonlocal cooperativity did not feature strongly in our results is due to the lack of quality examples in which both biostructure and SAR information from double replacement cycles are available.9,11,12 Details regarding weakly binding ligands are rarely elaborated upon, and only two well characterized examples could be identified for our training sets (Table 5, indices 13 and 14). A consequence of the structure of the training sets is that subgraph network descriptors connecting different ligand atoms (LPL_l, HLH), which would be especially suitable to describe nonadditive SAR, might not get enough weight compared to the other network elements (LPL_c, LPP, PLP).
We have made a first attempt to identify cooperative pairs of ligand moieties by considering only the LPL_l and HLH subset of network elements and requiring that both atoms of the pair are (a) strongly interacting with the protein, i.e., with more than one favorable interaction, (b) considerably networked, i.e., with a network contribution above threshold, and (c) connected to each other by less than six network nodes. Surprisingly, this simple approach was able to identify cooperative pairs in agreement with experimental SAR for a number of different systems. In the DPP-IV example (Figure 15), a roughly 8-fold lower IC50 is observed when both ortho- and para-chlorine atoms are attached to the 6-phenyl ring compared to an extrapolation from single Cl substitutions at this site.(9) Our calculations identify these two chlorine atoms as well as the ring α-carbon atom (C16) and the amino group (N21) as strongly networked atoms that are connected to each other through relatively short network paths. Different network paths of length 5 connect the two Cl atoms in the S1 binding site of DPP-IV, one of which is shown in Figure 15 traversing His 740, Val 711, Tyr 662, and Trp 659.
Figure 15.
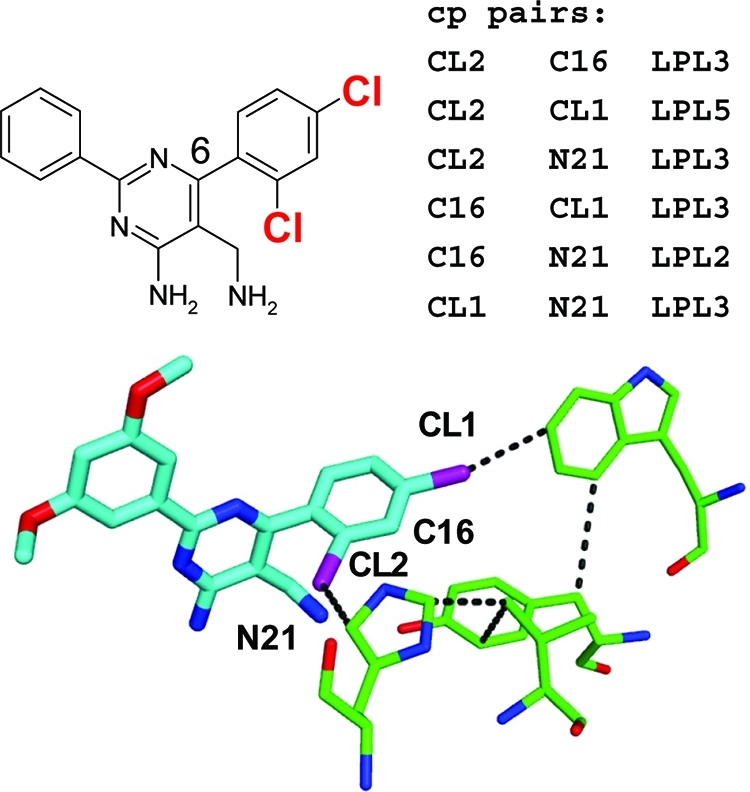
Example of cooperativity between two ligand chlorine atoms in a DPP-IV inhibitor series.(9) Adding both ortho- and para-Cl atoms to the 6-phenyl ring reduces the IC50 against the target 8-fold more than extrapolated from the IC50 values of the two single-Cl substituted and the unsubstituted analogues. The “cp pairs” list gives the predicted cooperative pairs, and the atom labels in the binding site view denote the atoms involved. An LPL_l path of length of 5 connecting the two chlorine atoms involved in cooperativity is displayed (PDB code 1rwq).
A second example stems from an Hsp90 fragment inhibitor optimization program in which substitution of a phenyl with a hydroxyl group in the 2 position leads to a drastic boost in binding affinity but only when an OH group is jointly present in the 4 position.(79) Our program identifies these two hydroxyl groups as potential cooperative atom pairs. Two of the strong hydrogen bonding networks of a path length of 4, involving Ser 52, Asp 93, and two water molecules with high Rank scores, are displayed in Figure 16.
Figure 16.
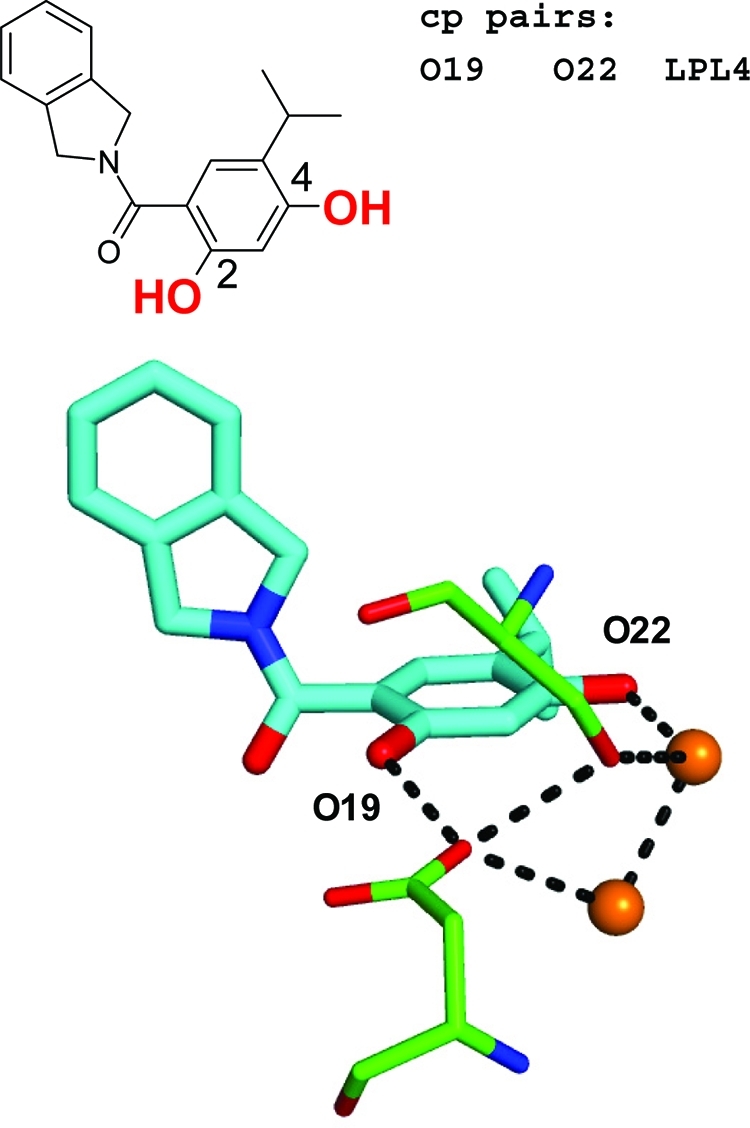
Example of cooperativity between two ligand hydroxyl groups in a Hsp90 inhibitor series.(79) Replacing the 4-OH group (O22) with 2-OH (O19) leads to a significant reduction in ligand efficiency, while having both 2-OH and 4-OH substitutions results in a significant gain in ligand efficiency. The “cp pairs” list gives the computed cooperative pairs, and the atom labels in the binding site view denote the atoms involved. Two LPL_l paths of a length of 4 connecting the two hydroxyl groups involved in cooperativity are displayed (PDB code 2xab).
Conclusions and Outlook
We have described the development of an approach that goes beyond the standard additive treatment of molecular interactions and provides a framework for the description of cooperative effects. We construct interaction networks by means of a newly defined comprehensive set of noncovalent contacts that encode state-of-the-art knowledge about molecular interactions. Through the optimization of a scoring function, ScorpionScore, against several high-quality test sets, we have obtained statistical evidence that the incorporation of a small world network description improves the prediction of binding affinities, in particular when small local changes in a ligand cause strong affinity changes. Examples combining structural and SAR data from drug discovery projects show that tight binding is associated with the formation of extended interaction networks. The tools that have been implemented enable visual analysis of these networks and of binding hot spots and are available as extensions of the Proasis3 software system.(31)
As a logical extension of this work, we plan to implement a ligand design tool that points out opportunities for creating tighter interaction networks in a binding site. Another extension will be the characterization of hot spots in protein–protein interactions, where cooperative stabilization is likely.(80) We also plan to investigate whether our network approach can help us to understand, and possibly predict, selectivity within protein families, particularly kinases.
During the derivation of the scoring function, we have become painfully aware of the absence of a good training set exhibiting both highest quality structural information and consistently measured binding affinities. Many researchers have optimized and validated scoring functions against data from a diverse set of proteins. We have come to realize that mixing affinity values measured against different proteins in different assays adds considerable noise, rendering an analysis of the deficiencies of current scoring methods almost impossible. As a consequence, we have optimized our scoring function against a combination of data sets, each with binding affinities measured against one assay and one protein only, and we have only taken into account very high quality X-ray structures. Due to the lack of sufficient public data, we had to complement the training set with proprietary data. On the basis of the stringent quality criteria outlined in this paper, we have started to filter the entire PDB and will publish this data set in due course together with consistently measured binding data.
While we believe that the network model can be extended to capture cooperativity effects more broadly and also more quantitatively, we are of course aware of its limitations. A single complex structure cannot prove, but only suggest, the possibility of cooperative binding. In particular, a tight interaction network is not a proof of structural tightening.19,81 There are probably cases where a high network score does not indicate a particularly strong gain in binding affinity but simply a high binding specificity—especially since we exclude unfavorable interactions and desolvation from the network analysis. The network model also cannot capture purely entropic and long-range (allosteric) cooperativity effects.
Intuitive but imperfect models have always been an important part of chemistry. Such models are valuable aids in the interpretation of complex phenomena. Thus, the empirical nature of the interaction types used here can be seen as a strength of our approach. This strength can turn into a weakness if we forget that the set of parameters we use is only one of many possibilities and provide only approximate solutions. Details of the geometric parameters influence results, and the use of hard distance and angle cutoffs leads to discontinuous energy changes. Initial attempts to use distance-dependent interaction energies led to a slightly poorer performance of the scoring function. We will explore this further as a continuous energy function would allow for geometry optimization of a protein–ligand complex, enabling additional use of our sets of nonclassical interactions and contact networks.
Finally, it must be remarked that a full description and understanding of protein–ligand binding must of course consider the entire thermodynamic cycle including solvation and desolvation steps. The network model only takes into account the recognition of protein and ligand. Where we identify tight interaction networks in narrow lipophilic pockets, others have attributed the observed large gains in binding affinity to the particularly poor solvation of the pocket.82,83 Both arguments are typically valid: the desolvation argument hints at the opportunity of large affinity gains, whereas the recognition/network argument focuses on how to seize this opportunity with specific ligand moieties. The examples that we have found provide the evidence that our broader analysis of noncovalent interactions and network approach indeed help rationalize tight binding ligands, and we are confident that our new concepts will lead to more success in structure-based design programs.
Acknowledgments
Dr. Wolfgang Guba is acknowledged for extensive feedback on the implementation. We thank Dr. Bradford Graves for help in collecting X-ray structures of the neuraminidase training set and Dr. Markus Rudolph for assistance in the calculation of the RSCC values. Computational support from Dr. Ken Brameld for the calculation of ligand strain energies is greatly acknowledged. Annabelle Taylor is acknowledged for many invaluable discussions on network approaches and the analysis of statistics results. We thank the EDS in Uppsala for permitting the download of a larger number of structure factor files.
Supporting Information Available
One figure (Figure S1) with ligand depictions and potency values for the neuraminidase training set. Three tables (Tables S2–S4) with details about the training set (public PDB structures), optimized parameters, and external performance of the scoring function derived for pose prediction. One table (Table S5) detailing the external performance of SScorpion in ranking binding affinities. One table (Table S6) with virtual screening results of SScorpion on targets of the DUD data set. This information is available free of charge via the Internet at http://pubs.acs.org/.
Author Present Address
§ Institute of General, Inorganic and Theoretical Chemistry, University of Innsbruck, A-6020 Innsbruck, Austria
Author Present Address
∥ Institute of Pharmaceutical Sciences, Swiss Federal Institute of Technology Zurich, CH-8093 Zurich, Switzerland
Supplementary Material
References
- Warren G. L.; Andrews C. W.; Capelli A.-M.; Clarke B.; LaLonde J.; Lambert M. H.; Lindvall M.; Nevins N.; Semus S. F.; Senger S.; Tedesco G.; Wall I. D.; Woolven J. M.; Peishoff C. E.; Head M. S. A Critical Assessment of Docking Programs and Scoring Functions. J. Med. Chem. 2005, 49, 5912–5931. [DOI] [PubMed] [Google Scholar]
- Kuhn B.; Gerber P.; Schulz-Gasch T.; Stahl M. Validation and Use of the MM-PBSA Approach for Drug Discovery. J. Med. Chem. 2005, 48, 4040–4048. [DOI] [PubMed] [Google Scholar]
- Foloppe N.; Hubbard R. Towards predictive ligand design with free-energy based computational methods?. Curr. Med. Chem. 2006, 13, 3583–3608. [DOI] [PubMed] [Google Scholar]
- Bissantz C.; Kuhn B.; Stahl M. A Medicinal Chemist’s Guide to Molecular Interactions. J. Med. Chem. 2010, 53, 5061–5084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clark T.; Hennemann M.; Murray J. S.; Politzer P. Halogen bonding: the sigma hole. J. Mol. Model. 2007, 13, 291–296. [DOI] [PubMed] [Google Scholar]
- Hardegger L. A.; Kuhn B.; Spinnler B.; Anselm L.; Ecabert R.; Stihle M.; Gsell B.; Thoma R.; Diez J.; Benz J.; Plancher J.-M.; Hartmann G.; Banner D. W.; Haap W.; Diederich F. Systematic Investigation of Halogen Bonding in Protein-Ligand Interactions. Angew. Chem., Int. Ed. 2011, 50, 314–318. [DOI] [PubMed] [Google Scholar]
- Paulini R.; Müller K.; Diederich F. Orthogonal multipolar interactions in structural chemistry and biology. Angew. Chem., Int. Ed. 2005, 44, 1788–1805. [DOI] [PubMed] [Google Scholar]
- Quinn J. R.; Zimmerman S. C.; Del Bene J. E.; Shavitt I. Does the A·T or G·C Base-Pair Possess Enhanced Stability? Quantifying the Effects of CH···O Interactions and Secondary Interactions on Base-Pair Stability Using a Phenomenological Analysis and ab Initio Calculations. J. Am. Chem. Soc. 2007, 129, 934–941. [DOI] [PubMed] [Google Scholar]
- Peters J.-U.; Weber S.; Kritter S.; Weiss P.; Wallier A.; Boehringer M.; Hennig M.; Kuhn B.; Loeffler B.-M. Aminomethylpyrimidines as novel DPP-IV inhibitors: A 100 000-fold activity increase by optimization of aromatic substituents. Bioorg. Med. Chem. Lett. 2004, 14, 1491–1493. [DOI] [PubMed] [Google Scholar]
- Patel Y.; Gillet V. J.; Howe T.; Pastor J.; Oyarzabal J.; Willett P. Assessment of Additive/Nonadditive Effects in Structure-Activity Relationships: Implications for Iterative Drug Design. J. Med. Chem. 2008, 51, 7552–7562. [DOI] [PubMed] [Google Scholar]
- Baum B.; Muley L.; Smolinski M.; Heine A.; Hangauer D.; Klebe G. Non-additivity of Functional Group Contributions in Protein-Ligand Binding: A Comprehensive Study by Crystallography and Isothermal Titration Calorimetry. J. Mol. Biol. 2010, 397, 1042–1054. [DOI] [PubMed] [Google Scholar]
- Muley L.; Baum B.; Smolinski M.; Freindorf M.; Heine A.; Klebe G.; Hangauer D. Enhancement of Hydrophobic Interactions and Hydrogen Bond Strength by Cooperativity: Synthesis, Modeling and MD-Simulations of a Congeneric Series of Thrombin Inhibitors. J. Med. Chem. 2010, 53, 2126–2135. [DOI] [PubMed] [Google Scholar]
- Jeffrey G. A.An Introduction to Hydrogen Bonding; Oxford University Press: New York, 1997. [Google Scholar]
- Kar T.; Scheiner S. Comparison of Cooperativity in CH···O and OH···O Hydrogen Bonds. J. Phys. Chem. A 2004, 108, 9161–9168. [Google Scholar]
- Tsuzuki S.; Houjou H.; Nagawa Y.; Goto M.; Hiratani K. Cooperative Enhancement of Water Binding to Crownophane by Multiple Hydrogen Bonds: Analysis by High Level ab Initio Calculations. J. Am. Chem. Soc. 2001, 123, 4255–4258. [DOI] [PubMed] [Google Scholar]
- Tsemekhman K.; Goldschmidt L.; Eisenberg D.; Baker D. Cooperative hydrogen bonding in amyloid formations. Protein Sci. 2007, 16, 761–764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jadzyn J.; Zywucki B. Molecular structure of hydrogen bonded N,N’-diethylurea in nonpolar solvents. J. Mol. Struct. 1987, 158, 293–300. [Google Scholar]
- Williams D. H.; Maguire A. J.; Tsuzuki W.; Westwell M. S. An Analysis of the Origins of a Cooperative Binding Energy of Dimerization. Science 1998, 280, 711–714. [DOI] [PubMed] [Google Scholar]
- Williams D. H.; Stephens E.; Zhou M. Ligand Binding Energy and Catalytic Efficiency from Improved Packing within Receptors and Enzymes. J. Mol. Biol. 2003, 329, 389–399. [DOI] [PubMed] [Google Scholar]
- Dorogovtsev S. N.; Mendes J. F. F.. Evolution of Networks; Oxford University Press: Oxford, 2006. A small world network is a type of mathematical graph in which most nodes are not neighbors of one another, but most nodes can be reached from every other one by a small number of steps. They have an unexpectedly low average shortest path length between any pair of nodes and a fat-tailed degree distribution; that is, the number of connections for some nodes is many orders of magnitude higher than the average number. Numerous studies have identified them throughout nature, in many different systems of biology, communication, finance, and throughout human social organizations. The reason why small world networks are so frequently observed is believed to be due to their stability, which arises from a low average shortest path length. [Google Scholar]
- Vendruscolo M.; Dokholyan N. V.; Paci E.; Karplus M. Small-world view of the amino acids that play a key role in protein folding. Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys. 2002, 65, 061910/1–061910/4. [DOI] [PubMed] [Google Scholar]
- Atilgan A. R.; Akan P.; Baysal C. Small-world communication of residues and significance for protein dynamics. Biophys. J. 2004, 86, 85–91. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Juanico B.; Sanejouand Y. H.; Piazza F.; De Los Rios P. Discrete Breathers in Nonlinear Network Models of Proteins. Phys. Rev. Lett. 2007, 99, 238104/1–238104/4. [DOI] [PubMed] [Google Scholar]
- Bode C.; Kovacs Istvan A.; Szalay Mate S.; Palotai R.; Korcsmaros T.; Csermely P. Network analysis of protein dynamics. FEBS Lett. 2007, 581, 2776–82. [DOI] [PubMed] [Google Scholar]
- Chang S.; Gong X. Q.; Jiao X.; Li C. H.; Chen W. Z.; Wang C. X., Network analysis of protein-protein interaction. Chin. Sci. Bull. 2010, 55, 814–822. [Google Scholar]
- Jacobs D. J.; Rader A. J.; Kuhn L. A.; Thorpe M. F. Protein flexibility predictions using graph theory. Proteins: Struct., Funct., Genet. 2001, 44, 150–165. [DOI] [PubMed] [Google Scholar]
- Gohlke H.; Kuhn L. A.; Case D. A. Change in protein flexibility upon complex formation: Analysis of Ras-Raf using molecular dynamics and a molecular framework approach. Proteins: Struct., Funct., Bioinf. 2004, 56, 322–337. [DOI] [PubMed] [Google Scholar]
- Grigorov M. G. Global properties of biological networks. Drug Discovery Today 2005, 10, 365–372. [DOI] [PubMed] [Google Scholar]
- Daylight Chemical Information Systems: Laguna Niguel C. A.http://www.daylight.com (accessed June 16, 2011).
- Schreyer A.; Blundell T. CREDO: a protein-ligand interaction database for drug discovery. Chem. Biol. Drug Des. 2009, 73, 157–167. [DOI] [PubMed] [Google Scholar]
- Proasis, version 2 & 3; Desert Scientific Software: Sydney, Australia. http://www.desertsci.com (accessed June 16, 2011).
- Sedgewick R.Algorithms in C; Addison-Wesley: Boston, 2002. [Google Scholar]
- Labute P.Chemical Computing Group, 'line of sight' part of 'Contact Criteria'. http://www.chemcomp.com/journal/cstat.htm (accessed June 16, 2011).
- Bondi A. van der Waals volumes and radii. J. Phys. Chem. 1964, 68, 441–51. [Google Scholar]
- Amadasi A.; Surface J. A.; Spyrakis F.; Cozzini P.; Mozzarelli A.; Kellogg G. E. Robust Classification of ″Relevant″ Water Molecules in Putative Protein Binding Sites. J. Med. Chem. 2008, 51, 1063–1067. [DOI] [PubMed] [Google Scholar]
- Allen F. H. The Cambridge Structural Database: A Quarter of a Million Crystal Structures and Rising. Acta Crystallogr. 2002, B58, 380–388. [DOI] [PubMed] [Google Scholar]
- Friesner R. A.; Murphy R. B.; Repasky M. P.; Frye L. L.; Greenwood J. R.; Halgren T. A.; Sanschagrin P. C.; Mainz D. T. Extra Precision Glide: Docking and Scoring Incorporating a Model of Hydrophobic Enclosure for Protein–Ligand Complexes. J. Med. Chem. 2006, 49, 6177–6196. [DOI] [PubMed] [Google Scholar]
- Stahl M.; Mauser H.; Tsui M.; Taylor N. R. A robust clustering method for chemical structures. J. Med. Chem. 2005, 48, 4358–4366. [DOI] [PubMed] [Google Scholar]
- Hawkins P.; Warren G.; Skillman A.; Nicholls A. How to do an evaluation: pitfalls and traps. J. Comput.-Aided Mol. Des. 2008, 22, 179–190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Macromodel, version 9.7; Schrödinger, LLC: New York. http://www.schrodinger.com (accessed June 16, 2011). [Google Scholar]
- Bailey S. The CCP4 suite: programs for protein crystallography. Acta Crystallogr. 1994, D50, 760–763. [DOI] [PubMed] [Google Scholar]
- Pham T. A.; Jain A. N. Parameter Estimation for Scoring Protein-Ligand Interactions Using Negative Training Data. J. Med. Chem. 2006, 49, 5856–5868. [DOI] [PubMed] [Google Scholar]
- Glide, version 5.0; Schrödinger, LLC: New York. http://www.schrodinger.com (accessed June 16, 2011). [Google Scholar]
- Englebienne P.; Moitessier N. Docking Ligands into Flexible and Solvated Macromolecules. 4. Are Popular Scoring Functions Accurate for this Class of Proteins?. J. Chem. Inf. Model. 2009, 49, 1568–1580. [DOI] [PubMed] [Google Scholar]
- Huang N.; Shoichet B. K.; Irwin J. J. Benchmarking Sets for Molecular Docking. J. Med. Chem. 2006, 49, 6789–6801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nicholls A. What do we know and when do we know it?. J. Comput.-Aided Mol. Des. 2008, 22, 239–255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fraser A. S. Simulation of genetic systems by automatic digital computers. I. Introduction. Aust. J. Biol. Sci. 1957, 10, 484–491. [Google Scholar]
- Leardi R. Genetic algorithms in chemistry. J. Chromatogr. A 2007, 1158, 226–233. [DOI] [PubMed] [Google Scholar]
- PyMOL Molecular Graphics System, version 1.3; Schrödinger, LLC: New York. http://www.pymol.org (accessed June 16, 2011). [Google Scholar]
- Gerber P. R.; Müller K. MAB, a generally applicable molecular force field for structure modelling in medicinal chemistry. J. Comput.-Aided Mol. Des. 1995, 9, 251–268. [DOI] [PubMed] [Google Scholar]
- Schweizer E.; Hoffmann-Roeder A.; Olsen J. A.; Seiler P.; Obst-Sander U.; Wagner B.; Kansy M.; Banner D. W.; Diederich F. Multipolar interactions in the D pocket of thrombin: large differences between tricyclic imide and lactam inhibitors. Org. Biomol. Chem. 2006, 4, 2364–2375. [DOI] [PubMed] [Google Scholar]
- Jorgensen W. L.; Pranata J. Importance of secondary interactions in triply hydrogen bonded complexes: guanine-cytosine vs uracil-2,6-diaminopyridine. J. Am. Chem. Soc. 1990, 112, 2008–2010. [Google Scholar]
- Blight B. A.; Hunter C. A.; Leigh D. A.; McNab H.; Thomson P. I. T. An AAAA-DDD quadruple hydrogen-bond array. Nat. Chem. 2011, 3, 244–248. [DOI] [PubMed] [Google Scholar]
- Anselm L.; Banner D. W.; Benz J.; Groebke Zbinden K.; Himber J.; Hilpert H.; Huber W.; Kuhn B.; Mary J.-L.; Otteneder M. B.; Panday N.; Ricklin F.; Stahl M.; Thomi S.; Haap W. Discovery of a factor Xa inhibitor (3R,4R)-1-(2,2-difluoro-ethyl)-pyrrolidine-3,4-dicarboxylic acid 3-[(5-chloro-pyridin-2-yl)-amide] 4-{[2-fluoro-4-(2-oxo-2H-pyridin-1-yl)-phenyl]-amide} as a clinical candidate. Bioorg. Med. Chem. Lett. 2010, 20, 5313–5319. [DOI] [PubMed] [Google Scholar]
- Roehrig S.; Straub A.; Pohlmann J.; Lampe T.; Pernerstorfer J.; Schlemmer K.-H.; Reinemer P.; Perzborn E. Discovery of the Novel Antithrombotic Agent 5-Chloro-N-({(5S)-2-oxo-3- [4-(3-oxomorpholin-4-yl)phenyl]-1,3-oxazolidin-5-yl}methyl)thiophene-2-carboxamide (BAY 59–7939): An Oral, Direct Factor Xa Inhibitor. J. Med. Chem. 2005, 48, 5900–5908. [DOI] [PubMed] [Google Scholar]
- Fleming P. J.; Rose G. D. Do all backbone polar groups in proteins form hydrogen bonds?. Protein Sci. 2005, 14, 1911–1917. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cotesta S.; Stahl M. The environment of amide groups in protein-ligand complexes: H-bonds and beyond. J. Mol. Model. 2006, 12, 436–444. [DOI] [PubMed] [Google Scholar]
- Zbinden K. G.; Anselm L.; Banner D. W.; Benz J.; Blasco F.; Decoret G.; Himber J.; Kuhn B.; Panday N.; Ricklin F.; Risch P.; Schlatter D.; Stahl M.; Thomi S.; Unger R.; Haap W. Design of novel aminopyrrolidine factor Xa inhibitors from a screening hit. Eur. J. Med. Chem. 2009, 44, 2787–2795. [DOI] [PubMed] [Google Scholar]
- Hagberg A. A.; Schult D. A.; Swart P. J., Exploring network structure, dynamics, and function using {NetworkX}. In Proceedings of the 7th Python in Science Conference (SciPy2008), Varoquaux G., Travis V., Jarrod M., Eds.; Pasadena, CA, 2008; pp 11–15. [Google Scholar]
- Krammer A.; Kirchhoff P. D.; Jiang X.; Venkatachalam C. M.; Waldman M. LigScore: a novel scoring function for predicting binding affinities. J. Mol. Graphics Modell. 2005, 23, 395–407. [DOI] [PubMed] [Google Scholar]
- Catana C.; Stouten P. F. W. Novel, Customizable Scoring Functions, Parameterized Using N-PLS, for Structure-Based Drug Discovery. J. Chem. Inf. Model. 2006, 47, 85–91. [DOI] [PubMed] [Google Scholar]
- Li X.; Li Y.; Cheng T.; Liu Z.; Wang R. Evaluation of the performance of four molecular docking programs on a diverse set of protein-ligand complexes. J. Comput. Chem. 2010, 31, 2109–2125. [DOI] [PubMed] [Google Scholar]
- Plewczynski D.; Łaźniewski M.; Augustyniak R.; Ginalski K. Can we trust docking results? Evaluation of seven commonly used programs on PDBbind database. J. Comput. Chem. 2011, 32, 742–755. [DOI] [PubMed] [Google Scholar]
- Tirado-Rives J.; Jorgensen W. L. Contribution of Conformer Focusing to the Uncertainty in Predicting Free Energies for Protein-Ligand Binding. J. Med. Chem. 2006, 49, 5880–5884. [DOI] [PubMed] [Google Scholar]
- Cross J. B.; Thompson D. C.; Rai B. K.; Baber J. C.; Fan K. Y.; Hu Y.; Humblet C. Comparison of Several Molecular Docking Programs: Pose Prediction and Virtual Screening Accuracy. J. Chem. Inf. Model. 2009, 49, 1455–1474. [DOI] [PubMed] [Google Scholar]
- Oslob J. D.; Romanowski M. J.; Allen D. A.; Baskaran S.; Bui M.; Elling R. A.; Flanagan W. M.; Fung A. D.; Hanan E. J.; Harris S.; Heumann S. A.; Hoch U.; Jacobs J. W.; Lam J.; Lawrence C. E.; McDowell R. S.; Nannini M. A.; Shen W.; Silverman J. A.; Sopko M. M.; Tangonan B. T.; Teague J.; Yoburn J. C.; Yu C. H.; Zhong M.; Zimmerman K. M.; O’Brien T.; Lew W. Discovery of a potent and selective Aurora kinase inhibitor. Bioorg. Med. Chem. Lett. 2008, 18, 4880–4884. [DOI] [PubMed] [Google Scholar]
- Green N. M. Avidin. Adv. Protein Chem. 1975, 29, 85–133. [DOI] [PubMed] [Google Scholar]
- Weber P. C.; Wendoloski J. J.; Pantoliano M. W.; Salemme F. R. Crystallographic and thermodynamic comparison of natural and synthetic ligands bound to streptavidin. J. Am. Chem. Soc. 1992, 114, 3197–3200. [Google Scholar]
- Boehm H.-J. The development of a simple empirical scoring function to estimate the binding constant for a protein-ligand complex of known three-dimensional structure. J. Comput.-Aided Mol. Des. 1994, 8, 243–256. [DOI] [PubMed] [Google Scholar]
- Kuntz I. D.; Chen K.; Sharp K. A.; Kollman P. A. The maximal affinity of ligands. Proc. Natl. Acad. Sci. U.S.A. 1999, 96, 9997–10002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hyre D. E.; Le Trong I.; Merritt E. A.; Eccleston J. F.; Green N. M.; Stenkamp R. E.; Stayton P. S. Cooperative hydrogen bond interactions in the streptavidin-biotin system. Protein Sci. 2006, 15, 459–467. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeChancie J.; Houk K. N. The origins of femtomolar protein-ligand binding: hydrogen-bond cooperativity and desolvation energetics in the biotin-(strept)avidin binding site. J. Am. Chem. Soc. 2007, 129, 5419–5429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chan L.; Pereira O.; Reddy T. J.; Das S. K.; Poisson C.; Courchesne M.; Proulx M.; Siddiqui A.; Yannopoulos C. G.; Nguyen-Ba N.; Roy C.; Nasturica D.; Moinet C.; Bethell R.; Hamel M.; L’Heureux L.; David M.; Nicolas O.; Courtemanche-Asselin P.; Brunette S.; Bilimoria D.; Bédard J. Discovery of thiophene-2-carboxylic acids as potent inhibitors of HCV NS5B polymerase and HCV subgenomic RNA replication. Part 2: Tertiary amides. Bioorg. Med. Chem. Lett. 2004, 14, 797–800. [DOI] [PubMed] [Google Scholar]
- Paruch K.; Dwyer M. P.; Alvarez C.; Brown C.; Chan T.-Y.; Doll R. J.; Keertikar K.; Knutson C.; McKittrick B.; Rivera J.; Rossman R.; Tucker G.; Fischmann T. O.; Hruza A.; Madison V.; Nomeir A. A.; Wang Y.; Lees E.; Parry D.; Sgambellone N.; Seghezzi W.; Schultz L.; Shanahan F.; Wiswell D.; Xu X.; Zhou Q.; James R. A.; Paradkar V. M.; Park H.; Rokosz L. R.; Stauffer T. M.; Guzi T. J. Pyrazolo[1,5-a]pyrimidines as orally available inhibitors of cyclin-dependent kinase 2. Bioorg. Med. Chem. Lett. 2007, 17, 6220–6223. [DOI] [PubMed] [Google Scholar]
- Komoriya S.; Haginoya N.; Kobayashi S.; Nagata T.; Mochizuki A.; Suzuki M.; Yoshino T.; Horino H.; Nagahara T.; Suzuki M.; Isobe Y.; Furugoori T. Design, synthesis, and biological activity of non-basic compounds as factor Xa inhibitors: SAR study of S1 and aryl binding sites. Bioorg. Med. Chem. 2005, 13, 3927–3954. [DOI] [PubMed] [Google Scholar]
- Kuhn B.; Hennig M.; Mattei P. Molecular recognition of ligands in dipeptidyl peptidase IV. Curr. Top. Med. Chem. 2007, 7, 609–619. [DOI] [PubMed] [Google Scholar]
- Patnaik S.; Stevens K. L.; Gerding R.; Deanda F.; Shotwell J. B.; Tang J.; Hamajima T.; Nakamura H.; Leesnitzer M. A.; Hassell A. M.; Shewchuck L. M.; Kumar R.; Lei H.; Chamberlain S. D. Discovery of 3,5-disubstituted-1H-pyrrolo[2,3-b]pyridines as potent inhibitors of the insulin-like growth factor-1 receptor (IGF-1R) tyrosine kinase. Bioorg. Med. Chem. Lett. 2009, 19, 3136–3140. [DOI] [PubMed] [Google Scholar]
- Dai Y.; Hartandi K.; Ji Z.; Ahmed A. A.; Albert D. H.; Bauch J. L.; Bouska J. J.; Bousquet P. F.; Cunha G. A.; Glaser K. B.; Harris C. M.; Hickman D.; Guo J.; Li J.; Marcotte P. A.; Marsh K. C.; Moskey M. D.; Martin R. L.; Olson A. M.; Osterling D. J.; Pease L. J.; Soni N. B.; Stewart K. D.; Stoll V. S.; Tapang P.; Reuter D. R.; Davidsen S. K.; Michaelides M. R. Discovery of N-(4-(3-Amino-1H-indazol-4-yl)phenyl)-N‘-(2-fluoro-5-methylphenyl)urea (ABT-869), a 3-Aminoindazole-Based Orally Active Multitargeted Receptor Tyrosine Kinase Inhibitor. J. Med. Chem. 2007, 50, 1584–1597. [DOI] [PubMed] [Google Scholar]
- Murray C. W.; Carr M. G.; Callaghan O.; Chessari G.; Congreve M.; Cowan S.; Coyle J. E.; Downham R.; Figueroa E.; Frederickson M.; Graham B.; McMenamin R.; O’Brien M. A.; Patel S.; Phillips T. R.; Williams G.; Woodhead A. J.; Woolford A. J. A. Fragment-Based Drug Discovery Applied to Hsp90. Discovery of Two Lead Series with High Ligand Efficiency. J. Med. Chem. 2010, 53, 5942–5955. [DOI] [PubMed] [Google Scholar]
- Keskin O.; Ma B.; Nussinov R. Hot Regions in Protein-Protein Interactions: The Organization and Contribution of Structurally Conserved Hot Spot Residues. J. Mol. Biol. 2005, 345, 1281–1294. [DOI] [PubMed] [Google Scholar]
- Choi J. H.; Banks A. S.; Estall J. L.; Kajimura S.; Bostrom P.; Laznik D.; Ruas J. L.; Chalmers M. J.; Kamenecka T. M.; Bluher M.; Griffin P. R.; Spiegelman B. M. Anti-diabetic drugs inhibit obesity-linked phosphorylation of PPAR[ggr] by Cdk5. Nature 2010, 466, 451–456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Young T.; Abel R.; Kim B.; Berne B. J.; Friesner R. A. Motifs for molecular recognition exploiting hydrophobic enclosure in protein-ligand binding. Proc. Natl. Acad. Sci. U.S.A. 2007, 104, 808–813. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Abel R.; Young T.; Farid R.; Berne B. J.; Friesner R. A. Role of the Active-Site Solvent in the Thermodynamics of Factor Xa Ligand Binding. J. Am. Chem. Soc. 2008, 130, 2817–2831. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.