Visual Motion and the Perception of Surface Material

Summary

Many critical perceptual judgments, from telling whether fruit is ripe, to determining whether the ground is slippery, involve estimating the material properties of surfaces. Very little is known about how the brain recognizes materials, even though the problem is likely as important for survival as navigating or recognizing objects. Though previous research has focused nearly exclusively on the properties of static images [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14,15,16], recent evidence suggests that motion may affect the appearance of surface material [17, 18, 19]. However, what kind of information motion conveys and how this information may be used by the brain is still unknown. Here, we have identified three motion cues that the brain could rely on to distinguish between matte and shiny surfaces. We show that these motion measurements can override static cues, leading to dramatic changes in perceived material depending on the image motion characteristics. A classifier algorithm based on these cues correctly predicts both successes and some striking failures of human material perception. Together these results reveal a previously unknown use for optic flow in the perception of surface material properties.

Results

Behavioral Results

When asked to visually assess the appearance of glossy objects, observers commonly rotate them back and forth in their hands to watch the highlights slide over the surface. This suggests that useful information may be carried by the characteristic way that features move during object motion or changes in viewpoint. While pigmentation patterns are usually rigidly attached to the surface, the position of reflected features depends on the relationship between viewer, object and light source [20, 21, 22]. This causes them to move relative to the surface whenever the object or viewer moves.

To test whether image motion conveys surface material, we devised a computer graphics procedure for rigidly attaching reflected patterns to the surface of an object during object or viewer motion, thus bringing static and motion cues to shininess into conflict. For any given frame in the motion sequence, the distorted patterns on the surface are consistent with specular reflections of the surrounding environment, and the object appears shiny. However, when viewed as a sequence, the patterns move with the surface, as if they were painted on instead of being reflections. The result is the distinct impression that the surface is not shiny and homogeneous, but rather matte and patterned (see Figure 1A, Movie S1: panels (1,1) and (1,2)).

Figure 1. Multiple Interpretations of Visual Input and Behavioral Experiment.

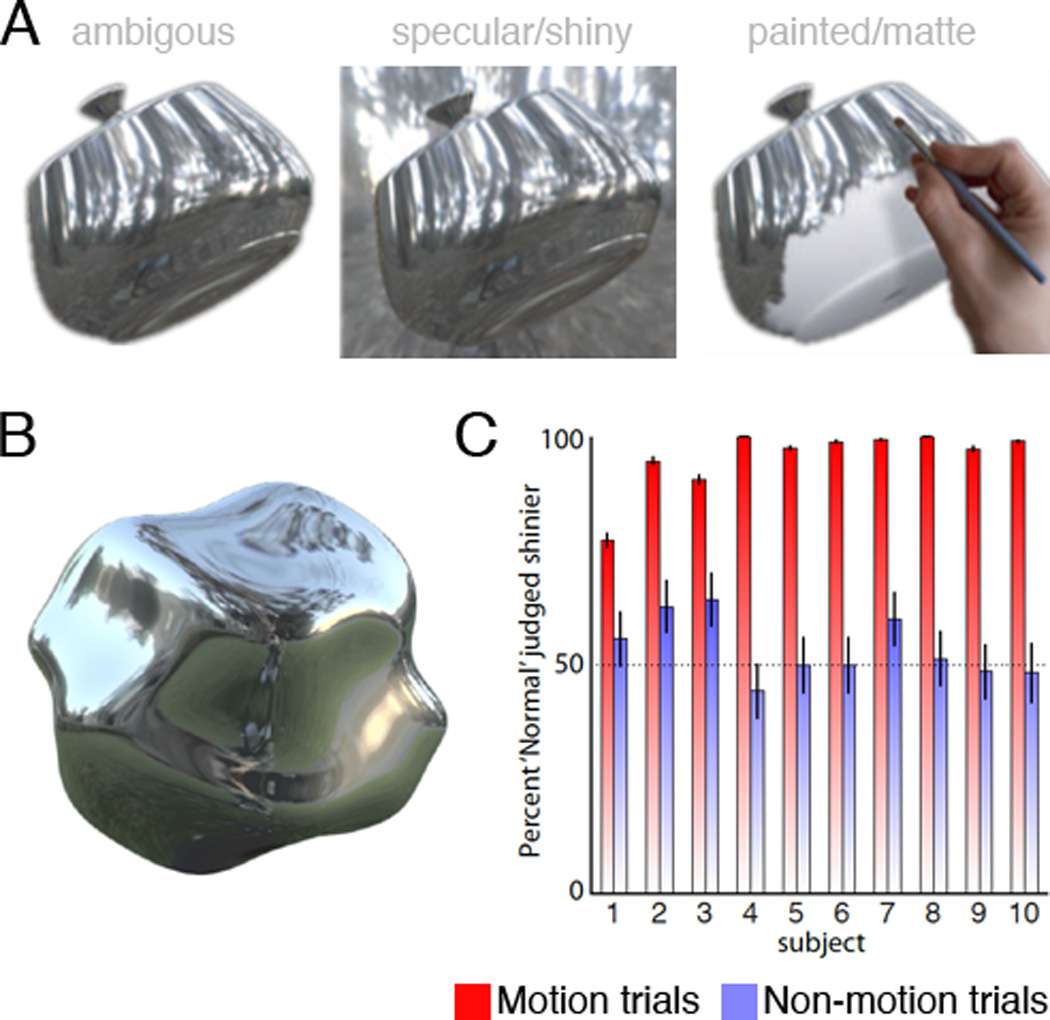
(A) Consider the object on the left. What does it appear to be made of? Most observers agree that it looks like a uniform, lustrous material reflecting a complex environment (center). However the image could also have been generated by carefully painting the pattern onto the surface with matte paint (right). This is an example of the ambiguity faced by the visual system when inferring the material composition of objects what appears to be a shiny surface might in fact be matte, but the converse is also possible. Despite the ambiguity, we rarely experience any difficulty distinguishing between diffuse and specular surfaces in daily life.

(B) Stimuli in the behavioral experiment.

(C) Grand average across all objects, illuminations and repetitions from ten naive subjects. In the experimental condition (red bars) observers almost always perceived the “Normal” stimulus as shinier. Without motion (control condition, blue bars) subjects were close to chance performance (dotted line). Error bars indicate standard error.

Also see Movie S1: panels (1,1) and (1,2).

We used movies similar to these as stimuli in an experiment to test whether human vision exploits motion cues to distinguish between shiny and matte materials (Figure 1B). In each trial, subjects were presented with two objects rotating back and forth, one with standard specular motion (“Normal” reflections), and the other with reflections that were rigidly attached to the surface (“Sticky” reflections). The task was to report which of the two objects appeared to be more shiny. Note that corresponding frames (except the first ones) of sticky and shiny movies appeared similar, but were not identical. Thus, to confirm all non-motion cues were balanced, in one tenth of trials the stimuli consisted of single static frames taken at random from the shiny and sticky motion sequences. For the moving stimuli, subjects reported objects with normal specular motion to appear shinier than those with sticky reflections (Figure 1C). By contrast, they were at chance performance for no-motion trials, indicating that motion cues created the differences in appearance between Normal and Sticky. Thus, the visual system does indeed rely on the characteristic motion patterns of features to determine whether a surface is shiny or matte.

Computational Results

Given the behavioral results we next wanted to understand what kind of information from material-specific image motion is available for the estimation of surface properties. The motion patterns produced by specular reflections depend crucially on surface curvature. Reflected features tend to “rush” across low curvature regions and “stick” to points of high curvature [20, 23], thus the resulting optic flow consists of a multitude of motion directions and image velocities. In contrast, matte, textured objects produce optic flow that is rather homogenous in direction and velocity (except for rotations around the viewing axis). Optic flow patterns may thus contain diagnostic features about an object’s surface material.

Computational analysis of the motion patterns of shiny and sticky objects used in the behavioral experiment yielded three optic flow statistics we call Coverage, Divergence, and 3D Shape Reliability. These statistical measures have perceptual interpretations, and are predictive of surface material class, each generalizing to complex objects and arbitrary rotation axes, and each capturing a different aspect of the motion pattern (See Supplemental Information). Each measure or cue is briefly introduced in the following section and illustrated in Figure 2.

Figure 2. Illustration of the three flow features.

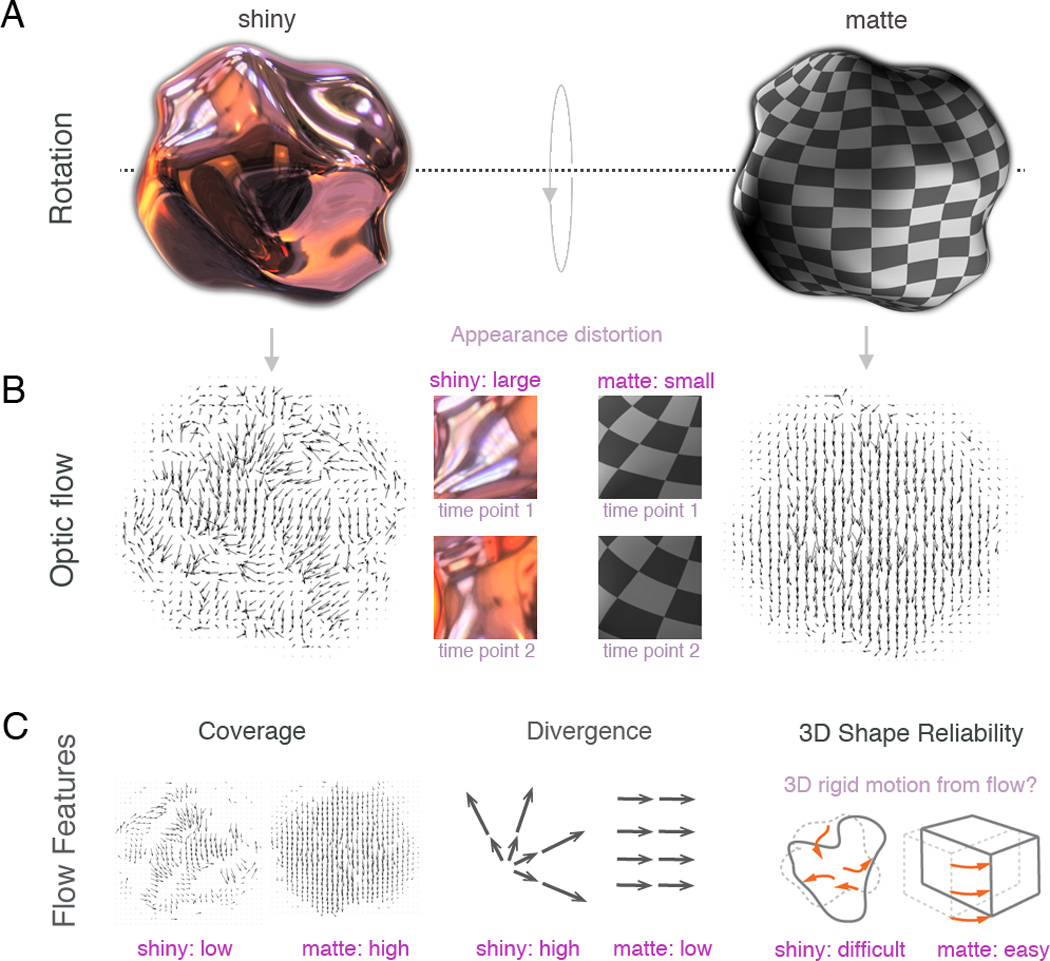
(A) A complex shiny (left) and matte, textured object (right) are rotating about the horizontal axis, front downwards towards the observer.

(B) This rotation gives rise to distinct flow pattern for each surface material. The shiny object exhibits a marked amount of appearance distortion, i.e. feature absorption and genesis, whereas the appearance of the matte object does not change substantially.

(C) Three flow features arise from this characteristic appearance distortion: 1. Coverage, 2. Divergence, 3. 3D Shape Reliability. See Supplemental Information for computational details of these measures, as well as Figure S1 for a more detailed illustration of the coverage feature.

Within a few frames of image motion, specular features that accelerate towards high curvature points become “absorbed” due to the compression at these locations [7]. Additionally, “feature genesis” occurs at local concavities on the object’s surface. The resulting distortion of appearance during object motion impairs the trackability of these features by optic flow mechanisms. When the image features change in appearance too rapidly, they cannot be tracked for sufficient time to estimate their motion. The proportion of features that are untrackable indicates shininess, and is captured by a cue we call Coverage.

For features that are trackable, appearance distortion can broadly be categorized into expansions and contractions. Specular features tend to move towards convexities (contractions) and conversely, radiate out from concavities (expansions). Moreover, as a specular feature approaches a local convexity its velocity reduces, whereas features closer to the trough of a concavity move faster than those further away. This local interplay of image motion direction and magnitude creates a potentially useful cue for the visual system to use when judging surface material – especially as contractions are usually not generated by rotating matte, textured objects. It has been shown that the first order structure of a flow field, such as that generated by the trajectories of specular features, can be decomposed into rotation, divergence and two deformation components [24]. Divergence quantifies the strength of sinks (concavities) and sources (convexities) that cause expansions and contractions in the flow field. These inhomogeneities are particularly dramatic near the interface between regions of low and high 3D-curvature (for specular surfaces).

The appearance distortions that occur on specular objects tend to adversely affect structure from motion (SfM) estimation – the computation of 3D shape from optic flow. However, the very fact that 3D rigid motion computations may be problematic for specular surfaces may itself serve as an important source of information for discriminating shiny and matte materials. Robust computation of 3D shape depends on tracking image features that correspond to surface points–i.e. that are stuck to the surface. The optic flow vector for such a feature is constrained to lie along an epipolar line. Because specular flow fields have features that slip relative to the surface, they exhibit epipolar deviations [25]. We measured how consistently the optic flow vectors are constrained by epipolar geometry and call this measure 3D Shape Reliability. Note that even with low values of 3D Shape Reliability it may still be possible to reliably compute 3D shape from SfM and other cues. In other words, the fact that a moving object appears shiny does not predict that we should not be able to see its shape. The important point for the current argument is that the presence of optic flow inconsistent with 3D rigid motion signals shininess. See Experimental Procedures for further details on the computation of each measure.

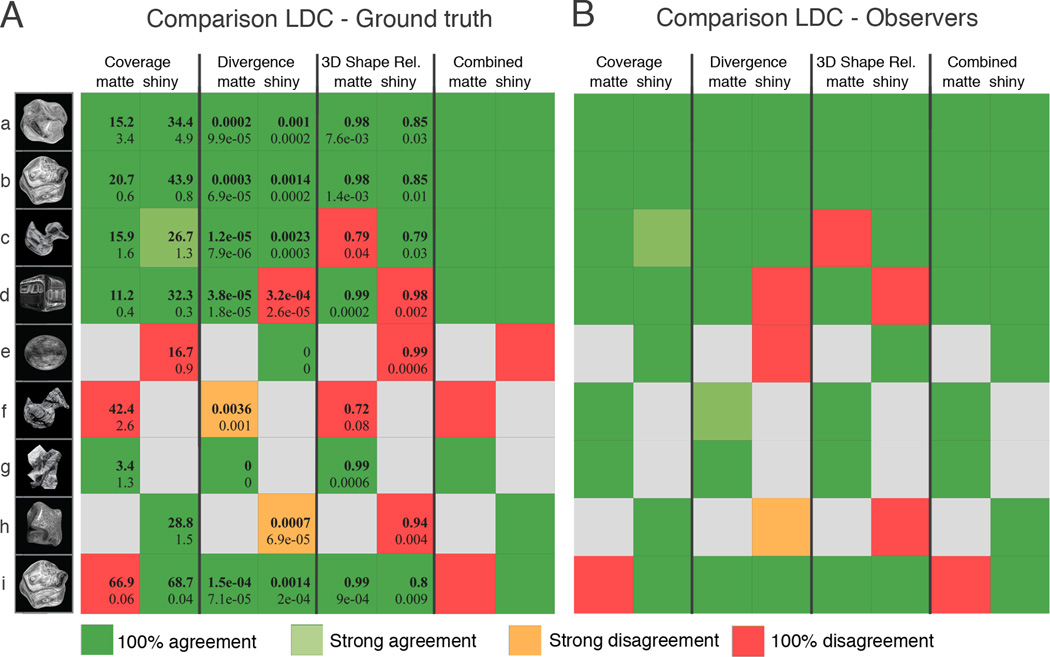
Inspection of the means and standard errors of the three cues reveals that they were individually highly diagnostic of material type for each object in the behavioral set (Figure 3, and Figure 4A, row a). Next we trained linear classifiers [26] on each of the flow measures for surface material class on eight, 15-frame image sequences taken from the behavioral experiment (Figure 1B). We classified 20 stimuli samples (10 shiny, 10 sticky, Figure 4A, row a), taken at random from the stimulus set, according to surface material. We then qualitatively compare classification results with ground truth (Figure 4A) as well as with observers' performance in the behavioral experiment (Figure 4B). The former comparison highlights the relation between physical properties and motion cues while the latter provides an indication of the predictability of the cues for human surface material perception. For the behavioral stimuli the classifiers were perfectly successful in predicting ground truth as well as observers' performance (Figure 4 A and B, row a, dark green squares). We next trained a classifier on a combination of all three cues [27] (on the same subset of stimuli from the behavioral experiment described above). Not surprisingly, the combined classifier was also in perfect agreement with observer performance.

Figure 3. Classification results.

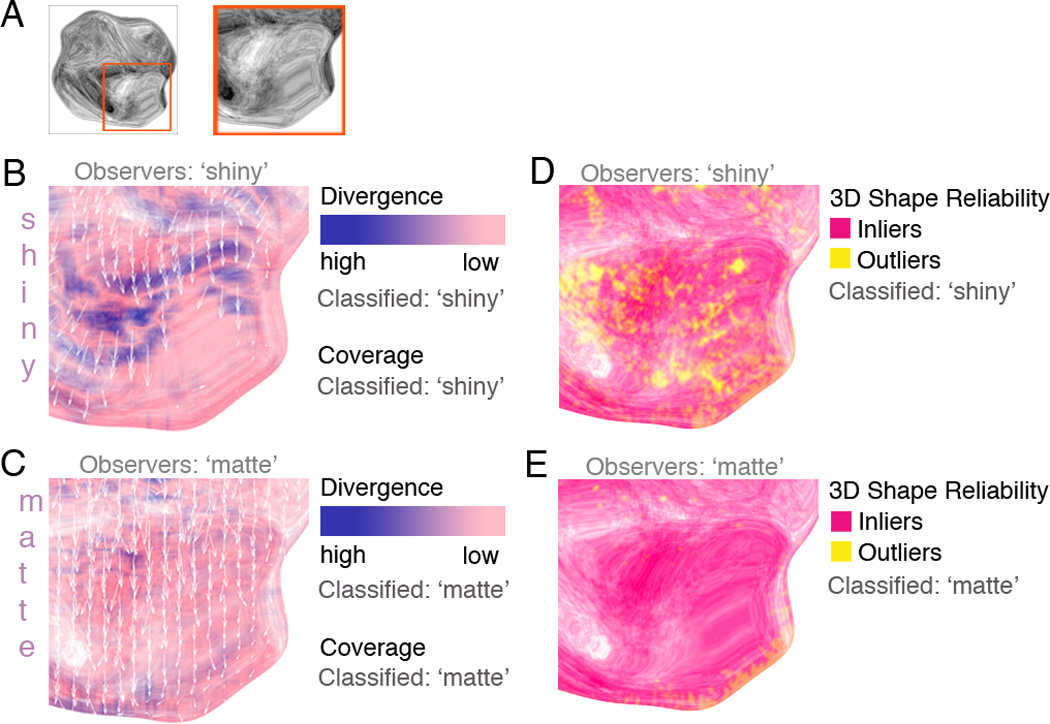
(A) A sample stimulus as well as a partial, close-up view on which classification results for the behavioral stimulus set are illustrated.

(B) White arrows indicate regions in which flow vectors could be computed over a distance of three frames. Classification results for divergence and coverage are shown to the right.

(C) Same as (B) but for matte objects.

(D) Pixels classified as inliers are those which show a flow pattern consistent with a 3D rigid motion. (E) Same as (D) but for matte objects.

Figure 4. Cue performances.

This figure illustrates cue values,- variability, and generalizability across a broad range of testing conditions.

(A) For test movies a–i we show numerical averages as well as corresponding standard errors for each measure (columns 1–6). Sample frames as well as sample images of each measure of the respective test scenarios can be found in Figure S2. We further qualitatively (by color) indicate the amount of agreement between the linear discriminant analysis (LDA) of the individual (columns 1–6) and the combined measures (last 2 columns) with the ground truth of the stimuli (shiny or matte).

(B) Same as (A) except that classifier performance is compared to observers” percepts. We find that no single cue correctly predicts observers” judgements under all conditions. Thus we argue observers may be using a combination of motion cues when estimating surface material. Rows a–i: (a) Samples taken from the behavioral set. (b) A shape moving about an arbitrary rotation axis and rendered with an arbitrary environment map (Movie S1: panels (2,1) and (2,2). (c) Novel 3D specular shape with arbitrary rotation axis, rotation speed, and environment map (Movie S1: panels (3,1). (d) A cube rotating and translating (Movie S1, panel (3,2)) (e) A motion-based perceptual surface material illusion (Movie S2: panel (1,1)). The specular object appears matte to most observers. This is not surprising since the optic flow generated by the ellipsoid lacks the multitude of motion directions and image velocities characteristic for shiny surfaces, and is instead more similar to the homogenous optic flow produced by matte, textured objects. (f) Non-rigidly deforming matte objects. Interestingly, these have a somewhat specular appearance (Movie S2: panel (1,2)). (g) An, about the vertical axis rotating, crumpled sheet of matte textured paper has moving self shadows ((Movie S2: panel (2,1)), which is problematic for fitting a 3D surface model (3D shape reliability), and may thus have a chance of being classified as specular. This was included to test the robustness of our flow measures. (h) A glossy object rotating about the horizontal axis (Movie S2: panel (2,2)). (i) The same object as in (b) but with an accelerated motion. This manipulation affects the coverage measure but leaves the other two intact. The combined classifier results weighs in favor of the coverage feature. This is not surprising as this measure has the largest effect size (Also see Supplemental Information).

Snapshots from the tested movies as well as images of the corresponding computed measures are shown in Figure S2. Test movies are shown in Movies S1 and S2.

A good model of perception should predict errors as well as successes. To make a stronger test of the proposed cues we measured their values across a number of additional conditions, including arbitrary rotation axes and environment maps (Figure 4, row b), a more complex shape (Figure 4, row c), a simpler shape (row d), new motions, including translations (row d), and accelerations (row i), a matte material with self-shadowing (row g), and a glossy shiny material (row h). As an additional test, we included two motion-based surface material illusions (rows e and f, and Movie S2 panels (1,1)-(2,2)) in which human observers perceive the wrong material property [28]. As above, we tested whether our cues can predict ground truth and whether they parallel observers' judgements. Fourteen naive observers viewed test movies (every movie once) in a random order on a laptop computer, and indicated whether a given stimulus appeared shiny or matte. For each test movie we computed % seen shiny.

For several test stimuli (compare pairs of means in Figure 4A, rows c, d and i) we find a considerable lessoning of the differences between shiny and matte for individual cues. When comparing the results of the individual and combined-measure classifiers (the training sets were the same as above) to ground truth and observers' performance we find that: 1. Our measures capture observers' performance rather than the physical reflectance properties of the stimuli (compare the proportion of reddish and greenish cells for illusory stimuli in rows e and f in Figure 4A and Figure 4B). In other words, our classifier yielded the same “perceptual errors” as our observers; 2. While each of the three individual-cue classifiers show instances of total failure in predicting observers percepts (see red squares in Figure 4B), results of the combined - cue the classifier, with the exception of one test (row i, discussed in the Supplemental Information) closely mimicked observers” performance (Figure 4B, last two columns). Snapshots from the tested movies as well as images of the corresponding computed measures are shown in Figure S2.

Discussion

Visual estimation of material properties is a difficult task, because the light arriving at the eye provides ambiguous information about the surface reflectance properties, mesoscale structure, object shape and incident illumination (Figure 1A). Despite this, humans and also some non-human animals [29, 30, 31] effortlessly discriminate between different types of surface material, yet little is known about what visual cues the brain can extract from the retinal images to estimate the “stuff” [32, 33] a surface is made of. Recent research suggested that motion may affect the appearance of surface material [17, 18, 19]. However, an explanation of this phenomenon has been missing. Here, we devised procedures that allowed us to single out motion from static cues. We found that motion can override static cues to surface properties, and that in general, optic flow characteristics play a significant role in the estimation of surface material qualities such as shininess.

The proposed flow properties may be extracted by hypothetical, yet plausible cortical mechanisms, such as those suggested by [34] for the computation of local divergence. Coverage relates to correspondence, i.e. the ability of the visual system to keep track of visual features across frames (or a certain time interval). Previous research by Todd [35], has shown that observers' judgements of 3D rigid motions were detrimentally affected by a decreased correspondence indicating that the visual system may indeed be partially sensitive to this motion cue. Interestingly, Todd noted that at intermediate levels of correspondence a rigid surface appeared to be “scintillating” [35]. 3D shape reliability might be extracted by neural mechanisms involved in the estimation of both shape and motion from optic flow [36, 37].

It is important to note, however, that optical flow is probably not sufficient on its own to induce a percept of a matte or shiny surface. For example, patterns of moving dots with given optical flow statistics do not look like specular or matte surfaces. The image velocities must have meaningful spatial organizations to be interpreted as a moving surface with certain material properties (See also [11, 13, 14] for shape-dependent static cues to surface glossiness). We have shown in previous work [28] that for simple objects (e.g. cuboidal shapes) with distinct high and low curvature regions, rushing and sticking (slow) specular features give rise to bimodal distributions of image velocity. Bi-modality in the image velocity histogram may thus signal the presence of a shiny surface, because matte, textured objects tend to produce unimodal velocity distributions. However, bi-modality essentially vanishes as the specular objects” shape becomes more complex or when the object rotates around the viewing axis yet under these conditions objects appear just as shiny (Also see Figure S2).

Because the image of a specular object is simply a distorted reflection of the surrounding world, the properties of the reflected scene can also affect how useful optical flow is for material perception. Classification of matte and shiny surfaces requires that there are sufficiently dense features in the reflected environment, and that these features are oriented such that they produce visible motion across the object. In degenerate cases where the motion of the object is parallel to elongated features in the environment (Movie S2: panels (3,1) and (3,2)), the reflected patterns produce no motion energy in the image, and therefore statistics computed on the optical flow are not reliable. Under these conditions an object appears matte to most observers. In addition to sufficient structure in the environment, the specular object must also exhibit sufficient variation in 3D curvature to be perceived as shiny (also see [28] and Hurlbert et al. [38] for the link between specular feature velocity and perceived 3D curvature).

A natural next question to ask is how the three cues are related to one another, and whether all three cues are needed for surface material estimation. We argue that these cues have independent origins, and thus can be inconsistent with one another, and in support of this notion we find that the three cues are only weakly correlated with one another (see Supplemental Information). In addition, we found that there are cases when one or two of the cues can fail to predict performance (Figure 4B). Also see Supplemental Information.

While the three motion cues we identified may not be the only ones that the brain could extract, we have demonstrated that the flow mechanisms proposed here generalize across many viewing conditions and even successfully predict motion-based perceptual surface material illusions. Thus, they capture aspects of the image motion that are relevant for the estimation of surface properties; they can override static cues to surface material; and, suggest hypothetical mechanisms to extract them from retinal motion sequences. Taken together, our findings imply a much more general role of optic flow in visual perception than previously believed [39, 40, 41].

Experimental Procedures

Behavioral experiments

Stimuli

Stimuli in the behavioral experiment consisted of 3 different shapes each rotating back and forth 15deg around six different axes (three cardinal, three random) illuminated under four “light probes” (thre debevec/Probes, one random 1/f noise). Shapes consisted of a unit “Geosphere” primitive perturbed with five sine waves of different orientations and wavelengths. We chose these irregular “blob-like” objects to be (i) novel (i.e. unfamiliar to the observers) so that observers would not be affected by pre-existing shape-material associations, and (ii) sufficiently complex to contain rich optical flow patterns that could drive motion-based material classification. Additionally, the shapes were designed to have no clearly defined principal axis, as in other experiments we have found interactions between shape and perceived axis of rotation. Images were rendered using Radiance [42].

Task

Ten naive subjects viewed stimuli, roughly 10deg visual angle across, on a laptop and responded via the keyboard. On each trial they viewed “Sticky” and “Normal” versions of a given stimulus side by side, and indicated which appeared more shiny. Trials were shown in random order, and the entire set was shown ten times.

Analysis

We computed the percent of trials on which the “Normal” stimulus was judged shinier than the “Sticky” stimulus for the objects in motion (experimental condition) and for static frames taken at random from the “Normal” and “Sticky” movies (control condition). Subjects almost always perceived the “Normal” stimulus as shinier in the motion condition. Without motion, subjects were close to chance performance (Figure 1C).

The second behavioral experiment is described in the main text. The stimulus set consisted of a range of different surface structures, including both familiar (e.g. duck) and unfamiliar (e.g. blobs) objects, as well as perceptual material illusions.

Computational Analysis

The training set consisted of 8, 15-frame image sequences taken from the behavioral experiment. Optic flow was computed using the algorithm of [43] (linearity threshold: 0.01; minimum number of valid component velocities: 7).

Coverage

Image features (pixels) need to be tracked between frames in order to assign a velocity vector. However, for long sequences or rapidly deforming regions, the corresponding features cannot be found and thus flow vectors cannot be computed. Coverage quantifies the ratio of pixels with computed flow vectors to the number of all pixels. Coverage change is the reduction in coverage due to lengthening of the frame sequence (from 2 to 3) quantifying the amount of trackability. We use the percent decrease in coverage to classify stimuli as matte or shiny.

Divergence

Divergence captures the strength of concavities and convexities that cause expansions and contractions in the flow field. This feature was computed as the number of pixels with divergence values above 2 (high divergence) divided by the total pixels with nonzero divergence values. This feature was computed over a 2-frame distance.

3D Shape Reliability

Estimation of 3D rigid motion from optic flow is problematic for specular flow fields since these exhibit epipolar deviations [24]. This poses a challenge for SfM. Corresponding points across image frames that were consistent with 3D motion, adhering to epipolar constraints, were termed “inliers” and were computed as follows. First, in order to de-noise the data, we retained only flow vectors (computed over a 2-frame distance) that had a magnitude > 0.25 * SD, where SD is the standard deviation of the magnitudes of all flow vectors in a given frame. The obtained flow vectors were then randomly separated into batches each containing 3000 motion vectors. Hundred RANSAC [44] iterations with 8 point DLT fundamental matrix estimation [45] were then applied to each batch. Vectors with Sampson error [46] less than 1 were accepted as inliers. The ratio of inliers to outliers denotes the 3D Shape Reliability feature.

PRTools Matlab toolbox [27] was used to train a normal density based linear classifier (no regularization) on the combined flow features for surface material class (ground truth). Classification was performed on non-training stimuli

katja/Smovies.

Highlights.

• Image motion determines surface material appearance

• Optic flow characteristics predict surface material illusions