Abstract
Functional RNA molecules are conformationally dynamic and sample a multitude of dynamic modes over a wide range of frequencies. Thus, a comprehensive description of RNA dynamics requires the inclusion of a broad range of motions across multiple dynamic rates which must be derived from multiple spectroscopies. Here we describe a slow conformational exchange theoretical approach to combining the description of local motions in RNA that occur in the ns-μs window and are detected by solid-state NMR with non-rigid rotational motion of the HIV-1 TAR RNA in solution as observed by solution NMR. This theoretical model unifies the experimental results generated by solution and solid-state NMR and provides a comprehensive view of the dynamics of HIV-1 TAR RNA, a well-known paradigm of an RNA where function requires extensive conformational rearrangements. This methodology provides a quantitative atomic level view of the amplitudes and rates of the local and collective displacements of the TAR RNA molecule, and provides directly motional parameters for the conformational capture hypothesis of this classical RNA-ligand interaction.
Keywords: HIV-1 TAR RNA, nucleic acids, conformational capture, relaxation times, rotational diffusion
1. Introduction
The transactivation response element (TAR) RNA from the human immunodeficiency virus type-1 (HIV-1) is required for HIV replication making it an important drug target, but it is also an ideal example of the way in which structural flexibility facilitates the interaction of RNA with ligands.1–4 Binding of HIV-1 Tat protein to TAR RNA requires a large conformation change of the RNA and a significant decrease in conformational disorder in both RNA and the polypeptide.5–9 The structural properties of these conformational states are partly known,5,10–12 yet, despite some recent progress,13,14 the exact atomic level displacements leading to these changes and many aspects of the changes in dynamics that accompany them remain to be studied.
The local dynamics of TAR RNA have been analyzed by solution NMR relaxation methods and analyzed extensively, using for the most part the Model-Free approximation.7,13,15 More recently, heterogeneities in 13C/1H line widths and relaxation rates in and around the bulged loop of TAR and the measurement of residual dipolar couplings (RDCs) have provided strong evidence for the existence of collective motions at ns-μs rates of the distal helices about a dynamic hinge associated with the bulged loop of TAR. 13,16 A meso-scale view of TAR functional dynamics derived from these studies suggest that TAR samples a manifold of structures that includes those observed when TAR is bound to various ligands, implying that TAR RNA is recognized through the opportunistic capture of pre-existing and possibly rare conformations (conformational capture). However, while RDCs can report on the amplitudes of motion occurring at any rate fast enough to pre-average the 13C-1H dipolar coupling constant (< ms), they do not provide any direct information on rates. Therefore, the time scale of these internal motions could only be broadly and indirectly inferred by a process of elimination when faster (sub-ns) and slower (ms) motions are not observed.13,17,18 Solution NMR relaxation methods can probe ms and ns-ps motions, but cannot directly detect motions within the ns-μs time frame. In contrast, 2H solid-state NMR (ssNMR) line shape and relaxation studies provide direct information on motions occurring at this rate. By combining solution and solid-state NMR studies, it should become possible to study the complete range of motions experienced by this paradigmatic RNA. However, this requires the development of theoretical methods to merge the results provided by the two techniques into a common interpretative model. Here we achieve this goal by first extracting detailed information on internal motions from the solid-state data, and then by incorporating these motions into a model of overall tumbling obtained from hydrodynamic considerations.
Local motions alter the global structure of the RNA, so that it is necessary to consider how the concerted motions of helical domains or single nucleotides modulate the macroscopic rotational diffusion of the RNA in solution and thus impact NMR relaxation rates.. However, the correct treatment of non-rigid tumbling of RNA poses a serious challenge because: 1) the correlation times of their motion may approach those of the overall tumbling,13,17 and 2) these motions may deform the tumbling molecule and affect its hydrodynamics.19 To solve the problem of motional coupling, several creative approaches have been taken, among them mode coupling analyses and domain elongation.13,17,20 In this paper we consider the situation, motivated by ssNMR models,14 where the rate of hydrodynamically-significant domain motions is substantially slower than the tumbling correlation time. This slow-exchange formalism considers weighted populations of conformers with arbitrary diffusion tensors, each of which contributes independently to the relaxation rates. Faster local motions that are reasonably assumed to have little effect on the tumbling rates are integrated into the separate conformer populations.
Using this slow-exchange model, we study dynamics at U-38, a helical base site in HIV-1 TAR RNA at which the assumption of motional decoupling is valid (Figure 1). Rates and amplitude of motions of the upper helix were obtained using 2H ssNMR applied to a TAR sample where uridine-5,6-2H2 was incorporated at U38.14,21 While comparisons to solution data in this manuscript are limited to solution relaxation times for the U38-13C6 site, the method is applicable to any site and residue.
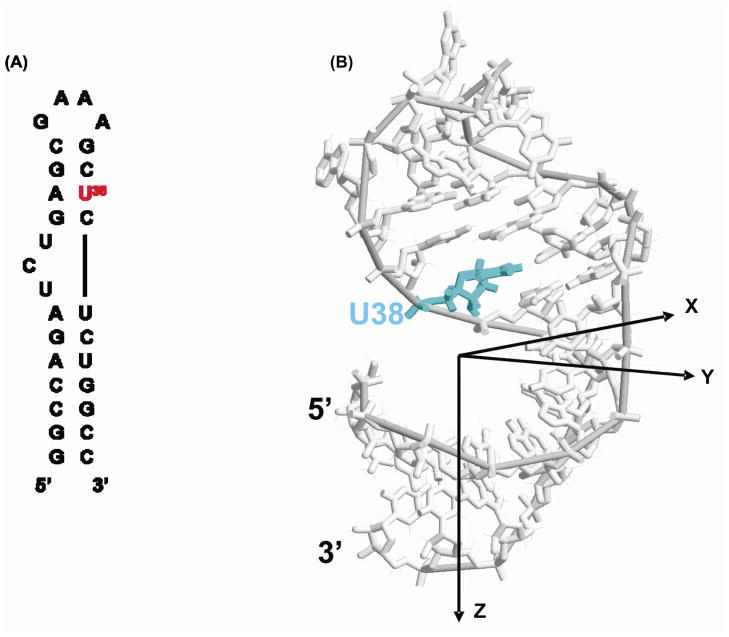
Figure 1.
A) Sequence and secondary structure of the HIV-1 TAR RNA construct used in this study, which includes a stable tetraloop for convenience instead of the native TAR loop. The U38 residue, which was deuterium labeled at the H5 and H6 sites for solid-state NMR and which is the subject of the present theoretical study, is highlighted in red. B) Lowest energy free TAR structure 1ANR. Hydrogen atoms have been removed from the figure for clarity. The Principal Axis System of the rotational diffusion tensor (PASd) is superimposed upon the molecule.
We focus this manuscript on the concerted dynamics of the TAR RNA construct shown in Figure 1A. In section 2 we introduce a slow exchange theory of concerted dynamics. In section 3A, constraints on the internal motions of TAR RNA obtained from solid-state NMR are explicitly stated and subsequently incorporated into the slow exchange correlation functions. A brief summary is also provided in section 3B of the method for calculating rotational diffusion tensors as implemented by HYDRONMR. In section 4, the theory of slow conformational exchange of section 2 is used to simulate the spin lattice and transverse relaxation rates for a 13C spin in the upper helix of TAR. In section 5, the validity of the assumptions made in constructing a slow conformational exchange correlation function for TAR RNA rotational diffusion is discussed.
2. Theory
NMR Relaxation in the Presence of Slow Conformational Exchange
Structural changes that alter significantly the shape of the TAR RNA molecule can perturb the global rotational motions of TAR in solution. Here we consider the problem of how slow conformational exchange perturbs the overall molecular tumbling motion and thus affects the relaxation of nuclear spins in the TAR RNA.
In deriving the model, we assume the existence in a RNA molecule of several types of motion occurring at different time scales. These include: 1) localized motions of individual structural units (nucleotide bases, furanose rings and small segments of the phosphodiester backbone); 2) long range conformational changes involving helical domains, the bulged loop, etc.; and 3) overall rotational motions of the TAR RNA molecule in solution. Prior studies of DNA oligonucleotides indicate that localized motions of small structural units in nucleic acids occur on the ns-ps timescale and are independent of overall rotational motions,22,23 which for a small RNA like TAR occurs on a time scale of 5–10 ns. In the theory that follows we therefore assume the localized base librations have no effect on overall molecular rotational diffusion. However, larger conformational rearrangements such as the reorientation of the helical domains of TAR will change the molecular shape, thereby modulating the molecular rotational diffusion tensor.17 Zhang and Al-Hashimi have similarly considered the modulation of the magnetic susceptibility tensors due to domain motion.24
The general problem of the coupling of molecular conformational changes to overall molecular tumbling has been treated recently in the context of the model-free analysis by Wong et al.25 for changes in the dimensions of idealized molecular shapes including the radii of spheres and the aspect ratio of cylinders. As in the theory of Wong et al.,25 we simplify the problem by treating the conformational motions in RNA as exchange between discrete structural forms, and we then solve the molecular diffusion problem in the presence of exchange between discrete conformers with distinct diffusion tensors.
Below we present the standard theory of correlation functions for single conformer diffusion (Equations 1 – 6), the diffusion equation for multiple conformers (Equation 7), as well as our own contribution in the form of the slow exchange formalism (Equations 8 and 9).
The free-diffusion equation can be written in terms of the diffusion tensor elements and the angular momentum operators:26
| (1) |
In equation 1, L̂i is the angular momentum operator about the ith axis, Dij is the ij component of the rotational diffusion tensor, and P(Ω⃗,t) is the probability that the molecular axis system will have rotated through an Euler angle vector of Ω⃗ at a time t relative to its initial orientation in the laboratory frame at time t = 0. Following Favro,26 the right hand side (RHS) of equation 1 can be expanded in the principal axis frame of the diffusion tensor (PASd) as follows:
| (2) |
where , and Dx, Dy and Dz are the eigenvalues of the diffusion tensor. In this formalism, the problem is thus reduced to finding the eigenvalues and eigenfunctions of the operator shown on the RHS of Equation 2. However, L̂z does not commute with the RHS operator, and a complete set of eigenfunctions cannot be found for this operator as long as Dx ≠ Dy. It is nonetheless possible to find eigenfunctions of the RHS operator in equation 2 for the first few eigenvalues of in an iterative manner. Utilizing the orthogonality of the first few resulting eigenfunctions, and the fact that the vector orientation of the C-H bond can be expressed as an expansion in these eigenfunctions, it is possible to calculate exactly two-time correlation functions of the C-H bond orientations relative to the laboratory frame, which has the form:
| (3) |
In equation 3, P2(x) is the second order Legendre polynomial, n̂(t) is the C-H bond orientation at time t, n̂(0) is the C-H bond orientation at t=0, and the amplitude al(A⃗0,B⃗0) are functions of the C-H bond orientation vector in the PASd frame, designated A⃗0 = (A1, A2, A3) and B⃗0 = (B1, B2, B3), where the superscript 0 indicates that the vector orientation is referenced to the PASd frame. In the absence of internal motion, A⃗0 = B⃗0. Equation 3 is equivalent to equation 6.29 in Favro26 and equation 35 in Woesner.27 The five amplitudes are defined as:
| (4) |
where , and . The correlation times are functions of the diffusion tensor eigenvalues alone and are given by:
| (5) |
where , and Δ is the same as above. The diffusion tensor eigenvalues are designated such that D3>D2>D1.
The occurrence of five correlation times in these expressions can be understood in terms of the number of parameters needed to describe a diffusion tensor with three different eigenvalues. Given the symmetry of the solvent, the diffusion tensor in an arbitrary frame is symmetric; thus, five unique parameters plus the trace are required to describe the tensor completely. The trace quantifies the overall scale of the diffusion tensor eigenvalues, and occurs in the exponential term e−6Dt = e−2Tr{D↔}t that multiplies the entire correlation function. This leaves five unique times and a scale-setting trace term in the correlation function.
We can incorporate discrete site jump models for local motions of the C-H bond vector into the rigid tumbling correlation function (equation 3) by averaging the amplitudes (al’s) over the local motion. The resulting expression for the general case of Nsite local discrete-site jumps is then:
| (6) |
Additional angular brackets show explicitly the averaging of the correlation function C(t) over the internal degrees of freedom. In the second line of Equation 6, the sites at time t are labeled by the index j and the sites at time t=0 are labeled by k. As seen here more explicitly, the al are functions of: A⃗0 (t), the orientation of the C-H bond in the diffusion tensor frame at time t, A⃗0 (0), the orientation of the bond at time t = 0, and of the diffusion tensor eigenvalues. The probability that a C-H bond lies at the orientation site j given that it was in site k at t=0 is given by the transition probability P(A⃗0(t, j)|A⃗0 (0,k)), while the a priori probability is given by P0(A⃗0(0,k)).
Equation 6 implicitly assumes that small amplitude local motions of the bases in RNA do not result in significant changes in the rotational diffusion tensor, and are thus independent of the overall molecular tumbling. This assumption is supported by the experimental data for U38, U25, and U23 in TAR RNA.28 However, reorientational motions of the helical domains of TAR RNA observed in RDC studies and in solid-state NMR studies of U38 are expected to modify the shape of the molecule in such a way as to perturb its hydrodynamic properties, effectively making the rotational diffusion tensor time-dependent. Treating these additional motions as exchanges of the TAR RNA molecule between N discrete structures, the diffusion equation becomes25
| (7) |
where the second term describes conformational transitions from conformer β to conformer α with rate Rαβ. The assumption in this equation is that the individual conformers tumble rigidly, punctuated by instantaneous shifts to rigidly-tumbling conformers with different diffusion tensors, so that relaxation times are obtained as averages over these multiple conformations. Wong et al.25 solved equation 7 for exchange between idealized structures like spheres and cylinders, but equation 7 can also be treated in a straightforward manner for completely anisotropic diffusion tensors, provided a significant rate separation exists between the molecular tumbling and the motions responsible for conformational exchange. For example, if conformational exchange can be described as a 2-site exchange with rates that are very slow compared to the rate of overall tumbling, then two independent populations of conformers exist, each representing one of the sites in the two-site motion. The contributions to the solution relaxation parameters from each of these conformers can be calculated by weighting the correlation functions by the population fraction of the ith conformational state (wi):
| (8) |
where the additional indices in and reflect the fact that diffusion tensor elements differ between distinct structural conformers. Fourier transformation of equation 8 results in the slow exchange expressions for solution longitudinal relaxation rate 1/T1, transverse relaxation rate 1/T2 and nuclear Overhauser relaxation, averaged over the distribution of N slow exchange conformers:
| (9) |
where the angular brackets in equation 9 indicate averaging over structural conformers. In equation 9, the following well known expressions are used in the calculation of the relaxation times and NOEs for individual rigidly-tumbling conformers:29
| (10) |
| (11) |
| (12) |
| (13) |
In equations 10–13, the spectral density is the cosine Fourier transform of C(t), , ωH and ωC are the Larmor frequencies of 1H and 13C respectively, μ0 is the permeability of a vacuum, γH and γC are the magnetogyric ratios of 1H and 13C, h is Planck’s constant (= 6.626 ×10−34 J.sec), rCH is the length of the C-H bond, and Δ is the chemical shift anisotropy (CSA). The effect of CSA tensor asymmetry has been neglected in these expressions. The errors associated with this assumption are discussed in section 4. For the 13C6-H6 bond length we used a value of 1.1 Å; the CSA of 13C6 is set at Δ = 212 ppm. The choice of CSA was based on the magnitude of the CSA tensor calculated by Ying et al for a Uracil-C6 atom.30 While the value used here is the mean value given in that reference (CSA = 212 ± 4 ppm), Ying et al. suggest using the lower end of the error range, i.e., 208 ppm. The difference in the results caused by assuming this lower value will be discussed in section 4.
The choice of rCH is of greater significance due to the r−6 dependence of the expressions for the relaxation times. Ying et al.30 suggest a value of 1.104 Å for rCH based on computational and RDC analysis. A neutron diffraction study of 1-Methylthymine by Frey et al.31 yielded a value for the C6-H6 bond length of 1.096 Å. The average of these two values gives our chosen value of 1.1 Å. However, it is important to note the different values used by other authors: Duchardt and Schwalbe32 used a value of 1.08 Å (not averaged over zero-point motion) in their analysis, while a survey of aromatic carbon-to-hydrogen bond lengths derived from neutron diffraction experiments gave a mean value of 1.083 Å.33 We briefly consider the effect of making a different choice of rCH in section 4. The selection of the value of 1.1 Å over a lower value can be justified by the fact that the value of 1.083 Å in Reference 33 was derived as an average over several aromatic compounds and did not specifically address nucleic acid bases, while both Ying et al.30 and Frey et al.31 target nucleic acids, with more specific data on thymine (similar to uracil) in the case of Frey et al. Moreover, the value used by Duchardt and Schwalbe32 is not averaged over the vibrational motion of the bond, a choice made to ensure that their order parameters did not exceed unity.
3. Methods
A. Rates, Amplitudes and Coordinate Frames for Internal Motions in TAR RNA
To extract 13C relaxation rates measured in solution from the slow exchange equation 9, the identities and weightings of the structural conformers of TAR involved in the exchange process(es) are required. In accordance with the conformational capture hypothesis, exchange occurs between the unbound TAR and a state that is structurally similar to the form of TAR in complexes with Tat-like peptides. We assume that one of the conformers involved in the slow exchange can be modeled as the lowest energy unbound TAR RNA structure reported by Aboul-ela et al.,12 hereafter referred to as 1ANR-1 (Figure 1B). On the basis of model free solution relaxation and RDC studies,13,17 the other exchange conformers are hypothesized to differ from 1ANR-1 in the mutual orientation of the upper and lower helices. Therefore, starting with the 1ANR-1 structure, other conformational forms of TAR RNA were generated by twisting and bending the distal helices about the bulged loop.
Further information on the rate of conformational exchange is provided by a recent solid-state deuterium NMR (ssNMR) study of selectively deuterated TAR, that monitored the solid-state exchange dynamics of uridine-5,6-2H2 incorporated at position U38 in the upper helix (Figure 1A) and at positions U25 and U23 in bulged loop, respectively.14 Of the three sites for which data were collected, only the dynamics of U38 is amenable to a slow exchange theoretical analysis. The repositioning of U23 and U25 observed by solid-state NMR are almost coincident with the time scale of overall molecular rotations, violating the separation of motional time scales used to derive equations 8 and 9.
The localized dynamics of U38 in the upper helix at a hydration of 16 waters per nucleotide include small-amplitude local motions (±4°) of the base at a rate of 2.2×108 s−1, superimposed upon a combination of 15° twisting and 9° bending of the entire nucleotide occurring at a much lower rate of 1.4×106 s−1. Because of its slow rate and the motional restrictions imposed upon U38 by its position within the upper helix, the combined twisting and bending motion is interpreted as a collective movement of the entire upper helix and likely corresponds to the domain motions observed in RDC studies.13,24 Since solid-state relaxation rates and the 2H NMR line shape for U38 do not change markedly at hydration levels of at least 30 waters per nucleotide,28 we assume that the rate of upper helix reorientation remains longer than the time scale of overall rotational motion in solution as well. Thus, the rates of collective dynamics of U38 and of the upper helix of TAR are separated in time scale from the rate of overall molecular rotation and are therefore amenable to analysis using equations 8 and 9. An order of magnitude estimate substantiating the claim of rate separation is provided in the following section (section 3B). Previously, Zhang, Al-Hashimi and co-workers have artificially produced such a separation in conformational and diffusion time-scales by elongating alternately the two TAR-RNA helices.13,17,19,34
To implement equation 8, relative orientations of the principal axis frame of the C6-1H6 dipolar tensor, the dynamic axis system C for local libration of the U38 base, and the axis frame M for the collective motion of the upper helix, were all inferred from the 2H ssNMR line shape and relaxation studies.14 The principal axis systems for the C6-1H dipolar and the 2H6 EFG tensor are axially symmetric about the C6-1H6 bond axis. The dynamic axis system C used to produce the small amplitude fast libration shown in Figure 2A has its zC axis normal to the plane of the base, while the xC axis bisects the two C6-1H6 bond orientations and the yC axis completes a right-handed coordinate system. The local motion of the U38 base is then treated as a two site exchange about the zC axis, making the solid angle ΩPC(t) = (0, βPC, γPC(t)) time dependent. Based on the analysis of the solid-state data, the difference between γPC in each of the two exchanging sites is 8 degrees and the rate of exchange is 2.2×108 s−1 and βPC is set to 90° in the above coordinate frame definition.14
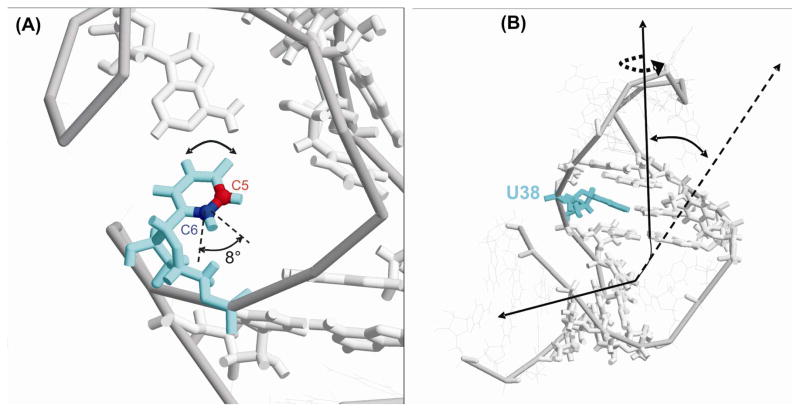
Figure 2.
A) Base-libration of U38 (light blue) relative to its pair-based nucleotide A27; the C5 (red) and C6 (dark blue) atoms are shown. The total amplitude of the best-fit base-libration model was found to be ±4o, corresponding to an 8° total angular excursion. B) Conformational exchange carries U38 (blue) within the entire upper helix between two distinct conformational states. Shown here is the transformation from the C frame to the M frame. The z axis of the C frame is indicated by the dotted line, and it is approximately perpendicular to the plane of the U38 base in 1ANR. The localized libration of the U38 base shown in Figure 2A is generated by a ±4o rotation about the zC axis. A bend of the entire upper helix is rendered by a rotation about yM and a twist and is affected by a rotation about zM. Both rotations are indicated in this figure.
For the collective motions of the upper helix, the M frame coincides with the crystal frame of one of the sites. To bring the crystal frame of the second site into coincidence with the M frame, two transformations are required. A bend of the entire upper helix is rendered by a rotation about yM and a twist is effected by a rotation about the z’ axis that results from the bend transformation, which together carry the upper helix into its orientation within the second conformer. The direction of yM determines the sense of the upper helix rotation relative to the bulged loop. Both rotations are depicted in Figure 2B.
B. Rotational Diffusion Tensors
To complete the definition of dynamic axes relevant to the TAR RNA relaxation problem, we need to establish the orientation of the principal axis frame of the rotational diffusion tensor (PASd) relative to the M, C, and C6-H6 bond axis frames. This in turn requires a determination of the eigenvalues and eigenvectors for the diffusion tensors of each of the two slowly exchanging conformers, which are characterized by different orientations of the upper helix relative to the lower helix. Equations 14 – 19 provide an overview of the standard method of calculating the diffusion tensors using a bead analysis. The well-known methodology is included in this paper to provide the reader with a clear picture of where the atomic element radius (AER) occurs in the calculation. The AER is defined below and is considered at some length in the interpretation of subsequent results.
Eigenvalues and eigenvectors for the rotational diffusion tensors of TAR are derived formally from a generalized Einstein relation35
| (14) |
where Drr and Dtt are 3×3 rotational and translational diffusion tensors, respectively. The off diagonal terms Dtr express the influence on diffusion of translational-rotational coupling. Similarly, Ξtt and Ξrr are the 3×3 translational and rotational friction tensors, respectively, and the matrix Ξtr represents the friction due to translational-rotational coupling. The rotational friction tensor is derived from the relation:
| (15) |
where U is a matrix with elements composed of non-hydrogenic atomic coordinates:
| (16) |
and C=B−1 is a 3N × 3N supermatrix (for a molecule composed of N discrete elements) composed of 3 × 3 blocks derived as follows
| (17) |
where ςi = 6πη0σi is the Stokes law friction, η0 is the solvent viscosity and Tij is the ij element of the hydrodynamic interaction tensor between two beads:35,36
| (18) |
Equation 18 expresses the fact that elements ij of the Oseen tensor are obtained by assuming non-hydrogenic atoms i and j can be treated as spherical beads with radii σi and σj, the centers of which are separated by a displacement vector R⃗ij and a distance Rij. I represents the 3 × 3 identity matrix. The atomic radii must however account for covalently attached protons and hydration. For i = j, Bij = (1/ςi)I. For the case in which the spheres are overlapping (Rij < σi + σj), equation 18 becomes
| (19) |
where the simplification σi = σj = σ has been made.
Several numerical algorithms based on modified Oseen tensors and bead models have been developed to obtain eigenvalues and eigenvectors for diffusion tensors.36,37 Here we use the public domain version of HYDRONMR.38 An important simplification in calculating the diffusion tensors with HYDRONMR is the assumption that a single value for σ, also called the Atomic Element Radius (AER), can be applied to all non-hydrogenic atoms in the molecule, as in equation 19. Although this is a significant simplification, it is questionable to use multiple independent atomic radii given a lack of detailed information on hydration in RNA on an atom-by-atom basis. The choices of AER used in this study are evaluated and described in Section 4 below.
As will be shown below in Figures 4A and 4B, the rotational diffusion eigenvalues for TAR RNA are on the order of 3×108 rad2 s−1. An order of magnitude estimate for the tumbling rate can be obtained by assuming spherical symmetry: rate ~ 6D0 ~ 109 s−1, where D0 is the diffusion coefficient for a sphere. This is almost three orders of magnitude higher than the exchange rate, justifying the use of a slow exchange methodology for motion of the U38 residue. Moreover, the effects of time-scale overlap start to become significant for a CE rate greater than about 1×107 sec−1, as established using a more general theory that does not require separation of time scales.
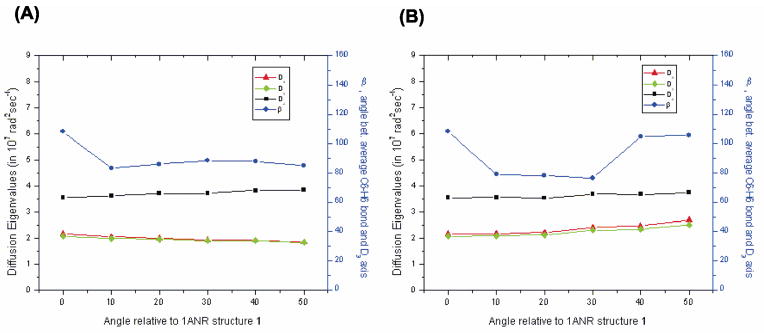
Figure 4.
Eigenvalues of the rotational diffusion tensor and the angle b between the 13C6-2H6 bond axis of U38 and the largest eigenvalue axis of the principal axis frame of the diffusion tensor (PASd) plotted as a function of rotation angle for the two set of structures generated by bending the TAR structures through two independent directions. The calculations use an AER of 2.3 Å. A) corresponds to the structures of Figure 3A, while B) corresponds to the structures of Figure 3B.
4. Results
Calculation of Relaxation Times of TAR RNA from the Slow Conformational Exchange Model
To apply the slow conformational exchange relaxation model to the calculation of relaxation times we assume that 13C6 relaxation is dominated by the fluctuations of its dipolar coupling to H6 and of its own CSA. For the 13C6-H6 bond length we used a value of 1.1 Å; the CSA of 13C6 is set at Δ = 212 ppm. The asymmetry of the CSA as well as the non-colinearity of the principal CSA axis and the dipole interaction axis were neglected in the relaxation equations. An estimate for the percentage error introduced by these approximations for pyrimidine C6 atoms is about 6–7%, for a CSA of 212 ppm.39 The error bars shown in all figures do not include this systematic error.
The values of the CSA and rCH chosen for this study were chosen from references discussed in section 2. To consider the effect of changing these parameters, we lowered the CSA down to 208 ppm, as recommended by Ying et al.30 The resulting T1 times increased by ~5 ms and the T2 times increased by ~0.4 ms. The magnitudes of these changes were considered to be sufficiently close to the error bars to be negligible.
An independent variation of rCH down to 1.096 Å31 or up to 1.104 Å30 resulted in a decrease or increase, respectively for the two changes, of T1 by ~5 ms and T2 by ~0.4 ms, again within experimental error. Lowering rCH to 1.08 Å,33 on the other hand, caused T1 to decrease by ~25 ms, and T2 by ~1.7 ms. These variations are significant enough to alter the best-fit parameters considered below. However, for reasons mentioned in section 2 above, we chose a higher value of 1.1 Å for all of the following analysis.
As discussed in section 3, one of the slowly exchanging conformers is very reasonably assumed to be represented by 1ANR-1, the lowest energy NMR structure reported for unbound TAR. To obtain the structure of the second TAR conformer, we systematically probed the conformational space sampled by the upper helix to test the possibility that, in solution, the angular displacement of the upper helix may differ from the bend angle of ~10° observed by ssNMR (the twist angle was assumed to have a negligible effect on the hydrodynamic properties, when considering an idealized upper helix with near-cylindrical symmetry). Specifically, the upper helix was reoriented relative to a fixed lower helix, starting with 1ANR-1 and systematically increasing the inter-helical angle in 10° increments up to 50°, which is the difference between the interhelical angles of free TAR and TAR bound to Tat. The change in the inter-helical bend angle relative to 1ANR-1 is referred to here as the conformation exchange (CE) rotation angle. For each structural model associated with a specific CE rotation angle, we evaluated the diffusion tensor using HYDRONMR and incorporated the localized base-libration motion (amplitude of ±4°, rate of 2.2×108 s−1) into the relaxation time calculations according to equation 8. The relaxation times for each structure associated with a CE rotation angle were subsequently averaged with those of 1ANR-1 using the slow exchange formalism of equation 9, assuming an equal population of conformers, as observed in solid-state NMR studies.14
Several sets of rotated structures were generated with the yM reorientation axis chosen perpendicular to the lower helix. To study how changing the direction of helical bending would change hydrodynamics and relaxation, the orientation of the yM axis (within the plane perpendicular to the lower helix) was varied through 30° increments. The arbitrarily chosen starting orientation was designated as the “0 degree series,” with subsequent increments labeled similarly as the “30 degree series,” “60 degree series,” etc. A superposition of atomic-detail TAR RNA structures of 1ANR-1 with CE rotation angles up to 50°, are shown for the “90 degree series” and “30 degree series” in Figures 3A and 3B, respectively. The following discussion will focus mainly on these two sets of structures for the sake of brevity (except for an inclusion of the “150 degree series” in Figures 7A and 7B). In practice, these structures were generated by shearing one of the bonds, and rotating the upper helix about the designated yM axis, keeping the lower helix and trinucleotide bulge positions fixed. It is important to note that the procedure of artificially modifying the 1ANR-1 TAR structure by rotating the upper helix was done only to approximate the hydrodynamic effect of rotating one helix relative to the other. We justify this approximation by observing that the hydrodynamic beads used in the diffusion tensor calculations overlapped sufficiently to wash out details of atomic-level bonding. Moreover, the U38 residue is rotated along with the upper helix and is thus not affected by the shearing and reattachment of the bonds. We have attempted to avoid steric clashes as much as possible, but for higher CE angles of 50° and above there are minimal instances of overlapping bonds and atoms (results for CE angles > 50°, while available were not included in the following analysis for this reason). These overlaps were not deemed to be significant enough to affect the sets of results shown in this manuscript.
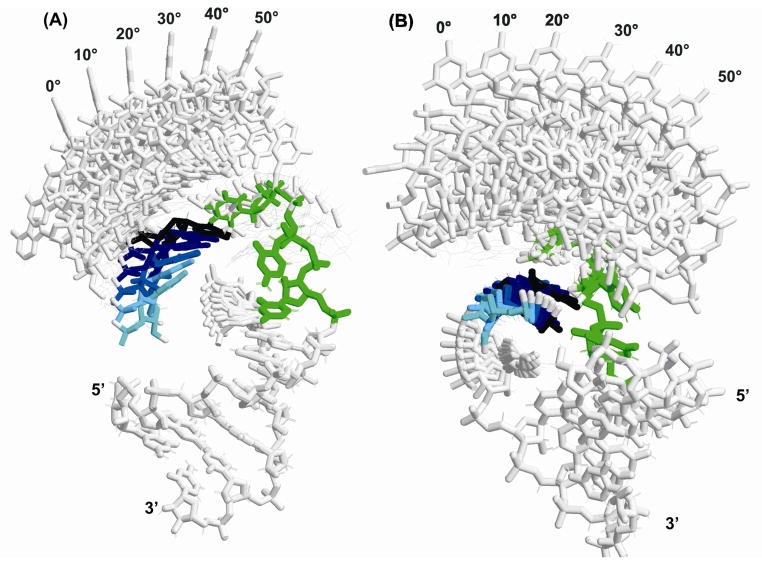
Figure 3.
Representation of the family of TAR structures differing in the rotation of the upper helix of TAR RNA relative to the lower helix starting from 1ANR-1 and systematically increasing the bend angle. The conformational exchange (CE) angle was varied in 10° increments from 0° to 50°. Both sets of structures are oriented in the figures such that the axis of helix reorientation is approximately out of the plane of the page. A) The “90 degree series”; and B) the “30 degree series”; conformational exchange in the two sets of structures is represented as a rotation about axes that are 60° apart in a plane perpendicular to the lower helix (The coloring of the U38 residue is varied from light blue to black for clarity in going from a CE angle of 0° to 50°. The bulge residues are highlighted in green in both panels.)
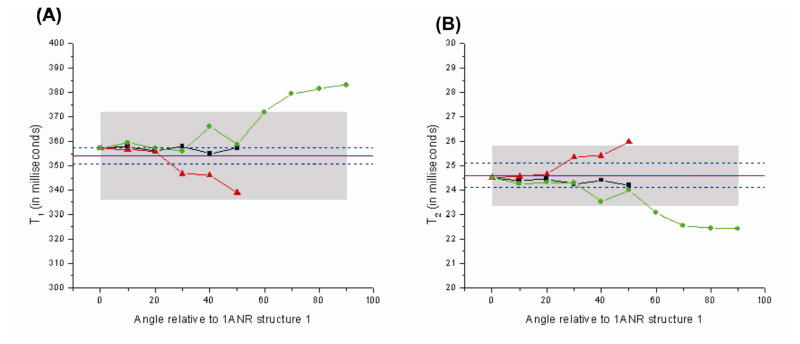
Figure 7.
A) T1 and B) T2 relaxation times calculated for the 13C6 spin of U38 with an AER of 2.3 Å for the TAR RNA structures designated as the “90 degree series” (Figure 3A; black), the “30 degree series” (Figure 3B; red), and for the “150 degree series” (green; the “150 degree series” has been extended to a CE angle of 90 degrees as there were no steric clashes even for high CE angles). The solid purple line and dashed blue lines represent the experimental values and error bars respectively of A) T1 = 354 ± 3.2 ms, and B) T2 = 24.6 ± 0.5 ms. The shaded regions in both panels represent error regions of ±5%.
Figures 4A and 4B display the eigenvalues of the diffusion tensor as functions of the CE rotation angle for the two choices of helical bending axes of Figures 3A and 3B, respectively. Also shown is the orientation of the 13C6-1H6 bond vector relative to the principal axis frame of the diffusion tensor (PASd), expressed as the angle β between the C6-H6 bond and the axis of PASd associated with the largest eigenvalue D3. The magnitudes of the diffusion eigenvalues are high enough to amply support the case for using a slow exchange theory (see estimate of tumbling rate in section 3B).
The model parameters that were adjusted independently of the experimental results include primarily the bead radius or atomic element radius (AER) and the sense of the direction of the upper helix rotation relative to the lower helix of TAR. Based on the solution conditions,16 the solvent viscosity in HYDRONMR was chosen to be the viscosity of 99.9% D2O at 25° C, η0 = 0.01096 Poises.40 Simulated T1 and T2 relaxation times were compared to solution NMR experimental relaxation times reported for the 13C6 spin of U38 as: T1 = 354 ± 3.2 ms, T2 = 24.6 ± 0.5 ms, and a heteronuclear NOE of 1.13 ± 0.01.16
A. AER dependence
Previous studies into the hydration radii of atoms in nucleic acids have yielded a range of results. In a study of several short oligonucleotides using HYDROPRO, a bead-modeling hydrodynamics program, Fernandes et al.41 showed that fits to hydrodynamic properties required different AER values for different molecules ranging from 1.6 to 3.8 Å. The authors assumed an average van der Waals radius of 1.7 Å for non-hydrogenic atoms. Aragon et al.42 found good agreement with optical Kerr effect rotational correlation times of tRNAphe using solvent-accessible surface-based hydrodynamic simulations with the BEST43 program, that included uniform hydration 1.1 Å in thickness. When added to the van der Waals radius of about 1.7 Å above, this yields an atomic radius of 2.8 Å.
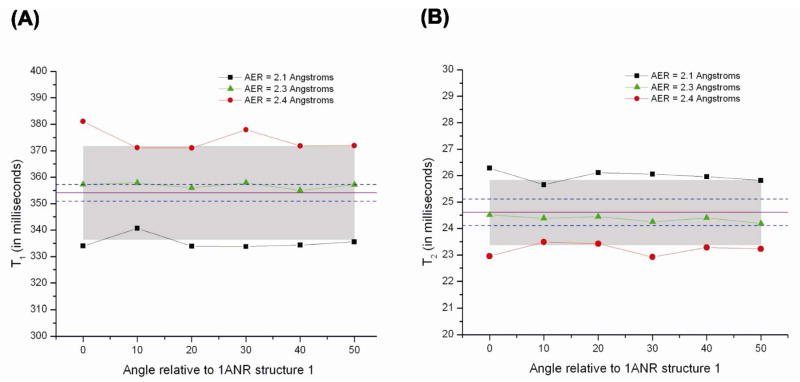
In view of this diversity of values for nucleic acids, we chose to vary the AER in order to get the best-fit to the solution data and the resulting range of values is from 2.1 to 2.4 Å (which lies within the range quoted by Fernandes et al.41). In Figures 5A and 5B, values of T1 and T2 are shown for three AER values of 2.1, 2.3 and 2.4 Å for the “90 degree series” (Figure 3A; AER = 2.2 Å was left out for clarity). In Figures 5A and 5B the experimental T1 and T2 values for 13C6 of 354 ms and 24.6 ms, respectively, are indicated by the solid, purple line, with dotted lines indicating the experimentally-determined uncertainties. Based on these calculations we see T1 values increase and T2 values decrease with increasing AER due to a corresponding increase in the tumbling times. However, for a given AER there is no discernible trend for this series as a function of CE angle, and relaxation times for all CE angles ≤ 50° fit the experimental data. A visual inspection of the structures as well as the trend in diffusion tensor eigenvalues in Figure 4A show that the rotational diffusion tensors remain fairly cylindrical throughout the reorientation process, and the β angle does not change significantly. Thus, no drastic changes in the rotational diffusion of the C-H bond are to be expected and the relaxation times do not vary. In the physical sample, however, as the upper helix begins to line up with the lower helix, the bulge would have to reconfigure itself and would possibly lead to a discernible asymmetry in the diffusion tensor.
Figure 5.
A) T1 and B) T2 values derived using equation 25 for the “90 degree series” (Figure 3A) as a function of AER and CE rotation angle. The solid purple line and dashed blue lines represent the experimental values and error bars respectively of A) T1 = 354 ± 3.2 ms, and B) T2 = 24.6 ± 0.5 ms. The shaded regions in both panels represent error regions of ±5%.
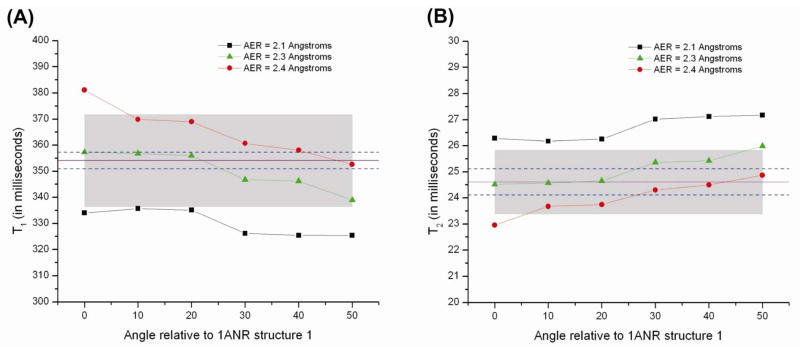
We repeated the same calculations for the “30 degree series” (Figure 3B). The results for T1 and T2 are shown in Figures 6A and 6B, respectively. The relaxation times for this series show more variation as a function of CE angle. This increased variation is due not only to changes in the principal elements of the rotational diffusion tensor, but also because of changes in the angle β which orients the C6-H6 bond relative to the PASd frame. Best fits to experimental T1 and T2 values occur for AER=2.3 Å and for smaller bend angles of < 20° – 30°.
Figure 6.
A) T1 and B) T2 values derived using equation 25 for the “30 degree series” (Figure 3B) as a function of AER and CE rotation angle. The solid purple line and dashed blue lines represent the experimental values and error bars respectively of A) T1 = 354 ± 3.2 ms, and B) T2 = 24.6 ± 0.5 ms. The shaded regions in both panels represent error regions of ±5%.
There is a correlation between the AER and the CE angle where an increase in the AER allows higher bend angles to be fit. For example, in addition to the fit parameters above, an AER of 2.4 Å together with CE angles between 30° and 40° fit the experimental data fairly well. Continuously increasing the AER from 2.3 Å to 2.4 Å and more will result in increasingly larger CE angles fitting the experimental data. It is possible to explain the correlation between the AER and CE angles in terms of the effect of increasing the AER upon the hydrodynamic models: if a model is composed of larger spheres, the anisotropies are partially “washed out.” Therefore, by scaling up the AER, increasingly bent molecules with large CE angles can start to approximate the experimental data better (while at the same time lower CE angle structures will hydrodynamically approach the ideal spherical case). In general, however, we believe that the results for smaller CE angles are more reliable due to the fact that the bulge configuration, frozen in the 1ANR-1 state, would be less representative of the physical structure of the bulge as the upper helix deviated further and further from the 1ANR-1 orientation.
Due to the correlation between the AER and the CE angle, to isolate best-fit CE angles an independent assessment of the AER is needed. This can be achieved by considering more explicit hydration models for nucleotides, attempts at which have been described at the beginning of this sub-section. An establishment of the AER would then allow the selection of best-fit CE angles. Conversely, if we consider the CE angles to be constrained by ssNMR models, it is possible to establish the AER associated with a given molecule: the ssNMR best-fit value for the upper helix bend of 9° supports an AER of 2.3 Å. Again, if we allow the angle to vary under solution conditions, it is possible to extract slightly different AERs.
B. Dependence on direction of helical bending
Figure 7A shows calculated T1 values as a function of CE rotation angle for the set of structures of Figures 3A and 3B, as well as the “150 degree series” with an AER of 2.3 Å. The results for the “150 degree series” were extended to a CE angle of 90 degrees as there were no steric clashes in this series, even at high CE angles. For the structures of Figure 3A, the calculated T1 relaxation time is almost invariant as a function of CE angle and lies partly within experimental uncertainty. For the set of structures of Figure 3B, only CE angles < 30° produce simulated T1 values that are within experimental error of the measured value. The data for the “150 degree series” shows some variation in the range of CE angles between 30° and 50° degrees, and then shows a clear deviation away from the experimental data for angles > 50°. This series is similar to the structures in Figure 3A (the “90 degree series”) in that the upper helix “straightens out” relative to the lower helix (not shown) and is thus a good representation of the solid-state models which predict such a helical realignment in the transition from free to bound TAR. The “150 degree series” does however differ from the series in Figure 3A in the position of the bulge relative to the upper helix during the reorientation. From Figure 7A one can therefore conclude that the CE angles that match the data are sensitive to the direction of reorientation of the helix, as evidenced by the graphs for both the structures in Figure 3B and the “150 degree series.” Similar considerations apply to the results for the T2 calculation shown in Figure 7B.
If we were to select a range of CE angles based on ssNMR simulations, it would be possible to select out a preferred helical reorientation direction. Conversely, an independent determination of the direction of reorientation, perhaps based on solid-state models and/or steric considerations might allow the CE angles to be determined from the above data.
In the above analyses the NOE values were not considered as the values varied negligibly over the entire range of parameter values.
5. Discussion
We have developed a slow exchange model to describe the solution behavior of TAR RNA in the presence of internal motions that alter the shape of the RNA and therefore its rotational diffusion. Our theory of solution NMR relaxation accounts for the non-rigid rotational motion of a molecule of arbitrary structure possessing a rotational diffusion tensor with arbitrary eigenvalues. The application of the model requires a significant separation in time scales between internal and global motion, a condition that is satisfied in the present system. The slow exchange correlation function given in equation 8, when parameterized exactly according to models of the internal dynamics of TAR RNA obtained by prior solid-state NMR studies, simulates to within experimental error the T1 and T2 data for a 13C spin in U38 within the upper helix of TAR RNA, the same nucleotide for which the solid-state models were developed. The results of the slow exchange model applied to TAR in section 4, together with prior 2H ssNMR and solution relaxation/RDC studies, indicate that conformational capture is a feasible paradigm for describing recognition between TAR RNA and Tat-like peptides.
By its very nature, a theory of relaxation that involves non-rigid rotation will have more parameters than a theory of rigid rotation, even when the diffusion equation is simplified by treating motion as exchange between discrete conformers with distinct rotation tensors, as was done in equation 7 and in the theory of Wong et al.25 Thus, a serious concern is that relaxation and line shape data are better simulated by assuming extra motions and additional fitting parameters. However, the motions that were introduced into the present model of TAR dynamics are supported by other data including solid-state relaxation times and line shapes, as well as RDC data, all of which indicate the presence of collective motions of the helices of TAR RNA about a putative flexible bulged loop. It can be also seen that even the single conformer 1ANR-1 (the CE angle = 0° data point in all graphs) fits the solution experimental data well, without recourse to the conformational exchange formalism. This is to be expected if the change in the hydrodynamic behavior of the molecule is not large in the transition to the proposed exchange partner. Also, we do not believe that a single conformer can accurately represent the physical condition of the molecule in solution conditions given that the ssNMR results support the presence of such a motion, and it is unlikely that there would be a reduction in the types of motion available to the molecule in going from solid-state to solution sample conditions.
It is certainly possible that the values of the slow exchange model parameters derived from solid-state NMR might not accurately portray the amplitudes and rates of these motions in solution. However, solid-state relaxation rates for the relaxation of the base deuterons of U38, U25, and U23 in TAR RNA change very slowly at high levels of hydration,28 indicating that internal motions converge to stable amplitudes and rates long before the bulk solution state is reached. In order to further address this issue, we probed a wide range of models of conformational exchange generated by systematically increasing the conformational exchange angle from 0° (starting structure) to a distorted structure with a rotation angle of 50° (the maximum CE angle can be raised to any arbitrary value as long as physically reasonable conformers are available). The results of section 5 show that solution experiments are in agreement with different CE angles depending on the AER and the direction of helical reorientation.
With regard to the rates of conformational exchange, it was assumed the time scale separation between conformational exchange and overall rotational motion exists in solution, but the solid-state value of 1.4×106 s−1 was not explicitly used. To test the assumption of slow conformational exchange, a more general solution would require solving equation 7 for arbitrarily structured molecules without a time scale separation. Such a theory would allow the analysis of the relaxation of spins of the U23 and U25 nucleotides as well. We have recently obtained such a solution and will report the ensuing results in the near future.
In order to compare our results to previously published results by Zhang, Al-Hashimi and co-workers13,17 we examined the order tensor-derived inter-helical bending angles, as well as the ensemble-derived motional parameters in reference 13. The order tensor analysis yields average inter-helical bending angles of 25° (short upper helix relative to elongated lower helix) and 54° (short lower helix relative to elongated upper helix), with the difference being interpreted as the effect of twisting motions affecting the two helices. While solid-state results reported in Olsen et al.14 disagree with the magnitude of the order tensor-derived bending motions, they do indicate the presence of simultaneous twisting and bending motions, and the results reported in this manuscript do not exclude inter-helical bend angles of 25°, or even 54°, for appropriate choices of the AER and the direction of helical bending. Furthermore, the three-conformer ensemble study in reference 13 yielded an overall helical bend of 94° along with an upper helical twist of 110° and lower helical twist of 53°. While these angles are much larger than the equivalent solid-state parameters14, they can potentially be reconciled with the results of this paper, albeit with an AER outside of the range of values considered here (> 2.4 Å). Finally, we considered the timescale of domain motions reported in reference 17 to be on the order of 1.5 ns to 1.9 ns. These are several orders of magnitude faster than the slow exchange suggested by the solid-state models of reference 14. Thus, if it is assumed that the solid-state models are a fair representation of the solution motions, then there is a sharp discord between the results presented herein and those of references 13 and 17. It is possible that the solid state matrix imposes some constraints on the motions compared to solution, although a thorough study of dynamics as a function of hydration in the solid state indicates that this is unlikely. Additional experiments and theoretical studies will be required to address the origin of this difference.
Finally, the structures generated above assume a frozen configuration for the bulge. In the physical sample, however, as the upper helix begins to line up with the lower helix, the bulge would have to reconfigure itself possibly leading to a discernible asymmetry in the diffusion tensor. This is a significantly more difficult problem given the number of under-constrained bulge degrees of freedom, and will have to be addressed in the future.
In this manuscript we have modeled only the U38 residue. Our justification in doing so is the relative degree of certainty in the available degrees of motion of this residue which allowed us to demonstrate the slow exchange methodology. Nevertheless, solution NMR relaxation studies show that for all pyrimidine 13C6 spins in the upper helix of TAR, T1 values lie within the narrow range of 354±14 ms and T2 values are similarly distributed narrowly within 25.2±0.2 ms. The slow exchange model can therefore account for the relaxation of all the 13C6 pyrimidine spins by adjustment of the orientation of the base relative to the frame of the diffusion tensor.
6. Conclusions
We have simulated solution NMR experimental relaxation times with models derived from solid-state NMR studies for the U38 residue in HIV-1 TAR RNA. In addition to incorporating base-libration into single conformers, this also involved using a formalism of conformational exchange between conformers at a rate slower by over two orders of magnitude than tumbling rates. The slow conformational exchange simulation procedure is completely general, and for sufficient rate separation, can easily be applied to a discrete set of conformers. Starting with solid-state models, and incorporating them into molecular tumbling equations, it is possible to address the question of whether the same motions are common to both sample conditions: if the solution results can be simulated through this method, then we have extended the domain of support for such motions to a larger data set; however, even if ssNMR models are at odds with solution NMR experiments, we can iterate the procedure for modified internal motional rates and/or amplitudes, or change the motional models altogether. We have endeavored to provide atomic detail in the combined modeling of solid-state and solution NMR experiments without recourse to hydrodynamic symmetry. Future research will attempt to characterize situations of conformational exchange with rates overlapping tumbling rates, as well as accounting for accompanying modifications of bulge configurations.
Acknowledgments
This work was supported by grants from the NSF (MCB-0642253) and NIH (RO1-EB03152) to G.P.D. and G.V.. We are grateful to Michael Bardaro for providing the TAR relaxation data and their error analysis and to Kari Pederson for help with the editing of the manuscript.
References
- 1.Dethoff EA, Hansen AL, Musselman C, Watt ED, Andricioaei I, Al-Hashimi HM. Biophysical Journal. 2008;95:3906–3915. doi: 10.1529/biophysj.108.140285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Shajani Z, Deka P, Varani G. Trends in Biochemical Sciences. 2006;31:421–424. doi: 10.1016/j.tibs.2006.06.002. [DOI] [PubMed] [Google Scholar]
- 3.Koplin J, Mu Y, Richter C, Schwalbe H, Stock G. Structure. 2005;13:1255–1267. doi: 10.1016/j.str.2005.05.015. [DOI] [PubMed] [Google Scholar]
- 4.Al-Hashimi HM. Biopolymers. 2007;86:345–347. doi: 10.1002/bip.20754. [DOI] [PubMed] [Google Scholar]
- 5.Aboul-ela F, Karn J, Varani G. Journal of Molecular Biology. 1995;253:313–332. doi: 10.1006/jmbi.1995.0555. [DOI] [PubMed] [Google Scholar]
- 6.Hennig M, Williamson JR. Nucleic Acids Research. 2000;28:1585–1593. doi: 10.1093/nar/28.7.1585. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Brodsky AS, Williamson JR. Journal of Molecular Biology. 1997;267:624–639. doi: 10.1006/jmbi.1996.0879. [DOI] [PubMed] [Google Scholar]
- 8.Long KS, Crothers DM. Biochemistry. 1999;38:10059–10069. doi: 10.1021/bi990590h. [DOI] [PubMed] [Google Scholar]
- 9.Puglisi JD, Tan R, Calnan BJ, Frankel AD, Williamson JR. Science. 1992;257:76–80. doi: 10.1126/science.1621097. [DOI] [PubMed] [Google Scholar]
- 10.Puglisi JD, Chen L, Frankel AD, Williamson JR. Proceedings of the National Academy of Sciences of the United States of America. 1993;90:3680–3684. doi: 10.1073/pnas.90.8.3680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Long KS, Crothers DM. Biochemistry. 1995;34:8885–8895. doi: 10.1021/bi00027a041. [DOI] [PubMed] [Google Scholar]
- 12.Aboul-ela F, Karn J, Varani G. Nucleic Acids Research. 1996;24:3974–3981. doi: 10.1093/nar/24.20.3974. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Zhang Q, Stelzer AC, Fisher CK, Al-Hashimi HM. Nature. 2007;450:1263–1267. doi: 10.1038/nature06389. [DOI] [PubMed] [Google Scholar]
- 14.Olsen GL, Bardaro MFJ, Echodu DC, Drobny GP, Varani G. Journal of the American Chemical Society. 2010;132:303–308. doi: 10.1021/ja907515s. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Shajani Z, Varani G. Biopolymers. 2007;86:348–359. doi: 10.1002/bip.20650. [DOI] [PubMed] [Google Scholar]
- 16.Bardaro MFJ, Shajani Z, Patora-Komisarska K, Robinson JA, Varani G. Nucleic Acids Research. 2009;37:1529–1540. doi: 10.1093/nar/gkn1074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Zhang Q, Sun X, Watt ED, Al-Hashimi HM. Science. 2006;311:653–656. doi: 10.1126/science.1119488. [DOI] [PubMed] [Google Scholar]
- 18.Lange OF, Lakomek N-A, Farès C, Schröder GF, Walter KFA, Becker S, Meiler J, Grubmüller H, Griesinger C, Grootfaster BLd. Science. 2008;320:1471–1475. doi: 10.1126/science.1157092. [DOI] [PubMed] [Google Scholar]
- 19.Zhang Q, Al-Hashimi HM. RNA. 2009;15:1941–1948. doi: 10.1261/rna.1806909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Tugarinov V, Liang Z, Shapiro YE, Freed JH, Meirovitch E. Journal of the American Chemical Society. 2001;123:3055–3063. doi: 10.1021/ja003803v. [DOI] [PubMed] [Google Scholar]
- 21.Olsen GL, Echodu DC, Shajani Z, Bardaro MFJ, Varai G, Drobny GP. Journal of the American Chemical Society. 2008;130:2896–2897. doi: 10.1021/ja0778803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Echodu D, Goobes G, Shajani Z, Pederson K, Meints G, Varani G, Drobny G. Journal of Physical Chemistry B. 2008;112:13934–13944. doi: 10.1021/jp801723x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Schurr JM, Fujimoto BS, Nuutero S. Journal of Magnetic Resonance Series A. 1994;106:1–22. doi: 10.1006/jmrb.1995.1009. [DOI] [PubMed] [Google Scholar]
- 24.Zhang Q, Al-Hashimi HM. Nature Methods. 2008;5:243–245. doi: 10.1038/nmeth.1180. [DOI] [PubMed] [Google Scholar]
- 25.Wong V, Case DA, Szabo A. Proceedings of the National Academy of Sciences of the United States of America. 2009;106:11016–11021. doi: 10.1073/pnas.0809994106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Favro LD. Physical Review. 1960;119:53–62. [Google Scholar]
- 27.Woessner DE. Journal of Chemical Physics. 1962;37:647–654. [Google Scholar]
- 28.Olsen GL, Bardaro MFJ, Echodu DC, Drobny GP. Journal of Biomolecular NMR. 2009;45:133–142. doi: 10.1007/s10858-009-9355-6. [DOI] [PubMed] [Google Scholar]
- 29.Abragam A. Principles of Nuclear Magnetism. Clarendon Press; Oxford: 1961. [Google Scholar]
- 30.Ying JF, Grishaev A, Bryce DL, Bax A. Journal of the American Chemical Society. 2006;128:11443–11454. doi: 10.1021/ja061984g. [DOI] [PubMed] [Google Scholar]
- 31.Frey MN, Koetzle TF, Lehmann MS, Hamilton WC. Journal of Chemical Physics. 1973;59:915–924. [Google Scholar]
- 32.Duchardt E, Schwalbe H. Journal of Biomolecular NMR. 2005;32:295–308. doi: 10.1007/s10858-005-0659-x. [DOI] [PubMed] [Google Scholar]
- 33.Allen FH, Kennard O, Watson DG, Brammer L, Orpen AG, Taylor R. Journal of the Chemical Society, Perkin Transactions II. 1987:S1–S19. [Google Scholar]
- 34.Hansen AL, Al-Hashimi HM. Journal of the American Chemical Society. 2007;129:16072–16082. doi: 10.1021/ja0757982. [DOI] [PubMed] [Google Scholar]
- 35.Carrasco B, de la Torre JG. Biophysical Journal. 1999;76:3044–3057. doi: 10.1016/S0006-3495(99)77457-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Yamakawa H. Journal of Chemical Physics. 1970;53:436–443. [Google Scholar]
- 37.de la Torre JG, Bloomfield VA. Biopolymers. 1977;16:1747–1763. doi: 10.1002/bip.1977.360160813. [DOI] [PubMed] [Google Scholar]
- 38.de la Torre JG, Huertas ML, Carrasco B. Journal of Magnetic Resonance. 2000;147:138–146. doi: 10.1006/jmre.2000.2170. [DOI] [PubMed] [Google Scholar]
- 39.Shajani Z, Varani G. Journal of Molecular Biology. 2005;349:699–715. doi: 10.1016/j.jmb.2005.04.012. [DOI] [PubMed] [Google Scholar]
- 40.Millero FJ, Dexter R, Hoff E. Journal of Chemical and Engineering Data. 1971;16:85–87. [Google Scholar]
- 41.Fernandes MX, Ortega A, Martinez MCL, de la Torre JG. Nucleic Acids Research. 2002;30:1782–1788. doi: 10.1093/nar/30.8.1782. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Aragon SR, Perez M, Ng K, Eden D. Optical Kerr Effect of DNA Oligomers and RNA. In: Stoylov SP, Stoimenova MV, editors. Molecular and Colloidal Electro-Optics. Vol. 134 Taylor & Francis; Boca Raton: 2006. [Google Scholar]
- 43.Aragon SR, Flamik D. Macromolecules. 2009;42:6290–6299. [Google Scholar]