Connecting Rare DNA Conformations and Surface Dynamics using Single-Molecule Resonance Energy Transfer

Abstract

A mechanistic understanding of single-stranded DNA (ssDNA) behavior in the near-surface environment is critical to advancing DNA-directed self-assembled nanomaterials. A new approach is described that uses total internal reflection fluorescence microscopy to measure resonance energy transfer at the single-molecule level, providing a mechanistic understanding of the connection between molecular conformation and interfacial dynamics near amine-modified surfaces. Large numbers (>10⁵) of ssDNA trajectories were observed, permitting dynamic correlation of molecular conformation with desorption and surface mobility. On the basis of dynamic behavior, molecules could be designated as members of the more common coiled population or a rare, weakly bound conformation. Molecules in the coiled state generally exhibited slow diffusion and conformational fluctuations that decreased with increasing average end-to-end distance. Lattice simulations of adsorbed self-avoiding polymers successfully predicted these trends. In contrast, the weakly bound conformation, observed in about 5% of molecules, had a large end-to-end distance but demonstrated conformational fluctuations that were much higher than predicted by simulations for adsorbed flexible chains. This conformation correlated positively with desorption events and led to fast diffusion, indicating weak surface associations. Understanding the role of the weakly bound conformation in DNA hybridization, and how solution conditions and surface properties may favor it, could lead to improved self-assembled nanomaterials.

Many nanomaterials and nanodevices rely on DNA as a recognition element to guide supramolecular self-assembly,^1–5 a process that involves a delicate balance between competing non-covalent interactions. Watson-Crick base-pairing between partially complementary DNA strands leads to double helical secondary structure that further directs self-assembly of DNA, along with any tethered nanocomponents, into specific supramolecular structures. For example, sophisticated DNA origami has been demonstrated in two and three dimensions.^6–9 These structures, with nanoscale organization, have been decorated with antibodies¹⁰ and nanoparticles,^11–13 or used as a template for metallic nanowire formation.¹⁴

Specific interactions that lead to DNA hybridization are influenced both by environmental factors (e.g. pH, temperature, concentration, ionic strength, etc.) and chemical properties of vicinal surfaces (e.g. microchips, nanoparticles, nanotubes, etc.). Particularly in the case of surfaces, several nanomaterials, specifically carbon nanotubes and metal nanoparticles, interact strongly with single-stranded DNA (ssDNA), presumably inhibiting its ability to hybridize and direct supramolecular assembly.^15–17 It is certainly possible that many other surface chemistries used in nanomaterials, to some degree, inhibit hybridization via a combination of electrostatic, hydrogen bonding, π-stacking, and hydrophobic interactions. Thus one important challenge in supramolecular DNA nanotechnology is to mechanistically link DNA-surface interactions with the ability of DNA to hybridize and drive self-assembly.

While static intermolecular interactions leading to DNA molecular recognition are well understood, simulations point to the significant role of surface dynamics in DNA hybridization.¹⁸ Dynamic surface effects remain mysterious partly because existing experimental methods cannot probe the complex choreography of successive rare events leading to self-assembly. Ensemble-averaging methods are insensitive to such events, and current single-molecule approaches, capable of tracking a few hundred molecular trajectories, are inadequate. Thus the goal of this work is to develop experimental techniques to provide mechanistic information about ssDNA dynamics and conformation in near-surface environments. We have chosen to study ssDNA on the assumption that the surface behavior of the unhybridized strand will ultimately determine its ability to cross any kinetic barriers to self-assembly. Put another way, conformation and mobility of ssDNA is expected to play a large role in hybridization dynamics and understanding these phenomena is a precondition for studying the hybridization process. Furthermore, by using freely adsorbing, desorbing, and diffusing ssDNA, we can use dynamic behaviors such as desorption frequency and interfacial diffusion to assess the strength of DNA-surface interactions and their relationship with molecular conformation.

Total internal reflection fluorescence microscopy (TIRFM) with single-molecule (SM) resolution can provide information on rare events leading to self-assembly due to its sensitivity to heterogeneous behavior.^19–25 When combined with resonance energy transfer (RET) techniques, SM-TIRFM can also track macromolecular conformation.^26–28 Despite this potential, SM-TIRFM methods to date have been limited by poor statistics, making the technique insensitive to important rare events; this is due to the low number of molecules (10²–10³) typically tracked in SM-TIRFM.^{20–21, 23, 29–31} Furthermore, while RET provides useful information by itself, the ability of SM-RET to correlate conformation with other dynamic phenomena, such as surface affinity, mobility, or hybridization has yet to be realized. In this manuscript, we describe a new molecular tracking approach, based on dynamic SM-RET, capable of making direct connections between the conformation of individual molecules and their surface affinity and mobility at nanometer and micron length scales. Additionally, by developing methods that allowed the observation of >10⁵ molecular trajectories, we are able to identify direct correlations between rare extended DNA conformations and important dynamic events such rapid surface mobility, conformational fluctuations, and desorption. These methods illustrate the potential of SM-RET in order to inspire a new level of mechanistic understanding of DNA-surface interactions.

Results and Discussion

In our experiments, dual-channel image sequences were acquired of RET-labeled ssDNA 15-mers at the interface between aqueous solution (10 mM phosphate buffer, pH = 8.0) and amine-modified fused silica surfaces. At pH<9, the cationic amine functionality has a favorable electrostatic interaction with the anionic DNA backbone although it must be noted that many other non-covalent interactions (e.g. hydrogen-bonding or hydrophobic effects) may also be important in the ssDNA interaction with the surface. Trajectories of 3x10⁵ molecules were identified; however, the vast majority (>90%) represented very short-lived interfacial species. While molecules belonging to this population would dominate the data associated with ensemble-averaging techniques, it seems unlikely that they play an important role in surface self-assembly due to their short surface residence time. Because of the large number of trajectories initially captured, we identified >10⁴ molecules with residence times≥2.7s for detailed analysis. The complete residence time distribution and discussion of this choice of 2.7s is addressed in Supporting Information. We characterized the instantaneous conformation of each ssDNA molecule by the relative end-to-end distance, d = (F_D/F_A)^1/6, where F_D and F_A are the fluorescence intensities of donor and acceptor species, respectively. This quantity is proportional to the absolute end-to-end distance through a scale-factor that depends on fluorophore- and machine-specific parameters, as described in the Methods.

In this work, the vast majority of observed conformations fell in the range 0.2 < d < 1.4. Although d is a relative measure of end-to-end distance, it is instructive to estimate what this corresponds to on an absolute scale. Assuming a Förster radius of 5.0 nm ³² and a machine constant of ~1 (cf. equation (1)) we approximate that ssDNA end-to-end distances between 1.0–7.0 nm are resolved in this experiment. Notably, this assumption neglects the change in Förster radius that may be induced by hindered fluorophore rotation at the surface. Hindered rotation has been demonstrated in single-molecule RET experiments²⁶ but this effect is not expected to change the Förster radius by more than 10–20% unless the transition dipoles of the fluorophores are frozen in nearly perpendicular orientations.³² Given a ssDNA length of 15 bases and a repeating unit length of 0.59 nm,³³ the contour length of this sequence is at least 8.9 nm and this does not include the length of dye spacers (shown in Supporting Information) which may contribute an additional 1–2 nm to the contour length. This contour length is larger than the longest distances that we observe here, suggesting that even highly extended molecules are not stretched to their full contour length. To assess the lower limit of our measured distances, we turn to the work of Bishop and Clarke, which gives the probability distribution of end-to-end distances for self-avoiding walks in two and three dimensions.³⁴ Their work indicates that over 70% of ssDNA configurations will have an end-to-end distance greater than 1.0 nm in three dimensions while nearly 90% will exceed this value in two dimensions (calculations provided in the Supporting Information). Thus, our estimated sensitivity of 1.0–7.0 nm is well suited to resolve conformations of the 15-mer chosen in this work.

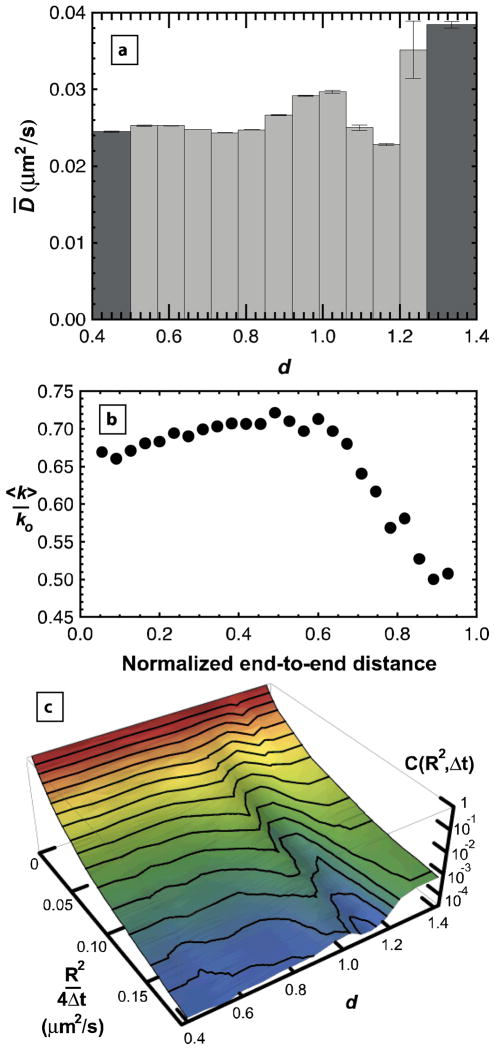
Interfacial mobility of molecules was observed to directly correlate with molecular conformation (d) in an interesting way (Fig. 1a). In this analysis, individual diffusive steps of trajectories were binned by the value of d immediately following the step, and the mean diffusion coefficient, D̄, was extracted from this distribution of step sizes (Fig 1c) as described in the Methods. Since molecules regularly changed conformation throughout their trajectories, this type of analysis enabled us to examine instantaneous correlations between conformation and mobility. Particularly surprising was the anomalously fast interfacial mobility associated with highly extended molecules, e.g. d≥1.2. The increased mobility for some values of D̄ can also be seen as elevated “ridges” in the cumulative squared-displacement distributions for different values of d (Figure 1c). In this plot, the function, C(R²,Δt), represents the probability of a squared-step size that is ≥ R²/4Δt. With a log-scale for the cumulative probability, C(R²,Δt), a straight line in the ln C-R² plane would indicate a single diffusive mode, but these distributions are clearly curved, indicating multiple diffusive modes for objects with a given d. This multi-mode diffusive behavior is commonly observed in molecules that can have multiple mechanisms of interaction with a solid substrate.^21–22

Figure 1.

Mean surface diffusion coefficient ( D̄ ) depends on relative end-to-end distance (d). (a) is elevated in the range 0.9<d<1.05 and also for 1.2≤d, indicating weaker surface interactions in this range. Bin sizes are demonstrated by the width of each bar except for the dark grey bars which also include values more extreme than the shown range for d. Error bars are calculated from the standard error determined from multimodal fits to each cumulative squared-displacement distribution. (b) Simulated average off-rate <k> is shown as a function of end-to-end distance normalized by contour length for a model adsorbed polymer with a surface interaction energy of – 0.1 kT per adsorbed monomer. An increase in <k> with increasing molecular extension is followed by a sharp drop at larger extension. This result qualitatively explains elevated D̄ for d<1.2. Off-rates are normalized by k_o which is the off-rate for a polymer that doesn’t interact with the surface. (c) The cumulative squared-displacement distribution is shown as a function of d, using the d-bins shown in (a). The two ridges correspond to elevated values of D̄.

In order to understand this behavior, it is useful to consider these data in the context of the “partial detachment” model, where surface diffusion is considered an activated process with an activation energy associated with the strength of adsorbate-surface interactions.^21–22 Within this paradigm, one can calculate the expected behavior of the interfacial diffusion coefficient for an adsorbed flexible chain. The Boltzmann-weighted average of the “off-rate” (<k>), is shown as a function of end-to-end distance in Figure 1b for an adsorbed flexible chain on a cubic lattice (details provided in the Methods). The modest increase with d for compact coiled chains is an entropic effect due to the large number of coiled configurations that involve excursions away from the surface and therefore have fewer surface contacts. The dramatic decrease in <k> for more extended chains (d>1) reflects the fact that most extended conformations have more attractive surface contacts. Thus the experimental data in Fig. 1a for d<1.2, exhibiting a modest rise in D̄ with increasing d followed by a decline in D̄, are consistent with expectations for an adsorbed chain. For d≥ 1.2, an unexpected, sharp increase in mobility was observed that was not predicted by the simulated conformations of an adsorbed chain. This discrepancy suggests the presence of a distinct population representing a separate conformational state where extreme molecular extension is correlated with a decrease in surface affinity and a concomitant increase in mobility, i.e. a weakly bound state. This state must be stabilized, either kinetically or thermodynamically, by factors other than favorable monomer contacts with the surface that were accounted for in the lattice simulations.

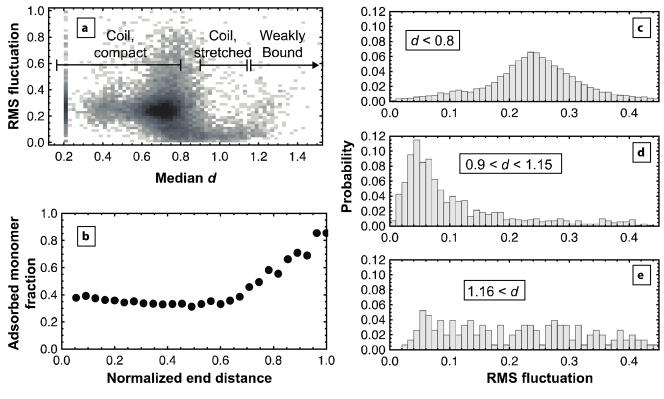
This distinct population of weakly bound molecules also exhibited anomalously large conformational fluctuations. For every trajectory, fluctuations in d were observed that correlated with the median d. A density plot comparing these parameters (Figure 2a) shows that, within the coil state, relatively compact molecules (d<0.8) fluctuate more than molecules with extended conformations (0.9<d<1.15). In particular, the distribution of root mean squared (rms) fluctuations for compact coils (Fig. 2c) is symmetrical and peaked at ~0.25, suggesting dynamically fluctuating molecules. Conformational fluctuations of stretched coils, on the other hand, are much smaller; the distribution peaks at ~0.05 (Fig. 2d). Again, our model of adsorbed flexible chains anticipates these results. If we presume that the number of adsorbed monomers represents a barrier to major conformational changes in a polymer chain, chains with more adsorbed monomers will have lower fluctuations in end-to-end distance than those with fewer adsorbed monomers. In Fig. 2b, the fraction of adsorbed monomers remains relatively constant at 0.4 for normalized end distances <0.6. If this simulated region represents the compact coils in Fig. 2c, they may change configurations often, leading to the large observed fluctuations. For normalized end distances >0.6, adsorbed monomer fraction increases substantially, suggesting that when adsorbed coils adopt extended conformations, they are strongly bound and likely to exhibit decreased fluctuations. In contrast to expectations for adsorbed flexible chains from Fig. 2b, a population was experimentally observed for d > 1.16 whose fluctuations were anomalously high (Fig. 2e). We suggest this population again represents the weakly bound state whose surface contacts are not as numerous, despite its large end-to-end distance.

Figure 2.

Conformational fluctuations suggest two states of adsorbed ssDNA. Each trajectory of ssDNA was analyzed for its rms fluctuation in d and its median value of d. (a) A density plot of all trajectories shows that trajectories with median d<0.8 have higher fluctuations than those with median 0.9<d<1.15. As median d increases above 1.15, the magnitude of fluctuations increases again. Darker regions indicate increased probability density. The population at median d=0.2 represents all “extreme” trajectory segments whose median conformation was more compact than the instrument could measure. (b) Simulations of an adsorbed polymer chain with a surface interaction energy of −0.1 kT per adsorbed monomer show the average adsorbed monomer fraction as a function of end distance, normalized by contour length. Up to a normalized end distance of 0.6, adsorbed monomer fraction remains relatively low, possibly explaining the ability of chains with median d<0.8 to fluctuate strongly. As the simulated chain extends, the adsorbed monomer fraction increases substantially, increasing the energy barrier to major conformational changes for these extended chains (0.9<d<1.15). The behavior of the weakly bound state is not captured by the simulation. (c–e) The probability distribution of rms fluctuations is shown for all trajectories that are: (c) compact coils, (d) stretched coils, or (e) weakly bound.

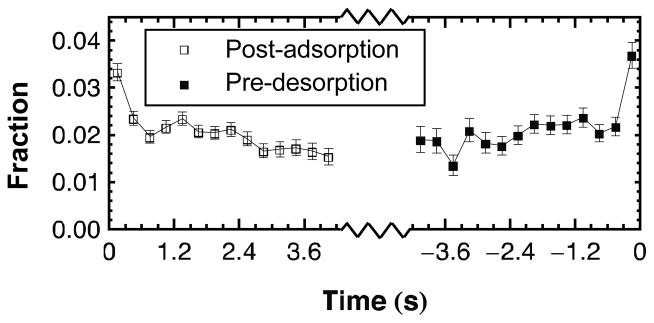
The weakly bound state should also exhibit a characteristic bias towards desorption; i.e. molecules should be more likely to desorb from an extended weakly bound state than from a more strongly bound coil state. This premise was tested by tracking molecular extension over time, either before desorption or after adsorption. The fraction of molecules in highly extended conformations (d≥ 1.2) was calculated as a function of time for each molecular trajectory. Figure 3 shows that the fraction of highly extended ssDNA remains relatively constant (at ~0.02) until immediately before desorption when this fraction nearly doubles. Although not all highly extended conformations are weakly bound, this positive correlation between extension and desorption supports the notion that the weakly bound state experiences decreased surface attraction. Figure 3 also indicates that the fraction of highly extended ssDNA decreases following adsorption, indicating post-adsorption relaxation to a compact coiled state. We reiterate that these data result from the analysis of long-lived populations; the vast majority of weakly bound adsorbing ssDNA will quickly desorb rather than undergo a relaxation process.

Figure 3.

Kinetics of conformational extension. The fraction of ssDNA with d≥1.2 is shown as a function of time either before desorption or after adsorption. Error bars represent the standard deviation in each fraction, assuming Poisson statistics. The fraction of highly extended conformations (d≥1.2) nearly doubles immediately before desorption and also decreases following adsorption.

Notably, the fractions of highly extended ssDNA are small, representing less than 5% of the long-lived population. These molecules would almost certainly be overlooked in ensemble-averaging experiments or SM-TIRFM experiments without the ability to observe large numbers of rare events. However, while rarely observed, the weakly bound state dramatically affects the dynamic behavior of ssDNA. Furthermore, rapid desorption following strong extension observed in Figure 3 suggests that many more molecules may exhibit this behavior, but desorption is so fast that the extension-desorption process is not captured by a 0.3s acquisition time.

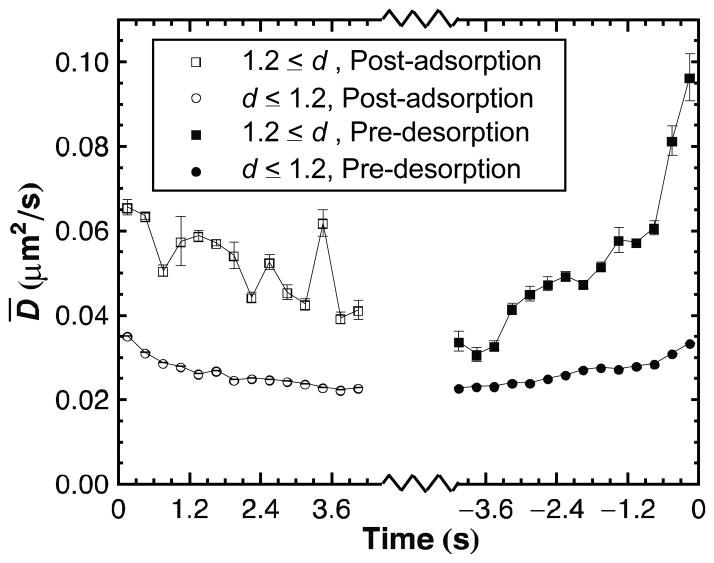
We previously hypothesized that the higher mobility of highly extended molecules reflected weaker surface interactions. If true, then molecules should diffuse more rapidly as they approach desorption. Figure 4 shows that highly extended ssDNA molecules exhibit a dramatic increase in D̄ immediately prior to desorption as well as a more gradual increase in D̄ beginning well before desorption. Interestingly, the magnitude of D̄ for highly extended ssDNA just prior to desorption is much larger than D̄ at times well before desorption or when averaged over all time as displayed in Figure 1a. This demonstrates that the broad category of highly extended ssDNA includes both weakly bound and stretched coil states but that the weakly bound state becomes increasingly prevalent and mobile closer to desorption. A decrease in D̄ is also observed after adsorption, reinforcing the idea that ssDNA adsorbing in a weakly bound conformation gradually increases its surface attractions, slowing its diffusion, as it settles on the surface. Finally, Figure 4 shows that D̄ also decreases weakly with time after adsorption and increases leading up to desorption in compact conformations. Thus, coil molecules also pass through conformations with progressively weaker affinity prior to desorption but these conformations still have higher surface affinity than the weakly bound state.

Figure 4.

Kinetics of surface attraction as determined by diffusive behavior. The mean diffusion coefficient ( D̄ ) is shown as a function of time either before desorption or after adsorption for ssDNA meeting the given criteria for d. Compact conformations (d < 1.2) show increasing D̄ prior to desorption and decreasing D̄ after adsorption. A strong trend with time, particularly before desorption, is seen for highly extended conformations (d≥1.2). Error bars are calculated in the same manner as for Figure 1.

It is important to note that the dynamic correlations between conformation and adsorption, desorption and diffusion cannot be explained by photophysical phenomena such as blinking or photobleaching that effectively turn off the donor or acceptor fluorophore. For example, if donor fluorescence were turned off, the molecule could be counted as desorbed in either that frame or the next. However, this would not result in either the fast diffusion that precedes desorption, or the pre-desorption extension. As another example, a rare double photobleaching event, where the acceptor is first turned off, and then the donor is subsequently turned off in the next 0.3s window, could conceivably be interpreted as an extension followed by desorption. However, this behavior would not lead to the fast diffusion of pre-desorption molecules and cannot explain any of the post-adsorption trends in conformation or diffusion. Similar arguments can be made for any attempt to comprehensively explain the data using blinking or photobleaching phenomena and it is the independent dynamic correlations between conformation and adsorption, desorption and diffusion that bolsters our stated interpretation of the data.

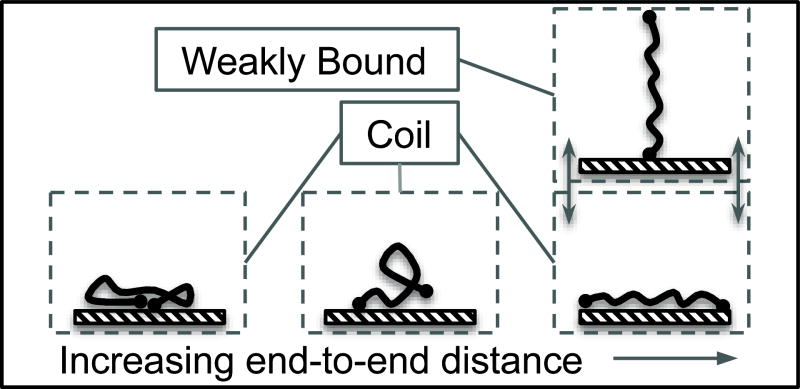
Thus far, we have demonstrated that the weakly bound state, with a highly extended conformation, diffuses quickly, correlates positively with desorption, and undergoes relatively high conformational fluctuations. As shown by lattice simulations of an adsorbed polymer chain, these dynamic behaviors are not expected for a highly extended molecule that is strongly-adsorbed to the surface. Consequently, we hypothesize that this second state may involve extension away from the surface as depicted in Figure 5. While this depiction reflects a plausible explanation for the above experimental observations of a distinct weakly bound population, there is no direct evidence for this interpretation and it is not clear what molecular-level mechanism would stabilize an upright state. Further work must be done to explore this interpretation.

Figure 5.

Physical interpretation of the coil and weakly bound states. One hypothesis is that the weakly bound state extends away from the surface and its fewer surface contact points lead to fast diffusion and likelihood of desorption. The coil state can extend in the plane of the surface but has many favorable surface contacts.

In conclusion, we have demonstrated the benefits of correlating molecular conformation with surface mobility, adsorption, and desorption in ssDNA adsorbed onto amine-modified glass. In a small fraction of molecules, an important correlation was identified in which extreme molecular extension strongly correlated with fast diffusion, large conformational fluctuations, and desorption events, and it was proposed that this conformation represents a weakly bound state whereby ssDNA extends away from the glass surface. A coiled state, whose conformation was generally compact, behaved as predicted by simulations of adsorbed polymer chains. Future work will seek to identify whether the weakly bound state is important for hybridization and whether vicinal surface chemistry affects its prevalence and properties.

Methods

Solutions of end-labeled ssDNA solutions

Single-stranded DNA was purchased from BioSearch Technologies and was purified by the company using HPLC to greater than 90%. The DNA sequence was 5′-TAA AAC GAC GGC CAT-3′ and was labeled on the 5′ end with carboxyfluorescein (FAM) and on the 3′ end with tetramethylrhodamine (TMR). This molecule is depicted in Supporting Figure S1. Phosphate buffer (10 mM) was created from a mixture of monobasic and dibasic sodium phosphate and pH-adjusted to 8.0 using trace amounts of sodium hydroxide and hydrogen chloride. The concentration of ssDNA in solution was 7 x 10⁻¹¹ M in order to achieve surface densities low enough to observe individual molecules but high enough to provide many molecules for tracking in each frame.

Surface preparation and characterization

Fused silica (FS) wafers were washed with cationic detergent (Micro 90, International Product Corp.) and thoroughly rinsed with water purified to 18 MΩ-cm. Wafers were then immersed in warm piranha solution for 1 hour followed by UV-ozone treatment for 1 hour. Following this treatment, FS wafers were coated with monolayers of 3-aminopropyltriethoxysilane (APTES) by exposing wafers to APTES vapors for 24 hours at room temperature. Following deposition, wafers were rinsed with toluene, dried under nitrogen and used for experiments.

In order to characterize the surface, static contact angles of APTES-functionalized fused silica were measured with a custom-built contact angle goniometer. A 1 μL drop of deionized water was deposited on the surface and at least six drops on three independent samples were averaged for reported values here. The static contact angle of APTES-functionalized fused silica was 45 ± 4°, a value consistent with reported values for vapor deposition of APTES monolayers.^35–36

Resonance energy transfer

Resonance energy transfer is commonly used to obtain spatial information in the range of 1–10 nm.³² In this photophysical phenomenon, a photon excites a fluorophore that either fluoresces or nonradiatively transfers its excess energy to an acceptor molecule at a rate that is proportional to r⁻⁶ where r is the separation between fluorophores. In this work, FAM is the energy donor and TMR is the energy acceptor. This separation can be expressed as a function of the fluorescence intensities of the donor and acceptor species as shown in equation (1) where R_o is a characteristic distance for energy transfer (i.e. Förster radius), F is fluorescence intensity, and subscripts A and D represent acceptor and donor, respectively.

$$r=R_o{\left(\frac{F_A{\mid }_{r\to 0}}{F_D{\mid }_{r\to \infty }}\right)}^{1/6}{\left(\frac{F_D}{F_A}\right)}^{1/6}$$ (1)

The Förster radius for FAM and TMR is between 4.9 and 5.4 nm although the exact value depends on pH and may change if the rotation of one or both fluorophores is hindered.³⁷ Also in equation (1), the ratio of acceptor fluorescence at zero separation to donor fluorescence at infinite separation is a constant that depends both on properties of the fluorophores as well as the optical properties of the detection system. This parameter was not measured in the present work but is expected to be of order 1. Even if this “machine constant” deviates significantly from 1, errors have a minimal effect given that the ratio is raised to the one-sixth power. Nevertheless, the above uncertainties make it difficult to place r on an absolute distance scale. Furthermore, absolute distance is unnecessary for identifying trends in r, as the present work seeks to do. Thus we use the relative end-to-end distance, d, to characterize ssDNA conformations as defined in equation (2).

$$\begin{array}{ll}d& =\frac{r}{R_o}{\left(\frac{F_A{\mid }_{r\to 0}}{F_D{\mid }_{r\to \infty }}\right)}^{1/6}\\ & ={\left(\frac{F_D}{F_A}\right)}^{1/6}\end{array}$$ (2)

The experimental fluorescence intensity of acceptors must be corrected for bleeding of donor fluorescence into the acceptor channel and for direct excitation of donors by the excitation source. Careful choice of bandpass filters effectively negates donor bleeding and this is verified experimentally by the observation of ssDNA with strong fluorescence in the donor channel that does not appear over background noise in the acceptor channel. Direct excitation is determined by examination of the intensity distribution of objects in the acceptor channel. A representative distribution is shown in Supporting Figure S2 where two peaks can be seen in the acceptor channel. The broad peak at higher intensity values is due to energy transfer events whereas the narrow peak at low intensity values represents direct excitation. The intensity corresponding to this latter peak is subtracted from all acceptor intensities. For analyses in which the value of d is required, segments of a trajectory are ignored if the intensity in either channel does not appear above background plus the contribution from direct excitation in the acceptor channel in order to minimize the effects of donor photobleaching or blinking. However, the molecule is not assumed to have desorbed as long as direct acceptor excitation permits object identification.

After subtraction of background and direct excitation contributions in the acceptor channel, intensity values in one channel or the other may be negative. In this case, d is set to an arbitrary “extreme” value that represents a practical point beyond which energy transfer cannot be quantified. The “extreme” values used in this work were 0.2 and 2.0 which were just beyond the lowest and highest values of d that were calculated for objects that had positive intensity in both channels. If an entire trajectory exhibited the same “extreme” value of d, that trajectory was neglected, and this led to the elimination of ~1% of trajectories. Such trajectories were assumed to be mislabeled, either having only FAM (leading to infinite d) or only TMR (leading to zero d). The ability to filter out subsets of molecules that are suspected to be trivial outliers makes these single-molecule methods relatively insensitive to impurities.

Single-molecule total internal reflection fluorescence microscopy

TIRFM measurements were performed using a custom-built prism-based illumination system, flow cell, Nikon TE-2000 microscope with 60x objective and 491 nm DPSS laser (Cobolt) that have been described previously.^{20, 22} The flow cell was maintained at 25.0 ± 0.1°C and flow was stopped after introduction of the ssDNA solution. The intensity of the laser illumination was high enough to resolve individual objects in sequential images with a 0.3s acquisition time. It should be noted that although this acquisition time is too slow to capture microsecond dynamics typical of unhindered molecular motion, it is possible that macromolecules adsorbed to an interface experience persistent conformational states and transition between these states with time scales much slower than would be expected for molecular motion alone. Indeed, the observation of heterogeneous behavior in the same molecule suggests that there is a time scale of ssDNA dynamics that is well-captured with a 0.3s acquisition time.

The evanescent wave created by total internal reflection has a penetration depth of less than 100 nm and consequently only objects near the surface are excited. While any object within this penetration depth may become excited and fluoresce, those that are not adsorbed to the surface are typically not observed. This is because diffusion coefficients in solution are orders of magnitude higher than even the fastest surface diffusion coefficients observed in these experiments and the residence time of any one molecule in the capture region of a single imaging pixel is negligible unless it is adsorbed to the surface. Consequently, objects in solution contribute to higher background levels but are not identified as objects themselves.

Dual-channel imaging was provided by an Optosplit II (Cairn Research) image splitter. In this device, a dichroic mirror (Chroma) with a nominal cut-on wavelength of 540 nm was used to separate fluorescence emission of FAM and TMR. Bandpass filters (Semrock) were then used to further select for fluorescence emission in each channel. The FAM channel used a bandpass filter centered at 529 nm with a 90% transmission width of 28 nm. The TMR channel used a bandpass filter centered at 585 nm with a 90% transmission width of 29 nm. After fluorescence emission was split and filtered, each channel was projected onto a separate region of an EMCCD camera (Photometrics) cooled to −70°C.

The two channels were aligned to within 1–2 pixels prior to the experiment using an alignment grid provided by the manufacturer. Fine alignment was performed after the experiment by aligning single-molecule images taken during the experiment. This was done by convolving the two channels as a function of the offset between the two and looking for the offset parameters that produced the maximum product. Essentially, this procedure aligns patterns of single-molecules that appear in each channel to less than 1 pixel.

Diffraction-limited objects were identified in each channel of each frame via image convolution with a disk matrix and thresholding.^{22, 25} An object’s position was calculated as its centroid of intensity and its total intensity was determined by integration (after local background subtraction) of all pixels assigned to that object by the disk convolution and thresholding algorithm. Objects identified in the two channels were compared for each frame by identifying objects that had the same position in each channel to within 2 pixels (455 nm). If duplicate objects were found, the object position was taken from the channel with greater signal-to-noise. The intensity for duplicate objects was recorded in each channel for future calculation of energy transfer efficiency. If an object was only identified in one channel, the positions of its pixels in that channel were used to determine the intensity of the object in the opposite channel. Such a strategy is necessary because either very strong or very weak energy transfer could make an object appear in one channel but fall below the identification threshold in the other. Object tracking between frames was then accomplished by identifying the closest objects in sequential frames while also requiring the distance between these closest objects to be less than 4 pixels (910 nm) to allow for diffusion.

This automated tracking algorithm is capable of quickly tracking a large number of objects in a relatively short amount of time. Furthermore, it is insensitive to errors typically made by humans such as ignoring objects that appear less bright than neighboring objects. This is particularly important in RET experiments where the intensity in each channel, for the same object, can fluctuate as RET efficiency changes. On the other hand, automated tracking is more sensitive to noise, occasionally identifying anomalously high single pixels as real objects. This source of error is easy to eliminate by ignoring objects that appear in only one frame, as noise is unlikely to cause a false identification in the same place in successive frames. This work goes even further by ignoring objects that appear in fewer than 9 frames, although this choice was not solely based on noise considerations. It was found that some molecules exhibited pre-desorptive and post-adsorptive behavior, within ~1 second of each event, that was different than their steady, surface-bound behavior. Thus, long trajectories, lasting for at least 2.7s, were used to allow unbiased comparisons between each type of above-mentioned behavior while still having a large dataset for good statistical significance.

Analysis of squared-displacement distributions

Analysis of two-dimensional diffusion in SM-TIRFM experiments has been described in detail elsewhere.²² Essentially, the probability distribution of squared displacements is assumed to be the sum of multiple Gaussians, each characterized by a different diffusion coefficient representing a different diffusive mode. To minimize binning artifacts, it is better to analyze the cumulative squared-displacement distribution, which represents the probability that an object will diffuse a distance ≥ R in a time interval Δt. For multiple diffusive modes, each characterized by a diffusion coefficient, D_i, the cumulative squared-displacement distribution (C) is given by equation (3) in which x_i represents the fraction of observed steps corresponding to mode i.

$$C(R^2,\mathrm{\Delta }t)=\sum _i{x}_i{e}^{-\frac{R^2}{4D_i\mathrm{\Delta }t}}$$ (3)

The mean diffusion coefficient is taken to be the fraction-weighted average of each mode and is given in equation (4).

$$\overline{D}=\sum _i{x}_i{D}_i$$ (4)

This mean diffusion coefficient shown in equation 4 is proportional to the mean squared-displacement for a random-walk with multiple modes of diffusion. That is: D̄= 〈R²〉/4Δt.

The experimental cumulative squared-displacement distribution was calculated by sorting the squared-displacement data in ascending order and ranking each data point. Thus, C(R_k², Δt) is given by:

$$C\left(R_k^2,\mathrm{\Delta }t\right)=1-k/N$$

where k is the rank in the sorted order and N is the total number of sorted data points. The error of each data point in the cumulative distribution represents 68% confidence intervals for a Poisson distribution with a mean of N+1-k.

The experimental cumulative squared-displacement distribution was fit to equation (3) by minimizing the variance, weighted by the squared error, for each data point. For a given dataset, the number of populations used for the fit was increased until populations were found with diffusion coefficients that were not statistically different from one another as determined by a t-test to 90% confidence. This modest confidence value generally excluded models with diffusion coefficients that had the same first significant digit.

Analysis of fluctuations

The root mean squared fluctuation value of each trajectory was calculated by comparing the value of d at each time in the trajectory to the mean d over a five frame window as shown in equation (5). The subscripts j and k represent the position along a trajectory of length N. While necessary to preserve a 1.5s averaging window, neglect of the first and last two positions in a trajectory also minimize bias due to conformational changes after adsorption and before desorption.

$$\mathit{rms}={\left[\frac{1}{N-4}{\sum _{j=3}^{N-3}\left(d_j-\frac{1}{5}\sum _{k=j-2}^{j+2}{d}_k\right)}^2\right]}^{1/2}$$ (5)

Analysis of pre-desorption and post-adsorption behavior

Pre-desorption and post-adsorption analysis, unique to molecular tracking techniques, provides information on the sequence of events that can stabilize or destabilize a molecule on the surface. To do this, each trajectory was aligned in time so that either its desorption or adsorption event was at time zero. Trajectories were then broken apart and each step in the trajectory grouped according to its time either before desorption or after adsorption. Analyses of molecular conformation or diffusive motion were then performed on these new, temporally grouped datasets. In order to isolate pre-desorption behavior from post-adsorption behavior and vice versa, the first 0.9s of each trajectory was ignored in the pre-desorption analysis and the last 0.9s was ignored in the post-adsorption analysis.

The effect of molecular conformation, characterized by d, was analyzed before desorption and after adsorption. Within each time-group, the fraction of observations that met the criterion of 1.2≤d was determined. Assuming Poisson statistics, the error in this fraction was taken as the square root of the number of observations of 1.2≤d divided by the total number of observations in the time-group. Surface mobility, characterized by D̄, was also analyzed within each time-group. First, each time-group was divided into two categories according to the value of d that followed the diffusive step: d<1.2 or 1.2≤d. The mean diffusion coefficient was then calculated as described previously, with the reported error being derived from the standard error used to determine the fraction (x_i) and diffusion coefficient (D_i) of each population.

Finally, it should be noted that linking a squared-displacement with the value of d immediately following that displacement might seem like an arbitrary choice as opposed to d immediately before the step or the average of the two. However, we feel that the value of d immediately following the step best represents the average conformation of the molecule while it was taking the observed step.

Simulation of adsorbed polymer conformations

In order to predict the relationship between diffusion coefficient and end-to-end distance, the conformations of a self-avoiding, adsorbed polymer in a cubic lattice were exhaustively enumerated for an 11-mer. An 11-mer was chosen because exhaustive enumeration is reasonable for this length in three dimensions. The activation energy required to desorb the polymer chain was taken as the sum of weak attractions between the surface and adsorbed monomers. The average number of adsorbed monomers was expected to depend on end-to-end distance creating a link between molecular conformation and off-rate constant, k. It is believed that the diffusion coefficient should correlate positively with k.^21–22

No restrictions were placed on starting or ending positions of the 11-mer relative to the surface and any configuration was thrown out if it penetrated the surface or overlapped onto itself. The number of adsorbed monomers for each conformation was determined as the number of monomers that lay in the plane of the surface and each adsorbed monomer was assigned an energy of a. For this work, a = −0.1 kT representing weakly favorable monomer-surface interactions. The statistical weight of each chain (w_i) was given as the Boltzmann factor associated with total chain energy, as shown in equation (6) where n_i is the number of adsorbed monomers on the i^th chain:

$$w_i=e^{-\frac{n_{i}a}{kT}}$$ (6)

The off-rate for each chain is assumed to follow first-order kinetics for a single desorption step with a rate constant given by the Arrhenius equation, shown in equation (7) where E_i is the activation energy and k_o is the frequency factor, or off-rate in the absence of an energy barrier:

$$k_i=k_o{e}^{-\frac{E_i}{kT}}$$ (7)

The assumption of a single desorption step may seem like an oversimplification for polymer chains in which sequential desorption of individual monomers may also be an important mechanism. Indeed, a more complicated sequential desorption model, which requires additional kinetic parameters, would deviate quantitatively from single-step desorption at long times. However, this added complication would reproduce the same qualitative trend in which desorption rate decreases roughly exponentially with the number of initially adsorbed monomers. Thus equation (7) is a reasonable approach for using the number of initially adsorbed monomers to predict the trend in off-rate with end-to-end distance.

The average off-rate over an ensemble of molecules is determined by the statistical average given in equation (8) where the ensemble includes all molecules with equivalent end-to-end distances:

$$\begin{array}{ll}\frac{\langle k\rangle }{k_o}& =\sum _i\frac{k_i}{k_o}{w}_i/\sum _i{w}_i\\ & =\sum _i{e}^{-\frac{E_i+n_{i}a}{kT}}/\sum _i{e}^{-\frac{n_{i}a}{kT}}\end{array}$$ (8)

We assume that the activation barrier for desorption is equal in magnitude to the total adsorption energy of the chain so that E_i = −n_i a and <k>/k_o is simply the inverse of the partition function. This analysis neglects other factors, such as chain rigidity and any unfavorable, conformation-dependent DNA-surface interactions that may contribute to the total chain energy.

These factors would affect the weight of each chain in equation (6) but are not accounted for here because we wish to focus solely on the relationship between the end-to-end distance and the number of monomer contacts that can be made by conformations with that distance.

With average off-rate calculated for each end-to-end distance, the results are displayed as a function of normalized end-to-end distance, which is the absolute end-to-end distance divided by the contour length of the chain. This is done to compare the results of this simulation of an 11-mer to the 15-mer ssDNA used in this work. This comparison of distance should only be taken as approximate since d is not placed on an absolute scale, and even if this were done, it is difficult to exactly compare lattice simulations to real polymer chains. In addition, a lattice model introduces artifacts into the distribution of end distances by dramatically favoring some lattice positions more than others with nearly equivalent end-to-end distances. In this work, we minimized this artifact by grouping end-to-end distances using bins of 0.4 monomer units, or 0.036 units in the normalized end distance scale.