Abstract
Long-term storage of natural tissues or tissue-engineered constructs is critical to allow off-the-shelf availability. Vitrification is a method of cryopreservation that eliminates ice formation, as ice may be detrimental to the function of natural or bioartificial tissues. In order to achieve the vitreous state, high concentrations of CPAs must be added and later removed. The high concentrations may be deleterious to cells as the CPAs are cytotoxic and single-step addition or removal will result in excessive osmotic excursions and cell death. A previously described mathematical model accounting for the mass transfer of CPAs through the sample matrix and cell membrane was expanded to incorporate heat transfer and CPA cytotoxicity. Simulations were performed for two systems, an encapsulated system of insulin-secreting cells and articular cartilage, each with different transport properties, geometry and size. Cytotoxicity and mass transfer are dependent on temperature, with a higher temperature allowing more rapid mass transfer but also causing increased cytotoxicity. The effects of temperature are exacerbated for articular cartilage, which has larger dimensions and slower mass transport through the matrix. Simulations indicate that addition and removal at 4°C is preferable to 25°C, as cell death is higher at 25°C due to increased cytotoxicity in spite of the faster mass transport. Additionally, the model indicates that less cytotoxic CPAs, especially at high temperature, would significantly improve the cryopreservation outcome. Overall, the mathematical model allows the design of addition and removal protocols that ensure CPA equilibration throughout the sample while still minimizing CPA exposure and maximizing cell survival.
Keywords: osmotic excursions, cytotoxicity, CPA addition/removal, CPA transport, mathematical modeling, vitrification
Introduction
Significant progress has been made in the field of Tissue Engineering towards designing and developing living biological substitutes for the repair, replacement or regeneration of certain tissues or organs [6; 38; 40; 47]. However, cryopreservation technologies are often overlooked until a construct is very close to being clinically available. Preservation during manufacturing and transportation is critical in bringing constructs to off-the-shelf, clinical use [24; 39; 40]. The need for preservation also extends to natural tissues which are in limited supply. Cryopreservation may be relatively simple for cells in suspension, but the addition of a three-dimensional matrix introduces resistance to heat and mass transport and increases the complexity of the cryopreservation methods [3; 4; 24]. Additionally, ice formation is critical, as ice has been shown to be detrimental to the mechanical properties of both tissue-engineered constructs [10] and natural tissues [42]. Therefore, the cryopreservation of three-dimensional natural or bioartificial tissues is rarely straightforward and often requires significant experimental work to achieve success.
Vitrification, or ice-free cryopreservation, is therefore a promising method of preservation [26]. Vitrification requires high concentrations of cryoprotective agents (CPAs) and rapid cooling to achieve a vitreous, or glassy, state. This method eliminates the problem of ice formation both within cells and in the extracellular matrix [8]. Generally, the high CPA concentrations in vitrification are achieved using a CPA cocktail solution which is added and removed using multi-step protocols to minimize cellular osmotic excursions. After addition, samples are rapidly cooled and stored in the vitreous state before rapid warming, stepwise removal of the CPAs and eventual use.
Significant theoretical work has been performed to better understand cryopreservation; however, many of the previous studies have focused on understanding processes during the cooling and warming of samples in conventional freezing. Specifically, these efforts cover important issues such as intracellular ice formation [29; 37], solute interactions [27], effects of temperature on cell membrane function [11], and synthetic phase diagrams [17]. While such studies are important in improving our fundamental understanding of these processes, little work has been done to investigate the methods of vitrification. Vitrification requires rapid cooling at a critical rate necessary for the solution to achieve a glassy state; similarly, warming should also be rapid to prevent the water from crystallizing. There is therefore little room for improvement of these critical cooling and warming rates. On the other hand, little modeling work has been done to address the other critical issue of vitrification, i.e., the addition and removal of CPAs and their effect on cells, constructs or natural tissues. A successful protocol should achieve full equilibration of the CPA or CPA cocktail throughout the sample to ensure successful vitrification, while minimizing osmotic excursions and CPA-induced cytotoxicity; the latter is dependent on the CPA identity and concentration as well as the exposure time and temperature [28].
To address these complexities, a previously published mathematical model [31] of mass transfer through the extracellular matrix and cellular membrane was expanded to incorporate heat transfer and CPA cytotoxicity. This model describes the CPA addition and removal and does not consider the rapid cooling, low temperature storage, or warming that would occur during the complete vitrification process. Addition and removal protocols were designed to maintain osmotic excursions of the cells within tolerable limits and achieve CPA equilibration throughout the entire construct. The temperature and duration of addition and removal steps were varied to determine their effects on cytotoxicity. To gain insight, simulations were carried out for two systems with different transport properties, geometry and size. The first was an encapsulated cell system of spherical geometry that is small in size (500 μm in diameter) and in which the matrix poses little resistance to mass transfer, exhibiting CPA diffusivities equal to approximately 80% of those in water [32]. The second system was based on articular cartilage of slab geometry, a tissue that is notoriously difficult to cryopreserve [7; 22; 34]. This system had larger dimensions with a clinically relevant overall thickness of 2 mm and significantly higher resistance to mass transfer with CPA diffusivities approximately 30% of those in water [31]. These two systems were chosen to cover different tissues and tissue-engineered constructs and to generate results that would be more broadly applicable to CPA addition and removal in the vitrification of tissues.
Mathematical Modeling
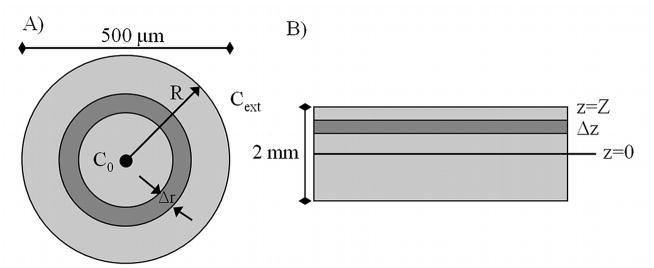
CPA cytotoxicity kinetics were evaluated on the basis of previously published experimental data obtained with encapsulated βTC-tet cells [28]; these kinetics were used for the simulations with both the encapsulated cell system and cartilage. Transport of CPAs through the extracellular matrix and the cell membranes was described with a two-compartment mathematical model [31]. Heat transfer and an additional equation describing the cytotoxicity kinetics of CPAs towards cells were incorporated into the mathematical model. The transport equations through the matrix were written for spherical geometry for the encapsulated system (Fig. 1A) and for slab geometry for cartilage (Fig. 1B). The parameter values used in simulations are shown in Table 1. Chondrocytes, as would be present in articular cartilage, were assumed to have the same parameters as βTC-tet cells. Additionally, the dependence of diffusivity and cell permeability on temperature were assumed to follow the Arrhenius relationship (similar to equation 15).
Figure 1.
Schematic for A) alginate bead and B) articular cartilage.
Table 1.
Values of Model Parameters used in this Study for Mass and Heat Transfer, Permeability & Cytotoxicity. Cell permeability parameters and cytotoxicity parameters were assumed to be the same for both cell types. Water permeability values (Lp) were higher for DMSO than for PD and were used for all simulations.
| Deff/Dbulk | α (μm2/s) | Lp (A) (μm/min atm) | Lp (Ea) (cal/mol) | Ps (A) (μm/s) | Ps (Ea) (cal/mol) | B (mol/kg)−1 | b (L/mol min) | d (K) | f (L/mol) | |
|---|---|---|---|---|---|---|---|---|---|---|
| Alginate | 0.8 | 1.46E11 | -- | -- | -- | -- | -- | -- | -- | -- |
| Cartilage | 0.3 | 1.32E5 | -- | -- | -- | -- | -- | -- | -- | -- |
| Me2SO | -- | -- | 6.67E-4 | 15400 | 4.73E-2 | 14100 | 0.0843 | 2.0E4 | 4270 | 0.08 |
| PD | -- | -- | -- | -- | 5.81E-2 | 14600 | 0.0576 | 1.2E5 | 4930 | 0.17 |
CPA Transport and Heat Transfer through Matrix
Effective diffusivities were previously determined for CPAs through 2% calcium-alginate beads [30] and through articular cartilage [31]. These values are reported in Table 1. Thermal diffusivity for 2% calcium-alginate beads was assumed to be that of water [5]. A value from literature for the thermal diffusivity of nasal septal cartilage was used to approximate this parameter value for articular cartilage. Although these tissues are different, the thermal properties for biological tissues, ranging from skeletal muscle to cardiac tissue, are of the same order of magnitude, therefore the thermal diffusivity used in this study for cartilage is an acceptable approximation [46]. The values for both of these parameters are also given in Table 1.
Model Assumptions
The following assumptions were incorporated in developing the model equations for the two types of tissue considered.
No CPA reaction or consumption by the cells or matrix.
Homogenous cell distribution throughout matrix. This is a good assumption for freshly encapsulated cells and immature cartilage which are both relatively homogenous [21]
CPA transport through the matrix is described by Fick’s law of diffusion.
Effective diffusivities and thermal diffusivities are isotropic.
Cell membrane permeability values are only affected by a change in temperature and are independent of CPA concentration.
No solute-solute interactions for multi-solute CPA transport across cell membrane or in matrix.
With these assumptions, the mass transport through the spherical alginate matrix is described in Eq. (1) below. In this equation, C = CPA concentration (mol/L), r = radial position (μm) and Deff = effective diffusivity (μm2/s).
| (1) |
The initial and boundary conditions used to solve Eq. (1) are as follows:
| (2) |
| (3) |
| (4) |
Mass transport through the slab geometry of articular cartilage is described in Eq. (5). Initial and boundary conditions are similar to Eq. (2)–(4).
| (5) |
C(z, t=0) = 0 (no CPA initially present in the slab)
C(z=Z, t) = Cexternal (CPA concentration at the slab surface is equal to the external concentration in the bulk liquid, i.e. no boundary layer and partition coefficient of 1)
It should be noted that more advanced models of transport in articular cartilage have recently been published, which take into account the effects of osmotic deformation caused by CPA addition on the transport of solutes [41], or adjust the transport equations for the volume fraction and frictional coefficients of the solutes [1]. These models indeed provide better approximations of solute transport through cartilage for concentrated CPA solutions, however, incorporation of such transport equations was beyond the scope of the present study, which additionally accounts for membrane transport and cytotoxicity effects, and Fickian diffusion of solutes was assumed.
Heat transfer through the spherical alginate matrix is analogous to mass transport as described in Eq. (1) and is shown in equation (6). Eq. (7) describes heat transfer through the slab geometry. In both equations, α = thermal diffusivity (μm2/s) and T = temperature (K).
| (6) |
| (7) |
Initial and boundary conditions for the heat transfer equations (Eqs. 6 & 7) are similar to those for mass transport and are shown for the slab geometry (Eq. 7).
| (8) |
| (9) |
| (10) |
CPA Transport across Cell Membrane
Parameters for βTC-tet cell membrane permeabilities were previously determined [32]. A two-parameter formalism with modifications was used to describe solute transport across the cell membrane [25]. This is described in Eqs. (11) and (12).
| (11) |
| (12) |
Eq. (11) describes the water flux through the cell membrane while Eq. (12) describes the solute flux. In these equations, Vw (μm3) is the volume of water inside the cell, Lp (μm/s·atm) is the water permeability, A(μm2) is the cell surface area, R (μm3·atm/mol·K) is the gas constant, T (K) is the absolute temperature, Me and Mi (osmoles/μm3) are the total external and internal osmotic concentrations, respectively, Ps (μm/s) is the ith solute permeability, Nsi (osmoles) is the intracellular amount of the ith solute and and (osmoles/μm3) are the external and internal osmotic concentrations for the ith solute, respectively. Although the driving force for transport in Eqs. (11) and (12) is more correctly the difference in chemical potential, the use of osmolality is a common approximation [12]. Me and Mi were determined using the osmotic virial equation (Eq. 13) and parameters published by Prickett [36] (shown in Table 1). In Eq. (13), π is the osmolality of the solution (osmole/kg solvent), mi is the molal concentration (moles solute/kg solvent), and B is the osmotic virial coefficient (kg solvent/moles solute). Osmolality was then converted to osmolarity for use in the permeability equations.
| (13) |
Cytotoxicity Kinetics
CPA cytotoxicity is governed by the time and temperature of exposure, CPA identity and concentration. Chemical and thermal cytotoxicity experienced by cells has been well characterized in the field of sterilization. First-order kinetics are often used (shown in equation 14), although these kinetics indicate that the reaction rate constant is independent of time which may not be the case in a biological system.
| (14) |
If the cells within the system are not homogenous, some being more robust than others, this should be reflected in the cytotoxicity kinetics. These states of varying resistance to CPA toxicity could be described as a continuous distribution of states in the cell population. In order to appropriately reflect this in a system, the subpopulations would need to be isolated and the rate constant determined for each. Alternatively, work done by Peleg, et al. suggests that the reaction rate constant could be made dependent on time [35]. This method is shown in Eqs. (15) and (16). If the exponent m is greater than 1, this indicates that cells are progressively weakened due to exposure. Based on previous experimental work [28], the exponent for encapsulated βTC-tet cells is less than 1, indicating that cells that are more susceptible to cytotoxicity are killed first, leaving more robust cells. Although this is not a mechanistic model, it was chosen for the sake of simplicity. The reaction rate constant also is dependent on temperature (Arrhenius relationship) as seen in Eq. (16).
| (15) |
| (16) |
In Eq. (16), E is activation energy (cal/mol), R is the gas constant (cal/(mol*K)) and T is the absolute temperature (K). Work done by Char [9] on sterilization that combines temperature and chemical cytotoxicity indicates that the concentration of the chemical affects the rate constant, kd, as well as the exponent m. Therefore, the pre-exponential factor in equation 16, A, was replaced by bmC, where b is an experimentally fit parameter and C is CPA concentration. Additionally, E/R is replaced by an experimentally fit parameter, d. Finally, the exponent m is replaced by fC where f is an experimentally fit parameter. Equation 17 is the result. This equation was fit to previously published experimental cytotoxicity data to determine all parameters [28]. Equation 14 was also fit to experimental data as a comparison and yielded a coefficient of determination (R2) of 0.60 compared to 0.93 for equation 17. While equation 17 uses an additional parameter (f), it also better reflects experimental data in the field of sterilization.
| (17) |
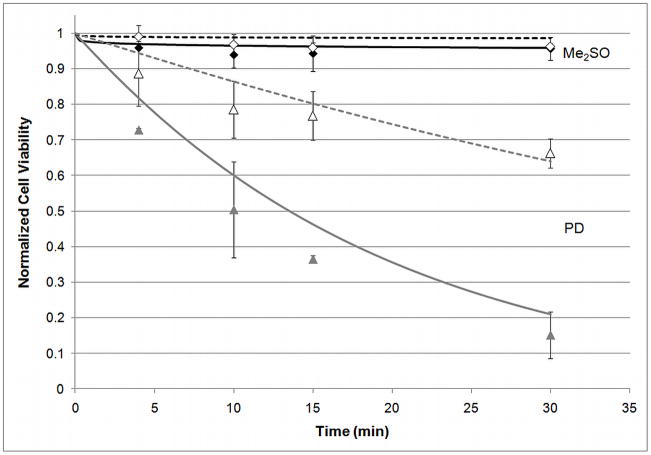
In this equation, n is viable cell number, no is initial viable cell number, resulting in a survival curve in terms of normalized viable cell number. Additionally, C is concentration in mol/L, T is temperature in Kelvin, t is time in minutes and b, d and f have units of L/(mol·min), K, and L/mol, respectively. Figure 2 shows experimental data in comparison to the fitted cytotoxicity equation. This comparison was made for the single-component experimental data at concentrations similar to the concentrations present in the cocktail solution. Parameters were determined by least squares fit of Eq. (17) to previously published cytotoxicity data [28], and the resulting values are shown in Table 1. All single-component data from [28] were used for parameter estimation.
Figure 2.
Comparison of cytotoxicity equation, equation 17, (lines) with experimentally determined normalized cell viability (n/n0) (data points) for 2M DMSO (black, diamond) or 6M PD (gray, triangle) with addition steps carried out at 25°C (solid) or 4°C (empty points, dashed line). Experimental data from [28]. n=3 for experimental data, error bars indicate standard deviation. Statistical significance not shown.
Solution of the model equations
The cytotoxicity Eq. (17) was fit to experimental data to determine parameter values by minimizing the sum of the squares of the differences using Microsoft® Excel® Solver. The equations for CPA transport through the extracellular matrix and through cell membranes, and the heat transport equation, were solved in MATLAB. The main MATLAB program passed variables to sub-programs, which converted CPA concentrations from molarity to osmolarity, calculated CPA concentrations within the matrix, the water volume and solute concentrations within cells, and the CPA cytotoxicity all as functions of time and position in the spherical encapsulated cell system or the cartilage slab.
Results
Heat Transfer
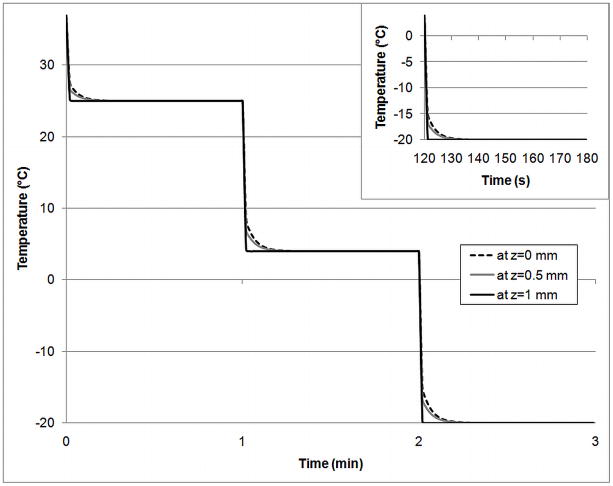
Heat transfer was incorporated into the mathematical model for two reasons. Previously, the assumption was made that heat transfer would be very rapid compared to mass transfer [31]. It was necessary to confirm this. If not, then it might have been beneficial to add CPAs as the sample was cooled to minimize cytotoxicity. Figure 3 shows the temperature profile for different positions throughout the articular cartilage slab in response to step changes in temperature at the edge of the slab. The slab geometry of articular cartilage was chosen as a “worst-case” scenario due to the large dimension and slower thermal diffusivity. Step changes were simulated from 37°C (physiological) to 25°C (approximate room temperature), 25°C to 4°C (ice water bath) and 4°C to −20°C (freezer). Even for the largest of these step changes, 4°C to −20°C, the target temperature is achieved throughout the slab within approximately 10 seconds. The time necessary for heat transfer is therefore negligible compared to the time necessary for mass transfer, which is 40–80 minutes (see Figure 6). Hence, all other simulations were performed isothermally.
Figure 3.
Temperature profile at center of slab (z=0), midway through slab (z=0.5mm), and at edge of slab (z=1) in response to temperature step changes at the edge of the slab.
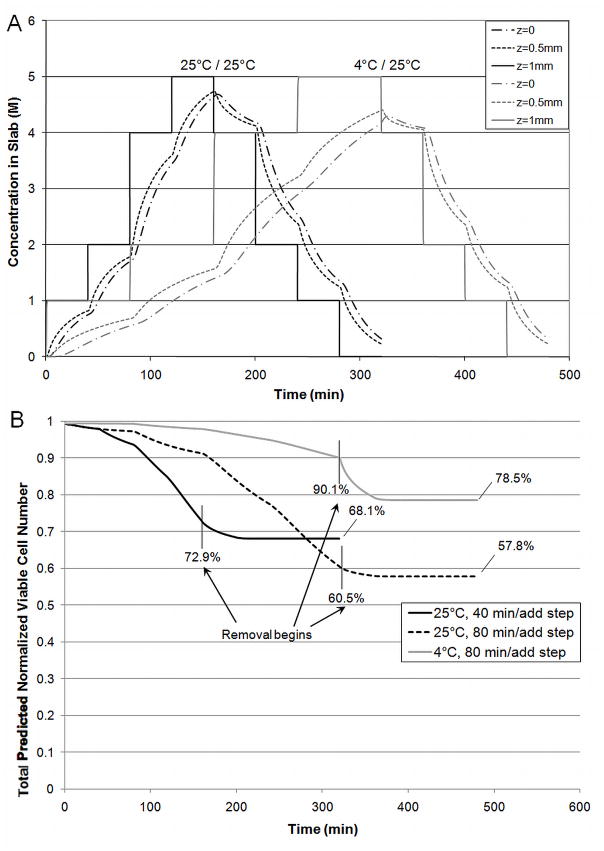
Figure 6.
A) Concentration Profiles of predominant CPA, PD, throughout slab for two temperatures and B) Total Predicted Normalized Viable Cell Number (n/n0) in slab for different exposure times and temperatures. All removal steps occurred at 25°C (40 minutes/step).
Mass Transfer through Alginate Bead
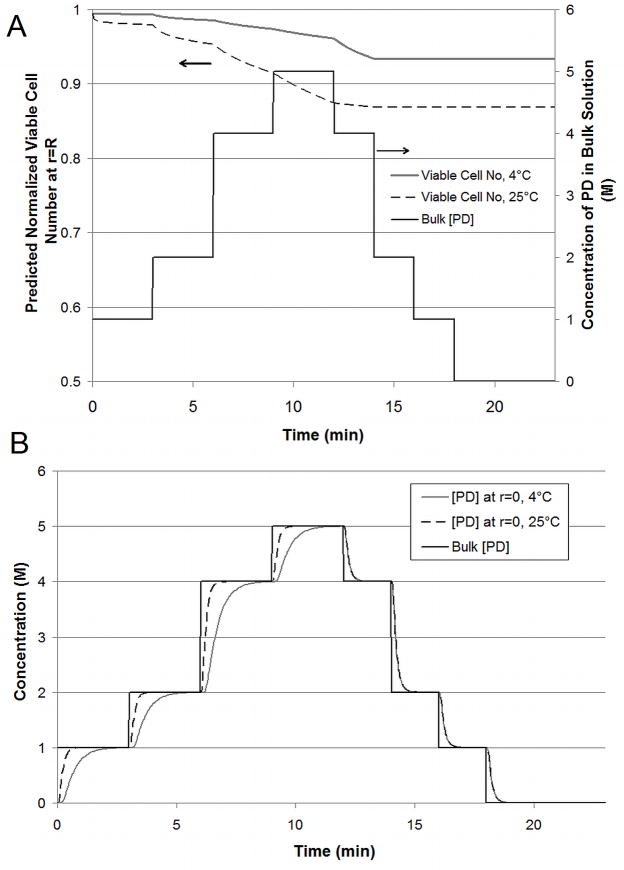
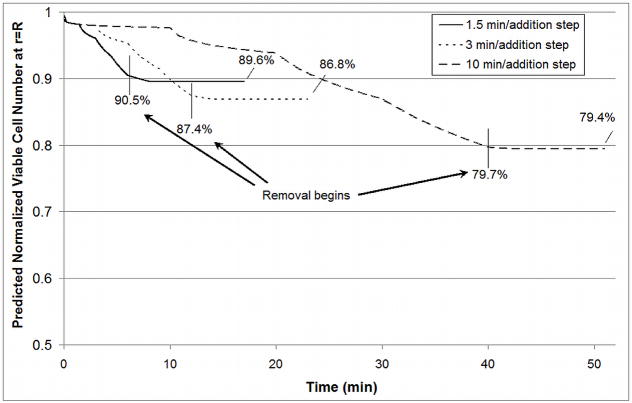
The case of the alginate bead presents little resistance to mass or heat transfer. To be vitrification-relevant, a vitrification solution consisting of dimethyl sulfoxide (Me2SO), propanediol (PD) and polyethylene glycol (MW 400) was used. The standard addition and removal protocol is given in Table 2. This protocol was designed to ensure that the osmotic excursions experienced by the cells within the matrix remained within the tolerable range as determined for βTC-tet cells previously [32]. Figure 4A shows results for 4°C or 25°C addition with all removal steps occurring at 25°C. The viable cell number at the edge of the bead is shown because cells at the edge are exposed to the CPAs longer than those at the center. This position serves as a “worst-case” scenario although viable cell number varies little (~2%) over the radius of the bead due to the small dimension (diameter of 500 μm) and high diffusivity. These results indicate that temperature has a significant effect on the CPA cytotoxicity experienced by βTC-tet cells at relatively short timescales. These short timescales are well within the experimental timescales used to determine the cytotoxicity equation parameters. As such, they are a direct reflection of experiment and are interpolated rather than extrapolated from experimental data. Additionally, removal at room temperature causes a greater loss in viable cell number (~3%) when addition occurred at 4°C than when addition occurred at room temperature (<1%) as shown in Figure 4A. This difference is relatively small and may not be detectable experimentally. This difference indicates that the temperature of removal may not be as critical for constructs that exhibit rapid mass transfer. The minimal loss in viable cell number that occurs during removal when all exposure is carried out at 25°C indicates that the more susceptible cells die during the addition steps leaving more robust cells behind. Figure 4B shows the concentration of CPA at the center of the bead during addition and removal. Achieving or approaching equilibration of CPAs is critical to the success of vitrification. The temperature of addition and removal significantly affects the amount of time necessary to achieve full equilibration. At a higher temperature, equilibration occurs much more quickly, allowing shorter incubation times and decreasing the cell’s exposure to CPAs during addition and removal. Cell viability at the edge of the bead for different exposure times is shown in Figure 5. Due to faster mass transport at 25°C, equilibration through the bead occurs within 1.5 minutes/step as opposed to 3 minutes/step at 4°C. A direct comparison of the results of properly designed protocols at 4°C (Figure 4A, 3 minutes/step) and at 25°C (Figure 5, 1.5 minutes/step) still indicate slightly more cell loss at the higher temperature with a resulting normalized viable cell number for exposure at 25°C of 89.6% compared to 93.3% at 4°C. Overexposure to CPAs, as seen for 3 or 10 minute steps at 25°C (Figure 5), further decreases the cell viability in the bead after addition and removal.
Table 2.
Simulated Addition and Removal Protocol for Alginate Beads. All removal steps were carried out at 25°C. Addition and removal exposure times were lengthened for simulations of articular cartilage.
| Component concentration (M) | Time (min) | Temperature (°C) | |||
|---|---|---|---|---|---|
| Step | PEG400 | PD | Me2SO | ||
| A1 | 0 | 1 | 0.5 | 3 | 4 or 25 |
| A2 | 0 | 2 | 1 | 3 | 4 or 25 |
| A3 | 0 | 4 | 1 | 3 | 4 or 25 |
| A4 | 0.34 | 5 | 1 | 3 | 4 or 25 |
| R1 | 0.2 | 4 | 0.75 | 2 | 25 |
| R2 | 0.2 | 2 | 0.5 | 2 | 25 |
| R3 | 0 | 1 | 0.25 | 2 | 25 |
| R4 | 0 | 0 | 0 | 5 | 25 |
Figure 4.
A) Predicted Normalized Viable Cell Number (n/n0) at edge of bead and B) concentration profile for predominant CPA, PD, at center of bead for 4°C (solid gray) and 25°C (dashed black) addition and concentration in bulk solution (solid black) for 3 min/addition step. All removal steps carried out at 25°C.
Figure 5.
Predicted Normalized Viable Cell Number (n/n0) at edge of bead for different exposure times at 25°C. At this temperature, 1.5 min/addition step is sufficient to achieve equilibrium. 3 min/addition step and 10 min/addition step are overexposures.
Mass Transfer through Articular Cartilage
Mass transfer through articular cartilage is hindered due to the dense nature of the tissue. The composition of each addition and removal step for articular cartilage was the same as for alginate beads. To address the mass transfer issues, the duration of the addition and removal steps was adjusted. The duration of all addition and removal steps were equal to each other, and this time was adjusted to ensure approximately 90% equilibration at the center of the slab by the end of all addition steps. Concentration profiles throughout the slab for exposure at both temperatures are shown in Figure 6A. The temperature effects on mass transfer are exacerbated for articular cartilage due to the reduced diffusivity and increased sample dimension. Simulations indicate that addition steps must be twice as long when carried out at 4°C (80 min/step) than 25°C (40 min/step).
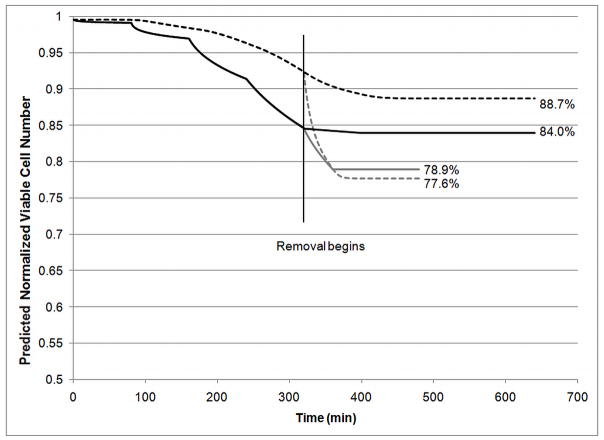
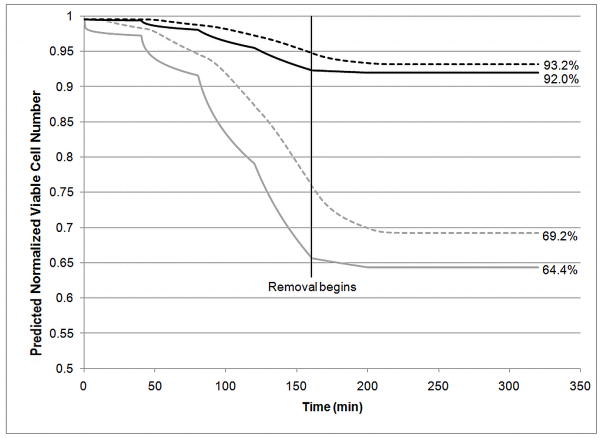
Figure 6B shows the effects of temperature and overexposure on cytotoxicity by comparing three scenarios. In the first scenario, addition steps occurred at 4°C and required 80 min/step to achieve approximately 90% equilibration. Addition steps for the second scenario occurred at 25°C and required only 40 min/step. These two scenarios were compared to overexposure: addition steps carried out at 25°C for 80 min/step. All removal steps were carried out at 25°C and at 40 min/step. The total normalized viable cell number was calculated by integrating the viable cell number over the entire slab using the trapezoidal rule. Results indicate that while overexposure increases cell death, temperature also plays a significant role. Additionally, more cell death is seen during removal at 25°C when addition was carried out at a lower temperature (4°C). These effects can be seen more clearly in Figure 7, where the normalized viable cell number at the center and edge of the slab is shown for two scenarios: addition and removal at 4°C (80 min/step) or addition at 4°C (80 min/step) and removal at 25°C (40 min/step). These results clearly indicate that temperature is critical, even for removal steps. In the second scenario, where addition occurs at 4°C and removal occurs at 25°C, there is a significant loss in viable cell number during removal. The steep decrease in normalized viability at the center of the slab during removal at 25°C reflects two distinct phenomena. The high viable cell number present at the beginning of removal indicates the presence of many cells that are still quite susceptible to CPA toxicity. These cells will rapidly die when exposed to the higher temperature during removal. The edge of the slab experiences this phenomenon to a lesser extent as the edge of the slab equilibrates with the bulk solution concentration almost instantaneously which decreases the CPA concentration and time of exposure that occurs during removal. At the center of the slab, this issue is compounded by the slow mass transfer. Even at the higher temperature, Figure 6A clearly shows that the center of the slab, as well as the point half way between the edge and center of the slab, experience prolonged exposure to the CPAs during removal when compared to the outer edge of the slab. This is the most likely cause for the lower final viable cell number at the center of the slab as compared to the edge. This prolonged exposure also occurs for removal at 4°C although the cytotoxicity at this temperature causes the decrease in viable cell number to be much less dramatic. Overall, removal at 4°C causes an additional viable cell loss of 3.7% at the center of the slab compared to 0.6% at the edge the slab. These simulations indicate that temperature is even more critical for larger constructs. The previously published experimental results indicate that Me2SO toxicity is much less dependent on temperature than PD [28]. Therefore, additional simulations were carried out using the cytotoxicity parameters for Me2SO rather than the combined cytotoxicity that would be expected for the cocktail used in these studies. Me2SO is slightly less cytotoxic than PD at low temperatures but Me2SO cytotoxicity is much less sensitive to a change in temperature making it significantly less cytotoxic at higher temperatures than PD. Figure 8 compares the normalized viable cell number for normal parameters to the “less temperature sensitive” cytotoxicity parameters of Me2SO. These results indicate that the use of a CPA that exhibits similar cytotoxicity at 4°C and 25°C will yield higher viable cell number after addition and removal than a CPA that exhibits cytotoxicity which significantly increases with temperature. Even with addition and removal occurring at 25°C, 6M Me2SO will result in less cell loss throughout the slab (92–93.2% viable cell number, Figure 8) than the cocktail solution including PD with all exposure carried out at 4°C (84–88.7% viable cell number, Figure 7). However, Me2SO, even at 6M is not vitrifiable, whereas the cocktails that are vitrifiable, such as Me2SO with PD, are more cytotoxic than Me2SO at 25°C.
Figure 7.
Predicted Normalized Viable Cell Number (n/n0) at center of slab (dashed) or edge of slab (solid) for addition steps at 4°C (80 min/step) and removal at 4°C (80 min/step, black) or 25°C (40 min/step, gray).
Figure 8.
Predicted Normalized Viable Cell Number (n/n0) at center of slab (dashed) and at edge of slab (solid) for 25°C, 40 minute addition and removal steps for DMSO values of cytotoxicity parameters (black) vs cocktail parameters (gray).
Discussion
The cryopreservation of different tissue-engineered constructs or natural tissues presents a significant challenge in bringing them to the clinic. Due to the wide array of tissues, geometries and clinically relevant sizes, it is desirable to be able to design addition and removal protocols based on the specific tissue being preserved. Significant work has been done in the area of cryopreservation to better understand the cooling and warming process, but little work has been done to better understand and design CPA addition and removal protocols. This study addresses this deficiency. Although cooling and warming rates are dictated by the vitrification solution, the proper design of addition and removal protocols can improve the success of the vitrification process. Three main concerns arise when designing addition and removal procedures: osmotic excursions, mass transfer and CPA cytotoxicity. The addition of vitrification-relevant concentrations of CPAs in a single step is generally recognized to cause excessive osmotic excursions. Previously published work from our laboratory and others has addressed this issue and validated the need to minimize osmotic excursions and maintain them in a tolerable normalized cell volume range [19; 20; 31; 32]. All simulations carried out in this work maintain osmotic excursions within the previously determined tolerable range for βTC-tet murine insulinomas.
The success of vitrification is also contingent upon achieving sufficient mass transfer of the vitrifiable solution. Although recent publications utilize macroscopic observation to prove successful vitrification [45], it is preferable to determine a solution’s ability to vitrify using differential scanning calorimetry or another method of thermal analysis. Ensuring equilibration throughout the sample lends credence to the successful vitrification of macro constructs that cannot easily be tested by calorimetry. The mathematical model allows determination of the necessary time of exposure for each CPA to achieve equilibrium throughout the construct. Although this can be determined experimentally [31], the use of a mathematical model is more broadly applicable and can be applied to novel tissue-engineered constructs.
Due to the dependence of cytotoxicity on CPA concentration, exposure time and temperature, mass transfer and cytotoxicity are inextricably linked. The incorporation of a cytotoxicity equation based on experimental results for βTC-tet cells allows for insight into the importance of each of these variables in the addition and removal protocols. It is important to realize, however, that cytotoxicity parameters dictate the results and will vary with cell type. Cytotoxicity has been shown to increase with increased temperature for relatively long exposure times of ~30 minutes [28; 43]. This has led to the general assumption that CPA exposure should be carried out at low temperatures (≤ 4°C). Our results clearly indicate the importance of temperature of CPA addition and removal. The effects of temperature on cytotoxicity are clearly exacerbated for the longer exposure times necessary for larger constructs. Articular cartilage is particularly challenging due to the clinically relevant size and dense nature of the tissue. The challenge of mass transfer in articular cartilage is well known and has been investigated experimentally. Pegg’s group has used the “liquidus-tracking method” in which CPAs are added as the sample is cooled. This method attempts to follow the liquidus curve of the vitrification solution’s phase diagram to minimize the concentration of CPA that the cells are exposed to while ensuring that ice will not form [34; 44]. Although our cytotoxicity parameters were chosen based on experimental results with βTC-tet cells, Pegg’s experiments corroborate the need for improved mass transfer. Our simulations indicate that if the first addition step, A1, is carried out at 25°C rather than 4°C, the viable cell number will only drop by 1%. If A2 is also carried out at 25°C, the viable cell number after A1 and A2 will decrease 5%. As the concentration of the addition steps increases, the viable cell number will only decrease. While the introduction of the first two steps at room temperature may decrease the time necessary for CPA equilibration, the resulting viable cell number will be lower. Therefore, the “liquidus-tracking method” or any method that begins CPA exposure at a higher temperature and cools during the subsequent addition steps may have limited benefit, depending upon the CPA used.
The issue of overexposure is not often addressed in cryobiology although its effects can be significant. When working with a relatively simple system, such as encapsulated cells, overexposure of 1.5 minutes per step can result in additional loss in viable cell number (~3%). While this cell loss may be minimal, these effects are clearly exacerbated for larger constructs with more resistance to mass transfer. In the case of articular cartilage, chondrocyte viability is clearly critical to overall performance [18]. Some have suggested the possibility of utilizing lower molecular weight CPAs to improve mass transfer and minimize cytotoxicity [18]. In order to determine whether a significant increase in diffusivity, either due to a change in the matrix or the size of the CPAs, aids the addition and removal process, additional simulations were done. Mass transfer through the articular cartilage slab geometry but with mass transfer properties of alginate still requires 30 minutes/step to achieve approximately 90% equilibration, as compared to 80 minutes/step for the articular cartilage slab (4°C, results not shown). Although improvement in mass transfer properties would slightly decrease cytotoxicity by approximately 4%, the dimension of a clinically relevant cartilage disc plays a larger role in the success or failure of vitrification. Studies on CPA cytotoxicity in chondrocytes in situ indicate that this result may be an underestimate, as chondrocytes appear more sensitive to CPA cytotoxicity than the βTC-tet cells [13]. It is likely that many researchers, instead of improving diffusivity, are achieving only partial equilibration and therefore partial vitrification. While this may minimize CPA toxicity, it will increase the possibility of cryoinjury for cells in the center of the disc. This has been experimentally shown for the vitrification solution VS55, composed of Me2SO, PD and formamide. Exposure to VS55 resulted in a decrease in chondrocyte viability in articular cartilage discs to 51% although rapid cooling without the solution resulted in viability of less than 5% [16]. These results indicate that the cryoinjury that occurs in the absence of CPAs causes more cell death than would be seen due to CPA cytotoxicity experienced by the cells during addition and removal. Cells within the matrix that are exposed to lower concentrations of CPAs that are not vitrifiable will likely experience intracellular ice formation, which is almost always lethal [33]. More recent studies with articular cartilage show significant improvement in mass transfer with dynamic loading [2]. These studies would be directly applicable to the cryopreservation of articular cartilage and may indeed improve the cryopreservation outcome.
Although experimentally determined, questions may remain about the cytotoxicity equation used in these simulations. The simulated viable cell number after addition and removal relies heavily on the parameters chosen. The cytotoxicity equation is most sensitive to a change in parameter f. When parameter f is halved, f/2, the viable cell number is also approximately halved. Clearly, the need to minimize cytotoxicity can be met, in part, with less toxic CPAs. The theory of cryoprotectant toxicity neutralization has been suggested by Fahy [14]. This theory indicates that specific chemicals can neutralize the toxicity of CPAs although this has only been shown conclusively for the combination of amides with Me2SO. Additionally, many have tried to minimize the concentrations of CPAs necessary to achieve vitrification by using non-permeating solutes, such as trehalose or sucrose. Non-permeating solutes may not contribute as significantly to overall toxicity as permeating solutes [15], but previous studies have shown that these additives are not innocuous and do contribute to toxicity [28]. Less cytotoxic CPAs may be beneficial, but these simulations indicate that it may be more critical to use CPAs that exhibit cytotoxicity that is less temperature sensitive. The previous experimental studies indicate that Me2SO toxicity is less temperature sensitive than that of PD. Recent studies corroborate that PD is more cytotoxic than Me2SO for chondrocytes [23]. Unfortunately, 6M Me2SO is not vitrifiable in our hands. The temperature sensitivity of single-component CPAs also carry over to the cocktails that are a combination of these CPAs [28]. Nevertheless, the issue of CPA cytotoxicity remains the most critical challenge for the successful vitrification of tissues or tissue-engineered constructs [14].
Finally, the use of a time-dependent death rate appears to reflect the experimentally determined cytotoxicity kinetics. The value of parameter f indicates that βTC-tet cells become somewhat resistant to CPA cytotoxicity over time. Depending on the mechanism of resistance, it may be possible to select for CPA resistant cells and preferentially use these in tissue-engineered constructs. This phenomenon may be present in other cell types to a greater or lesser extent. It is currently unclear whether the use of discrete subpopulations would better represent the physiological phenomenon that is occurring although further experiments would be required before the subpopulations could be accurately described. It is clear that investigation into the mechanisms of cytotoxicity and resistance would provide insight and allow for better design of CPA solutions and addition/removal protocols.
Conclusions
Vitrification has been touted for use with larger tissue engineered constructs or natural tissues where ice formation can be especially detrimental [26; 33]. The issue of CPA cytotoxicity is unavoidable when using the high concentrations of CPAs necessary to successfully vitrify a sample. Simulations indicate that temperature of exposure to CPAs is particularly deleterious to viable cell number. Cell death can be significantly reduced by using less cytotoxic CPAs. Additionally, the use of CPAs that exhibit less temperature sensitive cytotoxicity would allow the addition and removal steps to occur faster at a higher temperature without excessive cell death. CPA overexposure also results in significant cell loss, especially when working with larger constructs. On the other hand, CPA underexposure would achieve vitrifiable concentrations only at the outer part of a tissue. These results point to the critical need for properly designed protocols that allow for sufficient CPA equilibration while minimizing CPA cytotoxicity. This mathematical model is a useful tool in the design and optimization of such protocols for natural tissues and tissue-engineered constructs.
Model of mass transfer through extracellular matrix & cell membrane, heat transfer & toxicity
Simulations performed for encapsulated cells and articular cartilage
Addition and removal at 4°C is preferable to 25°C, as cell death is higher at 25°C
Temperature effect is exacerbated in articular cartilage due to size & diffusivity
Less cytotoxic CPAs would significantly improve the cryopreservation outcome
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Abazari A, Elliott JA, Law GK, McGann LE, Jomha NM. A biomechanical triphasic approach to the transport of nondilute solutions in articular cartilage. Biophys J. 2009;97:3054–64. doi: 10.1016/j.bpj.2009.08.058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Albro MB, Li R, Banerjee RE, Hung CT, Ateshian GA. Validation of theoretical framework explaining active solute uptake in dynamically loaded porous media. Journal of Biomechanics. 2010;43:2267–2273. doi: 10.1016/j.jbiomech.2010.04.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Arav A, Natan Y. Directional Freezing: A Solution to the Methodological Challenges to Preserve Large Organs. Seminars in Reproductive Medicine. 2009;27:438–442. doi: 10.1055/s-0029-1241052. [DOI] [PubMed] [Google Scholar]
- 4.Balasubramanian SK, Coger RN. Heat and mass transfer during the cryopreservation of a bioartificial liver device: A computational model. Asaio Journal. 2005;51:184–193. doi: 10.1097/01.mat.0000161079.35897.7d. [DOI] [PubMed] [Google Scholar]
- 5.Bird RB, Stewart WE, Lightfoot EN. Transport Phenomena. John Wiley & Sons, Inc; New York, NY: 2002. [Google Scholar]
- 6.Black SP, Constantinidis I, Cui H, Tucker-Burden C, Weber CJ, Safley SA. Immune responses to an encapsulated allogeneic islet beta-cell line in diabetic NOD mice. Biochemical and Biophysical Research Communications. 2006;340:236–243. doi: 10.1016/j.bbrc.2005.11.180. [DOI] [PubMed] [Google Scholar]
- 7.Brockbank KG, Chen ZZ, Song YC. Vitrification of porcine articular cartilage. Cryobiology. 2010;60:217–21. doi: 10.1016/j.cryobiol.2009.12.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Brockbank KGM, Walsh JR, Song YC, Taylor MJ. Vitrification: Preservation of Cellular Implants. In: Ashammakhi N, Ferretti P, editors. Topics in Tissue Engineering. University of Oulu; Oulu, FI: 2003. pp. 1–26. [Google Scholar]
- 9.Char CD, Guerrero SN, Alzamora SM. Mild Thermal Process Combined with Vanillin Plus Citral to Help Shorten the Inactivation Time for Listeria innocua in Orange Juice. Food and Bioprocess Technology. 2010;3:752–761. [Google Scholar]
- 10.Dahl SL, Chen Z, Solan AK, Brockbank KG, Niklason LE, Song YC. Feasibility of vitrification as a storage method for tissue-engineered blood vessels. Tissue Engineering. 2006;12:291–300. doi: 10.1089/ten.2006.12.291. [DOI] [PubMed] [Google Scholar]
- 11.Dragomir CT, Pausescu E. Theoretical considerations regarding the cell membrane function during cold-induced preservation of tissues and organs: new possibilities for optimizing the process. Journal of Theoretical Biology. 1974;47:281–93. doi: 10.1016/0022-5193(74)90198-2. [DOI] [PubMed] [Google Scholar]
- 12.Elmoazzen HY, Elliott JAW, McGann LE. Osmotic Transport across Cell Membranes in Nondilute Solutions: A New Nondilute Solute Transport Equation. Biophysical Journal. 2009;96:2559–2571. doi: 10.1016/j.bpj.2008.12.3929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Elmoazzen HY, Poovadan A, Law GK, Elliott JA, McGann LE, Jomha NM. Dimethyl sulfoxide toxicity kinetics in intact articular cartilage. Cell Tissue Bank. 2007;8:125–33. doi: 10.1007/s10561-006-9023-y. [DOI] [PubMed] [Google Scholar]
- 14.Fahy GM. Cryoprotectant toxicity neutralization. Cryobiology. 2010;60:S45–53. doi: 10.1016/j.cryobiol.2009.05.005. [DOI] [PubMed] [Google Scholar]
- 15.Fahy GM, Wowk B, Wu J, Phan J, Rasch C, Chang A, Zendejas E. Cryopreservation of organs by vitrification: perspectives and recent advances. Cryobiology. 2004;48:157–178. doi: 10.1016/j.cryobiol.2004.02.002. [DOI] [PubMed] [Google Scholar]
- 16.Guan J, Urban JP, Li ZH, Ferguson DJ, Gong CY, Cui ZF. Effects of rapid cooling on articular cartilage. Cryobiology. 2006;52:430–9. doi: 10.1016/j.cryobiol.2006.03.004. [DOI] [PubMed] [Google Scholar]
- 17.Han X, Liu Y, Critser JK. Determination of the quaternary phase diagram of the water-ethylene glycol-sucrose-NaCl system and a comparison between two theoretical methods for synthetic phase diagrams. Cryobiology. 2010;61:52–7. doi: 10.1016/j.cryobiol.2010.04.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Hayashi M, Tsuchiya H, Otoi T, Agung B, Yamamoto N, Tomita K. Influence of freezing with liquid nitrogen on whole-knee joint grafts and protection of cartilage from cryoinjury in rabbits. Cryobiology. 2009;59:28–35. doi: 10.1016/j.cryobiol.2009.04.002. [DOI] [PubMed] [Google Scholar]
- 19.Heo YS, Lee HJ, Hassell BA, Irimia D, Toth TL, Elmoazzen H, Toner M. Controlled loading of cryoprotectants (CPAs) to oocyte with linear and complex CPA profiles on a microfluidic platform. Lab Chip. 11:3530–7. doi: 10.1039/c1lc20377k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Hunt CJ, Pegg DE, Armitage SE. Optimising cryopreservation protocols for haematopoietic progenitor cells: A methodological approach for umbilical cord blood. Cryoletters. 2006;27:73–83. [PubMed] [Google Scholar]
- 21.Jadin KD, Wong BL, Bae WC, Li KW, Williamson AK, Schumacher BL, Price JH, Sah RL. Depth-varying density and organization of chondrocytes in immature and mature bovine articular cartilage assessed by 3d imaging and analysis. J Histochem Cytochem. 2005;53:1109–19. doi: 10.1369/jhc.4A6511.2005. [DOI] [PubMed] [Google Scholar]
- 22.Jomha NM, Lavoie G, Muldrew K, Schachar NS, McGann LE. Cryopreservation of intact human articular cartilage. Journal of Orthopaedic Research. 2002;20:1253–5. doi: 10.1016/S0736-0266(02)00061-X. [DOI] [PubMed] [Google Scholar]
- 23.Jomha NM, Weiss ADH, Forbes JF, Law GK, Elliott JAW, McGann LE. Cryoprotectant agent toxicity in porcine articular chondrocytes. Cryobiology. 2010;61:297–302. doi: 10.1016/j.cryobiol.2010.10.002. [DOI] [PubMed] [Google Scholar]
- 24.Karlsson JOM, Toner M. Long-term storage of tissues by cryopreservation: Critical issues. Biomaterials. 1996;17:243–256. doi: 10.1016/0142-9612(96)85562-1. [DOI] [PubMed] [Google Scholar]
- 25.Kleinhans FW. Membrane permeability modeling: Kedem-Katchalsky vs a two-parameter formalism. Cryobiology. 1998;37:271–89. doi: 10.1006/cryo.1998.2135. [DOI] [PubMed] [Google Scholar]
- 26.Kuleshova LL, Gouk SS, Hutmacher DW. Vitrification as a prospect for cryopreservation of tissue-engineered constructs. Biomaterials. 2007;28:1585–1596. doi: 10.1016/j.biomaterials.2006.11.047. [DOI] [PubMed] [Google Scholar]
- 27.Kyrychenko A, Dyubko TS. Molecular dynamics simulations of microstructure and mixing dynamics of cryoprotective solvents in water and in the presence of a lipid membrane. Biophys Chem. 2008;136:23–31. doi: 10.1016/j.bpc.2008.04.004. [DOI] [PubMed] [Google Scholar]
- 28.Lawson A, Ahmad H, Sambanis A. Cytotoxicity effects of cryoprotectants as single-component and cocktail vitrification solutions. Cryobiology. 2011;62:115–122. doi: 10.1016/j.cryobiol.2011.01.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Li F-F, Liu J. Characterization of Micro-/Nano-Scale Ice Crystal Formation in Cryo-Biomedical Engineering: A Review. Journal of Computational and Theoretical Nanoscience. 2010;7:85–96. [Google Scholar]
- 30.Mukherjee IN. Chemical & Biomolecular Engineering. Georgia Institute of Technology; Atlanta, GA: 2008. A Rational Design Approach for the Cryopreservation of Natural and Engineered Tissues; p. 219. [Google Scholar]
- 31.Mukherjee IN, Li Y, Song YC, Long RC, Sambanis A. Cryoprotectant transport through articular cartilage for long-term storage: experimental and modeling studies. Osteoarthritis and Cartilage. 2008;16:1379–1386. doi: 10.1016/j.joca.2008.03.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Mukherjee IN, Song YC, Sambanis A. Cryoprotectant delivery and removal from murine insulinomas at vitrification-relevant concentrations. Cryobiology. 2007;55:10–18. doi: 10.1016/j.cryobiol.2007.04.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Pegg DE. The relevance of ice crystal formation for the cryopreservation of tissues and organs. Cryobiology. 2010;60:S36–44. doi: 10.1016/j.cryobiol.2010.02.003. [DOI] [PubMed] [Google Scholar]
- 34.Pegg DE, Wang L, Vaughan D. Cryopreservation of articular cartilage. Part 3: the liquidus-tracking method. Cryobiology. 2006;52:360–8. doi: 10.1016/j.cryobiol.2006.01.004. [DOI] [PubMed] [Google Scholar]
- 35.Peleg M, Normand MD. Calculating microbial survival parameters and predicting survival curves from non-isothermal inactivation data. Crit Rev Food Sci Nutr. 2004;44:409–18. doi: 10.1080/10408690490489297. [DOI] [PubMed] [Google Scholar]
- 36.Prickett RC, Elliott JA, McGann LE. Application of the osmotic virial equation in cryobiology. Cryobiology. 2010;60:30–42. doi: 10.1016/j.cryobiol.2009.07.011. [DOI] [PubMed] [Google Scholar]
- 37.Ross-Rodriguez LU, Elliott JA, McGann LE. Investigating cryoinjury using simulations and experiments. 1: TF-1 cells during two-step freezing (rapid cooling interrupted with a hold time) Cryobiology. 2010;61:38–45. doi: 10.1016/j.cryobiol.2010.04.004. [DOI] [PubMed] [Google Scholar]
- 38.Safley S, Cui H, Cauffiel S, Weber C. Long-term metabolic control of spontaneous diabetes by microencapsulated allogeneic and xenogeneic islets. American Journal of Transplantation. 2007;7:206–206. [Google Scholar]
- 39.Sambanis A. Engineering challenges in the development of an encapsulated cell system for treatment of type 1 diabetes. Diabetes Technol Ther. 2000;2:81–9. doi: 10.1089/152091599316784. [DOI] [PubMed] [Google Scholar]
- 40.Sambanis A. Bioartificial Pancreas. In: Lanza R, Langer R, Vacanti J, editors. Principles of Tissue Engineering. Academic Press; Boston: 2007. pp. 619–630. [Google Scholar]
- 41.Shaozhi Z, Pegg DE. Analysis of the permeation of cryoprotectants in cartilage. Cryobiology. 2007;54:146–53. doi: 10.1016/j.cryobiol.2006.12.001. [DOI] [PubMed] [Google Scholar]
- 42.Thakrar RR, Patel VP, Hamilton G, Fuller BJ, Seifalian AM. Vitreous cryopreservation maintains the viscoelastic property of human vascular grafts. Faseb Journal. 2006;20:874–81. doi: 10.1096/fj.05-5304com. [DOI] [PubMed] [Google Scholar]
- 43.Tomford WW, Fredericks GR, Mankin HJ. Studies on cryopreservation of articular cartilage chondrocytes. J Bone Joint Surg Am. 1984;66:253–9. [PubMed] [Google Scholar]
- 44.Wang L, Pegg DE, Lorrison J, Vaughan D, Rooney P. Further work on the cryopreservation of articular cartilage with particular reference to the liquidus tracking (LT) method. Cryobiology. 2007;55:138–47. doi: 10.1016/j.cryobiol.2007.06.005. [DOI] [PubMed] [Google Scholar]
- 45.Weiss AD, Forbes JF, Scheuerman A, Law GK, Elliott JA, McGann LE, Jomha NM. Statistical prediction of the vitrifiability and glass stability of multi-component cryoprotective agent solutions. Cryobiology. 2010;61:123–7. doi: 10.1016/j.cryobiol.2010.05.008. [DOI] [PubMed] [Google Scholar]
- 46.Youn JI, Telenkov SA, Kim E, Bhavaraju NC, Wong BJ, Valvano JW, Milner TE. Optical and thermal properties of nasal septal cartilage. Lasers Surg Med. 2000;27:119–28. doi: 10.1002/1096-9101(2000)27:2<119::aid-lsm3>3.0.co;2-v. [DOI] [PubMed] [Google Scholar]
- 47.Zhang L, Hu J, Athanasiou KA. The role of tissue engineering in articular cartilage repair and regeneration. Crit Rev Biomed Eng. 2009;37:1–57. doi: 10.1615/critrevbiomedeng.v37.i1-2.10. [DOI] [PMC free article] [PubMed] [Google Scholar]