Joint Segmentation and Deformable Registration of Brain Scans Guided by a Tumor Growth Model

Abstract

This paper presents an approach for joint segmentation and deformable registration of brain scans of glioma patients to a normal atlas. The proposed method is based on the Expectation Maximization (EM) algorithm that incorporates a glioma growth model for atlas seeding, a process which modifies the normal atlas into one with a tumor and edema. The modified atlas is registered into the patient space and utilized for the posterior probability estimation of various tissue labels. EM iteratively refines the estimates of the registration parameters, the posterior probabilities of tissue labels and the tumor growth model parameters. We have applied this approach to 10 glioma scans acquired with four Magnetic Resonance (MR) modalities (T1, T1-CE, T2 and FLAIR ) and validated the result by comparing them to manual segmentations by clinical experts. The resulting segmentations look promising and quantitatively match well with the expert provided ground truth.

1 Introduction

Statistical atlases constructed from MR scans are powerful tools for aiding the analysis and understanding of brain tumor development. The atlases are used for tasks such as learning the relative location of tumors with respect to healthy tissue [4] or guiding the automatic segmentation of brain tumor scans [13]. An important component in the construction and application of the atlases is the registration of brain tumor MR scans to the a common coordinate system. This coordinate system is often represented by a MR scan of a healthy subject due to the subject specific nature of brain tumors. Although a plethora of methods for image registration exists [2], this registration task is generally considered very challenging as there is no correspondence for the pathology in the healthy scans. In addition, the healthy tissue in the brain scan is often severely deformed by the mass-effect of the tumor so that its shape is very different from that in the healthy brain scan. In this paper, we address this issue by developing a new approach for brain tumor registration that explicitly models the mass effect of the pathology.

A popular approach for registering brain images to an atlas coordinate system is to mask out the pathology and then perform the registration to the healthy tissue [11, 13, 14]. Alternative methods use atlas seeding, in which a tumor is seeded in the healthy (atlas) scan [10]. Both of these frameworks essential ignore edema as they fail to explicitly model the diffusion of the tumor cells into the neighboring healthy tissue. This limitation was addressed by [1], whose registration incorporated a biophysical (diffusion-reaction) tumor growth model simulating the mass-effect and diffusion caused by the pathology. However, the approach requires accurate segmentations of the pathology which are difficult to produce automatically. We now derive a joint atlas registration and segmentation framework to circumvent this problem.

Similar to joint segmentation and registration methods targeted towards healthy brains [6, 8], our method iteratively estimates the posterior probabilities of tissue classes and registers the atlas via the EM algorithm. However, our approach also computes the diffusion-reaction parameters of the tumor growth model and the coordinates for atlas seeding. These additional parameters greatly increase the complexity of the optimization problem compared to [6,8] which required us to carefully adopt the EM model to this specific application. The remainder of this paper is organized as follows: In Section 2 we review the diffusion-reaction model and describe the construction of the atlas. The atlas is then used in Section 3 to guide our joint registration and segmentation framework. In Section 4 we present our quantitative evaluation and results of the application to sample patients, and conclude the paper in Section 5.

2 Atlas Generation

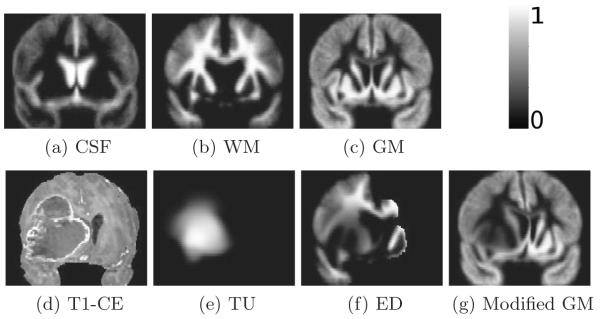
In this section, we use a glioma growth model to embed a tumor in an originally healthy atlas. We define the atlas as a set of probability maps that specify the spatial distribution of brain tissues (see Fig.1.(a)-(c)). This modified atlas then guides the EM algorithm in registering and segmenting of subjects with glioma.

Fig. 1.

(a)-(c) Healthy white matter (WM), gray matter (GM) and cerebro spinal fluid (CSF) probability maps, (d) sample glioma scan, (e) corresponding estimated tumor (TU), (f) edema (ED), and (g) gray matter probability maps before registration to the patient.

As in [1], a model of the glioma is implanted into the healthy brain scan by artificially seeding a tumor in the healthy atlas and growing it using the biophysical model proposed in [3]. Let Ω_A and [0, T] denote the space of atlas and a time interval for growing the tumor. The evolution of tumor probability π_TU (x, t) in Ω_A × [0, T] is determined by the following diffusion-reaction model:

$$\begin{array}{cc}\hfill & \frac{\partial {\pi }_{\mathit{TU}}}{\partial t}-\nabla (D\nabla {\pi }_{\mathit{TU}})+\nabla \left({\pi }_{\mathit{TU}}\mathbf{v}\right)=\rho {\pi }_{\mathit{TU}}(1-{\pi }_{\mathit{TU}}),\hfill \\ \hfill & \nabla [\lambda \mathbf{I}\nabla \cdot \mathbf{u}+\mu (\nabla \mathbf{u}+\nabla {\mathbf{u}}^T\left)\right]=p\nabla {\pi }_{\mathit{TU}}\hfill \end{array}$$ (1)

where Δ is the differential operator, u is the mass effect displacement field caused by the presence of the tumor, v = ∂u/∂t is the relevant velocity field, p is a scalar which determines the strength of the tumor mass effect, D is a spatially variable function capturing diffusion coefficient within white (D_WM) and gray matters (D_GM), and ρ is proliferation coefficient. We fix ρ = 0.025 and D_GM = 1e⁻¹⁰ (the default values of [3]) as the method is relatively insensitive to these parameters. Now, if we denote with x₀ the initial seed location of the tumor and with d the voxel size of the Ω_A, then our tumor growth model is completely defined by the parameters q ≡ {x₀, p, D_WM, T} given the initial conditions for the u(x|q, t = 0) = 0 and π_TU (x|q, t = 0) = exp(−(x − x₀)²/d²).

Once we solve the above equation for u and π_TU, we combine those results at t = T with the original atlas of healthy brains ${\pi }_X^o(\cdot )$ to infer tissue probability π_X(·|q) for tissue X. To simplify notation, we omit t = T from u and π_TU and simply denote with π_TU(x|q) the spatial probability map of glioma being present at location x ∈ Ω_A at time T and u(x|q) the corresponding mass effect at that location and time. We then construct π_X(·|q) for GM and CSF by deforming the corresponding spatial probabilities ${\pi }_X^o(\cdot )$ of the healthy population via the mass-effect u and weighing them with (1 − π_TU):

$$\begin{array}{cc}\hfill {\pi }_{\mathit{GM}}(\mathbf{x}\mid \mathbf{q})& \equiv {\pi }_{\mathit{GM}}^o\left(\mathbf{u}\right(\mathbf{x}\left)\right)\cdot (1-{\pi }_{\mathit{TU}}(\mathbf{x}\left)\right)\hfill \\ \hfill {\pi }_{\mathit{CSF}}(\mathbf{x}\mid \mathbf{q})& \equiv {\pi }_{\mathit{CSF}}^o\left(\mathbf{u}\right(\mathbf{x}\left)\right)\cdot (1-{\pi }_{\mathit{TU}}(\mathbf{x}\left)\right)\hfill \end{array}$$ (2)

We construct the spatial probability map of edema π_ED based on the assumption that edema is in close proximity of the tumor, which we model via the Heaviside function H(π_TU(x)) (H(a) = 0 for a ≤ 0 and H(a) = 1 otherwise), and be confined to the mass deformed white matter of the healthy brain, which we model with ${\pi }_{\mathit{WM}}^o\left(\mathbf{u}\right(\mathbf{x}\left)\right)$. Thus:

$${\pi }_{\mathit{ED}}(\mathbf{x}\mid \mathbf{q})\equiv {\pi }_{\mathit{WM}}^o\left(\mathbf{u}\right(\mathbf{x}\left)\right)\cdot (1-{\pi }_{\mathit{TU}}(\mathbf{x}\left)\right)\cdot H\left({\pi }_{\mathit{TU}}\right(\mathbf{x}\left)\right).$$ (3)

We define the subject specific spatial probability map of the white matter as:

$${\pi }_{\mathit{WM}}(\mathbf{x}\mid \mathbf{q})\equiv 1-\left[{\pi }_{\mathit{TU}}\right(\mathbf{x}\mid \mathbf{q})+{\pi }_{\mathit{ED}}(\mathbf{x}\mid \mathbf{q})+{\pi }_{\mathit{CSF}}(\mathbf{x}\mid \mathbf{q})+{\pi }_{\mathit{GM}}(\mathbf{x}\mid \mathbf{q}\left)\right]$$ (4)

A sample set of the generated probability maps π_TU(·|q), π_ED(·|q) and π_GM(·|q) is shown in Fig.1, illustrating the impact of the mass effect and tumor invasion in originally healthy atlas.

Finally, we note that we use the same probability map for enhancing tumor and necrosis as our tumor growth model does not distinguish between these two tissue types. In addition, we simplify notation by denoting the probability maps generated in this section with π_k(·|q), 1 ≤ k ≤ K = 6.

3 Joint Segmentation-Registration

We now describe the framework for joint segmentation-registration which is guided by the atlas defined in the previous section. We assume that a set of J co-registered, inhomogeneity-corrected, and skull stripped MR images is given in the reference (fixed) domain Ω_F so that for any sample voxel x ∈ Ω_F, y(x) ≡ [y₁(x), ⋯ , y_J(x)]^T is an independent observation vector that corresponds to the J image intensities. We then define observation set as: Y = {y(x)|x ∈ Ω_F}. The goal of this section is to derive an algorithm for estimating the intensity distributions of each structure Φ, the atlas coefficient q, and the deformation between the atlas and the reference domain h.

We further specify Φ by assuming the conditional probability distribution function (pdf) of each y(x) is a weighted mixture of K Gaussians: $f(\mathbf{Y}\mid \Phi ,\mathbf{h},\mathbf{q},\mathbf{x})\equiv {\sum }_{k=1}^K{\pi }_k\left(\mathbf{h}\right(\mathbf{x})\mid \mathbf{q})f_k\left(\mathbf{y}\right(\mathbf{x})\mid \Phi )$ where f_k ~ N(m_k, Σ_k) is a multivariate Gaussian distribution with mean m_k and the covariance matrix Σ_k, and Φ ≡ {m₁, ⋯ , m_K, Σ₁, ⋯ , Σ_K). The mixture weights are determined by π_k(h(x)|q) which are originally defined in the atlas space Ω_A (see Section 2) and registered to the patient space through h : Ω_F → Ω_A, a vector field mapping the atlas into the patient space. Based upon these assumptions, we write the conditional likelihood of Y as: f(Y|Φ, h, q) = Π_x∈ΩF f(Y|Φ, h, q, x).

Our problem of joint segmentation registration and atlas parameter estimation can be defined as the solution of the following:

$$({\Phi }_o,{\mathbf{h}}_o,{\mathbf{q}}_o)\equiv \underset{\Phi ,\mathbf{q},\mathbf{h}}{\mathrm{argmax}}\mathit{log}f(\mathbf{Y}\mid \Phi ,\mathbf{h},\mathbf{q}).$$ (5)

One way of computing the solution to this problem is via Expectation-Maximization algorithm [8]. EM is an iterative algorithm which in stead of directly solving (5), maximizes a lower bound on logf(Y|Φ, h, q). At every iteration, given the current estimate of the unknown parameters Φ’, h’ and q’, the lower bound of the log-likelihood in (5) is written as:

$$Q(\Phi ,\mathbf{h},\mathbf{q}\mid {\Phi }^{\prime },{\mathbf{h}}^{\prime },{\mathbf{q}}^{\prime })\equiv \sum _{\mathbf{x}\in {\Omega }_F}\sum _{k=1}^K{p}_k\left(\mathbf{x}\right)\mathit{log}\left({\pi }_k\right(\mathbf{h}\left(\mathbf{x}\right)\mid \mathbf{q}\left)f_k\right(\mathbf{y}\left(\mathbf{x}\right)\mid \Phi \left)\right),$$ (6)

where p_k(x) stands for the posterior probability of class k at voxel x (see equ.(7)) The structure of the proposed EM algorithm consists of iterations between the E-Step and M-Step, during which the posteriors and parameters {Φ, h, q} are respectively updated. Further detail is as follows:

E-Step

In this step, label estimation is achieved by updating the computed posterior probabilities given the current estimate of the parameter:

$$p_k\left(\mathbf{x}\right)=\frac{f_k\left(\mathbf{y}\right(\mathbf{x})\mid {\Phi }^{\prime }){\pi }_k\left({\mathbf{h}}^{\prime }\right(\mathbf{x})\mid {\mathbf{q}}^{\prime })}{\sum _{l=1}^K{f}_l\left(\mathbf{y}\right(\mathbf{x})\mid {\Phi }^{\prime }){\pi }_l\left({\mathbf{h}}^{\prime }\right(\mathbf{x})\mid {\mathbf{q}}^{\prime }}.$$ (7)

M-Step

The update of the distribution parameters, (i.e. means and covariance matrices) in Φ have closed form solutions which can be found in the literature [9] and are not mentioned here. We optimize h by the following variational framework which computes the differential of (6) with respect to an infinitely small test function v:

$$0=Q(\Phi ,{\mathbf{h}}^{\prime }+\mathbf{v},{\mathbf{q}}^{\prime }\mid {\Phi }^{\prime },{\mathbf{h}}^{\prime },{\mathbf{q}}^{\prime })-Q({\Phi }^{\prime },{\mathbf{h}}^{\prime },{\mathbf{q}}^{\prime }\mid {\Phi }^{\prime },{\mathbf{h}}^{\prime },{\mathbf{q}}^{\prime })=\sum _{\mathbf{x}\in {\Omega }_F}{\mathbf{v}}^t\left(\mathbf{x}\right).\left\{\mathbf{r}\right(\mathbf{x})+\mathbf{W}(\mathbf{x}).\mathbf{v}(\mathbf{x}\left)\right\}$$ (8)

In this equation, the gradient vector r(x) and the matrix W(x) are defined as:

$$\mathbf{r}\left(\mathbf{x}\right)=2\sum _{k=1}^K\frac{p_k\left(\mathbf{x}\right)}{{\pi }_k\left({\mathbf{h}}^{\prime }\right(\mathbf{x})\mid {\mathbf{q}}^{\prime })}\nabla {\pi }_k\left({\mathbf{h}}^{\prime }\right(\mathbf{x})\mid {\mathbf{q}}^{\prime }),$$ (9)

$$\mathbf{W}\left(\mathbf{x}\right)=\sum _{k=1}^K{p}_k\left(\mathbf{x}\right)[\frac{\mathbf{H}\left({\pi }_k\right({\mathbf{h}}^{\prime }\left(\mathbf{x}\right)\mid {\mathbf{q}}^{\prime }\left)\right)}{{\pi }_k\left({\mathbf{h}}^{\prime }\right(\mathbf{x})\mid {\mathbf{q}}^{\prime })}-\frac{\nabla {\pi }_k\left({\mathbf{h}}^{\prime }\right(\mathbf{x})\mid {\mathbf{q}}^{\prime }){(\nabla {\pi }_k({\mathbf{h}}^{\prime }\left(\mathbf{x}\right)\mid {\mathbf{q}}^{\prime }\left)\right)}^t}{{\left({\pi }_k\right({\mathbf{h}}^{\prime }\left(\mathbf{x}\right)\mid {\mathbf{q}}^{\prime }\left)\right)}^2}]$$ (10)

where H is the Hessian matrix. The detailed derivations are omitted due to space limitations. Equation (8) leads to r(x) + W(x).v(x) = 0, hence v can be found as: v(x) = W⁻¹(x) · r(x). For further numerical stability, we add an identity matrix component to W, therefore the update of h(x) can be written as:

$${\mathbf{h}}^{\prime }\left(\mathbf{x}\right)\leftarrow {\mathbf{h}}^{\prime }\left(\mathbf{x}\right)-{\left[\mathbf{W}\right(\mathbf{x})+c\mathbf{I}]}^{-1}\mathbf{r}\left(\mathbf{x}\right),$$ (11)

where I is the identity matrix and c is a constant. In this paper, we found c = 0.1 to produce a robust and reasonable deformation field. Notice the update equation is computed independently at every voxel, which in general results in a non-smooth deformation field. In order to apply the smoothness constraint, similar to Thirions’ demons framework [7] we di use the estimated deformation vectors by a Gaussian convolution filter with a band width of 2.

To update the atlas parameters q, since no analytical expression for the derivatives of Q(Φ’, h’, q|Φ’, h’, q’) w.r.t q exists, we follow a numerical scheme. We maximize (6) using a derivative free pattern search library [5]. Subsequently, each process returns its corresponding Q value to the library and the procedure is iterated until a maximum is found. Since this operation is computationally expensive it is performed only after having an adequate convergence on estimated deformation field otherwise we keep it fixed.

4 RESULTS

We applied our proposed joint segmentation-registration method to 10 glioma patients. Our preprocessing pipeline starts with skull stripping of all modalities (FLAIR,T2,T1, and T1CE) and MR field inhomogeneity correction [15]. These images are co-registered to the atlas using an affine registration based on mutual information [12]. We solved (1) on a lattice of 64 × 64 × 64 nodes for efficiency reasons. We numerically compared our EM based segmentation results to the expert provided references for edema and tumor labels using Dice volume overlap ratio. For the S1-S5 cases (see the first five columns in Table.1) total volumes of pathology were delineated and for the S6-S10 cases every third slice was segmented by our specialist. We also computed the dice scores with respect to every third slice in S1-S5. The average difference between these scores and those obtained based on entire volume was less than 0.75%.

Table 1.

Dice overlap ratios (%) of the segmented tumor and edema with the expert provided ground truths for fully and partly optimized tumor models. For S1-S5 subjects total volumes of edema and tumor were manually segmented whereas for subjects S6-S10 every third slice was delineated by our specialist.

Opt.	Lab.	S.1	S.2	S.3	S.4	S.5	S.6	S.7	S.8	S.9	S.10	Avg.
Fully	TU	89.4	89.7	87.2	83.0	91.8	70.0	81.6	84.0	82.7	90.8	85.4
	ED	85.7	80.0	60.4	59.5	83.3	81.6	81.7	87.6	75.6	66.0	76.0
Partly	TU	83.9	89.0	87.9	80.3	86.1	51.8	78.7	71.8	80.2	79.5	71.7
	ED	83.7	79.2	59.0	46.2	83.1	63.0	78.2	84.8	74.1	64.8	71.6

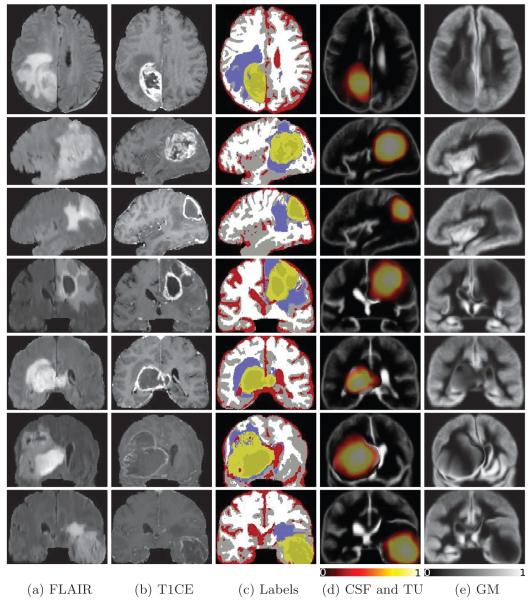
Sample results of seven patients in Fig.2 show a high visual correspondence with patients anatomies. Moreover, it is interesting to observe that the registered atlas probability maps closely match the patient segmented labels, which indicates good registration as well.

Fig. 2.

Segmentation and registration results for seven sample patients. Each row corresponds to a single patient and represents the results in the slice with largest tumor section. (a)-(b) FLAIR,T1-CE images,(c) segmentation results indicating enhancing tumor, necrosis, edema, CSF, gray and white matters in light and dark yellows, purple, red, gray and white colors respectively, (d) overlay of the tumor and CSF probability maps registered to the patient scans, (e) probability map of GM registered to the patient scans.

This observation is further verified by our numerical evaluations in Table.1 which shows that the segmentations using our method have reasonable matches with the reference volumes. Also, the Dice scores favorably compare to the values reported in [13], though the data sets are different. Regarding the observed discrepancy between the expert provided segmentations and our results, we believe that it is due to the fact that the proposed method takes a voxel-based classification approach, while a human rater considers other complex feature such as the shape and appearance.

Moreover, in order to investigate the sensitivity of the results w.r.t. optimality of parameters of model, two different sets of experiments were performed. In the first case, all model parameters in q were optimized (denoted by Fully), and in the second case only D_WM was optimized and the expert chosen parameters such as seed location and tumor growth length were not refined (denoted by Partly). As shown in Table.1, the Dice coefficients in fully optimized mode are in general higher and imply better overlaps compared to partly optimized model.

5 CONCLUSION

We developed a joint segmentation registration tool for glioma images. Our proposed method utilizes multi-channel MR images as the patient feature images, and an originally healthy atlas as the spatial probability maps for various tissue labels. We utilized a tumor growth model to modify the probability maps of the original atlas. The model impacts the atlas original probability maps by both deforming and masking them the due to tumor mass-effect and diffusion. We employed an EM algorithm to iteratively refine the estimates of posterior probabilities of various tissue labels, registration field and tumor growth parameters. Validation using 10 data sets reveals that the method can handle large mass effects and tumor sizes with various tissue types such as necrosis, edema and tumor infiltration. Quantitative evaluations of segmentations of our method were based on Dice overlap ratios with expert provided reference volumes, and in general are higher than values reported in the state-of-the-art literature.