Statistical Interior Tomography

Abstract

This paper presents a statistical interior tomography (SIT) approach making use of compressed sensing (CS) theory. With the projection data modeled by the Poisson distribution, an objective function with a total variation (TV) regularization term is formulated in the maximization of a posteriori (MAP) framework to solve the interior problem. An alternating minimization method is used to optimize the objective function with an initial image from the direct inversion of the truncated Hilbert transform. The proposed SIT approach is extensively evaluated with both numerical and real datasets. The results demonstrate that SIT is robust with respect to data noise and down-sampling, and has better resolution and less bias than its deterministic counterpart in the case of low count data.

I. Introduction

Since its introduction, X-ray computed tomography (CT) has been greatly improved and extensively applied to a large number of applications in biomedical imaging and nondestructive detection. In principle, a CT scanner measures integrals of the X-ray linear attenuation coefficients along lines through an object in parallel or divergent beam geometry. While medical CT has excellent diagnostic performance, there is an increasing concern over the risk associated with X-ray exposure [1]–[3]. To reduce the radiation dose, the well-known as-low-as-reasonably-achievable (ALARA) principle is widely accepted in the medical CT community. A primary strategy is to decrease the total dose to a patient by reducing both the amount of projection data and the current of the X-ray source during the data acquisition process.

For many clinical applications, physicians usually focus on only a relatively small region of interest (ROI) such as the heart, breast, and other organs. If only the ROI is irradiated by the X-ray source, the radiation will be significantly reduced. Theoretically exact reconstruction from local projections acquired in this mode is well known as the interior problem, which has been studied over many years [4]–[6]. The conventional wisdom is that the interior problem does not have a unique solution [6]. In other words, to accurately reconstruct an ROI inside the object, the conventional approach requires that the X-ray beam cover the whole object support [7].

Recently, it has been reported that the interior problem is solvable if some additional prior information is available. This new theoretically-exact local reconstruction methodology is referred to as interior tomography [8], which is based on several pieces of important work. First, the concept of differentiated back-projection (DBP) gives a link between local projections and the Hilbert transform of an object to be reconstructed on a chord/PI-line across an ROI [9], [10]. Then, it was proven that an image on a chord in the field-of-view (FOV) can be exactly reconstructed if one end of the chord is outside the object [11]. After that, it was proven that the interior problem can be exactly and stably solved if a subregion is known in the ROI [12]–[17]. The main idea behind this progress relates to the analytic continuation from the known subregion to the whole ROI. In a numerical implementation, a chord/PI-line can be defined through the known subregion, the DBP can be performed along the chord, and the resultant truncated Hilbert transform (THT) can be inverted to determine the 1D image on the chord. At present, there are at least two methods to invert the THT [8]: 1) projection onto convex set (POCS) [11], [12], [16] and 2) singular value decomposition (SVD) [15].

Further progress on interior tomography was inspired by compressed sensing (CS) theory. CS theory shows that signals and images can be reconstructed from far less data/measurements than what is usually considered necessary according to the Nyquist sampling theory [18], [19]. In this regard, it was found that an interior ROI can be exactly and stably reconstructed via a total variation (TV) minimization if the ROI is piecewise constant or polynomial [20]–[23]. The main idea is to use an appropriate sparsifying transform and an associated objective function to regularize ambiguity into the null space.

The two aforementioned methods based on THT or CS is exact for noiseless data when the precise prior knowledge on a subregion in an ROI is known or the ROI is indeed piecewise constant or polynomial [24]. However, these methods did not take into account the statistical nature of projection data, and will not work well in the case of low count data. Traditionally, the number of the detected X-ray photons is modeled as a Poisson distribution plus a background Gaussian noise with zero mean [25]. Also, a compound Poisson distribution was proposed for the polychromatic energy spectrum and the energy-integrating detection [26], [27]. In physical experiments, Li et al. [28] validated that the noise in projection data after a logarithm transform approximately follows a Gaussian distribution with a nonlinear signal-dependent variance.

Because the well-known statistical iterative reconstruction (SIR) framework utilizes a very accurate projection data model, over the past years several SIR algorithms were proposed for X-ray CT applications [25], [29]–[35]. Sukovic et al. [30] developed the penalized weighted least square (PWLS) algorithm for dual energy CT. Elbakri et al. [25] and De Man et al. [31] proposed the polychromatic SIR algorithms for beam hardening artifact reduction. Snyder et al. [36] developed two maximum-likelihood (ML) methods for reconstruction from incomplete projection data. Tang et al. [37] evaluated the CS algorithm in the statistical reconstruction framework. Defrise et al. [38], [39] investigated the applicability of the TV-regularized ML algorithm [33] for micro-CT. These SIR algorithms all yielded satisfactory imaging performance.

To improve interior tomography for further radiation dose reduction and faster data acquisition, it is natural to consider the statistical nature of local projection data. In this paper, we propose a statistical interior tomography (SIT) approach. Our contributions are two-fold. First, the CS-based interior tomography is performed in a statistical fashion, which is optimized using an alternating minimization algorithm. Second, a deterministic interior reconstruction, which is based on the inversion of THT via POCS, is used as the initial guess for the SIT reconstruction. The rest of this paper is organized as follows. In Section II, the proposed SIT algorithm is developed. In Sections III and IV, experimental design and reconstruction results are presented. Finally, we discuss the related issues and conclude the paper in Section V.

II. Methodlogy

In this section, a SIT algorithm will be developed to solve the interior problem statistically. First, the CS-based statistical objective function is formulated. Then, the problem is optimized in an alternating fashion. Furthermore, the THT based interior reconstruction result is used to initialize the SIT reconstruction. Finally, the overall scheme is pseudo-coded.

A. Statistical Model and Objective Function

For simplicity, we assume that the X-ray source is monochromatic. Under the ideal condition, X-ray photons from an X-ray tube are attenuated by an object along the path l_i, i = 1, ···, N_I, where N_I is the number of total X-ray paths through an ROI. The detected photons can be estimated by Beer’s law

$$I_i=b_{i}exp\left(-\underset{l_i}{\int }\mu (\stackrel{\rightharpoonup }{r})dl\right),i=1,\cdots ,N_I$$ (1)

where I_i is the number of the detected X-ray photons after attenuation, b_i the number of the detected X-ray photons without the object, and μ(r⃑) the linear attenuation coefficient of the object at a location r⃑ = (r₁, r₂) in the 2D real space.

For iterative reconstruction, the object is discretized as rectangular pixels. Then, the task is to estimate the discrete attenuation coefficient at those pixel locations. Let the number of the pixels be N_J, the integral along the ith projection path ∫_li μ(r⃗)dl can be discretized as

$$p_i=\underset{l_i}{\int }\mu (\stackrel{\rightharpoonup }{r})dl\approx \sum _{j=1}^{N_J}{a}_{ij}{\mu }_j={[\mathbf{A}\mathit{\mu }]}_i,i=1,\cdots ,N_I$$ (2)

where A = {a_ij} is the system matrix which accounts for the system geometry, μ = (μ₁, ···,μ_NJ)^T, μ_j, the linear attenuation coefficient of the jth pixel and the symbol “T” represents a transpose operator. For the ith X-ray path and the jth pixel, a_ij can be calculated as the normalized intersection area between the pixel and the ray path.

In a real CT system with a low dose setting, the data acquisition process is not deterministic as defined by (1). Hence, a statistical model should be utilized to describe the physical process. The Poisson probability model is well established for this purpose

$$y_i\sim \text{Poisson}\{{\overline{y}}_i\},i=1,\cdots ,N_I$$ (3)

where y_i is the measurement along the ith X-ray path with ȳ_i = b_ie^−p_i being the expected value of y_i. Because data along X-ray paths are independent of each other, given the distribution of linear attenuation coefficients, the joint probability distribution of the data acquisition process can be expressed as

$$P(\mathbf{y}\mid \mathit{\mu })=\prod _{i=1}^{N_I}P(y_i\mid \mathit{\mu })=\prod _{i=1}^{N_I}(e^{-{\overline{y}}_i}{\overline{y}}_i^{y_i}/{\overline{y}}_i!)$$ (4)

and the corresponding log-likelihood function can be written as

$$L(\mathbf{y}\mid \mathit{\mu })=lnP(\mathbf{y}\mid \mathit{\mu })=\sum _{i=1}^{N_I}(y_{i}ln(b_i{e}^{-p_i})-b_i{e}^{-p_i}-ln{y}_i!).$$ (5)

Ignoring the constant terms, we obtain

$$\begin{array}{l}L(\mathbf{y}\mid \mathit{\mu })=-\sum _{i=1}^{N_I}(y_i{p}_i+b_i{e}^{-p_i})\\ =-\sum _{i=1}^{N_I}\left(y_i{[\mathbf{A}\mathit{\mu }]}_i+b_i{e}^{-{[\mathbf{A}\mathit{\mu }]}_i}\right).\end{array}$$ (6)

From the statistical perspective, the original image can be reconstructed by maximizing a posteriori (MAP) of function P(μ|y). Since the natural logarithm is monotonically increasing, the maximization of a posteriori P(μ|y) can be carried out by maximizing its logarithm. According to the Bayesian rule

$$P(\mathit{\mu }\mid \mathbf{y})=P(\mathbf{y}\mid \mathit{\mu })P(\mathit{\mu })/P(\mathbf{y}).$$ (7)

Consequently, the reconstruction is equivalent to maximize the following objective function Φ̃(μ) = L(y|μ) + ln P(μ), where ln P(μ) expresses the prior knowledge on the object. Because ln P(μ) is a regularization term, we denote −ln P(μ) as R(μ) and have

$$\stackrel{\sim }{\mathrm{\Phi }}(\mathit{\mu })=-\sum _{i=1}^{N_I}\left(y_i{[\mathbf{A}\mathit{\mu }]}_i+b_i{e}^{-{[\mathbf{A}\mathit{\mu }]}_i}\right)-R(\mathit{\mu }).$$ (8)

With the negative signs in (8), the task is to minimize the following objective function:

$$\mathrm{\Phi }(\mathit{\mu })=\sum _{i=1}^{N_I}\left(y_i{[\mathbf{A}\mathit{\mu }]}_i+b_i{e}^{-{[\mathbf{A}\mathit{\mu }]}_i}\right)+R(\mathit{\mu }).$$ (9)

Applying a second-order Taylor’s expansion to g_i(p_i) = y_ip_i + b_ie^−p_i around an estimated line integral p̂_i = ln(b_i/y_i) [25], we have

$$\begin{array}{l}{g}_i(p_i)\approx g_i({\widehat{p}}_i)+{\stackrel{.}{g}}_i({\widehat{p}}_i)(p_i-{\widehat{p}}_i)+\frac{{\ddot{g}}_i({\widehat{p}}_i)}{2}{(p_i-{\widehat{p}}_i)}^2\\ =y_{i}ln(b_i/y_i)+y_i+\frac{1}{2}{y}_i{(p_i-{\widehat{p}}_2)}^2.\end{array}$$ (10)

Omitting the irrelevant terms, (9) becomes

$$\mathrm{\Phi }(\mathit{\mu })=\sum _{i=1}^{N_I}\frac{y_i}{2}{({[\mathbf{A}\mathit{\mu }]}_i-{\widehat{p}}_i)}^2+R(\mathit{\mu }).$$ (11)

According to the CS-based interior tomography theory [20]–[23], the interior ROI can be exactly reconstructed via minimizing an objective function which is associated with an appropriate sparsifying transform. Among all the existing sparsifying transforms, the discrete gradient transform (DGT) is most commonly used. The sum of DGT for each pixel is the so-called TV of an image.

In a 2D image space, the linear attenuation coefficient μ_j of the jth pixel can be denoted in dual subscripts as

$$\begin{array}{l}{\mu }_j={\mu }_{m,n},j=(m-1)\times W+n,m=1,2,\cdots ,H,\\ n=1,2,\cdots ,W\end{array}$$ (12)

where W and H are respectively the width and height of the 2D image matrix, and N_J = W × H. Then, the image TV can be expressed as

$$TV(\mathit{\mu })={\left|\right|D\mathit{\mu }\left|\right|}_1$$ (13)

where Dμ = (D₁μ, ···,D_NJμ)^T and $D_j\mathit{\mu }=D_{m,n}\mathit{\mu }=\sqrt{{({\mu }_{m,n}-{\mu }_{m+1,n})}^2+{({\mu }_{m,n}-{\mu }_{m,n+1})}^2}$.

When the TV term is selected for regularization of (11), the interior problem can be solved statistically by minimizing the following objective function:

$$\mathrm{\Phi }(\mathit{\mu })=\sum _{i=1}^{N_I}\frac{y_i}{2}{({[\mathbf{A}\mathit{\mu }]}_i-{\widehat{p}}_i)}^2+\beta TV(\mathit{\mu })$$ (14)

where β is a positive parameter to balance the log-likelihood and TV terms.

B. Optimization Via Alternating Minimization

Taking the following transformation:

$${\mathbf{A}}_{\mathrm{\Lambda }}=\mathrm{\Lambda }\mathbf{A}=\{a_{{\mathrm{\Lambda }}_{ij}}\},{\widehat{\mathbf{p}}}_{\mathrm{\Lambda }}=\mathrm{\Lambda }\widehat{\mathbf{p}},\widehat{\mathbf{p}}={({\widehat{p}}_1,{\widehat{p}}_2,\cdots ,{\widehat{p}}_{N_I})}^T$$ (15)

where $\mathbf{\Lambda }=\mathit{diag}(\sqrt{y_i/2})\in {\mathbb{R}}^{N_I}\times {\mathbb{R}}^{N_I}$ be a diagonal matrix, the objective function (14) can be rewritten as

$$\mathrm{\Phi }(\mathit{\mu })={\left|\right|{\mathbf{A}}_{\mathrm{\Lambda }}\mathit{\mu }-{\widehat{\mathbf{p}}}_{\mathrm{\Lambda }}\left|\right|}_2^2+\beta TV(\mathit{\mu })$$ (16)

The above objective function represents a common TV-regularized problem, and minimizing Phi;(μ) is a typical convex problem. Goldfarb and Yin [40] first reformulated this TV-regularized problem into a second-order cone programming (SOCP) setting, and the efficient interior point methods can produce an accurate solution at a polynomial computing cost. This approach has been widely used in image processing and analysis [40]–[42]. However, because the system matrix size is typically enormous in the CT field, an alternating minimization algorithm is usually chosen to solve the TV-regularized problem. Sidky and Pan [43] proposed an ASD-POCS algorithm, in which the minimization of the objective function is performed in an alternating fashion for the data fidelity term via projections onto the convex sets and the TV term through adaptive steepest descent searching. The analysis by Daubechies et al. [44] shows the convergence of the powerful soft-threshold filtering scheme. Inspired by her theory, Yu and Wang [45] recently adapted the soft-threshold filtering method for image reconstruction with the simultaneous algebraic reconstruction technique (SART) [46] for data fidelity and a pseudo-inverse of DGT for a TV-type regularization. In light of these state of the art results, here we present an alternating minimization strategy to minimize the objective function (16).

Introducing an auxiliary variable ν = Dμ, (16) becomes the following problem:

$$\mathrm{\Phi }(\mathit{\mu })={\left|\right|{\mathbf{A}}_{\mathrm{\Lambda }}\mathit{\mu }-{\widehat{\mathbf{p}}}_{\mathrm{\Lambda }}\left|\right|}_2^2+\beta {\left|\right|\mathit{\nu }\left|\right|}_{1}s.t.\mathit{\nu }=D\mathit{\mu }.$$ (17)

Relaxing the equality constraint and penalizing any discrepancy quadratically, an unconstraint objective function is obtained as follows:

$$\mathrm{\Psi }(\mathit{\mu })={\left|\right|{\mathbf{A}}_{\mathrm{\Lambda }}\mathit{\mu }-{\widehat{\mathbf{p}}}_{\mathrm{\Lambda }}\left|\right|}_2^2+\beta {\left|\right|\mathit{\nu }\left|\right|}_1+\alpha {\left|\right|\mathit{\nu }-D\mathit{\mu }\left|\right|}_2^2$$ (18)

where α > 0 is the Lagrange multiplier, and a suitable choice of α will make the solution of Ψ(μ) approximate the solution of Φ(μ) closely.

The optimization of Ψ(μ) can be implemented in the following three steps in an alternating manner until the stopping criterion is met.

• Step 1)
  Minimize the log-likelihood term

  $${\left|\right|{\mathbf{A}}_{\mathrm{\Lambda }}\mathit{\mu }-{\widehat{\mathbf{p}}}_{\mathrm{\Lambda }}\left|\right|}_2^2=\sum _{i=1}^{N_I}\frac{y_i}{2}{({[\mathbf{A}\mathit{\mu }]}_i-{\widehat{\mathbf{p}}}_i)}^2.$$
  This step can be implemented via a typical iterative reconstruction algorithm. In this paper, we utilize the separable paraboloid surrogate method [25]

  $${\stackrel{\sim }{\mu }}_j^t={\mu }_j^{t-1}-\frac{{\displaystyle \sum _{i=1}^{N_I}}(a_{ij}{y}_i({[\mathbf{A}{\mathit{\mu }}^{t-1}]}_i-{\widehat{p}}_i))}{{\displaystyle \sum _{i=1}^{N_I}}\left(a_{ij}{y}_i{\displaystyle \sum _{k=1}^{N_J}}{a}_{ik}\right)},j=1,\cdots ,N_J$$ (19)

  where the superscript t = 1, 2, ··· is the iteration number, and μ⁰ the initial guess of the image.

  According to (15), (19) can be rewritten as

  $${\stackrel{\sim }{\mathit{\mu }}}^t={\mathit{\mu }}^{t-1}+\mathbf{M}{\mathbf{A}}_{\mathrm{\Lambda }}^T({\widehat{\mathbf{p}}}_{\mathrm{\Lambda }}-{\mathbf{A}}_{\mathrm{\Lambda }}{\mathit{\mu }}^{t-1})$$ (20)

  where $\mathbf{M}=\mathit{diag}(1/{\sum }_{i=1}^{N_I}(a_{\mathrm{\Lambda }ij}{\sum }_{k=1}^{N_J}{a}_{\mathrm{\Lambda }ik}))\in {\mathbb{R}}^{N_J}\times {\mathbb{R}}^{N_J}$ is a diagonal matrix.

• Step 2)

  Fixing μ = μ̃^t, minimize the last two terms $\beta {\left|\right|\mathit{\nu }\left|\right|}_1+\alpha {\left|\right|\mathit{\nu }-D{\stackrel{\sim }{\mathit{\mu }}}^t\left|\right|}_2^2$ of (18) to update ν.

  This problem can be solved using a 1D shrinkage method. Since Dμ ≥ 0, we have

  $${\mathit{\nu }}^t=max\{D{\stackrel{\sim }{\mathit{\mu }}}^t-\beta /2\alpha ,0\}.$$ (21)

  This process is a soft-threshold filtration of the DGT with a threshold β/2α.

• Step 3)

  Fixing ν = ν^t, minimize $\alpha {\left|\right|{\mathit{\nu }}^t-D{\stackrel{\sim }{\mathit{\mu }}}^t\left|\right|}_2^2$ to obtain μ^t.

If Dμ = ν^t, $\alpha {\left|\right|{\mathit{\nu }}^t-D{\stackrel{\sim }{\mathit{\mu }}}^t\left|\right|}_2^2$ will reach the minimum value zero. Clearly, finding μ from Dμ = ν^t is to invert DGT. Because DGT is not uniquely invertible, here we use a pseudo-inverse of DGT [45].

The above three steps will be alternately executed to minimize the objective function. The second and third steps of the above alternating minimization algorithm are equivalent to the soft-threshold nonlinear filtration based on the pseudo-inverse of DGT [45], which is performed with

$${\mu }_{m,n}^t=\frac{1}{4}(2{\mu }_{m,n}^{t,a}+{\mu }_{m,n}^{t,b}+{\mu }_{m,n}^{t,c})$$ (22)

where

$$\begin{array}{l}{\mu }_{m,n}^{t,a}=\{\begin{array}{ll}\frac{2{\stackrel{\sim }{\mu }}_{m,n}^t+{\stackrel{\sim }{\mu }}_{m+1,n}^t+{\stackrel{\sim }{\mu }}_{m,n+1}^t}{4}\hfill & if{D}_{m,n}{\stackrel{\sim }{\mathit{\mu }}}^t<\omega \hfill \\ {\stackrel{\sim }{\mu }}_{m,n}^t-\frac{\omega (2{\stackrel{\sim }{\mu }}_{m,n}^t-{\stackrel{\sim }{\mu }}_{m+1,n}^t-{\stackrel{\sim }{\mu }}_{m,n+1}^t)}{4D_{m,n}{\stackrel{\sim }{\mathit{\mu }}}^t}\hfill & if{D}_{m,n}{\stackrel{\sim }{\mathit{\mu }}}^t\ge \omega \hfill \end{array}\\ {\mu }_{m,n}^{t,b}=\{\begin{array}{ll}\frac{{\stackrel{\sim }{\mu }}_{m,n}^t+{\stackrel{\sim }{\mu }}_{m-1,n}^t}{2}\hfill & if{D}_{m-1,n}{\stackrel{\sim }{\mathit{\mu }}}^t<\omega \hfill \\ {\stackrel{\sim }{\mu }}_{m,n}^t-\frac{\omega ({\stackrel{\sim }{\mu }}_{m,n}^t-{\stackrel{\sim }{\mu }}_{m-1,n}^t)}{4D_{m-1,n}{\stackrel{\sim }{\mathit{\mu }}}^t}\hfill & if{D}_{m-1,n}{\stackrel{\sim }{\mathit{\mu }}}^t\ge \omega \hfill \end{array}\\ {\mu }_{m,n}^{t,c}=\{\begin{array}{ll}\frac{{\stackrel{\sim }{\mu }}_{m,n}^t+{\stackrel{\sim }{\mu }}_{m,n-1}^t}{2}\hfill & if{D}_{m,n-1}{\stackrel{\sim }{\mathit{\mu }}}^t<\omega \hfill \\ {\stackrel{\sim }{\mu }}_{m,n}^t-\frac{\omega ({\stackrel{\sim }{\mu }}_{m,n}^t-{\stackrel{\sim }{\mu }}_{m,n-1}^t)}{2D_{m,n-1}{\stackrel{\sim }{\mathit{\mu }}}^t}\hfill & if{D}_{m,n-1}{\stackrel{\sim }{\mathit{\mu }}}^t\ge \omega \hfill \end{array}\end{array}$$

and ω is a threshold.

As far as the threshold ω is concerned, it can be adaptively determined using the projected gradient method [45], [47], [48]. In each filtering step, the threshold ω should make the TV of a current image be approximately equal to a desirable value, that is

$$TV({\mathit{\mu }}^t)={\left|\right|{\mathit{\nu }}^t\left|\right|}_1=\sum _m\sum _n{S}_{\omega }(D_{m,n}{\stackrel{\sim }{\mathit{\mu }}}^t)\approx TV({\mathit{\mu }}^{\ast }),$$ (23)

where $S_{\omega }(x)=\{\begin{array}{ll}x-\omega \hfill & ifx\ge \omega \hfill \\ 0\hfill & ifx>\omega \hfill \end{array}$, and μ* is an ideal image. TV(μ*) can be estimated in several ways; for example, by down-scaling the TV of a corresponding image reconstructed using another method, such as filtering back-projection (FBP) for full-scan reconstruction or THT-based interior tomography for ROI reconstruction. Equation (23) can be easily solved by dichotomy.

C. Inversion of THT by POCS for Initialization

When there is a known subregion inside the ROI, the interior problem can be solved as the inversion of THT using the POCS method [12]–[14], [16], [17].

First, a set of chord/PI-lines are constructed, which go through both the known and unknown regions in the ROI. The linear attenuation coefficient distribution &mu;(r⃑) along such a chord/PI-line L can be denoted as f(x), where x is the 1D coordinate along L. Let the support of f(x) on L be [c₁, c₂] , the interval of the ROI on L be (c₃, c₄), the interval of the known subregion on L be (c₅, c₆), and these constants satisfy c₁ ≤ c₃ ≤ c₅ ≤ c₆ ≤ c₄ ≤ c₂.

Second, THT along each chord/PI-line inside the ROI is computed using the DBP method, which can be expressed as

$$\begin{array}{l}(H_{L}f)(x)=\frac{1}{\pi }\text{P}.\text{V}.\underset{c_1}{\overset{c_2}{\int }}f(z)\frac{dz}{x-z}\\ g(x)={-\frac{1}{2\pi }\underset{{\phi }_0}{\overset{{\phi }_0+\pi }{\int }}\frac{\partial p(s,\phi )}{\partial s}|}_{s=\overline{r}•\overline{u}(\phi )}d\phi \\ (H_{L}f)(x)=g(x)\end{array}$$ (24)

where P.V denotes the Cauchy principal value, H_L the Hilbert transform along L, u⃑(φ) = (cos φ, − sin φ), and $p(s,\phi )={\int }_{-\infty }^{\infty }\mu (s\stackrel{\rightharpoonup }{u}(\phi )+v{\stackrel{\rightharpoonup }{u}}^{\perp }(\phi ))dv$, s, φ ∊ ℝ (with p(s, φ + π) = p(−s, φ)) being the integral along a line paralleled to u⃑^⊥(φ) = (−sin φ, cos φ) at a signed distance from the origin of the coordinate. p(s, φ) can be interpolated from ${\{\widehat{p}\}}_{i=1}^{N_I}$.

By the Tricomi formula [49], f(x) can be recovered from its finite Hilbert transform g(x)

$$\sqrt{(c_2-x)(x-c_1)}f(x)=C_f+\frac{1}{\pi }\text{P}.\text{V}.\underset{c_1}{\overset{c_2}{\int }}g(z)\sqrt{(c_2-z)(z-c_1)}\frac{dz}{z-x}$$ (25)

where $C_f=(1/\pi ){\int }_{c_1}^{c_2}f(x)dx$ is a known quantity (the projection value along the chord).

Third, THT along each chord is inverted using the POCS method. Because (25) cannot be directly used to solve the interior problem, the POCS method is commonly used to solve f based on (24). It is assumed that the 1D function f belongs to the intersection of J convex sets C₁, C₂, ···, C_J. If the projection operators onto these convex sets are denoted as P₁, P₂, ···, P_J, POCS can be expressed as f^t+1 = P_JP_J−1 ··· P₁f^t, where t indicates the iteration index. In other words, the interior reconstruction is to find f(x) ∈ L²(ℝ) in the intersection of the convex sets

$$\begin{array}{l}{C}_1=\{f\in L^2(\mathbb{R})\mid (H_{L}f)(x)=g(x),x\in (c_3,c_4)\}\\ C_2=\{f\in L^2(\mathbb{R})\mid f(x)=f_0(x),x\in (c_5,c_6)\}\\ C_3=\left\{f\in L^2(\mathbb{R})\mid \frac{1}{\pi }\underset{c_1}{\overset{c_2}{\int }}f(x)d(x)=C_f\right\}\\ C_4=\{f\in L^2(\mathbb{R})\mid f(x)\ge 0,x\in [c_1,c_2]\}\\ c_5=\{f\in L^2(\mathbb{R})\mid f(x)\le f_{max},x\in [c_1,c_2]\}\end{array}$$

where f₀(x) and f_max are the ideal image function and its upper bound, respectively. More convex sets can be introduced if additional convex constraints are available.

After the values on all of the chords are reconstructed, we can use a coordinate transformation to form the reconstructed image μ. However, this POCS algorithm does not take the statistical property of the projection data into account, and may produce noisy results under low-dose conditions. In this paper, we only use this result as an initial guess for the statistical iteration.

D. Overall Scheme

Overall, the proposed SIT scheme is described in Table I. After the inversion of THT is used as the initial guess, an alternating minimizing algorithm is employed to optimize (16). Mathematically speaking, in general the convergence study on an alternating algorithm is challenging. In particular, the pseudo-inverse of DGT makes the convergence analysis of our algorithm tougher. Encouragingly, Daubechies et al. [44] proved the convergence of a general iterative soft-threshold filtering algorithm to solve the linear inverse problem with a sparse expansion. Although the DGT is not uniquely invertible, the theoretical justification in [44] is suggestive that our heuristically adapted alternating minimization approach would produce excellent results. With an appropriate parameter selection, our proposed alternating minimization algorithm will indeed minimize the above TV-regularized objective function and yield a satisfactory solution of the optimization problem, as seen in our extensive numerical and experimental studies that will be reported below in detail. We will rigorously analyze the theoretical convergence of the proposed algorithm in the future.

TABLE I.

Pseudo-Code of the Proposed Statistical Interior Tomography Algorithm

Input: ${\{y_i\}}_{i=1}^{N_I}$

Output: μ

Part 1: Inversion of THT

For each chord,

Initialize f(x) = 0

—For t = 1,2, ···, t1

POCS on C1 ~ C5;

—End

Coordinate transform μTHT = μChord

Part 2: CS-based SIR

Initialize μ0 = μTHT, TV(μ*)

—For t = 1,2, ···, t2

1) Update the image using Eq. (20);

2) Determine the threshold using Eq. (23);

3) Nonlinear filtering using Eq. (22);

—End

III. Experimental Design

A. Representative Algorithms

In this paper, our focus is to study the general THT-based interior tomography (denoted by THT) described as Part 1 in Table I, the CS-based statistical reconstruction from a zero image (denoted by SIRCS-Zero) described as part 2 in Table I with a modification of zero initial guess, and the CS-based statistical reconstruction from the THT (denoted by SIRCS-THT) is described as Table I. Also, we studied the performance of the CS-based interior tomography without considering the statistical property of the projection data (denoted by NSIRCS-THT). For this purpose, (16) can be modified as

$$\mathrm{\Phi }(\mathit{\mu })={\left|\right|\mathbf{A}\mathit{\mu }-\widehat{\mathbf{p}}\left|\right|}_2^2+\beta TV(\mathit{\mu })$$ (26)

which can be solved using the algorithm in Table I. In the implementation, an ordered subset strategy [50]–[52] was used to speed up the convergence. Also, a nonnegative constraint was enforced on the reconstructed image μ.

B. Data Acquisition

A comprehensively numerical simulation was carried out to evaluate the performance of SIT quantitatively. Additionally, both nonhuman and human datasets were acquired to demonstrate the feasibility of the proposed algorithms in practical applications.

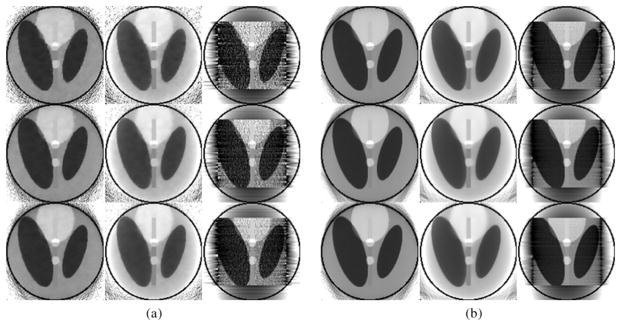
In the numerical simulation study, a 2D Shepp-Logan phantom was employed. The phantom consists of ten ellipses, whose parameters are listed in Table II, where a and b are the lengths of the two semi-axes of an ellipse, (x₀, y₀) specifies the ellipse’s center, θ the rotation angle, and du the relative attenuation coefficient normalized by the linear attenuation coefficient of water. A fan-beam geometry and an equi-spatial virtual detector was assumed. The virtual detector was centered at the system origin and made perpendicular to the line from the system origin to the X-ray source. The distance from the X-ray source to the system origin was 57 cm. The detector included 360 elements with a total length of 10.8 cm. For a full scan, 1080, 720, and 360 projections were equi-angularly collected to evaluate the effect of the number of projections on the performance of the proposed algorithms. In each case, 200, 100, 50, 20, 10, and 5 (×10⁴) photons per detector element were used to simulate six noise levels respectively. The phantom and the FOV were shown in Fig. 1.

TABLE II.

Parameters of the 2-D Shepp-Logan Phantom

No.	a (cm)	b (cm)	x0 (cm)	y0 (cm)	θ (degree)	du
1	6.900	9.200	0	0	0	2.0
2	6.624	8.740	0	−0.184	0	−0.98
3	1.100	3.100	2.200	0	−18	−0.08
4	1.600	4.100	−2.200	.	18	−0.08
5	2.100	2.500	0	3.500	0	0.04
6	0.460	0.460	0	1.000	0	0.04
7	0.460	0.460	.	−1.000	0	0.04
8	0.460	0.230	−0.800	−6.050	0	0.04
9	0.230	0.230	0	−6.050	0	0.04
10	0.230	0.460	0.600	−6.050	0	0.04

Fig. 1.

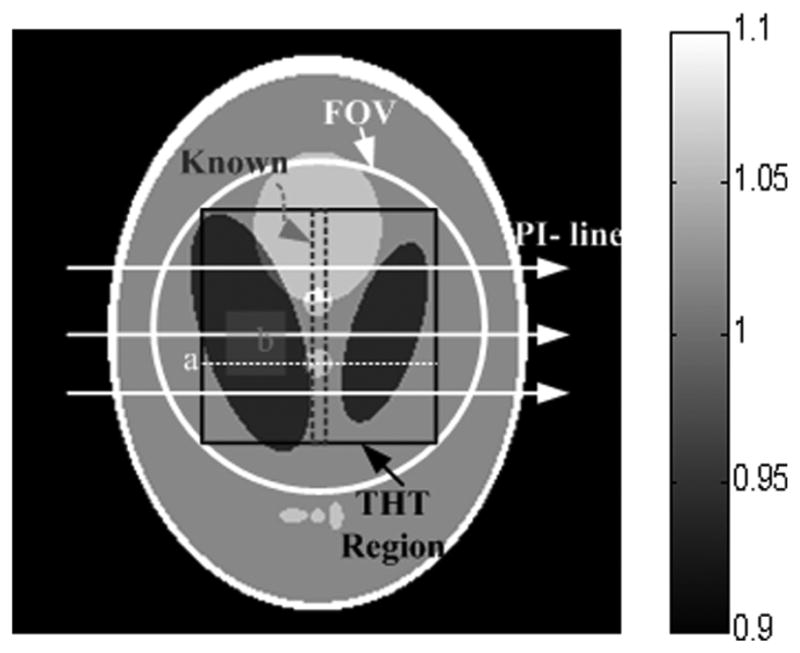
2D Shepp–Logan phantom within a display window [0.9 1.1]. The circular region indicates the FOV which is the ROI in SIRCS, the inscribed square indicates the ROI in THT, and the central stripe is known. The PI-lines were reconstructed along the horizontal direction, and the line labeled “a” and the region labeled “b” were used to evaluate the image quality.

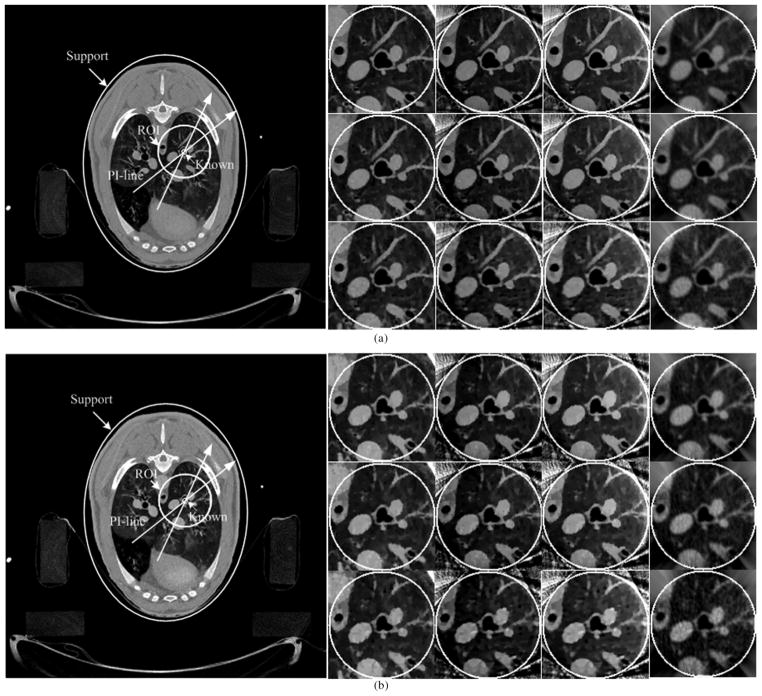
In the nonhuman application, we performed a CT scan of an anesthetized sheep, which was approved by both the University of Iowa and Virginia Tech IACUC committees. The chest of the sheep was scanned in cone-beam geometry on a SIEMENS Somatom Sensation 64-Slice CT scanner. We only extract the central slice, which is a typical fan-beam geometry. The radius of the X-ray source scanning trajectory was 57 cm. Over a 360° range, 1160 projections were uniformly collected. The data were the line integrals {p̂_i}, and the corresponding measurements were estimated from {y_i = b_i exp(−p̂_i)} by assuming a uniform blank scan. For each projection, 672 detector elements were equi-angularly distributed to define an FOV of radius 25.05 cm. In our experiments, two scans were performed. One used a normal dose (100 kVp, 150 mAs), and the other used a low dose (80 kVp, 17 mAs) protocol. We first reconstructed the entire lung cross-section in a 768 × 768 matrix covering a 43.63 cm × 43.63 cm region from each full-scan dataset. Then, a subregion of radius six pixels was selected in an endotracheal region, where the attenuation coefficient was known to be zero. After that, a circular region of radius 61 pixels around the trachea was chosen as an ROI. Finally, only the projection data through the ROI were kept to simulate an interior scan. To evaluate the performance of the proposed algorithms with fewer projections, the views were down sampled from 1160 to 580 and 290. The reconstructed images from the two full-scan datasets and their correspond ROI were shown in Fig. 5.

Fig. 5.

Reconstructed images in the nonhuman experiments. (a) and (b) The results from normal and low dose datasets, respectively. The left large images were reconstructed from full-scan datasets to show the ROIs and PI-lines. Among the right small images, the first, second, and third rows are the results from 1160, 580, and 290 views, respectively; the first column is the results obtained from a full-scan dataset using SIRCS-Zero, and second, third, and fourth columns are the results from a truncated dataset using SIRCS-THT, SIRCS-Zero and THT, respectively. The display window is [−700HU 800HU].

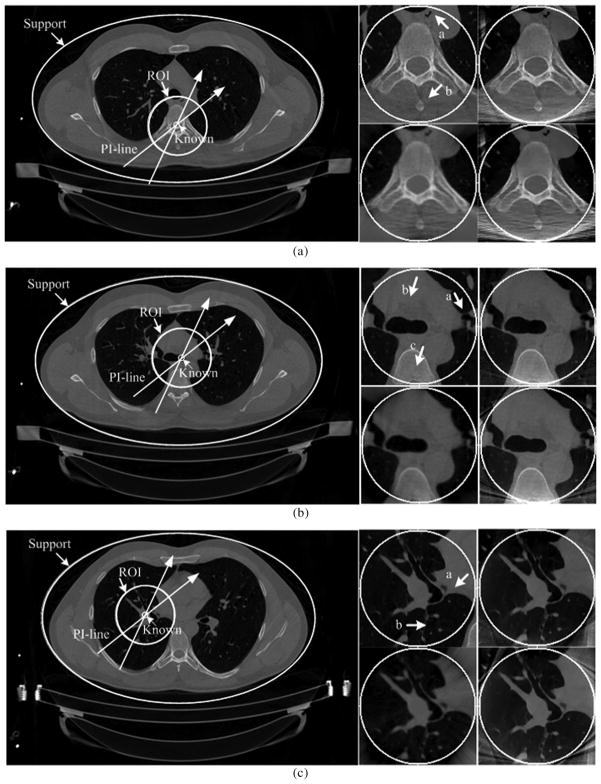
On the same CT scanner at the University of Iowa, a normal human male research subject, age 29, was selected and analyzed to evaluate our algorithms. The subject received two CT scans, one at full inspiration and one at full expiration lung volumes. This scan was carried out as part of a larger NIH funded study seeking to establish an atlas of the normal human lung which will serve as the basis from which early characterization of lung pathologies (NIH-HL-064368). The imaging parameters include 120 kVp, 100 mAs, 0.5 s rotation time, unit pitch, 0.75 mm slice thickness and 0.5 mm slice spacing in the same cone-beam geometry as that for the aforementioned sheep lung experiments. After the datasets were acquired, we converted each multislice dataset to a stack of fan-beam sinograms associated with pre-specified horizontal z-slices. Among these slices, we selected three representative ones to evaluate the proposed algorithms. The entire thorax cross-sections in a 600 × 900 matrix covering a 37.76 cm × 56.64 cm region were reconstructed from each full-scan dataset. Then, an ROI of radius 75 pixels was coupled with known subregion of radii 7 pixels located in center. Finally, only the projection data through the ROI were kept to simulate an interior scan. The reconstructed images of three slices from full-scan datasets and the corresponding ROIs were shown in Fig. 9.

Fig. 9.

Reconstructed images in the human experiment. (a), (b), and (c) The results of different Slices 1–3, respectively. The left large images were reconstructed from the full-scan datasets to show the ROIs and PI-lines. The ROI in Slice 1 contains a bony structure. The ROI in Slice 2 is mainly soft tissue. Most of the ROI in Slice 3 is a cavity. Among the right small figures, the upper left, upper right, lower left, and lower right images are the reference ROI, the ROI reconstructed using SIRCS-THT, THT, and SIRCS-Zero (for Slice 2 and 3)/NSIRCS-THT (for Slice 1), respectively. (a) Slice 1. (b) Slice 2. (c) Slice 3.

C. Image Evaluation

In the numerical simulation study, we used a root mean square error (RMSE) index to quantify the reconstructed results,

$$\text{RMSE}=\sqrt{\sum _{j\in \text{ROI},j\notin \text{Known}}{({\mu }_j^r-{\mu }_j^{\ast })}^2/N_R}$$ (27)

where ${\mu }_j^r$ is the reconstructed attenuation coefficient, ${\mu }_j^{\ast }$ the ideal value of the phantom, and N_R the number of the pixels in the ROI excluding the known subregion. Additionally, we selected a rectangular subregion b (see Fig. 1) in the fourth ellipse (see Table II) with the true attenuation coefficient 0.94. The average error, maximum error and standard variation were calculated in this subregion.

Because the ideal images were not known in nonhuman and human studies, the reference images were reconstructed from corresponding full-scan datasets, which may be corrupted by noise, error, etc. Thus, it would be meaningless to compute the RMSE and error indexes against the gold standard as done in the numerical simulation. Alternatively, we evaluated the reconstructed results of interior tomography in terms of spatial resolution and an image quality assessment (IQA) index of structural similarity (SSIM) [53]. While the SSIM measures were computed in reference to the globally reconstructed images, spatial resolution was estimated across the internal border of the trachea as the full-width-of-half-maximum (FWHM) of the line spread function fitted into the Gaussian form [54].

IV. Results

A. Numerical Simulation

The ROI for THT was an inscribed square inside the FOV as illustrated in Fig. 1. And chords/PI-lines were constructed through a vertical ROI stripe along the horizontal direction, and image values of each chord inside a subregion were precisely known in advance. The reconstructed image covered an FOV of radius 10 cm in a 256 × 256 matrix. On each chord, the ROI covered 96 pixels with a known subregion of six pixels. The DBP was carried out only in the square ROI. The maximum iteration number was 500. For the SIRCS, the ROI was defined by the local scanning beam. The maximum iteration numbers for the datasets of 1080 views, 720 views and 360 views were 70, 100, 200 with 30, 20, 10 order-subsets, respectively. A compact support covering the phantom was used.

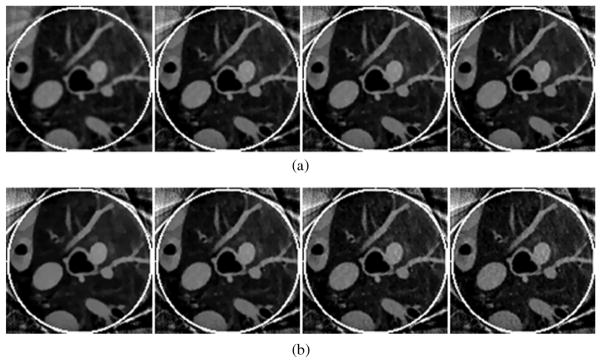
Fig. 2 shows the reconstructed images at the lowest and highest noise levels with different view numbers by different reconstruction methods. It is observed that the images reconstructed by THT are noisy, especially in case of low count 5 × 10⁴ photons. The noise level in the results reconstructed by other algorithms was lower and their reconstructions were more stable. Moreover, the results reconstructed by SIRCS-Zero had a bias but the SIRCS-THT achieved the best performance. When the number of views was decreased from 1080 to 360, the images reconstructed by the three algorithms degenerated indistinctively, especially the SIRCS ones.

Fig. 2.

Reconstructed ROIs in the Shepp-Logan phantom using interior tomography at different noise levels. (a) and (b) The results reconstructed with 5 × 10⁴ and 2 × 10⁶ photons per detector, respectively. The first, second, and third rows were reconstructed from 360, 720, and 1080 views, respectively. The left, middle and right columns were reconstructed using SIRCS-THT, SIRCS-Zero and THT, respectively. The display window is [0.9 1.1].

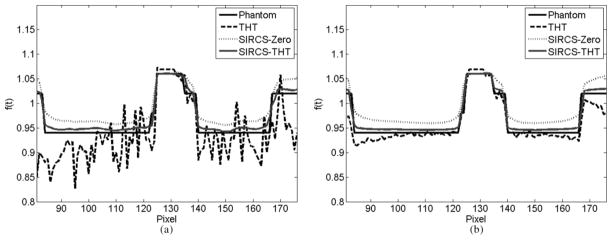
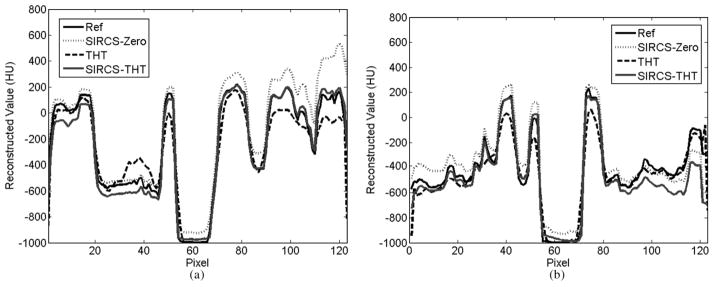
Representative profiles along the line a indicated in Fig. 1 of the reconstructed images are shown in Fig. 3. The reconstruction accuracy of THT was affected by the pixel position. That is, the closer to the known subregion, the more accurate the result is, which is consistent with the theoretical analysis of interior tomography [12]. Compared with other methods, THT shows stronger noise and is affected more by the number of photons per detector element. The SIRCS-Zero had weaker noise but a larger bias. However, SIRCS-THT seems always converging to the truth.

Fig. 3.

Profiles of the reconstructed ROIs along the line “a”; in Fig. 1. While the left one was from 360 views with 5 × 10⁴ photons per detector, the right one was from 1080 views with 2 × 10⁶ photons per detector.

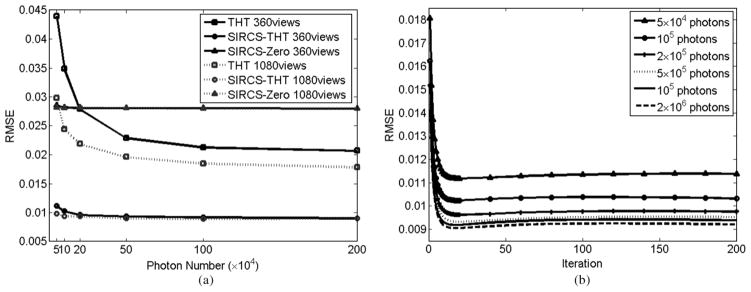
The RMSEs are shown in Fig. 4. Obviously, the RMSE of THT increases when the number of photons decreases. The RMSEs with other methods change less with the decrement in the number of photons. Because SIRCS-Zero had a significant bias, its RMSE is always higher. Down-sampling views from 1080 to 360, while the RMSE of THT increase distinctly, the changes with the SIRCS RMSEs are almost invisible. The RMSE’s change by SIRCS schemes is visible only in the case of very low counts. This is caused by down-sampling of views. In the case of 360 views, the RMSE of SIRCS-THT achieves the minimum after ~20 iterations, and more iteration will result in slight increase on RMSE than its minimum. This small increase changes very slowly and ceases after many more iterations, implying that our algorithm converges to a stable solution. The RMSEs change in the same fashion in the cases of 720 and 1080 views. Therefore, we can stop the iteration when the RMSE changes little. In addition, it can be seen that 2 × 10⁵ photon number is enough to get a very good result for the Shepp-Logan phantom via SIRCS-THT. There is no further improvement of the image quality with the addition of more photons.

Fig. 4.

RMSE variation over the ROI in the phantom. The left one shows the RMSE of different algorithms versus numbers of photons in the cases of 360 and 1080 views, respectively. The right one shows the RMSE of SIRCS-THT after different numbers of iterations in the case of 360 views.

Table III lists the variation range of the average error, maximum error and standard deviation of the results in the region b indicated in Fig. 1 from all kinds of the projection datasets by three interior tomography schemes. The standard deviation of THT was the largest. The bias of SIRCS-Zero was the greatest. The performance of SIRCS-THT outperforms others, being the closest to the ideal phantom image.

TABLE III.

Comparison of the Results Obtained Using THT, SIRCS-Zero, and SIRCS-THT, Respectively. In Each Case, A Minimum-to-Maximum Range is Given

	Average Error	Maximum Error	Standard Deviation
SIRCS-THT	0.0057~0.0060	0.0073~0.0126	0.0005~0.0027
SIRCS-Zero	0.0201~0.0206	0.0256~0.0300	0.0021~0.0037
THT	0.0057~0.0099	0.0266~0.1309	0.0066~0.0395

B. Sheep Study

The PI-lines were constructed along all radial directions from the center of the trachea. The maximum iteration number of THT was fixed to 500. The maximum iteration number of SIR to 1160, 580, 290 views were 50, 100, 200 with 40, 20, 10 subsets, respectively. The support was an ellipse covering the sheep as indicated in Fig. 5. Because it was an in vivo study, were slightly different due to physiological motion. Therefore, the reference images were reconstructed from the images of the two scans at normal and low dose levels full scan datasets without down-sampling of views, respectively. The SIRCS-Zero method was employed to reconstruct the reference images as shown in Fig. 5.

Fig. 5 shows the ROIs reconstructed by the SIRCS-Zero from full-scan datasets and the aforementioned three interior tomography schemes from truncated local datasets with different view numbers and dose levels. It is observed that the images reconstructed by THT had a lower spatial resolution. One reason was that the PI-lines were constructed along radial directions, and the additional interpolation operation was required for a coordinate transformation [55]. The results reconstructed by the other two algorithms demonstrated a higher spatial resolution, and the SIRCS-Zero showed a bias similar to that observed in the numerical simulations. For the normal dose dataset and SIRCS-THT method, down-sampling from 1160 to 580 views did not affect the image quality, whereas the result from 290 views degraded the image slightly. However, for the low dose dataset, view down-sampling makes the results distinctly worse, especially in the case of 290 views. In any case, with different views or doses, the ROIs reconstructed by the SIRCS-THT were always the best one compared to the results from the corresponding full-scan datasets.

Typical profiles of the reconstructed ROIs from the truncated normal dose data with 1160 views are shown in Fig. 6. It is noticed that the SIRCS algorithms preserved more details than the THT. SIRCS-Zero continued to suffer from a substantial bias. Although the SIRCS-THT performed much better than THT and SIRCS-Zero, there were still some residual artifacts especially near the peripheral region of the ROI. We are developing more sophisticated algorithms to suppress this kind of artifacts.

Fig. 6.

Profiles through the ROIs in the nonhuman experiments from the normal dose dataset using different interior tomography schemes, respectively. The left and right are along the horizontal and vertical central lines of the ROI, respectively.

Table IV lists the SSIM and spatial resolution indexes of the results from the truncated normal dose datasets. Compared to the reference image, SIRCS-THT has the best structural similarity according to SSIM. And SIRCS-THT also produces the highest spatial resolution. Although the SIRCS-Zero does not work as well as SIRCS-THT, it outperforms the THT.

TABLE IV.

Comparisons of the Reconstructions From Non-Human Truncated Normal Dose Data Using THT, SIRCS-Zero, and SIRCS-THT, Respectively

Number of view	SSIM			Resolution (mm)
	SIRCS-THT	SIRCS-Zero	THT	SIRCS-THT	SIRCS-Zero	THT
1160	0.9317	0.9096	0.7856	1.3413	1.5787	2.5757
580	0.8933	0.8741	0.7724	1.3772	1.5911	2.6589
290	0.8174	0.8035	0.7372	1.4255	1.6127	2.8557

To demonstrate the convergence of SIRCS-THT, we pick the result from normal dose 1160 views as an example. The ROIs after 5, 20, 35, and 50 iterations are shown in Fig. 7(a). Corresponding SSIM and resolution indexes are listed in Table V. It is observed that both the SSIM and resolution are improved quickly with the increase of iteration number at the beginning; after ten iterations, both the SSIM and resolution changes are minimal. From Fig. 7(a), we can see that the ROI after 35 iterations is almost the same as that after 50 iterations. Therefore, we can stop the iterative process when improvement slows.

Fig. 7.

Reconstructed ROIs in the nonhuman experiments using SIRCS-THT. (a) The results after different numbers of iterations. The objective TV was estimated as about 16. From the left to right, the numbers of iterations are 5, 20, 35, and 50, respectively. (b) The results with different objective TV values. From the left to right, the objective TV values are 14, 16, 18, and 20, respectively. The display window is [−700HU 800HU]

TABLE V.

Comparison of the Reconstructions From Nonhuman Truncated 1160-View Normal Dose Data Using SIRCS-THT After Different Numbers of Iterations

Iteration Number	5	20	35	50
SSIM	0.9000	0.9365	0.9345	0.9317
Resolution (mm)	1.9722	1.5002	1.3810	1.3413

Because the proposed SIT algorithms are based on soft-threshold filtering framework, the selection of threshold will affect the result. From the methodology section, an optimal threshold is determined using the projection gradient method, which is related to an objective TV. The reconstructed ROIs with different objective TV by SIRCS-THT are shown in Fig. 7(b), where the normal dose 1160 views dataset is pickup as an example and four objective TV values are tested. The corresponding SSIM and resolution index are listed in Table VI. It can be seen that either a bigger or a smaller objective TV can make the reconstructed image quality acceptable. The ROIs by the SIRCS-THT are all better than those by THT when the objective TV changes from 14 to 20.

TABLE VI.

Comparison of the Reconstructions From Non-Human Truncated 1160-View Normal Dose Data Using SIRCS-THT With Different Objective TV Values

Objective TV	14	16	18	20
SSIM	0.9107	0.9317	0.9233	0.9027
Resolution (mm)	1.3933	1.3418	1.3328	1.3328

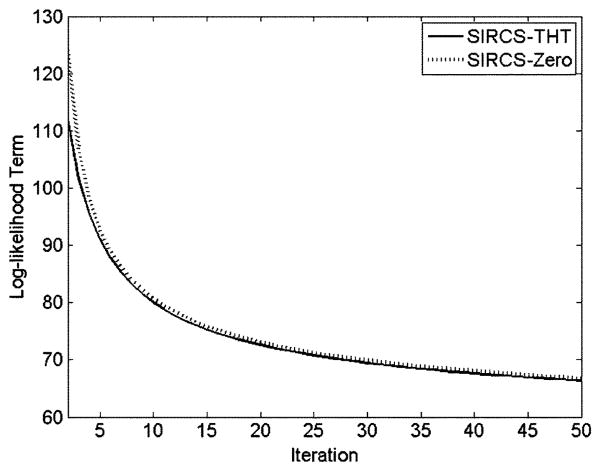
For the case of normal dose 1160 views, the log-likelihood term ${\sum }_{i=1}^{N_I}{y}_i/2{({[\mathbf{A}\mathit{\mu }]}_i-{\widehat{p}}_i)}^2$ in SIRCS algorithms is decreased with the iteration index increase as shown in Fig. 8. The SIRCS-THT always showed a smaller value than SIRCS-Zero after the same iterations. With the increment of the iteration index, the log-likelihood term decreases progressively more slowly.

Fig. 8.

Plot of the log-likelihood function with respect to the number of iterations.

C. Human Scan

The PI-lines were constructed along all radial directions from the center of ROI as in the sheep lung experiment. The maximum iteration number of THT was fixed to 500. The maximum iteration number of SIR was 50 with 40 subsets.

The support was an ellipse covering the imaging object as indicated in Fig. 9. The reference images were reconstructed by the SIRCS-Zero method from the corresponding full scan datasets, respectively.

The results of Slice 1 are shown in Fig. 9(a), which contains a bony structure. It can be seen that there are many streak artifacts in the region as indicated by the arrow “b” in the result reconstructed by the non-statistical methods. However, the reference ROI suppresses these streaks and preserves a good resolution. The ROI reconstructed by the SIRCS-THT is as good as the reference. The THT not only has a worse resolution (pay attention to the region indicated by the arrow “a”) as in previous experiments and many streaks artifacts remain. The NSIRCS-THT has a similar resolution as SIRCS-THT, but the streak artifacts cannot be eliminated.

Fig. 9(b) shows the results of Slice 2. Because the ROI contains a large region of soft tissue, we pay attention to the low contrast difference between soft tissues as indicated by the arrow “b.” From the regions indicated by the arrows “a” and “b,” we can see the THT still has the worst resolution and retains the fewest details. On the other hand, the SIRCS algorithms can distinguish low contrast variations keeping much more detail. However, in the region indicated by the arrow “c,” the results form SIRCS algorithms are brighter than the reference. Moreover, the SIRCS-Zero deviates even more. One reason causing this phenomenon is that the defined compact support does not contain the scanner table. Because the table is below the imaged object, its effect on the ROI is not symmetrical. The bottom of the ROI is affected stronger than the upper, which results in slightly higher values.

The ROI of Slice 3 is constituted mostly by many small details in a cavity. The reconstructed results are shown in Fig. 9(c). From the regions indicated by the arrows “a” and “b,” one can have the same conclusions as those of the slice 2.

V. Discussions and Conclusion

The THT-based interior tomography works well when a known subregion is available, which can often be assumed in practice, such as air in an airway, blood in an aorta, or implanted structures [12]–[14], [16], [17]. Generally speaking, THT-based interior tomography does not produce any significant bias around the known subregion in our simulation and experiments. However, as demonstrated in Fig. 3, the THT-based reconstruction quality becomes gradually less in term of noise and bias further away from the known subregion. From the above results, it has been seen that the THT-based method is noise-sensitive. Since the PI-lines are constructed across a known subregion, they are usually not consistent with the Cartesian grid, and the involved interpolation will compromise the spatial resolution. Recently, Schondube et al. [55] developed a 2D inverse Hilbert transform based on 2D filtering in the Fourier domain to avoid this type of interpolation. Nevertheless, the ringing artifact remains challenging for this method [55]. Since the THT-based reconstruction only serves as an initial guess for our proposed SIT algorithm, these artifacts do not pose any problem.

Our proposed CS-based statistical interior tomography has distinct merits in both noise and resolution aspects. In the numerical simulation, satisfactory results have been obtained even in the case of 360 views and 5 × 10⁴ photons as shown in Figs. 2 and 3. Using the IQA index SSIM to assess the results from real CT datasets, the images reconstructed using this method have produced a better structural similarity and spatial resolution as listed in Table IV. Therefore, they can keep more details under low count conditions. Moreover, the down-sampling operation on normal dose projections has shown a less effect on the final results, which means a major dose reduction.

Many kinds of other optimization algorithms with rigorous convergence analysis are potential candidates to solve (16) [40], [56], [57]. However, our three-step alternating minimization algorithm is rather desirable because of its easiness with the parameter choice and the structure for straightforward computation. When this alternating minimization algorithm is used to optimize the TV-regularized objective function, a pre-specified TV should be decided. This can be estimated from a reference image as described in Section II. Fig. 7(b) and Table VI indicate that different objective TV values only lead to slightly different results. With a suitable parameter choice, the alternating minimization algorithm can perform robustly. Both of the above numerical tests and nonhuman/human experiments show that the quality of the reconstructed images do not change significantly after a number of iterations. The log-likelihood term presenting the fidelity of projections also decreases only minimally after a number of iterations. Therefore, the iterative process can be terminated when the indices begin stabilizing.

Due to the Poisson property of raw data, projections along higher attenuation paths will have more noise. Using a general nonstatistical reconstruction method, this inconsistency will cause streak artifacts around higher attenuation regions. Because the SIRCS algorithm is statistically oriented, it can effectively suppress these artifacts. In Fig. 9(a), the nonstatistical reconstruction methods, such as THT and NSIRCS-THT, led to streak results, while the SIRCS clearly outperformed the competitors.

The TV minimization based interior tomography assumes a piecewise constant image model, and produces suboptimal results when this assumption is violated [20]. In this regard, the high order TV (HOT) minimization approach is a promising tool [23]. Additionally, this algorithm must be stopped after finitely many steps. In our experiments, SIRCS with a zero initial image usually led to a biased result. When the THT result was used as an initial guess, the SIRCS has been shown to arrive at a globally optimal result steadily. This is because the THT based initialization incorporates the Hilbert constraint and the known subregion. Therefore, the SIRCS-THT method is not only insensitive to noise but also immune to bias or distortion.

In conclusion, we have proposed a statistical interior tomography approach by combining THT-based interior tomography, CS-based regularization and statistical optimization. Our simulation and experiments have demonstrated that it is a powerful and useful tool for local CT reconstruction under low dose conditions. Therefore, this approach may find many preclinical and clinical applications. Currently, we are working to analyze the theoretical convergence of the proposed algorithm, and also unify the THT and CS constraints in a statistical framework to improve image quality further. Additionally, we are accelerating the key algorithmic steps, especially the forward and backward projection operations. Recently, a separable footprint (SF-TR) method was reported [58], which provides us a way to make more accurate forward and backward projections at a comparable computational time.