Measuring the Quality of Neuronal Identification in Ensemble Recordings

Abstract

Technological advances in electrode construction and digital signal processing now allow recording simultaneous extracellular action potential discharges from many single neurons, with the potential to revolutionize understanding of the neural codes for sensory, motor, and cognitive variables. Such studies have revealed the importance of ensemble neural codes, encoding information in the dynamic relationships among the action potential spike trains of multiple single neurons. Although the success of this research depends on the accurate classification of extracellular action potentials to individual neurons, there are no widely used quantitative methods for assessing the quality of the classifications. Here we describe information theoretic measures of action potential waveform isolation applicable to any dataset that have an intuitive, universal interpretation, that are not dependent on the methods or choice of parameters for single-unit isolation, and that have been validated using a dataset of simultaneous intracellular and extracellular neuronal recordings from Sprague Dawley rats.

Introduction

As we begin decoding spikes to understand brain function, it is critical to reliably identify distinct action potential trains from many neurons simultaneously (Wilson and McNaughton, 1993; Hampson et al., 2001; Csicsvari et al., 2003; Harris et al., 2003; Buzsáki, 2004; Hill et al., 2011). “Spike sorting” uses features of multiple simultaneously recorded action potential waveforms to divide signals into isolated categories, each corresponding to the discharge of an individual neuron.

Spike sorting remains difficult, perhaps more art than science. Currently, the quality of waveform isolation in most studies is unknown, a matter of trusting a particular laboratory or user. Identification uncertainty is problematic because conclusions about information processing mechanisms in the brain depend on the quality of action potential isolation (Quirk and Wilson, 1999; Schmitzer-Torbert et al., 2005; Fenton et al., 2008). Lack of a consistent method to determine single-unit isolation quality impedes progress in understanding how coordination of neuronal discharge produces behaviors and cognition or how failure of coordination produces pathology. A quantitative method could validate experiments in different laboratories and would be useful for developing waveform-isolation algorithms.

During spike sorting, features of extracellular waveforms, such as peak amplitude and energy, are extracted and placed in feature vectors. An expert user then uses subjective notions of spike-waveform isolation to create boundaries around clusters in two-dimensional (2-D) or three-dimensional scatter plots of these high-dimensional feature vectors. Cluster separation quality varies with operator expertise, choice of features, and visual assessment of cluster boundaries (Harris et al., 2000; Wood et al., 2004).

Although several measures of isolation quality were developed, they have not gained widespread use, generally only working on particular types of datasets, or favoring particular isolation methods and parameters used by one research group. For example, Isolation Distance (IsoD) and LRatio are two related measures of isolation quality (Schmitzer-Torbert et al., 2005). Although definable using any waveform parameter set, to make comparisons across datasets, it was necessary to use identical parameters for waveform isolation in each dataset. Therefore, that study proposed a standardization using only two waveform features: energy and the first principal component coefficient of the energy normalized waveform. In our experience, those two features alone rarely provide good waveform isolation, a process that generally requires a large number of features.

We sought a measure that can be interpreted consistently across datasets using feature spaces that differ in both the identities and number of features. We present an information theoretic approach to quantify the quality of extracellular waveform isolation. We provide a quality measure that can be compared across recordings and laboratories, without constraint as to the type of electrode, the data acquisition method, or the particular set of parameters used for waveform isolation. By providing a method allowing each study to use whatever set of parameters provides optimal isolation, we expect that these measures can begin to provide a standard for ensemble recording studies. These quality measures will also provide the quantitative basis needed to evaluate and compare the effectiveness of automated waveform-isolation methods extant or in development.

Materials and Methods

Electrophysiology

The data described here, which we used for this study, was recorded previously from male, Long–Evans rats (Taconic Farms). The methods have been described in detail previously (Fenton et al., 2008; Park et al., 2011). All procedures received Institutional Animal Care and Use Committee approval and were in accordance with institutional and National Institutes of Health guidelines. Briefly, tetrodes (O'Keefe and Recce, 1993; Gray et al., 1995) made by twisting four strands of 25 μm nichrome were used to aid unitary waveform discrimination. For the recordings from freely moving rats (male; Taconic Farms), eight tetrodes were loaded into a custom machined microdrive assembly (Bio-Signal Group). The assembly was surgically implanted under pentobarbital anesthesia (50 mg/kg) to position the tetrodes above the pyramidal cell layer in the dorsal hippocampus (centered at anteroposterior, 3.8 mm; lateral, 2.5 mm; dorsoventral, 2 mm relative to bregma; Paxinos and Watson, 2007). The rats were allowed to recover for at least 1 week before the tetrodes were individually advanced in <50 μm steps during the course of 1–2 weeks. The goal was to position as many of the eight tetrodes in the CA1, CA3, or dentate gyrus principal cell layer at the same time. A dataset of tetrode recordings from the hippocampus and medial prefrontal cortex (mPFC) of urethane-anesthetized Long–Evans rats (male; Taconic Farms) was also studied. These recordings were made using the methods described by Olypher et al. (2006).

Extracellular potentials were buffered by unitary gain amplifiers plugged into the microdrive connector on the rat's head. The buffered signals were transmitted to main amplifiers along wires. Action potential (300–10,000 Hz) bandpass-filtered signals were amplified (5000–10,000 times), digitized (32 or 48 kHz), and time stamped (100 μs resolution), and 2 ms tetrode waveforms were recorded using custom software (AcX; A.A.F.) or a commercial system (dacqUSB; Axona). Whenever an action potential voltage exceeded a threshold voltage, the voltages on all four wires of the tetrode were collected. The recorded action potential waveforms were aligned with the voltage at the threshold crossing set to the sample at 250 μs. This alignment produced a time-axis origin for measuring time-dependent waveform features, such as the waveform voltage at a particular time point relative to the threshold crossing at t = 250 μs.

Single-unit waveform isolation was done manually using custom software (WClust; A.A.F., S.A.N.) that allows the user to define unitary waveform parameter clusters by drawing convex polygon boundaries in 2-D slices of waveform parameter space, as described in Results. The waveform parameters included the positive and negative peak amplitudes on each tetrode wire, determined from a cubic spline (Press et al., 1992) of the digitized waveform; the principal components computed either from the waveform on each tetrode wire separately or computed from the concatenation of the four tetrode waveforms; the waveform energy between a user-selected pair of time points (defined in units of voltage as $\sqrt{{\displaystyle {\sum }_{i=n_1}^{n_2}{x}_i^2}}/\left(n_2-n_1+1\right)$, where x_i is the waveform value of sample i, and n₁ and n₂ are the starting and ending sample indices, respectively); the waveform voltage or slope at a user-selected time point; and the waveform voltage on each tetrode wire at the time of the peak voltage on the largest waveform in the tetrode event.

Nearest-neighbor estimates of probability with k-dimensional trees

The nearest-neighbor Kullback–Leibler divergence (KLD) (Kullback and Leibler, 1951) estimator (Wang et al., 2006) requires finding the nearest neighbors of arbitrary feature vectors in a high-dimensional space. To reduce the search time to find nearest neighbors, we stored the feature vectors in k-dimensional (KD) trees (Bentley, 1975; Cormen et al., 2001), which are a data structure allowing for O(logN) time lookup of nearest neighbors, where N is the size of a distribution. Before storing the feature vectors in the KD trees, we normalized the values of each dimension into the range of [0–1] by the following formula: $v=\frac{v_i-{\min }_i}{{\max }_i-{\min }_i}$. Here, v_i is element i of vector v, and min_i and max_i are the minimum and maximum values of dimension i. This normalization allows each dimension to play an equal role in calculating nearest-neighbor distances, regardless of magnitudes of values in the dimensions. One KD tree was created for the feature distribution of each cluster.

Simultaneous intracellular and extracellular neuronal recordings

The waveform isolation quality measures we developed were validated using publicly available simultaneous recordings of intracellular and extracellular voltages from hippocampal area CA1 of Sprague Dawley rats (Harris et al., 2000; Henze et al., 2000). Each recording had a single intracellular channel and four extracellular channels. This allowed the identity of spikes on the extracellular channels to be correctly classified as belonging to the intracellularly recorded neuron.

To extract action potential waveforms from the intracellular recordings, we calculated the discrete derivative and then set a threshold for spike crossing at a value above the average discrete derivative value. To extract putative spikes from the extracellular recordings, we first performed a zero-phase distortion bandpass filter between 500 Hz and 3 kHz. Any voltage level from the filtered signal that crossed a threshold indicated a spike. The portion of the signal surrounding the threshold crossing (including 0.3 ms before and 1.8 ms after) was extracted from each channel and stored. Next, commonly used features, including peak, energy, and principal components, were extracted from the extracellular waveforms on the four channels and used to form feature vectors. The extracellular waveforms were considered to originate from the intracellular neuron if the intracellular and extracellular peaks occurred within 0.4 ms (similar to Harris et al., 2000).

To assess correlation of our quality measures with false positives and negatives, we performed 28 increasing levels of corruption to the original intracellularly identified (IC) clusters. For each recording, to simulate false positives, we calculated the center of the IC cluster and added the waveform feature vectors from the background distribution that encroached on its borders. We defined an IC cluster border as 2 SDs above the mean from the center. To simulate false negatives, we excluded feature vectors that were known to belong to the IC cluster from its outermost borders, as measured by distance to center.

IsoD and LRatio

IsoD and LRatio are measures developed to assess the quality of spike feature clusters (Schmitzer-Torbert et al., 2005). Although these measures can operate on arbitrary features, we used an eight-dimensional (8-D) space in our standard implementation. This space consisted of energy and the first principal component of the energy-normalized waveforms, two dimensions for each of the four microwires of a tetrode. Both measures use a noise distribution for each cluster consisting of all feature vectors not in the cluster. To compute IsoD, we compute mean and covariance matrix for each cluster feature distribution and then calculate the squared Mahalanobis distance (Mahalanobis, 1936) for each feature vector in the noise distribution from the mean of the cluster. These distances are sorted in increasing order. IsoD is the nth largest squared distance, where n is the number of spikes in the cluster. IsoD tends to be larger for clusters that are well separated from the background.

For each cluster C, L is defined as L(C) = $\Sigma i\in C$ 1 − CDFχ_df² (D_i,C²), where i∉ C is the set of noise spikes not in cluster C, CDFχ_df² is the cumulative distribution function of the χ² distribution with eight degrees of freedom (Bulmer, 1979), and D_i,C² is the squared Mahalanobis distance of i to cluster C. Noise spikes close to the center of C contribute more to this sum than noise spikes far from the center. A low value of L indicates that C is well separated from the surrounding noise. LRatio is then defined as $\frac{L\left(C\right)}{n}$, where n is the number of spikes in cluster C. As shown, IsoD and LRatio are highly correlated (r = 0.91, p < 0.001) and thus redundant. The redundancy is a result of both being functions of the squared Mahalanobis distances of the noise spikes from the cluster center.

Software

The software for calculating the different measures of single-unit isolation quality and for extraction of waveform features was written in standard C++ and is available for download as a package at the International Neuroinformatics Coordinating Facility software center (http://software.incf.org/software/isoitools) and at ModelDB strategies that included surgery. (http://senselab.med.yale.edu/ModelDB/ShowModel.asp?model=141061). The software was tested and compiled independently on Linux OS and also as part of custom single-unit isolation software for the Windows platform WClust.

Results

Isolation information

Intuitively, the quality of a cluster is greatest when the cluster is well separated from the background, separated from all neighboring clusters, and compact. To capture this intuition, we propose isolation information (IsoI), which computes a symmetrized KLD (Kullback and Leibler, 1951) between two multidimensional probability distributions of action potential waveform features. In what follows, we primarily refer to this as a “cluster” or “feature cluster.” We refer to it as “probability distribution” or “distribution” when discussing KLD as a general measure. KLD measures the separation between two probability distributions, P and Q, with probability densities p and q:

where the integral is taken over the space of waveform features. Keeping with the information theory standard, logarithms in this paper are base 2, unless otherwise stated.

We sought a measure that increased monotonically as the uncertainty of waveform parameters decreased. KLD had the disadvantage of not being symmetrical: distance from P to Q is not the same as distance from Q to P. We therefore defined our new measure, isolation information (IsoI), to be the resistor average (Johnson and Sinanovic, 2001) of KLD(P, Q) and KLD(Q, P) to provide symmetry:

Graphing IsoI against the individual entropies of P, Q divided by the entropy of the joint distribution of P, Q demonstrated an additional advantage of this measure: it provided an approximately linear association with entropy reduction during classification of waveforms to their respective clusters (data not shown).

Given a dataset of classified action potential waveforms, we calculated two different IsoI values: IsoI(C, BG) (IsoI_BG, cluster vs background) and IsoI(C, NN) (IsoI_NN, cluster vs nearest neighbor). IsoI(C, BG) computes a distance measure between the waveform feature probability distribution of the isolated action potentials of a cluster of interest (C) and the waveform feature probability distribution of all the other recorded events in the background (BG). This quantifies how well isolated the feature vectors of the cluster are from all of the other feature vectors as well as measuring the compactness of the cluster, because high probabilities in the distribution result from tight clustering in feature space.

IsoI(C, NN) computes the distinction between a waveform feature probability distribution of a cluster and the nearest-neighbor distribution (NN):

IsoI(C, NN) is useful because a cluster may be far from a large proportion of the other feature vectors and hence have a large IsoI(C, BG) but be close to another cluster. In such situations, the IsoI(C, NN) value will be reduced and may thereby be used to more sensitively quantify the uniqueness of the cluster.

These two measures quantify the isolation quality in bits (units of information) across arbitrarily chosen waveform features and quantify judgments of cluster isolation quality in terms of separation and uniqueness.

Calculating KLD

With high-dimensional feature spaces, accurately determining probabilities becomes difficult when the size of the dataset is limited because of data points being sparse in the space. In particular, 0-probability events are often terms when calculating Equation 1, causing the KLD to be undefined. We therefore computed the KLD between probability distributions P and Q using a nearest-neighbor divergence estimator that has been shown to converge to the exact value of KLD with the increase of the sample size (Wang et al., 2006). To calculate the value using this estimator, we iterate over all of the elements in P. We then find the distance to their nearest neighbor in P and the distance to their nearest neighbor in Q. The log of the ratio of these distances is then summed:

where d is the number of dimensions, |P| signifies the number of elements in distribution P, min_j(dist(Q_j ϵ Q, P_i)) is the distance from element P_i to the nearest element in Q, and min_j(dist(P_j ϵ P |i ≠ j, P_i)) is the distance of element P_i to its nearest neighbor in distribution P. Euclidean distance was used:

with n the dimensionality of the vectors. Equation 4 indicates that when the elements of distribution P are well clustered, their nearest neighbors within P will be closer than their nearest neighbors in Q. In this case, the ratio of logs will contribute a positive value. If the nearest-neighbor distance to distribution P is larger than that of Q, the ratio will contribute a negative value. This occurs for poorly defined clusters that are not well isolated and for points near the boundary in the case of two adjoining distributions. In summary, KLD is a summation over all elements of the ratio of likelihoods that an element from the distribution is from that distribution and not from outside of it.

Dimensionality reduction

To compare IsoI values across different feature spaces of arbitrary dimensionality, we performed a dimensional reduction. For each cluster C, we found the eight features of 20–40 typically used that gave the highest pairwise 2-D IsoI_BG, F_C. These features are then used to compute the final 8-D IsoI_BG and 8-D IsoI_NN. Note that, for calculating the IsoI_NN of a particular cluster C, we use F_C when calculating each IsoI(C, X), where X is any other cluster than C. The automatically chosen features in F_C maximize cluster isolation and compactness. Although the selected features typically differ somewhat for each cluster, this technique allows estimation of isolation quality using the features best suited for isolating each individual single unit.

Although computing pairwise 2-D divergence for each cluster comes at the cost of increased computation time, it allows for selecting dimensions that maximize both isolation and compactness. Using one-dimensional (1-D) divergence to select for optimal dimensions does not allow selecting for compactness because 1-D divergence will only be maximal when the separation between the two clusters is high. The choice of 8-D for the final analysis was a conservative choice after testing assessment at different dimensions. In any case, the final 8-D calculation was not computationally expensive compared with the pairwise 2-D comparisons.

Sensitivity of isolation information measures to isolation errors

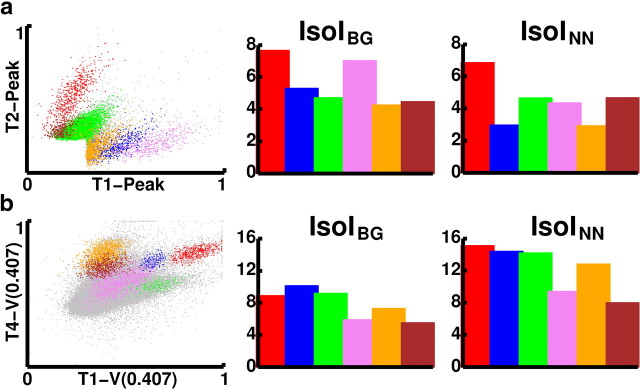
To measure the sensitivity of IsoI to classification error, we assessed various forms of cluster degradations, starting with high-quality clusters defined by an expert user and verified by our inspection. These clusters were compact and had a large separation from each other, as well as from the background, resulting in large IsoI values, ranging from −7 to 14 bits (Fig. 1). Cluster 1 (C1) (red) and C3 (green) have the highest separation from background and from their nearest-neighboring clusters. This can be seen in the larger distance of C1 and C3 from the other clusters and background spikes in Figure 1b in slices 1, 2, and 4, as well as slice 3 for C1. The other clusters, C2 (blue), C4 (purple), and C5 (light blue) are well isolated in some slices but not as well in others, particularly in slices 3 and 4. Although sometimes only a single slice is used to determine separation, separability in more dimensions does add to cluster quality. As a result, the IsoI values of C2, C4, and C5 are lower than those for C1 and C3. Degradations were tested on various clusters both from this dataset and others. Degradation effects (Fig. 2) were assessed on the clusters from Figure 1 after alterations to C1. Most of the alterations were performed in a single 2-D subspace (Fig. 1b3), which displays voltages at specific times on two different microwires. This 2-D slice contained the C1 boundary that contributed the most to isolating it from the background, as evidenced by it contributing the highest 2-D IsoI_BG of any 2-D feature slice. This shows an advantage of this method, with implications for future development of automated systems. By allowing the use of arbitrary features, higher isolation quality may be sought by keying in on peculiarities in waveform shape that are revealed through visual or automated inspection of the most influential slices. As a suggestion for best practice, we typically used standard features consisting of waveform peak amplitude, energy, principal components, and voltage level or derivative at different times.

Figure 1.

a, Extracellular action potential waveforms (negative up) of five well-defined clusters, C1–C5. Gray waveforms (C0) are unclustered spikes. The four signals recorded from each wire of the tetrode (T1–T4) are drawn next to each other, separated by vertical black lines. Waveforms were stored 250 μs before the upward threshold crossing and 1.75 ms afterward. b, Different 2-D slices of the clusters in feature-space. T1-peak is defined as the peak voltage on wire 1 (see Materials and Methods). T1-V(0.181) is a user-defined feature defined as the voltage on wire 1 at time 181 μs of the stored waveform. T3-V(0.307) is the voltage on wire 3 at 307 μs. These features were selected by an expert user to optimize waveform isolation, as reflected in the well-separated clusters. Only the five best clusters found are highlighted here. Voltage is in units of millivolts. c, Top, IsoI_BG of the five clusters shown in b. Bottom, IsoI_NN of the five clusters.

Figure 2.

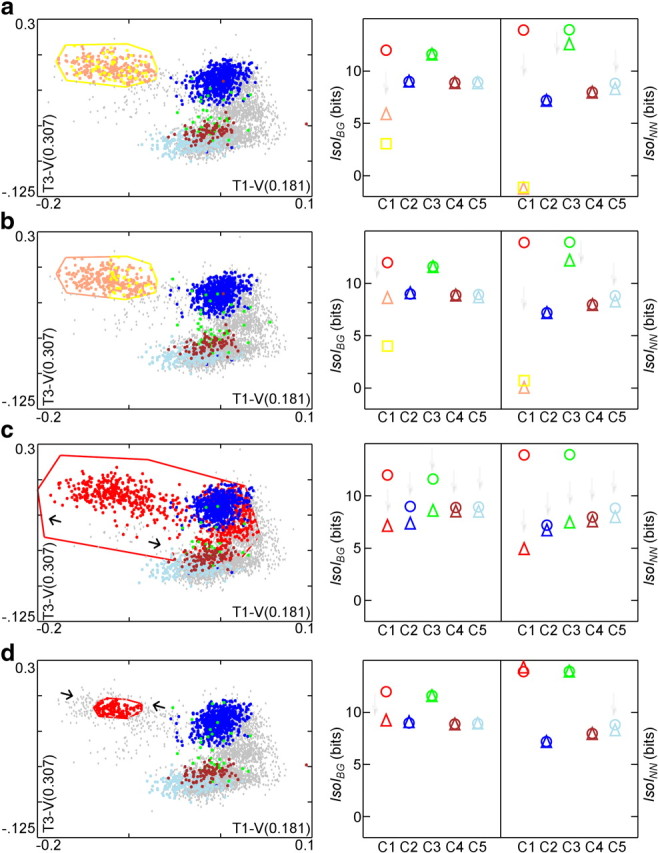
Sensitivity of IsoI measures to various cluster degradations. Left, Degradations are a high level of random intermingling, lower level of intermingling, expansion, and contraction. Scatter plots of the clusters in the same 2-D projections after the various degradations of C1 are shown in a–d. Voltage is in units of millivolts. Right, IsoI values before (circle) and after (triangle) degradation. Square in a and b shows IsoI value for the additional new cluster (color coded). Faint gray arrows pointing downward emphasize where decreases in IsoI values occur. a, Random 50% reassignment produces substantial decrease in IsoI values for the two derived clusters. Note that oscillatory behavior about the exact value, e.g., 0 for the new IsoI_NN of C1 here, during convergence is a general property of the nearest neighbor divergence estimator. b, Approximate bisection of cluster C1 within a 2-D feature slice also reduces IsoI values, despite the clear border between derived clusters. c, Expansion: C1 is brought closer to C2 and C3, so IsoI values of C2 and C3 also decrease. C3, nearest neighbor to C1, shows large decrease in IsoI_NN. C4 and C5 are also slightly degraded. d, Contraction primarily degrades C1 IsoI_BG as a result of poor isolation from points that are now part of background.

In the first degradation, we considered a common scenario in which features of two clusters are intermingled. Although a user would always avoid the extreme case of near complete intermingling (Fig. 2a), users commonly define what appears to be a single cluster in feature space and subsequently, during close inspection of the waveforms, find an additional feature with potential to partially split the cluster in two. In this scenario, a user would first “clone” the original cluster boundaries and then attempt to find new distinguishing features. To simulate this, we duplicated C1 boundaries, splitting the feature vectors into two C1 clusters shown in pink and yellow (C1′,C1″ respectively). The two derived clusters are now each other's nearest neighbor. Additionally, each derived cluster now has the other one as part of its background. As a result, the IsoI_BG, IsoI_NN values of C1′ and C1″ dropped significantly (note that oscillatory behavior about the exact value, 0 for IsoI_NN here, during convergence is a general property of the nearest-neighbor divergence estimator from the study by Wang et al., 2006). IsoI_BG values for all the other clusters remained unchanged. The IsoI_NN values were subject to minor change, because nearest-neighboring clusters can be changed by modifying a single cluster. As a result, C3 and C5 have lower IsoI_NN values than the originals.

The next degradation was a less extreme example of intermingling. Here, we contaminated C1 by creating a new cluster within its boundaries (Fig. 2b). In this instance, two clusters C1′ and C1″ were close in feature space but were still fairly well separated from the background distribution. As a result, IsoI_NN is lowered more significantly than IsoI_BG for these two clusters compared with C1. The degradation again slightly lowered the IsoI_NN values of clusters C3 and C5.

Another cause of overlap between clusters occurs when a user has difficulty determining precise demarcations, typically as a result of a high density of feature vectors in the area between two or more clusters. To replicate this situation, we expanded several of the 2-D boundaries of C1 by randomly reassigning a proportion of the points falling within this expanded boundary from their original clusters to C1 (Fig. 2c). C1 now encroached into the territory of the other clusters. This degradation lowered IsoI_BG for cluster C1, because it was now closer to the background distribution. Other clusters, with some of their points removed, were closer to the background distribution, resulting in reduced IsoI_BG values, most evident for C2 and C3. In addition, the IsoI_NN of C1, C2, and C3 were all significantly lowered, because their nearest-neighboring clusters became closer. Because the nearest-neighboring cluster of C3 is C1, its IsoI_NN value was lowered the most. Importantly, this demonstrates that our measures are sensitive to nonlocal changes. Here, IsoI_BG and IsoI_NN both show lower values for C2 and C3 as well as for C1 because these are clusters who have “given up” feature vectors to C1. A different problem occurs when the density of feature vectors around a cluster is low, making it difficult to determine where to place the border of a cluster. In this case, the user may exclude feature vectors that should belong to the cluster. To replicate this, we contracted one of the 2-D boundaries of C1, excluding feature vectors that lie outside the new boundary (Fig. 2d). These excluded vectors were added to the background, resulting in a lower IsoI_BG value. Contraction also produced an insignificant increase in the IsoI_NN value of C1 because C1 is now farther from its nearest-neighboring cluster, C3, as a result of the contraction.

Validation using simultaneous intracellular and extracellular recordings

We used publicly available simultaneous intracellular and extracellular neuronal recordings from hippocampal area CA1 (see Materials and Methods) to validate the IsoI measures (Fig. 3). We also used the same recordings and methods to compare the performance of two previously developed measures, IsoD and LRatio (see Materials and Methods). In each recording, all extracellular feature vectors belonging to the intracellularly recorded neuron were set to belong to the IC cluster. The remaining feature vectors belonged to the background distribution. To calculate correlation of IsoI_NN with error rates, a nearest-neighboring cluster was required for each IC cluster. To estimate this, we performed k-means clustering on the background distribution and selected the cluster with smallest IsoI_NN values as the nearest-neighboring cluster of IC. For IsoI_NN, false-positive and false-negative corruptions were performed using these two clusters (IC and NN).

Figure 3.

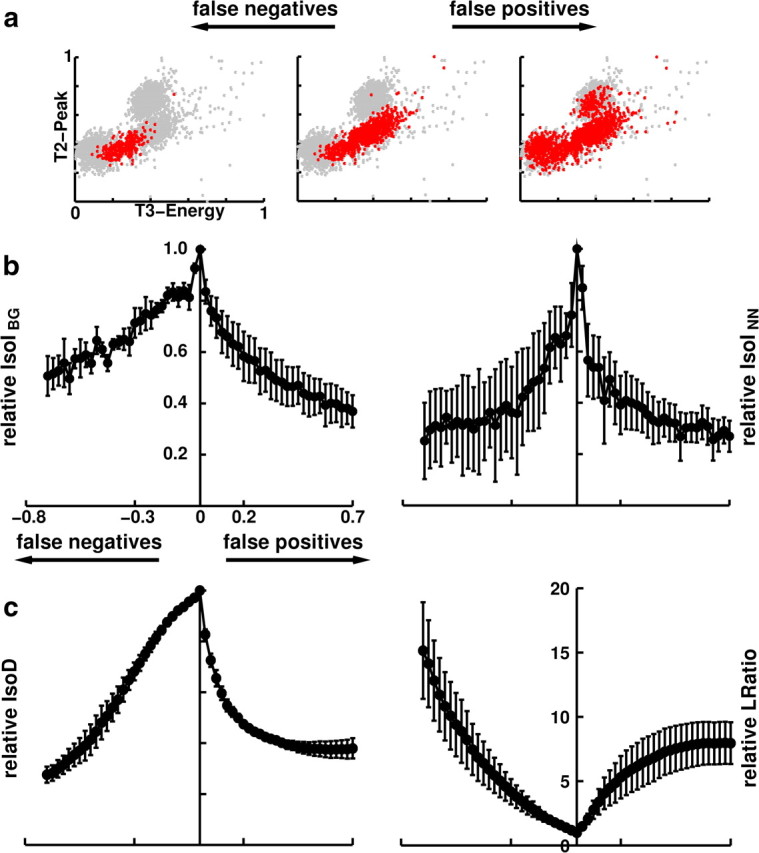
Correlation of IsoI measures with error rates. a, False positives (right) and false negatives (left) were incrementally added to the known IC feature distribution, and the corresponding relative IsoI values were calculated. The cluster displayed has 833 feature vectors. b, Correlation of relative IsoI_BG and IsoI_NN values with false-positive and false-negative error rates were found to be large and significant (p < 0.001). Peak IsoI value occurs at zero error rate. Error rates were defined by the percentage of points added to (false positives) and subtracted from (false negatives) the IC cluster. At high error rates, variability of relative IsoI values increased, but IsoI values remained non-negative. c, Correlation of relative IsoD and LRatio values with false-positive and false-negative error rates were found to be significant (p < 0.001). Note that LRatio increases with increasing error rate, indicating a drop in single-unit isolation quality.

We correlated each cluster quality measure with false positives and false negatives using 28 levels of corruption to the IC clusters (Fig. 3b). Error rates were defined by the percentage of points added to (false positives) and subtracted from (false negatives) the IC cluster. As an example of this procedure on the simultaneous intracellular and extracellular dataset for one corruption level, Figure 3a shows a cluster (center) containing 833 spikes, with a high IsoI_BG value of 5.2 bits and high values of IsoD (250.5) and LRatio (0.00836). We performed false-negative corruptions by removing up to 70% of the feature vectors of the cluster (Fig. 3a, left), bringing the new cluster closer to the background distribution. As a result, the IsoI_BG value dropped drastically, to 3.8 bits, and the IsoD and LRatio values decreased to 45.8 and 0.87, respectively. We performed false-positive corruptions of the original cluster (Fig. 3a, right), by adding 583 feature vectors from the background distribution (70% of the original 833 feature vectors). As a result, the IsoI_BG value dropped to 2.8 bits, and the IsoD and LRatio values worsened, changing to 59.8 and 0.56, respectively. All measures had their highest quality values at zero corruption and dropped off sharply with the corruption, illustrating that all the measures were able to objectively quantify cluster quality.

To calculate error rates for the measures, we performed corruptions on the four recordings. At baseline, the (IsoI_BG, IsoI_NN, IsoD, LRatio) values of the IC clusters from the four recordings had the following values: (3.6, 3.3, 18.8, 0.20), (4.2, 2.0, 25.8, 0.05), (3.1, 2.0, 20.7, 0.20), and (5.2, 4.7, 42.5, 0.04). The clusters ranged in size from 172 to 833 feature vectors, which allowed us to make significant reductions in cluster size when performing false-negative corruptions. For all recordings, the peak IsoI_BG (Fig. 3b, left) and IsoI_NN (Fig. 3b, right) values occurred when there was no corruption to the IC clusters, verifying the usefulness of our measures as an objective quantification of neuronal isolation quality. Similar results were obtained for the IsoD and LRatio measures (Fig. 3c).

We defined relative cluster quality values, for each of the cluster quality measures, as the cluster quality value at the given error rate divided by the uncorrupted IC cluster quality value. We found that increasing levels of corruption tended to monotonically decrease the relative quality indicated by IsoI_BG and IsoI_NN. Similar results were obtained with IsoD and LRatio.

We calculated the Pearson's correlation between false-positive and false-negative error rates with the relative cluster quality values, for each of the measures. The overall correlation levels between each of the measures and error rates were high and statistically significant at the p < 0.001 level for all recordings. The IsoI_BG correlation levels with false negatives ranged from −0.71 to −0.97 and had an average of −0.87. We found that IsoI_BG correlation with false positives had similarly high values, ranging from −0.82 to −0.99, with an average of −0.90. IsoI_NN correlation with false negatives ranged from −0.65 to −0.91, with an average of −0.78, and the IsoI_NN correlation with false positives ranged from −0.49 to −0.97, with an average of −0.71. The strong correlation levels of both IsoI measures with increasing error rates confirms that IsoI may be used to objectively validate the quality of single neuronal identification from extracellular recordings. Similar results were found for both IsoD and LRatio, which had (minimum, maximum, average) correlations with false negatives of (0.98,1.0, 0.99) and (0.94,0.99, 0.96) for IsoD and LRatio, respectively, and (minimum, maximum, average) correlations with false positives of (0.63, 0.89, 0.77) and (0.80, 0.99, 0.89), respectively. These results indicate the utility of these measures in quantifying single-unit isolation quality as well.

To determine whether the different measures were symmetrically sensitive to both types of errors, we calculated the skew of the relative values of each of the measures, defined as $\sum \frac{{\left(r_{fp}-r_{fn}\right)}^3}{N}$, where r_fp and r_fn represent the relative value of the measure at the given false-positive and false-negative corruption level, respectively, and N is the number of corruption levels (28). We found that IsoI_BG and IsoI_NN had average skews of −0.0143 and −0.0095, respectively, across the four recordings. These low skew values suggest nearly symmetric sensitivity to both types of errors and may be particularly useful where it is not known what type of error will occur. Although IsoD had a low average skew of −0.015, LRatio had a high average skew of −49.738.

Comparison of IsoI to other measures

We performed additional comparisons of the IsoI measures with two published measures of cluster quality, IsoD and LRatio (see Materials and Methods), on a dataset of 350 clusters from >45 different recordings. In these recordings, the number of clusters obtained ranged from 2 to 15. Detailed analysis of the comparisons is provided below.

The Pearson's correlation coefficient was computed between each pair of cluster quality measures, between the measures and the number of spikes in the cluster, and between the measures and the number of clusters that were isolated from the tetrode recording (Table 1). Before computing the correlation coefficients on IsoD and LRatio, we computed their natural logarithms first (Schmitzer-Torbert et al., 2005).

Table 1.

Pearson's correlations between different measures and the number of spikes in the cluster and the number of clusters in the recording

	IsoIBG	IsoINN	ln(IsoD)	ln(LRatio)	Clusters
IsoIBG	●	■	■	■	0.28
IsoINN	0.55	●	■	■	−0.11
ln(IsoD)	0.5	0.47	●	■	0.16
ln(LRatio)	−0.57	−0.46	−0.91	●	−0.13
Spikes	−0.02	0.21	0.37	−0.26	●

Circles represent diagonal elements of table which all have value of 1.0. Squares represent redundant values that are symmetrical across the diagonal and were left out. Significant correlations (p < 0.05, n = 350, two-tailed test) are in bold.

There is a high correlation between ln(IsoD) and ln(LRatio), showing significant redundancy. ln(IsoD) and ln(LRatio) also have high correlations with the number of spikes in the cluster. This property of these measures is undesirable because principal cells in hippocampus, striatum, entorhinal cortex, and other brain regions have low firing frequencies, whereas interneurons have high firing rates. Low values of these measures may wrongly exclude such cells from analysis. IsoI_BG is not correlated with cluster size.

There is a statistically significant but only small correlation between each of the IsoI_BG, IsoD, and LRatio measures with the number of clusters in the recording, suggesting that these measure perform well across a wide range of recording qualities. The correlation between IsoI_NN and the number of clusters in a recording is not significant, indicating enhanced robustness of this measure to the different recording conditions.

Importantly, IsoI_NN is not as strongly correlated with IsoI_BG as LRatio is with IsoD, demonstrating that IsoI_NN and IsoI_BG measure different aspects of cluster quality. This was of course our intention when designing these as complementary measures.

Comparison of IsoI_BG with IsoD

The standard implementations of IsoD and LRatio operate in the 8-D feature space consisting of the energy of the spike waveform and first principal component of the energy-normalized waveform on each microwire of a tetrode. Because IsoI has no such constraint, an operator that uses other features to isolate a single-unit waveform can more accurately evaluate the quality of isolation using IsoI than with the standard implementation of IsoD or LRatio. The correlation of IsoI_BG versus ln(IsoD) is significant and positive (r = 0.5, p < 0.001, n = 350, two-tailed test), and the correlation with IsoI_BG versus ln(LRatio) is significant and negative, although outliers are seen (Fig. 4a). We examined clusters where the measures agreed/differed to see the strengths/weaknesses of the measures. In exemplar 2-D slices of feature space, the examined cluster is shown in red, and its nearest neighbor is shown in blue. Because IsoD and LRatio are highly correlated (r = −0.91, p < 0.001, n = 350, two-tailed test), we focus on the IsoI_BG and IsoD comparisons.

Figure 4.

Comparison of IsoI_BG with ln(IsoD) and ln(LRatio) on all clusters in the 350 cluster dataset along with several case studies. a, Plot of IsoI_BG versus ln(IsoD) and ln(LRatio). Larger, labeled points represent clusters discussed in Results. These clusters are shown in b–e. In b–e, the red cluster is the cluster of interest (highlighted point from a), and the blue cluster is its nearest neighbor. The gray points are the remaining spikes. The left column of b–e shows the slices of the feature space used by IsoI_BG, and the right column shows slices of the feature space used by IsoD. Voltage is in units of millivolts. b, A well-isolated cluster according to both measures. c, A poorly isolated cluster according to both measures. d, A well-isolated cluster according to IsoI_BG and a poorly isolated cluster according to IsoD/LRatio. e, Poorly isolated cluster according to IsoI_BG and a well-isolated cluster according to IsoD/LRatio.

The first cluster examined had high ratings in both IsoI_BG (11.99 bits) and IsoD (203.98) (Fig. 4b). This cluster has good separation from the background distribution using both sets of features. The next cluster had low ratings in both of these measures: an IsoI_BG of 5.3 bits and IsoD of 2.82 (Fig. 4c). The cluster is poorly isolated from the background and dispersed in both sets of features.

The next cluster examined had a low IsoD of 8.64 and a high IsoI_BG of 13.12 (Fig. 4d). The operator selected the boundaries of this cluster using the voltage at two different times in the action potential waveform, which allows for good discrimination of this cluster. These features are not measured by IsoD, and, as a result, less than optimal features are used in calculating the quality of this cluster. In addition, this cluster comprises <0.001% of the spikes in the recording. This makes it difficult for IsoD to give this cluster a good score, because IsoD is proportional to the cluster size (see Materials and Methods). IsoI_BG does not share these problems. This case illustrates how relying on IsoD may exclude valid clusters that require nonstandard parameters for isolation or exclude low-frequency firing single units from analysis.

The next cluster examined (Fig. 4e) had a relatively low IsoI_BG of 5.28 bits and a relatively high IsoD of 47.37. Although this cluster is not so well isolated from the background distribution, it comprises ∼19% of the spikes in the recording. As a result, the IsoD score is inflated, because a large distance from the center of the cluster must be traversed to accumulate as many noise spikes as are in the cluster (see Materials and Methods). IsoI_BG has no such problem as reflected in the low score of 5.28 bits. This case again illustrates the problem of using a quality measure that depends on the number of spikes in the cluster.

Comparison of IsoI_NN with IsoD

IsoI_NN measures the separation between nearest-neighboring clusters, and IsoD measures the separation of clusters from the background distribution. The correlation between IsoI_NN and IsoD is significant and positive (r = 0.47, p < 0.001, n = 350, two-tailed test), and the correlation between IsoI_NN and LRatio is significant and negative (r = −0.46, p < 0.001, n = 350, two-tailed test), with outliers visible (Fig. 5a). We examined the highlighted cases in Figure 5a to see where the measures agree and disagree. Again, we focus on comparing IsoI_NN and IsoD.

Figure 5.

Comparison of IsoI_NN and ln(IsoD), ln(LRatio) on all clusters in the dataset along with several case studies. a, Plot of IsoI_NN versus ln(IsoD) and ln(LRatio). Larger, labeled points represent clusters discussed in Results. These clusters are shown in b–e. b–e, The red cluster is the cluster of interest, and the blue is its nearest-neighboring cluster. The gray points are the remaining unassigned spikes. The left column of b–e shows the slices of the feature space used by IsoI_NN, and the right column shows slices of the feature space used by IsoD. Voltage is in units of millivolts. b, A well-isolated cluster according to both measures. c, A poorly isolated cluster according to both measures. d, A well-isolated cluster from its nearest-neighbor cluster but poorly isolated from background. This example illustrates that neither IsoD nor LRatio is sensitive to separation between clusters. e, A cluster with poor separation from its nearest-neighbor cluster but good cluster-background separation. The overlap between the red and blue clusters indicates they may need to be merged into a single cluster or discarded.

The two measures agree when a cluster is well separated from both the background and from its nearest-neighboring cluster (Fig. 5b). This is shown in Figure 5b, where the cluster has a high IsoI_NN of 14.52 bits and a high IsoD of 531.66. The two measures also agree when a cluster is poorly separated from both the background and from its nearest-neighboring cluster. This is shown in Figure 5c, where the cluster has an IsoI_NN of 5.04 bits and an IsoD of 3.29. We next examined a cluster with good separation from the nearest-neighboring cluster, with an IsoI_NN of 14.47 bits, but poor separation from the background, with an IsoD of 7.73 (Fig. 5d). These measures indicate that the cluster is probably not a single unit and needs to be reclustered. This demonstrates that IsoI_NN provides additional information on the quality of a good cluster: only when it is already known that the cluster is isolated from the background distribution should IsoI_NN be used, providing a stricter criterion of cluster quality than either IsoD or IsoI_BG alone.

The next cluster examined (Fig. 5e) has poor separation from the nearest-neighboring cluster, with an IsoI_NN of 1.34 bits, but good cluster-background separation, with an IsoD of 53.62. The former can be seen in the overlap between the red and blue clusters and the latter in the relatively large distance of the red and blue clusters to the remaining feature vectors. This example demonstrates that a non-unique cluster, C, is only separated from the background (high IsoD or IsoI_BG) but not from its nearest-neighboring cluster (low IsoI_NN), NN. This may suggest that C and NN should be merged into a single, larger cluster, which will have better isolation and uniqueness. This example illustrates that IsoD is not sensitive to uniqueness and that IsoI_NN can help point out problems of over-splitting waveform feature clusters.

Comparison of isolation quality across electrode configurations

Although the IsoI measures were designed to work on arbitrary feature spaces, different laboratories use electrode configurations that vary in the number of microwires composing each electrode, and these differences can have a substantial impact on single-unit isolation quality (Gray et al., 1995). We therefore used a dataset of 31 recording sessions from hippocampal CA1, consisting of 437 single units, to measure how IsoI values change as a function of the number of electrode microwires used.

Initial clustering was performed by an expert, using features available from all four microwires of the tetrode. We then used the feature space derived from all four microwires to compute the baseline IsoI values. To allow for comparison across these feature spaces, RelIsoI(N) was defined as the IsoI value computed when using the best eight features available from N (1 or 2) microwires, divided by the baseline IsoI value. We performed these calculations for both IsoI_BG and IsoI_NN. As expected, our calculations confirm that using only one or two microwires degrades the isolation quality significantly (Table 2). It is noteworthy that the degradation in quality had a larger impact on IsoI_NN, which confirms that a particular benefit of using multiple microwire electrodes is in reducing the contamination that can often occur between two or more clusters of action potential waveforms that are of sufficiently large amplitude to be distinct from the background activity.

Table 2.

Average ± SEM of the RelIsoI values calculated using one or two microwires

RelIsoI(1)BG	0.698 ± 0.183
RelIsoI(2)BG	0.550 ± 0.020
RelIsoI(1)NN	0.165 ± 0.014
RelIsoI(2)NN	0.430 ± 0.027

Comparison of isolation quality across brain areas

Firing properties, including rates and action potential features, as well as the density of neurons, can differ significantly across different brain areas. These differences can impact the ability of experimenters to accurately identify single units from waveform feature distributions. We therefore tested IsoI sensitivity to differences in the extracellular waveform characteristics of different brain areas, using in vivo recording datasets from awake rats from multiple areas, including hippocampal CA1, CA3, and dentate gyrus (Table 3, using data from Fenton et al., 2008; Park et al., 2011). The average IsoI values had similar ranges from ∼6 to 11 bits, across regions. IsoI_BG values ranged from 3.7 to 14.6, whereas IsoI_NN values had a larger range, from ∼0.3 to 16.7 bits.

Table 3.

IsoI values from different hippocampal regions, recorded from awake, freely moving rats

	IsoIBG	IsoINN
Park et al. (2011)
CA1
Ave	6.76	8.67
SEM	0.19	0.31
Min	4.11	4.12
Max	11.86	16.46
n	167	167
CA3
Ave	7.14	8.39
SEM	0.21	0.39
Min	4.48	4.19
Max	10.55	15.8
n	79	79
DG
Ave	7.04	8.97
SEM	0.14	0.37
Min	4.01	4.07
Max	9.45	16.71
n	104	104
Fenton et al. (2008)
CA1
Ave	7.90	7.16
SEM	0.11	0.19
Min	3.66	0.34
Max	14.63	16.03
n	268	268

Ave, Min, Max, and n denote average, minimum, maximum, and number of recordings used, respectively. DG indicates dentate gyrus. Note that the Park et al. (2011) data displayed are obtained only from place cells.

We examined a recording of 56,005 spikes from CA3 in detail (Fig. 6a). Approximately 21% of the spikes recorded were considered noise (Fig. 6a, left, gray points). The remaining spikes formed six clusters, corresponding to putative single cells. These clusters were characterized as follows (color, number of spikes, IsoI_BG, IsoI_NN): red, (2358, 7.7, 6.9); blue, (2095, 5.4, 3.0); green, (33,213, 4.8, 4.7); purple, (1809, 7.1, 4.4); orange, (3616, 4.3, 3.0); maroon, (1274, 4.5, 4.7). Cluster 1 (red) showed the best separation from both background (IsoI_BG of 7.7 bits) and its nearest-neighboring cluster (IsoI_NN of 6.9 bits). Cluster 4 (purple) also showed strong background separation (IsoI_BG of 7.1 bits) and separation to its nearest-neighboring cluster (IsoI_NN of 4.4 bits). Although cluster 6 (maroon) appears to overlap cluster 3 (green), it has both substantial background separation (IsoI_BG of 4.5 bits) and nearest-neighbor separation (IsoI_NN of 4.7 bits), which is attributable to good separation in other planes of feature space. The other clusters had fairly high IsoI_BG values, all larger than 4 bits, whereas their IsoI_NN were usually only slightly less. Although firing activity of CA3 neurons can be fairly sparse, these substantial IsoI values demonstrate that, with a sufficiently large dataset, it is possible to accurately identify single units from this brain region.

Figure 6.

Comparison of single-unit isolation quality in CA3 (a) and mPFC (b). Left, Scatter plots of feature vectors from six different clusters. Features displayed are microwire voltages normalized to be between 0 and 1. Gray points represent feature vectors in the noise distribution. Note that T1-V(0.407) is a user-defined feature defined as the voltage on wire 1 at time 407 μs of the stored waveform. Middle and right panels display bar plots of the IsoI values, color coded to match the clusters in the scatter plots.

We evaluated IsoI from recordings made in mPFC and hippocampal CA1 from rats under urethane anesthesia (Table 4; unpublished observation). Both of these areas showed similar average IsoI_BG values of 7.6 ± 0.3 and 7.7 ± 0.3 for CA1 and mPFC, respectively. The IsoI_NN values were also similar, with averages of 10.4 ± 0.4 for CA1 and with a slightly higher value of 11.3 ± 0.6 for mPFC. Minimum and maximum values were similar to those from the awake, freely moving rats.

Table 4.

IsoI values from recordings from rats under urethane anesthesia

	IsoIBG	IsoINN
CA1
Ave	7.64	10.41
SEM	0.26	0.40
Min	4.34	4.06
Max	13.61	20.69
n	67	67
mPFC
Ave	7.69	11.32
SEM	0.27	0.59
Min	4.44	4.2
Max	15.18	25.05
n	58	58

Ave, Min, Max, and n denote average, minimum, maximum, and number of recordings used, respectively.

Next, we examined a recording of 283,469 spikes recorded from mPFC in detail (Fig. 6b). Approximately 95% of the spikes recorded were considered noise as a result of low-amplitude spikes on several channels (Fig. 6b, left, gray points). The remaining ∼12,000 spikes were isolated into six clusters. These clusters were characterized as follows (color, number of spikes, IsoI_BG, IsoI_NN): red, (1449, 9.0, 15.2); blue, (504, 10.2, 14.5); green, (617, 9.3, 14.3); purple, (4370, 6.0, 9.5); orange, (3326, 7.4, 12.9); maroon, (1872, 5.6, 8.1). All of the clusters showed high separation from both background and their nearest-neighboring clusters. Although each of the six clusters had high IsoI_BG values, ranging from 5.6 to 10.2 bits, each cluster had a higher IsoI_NN value, ranging from 8.1 to 15.2 bits. The higher IsoI_NN values found in these recordings were partially attributable to the higher level of noise present in the recording (95% of the spikes) compared with a hippocampal recording. However, because the IsoI_BG values were typically in the same range as those from hippocampal recordings, the single-unit isolation from background should be considered sufficiently high. The fact that this is so demonstrates that the IsoI measures are useful for quantifying single-unit isolation in hippocampal as well as neocortical structures.

The minimum IsoI values across the datasets described was typically near ∼3 bits. We have adopted a best practice of rejecting clusters in which the IsoI values are <4 bits. The similarity of IsoI values from these different brain regions demonstrates the utility of the methods in quantifying single-unit isolation quality in different recording conditions.

Comparison of computation time

We used a dataset of >400 single units from 31 different recordings from hippocampal CA1 to estimate computational costs for the different isolation quality measures. For IsoI calculations, we started with 12 feature vectors from the action potential energy, peak, and first principal component on each of the four microwires. The feature selection stage of IsoI, which iterates over all $\frac{n\left(n-1\right)}{2}$ pairs of 2-D slices, for each cluster, to find the best features for the final 8-D IsoI calculation, was the largest bottleneck of the IsoI calculation. This stage had a computational cost ranging from 1.24 to 35.37 s, with an average ± SEM of 7.28 ± 0.28 s (n = 440) per cluster. IsoI_BG had the next largest computational cost, ranging from 0.25 to 22.5 s and averaging 2.84 ± 0.13 s per cluster. IsoI_NN had a slightly lower computational cost, ranging from 0.01 to 27.85 s and averaging 1.43 ± 0.13 s per cluster. This lower cost for IsoI_NN was attributable to the smaller number of comparisons between feature vectors belonging to two distinct clusters, which are less than the large number of comparisons needed to compare feature vectors belonging to a cluster and its complement, as is done for IsoI_BG.

IsoD and LRatio both operate in an 8-D space, consisting of energy and the first principal component of the action potential waveform on each tetrode wire and do not use feature selection. Their lower computational costs are partly a result of these differences. IsoD and LRatio had the following values for minimum to maximum and average ± SEM (in ms/cluster): (5.6–46.4, 18.3 ± 0.5) and (10.0–82.2, 32.8 ± 0.8), respectively. Although the IsoI measures had a higher computational cost, judicious use of KD trees by caching nearest-neighbor values may help reduce the cost of the calculations. In addition, parallelizing the 2-D search across multiple threads would allow for additional time savings. Nonetheless, use of IsoI amounts to spending approximately a minute extra to compute estimates of single-unit isolation quality. This is an insignificantly short amount of time with enormous value, given that it can take an expert hours to select the waveform boundaries.

Discussion

We have developed and validated an information-theoretic measure for determining single-unit isolation quality in a standardized way that generalizes across brain regions and electrode configurations. The method, IsoI, calculates a symmetrized KLD between two sets of waveform-feature probability distributions in two complementary ways: between a cluster and the background (IsoI_BG) and between a cluster and the nearest-neighboring cluster (IsoI_NN). These two measures, respectively, quantify the isolation and uniqueness of a cluster. We selected the features maximizing 2-D IsoI_BG on a per-cluster basis to calculate a final IsoI. This approach permitted comparison of IsoI values across different feature spaces. This is important for comparing quality across different users, who will choose different features given the same dataset, and also for comparisons across laboratories. It is also important, as demonstrated, that the measures permit comparisons of single-unit isolation quality across recordings from different brain regions. In our datasets, single-unit isolation quality did not differ for recordings from the different hippocampal subfields, nor did isolation quality differ if recordings were made from mPFC or under anesthesia. This does not imply that it is just as easy to isolate single units in each of these areas and conditions, but rather that similar isolation quality standards were applied to the different datasets by the manual operators. Indeed, we have observed a reduction of isolation quality that was captured by a significant decrease of the IsoI measures in conditions when a larger proportion of the recordable cells were actively discharging (Fenton et al., 2008; Park et al., 2011). The IsoI measures were also lower for recordings that only used waveform information from one or two electrodes rather than from all four electrodes of a tetrode, which simply quantified the fact that multi-wire electrode configurations provide more information and power for single-unit isolation. There is substantial merit in the use of a single-unit isolation metric that has general applicability (Hill et al., 2011), and we suggest that the IsoI measures described here are well suited to quantify the quality of single-unit isolation, regardless of where the data were recorded from and regardless of how the units were recorded and isolated.

The isolation measures were applied to a database of clusters, and the values matched expert judgments of isolation quality. We simulated common clustering errors and demonstrated that IsoI reasonably quantified the degree of degradation whether changes were made locally (only a single cluster perturbed) or globally.

To objectively validate our IsoI measures, we used publicly available, simultaneous intracellular and extracellular neuronal recordings to demonstrate that reductions in both of our IsoI measures correlated strongly with false-positive and false-negative error rates. The strong correlation levels indicate that our IsoI measures may be used to objectively validate the quality of single neuronal identification from extracellular recordings.

Our new measures generally correlated well with older measures (IsoD and LRatio) but showed additional significant advantages. One advantage is that IsoI is intuitive via its standard information theoretic scaling, providing a consistent interpretation even when varying features are used for isolation. Another advantage is insensitivity to cell firing rate, particularly important when both fast-firing interneurons and slower-firing principal cells are recorded. An additional advantage occurs with “over-splitting,” a common problem in single-unit isolation. Over-splitting occurs when waveforms from a single-unit are inaccurately split into two or more clusters. This occurs, for example, when higher-amplitude spikes precede low-amplitude spikes in a complex-spike burst (Quirk and Wilson, 1999). IsoI_NN directly detects over-splitting by identifying clusters that are excessively entangled with their nearest neighbor. Here, as in all cases, IsoI_BG remains a necessary complement, because IsoI_NN is only useful to quantify uniqueness once minimal isolation quality has been established with IsoI_BG. IsoI_NN can of course only be used when there are at least two single units to compare.

Certifying students

Isolating single units from multiple extracellular electrodes is a time sink for many neuroscience laboratories (Buzsáki, 2004). It can take ∼2–4 h for an expert to manually cluster a 10 min ensemble recording. IsoI can speed up this process by identifying particular clusters that are not well defined. Such clusters can then be eliminated from consideration or examined using alternative feature sets. Because IsoI is agnostic to feature choice, it can be used as an aid in the choice of the most discriminative features that end up producing the best clusters. Spike clustering is even more frustrating for the student, who must also wonder when to stop refining clusters. Using the IsoI measures, the novice user can make several different clustering attempts and identify the best outcome. The measures also provide a laboratory with a criterion to use both while training new researchers in this skill and subsequently certifying the student to perform these assessments independently.

Certifying projects

Manual spike clustering includes use of subjective judgments of cluster quality: different clusters look better or worse to different researchers depending on their levels of expertise (Wood et al., 2004). As a result, incorrect conclusions may be drawn when clustering quality is inconsistent or lower than required for a particular investigation (Harris et al., 2000). For example, accurate characterization of the milliseconds scale temporal interactions among two or more neurons may require greater isolation quality than estimating the stability of the receptive fields (Quirk and Wilson, 1999). A standardized measure will permit data quality to be assessed during paper review and after publication. The generality of the IsoI measures, allowing comparison across different choices of feature sets, is a key advantage in its use and potential adaptation by neurophysiologists using different electrode designs and amplifier settings, and looking at different species and different brain location, factors that require the use of different features to provide optimal discrimination.

Usefulness for long-term recordings

Until now, widespread long-term recording on the scale of days and months has not been practical because of a variety of technical difficulties (Emondi et al., 2004). IsoI can provide a robust method for investigating the consequences of these problems and for determining recording periods that are stable enough for detailed analysis. In this application, the user would first cluster a minimal n-minute period of the recording, defining cluster boundaries. The duration of this period would then be incrementally augmented and the IsoI measures applied with these same cluster boundaries. With duration increase, the larger set of waveforms will blur the clusters, resulting in lower values of the IsoI measures. With experience, a threshold can be set that defines a distinction between “blurring” and cluster degradation, allowing identification of a time after which we can no longer be confident that the same units are being recorded. At this point, the user will need to recluster and find new cluster boundaries. This incremental “chunk-and-cluster” procedure will allow a quantified interpretation of whether it is reasonable to accept that individual units have been continuously isolated for periods of minutes or possibly hours (days or weeks seem unlikely with current technologies). Note that there will be nothing in this determination to distinguish whether unit appearance has changed or whether new units have been recorded.

Automation

The IsoI measures represent an important step toward spike-sorting automation, which has been investigated previously by multiple groups (Lewicki, 1998; Wheeler, 1999; Shoham et al., 2003; Quiroga et al., 2004). IsoI automates quality control, allowing methods to be developed that use IsoI as a fitness function in machine learning optimization algorithms. IsoI can also be used to determine whether and when the output of an algorithm approaches or exceeds expert efforts. Additional uses of IsoI include using the measures in a real-time system that assigns spikes and periodically prompts the user to adjust cluster boundaries (or recluster) when IsoI values fall below a threshold. Use of IsoI in such an automated manner would require optimizations, such as caching of values in KD trees and a single calculation of optimal dimensions. Once the KD trees and best dimensions are found, nearest neighbors can be found in logarithmic time, proportional to the number of elements in the KD tree. Because a nearest-neighbor lookup will be required for each element in a cluster, the runtime will also scale in proportion to cluster size. The complexity of iterative optimization algorithms would also be proportional to the number of iterations run. Additional development of partial or full automation methods will be a great time savings for many laboratories and also allow for inter-laboratory exchange of data, reducing error and bias.

Importance for neuroscience

Improved understanding of physiological and pathophysiological brain states will require long-term recordings that can determine how individual neurons perform computations over time and across different experimental conditions (Thompson and Best, 1990; Tolias et al., 2007; Dickey et al., 2009). Spike-sorting methods, already widely used for cortical recordings, will find increasing use in determining ensemble activity patterns in subcortical areas as well (Schmitzer-Torbert and Redish, 2004; Bryant et al., 2009). Furthermore, usage can be expected to expand beyond the classical assessments of sensory and place-cell ensembles and begin to look at the pathophysiology of ensemble discoordination and hypercoordination seen in the dynamical brain disorders: epilepsy, Parkinson's disease, and schizophrenia (Olypher et al., 2006; Lytton, 2008).