Skip to main content
NCBI home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2012 Dec 1.
Published in final edited form as: Magn Reson Med. 2011 Apr 26;66(6):1682–1688. doi: 10.1002/mrm.22952

Improved Temporal Resolution in Cardiac Imaging using Through-Time Spiral GRAPPA

Nicole Seiberlich 1,*, Gregory Lee 1, Philipp Ehses 2, Jeffrey L Duerk 1,3, Robert Gilkeson 1, Mark Griswold 1,3
PMCID: PMC3247784  NIHMSID: NIHMS281346  PMID: 21523823

Abstract

Previous work has shown that the use of radial GRAPPA for the reconstruction of undersampled real-time free-breathing cardiac data allows for frame rates of up to 30 images / s. It is well known that the spiral trajectory offers a higher scan efficiency compared to radial trajectories. For this reason, we have developed a novel through-time spiral GRAPPA method and demonstrate its application to real-time cardiac imaging. By moving from the radial trajectory to the spiral trajectory, the temporal resolution can be further improved at lower acceleration factors compared to radial GRAPPA. In addition, the image quality is improved compared to those generated using the radial trajectory due to the lower acceleration factor. Here we show that 2D frame rates of up to 56 images / s can be achieved using this parallel imaging method with the spiral trajectory.

Keywords: spiral, GRAPPA, parallel imaging, non-Cartesian, cardiac imaging, real-time imaging

INTRODUCTION

Non-Cartesian parallel imaging can be employed for fast imaging [1-7], typically allowing acceleration factors between R=2 and R=6 using trajectories such as radial or spiral. However, when working with unoptimized trajectories, the acceleration factors required to scan fast enough to capture the motion of the beating heart often exceed the encoding capabilities of the receiver coil. Previous work has shown that real-time cardiac images can be generated using a novel through-time/through-k-space parallel imaging scheme known as hybrid radial GRAPPA [8]. This method employs a GRAPPA-like k-space data reconstruction technique [9] where acquired lines are multiplied with a GRAPPA weight set in order to reconstruct the missing non-Cartesian points. The GRAPPA weight set for the specific geometry of the undersampled data can be found by using k-space points in a fully-sampled dataset with similar geometry in k-space (through-k-space calibration), or by using several fully-sampled datasets where the proper geometry appears several times through time (through-time calibration). Combining the through-time and through-k-space calibration leads to improved reconstructions in terms of both artifact power and total calibration time. However, in order to get to temporal resolutions of less than 50 ms / image, acceleration factors of greater than R=8 must be used, leading to potential blurring or residual aliasing in the reconstructed images because the receiver coil does not generally support these high acceleration factors.

The burden on the parallel imaging reconstruction can be reduced by either decreasing the acceleration factor or exploring the use of a more efficient k-space trajectory. The spiral trajectory, for example, has previously been used in fast cardiac imaging due to its rapid coverage of k-space [10]. In this work, a specially designed variable density spiral trajectory is employed and undersampled data are reconstructed using a slightly modified version of the novel through-time radial GRAPPA scheme described above. This spiral trajectory allows the acquisition of the complete k-space in approximately 60% of the time of the radial trajectory. Thus, temporal resolutions similar to those reported using the radial trajectory are possible at lower acceleration factors. Additionally, the amount of time required to collect the calibration data is reduced. Because the through-time radial GRAPPA method proposed in Seiberlich [8] is not trajectory specific, it can be used with a few minor modifications to reconstruct the undersampled spiral data. This method is known here as through-time non-Cartesian GRAPPA to reflect the fact that it can be used for any undersampled trajectory. In vivo cardiac images with temporal resolutions of less than 18 ms / image can be reconstructed with high SNR and few residual aliasing artifacts.

METHODS

In vivo cardiac data were acquired in eight healthy volunteers on a Siemens 1.5T Espree scanner (Siemens Medical Solutions, Erlangen, Germany) and 18 receive channels (a six-channel body matrix coil and 12 channels from the spine matrix) in compliance with our institution’s IRB. In order to maintain the standard balanced steady-state free precession (bSSFP) image contrast, we developed a spiral bSSFP trajectory. Due to the need for 0th and 1st moment gradient compensation per TR in the bSSFP sequence, the spiral trajectory was designed to loop back in on itself using code developed by Brian Hargreaves and available at the website http://mrsrl.stanford.edu/~brian/mritools.html to accomplish this gradient compensation as suggested by Nayak [11]. In order to cover the entire 1282 matrix while respecting the Nyquist criterion at the edges of k-space, a total of 48 spiral arms are required. All acceleration factors cited for the spiral trajectory in this manuscript assume that the acquisition of 48 spiral arms corresponds to R=1; 24 arms would be R=2, etc. The density of the spiral arms changes throughout the read out, such that the central 8×8 portion of k-space is fully-sampled using only 4 spiral arms. Outside of this central region, the density decreases linearly with k-space radius. Trajectories were created for a field-of-view (FoV) of 300 mm2 and 250 mm2. Rewinders for 0th and 1st order moment compensation were designedin a time-optimal fashion subject to a gradient slew rate limit of 161.5 mT/m/ms and amplitude limit of 22.8 mT/m [12] (95% of the maximum values of each). Trajectories were measured in the transverse plane using the technique of Duyn [13]. Two shots of the trajectory used for the 300 mm2 FoV are shown in Figure 1; note the variable density nature of the spiral and the rewinder which brings the trajectory back to the center while simultaneously providing 1st moment compensation. With a repetition time of 4.48 ms per arm for the FoV=300 mm2 and 4.78 ms for FoV=250 mm2, the total acquisition time for a single fully-sampled image was 215 ms and 230 ms, respectively. Note that the spiral trajectory requires approximately 60% of the time for a fully-sampled image when compared with the radial trajectory for a 300 mm2 FoV (TR = 2.74 ms, 128 projections) with a total acquisition time of 350 ms. It is important to note that to meet the Nyquist criterion for the radial trajectory, 200 projections are actually needed; thus, the truly full-sampled radial trajectory would require even more time.

Figure 1.

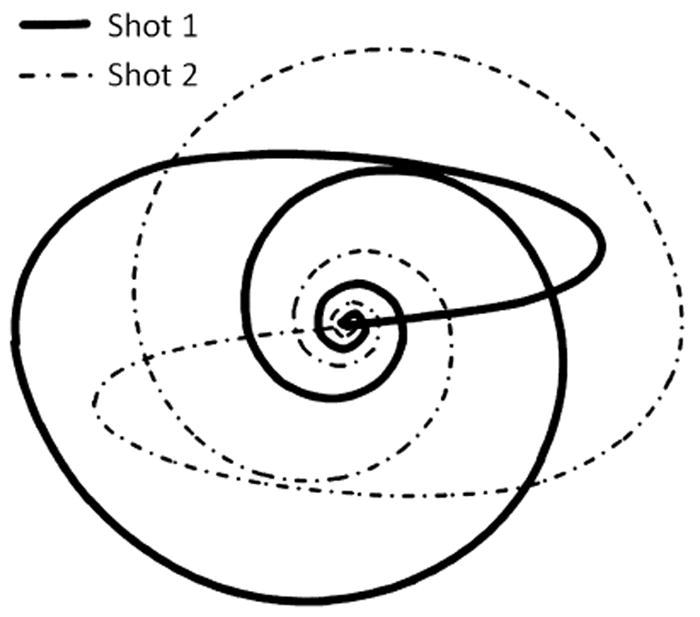
Figure 1

Open in a new tab

Two shots of the variable density, 0th and 1st moment compensated spiral trajectory used for the 300 mm2 FoV. When using only 4 shots, the central 8×8 portion of k-space is fully sampled

Fully-sampled and undersampled data were acquired with the spiral trajectory for both the 300 mm2 and 250 mm2 FoVs. The slice thickness for each of the datasets was 8 mm, the flip angle = 70°, and the TE=TR/2 using the spiral trajectories described above for each of the FoVs. As suggested in Seiberlich [8], a total of 80 calibration frames were acquired during free-breathing with no ECG gating. For the 300 mm2 FoV, the calibration phase took 17.2 s; for the 250 mm2 FoV, calibration required 18.4 s. A total of 100 accelerated undersampled repetitions were acquired with 12, 8, 6, and 4 spiral arms in order to achieve different temporal resolutions (the longest scan required 5.7s at a rate of 57 ms per image, and the shortest 1.8s at a rate of 18 ms per image). As in the fully-sampled data acquisition, the undersampled data were acquired with no gating or breathholding.

The undersampled data were reconstructed using the fully sampled calibration data and hybrid through-time / through-k-space non-Cartesian GRAPPA modified to fit the geometry of the spiral trajectory. The mechanics of this method are depicted schematically in Figure 2. A GRAPPA kernel of size 2 × 3 in the spiral-arm x read direction was used; the 2 × 3 kernel has been suggested previously by Seiberlich [8] and Codella [14]. It is important to note that other direct, non-iterative spiral GRAPPA methods such as those described by Heberlein [6] and Heidemann [7] would be more difficult to implement with this type of data due to the variable density, and thus irregularity, of the spiral data. All 80 calibration frames were used for the determination of the GRAPPA weights. The k-space block size in the through-k-space portion of the hybrid method included 8 points in the read direction to assure that enough information was available for calibration (a total of 80 × 8 = 640 equations for calibration). For the spiral formulation, the calibration blocks extended only in the read-out direction (azimuthally) and not into the spiral arm direction (radially), as in the original formulation of hybrid radial GRAPPA. Because the first 30 points of the trajectory offer a fully-sampled k-space center due to the variable density nature of the sampling, these points were not reconstructed for the missing spiral arms. Additionally, only the portions of the trajectory which spiral out were reconstructed; the 1st moment rewinder bringing the trajectory back to the center of k-space was acquired but not used for the final images. Thus, for the R=6 spiral data, 670 read-out points were reconstructed for each of the 40 missing arms (8 are acquired), leading to a 26,800 total points to be reconstructed. Because each of these points requires a different GRAPPA weight set due to its unique geometry in the dataset, a total of 26,800 blocks is used for calibration and reconstruction in this case. Following reconstruction using hybrid non-Cartesian GRAPPA, images were generated by gridding the now fully-sampled data using NUFFT [15] and the Image Reconstruction Toolbox provided by Jeff Fessler available at the website http://www.eecs.umich.edu/~fessler/code/. In order to demonstrate the severity of the artifacts in the undersampled data, zero-filled images were also generated using NUFFT.

Figure 2.

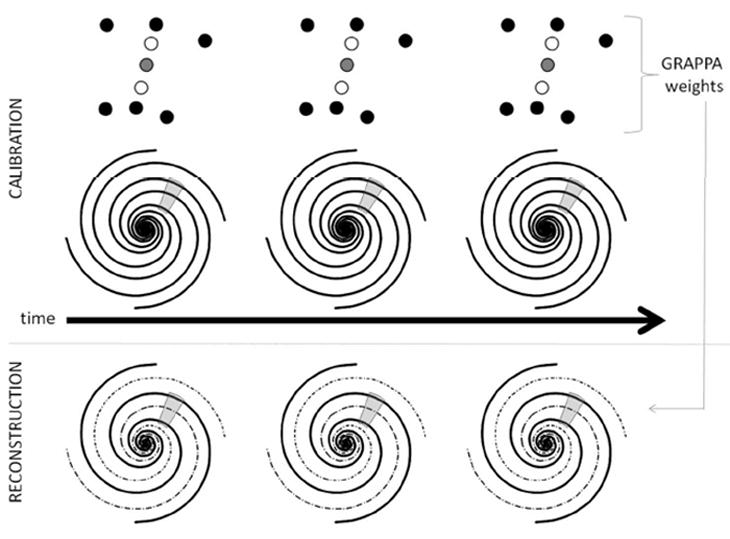
Figure 2

Open in a new tab

A schematic of the through-time non-Cartesian GRAPPA algorithm. A kernel is selected in the fully-sampled spiral k-space (top), where the source points are shown in black and the target point in gray. This segment occurs several times due to the multiple repetitions. Using these occurrences of the GRAPPA kernel through-time, the GRAPPA weights can be determined and then applied to undersampled data at the same geometric location to reconstruct the missing spiral arms (bottom). Hybrid through-time / through-k-space GRAPPA uses the same idea, but supplements kernel occurrences through time with kernel occurrences through-kspace. In this manuscript, the segment size for the through-k-space calibration was 8 points in the read direction in addition to 80 through-time kernel occurrences

In order to compare radial and spiral reconstructions for similar temporal resolutions, radial data were also acquired. As for the spiral data, both the calibration and accelerated acquisition phases were conducted under free breathing with no ECG triggering. The sequence parameters were as follows: FoV = 300mm2, slice thickness = 8 mm, matrix size = 1282, flip angle = 70°, TR=2.74ms, TE=1.37ms, metronome bSSFP radial trajectory (see Seiberlich [8] for details). A total of 80 calibration frames were acquired for the fully-sampled datasets. To match the temporal resolution of ~35 ms and ~18 ms which can be accomplished using the spiral trajectory and 8 or 4 spiral arms, respectively, undersampled datasets with 14 and 8 radial projections were collected for the accelerated acquisitions. The temporal resolutions for these radial datasets are slightly slower than their spiral counterparts (14 radial TRs = 38.4 ms/image vs. 8 spiral TRs = 35.8 ms/image; 8 radial TRs = 21.9 ms/image vs. 4 spiral TRs = 17.9ms/image). Image reconstruction followed using hybrid through-time/through-k-space radial GRAPPA with all 80 calibration frames and block sizes of 8 × 1 in the read × projection directions. Following the parallel imaging, the reconstructed data were gridded as described above.

RESULTS

Images comparing the radial and spiral reconstructions for similar temporal resolutions are shown in Figure 3. The top row contains only radial images and the bottom spiral images. The left block shows images acquired at a temporal resolution of approximately 35 ms and the right block shows images acquired at a temporal resolution of approximately 18 ms; undersampled and zero-filled images appear on the left to demonstrate their severity, and the reconstructions are on the right. For the 35 ms temporal resolution images, which correspond to an undersampling factor of R=9 for the radial data and R=6 for the spiral, the reconstructions for both trajectories yield images with few remaining artifacts. However, when moving to the higher temporal resolution of 18 ms/ image, the radial reconstruction with an acceleration factor of R=16 no longer accurately depicts the anatomy, and the resulting images are blurred. The spiral image corresponding to an acceleration factor of R=12 can still be reconstructed without significant residual aliasing artifacts. Note the blurring of the fat in the chest wall in the spiral images compared to the radial images due to the longer readout window of the spiral sequence.

Figure 3.

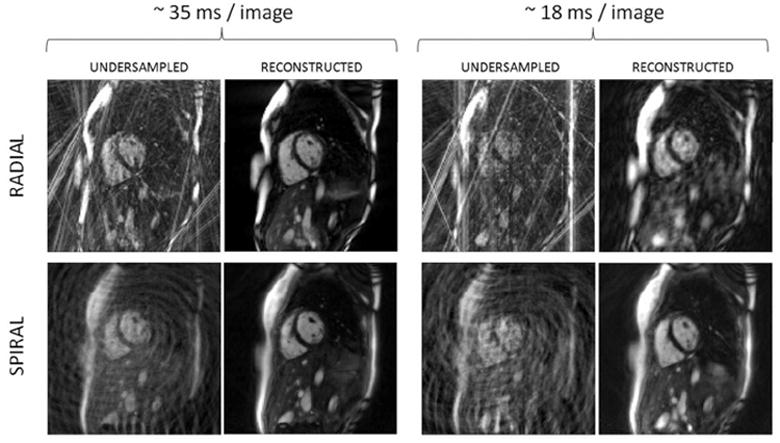
Figure 3

Open in a new tab

Example undersampled and reconstructed radial (top row) and spiral images (bottom row). The left group of images has a temporal resolution of ~35 ms, and the right ~18 ms. Undersampled and zero-filled images are shown to the left of each reconstructed image to illustrate the degree of the undersampling artifacts

Representative hybrid through-time/through-k-space spiral GRAPPA reconstructions over an entire heartbeat for the 300 mm2 and 250 mm2 FoV are shown in Figures 4 and 5. Figure 4 shows example images reconstructed using only four spiral arms (R=12) with a temporal resolution of 17.9 ms / image. Note that the entire heartbeat for the four arm images lasts for 50 frames, so only portions of a single heart beat are shown here (every fifth image is depicted). In order to demonstrate the quality of these images when examined sequentially, a movie showing the series of images from Figure 4 can be accessed here: Figure 5 shows an image reconstructed from 6 spiral arms (an acceleration factor of R=8) using the trajectory for the FoV = 250 mm2. Every fourth image over a single heartbeat is shown in this image. Note that even at this higher resolution (1.95 mm in plane resolution), it is still possible to generate images with a high temporal resolution (28.7 ms / image) without residual aliasing artifacts. Due to the limited time frame of data shown in these figures, breathing motion cannot be appreciated; when acquiring data over more than 4 or 5 seconds, the motion of the heart due to the displacement of the lungs can also be clearly observed.

Figure 4.

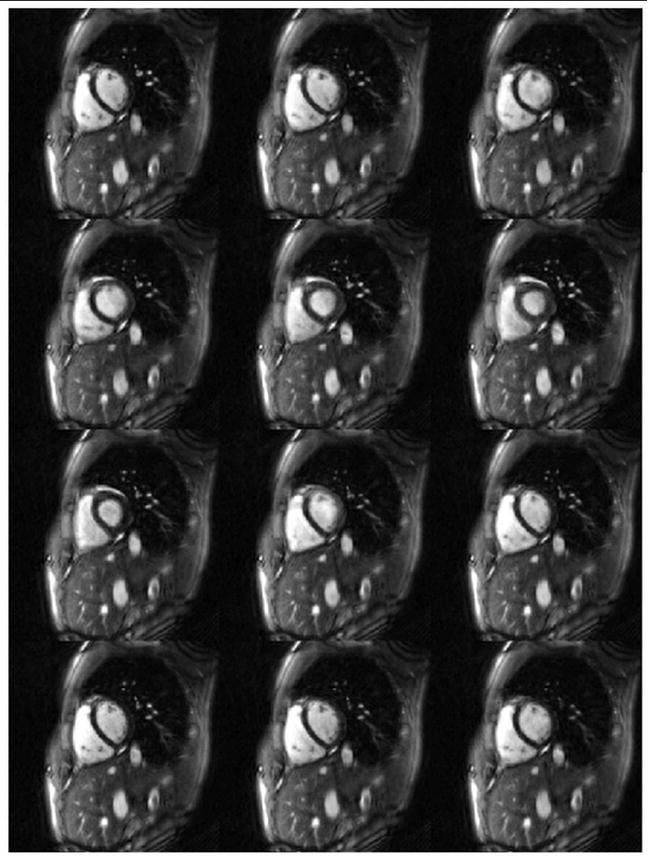
Figure 4

Open in a new tab

Example 300 mm2 FoV images reconstructed using 4 spiral arms (R=12), 80 fullysampled calibration frames, and a segment size of 16 in the read direction. Every fifth reconstructed image is shown here. Note the removal of aliasing artifacts despite the high temporal resolution (17.9 ms / image

Figure 5.

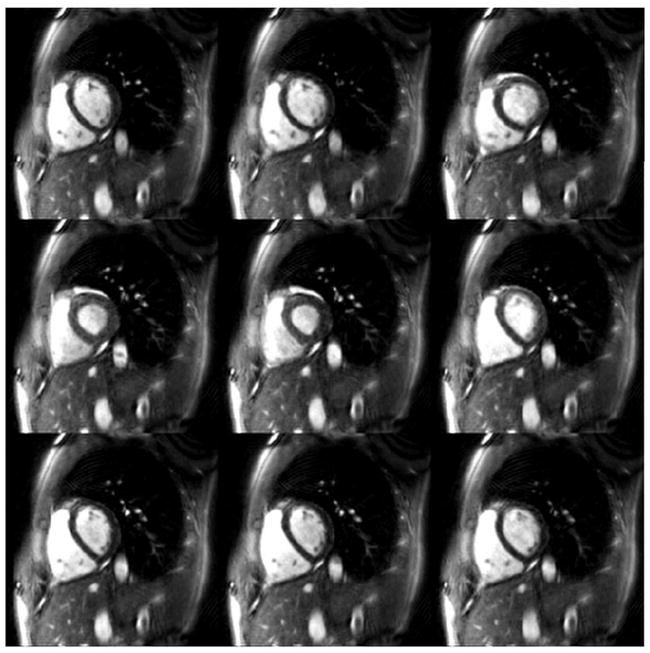
Figure 5

Open in a new tab

Example 250 mm2 FoV images reconstructed using 6 spiral arms (R=8), 25 fully-sampled calibration frames, and a segment size of 16 in the read direction. Every fourth reconstructed image is shown here. This figure demonstrates that a high temporal resolution (28.7 ms / image) can be achieved in combination of spatial resolutions of higher than 2 mm in plane.

DISCUSSION

Hybrid through-time/through-k-space spiral GRAPPA has been used to generate in vivo cardiac images using data acquired in less than 18 ms / image, allowing for true real-time cardiac imaging with no view sharing. This method requires additional fully-sampled calibration frames in order to determine the GRAPPA weights for the reconstruction, but these frames can be acquired in less than 6 seconds per slice. Because the volunteer or patient is allowed to breathe freely during the examination and no ECG gating is required and neither the 18 second calibration time nor the acquisition of several cardiac cycles worth of undersampled data is burdensome. Since the spiral trajectory covers the same area of k-space in approximately 60% of the time of a radial scan, lower acceleration factors can be used for similar temporal resolutions; whereas an acceleration factor of R=9 is required to collect radial data with a temporal resolution of 35 ms / image, only R=6 is required for the spiral trajectory and the same temporal resolution. This reduction in acceleration factor means that the images using the spiral trajectory will in general demonstrate fewer residual artifacts and a higher SNR at a fixed temporal resolution, or the frame rate can be further increased at a similar level of artifacts and SNR. The fastest temporal resolution shown here, 17.9 ms/image, required an acceleration factor of R=12 (a total of 4 spiral arms in relation to the fully-sampled 48), which is at the limit of the encoding capability of the receiver array used here. For the radial trajectory at the same temporal resolution, an acceleration factor of R=16 was needed and demonstrated significant artifacts.

The current implementation of the spiral trajectory does pose some challenges. Because the spiral arms do not “line up” like the radial projections, forming calibration segments along the spiral arm direction is more difficult for the spiral than for the radial. All of the images shown in this manuscript were generated using segments along only the read direction. This limitation means that more through-time repetitions of the fully-sampled dataset are required to yield enough occurrences of the GRAPPA kernel to allow accurate reconstruction. This issue could be alleviated by interpolating along the acquired spiral arms to generate additional points which do “line up” along the projection direction (as performed by Heidemann [7]).

Another potential limitation of the current study is that the form of the spiral trajectory as implemented depends on the FoV and the gradient system, and is currently determined off-line. For this work, two FoV sizes were selected (250 and 300 mm), and these two sets of trajectories were used exclusively. The fixed FoV sizes and trajectories did not pose any problems for the cardiac imaging performed here, but a method of generating and measuring spiral trajectories with the necessary requirements (0th and 1st moment balanced, maximum gradient strength and slew rate not exceeded, center of k-space oversampled, short TR) on the scanner for arbitrary FoVs would increase the utility of such a trajectory in a clinical setting.

The images shown here were acquired using the spiral bSSFP sequence, which places certain constraints on the form of the spiral. The TR of the sequence is relatively long for bSSFP (4.48 and 4.78 for the 300 and 250 mm2 FoVs, respectively), which can lead to banding in areas close to air-tissue boundaries, which can be appreciated in Figures 3 through 5. Faster imaging could be performed using the FLASH sequence with a modified spiral trajectory, which would no longer require the rewinding needed for the bSSFP sequence. Using FLASH would also remove the banding artifacts, and may be more practical when moving to higher field strengths than the 1.5T used here. However, due to the improved contrast between the blood and tissue in bSSFP for cardiac imaging compared to FLASH, the work here has focused on the bSSFP sequence.

While a set number of 80 frames was used for calibration based on previous work by our group [8], this number could be reduced. It is important to note that the 640 calibration equations per block is more than required to solve for the 108 unknowns in each GRAPPA weight set; theoretically, only 108 equations are needed. However, if fewer equations than unknowns are used to determine the GRAPPA weights, the resulting images will start to resemble the calibration images. This happens because the calibration data is effectively copied into the undersampled data when the calibration equations become underdetermined. In order to assure that the GRAPPA weights are appropriately calibrated for the through-time spiral GRAPPA cardiac examples shown here, a large number of calibration frames were acquired and employed. The actual factor by which the equations must be overdetermined has not been explored here and could be affected by other factors such as the SNR of the calibration data or the coil configuration used.

In many other dynamic parallel imaging methods with high acceleration factors, a strong noise enhancement due to the g-factor is observed. However, the smaller noise enhancement in through-time radial and spiral GRAPPA can be potentially understood by examining several factors. When the total acceleration factor is high, most of the k-space energy is actually captured in the fully-sampled center of k-space in the variable density acquisition scheme used here, and only the very outer portions of k-space has the maximum acceleration factor. The authors hypothesize that this leads to a significantly smaller SNR loss for the reconstructed radial and spiral images as compared to the more standard Cartesian acquisitions. Due to the variable density nature of the spiral trajectory, the maximum acceleration factor occurs only for the outer portions of k-space. For instance, in the R=8 spiral examples shown here, the average acceleration factor over the entire undersampled k-space is approximately R=4.33. Thus, while the acquisition requires only one eighth of the time of the fully-sampled spiral trajectory, the k-space covered still corresponds to a factor of R=4.33 according to the Nyquist criterion. Additionally, the g-factor losses that are present are more diffuse than in the Cartesian case because the aliasing in the non-Cartesian images is less coherent [16]. Thus, even at high acceleration factors, the reconstructed spiral images should not necessarily be expected to be coupled with a strong local noise enhancement. These hypotheses for the high signal level of the reconstructions are based on observations from the trajectory and average acceleration factor, and a more rigorous examination of the noise characteristics of the through-time GRAPPA method must be performed to validate these ideas.

While only short-axis cardiac images have been shown here, the spiral trajectory and hybrid through-time/through-k-space non-Cartesian GRAPPA method demonstrated can be used to depict anatomy other than the heart. Additionally, although a variable density spiral was used here, the parallel imaging reconstruction can be applied to many other trajectories. Thus, the hybrid non-Cartesian GRAPPA method is widely applicable and can be used for real-time imaging when frame rates as high as 56 images/s are required.

CONCLUSION

The hybrid through-time / through-k-space non-Cartesian GRAPPA method can be used to acquire images in real-time for cardiac imaging. In vivo short-axis bSSFP undersampled spiral datasets were used to generate cardiac images with temporal resolutions of 17.9 ms to 35 ms with no need for breathholding or ECG gating, and the entire imaging process required less than 22 seconds (approximately 18s for calibration followed by 4 s of data acquisition). This method can be applied to anatomy besides the heart and to trajectories besides the variable density spiral used here, making it a flexible option for real-time MRI.

Supplementary Material

Supp Movie S1
Download video file (30.4MB, avi)

Acknowledgments

The Case Center for Imaging Research MRI research group acknowledges support from SiemensMedical Solutions, Erlangen, Germany. This work was funded in part by NIH/NIBIB grants 1K99EB011527-01 and 1RO1HL094557. The authors would like to thank Dr. Vikas Gulani for his helpful comments.

References

  • 1.Griswold MA, Heidemann RM, Jakob PM. Direct parallel imaging reconstruction of radially sampled data using GRAPPA with relative shifts. Proceedings of the 11th Annual Meeting of the ISMRM; Toronto, Canada. 2003. p. 2349. [Google Scholar]
  • 2.Griswold MA, Blaimer M, Heidemann RM, Speier P, Kannengeiser S, Nittka M, Breuer F, Mueller M, Jakob PM. Rapid Evaluation of CardiacFunction Using Undersampled Radial TrueFISP with GRAPPA. Proceedings of the 12th Annual Meeting of the ISMRM; Kyoto, Japan. 2004. p. 737. [Google Scholar]
  • 3.Pruessmann KP, Weiger M, Boernert P, Boesiger P. Advances in sensitivity encoding with arbitrary k-space trajectories. Magn Reson Med. 2001;46:638–651. doi: 10.1002/mrm.1241. [DOI] [PubMed] [Google Scholar]
  • 4.Yeh EN, McKenzie CA, Ohliger MA, Sodickson DK. Parallel magnetic resonance imaging with adaptive radius in k-space (PARS): constrained image reconstruction using k-space locality in radiofrequency coil encoded data. Magn Reson Med. 2005 Jun;53(6):1383–92. doi: 10.1002/mrm.20490. [DOI] [PubMed] [Google Scholar]
  • 5.Seiberlich N, Breuer F, Heidemann R, Blaimer M, Griswold M, Jakob P. Reconstruction of undersampled non-Cartesian data sets using pseudo-Cartesian GRAPPA in conjunction with GROG. Magn Reson Med. 2008 May;59(5):1127–37. doi: 10.1002/mrm.21602. [DOI] [PubMed] [Google Scholar]
  • 6.Heberlein K, Hu X. Auto-calibrated parallel spiral imaging. MagnReson Med. 2006 Mar;55(3):619–25. doi: 10.1002/mrm.20811. [DOI] [PubMed] [Google Scholar]
  • 7.Heidemann RM, Griswold MA, Seiberlich N, Kruger G, Kannengiesser SA, Kiefer B, Wiggins G, Wald LL, Jakob PM. Direct parallel image reconstructions for spiral trajectories using GRAPPA. Magn Reson Med. 2006 Aug;56(2):317–26. doi: 10.1002/mrm.20951. [DOI] [PubMed] [Google Scholar]
  • 8.Seiberlich N, Ehses P, Duerk J, Gilkeson R, Griswold M. Improved radial GRAPPA calibration for real-time free-breathing cardiac imaging. Magn Reson Med. 2011 Feb;65(2):492–505. doi: 10.1002/mrm.22618. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.Griswold MA, Jakob PM, Heidemann RM, Nittka M, Jellus V, Wang J, Kiefer B, Haase A. Generalized autocalibrating partially parallel acquisitions (GRAPPA) Magn Reson Med. 2002 Jun;47(6):1202–10. doi: 10.1002/mrm.10171. [DOI] [PubMed] [Google Scholar]
  • 10.Meyer CH, Hu BS, Nishimura DG, Macovski A. Fast spiral coronary artery imaging. Magn Reson Med. 1992;28:202–213. doi: 10.1002/mrm.1910280204. [DOI] [PubMed] [Google Scholar]
  • 11.Nayak KS, Hargreaves BA, Hu BS, Nishimura DG, Pauly JM, Meyer CH. Spiral balanced steady-state free precession cardiac imaging. Magn Reson Med. 2005 Jun;53(6):1468–73. doi: 10.1002/mrm.20489. [DOI] [PubMed] [Google Scholar]
  • 12.Hargreaves BA, Nishimura DG, Conolly SM. Time-optimal multidimensional gradient waveform design for rapid imaging. Magn Reson Med. 2004 Jan;51(1):81–92. doi: 10.1002/mrm.10666. [DOI] [PubMed] [Google Scholar]
  • 13.Duyn JH, Yang Y, Frank JA, van der Veen JW. Simple correction method for k-space trajectory deviations in MRI. J Magn Reson. 1998 May;132(1):150–3. doi: 10.1006/jmre.1998.1396. [DOI] [PubMed] [Google Scholar]
  • 14.Codella NC, Spincemaille P, Prince M, Wang Y. A radial self-calibrated (RASCAL) generalized autocalibrating partially parallel acquisition (GRAPPA) method using weight interpolation. NMR Biomed. 2010 Dec 28; doi: 10.1002/nbm.1630. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Fessler JA. On NUFFT-based gridding for non-Cartesian MRI. J Magn Reson. 2007 Oct;188(2):191–5. doi: 10.1016/j.jmr.2007.06.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Breuer FA, Kannengiesser SA, Blaimer M, Seiberlich N, Jakob PM, Griswold MA. General formulation for quantitative G-factor calculation in GRAPPA reconstructions. Magn Reson Med. 2009 Sep;62(3):739–46. doi: 10.1002/mrm.22066. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supp Movie S1
Download video file (30.4MB, avi)

RESOURCES