Modelling population-based cancer survival trends using join point models for grouped survival data

Summary

In the United States cancer as a whole is the second leading cause of death and a major burden to health care, thus the medical progress against cancer is a major public health goal. There are many individual studies to suggest that cancer treatment breakthroughs and early diagnosis have significantly improved the prognosis of cancer patients. To better understand the relationship between medical improvements and the survival experience for the patient population at large, it is useful to evaluate cancer survival trends on the population level, e.g., to find out when and how much the cancer survival rates changed. In this paper, we analyze the population-based grouped cancer survival data by incorporating joinpoints into the survival models. A joinpoint survival model facilitates the identification of trends with significant change points in cancer survival, when related to cancer treatments or interventions. The Bayesian Information Criterion is used to select the number of joinpoints. The performance of the joinpoint survival models is evaluated with respect to cancer prognosis, joinpoint locations, annual percent changes in death rates by year of diagnosis, and sample sizes through intensive simulation studies. The model is then applied to the grouped relative survival data for several major cancer sites from the Surveillance, Epidemiology and End Results (SEER) Program of the National Cancer Institute. The change points in the survival trends for several major cancer sites are identified and the potential driving forces behind such change points are discussed.

1. INTRODUCTION

In recent decades, there has been considerable progress against cancer due to improvement in treatment, the development of cancer prevention, and the dissemination of early diagnosis and cancer screening techniques. These medical advances improved both the quality of life and the length of survival, permitting many survivors to continue full and productive lives. Joinpoint models (Kim et al. 2000) have been used to characterize cancer trends and progress as connected linear segments. The Cancer Statistics Review (Ries et al. 2006), an annual publication of the NCI, reports the trends of cancer incidence and mortality rates, using the joinpoint models. First issued in 1998, the Annual Report to the Nation, a collaboration among the NCI, the Centers for Disease Control and Prevention (CDC), the American Cancer Society (ACS), and the North American Association of Central Cancer Registries (NAACCR), also provides updated information on cancer incidence and mortality rates in the United States obtained from the joinpoint models. These trends help in understanding the impact of cancer control and interventions on cancer incidence and mortality. However, there is no analogous method for reporting trends in cancer survival, which is also an important measure for monitoring and evaluating the impact of early diagnosis and treatment breakthroughs.

Medical breakthroughs impact survival of patients diagnosed in a specific time frame. Including the joinpoints into the survival models enables us to identify and evaluate the impact of important medical breakthroughs. Feuer et al. (1991) and Weller et al. (1999) have modeled the impact of treatment breakthroughs on survival in testicular cancer and Hodgkins disease using joinpoint regression. In their work two joinpoints occur when a medical development is changing survival as a function of the year of diagnosis; the first joinpoint when the intervention is introduced, and the second one is when survival levels off, indicating the end of dissemination through the population. However, they only assumed a fixed number of joinpoints and do not solve the more general problem of determining the number of joinpoints. In this article, we extend the use of the joinpoint model to the population-based grouped survival data from the SEER Program. The main goal of the Joinpoint survival model (JPSM) is to describe the trends in cancer survival, i.e., to find out when the cancer survival starts to change its improvement pattern; and, if there is a leveling off of such realized improvement, how much of an improvement was finally attained.

The rest of the paper is organized as follows. In Section 2, we describe the importance and challenges of modeling the trends in population-based cancer survival. In Section 3, we propose the JPSM for population-based grouped cancer survival data, and describe the estimation method and the model selection criteria. While mainly developed for population-based grouped survival data, the method could also be applied to any arbitrary interval-censored survival data. Extensive simulation studies are carried out to assess the performance of the JPSMs in Section 4. In Section 5, the JPSMs are applied to the grouped cancer survival data for several major cancer sites from the SEER Program. Finally, the advantages and the utilities of the JPSMs are discussed.

2. TRENDS IN POPULATION-BASED CANCER SURVIVAL

Information on the survival of cancer patients after diagnosis is a key indicator of cancer control, alongside the cancer incidence and mortality. Such information is also required to plan and evaluate health services. This information can only be derived from population-based cancer registries (Coleman et al., 2003). Because the United States has no centralized data system for health outcomes, the effect of new treatment on the US population for potentially fatal diseases must be inferred from administrative records. The Surveillance, Epidemiology, and End Results (SEER) Program of the NCI is an authoritative source of information on cancer incidence and survival in the U.S. SEER currently collects and publishes cancer incidence and survival data from population-based cancer registries.

The SEER registries routinely collect data on patient demographics, primary tumor site, morphology, stage at diagnosis, first course of treatment, follow-up for vital status, etc. The SEER Program began collecting data on cancer cases in 1973, in the states of Connecticut, Iowa, New Mexico, Utah, and Hawaii and the metropolitan areas of Detroit and San Francisco-Oakland. In 1974–1975, the metropolitan area of Atlanta and the 13-county Seattle-Puget Sound area were added. These original 9 regions are referred to as the SEER 9 registries, covering 10% of the US population.

The population-based cancer survival data are typically grouped into annual or monthly intervals by the time after cancer diagnosis. With the ageing of populations, the number and proportion of elderly cancer patients keep rising. One challenge of the population-based cancer survival data is that competing risks of death other than cancer are common among cancer patients. When we evaluate the progress and trend in cancer survival, it is ideal that the confounding effects of death from other causes are removed. The cancer net survival is a hypothetical quantity that measures the excess mortality due to the cancer of interest as if other causes of death are eliminated. There are two common measures of net survival, namely, the cause-specific survival and the relative survival. In cause-specific survival analysis, the cause of death is identified and used. The event is the death due to the cancer of interest and the people dying from other causes or lost to follow-up are considered as censored. By modeling the trends of population-based cancer survival, the results are representative of the general population in the U.S. and thus can be used to evaluate the effectiveness of cancer treatment and services.

The cause-specific survival analysis requires accurate information on cause of death. The accuracy of death certificates for determining the underlying cause of death is problematic in some situations (Percy 1981). An alternative method of estimating cancer net survival is to use the relative survival ratio (Ederer et al. 1961), defined as the observed survival proportion in the patient group divided by the expected survival rate of a comparable group from the general population, who are assumed to be practically free of the cancer of interest. Both measures estimate the same conceptual quantity, i.e., cancer specific net survival, although in different ways. The major advantage of the relative survival is that the information on cause of death is not required, thereby circumventing problems with the inaccuracy or nonavailability of death certificates. Thus, the relative survival is a common metric used in the population-based cancer survival studies.

3. JOINPOINT SURVIVAL MODEL

Let x be the calendar time, which reflects the possible change point of cancer survival trends. In cancer survival studies, the survival time is usually defined as the time from diagnosis to death. We assume that the hazard rate of dying at time t follows a proportional hazards model with

$$\lambda (t\mid x)={\lambda }_0(t)exp\{h(x)\},$$ (1)

where λ₀(t) is the baseline hazard and

$$h(x)=\beta x+\sum _{k=1}^K{\delta }_k{(x-{\tau }_k)}^{+}+{\gamma }^{\prime }z,$$ (2)

indicates the trend of survival with respect to calendar time x. Here, u⁺ = u if u > 0 and = 0 otherwise. Throughout the paper, we use x to denote the year of diagnosis. The other covariates z, e.g., race, sex, and comorbidity status, can also be included in h(x). For simplicity, we omit the covariate z from now onwards. In the model, the regression parameters are β, δ₁, …, δ_K. The τ₁, …, τ_K are called the joinpoints because the function h(x) is continuous at, but has different slopes before and after, τ₁, …, τ_K. The continuity constraint on h(x) at the joinpoints is more realistic as the effect of the new treatment or intervention on the hazard rate usually takes place gradually. We call the survival model, with h(x) defined as in (2), a K-joinpoint JPSM. There are a total of (K + 1) segments, and for the k-th segment, the slope coefficient is ${\beta }_k=\beta +{\sum }_{l=1}^{k-1}{\delta }_l$, k = 1, …, K + 1.

The baseline hazard λ₀(t) can be modeled, for example, by a time-dependent function such as regression spline (Rosenberg 1995). Some have considered modeling λ₀(t) using one discontinuous change point, see, for example, Liang et al. (1990), Luo et al. (1997) and Lim et al. (2002), among others. Recently, Goodman et al. (2006) considered a multiple change point model and a multiple joinpoint model for the baseline hazard. So far, there is no literature on the multiple joinpoint models for the survival trends with respect to calendar year. Here we focus on modeling the secular trend in cancer survival by introducing joinpoints following the calendar time of cancer diagnosis and the baseline hazards are model by a nonparametric step function.

For the population-based cancer survival data, e.g., the SEER survival data, the survival times after diagnosis are usually grouped into intervals I_j = [t_j−1, t_j), j = 0, …, J, where t₀ = 0, and t_J is the end of the follow-up. We call it grouped survival data. The death rate during the interval I_j given that a patient is alive at the beginning of the interval is

$${\lambda }_j(x)=P(T<t_j\mid T\ge t_{j-1};x)=1-\frac{S(t_j\mid x)}{S(t_{j-1}\mid x)},j=1,\dots ,J.$$ (3)

Under the proportional hazards assumption, the survival function is given by

$$S(t\mid x)=S_0{(t)}^{exp\{h(x)\}},$$ (4)

where S₀(t) is the baseline survival function, and

$$log\left\{-log\left[1-{\lambda }_j(x)\right]\right\}=log\left\{-log\left[\frac{S_0(t_j)}{S_0(t_{j-1})}\right]\right\}+h(x).$$ (5)

Let ${\alpha }_j=log\left\{-log\left[\frac{S_0(t_j)}{S_0(t_{j-1})}\right]\right\}$. Then, the baseline survival function can be expressed as $S_0(t_j)=exp[-{\sum }_{l=0}^j{e}^{{\alpha }_l}]$.

When there is no joinpoint, h(x) = βx and we have $exp(\beta )=\frac{log(1-{\lambda }_j(x+1))}{log(1-{\lambda }_j(x))}$. If the death rates λ_j(x) are small for j = 1, …, J, then $exp(\beta )-1\approx \frac{{\lambda }_j(x+1)-{\lambda }_j(x)}{{\lambda }_j(x)}$. Thus, [exp(β)−1]100% can be interpreted as the annual percent change (APC) of the death rates, λ_j(x), with respect to the diagnosis year x. A negative value of the APC means that the death rates λ_j(x) decrease as x increases. When h(x) is defined by a joinpoint model (2), the APC of the death rates in the k-th segment is APC_k = [exp(β_k) − 1]100%. Because we did not assume interaction between covariates z and diagnosis year x, so the APC values are the same for different covariate levels. The collection of the parameters are denoted by θ = (α, β, δ, τ)^T, where α = (α₁, …, α_J), δ = (δ₁, …, δ_K), τ = (τ₁, …, τ_K).

3.1. The Likelihood function for the grouped cancer survival data

For the patient cohort diagnosed in the year x, let n_xj be the number of people alive at the beginning of interval I_j, let d_xj be the number of cancer deaths and let l_xj be the number of patients lost to follow-up or dying from other causes in interval I_j. By the actuarial assumption (Gail, 1975), the adjusted number of person-years at risk is $r_{xj}=n_{xj}-\frac{1}{2}{l}_{xj}$ and the number of cancer deaths in I_j follows a binomial distribution, i.e., d_xj ~ Bin(r_xj, λ_j(x)). Hence, the likelihood function for the cause-specific grouped survival data = {x, (r_xj, d_xj), j = 1, …, J} is

$$L(\mathit{\theta }\mid \mathcal{D})=\prod _x\prod _{j=1}^J{\left\{{\lambda }_j(x)\right\}}^{d_{xj}}{\left\{1-{\lambda }_j(x)\right\}}^{r_{xj}-d_{xj}}.$$ (6)

In relative survival analysis, the cause of death is not used. Let d_xj denote the number patients dying from all causes and l_xj denote the number of patients lost to follow-up during interval I_j. The conditional probability of surviving the interval I_j from all causes is p_j(x)E_j(x), where p_j(x) = 1 − λ_j(x) is the interval relative survival probability and E_j(x) is the expected probability of surviving interval I_j for the general population. We assume that d_xj follows a binomial distribution d_xj ~ Bin(r_xj, 1 − p_j(x)E_j(x)). The likelihood function for the relative survival data 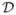= {x, (r_xj, d_xj, E_xj), j = 1, …, J} is

$$L(\mathit{\theta }\mid \mathcal{D})=\prod _x\prod _{j=1}^J{\left\{1-p_j(x)E_j(x)\right\}}^{d_{xj}}{\left\{p_j(x)E_j(x)\right\}}^{r_{xj}-d_{xj}}.$$ (7)

Here, E_j(x) are calculated from the life tables for the matched general population (National Center for Health Statistics, 2003).

3.2. Parameter estimation

When the covariates are fixed, the likelihood functions (6) and (7) correspond to generalized linear models with complementary log-log link function. For this case, the estimation methods are described by Prentice and Gloeckler (1978), and Hakulinen and Tenkanen (1987). For the general interval-censored survival data, the Expectation-Maximization algorithm has been proposed by Goetghebeur and Ryan (2000). If the locations of the joinpoints, τ₁, …, τ_K, are known, then (x − τ₁)⁺, …, (x − τ_K)⁺ are fixed and the above available methods apply. When the locations of the joinpoints are not known, we can use the grid search method (Lerman 1980) to find the estimates of joinpoints. We assume that the joinpoints only occur at the observed data points, i.e., τ_k ∈ Ξ, k = 1, …, K, where Ξ is the set of observed x values. Let ℓ(θ) = log L(θ| 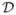) be the loglikelihood function. First the loglikelihood is maximized for fixed values of τ = (τ₁, …, τ_K) and the associated estimates of (α, β, δ) are denoted by (α̂_τ, β̂_τ, δ̂_τ). The maximum loglikelihood value of ℓ(θ) for given τ is a profile loglikelihood. All possible combinations of the joinpoints are tried by grid search and the maximum likelihood estimates (MLEs) of the joinpoints, τ̂ are the values that maximize ℓ_τ. Thus, the MLE of the parameters is θ̂ = (α̂_τ̂, β̂_τ̂, δ̂_τ̂, τ̂).

The asymptotic distribution theory in the joinpoint regression has been proved by Feder (1975a,b). With this approach, ℓ_max is the maximum value of ℓ_τ and ℓ_τ (τ₁, …, τ_K|τ_k = x) is the maximum value of ℓ_τ conditional on τ_k = x. Then the 100(1−q)% confidence interval (CI) for τ_k includes the x values such that

$$-2\left\{{\ell }_{\mathit{\tau }}({\tau }_1,\dots ,{\tau }_K\mid {\tau }_k=x)-{\ell }_{max}\right\}\le {({\chi }_1^2)}^{-1}(q),$$ (8)

where ${({\chi }_1^2)}^{-1}(q)$ is the quantile function of a chi-squared distribution with one degree of freedom.

Feder (1975b, p.53) proved that when the number of data points n goes to infinity, the MLE θ̂ has the same asymptotic normal distribution as the estimates for the data with a small number of observations deleted near the true joinpoints. In practice, the standard errors of the MLEs (α̂, β̂, δ̂) are estimated by fitting the JPSM after deleting the data points that are on the estimated joinpoints τ̂₁, …, τ̂_K (Lerman 1980; Feder 1975b). The standard errors for the slopes β̂_k, k = 1, …, K +1, and that of the estimated survival function S(t|x, θ̂) can be calculated from the delta method using Equations (4) and (2). The CIs for β_k are obtained from the normal approximation and the CIs for APC_k can be transformed from the CIs for β_k, k = 1, …, K + 1. Kim et al. (2006) have showed by simulations that the CIs for β̂ from this approach have good coverage rates. In practice, we limit the maximum number of joinpoints to 3 because the patient’s survival usually improves gradually and changes in survival are few in number. Also, we impose the restriction that two joinpoints may not be too close to each other and that a joinpoint may not occur too early or too late in the study period. We also restrict that, after excluding the joinpoints, the minimum number of data points between two consecutive joinpoints is 2 and that the minimum number of data points from a joinpoint to either end of the data is 2.

3.3. Model selection

There are several methods available for model selection, such as the Akaike’s information criterion (AIC) (Akaike 1973) and the Bayesian Information Criterion (BIC) (Schewarz 1978). The AIC tends to over fit the true model and the BIC is consistent when the number of true covariates does not increase with the sample size (Yang 2006; Zheng and Loh 1995). The BIC has been used for selecting the number of joinpoints in Bayesian models (Tiwari et al. 2005). Kim et al. (2000) used permutation tests for model selection in the joinpoint models for rates and proportion. The permutation-test based (PTB) model selection approach consists of a series of permutation tests for H₀: K = k₀ against H₁: K = k₁ by permuting the residuals. The PTB model selection method has been developed for the joinpoint model for cancer incidence and mortality rates by the NCI (http://srab.cancer.gov/joinpoint).

The PTB approach can also be used to select the number of joinpoints in JPSM. Let λ̂_j(x) be the predicted value of λ_j(x) in (3) under the null model. The predicted value for the number of deaths d_xj is given by d̂_xj = r_xjλ̂_j(x) and its variance V_xj = r_xjλ̂_j(x){1 − λ_j(x)}. Then the residuals d̂_xj − d_xj are standardized to e_xj with mean 0 and variance 1. The permuted residuals, $e_{xj}^{\ast }$ are added back to create permuted samples $d_{xj}^{\ast }$, where

$$d_{xj}^{\ast }={\widehat{d}}_{xj}+r_{xj}^{\ast }\sqrt{V_{xj}}.$$

Let F( 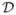) be the F-type statistic for testing the difference between the null and alternative model using the original data 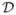. Because the joinpoints are estimated, F( 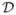) no longer follows an asymptotic F distribution, and its empirical distribution has to be estimated from the permuted sample 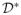. The p-value is the proportion of times that F( 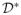) > F( 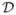) over a large number of permutations.

However, it is computationally too intensive to use the PTB approach for the survival data in practice. There are two major contributions of the difference in computation time using the PTB approach for model selection on survival data and for age-adjusted mortality and incidence rates (Kim et al. 1999). First, fitting a linear trend for grouped survival data involves maximizing the loglikelihood (6) or (7), which is an iterative calculation and thus is much slower than the simple linear regression for rates. Second, there is only one observation of rates per year for incidence and mortality, but L observations of follow-up intervals for survival for each diagnosis year, where L is the difference between the diagnosis year and the end of follow-up. For example, for the people diagnosed from 1975 to 2002 with study cutoff date December 31, 2002, the maximum follow-up time is 27 years for the people diagnosed in 1975, and there is one less year follow-up for each diagnosis year ahead. In total there are 27+26+···+1=378 observations. In contrast, there are only 28 observations of incidence or mortality rates for 1975 to 2002. To fit a single JPSM with fixed joinpoints it takes from 1000 to 5000 times longer with survival data than with a series of incidence or mortality data, depending on the number of joinpoints and the number of iterations necessary. To permute 378 observations takes about 75 times longer than permuting 28 observations. Since the fit of the JPSM’s are nested within the permutations, the computing time for fitting a PTB survival model is therefore from (1000×75)=75,000 to (5000×75)=375,000 times longer than for an analogous incidence or mortality model. For a typical problem, it takes 5 seconds for incidence or mortality data to select from 0–3 joinpoints using a PTB approach with 4499 permutations using a Pentium (R) 4 3.00GHz CPU and 1.00G RAM, and it would take about 22 days to fit the analogous survival model. Hence, the permutation test is not practical for fitting JPSMs.

Alternatively, BIC is often used as a model selection criterion in frequentist settings (Burham and Anderson, 2004). Based on an empirical study, Kim et al. (2006) compared the BIC with the PTB approach and found that, although liberal, the BIC approach is much less computationally intensive and is a strong competitor of the PTB approach. The AIC is even more liberal, and tends to pick a higher number of joinpoints. Therefore, we use the BIC for model selection. Let M_K denote a K-joinpoint model and let ℓ_K be the maximum loglikelihood value of model M_K as defined in (6) or (7), then

$$\mathit{BIC}(M_K)=-2{\ell }_K+p_{K}logn,$$ (9)

where n is the total number of follow-up years for all diagnosis years and p_K is the number of parameters under model M_K. For JPSM M_K with a maximum J years of follow-up, p_K = J + 1 + 2K. If the possible range of the number of joinpoints is from 0 to, a pre-defined value, K_max, the BIC approach selects the model M_K with the minimum BIC as the final model.

4. SIMULATION STUDY

The purpose of the simulation study is to evaluate how well the proposed JPSM picks the correct number of joinpoints during a long study period. The grouped survival data are simulated with various combinations of the number of new cancer incidences diagnosed each year, severity of the cancer, number of joinpoints, locations of the joinpoints and the APC of the death rates. The simulation study may provide a general reference of the performance of the method before proceeding to an analysis of the population-based survival data in practice. To avoid the use of the expected survival, we assume that the cause of death is known and use cause-specific analysis in the simulation. The results can be generalized to the relative survival case.

4.1. Simulation settings

We consider the range of the diagnosis year as x = 0, 1, …, 27, representing 1975 to 2002 in the SEER data. The study cutoff year is the end of the 27th year, so the maximum follow-up time is 27 years. After examining the new cancer cases diagnosed in each year in period 1975–2002 from the real SEER data, we found that the average numbers of new cases each year are over 5000 for the most common cancer sites, are around 1000–2000 for the common cancer sites and are in hundreds for the rare cancer sites. To simulate the grouped survival data, we assume that in each calendar year, there are 5000, 1000 and 500 new cancer cases diagnosed, representing the most common, moderately common, and rare cancer sites in the SEER 9 registries. These numbers correspond to n_x1, the number of people alive in the beginning of the first interval I₁ for each calendar year x. The number of people dying from other causes in the interval j is generated as a binomial variable l_xj ~ Bin(n_ij, p_0j), where p_0j are the probabilities of dying from other causes from the US life tables (Anderson, 1999) for the people with age (65+j), which is approximate the average age of cancer diagnosis. Hence the adjusted number of people at the risk of cancer death is $r_{xj}=n_{xj}-\frac{1}{2}{l}_{xj}$. The numbers of cancer deaths d_xj, j = 1, ···, 27, are generated using the binomial distributions for cause-specific survival data described in Section 2.1, where the death rate λ_j(x) is calculated from (3). The number of people alive at the beginning of the interval j + 1 is n_x;j+1 = n_xj − l_xj − d_xj.

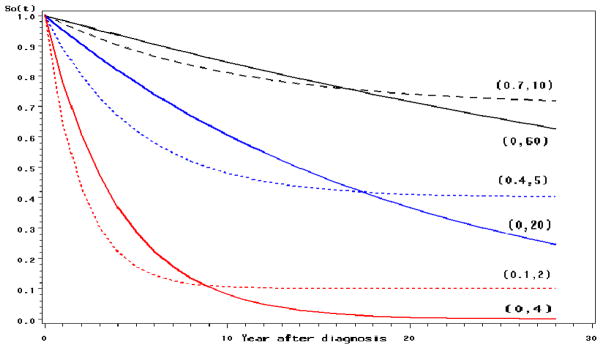
Cure becomes a possibility for certain cancers if diagnosed early. The mixture cure models (Boag 1949; Farewell 1982; Gamel et al. 2000; Yu et al. 2004), which postulate that a fraction of the patients are cured from the disease of interest, are widely used to model the survival data from clinical studies as well as population-based cancer survival studies. In the simulation study, we use the mixture cure model and the exponential model without cure as the baseline survival function S₀(t). The baseline survival function S₀(t) = c + (1 − c) exp(−t/μ), where c is the cure fraction and μ is the mean survival time in years for uncured patients. When c = 0, it reduces to an exponential model. For the purpose of illustration, the parameters (c, μ) are set to be (0, 60), (0, 20) and (0, 4) for the exponential model and (0.7, 10), (0.4, 5) and (0.1, 2) for the mixture cure model to represent cancer with best, moderate, and poor survival rates, respectively. The corresponding survival curves are shown in Figure 1. Notice that the population of patients with (c = 0, μ = 60) or (c = 0.7, μ = 10) have the best chance of survival and can live for a longer time, thus leaving not much room for the improvement in survival. For the patients with (c = 0, μ = 4) or (c = 0.1, μ = 2), the survival is poor, so if there is a big treatment improvement of the disease, it is easier to observe an increase in survival and to detect a significant joinpoint in the trend.

Fig. 1.

The baseline survival functions S₀(t) used in the simulation

The performance of the JPSM is also associated with the number and the locations of joinpoints. The total number of joinpoints K is selected to be 0, or 1, or 2. There are a total of 13 cases of joinpoint models as specified in Table 1. For example, there is no joinpoint in Case 1, one joinpoint at varying locations in Cases 2–7, and two joinpoints for Cases 8–13. In order to see whether the JPSM can detect the change occurring close to the end of study, some joinpoints are set to the year 23. For Case 2, there is one joinpoint at τ₁ = 10 with APC=−5% before, and APC=0% after, the year 10. The difference of the APC in the two segments 0–10 and 10–27 is 5%. When the difference of the APCs in two consecutive segments is big, we expect to detect that joinpoint, but when the difference is small, there is less chance to detect the joinpoint.

Table 1.

Locations of the joinpoints and APC values in the simulation for the K-joinpoint models

Case	K	(τ1, …, τK)	(APC1, …, APCK+1)(%)
1	0		−2
2	1	10	(−5, 0)
3	1	10	(−5, −2)
4	1	15	(−5, 0)
5	1	15	(−5, −2)
6	1	23	(−5, 0)
7	1	23	(−5, −2)
8	2	(10, 15)	(0, −5, 0)
9	2	(10, 15)	(0, −5, −2)
10	2	(10, 23)	(0, −5, 0)
11	2	(10, 23)	(0, −5, −2)
12	2	(15, 23)	(0, −5, 0)
13	2	(15, 23)	(0, −5, −2)

4.2. Performance of the model selection method using BIC

The percentages of picking the correct number of joinpoints for 0–1 joinpoint models and 2-joinpoint models are presented in Table 2.A and Table 2.B, respectively. The specifications of the 13 cases of joinpoint models are shown in the top rows of each subsection. The first column is the value of (c, μ). The next four columns show the percentages of selecting a k-joinpoint model M_k (k = 0, 1, 2, 3) for a common cancer site with new cancer cases n = 5000 each year. The middle four columns and the last columns correspond to n = 1000 and n = 500, respectively.

Table 2.

A. Percentages of selecting different joinpoint models M₀–M₃ using BIC for 0-joinpoint or 1-joinpoint models ^*

	n = 5000				n = 1000				n = 500
(c, μ)	M0	M1	M2	M3	M0	M1	M2	M3	M0	M1	M2	M3
Case 1: K = 0, APC=−2
(0.7,10)	99.8	0.2	.	.	99.6	0.4	.	.	99.6	0.4	.	.
(0,60)	99.4	0.6	.	.	99.4	0.5	0.1	.	99.7	0.3	.	.
(0.4,5)	99.7	0.3	.	.	99.8	0.2	.	.	99.5	0.5	.	.
(0,20)	99.8	0.2	.	.	99.8	0.2	.	.	99.5	0.5	.	.
(0.1,2)	99.3	0.6	0.1	.	99.0	1.0	.	.	98.6	1.3	0.1	.
(0,4)	99.5	0.5	.	.	100.0	.	.	.	100.0	.	.	.
Case 2: K = 1, JP=10, APC=(−5, 0)
(0.7,10)	.	99.4	0.6	.	3.3	96.6	0.1	.	37.9	62.0	0.1	.
(0,60)	.	99.6	0.4	.	6.0	93.9	0.1	.	46.4	53.6	.	.
(0.4,5)	.	99.1	0.9	.	.	99.8	0.2	.	0.1	99.3	0.6	.
(0,20)	.	99.5	0.5	.	.	99.4	0.6	.	1.2	98.3	0.4	0.1
(0.1,2)	.	99.2	0.8	.	.	98.6	1.3	0.1	.	98.4	1.5	0.1
(0,4)	.	99.0	1.0	.	.	99.4	0.6	.	.	100.0	.	.
Case 3: K = 1, JP=10, APC=(−5, −2)
(0.7,10)	.	99.9	0.1	.	61.1	38.8	0.1	.	87.4	12.5	0.1	.
(0,60)	0.2	99.3	0.5	.	68.8	31.0	0.2	.	90.8	9.1	0.1	.
(0.4,5)	.	99.1	0.9	.	4.4	95.0	0.6	.	33.2	66.4	0.4	.
(0,20)	.	99.5	0.5	.	11.1	88.5	0.4	.	55.6	44.2	0.2	.
(0.1,2)	.	99.2	0.8	.	.	99.0	0.9	0.1	1.2	97.5	1.3	.
(0,4)	.	99.0	1.0	.	.	100.0	.	.	1.4	98.6	.	.
Case 4: K = 1, JP=15, APC=(−5, 0)
(0.7,10)	.	99.1	0.9	.	16.2	83.4	0.4	.	59.4	40.4	0.2	.
(0,60)	.	99.6	0.4	.	32.3	67.1	0.6	.	74.1	25.9	.	.
(0.4,5)	.	99.4	0.5	0.1	.	99.7	0.3	.	1.7	97.8	0.5	.
(0,20)	.	99.4	0.6	.	0.5	99.0	0.5	.	14.6	85.4	.	.
(0.1,2)	.	99.0	1.0	.	.	98.9	1.0	0.1	.	98.9	1.1	.
(0,4)	.	99.3	0.7	.	.	99.5	0.5	.	.	98.8	1.2	.
Case 5: K = 1, JP=15, APC=(−5, −2)
(0.7,10)	1.6	98.2	0.2	.	77.5	22.5	.	.	93.6	6.3	0.1	.
(0,60)	5.8	93.8	0.4	.	84.9	14.9	0.2	.	95.4	4.6	.	.
(0.4,5)	.	99.8	0.2	.	10.9	88.5	0.6	.	53.1	46.8	0.1	.
(0,20)	.	99.5	0.5	.	36.4	63.3	0.3	.	75.0	25.0	.	.
(0.1,2)	.	99.0	1.0	.	.	98.7	1.3	.	2.3	96.8	0.9	.
(0,4)	.	99.3	0.6	0.1	.	99.5	0.5	.	6.0	92.8	1.2	.
Case 6: K = 1, JP=23, APC=(−5, 0)
(0.7,10)	87.9	11.8	0.3	.	99.3	0.7	.	.	99.8	0.2	.	.
(0,60)	95.1	4.9	.	.	99.3	0.7	.	.	99.8	0.2	.	.
(0.4,5)	27.8	71.8	0.3	0.1	93.3	6.7	.	.	96.7	3.3	.	.
(0,20)	68.5	31.5	.	.	97.8	2.1	0.1	.	99.1	0.9	.	.
(0.1,2)	.	99.5	0.5	.	42.8	56.2	0.9	0.1	73.3	26.4	0.3	.
(0,4)	0.9	99.0	0.1	.	76.1	23.9	.	.	87.7	11.1	1.2	.
Case 7: K = 1, JP=23, APC=(−5, −2)
(0.7,10)	98.0	2.0	.	.	99.7	0.3	.	.	99.5	0.5	.	.
(0,60)	98.6	1.4	.	.	99.8	0.2	.	.	99.7	0.3	.	.
(0.4,5)	80.5	19.4	0.1	.	99.1	0.9	.	.	99.3	0.7	.	.
(0,20)	94.5	5.4	0.1	.	99.3	0.7	.	.	99.5	0.5	.	.
(0.1,2)	14.5	85.0	0.5	.	84.1	15.9	.	.	91.6	8.4	.	.
(0,4)	45.7	54.0	0.3	.	91.1	8.9	.	.	98.8	1.2	.	.
Case 8: K = 2, JP=(10,15), APC=(0, −5, 0)
(0.7,10)	0.8	0.2	98.7	0.3	87.4	5.1	7.5	.	97.2	2.0	0.7	0.1
(0,60)	2.0	2.4	95.5	0.1	89.9	5.0	5.1	.	97.6	1.7	0.6	0.1
(0.4,5)	.	.	99.2	0.8	27.9	2.7	69.2	0.2	76.5	3.9	19.3	0.3
(0,20)	.	.	99.6	0.4	40.5	7.8	51.5	0.2	81.7	7.1	11.0	0.2
(0.1,2)	.	.	99.2	0.8	0.2	0.1	98.5	1.2	16.0	2.4	80.3	1.3
(0,4)	.	.	99.1	0.9	.	.	100.0	.	44.4	.	55.6	.
Case 9: K = 2, JP=(10,15), APC=(0, −5, −2)
(0.7,10)	.	47.2	52.8	.	50.5	47.7	1.8	.	86.8	12.7	0.5	.
(0,60)	.	61.3	38.7	.	53.8	44.4	1.8	.	86.6	13.0	0.4	.
(0.4,5)	.	1.5	97.8	0.7	2.2	74.2	23.6	.	36.9	56.0	7.1	.
(0,20)	.	7.5	92.1	0.4	6.4	79.7	13.8	0.1	44.0	52.5	3.5	.
(0.1,2)	.	.	98.8	1.2	.	28.8	70.0	1.2	3.7	61.7	34.2	0.4
(0,4)	.	.	99.6	0.4	.	37.9	58.6	3.4	.	42.9	57.1	.
Case 10: K = 2, JP=(10,23), APC=(0, −5, 0)
(0.7,10)	.	81.7	18.2	0.1	2.0	96.3	1.7	.	36.2	63.1	0.7	.
(0,60)	.	90.6	9.2	0.2	5.4	93.0	1.6	.	43.7	55.8	0.5	.
(0.4,5)	.	11.8	87.6	0.6	.	89.1	10.9	.	0.5	94.5	5.0	.
(0,20)	.	50.4	49.2	0.4	.	95.5	4.4	0.1	1.8	96.2	1.9	0.1
(0.1,2)	.	.	99.1	0.9	.	29.3	70.0	0.7	.	64.3	35.5	0.2
(0,4)	.	0.2	99.6	0.2	.	62.1	37.9	.	.	75.0	25.0	.
Case 11: K = 2, JP=(10,23), APC=(0, −5, −2)
(0.7,10)	.	95.0	4.9	0.1	2.6	96.4	1.0	.	34.6	64.7	0.7	.
(0,60)	.	98.0	1.9	0.1	3.9	95.5	0.6	.	37.9	61.8	0.3	.
(0.4,5)	.	72.6	27.4	.	.	97.9	2.1	.	0.2	98.4	1.4	.
(0,20)	.	88.8	11.2	.	.	98.2	1.7	0.1	1.0	98.4	0.6	.
(0.1,2)	.	7.9	91.7	0.4	.	80.6	19.3	0.1	.	90.6	9.4	.
(0,4)	.	28.3	71.4	0.4	.	88.3	11.7	.	.	92.3	7.7	.
Case 12: K = 2, JP=(15,23), APC=(0, −5, 0)
(0.7,10)	.	80.4	19.6	.	10.2	87.9	1.9	.	49.1	50.3	0.6	.
(0,60)	.	89.5	10.5	.	18.1	80.9	1.0	.	63.3	36.4	0.3	.
(0.4,5)	.	12.7	87.1	0.2	.	88.3	11.6	0.1	0.6	95.0	4.4	.
(0,20)	.	55.8	44.2	.	.	95.9	4.1	.	6.9	91.5	1.6	.
(0.1,2)	.	.	99.3	0.7	.	41.5	58.0	0.5	.	71.5	28.4	0.1
(0,4)	.	.	99.6	0.4	.	68.9	31.1	.	.	100.0	.	.
Case 13: K = 2, JP=(15,23), APC=(0, −5, −2)
(0.7,10)	.	96.0	3.9	0.1	5.0	94.2	0.8	.	41.5	58.1	0.4	.
(0,60)	.	96.7	3.2	0.1	13.5	85.9	0.6	.	61.2	38.4	0.4	.
(0.4,5)	.	77.0	23.0	.	.	97.7	2.3	.	0.2	98.5	1.2	0.1
(0,20)	.	90.9	9.1	.	.	99.0	0.9	0.1	3.6	95.6	0.8	.
(0.1,2)	.	12.9	86.3	0.8	.	82.0	17.8	0.2	.	90.7	9.2	0.1
(0,4)	.	34.0	66.0	.	.	88.1	11.9	.	.	100.0	.	.

^*K is the true number of jointpoints, M_k denotes a k-joinpoint model, k = 0, .., 3, JP is the location of the joinpoints

The effects of different parameter specifications are summarized below:

• Effect of sample size: For common cancers with the number of new cases n = 5000 every year, the JPSM finds the correct number of joinpoints most of the time. As the number of new cases decreases to n = 1000, the estimated number of joinpoints K̂ tends to be less than the true K. For n = 500, the model tends to find no joinpoint.

• Effect of cancer prognosis: The JPSMs select a lower number of joinpoints for less severe cancer with high survival rates. For the same value of APC, the higher baseline death rate λ_j(x) implies a larger absolute difference in death rates λ_j(x + 1) − λ_j(x). For example, if APC=−20%, then the referent death rate λ_j(x) = 50% induces an absolute reduction of 10% in death rates, while the λ_j(x) = 10% only leads to a 2% decrease in death rates. Thus, JPSMs have more capability to detect a joinpoint when the baseline death rates are high.

• Effect of the number of joinpoints: The chance of capturing the correct total number of joinpoints is higher for smaller K. When the true model is M₀, the percentages of selecting the correct model are close to 100% for all the data with different size and severity status, which implies that the false alarm rate of a significant improvement in survival is very low if the there is no trend variation. For the Cases 2–7 where the number of joinpoints K ≥ 1, there is a tendency to underestimate the total number of joinpoints, i.e., the JPSMs tend to be conservative.

• Effect of the locations of joinpoints: As the people diagnosed more recently have less follow-up, the JPSMs are not able to detect a joinpoint when the true joinpoint is very close to the end of the study period. See, e.g., Cases 6 and 7 with joinpoint located at 23, which is only 4 years away from the last year in the study. Even though, there exist some improvements in trend, there is not enough follow-up time to allow the model to detect the difference. Therefore, the closer are the joinpoints to the beginning or to the end of the study period, the harder it is to detect the joinpoints. These issues are worse near the end of the study period since the follow-up time is shorter.

• Effect of the change in APC on death rates: The model selection method tends to select a lower number of correct models when the APCs for the two consecutive segments are −5% and −2% (with absolute difference 3%) compared with APC=−5% and 0% or APC=0% and −5% (with absolute difference 5%). So larger changes in APC lead to better performance of the model for detecting the joinpoint.

• Effect of cure fraction c: The difference is minor between the standard survival model and the mixture cure model when the survival level is the same. For example, the percentage of correctly selecting one joinpoint is 99.4% for data with (c, μ) = (0.7, 10) and 99.1% for data with (c, μ)=(0, 60) when n = 5000 for Case 2. From Figure 1, the outcomes of these two cases are very close.

To assess the sensitivity of the results to the specification of baseline survival function, we used a lognormal baseline survival function S₀(t) = 1 − Φ[log(t) − α]. The values of α were chosen such that the mean survival times μ = exp(α + 0.5) as specified in Section 4.1. We selected Cases 2 and 8 for comparison. For Case 2 with 1-joinpoint model, the results remained similar that the true model M₁ was selected most of the times. For Case 8 with 2-joinpoint model, when (c, μ) = (0, 60) or (0.4, 5), the BIC method picked the correct model M₂ more times when baseline survival is lognormal than when the baseline is exponential. This is probably due to the different tails of the lognormal and the exponential distributions. Overall, the results for the lognormal and exponential survival functions are similar.

Generally, the JPSMs are conservative with low false alarm rate or Type I error, especially when the patient’s survival prognosis is good (less severe) and the cancer is rare.

4.3. Performance of the selection method using permutation tests

In modeling the trends of cancer incidence and mortality rates, the permutation tests have been used to select the correct number of joinpoints. Simulation studies (Kim et al. 2008) showed that the permutation-test based (PTB) model selection procedure is generally more conservative than the BIC method for incidence rates. We conducted a small scale simulation to examine the performances of the PTB procedure for survival data.

Table 4 presents the percentages of selecting a k-joinpoint model for Cases 2 and 8. Because the results for n = 1000 or 5000 for Case 2 are similar, so is that for n = 1000 or 500 for Case 8, we conducted new simulations using the PTB procedure for n = 1000, 500 for Case 2 and for n = 5000, 1000 for Case 8. Due to the constraint of computation time, we set the maximum number of joinpoints K_max = 2. The results in Table 4 were based on 1000 permutations for each simulated dataset. When we compared the results in Table 4 and Tables 2.A and 2.B, we found that:

Table 4.

Selected simulation for Cases 2 and 8 using permutation tests for model selection with K_max = 2

Case 2: K = 1, JP=10, APC=(−5,0)
	n = 1000			n = 500
	M0	M1	M2	M0	M1	M2
(0.7,10)	.	96	4	10	78	12
(0.4,5)	.	99	1	.	97	3
(0.1,2)	.	96	4	.	99	1
(0,60)	23	59	18	28	35	37
(0,20)	.	96	4	1	94	5
(0,4)	48	52	.	74	26	.
Case 8: K = 2, JP=(10,15), APC=(0,−5,0)
	n = 5000			n = 1000
	M0	M1	M2	M0	M1	M2
(0.7,10)	.	.	100	35	19	46
(0.4,5)	.	.	100	.	3	97
(0.1,2)	.	.	100	.	.	100
(0,60)	4	50	46	53	29	18
(0,20)	.	.	100	5	23	72
(0,4)	7	.	93	70	.	30

• Case 2: When there is a cure for the cancer (c > 0), the PTB method picked the correct model M₁ more times than the BIC method did, especially for rare cancer with n = 500. When the cure rate is 0, the PTB method could be liberal and picked the 2-joinpoint model 37% and the BIC method performed much better by pick M₁ above 98%.

• Case 8: When there is a cure, the PTB method performed better than the BIC method and picked the correct model M₂ more times, especially for n = 1000. However, when there is no cure, the BIC method performed better.

When K_max = 3, the PTB method is almost impossible for model selection. Overall, the BIC method is preferred for model selection when we model the trends of survival. Based on the simulation, the performances of the BIC method and the PTB method were comparable. The BIC method is much less computationally intensive and it is conservative.

5. APPLICATION

Because of the long history of the SEER 9 registries, we apply the JPSM to the survival data from the SEER 9 registries from 1975 to 2002, which was the most recent year with complete follow-up information at the time that the analysis was initiated. To avoid the inaccuracy of the cause of death information, we use the relative survival data.

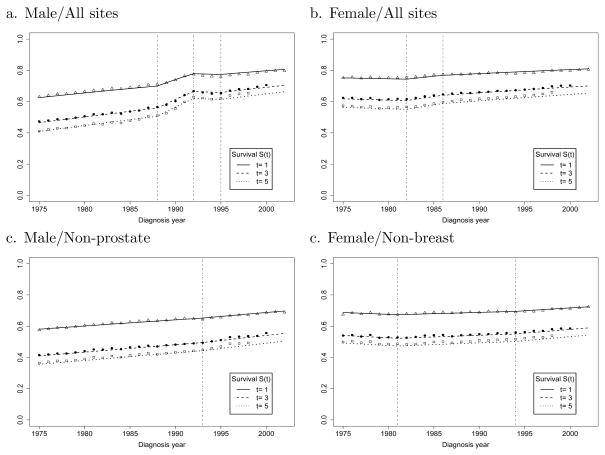
We start by presenting the survival trends for all cancer sites combined for males and for females (Figure 2a, b). The estimates of the joinpoints and APC are shown in Table 5. The standard errors of the APCs are not reported. Instead, the significant differences of the APC values are marked with asterisks. For men, the trend in survival is divided into four segments demarcated by joinpoints in 1988 (95% CI, 1987–1990), 1992 (95% CI, 1991–1993) and 1995 (95% CI, 1994–1996). The slopes of the four segments reveal that the APC in mortality was decreasing significantly by 2.1% in the first segment, by 8.5% in the second segment, and was not significantly different from zero with APC=0.7% and −2.5% for the last two segments. The joinpoints for 1988 and 1992 are suggestive of changes that were taking place in prostate cancer screening and diagnosis. The large and significant changes in prostate cancer incidence in 1989 and 1992 appear to be responsible for the major details of the overall survival curve for males. Because the prostate cancer contribution to the overall survival curve is related to several factors including PSA screening, a more detailed analysis and discussion is needed to address the organ specific details that contribute to the blended composite. With prostate cancer incidence included in the overall model, it is difficult to interpret what portion of the trend is artificial, or in other words generated by well recognized sources of bias. The introduction of screening in a population causes survival to improve, since the time of diagnosis is shifted to an earlier time point, even if the time of death is unchanged (lead time bias). In addition, screening can detect some cancers that never would have produced symptoms, if screening had not detected the cancer (over-diagnosis bias). Consequently, we elected to obtain a survival progress measure independent of prostate cancer, by generating a survival model for all male cancer excluding prostate. In this model, a single joinpoint remained for 1993 (95% CI, 1990–1995), with a steady significant improvement in survival through 1993 (APC=−1.3%) and with an acceleration of the improvement after that (APC=−1.9%). While screening influences cancers sites other than prostate cancer, factors that artificially increase survival are influenced mostly by the rapid introduction of screening, where prostate cancer is by far the prime example.

Fig. 2.

The trends of t-year relative survival rates S(t) by the year of diagnosis (t = 1, 3, 5)

Table 5.

Estimates of the joinpoints and the APC of annual death (hazard) rates for selected cancer sites

Cancer site	New cases per year	K	Estimated Joinpoints	APC
Male/All Sites	43173	3	(88, 92, 95)	(−2.1*, −8.5*, 0.7, −2.4)
Female/All Sites	40396	2	(82, 86)	(0.5, −2.9*, −1.4*)
Male/Non-prostate	31470	1	93	(−1.3*,−1.9*)
Female/Non-breast	28039	2	(81, 94)	(0.9*, −0.6*,−1.5*)
Distant Testicular	69	2	(77, 93)	(−32.2*, −4.2, 4.2)
Distant Pancreatic	1043	1	95	(−0.3*, −2.9*)
Regional Melanoma	261	1	98	(−1.1*,−14.8*)

We used a similar approach to examine the survival of females from cancer at all sites. The trend in overall survival for women was marked by joinpoints in 1982 (95% CI, 1979–1983) and 1986 (95% CI, 1984–1990), with the largest APC amounting to −2.9% in the middle segment, and a slowing of the improvements after that (APC=−1.4%) (Table 5). Major advances in adjuvant endocrine and multi-agent chemotherapy for breast cancer treatment influenced survival over this period. However, screening mammography undoubtedly affected trends in breast cancer incidence during the 1980s, introducing some level of artifact into the survival trends. When breast cancer cases were removed, the model showed significant improvements from 1981 (95% CI, 1979–1983) through 1994 (95% CI, 1992–1998) with APC=−0.6% and an acceleration after that (APC=−1.5%). The approach that we have used shows that it is preferable to examine joinpoints in organ specific survival curves when looking for their connection to patterns of care.

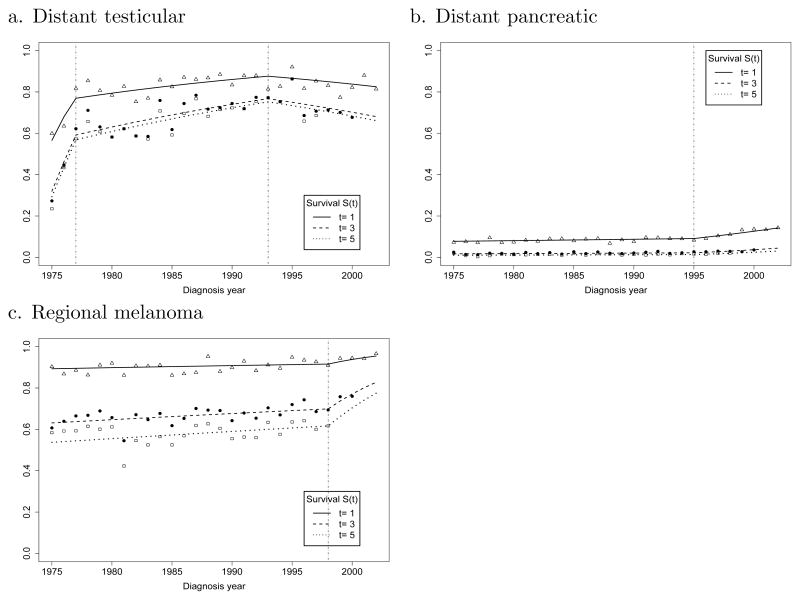
To illustrate the utility of the JPSM and certain characteristics of our results, we have selected three additional organ site examples: distant testicular cancer, distant pancreatic cancer, and regional melanoma (Figure 3). For distant testicular cancer in Figure 3a, two joinpoints observed in 1977 (95% CI, 1976–1979) and 1993 (95% CI, 1988–1997) separate 3 phases of survival improvement for distant testicular cancer. Distant testicular cancer is highlighted because the circumstances surrounding changes in survival of testicular cancer patients are particularly well documented. In the earliest time period, the APC of death rates is decreasing 32.2% each year. This period of dramatic survival improvement stabilizes in 1977 followed by a period of moderate but consistent gains in late stage survival from 1977 to 1993. Then in the period following 1993, the survival for late stage disease ceases to improve. In Figure 3b the data for distant pancreatic cancer also reveal a single joinpoint, indicating a modest change in survival in this subgroup starting in 1995 (95% CI, 1993–1998) and corresponding to a 2.9% annual improvement. For regional melanoma in Figure 3c, a single joinpoint is observed in 1998 (95% CI, 1996–1999). This joinpoint heralds a large improvement in survival corresponding to an APC of 14.8%.

Fig. 3.

The trends of t-year relative survival rates S(t) by the year of diagnosis for three selected cancer sites (t = 1, 3, 5)

Our confidence in the JPSM approach is strengthened by the data for testicular cancer. Changes in survival for testicular cancer are closely linked with the introduction of platinum therapy in 1974, a development which enabled a dramatic improvement in the survival of distant stage testicular cancer patients prior to 1977. The gain in survival in these patients was largely related to an increased cure fraction (Huang et al. 2007). From 1977 to 1993, the more modest gains in survival correspond to the optimization of platinum-based, multi-agent therapy. The decline in survival for distant stage testicular cancer after 1993 is probably associated with an increase of biologically aggressive disease in the distant stage category, as observed in other study populations. (Sonneveld et al. 1999) Over time, the stage distribution of testicular cancer has changed so that more Stage 1 cancer is diagnosed in conjunction with less of all other stages combined. This evidence of earlier detection is consistent with a shift to earlier stages of more indolent tumors with their extended opportunity for detection, leaving the more virulent and rapidly progressing forms of the disease to be diagnosed in the late stage setting.

Moving away from diagnoses where evolving patterns of care and their impact are relatively well characterized, it could not have been anticipated that JPSM would uncover a statistically significant joinpoint in the survival profile for regional melanoma or for distant pancreatic cancer. For regional melanoma, our results suggest that a change in practice somewhat prior to 1998 started a trend for a sizable increase in the survival of patients with a diagnosis of regional melanoma. This result underscores the difficulty in understanding a trend that is premised on data from a limited number of cases (259) subject to uncontrolled factors. From a review of clinical trials for patients receiving systemic adjuvant therapy for melanoma, there is no clear cut evidence that a breakthrough has been achieved or that long-term survival has been extended (Verma et al. 2006). However, after a landmark trial of high-dose Interferon alfa-2b (IFN alpha-2b) in 1996, (Kirkwood et al. 1996) a case can be made that increasing use of IFN alpha-2b may have contributed to improved survival. Indeed, a meta-analysis of 12 randomized trials suggested that recurrence free survival was improved by IFN alpha-2b with a statistically significant benefit associated with increasing dose (Wheatley et al. 2003). Based on this kind of information, it might be useful to return to the records for the regional melanoma cases involved in this study, to look for a trend of increasing interferon use in this cohort. In addition, alternative hypotheses for an apparent improvement in survival could also be considered.

A change in surgical practice associated with regional melanoma might also be a factor that could influence survival. Lymphatic mapping with sentinel node biopsy was the basis for the Multi-center Selective Lymphadenectomy Trial (MSLT-1) that started in 1994 and completed accrual in 2002 (Morton et al. 2006). The participants in this trial were individuals with relatively advanced lesions (Clark level IV, V, or level III with intermediate thickness). With randomization to observation versus sentinel node biopsy with immediate clearing of the lymphatic basin for a positive sentinel node, the MLST-1 showed that immediate lymphadenectomy increases the survival of patients with nodal metastases. The five year survival for immediate lymphadenectomy was 72% vs. 52% for delayed lymphadenectomy. However, it is debatable whether 1998 is a milestone in the use of sentinel node biopsy for melanoma patients. Nevertheless, the possibilities for explaining a survival trend of this magnitude starting in 1998 are limited in number. This experience highlights the potential for JPSM to improve cancer surveillance. When unrecognized trends are identified, there is an opportunity to return to the registries to collect additional data that may explain the trend and support wider application of beneficial interventions.

In the case of distant pancreatic cancer, JPSM has identified a trend in survival improvement starting in 1995. This result highlights another surveillance issue. Using SEER data from 1988 to 1999, investigators were able to appreciate survival improvements in distant pancreatic cancer when comparing 2-year survival rates for the years after 1992 compared with the years before 1991 (Riall et al. 2006). However, the authors noted that even though the trend they observed was statistically significant, they doubted that it was clinically significant. Using the more precise data obtained with JPSM, attention can be focused on identifying a change in treatment that could account for an improvement in survival starting around 1995. After many years when single agent 5-fluorouracil (5-FU) was the standard systemic treatment for unresectable pancreatic cancer, gemcitabine was approved for this indication by the FDA in May, 1996 (Storniolo et al. 1999). The introduction of this drug into practice is a likely explanation for a modest improvement in survival for patients with advanced pancreatic cancer. In a randomized clinical trial comparison of gemcitabine with 5-FU, patients treated with gemcitabine experienced a median survival extension of 5 weeks (Burris et al. 1997). The details of this example show that a relative improvement in survival for a cohort that experiences short survival can be pinpointed and identified as statistically significant; however, further information is needed to provide a scale to the benefit. Otherwise, large numbers of patients may serve as the basis for identifying statistically significant events of small magnitude without much insight as to benefit. In this event, the value of a more complex decision making model (Tennvall and Wilking, 1999) can be invoked, attempting an assignment of cost-effectiveness with the attendant risks of that process.

6. DISCUSSION

The JPSM is useful to describe the progress of cancer survival and to gain understanding about the effect of changes in medical practice. Although we used relative survival data in our application, it is also possible to use cause-specific survival data when the information on cause of death is more reliable. The JPSM can serve as a tool to find a potential change point in cancer survival. Compared to the cancer incidence or mortality trends, survival trends usually improve gradually, and there tends to be a smaller number of joinpoints.

Here we focus on the joinpoints in the year of cancer diagnosis, which is surrogate of treatment progress. The proposed JPSM assumes that the new treatment decreases (increases) the baseline hazard rate proportionally. A joinpoint can also be incorporated into the baseline hazard function in order to examine the effect of a new treatment versus the conventional treatment if the new treatment changes the shape of the baseline survival by transforming it to a different disease. If joinpoints are considered in both the baseline survival function and the diagnosis year, there might be different joinpoints for 5-year and 10-year survival and this possibility adds to the complexity of the model. Based on the application (see Figures 2 and 3), it is reasonable that the 1-, 3- and 5-year survival rates are proportional and share the same joinpoints. Thus, the JPSM with joinpoints only in the diagnosis year is appropriate for modeling the survival trends in our application.

When evaluating survival, one must be aware of various biases introduced by screening and new diagnostic technologies, e.g., lead time, length bias and over diagnosis. For instance, screening mainly influences survival by detecting earlier, either earlier stage or event at a smaller size within stage, and this shift to earlier disease is hard to control. Hanin et al. (2006) presented a biologically motivated model of breast cancer development and detection, and examined the effect of screening schedules and clinical covariates at the time of diagnosis on survival. It is useful to incorporate the models for screening effect in the change point modeling. Thus JPSM can be used when we have confidence in the effect of medical breakthroughs on survival or we are interested in the identification of possible change in trends. However, we need to be cautious about the possible biases due to screening or selection. It is not advised that one use the JPSM directly to evaluate the benefits of treatment using the population-based cancer survival data since the data are not from a randomized trial where the treated and untreated group are balanced in confounders. That is why we should look at population level data in a JPSM. By developing the JPSM to population data, the comparison of population level findings with the outcomes of clinical trials should allow use to refine our understanding of survival trends.

The simulation studies presented here evaluate the performance of the JPSM in picking the correct number of joinpoints. The model selection criterion used for the JPSM is the BIC, which tends to detect a lower number of joinpoints, especially when the sample size is small. An alternative model selection criterion such as AIC, which is more sensitive to changes in the trend could also be used. The focus of this paper is on the description of current survival trends and the identification of change points. However, the JPSM can also be used for the survival prediction. The standard survival models, such as the proportional hazards models, have been used to predict the survival rates for the newly diagnosed cancer patients (Mariotto et al. 2006). It is useful to compare the accuracy of the predictions resulting from the standard survival models with those from the JPSM.

As treatments progress, more and more patients are cured and become long-term survivors for certain types of cancers. The major medical breakthroughs can significantly increase the probability of cure as well as prolong the survival time for the uncured patients favoring the use of the mixture cure model. It is possible to include joinpoints in the mixture cure model to evaluate the change in trend for both cure fraction and the survival times for the uncured patients. Even though the JPSM described is primarily for cancer survival data, it can be applied to other similar survival data. Adding change points to the baseline hazard for relative survival data is useful to examine the survivals of cancer patients and general population, for example, whether the patients and general population have the same survival rates.

Table 3.

Selected simulation for Cases 2 and 8 using BIC for model selection with lognormal baseline survival function

	n = 5000				n = 1000				n = 500
	M0	M1	M2	M3	M0	M1	M2	M3	M0	M1	M2	M3
Case 2: K = 1, JP=10, APC=(−5, 0)
(0.7,10)	.	99.5	0.5	.	4.6	95.2	0.2	.	47.2	52.7	0.1	.
(0.4,5)	.	99.6	0.4	.	.	99.5	0.5	.	0.1	99.1	0.8	.
(0.1,2)	.	99.3	0.7	.	.	99.5	0.5	.	.	98.6	1.4	.
(0,60)	0.9	98.5	0.6	.	29.8	70.0	0.2	.	11.1	88.8	0.1	.
(0,20)	.	99.2	0.8	.	.	99.5	0.5	.	8.3	91.0	0.7	.
(0,4)	0.0	99.7	0.3	.	0.0	99.4	0.6	.	0.0	99.6	0.4	.
Case 8: K = 2, JP=(10,15), APC=(0, −5, 0)
(0.7,10)	0.7	1.3	97.8	0.2	87.2	6.5	6.3	.	96.4	2.7	0.9	.
(0.4,5)	.	.	99.7	0.3	28.4	3.4	67.8	0.4	73.9	5.8	20.1	0.2
(0.1,2)	.	.	99.3	0.7	0.5	0.1	98.5	0.9	19.4	2.5	77.5	0.6
(0,60)	29.2	53.9	16.5	0.4	93.1	6.6	0.3	.	97.0	2.9	.	0.1
(0,20)	.	0.1	99.4	0.5	44.5	26.2	29.1	0.2	81.6	14.1	4.3	.
(0,4)	0.0	.	99.5	0.5	Calculation failed to converge