Force-momentum-based self-guided Langevin dynamics: A rapid sampling method that approaches the canonical ensemble

Abstract

The self-guided Langevin dynamics (SGLD) is a method to accelerate conformational searching. This method is unique in the way that it selectively enhances and suppresses molecular motions based on their frequency to accelerate conformational searching without modifying energy surfaces or raising temperatures. It has been applied to studies of many long time scale events, such as protein folding. Recent progress in the understanding of the conformational distribution in SGLD simulations makes SGLD also an accurate method for quantitative studies. The SGLD partition function provides a way to convert the SGLD conformational distribution to the canonical ensemble distribution and to calculate ensemble average properties through reweighting. Based on the SGLD partition function, this work presents a force-momentum-based self-guided Langevin dynamics (SGLDfp) simulation method to directly sample the canonical ensemble. This method includes interaction forces in its guiding force to compensate the perturbation caused by the momentum-based guiding force so that it can approximately sample the canonical ensemble. Using several example systems, we demonstrate that SGLDfp simulations can approximately maintain the canonical ensemble distribution and significantly accelerate conformational searching. With optimal parameters, SGLDfp and SGLD simulations can cross energy barriers of more than 15 kT and 20 kT, respectively, at similar rates for LD simulations to cross energy barriers of 10 kT. The SGLDfp method is size extensive and works well for large systems. For studies where preserving accessible conformational space is critical, such as free energy calculations and protein folding studies, SGLDfp is an efficient approach to search and sample the conformational space.

INTRODUCTION

The self-guided molecular dynamics (SGMD) (Refs. ¹ and ²) and the self-guided Langevin dynamics (SGLD) (Ref. ³) simulation methods were developed for efficient conformational searching and have found many applications for the study of rare events such as protein folding,^{4, 5, 6, 7, 8, 9, 10, 11, 12} ligand binding,¹³ docking,¹⁴ conformational transition,^{15, 16, 17} and surface absorption.^{18, 19, 20, 21} While SGMD/SGLD can accelerate slow events to an affordable time scale, the perturbation in conformational distribution due to the self-guiding force was not quantitatively understood until recently.²² A common practice for SGMD or SGLD simulations is to limit the guiding factor to a small range so that the effect on conformational distribution is very small and can be neglected.³

For quantitative studies, it is important to obtain correct conformational distributions while accelerating conformational searching. Andricioaei et al. proposed a Monte Carlo procedure called the momentum-enhanced hybrid Monte Carlo method to include the benefit of the guiding force while preserving the ensemble average properties.²³ In molecular dynamics simulations, the difficulty in characterizing the effect of the guiding force on ensemble distributions is mainly due to the lack of quantitative definition for the low-frequency motion enhanced in SGLD simulations. Recently, a quantitative understanding of the guiding effect on the conformational distribution has been achieved.²² The low-frequency properties are defined with the local averaging mechanism used for the guiding force calculation. The partition function of the SGLD ensemble is derived based on the separation of the low-frequency properties and the high-frequency properties. Based on the SGLD partition function, the conformational distribution obtained in SGLD simulations can be converted to the canonical ensemble distribution, and ensemble average properties can be calculated from the SGLD simulations through reweighting.

Based on the SGLD partition function, we find that the perturbation due to the momentum based guiding force can be corrected with the force-based guiding force previously used in the SGMD simulation method.^{1, 2} Therefore, by combining the force-based guiding force with the momentum-based guiding force, this work developed a simulation method to achieve rapid conformational sampling while maintaining approximately the canonical ensemble. For the convenience of reference, we designate this simulation method as the force-momentum-based self-guided Langevin dynamics, abbreviated as SGLDfp. The details of the derivation are described in the Theory and Method section. Some demonstrations and applications of this method are provided in the Results and Discussions section.

THEORY AND METHOD

Most of simulation methods improve conformational searching and sampling through either modifying energy surfaces or raising temperatures so that energy barriers can be crossed easily. The SGLD method is unique in the way that it selectively enhances and suppresses molecular motions based on their frequency to accelerate conformational searching without modifying energy surfaces or raising temperatures. The concept of the low-frequency and high-frequency properties plays a central role in understanding the SGLD method. Even though this work is to present the SGLDfp method, we feel it is necessary to provide a brief description of this concept and how it lead to the SGLD partition function.²²

The low-frequency and high-frequency properties

Thermal motion in a molecular system makes all dynamic behaviors possible, such as diffusion, protein folding, and signal transduction. Thermal motion has a distribution of frequencies, from high-frequency motions such as chemical bond vibrations to low-frequency motions such as protein folding. High-frequency motions can repeat in a short time scale and are often easy to study in molecular simulations. Low-frequency motions are important for many macroscopic behaviors such as protein folding and ligand binding, but are often beyond the time scale accessible by molecular simulations with current computing resources.

Corresponding to the low-frequency motion and the high-frequency motion there are the low-frequency conformational space, Ω_lf, and the high-frequency conformational space, Ω_hf. The total conformational space is a combination of the two: Ω = Ω_lf · Ω_hf. A simple example is that in a box of water, water molecules diffuse around the box while their bonds stretch and bend quickly. The diffusion motion occurs in the box space while the bond vibrations cover the bond length and bond angle ranges. It is reasonable to separately consider the slow diffusion and the fast vibrations and in many practices, the fast vibrations are completely removed with constraint methods such as SHAKE (Ref. ²⁴) or the semi-flexible constraint dynamics.²⁵

Assume the potential energy surfaces in the low- and high-frequency conformational spaces are E_lf and E_hf, respectively. If we assume the temperatures of the low- and high-frequency motions are T_lf and T_hf, which normally equal to the system temperature, T, we can write the partition functions in the low- and high-frequency conformational spaces separately:

$$\begin{array}{c}\hfill {\Theta }_{\mathrm{lf}}(N,V,T_{\mathrm{lf}})=\sum _{{\Omega }_{\mathrm{lf}}}\exp \left(-\frac{E_{\mathrm{lf}}}{k{T}_{\mathrm{lf}}}\right),\end{array}$$ (1)

$$\begin{array}{c}\hfill {\Theta }_{\mathrm{hf}}(N,V,T_{\mathrm{hf}})=\sum _{{\Omega }_{\mathrm{hf}}}\exp \left(-\frac{E_{\mathrm{hf}}}{k{T}_{\mathrm{hf}}}\right).\end{array}$$ (2)

Here, k is the Boltzmann constant. By neglecting the coupling between the two conformational distributions, the total partition function can be expressed as

$$\begin{array}{ccc}\hfill \Theta (N,V,T)& =& {\Theta }_{\mathrm{lf}}(N,V,T_{\mathrm{lf}}){\Theta }_{\mathrm{hf}}(N,V,T_{\mathrm{hf}})\hfill \\ & =& \sum _{{\Omega }_{\mathrm{lf}}}\exp \left(-\frac{E_{\mathrm{lf}}}{k{T}_{\mathrm{lf}}}\right)\sum _{{\Omega }_{\mathrm{hf}}}\exp \left(-\frac{E_{\mathrm{hf}}}{k{T}_{\mathrm{hf}}}\right)\hfill \\ & =& \sum _{\Omega }\exp \left(-\frac{E_{\mathrm{lf}}}{k{T}_{\mathrm{lf}}}-\frac{E_{\mathrm{hf}}}{k{T}_{\mathrm{hf}}}\right).\hfill \end{array}$$ (3)

In the canonical ensemble, temperatures in all conformational spaces are the same, T_lf = T_hf = T, and the total potential energy of the system is a sum of the two, E_p = E_lf + E_hf. Therefore, the partition function from Eq. 3 becomes

$$\begin{array}{c}\hfill Q_{\mathit{NVT}}=\sum _{\Omega }\exp \left(-\frac{E_{\mathrm{lf}}}{kT}-\frac{E_{\mathrm{hf}}}{kT}\right)=\sum _{\Omega }\exp \left(-\frac{E_{\mathrm{p}}}{kT}\right).\end{array}$$ (4)

A slow conformational searching in molecular simulation is often related to a weak low-frequency motion. The central idea behind the SGMD/SGLD simulation method is to accelerate conformational searching through enhancing the low-frequency motion. In other words, in SGMD/SGLD simulations, temperatures in the low-frequency and high-frequency conformational space are no longer the same. Unlike high temperature simulations which accelerate motions in all frequencies, SGMD/SGLD simulations increase the temperature of the low-frequency motion, T_lf, and reduce the temperature of the high-frequency motion, T_hf, to achieve efficient conformational searching and sampling. The overall temperature in SGMD/SGLD simulations remains unchanged.

To quantitatively describe the conformational distribution of a SGLD simulation, we proposed previously to define a low-frequency property by a method we designated as the local averaging.²² Let us consider a system of N particles described by their positions, q_i, and momenta, p_i. For any conformation, Ω = {q_i}, we define L as its local conformational space where all conformations are within a certain distance from Ω. For a canonical ensemble at temperature T, a local average is an ensemble average over the local conformational space

$$\begin{array}{ccc}\hfill {〈P〉}_L& =& \frac{1}{Q_{\mathrm{L}}}\sum _{\Omega \in \mathbf{L}}P\left(\Omega \right)e^{-E_{\mathrm{p}}/kT}\approx \frac{1}{t_L}\sum _{t-t_L}^{t}P\left(\tau \right)\hfill \\ & \approx & \left(1-\frac{\delta t}{t_L}\right)\tilde{P}(t-\delta t)+\frac{\delta t}{t_L}P\left(t\right)=\tilde{P}\left(t\right).\hfill \end{array}$$ (5)

Here, P represents any conformational property. E_p is the potential energy at conformation Ω. $Q_{\mathrm{L}}={\sum }_{\Omega \in \mathbf{L}}{e}^{-(E_{\mathrm{p}}/kT)}$ is called the local partition function. As shown in Eq. 5, for computational feasibility, this local ensemble average is approximately calculated as a time average over a local average time, t_L, which is further approximately calculated as an evolving average. This evolving average is denoted with a “∼” cap: $\tilde{P}$. Because all local averages in this work are calculated as the evolving averages, we also use “〈P〉_L” to represent evolving averages when the cap “∼” is not easy to print.

Through the local averaging, high-frequency components are suppressed and low-frequency components remain. Therefore, $\tilde{P}$ represents the low-frequency portion of property P. Correspondingly, the high-frequency property is the deviation from the low-frequency property, $P-\tilde{P}$.

With the evolving averaging, many low-frequency properties can be obtained efficiently in a molecular simulation, for example, low-frequency forces

$$\begin{array}{c}\hfill {\tilde{\mathbf{f}}}_i\left(t\right)=\left(1-\frac{\delta t}{t_L}\right){\tilde{\mathbf{f}}}_i(t-\delta t)+\frac{\delta t}{t_L}{\mathbf{f}}_i\left(t\right),\end{array}$$ (6)

low-frequency momenta

$$\begin{array}{c}\hfill {\tilde{\mathbf{p}}}_i\left(t\right)=\left(1-\frac{\delta t}{t_L}\right){\tilde{\mathbf{p}}}_i(t-\delta t)+\frac{\delta t}{t_L}{\mathbf{p}}_i\left(t\right),\end{array}$$ (7)

and low-frequency potential energies

$$\begin{array}{c}\hfill {\tilde{E}}_{\mathrm{p}}\left(t\right)=\left(1-\frac{\delta t}{t_L}\right){\tilde{E}}_{\mathrm{p}}(t-\delta t)+\frac{\delta t}{t_L}{E}_{\mathrm{p}}\left(t\right).\end{array}$$ (8)

We can calculate some derived low-frequency quantities from these low-frequency properties, such as the low-frequency temperature,

$$\begin{array}{c}\hfill \tilde{T}=\frac{1}{N_{\mathrm{DF}}k}〈\sum \frac{{\tilde{\mathbf{p}}}_i^2}{m_i}〉.\end{array}$$ (9)

Here, N_DF is the number of degrees of freedom in all conformational spaces. m_i is the mass of particle i and the summation runs over all atoms in the system. The low-frequency temperature, $\tilde{T}$, measures the kinetic energy of the low-frequency motion in the temperature unit, K. Similarly, $T-\tilde{T}$ measures the kinetic energy of the high-frequency motion. Please note that $\tilde{T}$ is not T_lf. $\tilde{T}$ is calculated with the total number of degrees of freedom, N_DF, while T_lf should be calculated with only the number of degrees of freedom in the low-frequency space. A ratio of $\tilde{T}$ to T reflects the ratio of the kinetic energy of the low-frequency motion to the total kinetic energy.

The self-guided Langevin dynamics

The equation of motion for the self-guiding Langevin dynamics³ has the following form:

$$\begin{array}{c}\hfill {\dot{\mathbf{p}}}_i={\mathbf{f}}_i+{\mathbf{g}}_i-{\gamma }_i{\mathbf{p}}_i+{\mathbf{R}}_i,\end{array}$$ (10)

where ${\dot{\mathbf{p}}}_i$ and f_i are the time derivative of momentum and the interaction force of particle i, respectively. R_i is a random force, which is related to mass, m_i, the collision frequency, γ_i, and simulation temperature, T, by the following equation:

$$\begin{array}{c}\hfill ⟨{\mathbf{R}}_j\left(0\right){\mathbf{R}}_i\left(t\right)⟩=2m_{i}kT{\gamma }_i\delta \left(t\right){\delta }_{ij},\end{array}$$ (11)

where ${\delta }_{ij}=\{\begin{array}{cc}1,& i=j\\ 0,& i\ne j\end{array}$. The random force is independent in each direction.

In Eq. 10, g_i is called the guiding force. When g_i = 0, Eq. 10 reduces to the equation of motion for the Langevin dynamics. In SGLD simulations, g_i is calculated from the momentum

$$\begin{array}{c}\hfill {\mathbf{g}}_i\left(t\right)={\mathbf{g}}_i^{\mathrm{p}}\left(t\right)={\lambda }_i^{\mathrm{p}}{\gamma }_i\left({\tilde{\mathbf{p}}}_i\left(t\right)-{\xi }^{\mathrm{p}}{\mathbf{p}}_i\left(t\right)\right).\end{array}$$ (12)

Here, we use ${\mathbf{g}}_i^{\mathrm{p}}$ to represent the momentum-based guiding force to be distinct from the force-based guiding force, ${\mathbf{g}}_i^{\mathrm{f}}$, which will be introduced later. The parameter, ${\lambda }_i^{\mathrm{p}}$, is the momentum guiding factor. A subscript “i” indicates that ${\lambda }_i^{\mathrm{p}}$ can be set differently for different atoms. The parameter, ξ^p, is an energy conservation factor used to cancel any energy input from the guiding force

$$\begin{array}{c}\hfill \sum _i{\mathbf{g}}_i·{\dot{\mathbf{r}}}_i=\sum _i{\lambda }_i^{\mathrm{p}}{\gamma }_i{\tilde{\mathbf{p}}}_i·{\dot{\mathbf{r}}}_i-{\xi }^{\mathrm{p}}\sum _i{\lambda }_i^{\mathrm{p}}{\gamma }_i{\mathbf{p}}_i·{\dot{\mathbf{r}}}_i=0.\end{array}$$ (13)

Here, the summation runs over all particles in a simulation system. From Eq. 13, we have

$$\begin{array}{c}\hfill {\xi }^{\mathrm{p}}=\frac{{\sum }_i{\lambda }_i^{\mathrm{p}}{\gamma }_i{\tilde{\mathbf{p}}}_i·{\dot{\mathbf{r}}}_i}{{\sum }_i{\lambda }_i^{\mathrm{p}}{\gamma }_i{\mathbf{p}}_i·{\dot{\mathbf{r}}}_i}.\end{array}$$ (14)

The guiding forces defined by Eqs. 12, 13 produce no net work to a simulation system. They act in a direction orthogonal to the velocities. The ${\lambda }_i^{\mathrm{p}}{\gamma }_i{\tilde{\mathbf{p}}}_i\left(t\right)$ term accelerates the low-frequency motion, and the $-{\lambda }_i^{\mathrm{p}}{\gamma }_i{\xi }^{\mathrm{p}}{\mathbf{p}}_i\left(t\right)$ term dumps the high-frequency motion. Overall, the thermal temperature is maintained.

Conformational distribution in SGLD

In SGLD simulations, the guiding force has two effects in both the low-frequency conformational space and the high-frequency conformational space. First, it may correlate with the energy surface to have certain bias effects. The effective energy surfaces can be expressed as E_lf = λ_lf〈E_p〉_L and E_hf = λ_hf(E_p − 〈E_p〉_L). The factors, λ_lf and λ_hf, are called the low-frequency energy factor and the high-frequency energy factor, respectively. Second, the guiding force enhances motions in the low-frequency conformational space and reduces motions in the high-frequency conformational space. These effects cause changes in the effective temperatures in the two conformational spaces: T_lf = T/χ_lf and T_hf = T/χ_hf. The factors,χ_lfand χ_hf, are called the low-frequency collision factor and the high-frequency collision factor, respectively. Therefore, according to Eq. 3, the configurational partition function of a SGLD simulation has the following form:

$$\begin{array}{ccc}\hfill {\Theta }_{\mathrm{SGLD}}& =& \sum _{\Omega }\exp \left(-{\lambda }_{\mathrm{lf}}{\chi }_{\mathrm{lf}}\frac{{⟨E_{\mathrm{p}}⟩}_{\mathrm{L}}}{kT}-{\lambda }_{\mathrm{hf}}{\chi }_{\mathrm{hf}}\frac{E_{\mathrm{p}}-{⟨E_{\mathrm{p}}⟩}_L}{kT}\right)\hfill \\ & \approx & \sum _{\Omega }\exp \left(-{\lambda }_{\mathrm{lf}}{\chi }_{\mathrm{lf}}\frac{{\tilde{E}}_{\mathrm{p}}}{kT}-{\lambda }_{\mathrm{hf}}{\chi }_{\mathrm{hf}}\frac{E_{\mathrm{p}}-{\tilde{E}}_{\mathrm{p}}}{kT}\right).\hfill \end{array}$$ (15)

Here, the summation is over all microscopic states. For computational feasibility, the local average potential energy is approximated with the evolving average calculated with Eq. 8. This approximation makes it computationally feasible to estimate conformational distributions in the SGLD simulations.

The factors, λ_lf, λ_hf, χ_lf, and χ_hf, are related to the guiding force and the simulation systems. Their direct relations with simulation conditions are difficult to derive. Instead, based on their definitions, we can calculate them from quantities observable in the SGLD simulations. Through the local averaging, the equation of motion (Eq. 10) can be separated into that in the low-frequency conformational space,

$$\begin{array}{c}\hfill {\dot{\tilde{\mathbf{p}}}}_i={\tilde{\mathbf{f}}}_i+{\tilde{\mathbf{g}}}_i-{\gamma }_i{\tilde{\mathbf{p}}}_i+{\tilde{\mathbf{R}}}_i,\end{array}$$ (16)

and that in the high-frequency conformational space,

$$\begin{array}{c}\hfill {\dot{\mathbf{p}}}_i-{\dot{\tilde{\mathbf{p}}}}_i={\mathbf{f}}_i-{\tilde{\mathbf{f}}}_i+{\mathbf{g}}_i-{\tilde{\mathbf{g}}}_i-{\gamma }_i({\mathbf{p}}_i-{\tilde{\mathbf{p}}}_i)+{\mathbf{R}}_i-{\tilde{\mathbf{R}}}_i.\end{array}$$ (17)

These two equations correspond to motions on energy surfaces E_lf and E_hf, respectively. Based on the force-energy relation, we have

$$\begin{array}{c}\hfill {\tilde{\mathbf{f}}}_i+{\tilde{\mathbf{g}}}_i-{\gamma }_i{\tilde{\mathbf{p}}}_i\approx -\frac{d}{d{\mathbf{r}}_i}{E}_{\mathrm{lf}}\equiv -{\lambda }_{\mathrm{lf}}\frac{d}{d{\mathbf{r}}_i}{\tilde{E}}_{\mathrm{p}}\approx {\lambda }_{\mathrm{lf}}{\tilde{\mathbf{f}}}_i,\end{array}$$ (18)

$$\begin{array}{ccc}\hfill {\mathbf{f}}_i-{\tilde{\mathbf{f}}}_i+{\mathbf{g}}_i-{\tilde{\mathbf{g}}}_i-{\gamma }_i({\mathbf{p}}_i-{\tilde{\mathbf{p}}}_i)& \approx & -\frac{d}{d{\mathbf{r}}_i}{E}_{\mathrm{hf}}\equiv -{\lambda }_{\mathrm{hf}}\frac{d}{d{\mathbf{r}}_i}(E_{\mathrm{p}}-{\tilde{E}}_{\mathrm{p}})\hfill \\ & \approx & {\lambda }_{\mathrm{hf}}({\mathbf{f}}_i-{\tilde{\mathbf{f}}}_i).\hfill \end{array}$$ (19)

To achieve numerical stability, we multiply both sides of Eq. 18 by ${\tilde{\mathbf{f}}}_i$ and both sides of Eq. 19 by ${\mathbf{f}}_i-{\tilde{\mathbf{f}}}_i$. After summing over all particles and all simulation conformations, we obtain the following expressions:

$$\begin{array}{c}\hfill {\lambda }_{\mathrm{lf}}=1+\frac{〈{\sum }_i\left({\tilde{\mathbf{g}}}_i-{\gamma }_i{\tilde{\mathbf{p}}}_i\right){\tilde{\mathbf{f}}}_i〉}{〈{\sum }_i{\tilde{\mathbf{f}}}_i{\tilde{\mathbf{f}}}_i〉},\end{array}$$ (20)

$$\begin{array}{c}\hfill {\lambda }_{\mathrm{hf}}=1+\frac{〈{\sum }_i\left({\mathbf{g}}_i-{\tilde{\mathbf{g}}}_i-{\gamma }_i({\mathbf{p}}_i-{\tilde{\mathbf{p}}}_i)\right)({\mathbf{f}}_i-{\tilde{\mathbf{f}}}_i)〉}{〈{\sum }_i({\mathbf{f}}_i-{\tilde{\mathbf{f}}}_i)({\mathbf{f}}_i-{\tilde{\mathbf{f}}}_i)〉}.\end{array}$$ (21)

From Eqs. 20, 21, we can see that λ_lf represents the average projections of the total low-frequency force onto the low-frequency interaction forces and λ_hf represents the average projections of the total high-frequency force onto the high-frequency interaction forces.

The factors, χ_lf and χ_hf, describe the temperature change in low- and high-frequency conformational spaces

$$\begin{array}{c}\hfill {\chi }_{\mathrm{lf}}=\frac{T}{T_{l\mathrm{f}}}=\frac{{\tilde{T}}_0}{\tilde{T}},\end{array}$$ (22)

$$\begin{array}{c}\hfill {\chi }_{\mathrm{hf}}=\frac{T}{T_{\mathrm{hf}}}=\frac{T-{\tilde{T}}_0}{T-\tilde{T}}.\end{array}$$ (23)

Here, we assume the temperatures in the low-frequency and high-frequency conformational spaces are proportional to the low-frequency and high-frequency temperatures. ${\tilde{T}}_0$ is the low-frequency temperature when ${\lambda }_i^{\mathrm{p}}=0$, i.e., in a LD simulation. We call ${\tilde{T}}_0$ the reference low-frequency temperature. To calculate χ_lf and χ_hf with above equations, one need to know ${\tilde{T}}_0$ from a separate SGLD simulation with ${\lambda }_i^{\mathrm{p}}=0$ which is actually a LD simulation. Based on the definition, we know ${\tilde{T}}_0$ depends on the simulation conditions and the local average time, t_L.

Alternatively, we can calculate χ_lf and χ_hf directly from a SGLD simulation. From Eq. 11, we know that the temperature is inversely proportional to the collision frequency, if the random forces remain the same. Therefore, a change in temperature indicates a change in the effective collision frequency. For the low-frequency motion, a change in temperature from T to T_lf = T/χ_lf corresponds to a change in the collision frequency from γ_i to χ_lfγ_i. Similarly, for the high-frequency motion, a change in temperature from T to T_hf = T/χ_hf corresponds to a change in the collision frequency from γ_i to χ_hfγ_i. The guiding forces in the equations of motion (Eqs. 16, 17) behave like a modification in the collision frequency

$$\begin{array}{c}\hfill {\tilde{\mathbf{g}}}_i-{\gamma }_i{\tilde{\mathbf{p}}}_i\approx -{\chi }_{\mathrm{lf}}{\gamma }_i{\tilde{\mathbf{p}}}_i,\end{array}$$ (24)

$$\begin{array}{c}\hfill {\mathbf{g}}_i-{\tilde{\mathbf{g}}}_i-{\gamma }_i({\mathbf{p}}_i-{\tilde{\mathbf{p}}}_i)\approx -{\chi }_{\mathrm{hf}}{\gamma }_i({\mathbf{p}}_i-{\tilde{\mathbf{p}}}_i).\end{array}$$ (25)

To achieve numerical stability, we multiply both sides of Eq. 24 by ${\gamma }_i{\tilde{\mathbf{p}}}_i$ and both sides of Eq. 25 by ${\gamma }_i({\mathbf{p}}_i-{\tilde{\mathbf{p}}}_i)$. After summing over all particles and all simulation conformations, we obtain the following expressions:

$$\begin{array}{c}\hfill {\chi }_{\mathrm{lf}}\approx 1-\frac{〈{\sum }_i{\gamma }_i{\tilde{\mathbf{g}}}_i·{\tilde{\mathbf{p}}}_i〉}{〈{\sum }_i{\gamma }_i^2{\tilde{\mathbf{p}}}_i·{\tilde{\mathbf{p}}}_i〉},\end{array}$$ (26)

$$\begin{array}{c}\hfill {\chi }_{\mathrm{hf}}\approx 1-\frac{〈{\sum }_i{\gamma }_i({\mathbf{g}}_i-{\tilde{\mathbf{g}}}_i)·({\mathbf{p}}_i-{\tilde{\mathbf{p}}}_i)〉}{〈{\sum }_i{\gamma }_i^2({\mathbf{p}}_i-{\tilde{\mathbf{p}}}_i)·({\mathbf{p}}_i-{\tilde{\mathbf{p}}}_i)〉}.\end{array}$$ (27)

It is more accurate to estimate χ_lf and χ_hf from ${\tilde{T}}_0$ and $\tilde{T}$ using Eqs. 22, 23, if ${\tilde{T}}_0$ is available from a separate SGLD simulation with ${\lambda }_i^{\mathrm{p}}=0$. Otherwise, they can be estimated from Eqs. 26, 27 without knowing ${\tilde{T}}_0$.

From the SGLD partition function (Eq. 15), we can calculate the weighting factor, w_SGLD, for each conformation

$$\begin{array}{c}\hfill w_{\mathrm{SGLD}}=\exp \left(\left({\lambda }_{\mathrm{lf}}{\chi }_{\mathrm{lf}}-1\right)\frac{{\tilde{E}}_{\mathrm{p}}}{kT}+\left({\lambda }_{\mathrm{hf}}{\chi }_{\mathrm{hf}}-1\right)\frac{E_{\mathrm{p}}-{\tilde{E}}_{\mathrm{p}}}{kT}\right).\end{array}$$ (28)

Any canonical ensemble average, 〈P〉, can be calculated in a SGLD simulation as a weighted average

$$\begin{array}{c}\hfill 〈P〉=\frac{{〈P{w}_{\mathrm{SGLD}}〉}_{\mathrm{SGLD}}}{{〈w_{\mathrm{SGLD}}〉}_{\mathrm{SGLD}}}.\end{array}$$ (29)

In SGLD simulations, the thermal motions in the low-frequency and high-frequency conformational spaces are scaled by χ_lf and χ_hf, respectively. The conformational searching ability increases with the thermal temperature in the low-frequency conformational space. Because SGLD simulations do not change the simulation temperature, the thermal motion in the high-frequency conformational space decreases as the low-frequency conformational space increases. Therefore, the conformational searching ability can approximately be expressed as inversely proportional to χ_lf and directly proportional to χ_hf. To describe the conformational searching ability of a SGLD simulation, we define the self-guiding temperature as the following form:

$$\begin{array}{c}\hfill T_{\mathrm{sg}}=\frac{{\chi }_{\mathrm{hf}}}{{\chi }_{\mathrm{lf}}}T=\frac{\tilde{T}(T-{\tilde{T}}_0)}{{\tilde{T}}_0(T-\tilde{T})}T.\end{array}$$ (30)

The self-guiding temperature, T_sg, provides a qualitative measure of the conformational searching ability in the unit of temperature. An SGLD simulation with a self-guiding temperature of T_sg has a conformational searching ability comparable to that in a high temperature simulation at T = T_sg. As can be seen from Eq. 30, for a LD simulation, based on the definition, $\tilde{T}={\tilde{T}}_0$, we have T_sg = T. For an SGLD simulation with λ > 0, we have an increased low-frequency motion, $\tilde{T}>{\tilde{T}}_0$ ; therefore, T_sg > T. And with λ < 0, we have $\tilde{T}<{\tilde{T}}_0$; thus, T_sg < T. T_sg can be used as a guidance to choose the value of λ, which lacks physical meaning. For example, it is reasonable to choose a value of λ to reach T_sg = 2T. However, when λ is large and T_sg is too large as compared to T, it is difficult to obtain an accurate canonical ensemble through the reweighting with Eqs. 28, 29. Therefore, λ should be chosen to balance the acceleration in conformational searching and the accuracy in conformational reweighting.

Force-momentum-based self-guided Langevin dynamics

The SGMD method utilizes the local average forces, while the SGLD method uses the local average momentum to calculate the guiding force to achieve accelerated conformational searching. These two types of guiding forces have opposite bias effects on the low-frequency energy surface. The low-frequency force favors low ${\tilde{E}}_{\mathrm{p}}$ states, just as normal forces do, while the low-frequency momentum favors high ${\tilde{E}}_{\mathrm{p}}$ states, just as temperature does. These two types of low-frequency properties can be combined in such a way that the bias effects cancel each other. We call this kind of SGLD simulation as the SGLDfp.

In SGLDfp, the guiding force, g_i, is a combination of forces and momentums in the following form:

$$\begin{array}{c}\hfill {\mathbf{g}}_i\left(t\right)={\mathbf{g}}_i^{\mathrm{f}}\left(t\right)+{\mathbf{g}}_i^{\mathrm{p}}\left(t\right)={\lambda }^{\mathrm{f}}{\tilde{\mathbf{f}}}_i\left(t\right)-{\xi }^{\mathrm{f}}{\mathbf{f}}_i\left(t\right)+{\lambda }_i^{\mathrm{p}}{\gamma }_i\left({\tilde{\mathbf{p}}}_i\left(t\right)-{\xi }^{\mathrm{p}}{\mathbf{p}}_i\left(t\right)\right).\end{array}$$ (31)

Here, λ^f is defined as the force guiding factor and ξ^f is defined as the force damping factor. The energy conservation factor, ξ^p, is calculated according to Eq. 13 with the guiding force defined by Eq. 31

$$\begin{array}{c}\hfill {\xi }^{\mathrm{p}}=\frac{{\sum }_i{\left({\lambda }^{\mathrm{f}}{\tilde{\mathbf{f}}}_i-{\xi }^{\mathrm{f}}{\mathbf{f}}_i+{\lambda }_i^{\mathrm{p}}{\gamma }_i\tilde{\mathbf{p}}\right)}_i·{\dot{\mathbf{r}}}_i}{{\sum }_i{\lambda }_i^{\mathrm{p}}{\gamma }_i{\mathbf{p}}_i·{\dot{\mathbf{r}}}_i}.\end{array}$$ (32)

According to Eqs. 20, 21, the parameters λ_lf and λ_hf have the following relation to λ^f and ξ^f:

$$\begin{array}{ccc}\hfill {\lambda }_{\mathrm{lf}}& =& 1+\frac{〈{\sum }_i\left({\tilde{\mathbf{g}}}_i^{\mathrm{p}}-{\gamma }_i{\tilde{\mathbf{p}}}_i\right){\tilde{\mathbf{f}}}_i〉}{〈{\sum }_i{\tilde{\mathbf{f}}}_i{\tilde{\mathbf{f}}}_i〉}+\frac{〈{\sum }_i{⟨{\tilde{\mathbf{f}}}_i⟩}_L{\tilde{\mathbf{f}}}_i〉}{〈{\sum }_i{\tilde{\mathbf{f}}}_i{\tilde{\mathbf{f}}}_i〉}{\lambda }^{\mathrm{f}}-{\xi }^{\mathrm{f}}\hfill \\ & =& {\lambda }_{\mathrm{lf}}^{\mathrm{p}}+{\kappa }_{\mathrm{lf}}{\lambda }^{\mathrm{f}}-{\xi }^{\mathrm{f}},\hfill \end{array}$$ (33)

$$\begin{array}{ccc}\hfill {\lambda }_{\mathrm{hf}}& =& 1+\frac{〈{\sum }_i\left({\mathbf{g}}_i^{\mathrm{p}}-{\tilde{\mathbf{g}}}_i^{\mathrm{p}}-{\gamma }_i({\mathbf{p}}_i-{\tilde{\mathbf{p}}}_i)\right)({\mathbf{f}}_i-{\tilde{\mathbf{f}}}_i)〉}{〈{\sum }_i({\mathbf{f}}_i-{\tilde{\mathbf{f}}}_i)({\mathbf{f}}_i-{\tilde{\mathbf{f}}}_i)〉}\hfill \\ & & +\frac{〈{\sum }_i{⟨{\mathbf{f}}_i-{\tilde{\mathbf{f}}}_i⟩}_L({\mathbf{f}}_i-{\tilde{\mathbf{f}}}_i)〉}{〈{\sum }_i({\mathbf{f}}_i-{\tilde{\mathbf{f}}}_i)({\mathbf{f}}_i-{\tilde{\mathbf{f}}}_i)〉}{\lambda }^{\mathrm{f}}-{\xi }^{\mathrm{f}}={\lambda }_{\mathrm{hf}}^{\mathrm{p}}+{\kappa }_{\mathrm{hf}}{\lambda }^{\mathrm{f}}-{\xi }^{\mathrm{f}}.\hfill \end{array}$$ (34)

Here, ${\lambda }_{\mathrm{lf}}^{\mathrm{p}}=1+⟨{\sum }_i\left({\tilde{\mathbf{g}}}_i^{\mathrm{p}}-{\gamma }_i{\tilde{\mathbf{p}}}_i\right){\tilde{\mathbf{f}}}_i⟩/⟨{\sum }_i{\tilde{\mathbf{f}}}_i{\tilde{\mathbf{f}}}_i⟩,{\lambda }_{\mathrm{hf}}^{\mathrm{p}}=1+⟨{\sum }_i\left({\mathbf{g}}_i^{\mathrm{p}}-{\tilde{\mathbf{g}}}_i^{\mathrm{p}}-{\gamma }_i({\mathbf{p}}_i-{\tilde{\mathbf{p}}}_i)\right)({\mathbf{f}}_i-{\tilde{\mathbf{f}}}_i)⟩/⟨{\sum }_i({\mathbf{f}}_i-{\tilde{\mathbf{f}}}_i)({\mathbf{f}}_i-{\tilde{\mathbf{f}}}_i)⟩$, ${\kappa }_{\mathrm{lf}}=⟨{\sum }_i{⟨{\tilde{\mathbf{f}}}_i⟩}_L{\tilde{\mathbf{f}}}_i⟩/⟨{\sum }_i{\tilde{\mathbf{f}}}_i{\tilde{\mathbf{f}}}_i⟩$, and ${\kappa }_{\mathrm{hf}}=⟨{\sum }_i{⟨{\mathbf{f}}_i-{\tilde{\mathbf{f}}}_i⟩}_L({\mathbf{f}}_i-{\tilde{\mathbf{f}}}_i)⟩/⟨{\sum }_i({\mathbf{f}}_i-{\tilde{\mathbf{f}}}_i)({\mathbf{f}}_i-{\tilde{\mathbf{f}}}_i)⟩$. These quantities can be estimated from simulations.

We can adjust the values of λ^f and ξ^f to make

$$\begin{array}{c}\hfill {\chi }_{\mathrm{lf}}{\lambda }_{\mathrm{lf}}=1\end{array}$$ (35)

and

$$\begin{array}{c}\hfill {\chi }_{\mathrm{hf}}{\lambda }_{\mathrm{hf}}=1.\end{array}$$ (36)

Equation 35 will result in a canonical-like conformational distribution in the low-frequency space, and Eq. 36 will result in a canonical-like conformational distribution in the high-frequency space. When both Eqs. 35, 36 are satisfied, the partition function reduces to that of the canonical ensemble

$$\begin{array}{ccc}\hfill {\Theta }_{\mathrm{SGLDfp}}& =& \sum \exp \left(-{\chi }_{\mathrm{lf}}{\lambda }_{\mathrm{lf}}\frac{{\tilde{E}}_{\mathrm{p}}}{kT}-{\chi }_{\mathrm{hf}}{\lambda }_{\mathrm{hf}}\frac{E_{\mathrm{p}}-{\tilde{E}}_{\mathrm{p}}}{kT}\right)\hfill \\ & =& \sum \exp \left(-\frac{{\tilde{E}}_{\mathrm{p}}}{kT}-\frac{E_{\mathrm{p}}-{\tilde{E}}_{\mathrm{p}}}{kT}\right)=Q_{\mathit{NVT}}.\hfill \end{array}$$ (37)

From Eqs. 33, 34, we can solve

$$\begin{array}{c}\hfill {\lambda }^{\mathrm{f}}\approx \frac{1}{{\kappa }_{\mathrm{lf}}-{\kappa }_{\mathrm{hf}}}\left(\frac{1}{{\chi }_{\mathrm{lf}}}-\frac{1}{{\chi }_{\mathrm{hf}}}-{\lambda }_{\mathrm{lf}}^{\mathrm{p}}+{\lambda }_{\mathrm{hf}}^{\mathrm{p}}\right),\end{array}$$ (38)

$$\begin{array}{c}\hfill {\xi }^{\mathrm{f}}\approx \frac{{\kappa }_{\mathrm{lf}}}{{\kappa }_{\mathrm{lf}}-{\kappa }_{\mathrm{hf}}}\left({\lambda }_{\mathrm{hf}}^{\mathrm{p}}-\frac{1}{{\chi }_{\mathrm{hf}}}\right)-\frac{{\kappa }_{\mathrm{hf}}}{{\kappa }_{\mathrm{lf}}-{\kappa }_{\mathrm{hf}}}\left({\lambda }_{\mathrm{lf}}^{\mathrm{p}}-\frac{1}{{\chi }_{\mathrm{lf}}}\right).\end{array}$$ (39)

This solution is approximate because ${\lambda }_{\mathrm{lf}}^{\mathrm{p}}$, ${\lambda }_{\mathrm{hf}}^{\mathrm{p}}$, χ_lf, and χ_hf also depend on λ^f and ξ^f. In many cases, Eqs. 38, 39 can further be simplified with approximations κ_lf ≈ 1 and κ_hf ≈ 0.

By using λ^f and ξ^f calculated from Eqs. 38, 39, we can obtain a conformational distribution similar to that of the canonical ensemble as shown by Eq. 37. Therefore, ensemble average properties can be directly estimated from a SGLDfp simulation

$$〈P〉\approx {〈P〉}_{\mathrm{SGLDfp}}.$$

Four parameters, ${\lambda }_i^{\mathrm{p}}$, ξ^p, λ^f, ξ^f, are used to define the guiding force in Eq. 31. To maintain a canonical ensemble, only one parameter, e.g., ${\lambda }_i^{\mathrm{p}}$, is independent while the others depend on it. If we are interested in maintaining a canonical distribution only in the low-frequency conformational space, in addition to ${\lambda }_i^{\mathrm{p}}$, we can adjust either λ^for ξ^f to satisfy Eq. 35 and at the same time to achieve an optimal efficiency in conformational searching. In this work, we only focus on the case of maintaining a full canonical ensemble. A leap-frog Verlet simulation algorithm of the SGLDfp method is described in the Appendix. The force guiding parameters λ^f and ξ^f, as well as ${\lambda }_{\mathrm{lf}}^{\mathrm{p}}$, ${\lambda }_{\mathrm{hf}}^{\mathrm{p}}$, χ_lf, and χ_hf, are estimated during simulation according to Eqs. 26, 27, 33, 34, 35, 36, 37, 38, 39, with the ensemble average properties in these equations replaced by long evolving averages calculated in the following way:

$$\begin{array}{c}\hfill \overline{P}\left(t\right)=\left(1-\frac{\delta t}{t_{\mathrm{est}}}\right)\overline{P}(t-\delta t)+\frac{\delta t}{t_{\mathrm{est}}}P\left(t\right).\end{array}$$ (40)

Here, P(t) represents an instantaneous value of any property, and $\overline{P}\left(t\right)$ represents its estimated average. The estimation time, t_est, determines the estimation accuracy. Typically, we set t_est = 10t_L.

To run a SGLDfp simulation, one can either set ${\lambda }_i^{\mathrm{p}}$ and let λ^f and ξ^f be calculated from Eqs. 37, 38, or set a target self-guiding temperature,²²$T_{\mathrm{sg}}^0$, and adjust ${\lambda }_i^{\mathrm{p}}$ to make$T_{\mathrm{sg}}\to T_{\mathrm{sg}}^0$. Because an increase in ${\lambda }_i^{\mathrm{p}}$ always results in an increase in $\tilde{T}$, and so in T_sg, ${\lambda }_i^{\mathrm{p}}$ can be adjusted in the following way to make T_sg approach $T_{\mathrm{sg}}^0$:

$$\begin{array}{c}\hfill {\lambda }_i^{\mathrm{p}}\left(t\right)={\lambda }_i^{\mathrm{p}}(t-\delta t)+\frac{\delta t}{t_{\mathrm{est}}}\frac{T_{\mathrm{sg}}^0-T_{\mathrm{sg}}}{T}.\end{array}$$ (41)

Then, λ^f and ξ^f will be calculated according to Eqs. 37, 38 in the same way as when ${\lambda }_i^{\mathrm{p}}$ is set. Because T_sg is a derived quantity, its value range is limited by the simulation temperature, system size, and other SGLDfp parameters. The value of $T_{\mathrm{sg}}^0$ must be set within its T_sg limits to produce a converging, ${\lambda }_i^{\mathrm{p}}$. For example, one may set $T_{\mathrm{sg}}^0=1.2T$ for a SGLDfp simulation. For systems of unknown T_sg limits, it is suggested to set ${\lambda }_i^{\mathrm{p}}$ instead of $T_{\mathrm{sg}}^0$.

SIMULATION DETAILS

To demonstrate the application of the SGLDfp simulation method, we report the results for several simple systems. A leap-frog Verlet algorithm for the SGLDfp simulation shown in the Appendix has been implemented into CHARMM (Refs. ²⁶ and ²⁷) version 36. Because a SGLDfp simulation involves extra calculation only in the propagation of the equation of motion as compared to a normal LD simulation, the cost of SGLDfp simulation is almost identical to a LD simulation for the same number of time steps. SGLDfp simulations, as well as SGLD simulations, do use additional memory due to the need to store the guiding forces, as well as some arrays for the weighting factor calculation. In all SGLD and SGLDfp simulations reported here, we set the momentum guiding factor, ${\lambda }_i^{\mathrm{p}}$, instead of a target self-guiding temperature, $T_{\mathrm{sg}}^0$, for an easy comparison. Because only ${\lambda }_i^{\mathrm{p}}$ is set and is the same for all particles, in the following description the guiding factor, λ, represents the momentum guiding factor, ${\lambda }_i^{\mathrm{p}}$.

RESULTS AND DISCUSSIONS

The SGLDfp method includes forces in its guiding force to compensate the perturbation on the conformational distribution caused by the momentum-based guiding force. As described in the Theory and Method section, a series of approximations is introduced to make a SGLDfp simulation possible. To validate these approximations and to demonstrate the conformational searching efficiency of this method, we present the simulation results of three model systems.

The skewed double well system

A skewed double well system represents the simplest system with an energy barrier to cross. This system has only one particle, and the particle moves on a skewed double well energy surface of the following function:

$$\begin{array}{c}\hfill {\varepsilon }_{\mathrm{p}}(x,y,z)=a(x^2+z^2)+b{y}^2{(y-w)}^2+cy.\end{array}$$ (42)

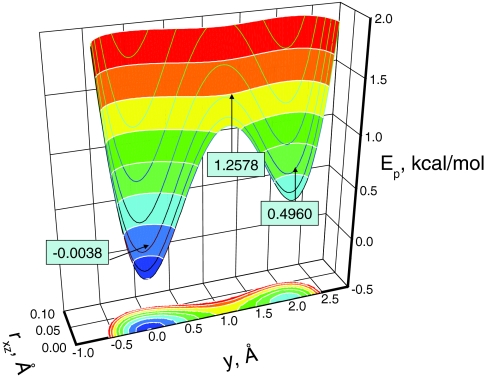
In this work, we chose a = 500 kcal/(molŲ), b = 1 kcal/(molÅ⁴), c = 0.25 kcal/(molÅ), and w = 2 Å. Figure 1 shows the energy surface of this double well potential. This energy surface is designed in such a way that it restricts the particle to move near the y axis with two energy minimums of different depths, −0.0038 kcal/mol and 0.4960 kcal/mol, along the y axis at (0, −0.0299 Å, 0) and (0, 1.9672 Å, 0), respectively. The potential is symmetric about the y axis with a strong dependence on the distance, r_xz, from the y axis, where $r_{\mathrm{xz}}=\sqrt{x^2+z^2}$. The minimum transition energy from one well to the other well is 1.2578 kcal/mol at (0, 1.0627 Å, 0) between the two wells. Such a design forces the particle to have a high-frequency motion in the x–z direction and a low-frequency motion in the y direction. An argon atom was used to represent the particle. The simulations were carried out with a local average time, t_L = 0.2 ps. A time step of 1 fs was used and the simulation length was 1000 ns for each simulation. The collision frequency was 10/ps unless otherwise noted.

Figure 1.

The energy surface of the skewed double well potential. The potential is symmetric about the y axis and $r_{xz}=\sqrt{x^2+z^2}$ is the distance to the y axis.

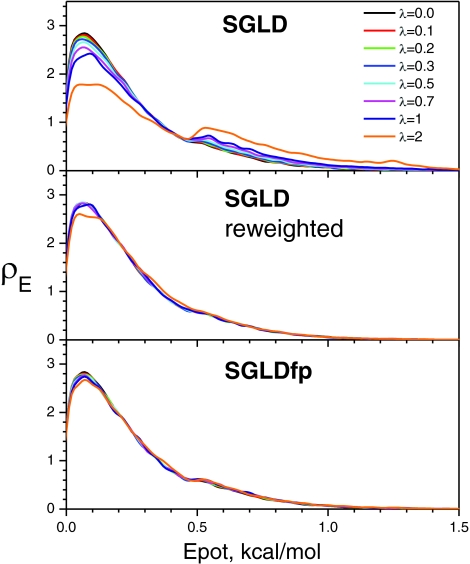
This system was simulated at 80 K with different guiding factors to examine the ensemble distributions from the SGLD and SGLDfp simulations. At 80 K, the average y-energy of the system is 0.107 kcal/mol. The energy barrier height from the average y-energy to the transition energy is 7.24 kT and the energy difference between the two wells is 3.14 kT. Figure 2 compares the potential energy distributions in the SGLD simulations and the SGLDfp simulations. To illustrate the deviations from the LD result, we show the SGLD and SGLDfp results with λ up to 2, far beyond the recommended range of λ < 1. In the SGLD simulations, as can be seen in the top panel of Fig. 2, as λ increases, the distribution decreases in the low energy region and increases in the high energy region. The middle panel of Fig. 2 shows the reweighted energy distributions.²² Clearly, all curves converge fairly well to the one with λ = 0, except for the case when the guiding factor is very large, λ = 2, validating the SGLD reweighting mechanism (Eqs. 28, 29) and in turn, validating the SGLD partition function (Eq. 15). The bottom panel of Fig. 2 shows the results from the SGLDfp simulations. The densities with different guiding factors converge together, even with λ = 2, proving that the SGLDfp simulations can preserve the energy distribution to a reasonable degree of accuracy.

Figure 2.

The potential energy distributions of the skewed double well system at different guiding factors. The collision frequency is 10/ps and the temperature is 80 K.

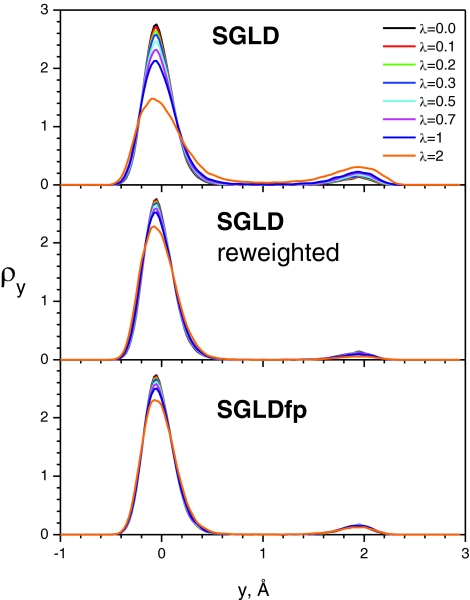
To further demonstrate the preservation of conformational distributions in SGLDfp simulations, we plot the conformational density as a function of the y coordinates in Fig. 3 at different guiding factors and in Fig. 4 at different local averaging times. The top panel of Fig. 3 shows the SGLD distributions at different guiding factors. There are two peaks with different heights, corresponding to the two skewed double wells. As λ increases, the left peak (the higher peak) decreases, while the right peak (the lower peak) grows. The middle panel of Fig. 3 shows the reweighted SGLD distributions. All distributions converge fairly well to the one with λ = 0, except for the one with λ = 2, validating the reweighting mechanism. The SGLDfp distributions are shown in the bottom panel of Fig. 3. The densities at different guiding factors almost overlap with each other, except for the one with λ = 2, proving that the SGLDfp simulation preserves the conformational distribution fairly well with λ < 1. When the guiding factor is too large, here, λ = 2, the approximation error becomes significant. Therefore, λ < 1 is recommended for the SGLD reweighting or the SGLDfp simulation.

Figure 3.

The y-coordinate distributions of the skewed double well system with different guiding factors. The local average time, t_L = 0.2 ps, is used for all SGLD and SGLDfp simulations. The collision frequency is 10/ps and the temperature is 80 K.

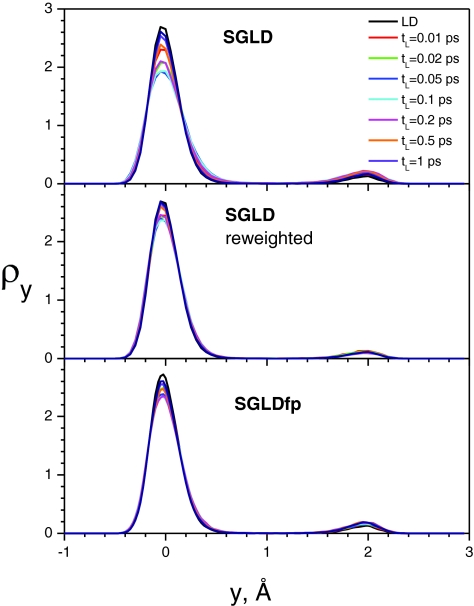
Figure 4.

The y-coordinate distributions of the skewed double well system with different local average times. The guiding factor, λ = 1, is used for all SGLD and SGLDfp simulations. The collision frequency is 10/ps and the temperature is 80 K.

In addition to the guiding factor, λ, the local average time, t_L, is another important parameter for SGLD and SGLDfp simulations. The local average time t_L determines the separation of the low-frequency and high-frequency properties. Figure 4 examines the distributions at various t_L values. The guiding factors are all set to λ = 1, except for the LD simulation which corresponds to a SGLD simulation with λ = 0. Again, as compared to the SGLD results (top panel), the reweighted SGLD results (middle panel) and the SGLDfp results (bottom panel) have much improved agreements with the LD result.

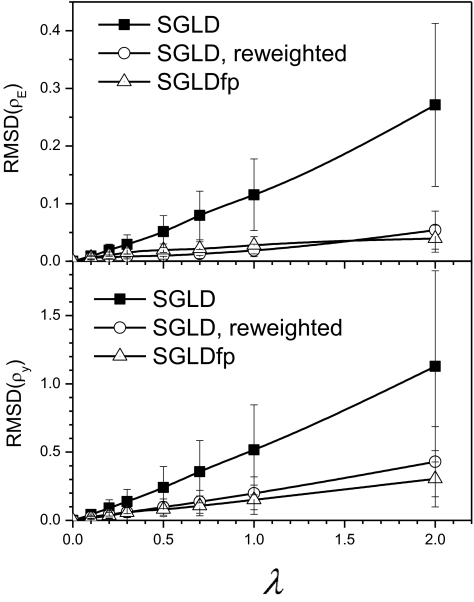
One should keep in mind that there are certain approximations in the SGLD reweighting and the SGLDfp method. The major approximations are the use of evolving averages (Equations 5, 40) to replace local averages in partition functions (Eqs. 15, 37), and to replace ensemble averages in the parameter calculations (Eqs. 26, 27, 33, 34, 38, 39). These approximations break down and cause significant errors when the guiding factor exceeds a certain range. To quantitatively compare the LD, SGLD, and SGLDfp results, we plot their root-mean-square deviations (RMSDs) in Fig. 5. The upper panel and the lower panel of Fig. 5 show the RMSDs of the energy distributions, δρ_E, and the RMSDs of the y distributions, δρ_y, respectively. The RMSDs of the SGLD results are much larger than that of the reweighted SGLD results and the SGLDfp results. The deviations of the SGLD and SGLDfp results increase with the guiding factor. These results confirm that λ < 1 is a recommended range for a reasonable accuracy to calculate ensemble average properties.

Figure 5.

Root-mean-square deviations of the SGLD and SGLDfp distributions from the LD distributions. The upper panel shows the deviations in the potential energy distributions shown in Fig. 2 and the lower panel shows the deviations in the y distributions shown in Fig. 3.

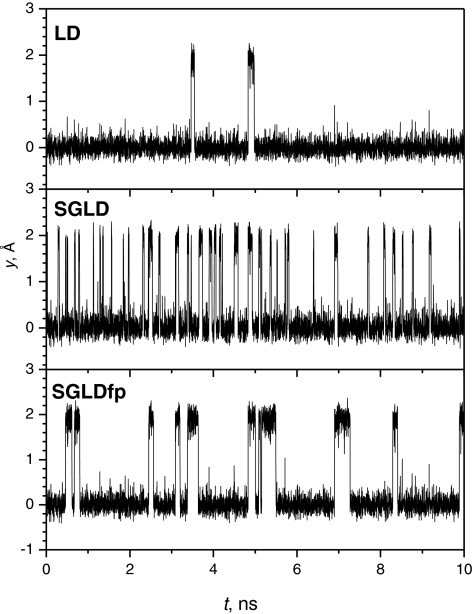
While the SGLDfp simulation preserves the ensemble distribution, it is interesting to see by how much it enhances conformational searching. Figure 6 shows the trajectories of the particle in the LD, SGLD, and SGLDfp simulations. Both the SGLD and SGLDfp simulations were run with a guiding factor, λ = 1. Clearly, both the SGLD and SGLDfp simulations increased transition rates as compared with the LD simulation. However, the SGLDfp simulation shows fewer transitions than the SGLD simulation.

Figure 6.

Trajectories of the particle in the skewed double well system during the LD, SGLD, and SGLDfp simulations. Here, t_L = 0.2 ps and λ = 1 are used for the SGLD and SGLDfp simulations. The collision frequency is 10/ps and the temperature is 80 K.

The collision frequency, γ, plays an important role in Langevin dynamics. It also plays an important role in SGLD and SGLDfp because it directly determines the strength of the guiding force (see Eqs. 12, 31). Through this skewed double well system, we can examine its effect on SGLD and SGLDfp simulations.

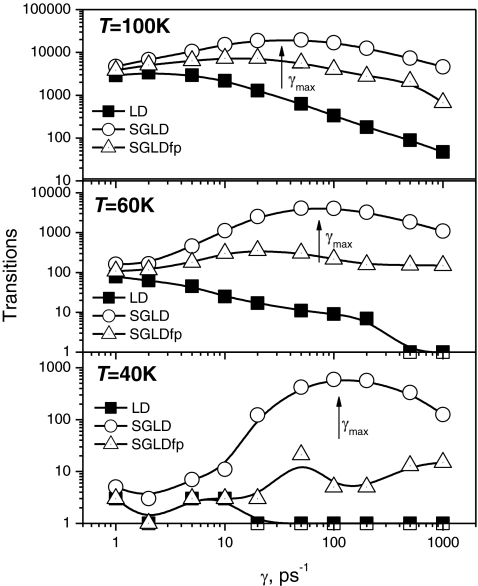
We performed a series of SGLD and SGLDfp simulations with λ = 1 at various γ and T, and the transition rates are shown in Fig. 7. For the convenience of plotting in a logarithm scale, the transition count starts with 1. A transition of 1 means that the particle has never crossed the energy barrier. The collision frequency controls the diffusion and the temperature controls the relative energy barrier heights. At T = 100 K, 60 K, and 40 K, the average y-energies are 0.152, 0.0793, and 0.0561 kcal/mol, respectively. The energy differences between the global minimum and the transition barrier are 6.35 kT, 10.58 kT, and 15.87 kT, and the relative barrier heights from the average y-energies to the transition barrier are 5.56 kT, 9.89 kT, and 15.1 kT at T = 100 K, 60 K, and 40 K, respectively.

Figure 7.

Transitions of the particle on the skewed double well potential at different collision frequencies and temperatures. A guiding factor of λ = 1 is used for all simulations. The transition count starts with 1. The simulation length is 1000 ns. The energy barrier heights from the y-average energies are 5.56kT at T = 100 K, 9.89kT at T = 60 K, and 15.1kT at T = 40 K.

In Fig. 7, we can see that the transition rates of the LD simulations generally decrease with γ at all temperatures. At 40 K, only a few transitions or no transitions at all are observed in the LD simulations. Higher γ reduces diffusion and slows down all events in LD simulations, regardless of their energy barriers. The transition rates of both the SGLD and SGLDfp simulations are higher than that in the LD simulations, except at T = 40 K and γ ≤ 10/ps where fewer than three transitions are observed for LD and SGLDfp and it is hard to tell the difference between LD and SGLDfp simulations. The accelerations increase with γ because the guiding force is proportional to γ, as shown in Eqs. 12, 31. Comparing the SGLD and the SGLDfp results, we can see that the SGLDfp simulations have much fewer transitions than the SGLD simulations. These results show that the SGLDfp method sacrifices the enhancement in conformational searching to maintain correct conformational distributions.

In Fig. 7, there are maximums in the transitions∼γ curves from the SGLD and SGLDfp simulations. These maximums are due to the competition of two control effects on the transition. One is the energy barrier effect and the other is the diffusion effect. An increase in γ will increase the guiding force, as well as the friction force. At low γ, the energy barrier controls the transition and an increase in the guiding force helps energy barrier crossing more than the slow down by the increase in the friction force. Therefore, an increase in γ results in more transitions. At high γ, the diffusion effect controls the transition and an increase in γ will result in fewer transitions. At γ_max, the energy barrier effect is balanced by the diffusion effect.

Alanine dipeptide

Alanine dipeptide is the simplest molecule that is relevant to proteins. The conformation of this molecule is mainly characterized by two dihedral angles, ϕ: C–N–Cα–C and ψ: N–Cα–C–N. The CHARMM all-atom force field²⁸ was used to describe the interactions. A distance-dependent dielectric constant of 4r was used to represent a solvent screening effect to simplify the example. The cutoff distance was set to 100 angstroms to avoid any cutoff effect in non-bonded interaction calculation within this small molecule.

All simulations were performed with a time step of 2 fs, and the SHAKE algorithm²⁴ was employed to fix bond lengths. Each simulation was 200 ns in length and conformations of every 2 ps were saved for post analysis. The SGLD and SGLDfp simulations were performed with a local average time of t_L = 0.2 ps and a temperature of 300 K. A collision frequency of 10/ps was used for all these simulations.

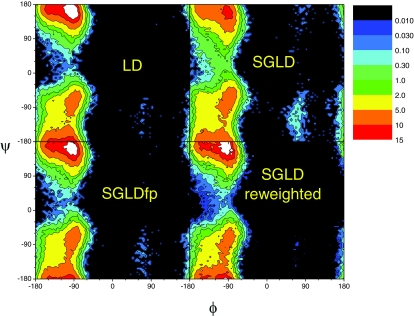
Figure 8 compares the ϕ–ψ dihedral angle distributions of the alanine dipeptide in the LD, SGLD, and SGLDfp simulations. To show the details in low density area, the contours are drawn in an exponential scale. For this small molecule at the simulation condition, LD can well sample the conformational space. There is a major peak at (−90°, 170°), and a secondary peak near (−90°, −70°). There is also a trace region around (70°, −120°). Comparing the LD and SGLD distributions, we can see the major peak from the SGLD simulation is significantly lower, while the trace region is much higher. The SGLD distribution has a broader baseline and the valley around ψ = 30° is less deep. After the reweighting, all characteristics of the LD distribution are recovered: the major peak is elevated, the trace region is reduced, and the baseline shrinks, which again, demonstrating that the SGLD distribution can be converted to the LD distribution through the reweighting. Comparing the ϕ–ψ distributions from the SGLDfp simulation and the LD simulation, we can clearly see that they agree with each other fairly well. The root-mean-square differences from the LD distribution are 1.08, 0.574, and 0.380 for the SGLD distributions before and after reweighting, and for the SGLDfp distribution, respectively.

Figure 8.

The ϕ–ψ dihedral angle distributions of the alanine dipeptide in the LD, SGLD, and SGLDfp simulations. A distant dependent dielectric constant, ɛ = 4r, is used to describe the solvation effect. The collision frequency is γ = 10/ps and the simulation temperature is 300 K. A guiding factor of λ = 1 is used for both the SGLD and SGLDfp simulations.

To demonstrate the conformational searching ability, we compare the SGLD and SGLDfp simulations with high temperature LD simulations. To quantitatively compare the conformational searching ability, we calculated the transition rate for the dihedral angles, (ϕ, ψ), to transfer from one local minimum at (−90°,−70°) to another local minimum at (−90°, 170°). One transfer is counted when (ϕ, ψ) changes from within 40° of one local minimum to within 40° of the other local minimum.

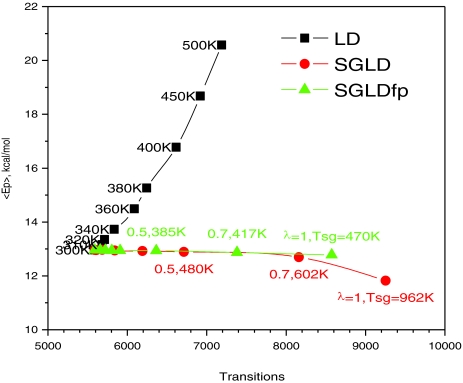
Figure 9 shows the average potential energies as a function of the transition rate in the high temperature LD simulations as well as in the SGLD and SGLDfp simulations. The average potential energy reflects the conformational distribution to a certain degree. A change in the average energy indicates a change in the conformational distribution. As can be seen from Fig. 9, the high-temperature simulation not only increases the transition rate, but also significantly increases the average potential energy. In the SGLD and SGLDfp simulations, the average potential energy experiences little change except for the SGLD simulations with λ = 1. The transition rate increases significantly with λ in both the SGLD and SGLDfp simulations, even though the SGLDfp simulations have fewer transitions as compared to the SGLD simulations with the same λ. It is also clear from Fig. 9 that the SGLDfp simulation preserves the average energy better.

Figure 9.

Average energies versus transition rates of the alanine dipeptide system in high temperature LD, SGLD, and SGLDfp simulations. The simulation temperatures of the LD simulations, as well as the guiding factors and the self-guiding temperatures of the SGLD and SGLDfp simulations, are labeled beside their data points. A distant dependent dielectric constant, ɛ = 4r, is used to describe the solvation effect. The collision frequency is γ = 10/ps for all simulations. The simulation temperature is 300 K for the SGLD and SGLDfp simulations.

Folding of a pentamer peptide

Protein folding is a major challenge for conformational searching. Due to many degrees of freedom of proteins, the conformational space of a protein is extremely large and an exhaustive conformational search is impossible. To reach the folded state, we believe the accessible conformational space for a protein is limited and the protein can find its folded state quickly by moving through this accessible conformational space. Many methods, such as high-temperature simulations, not only accelerate conformational searching but also increase the accessible conformational space. An increase in the accessible conformational space not only makes the conformational searching problem worse, but also may alter the global minimum and make it harder to identify the folded state. The ability to preserve the conformational distribution makes SGLDfp a suitable means to study problems where the preservation of conformational distribution is critical.

To demonstrate the application of the SGLDfp method in a protein folding study, we performed folding simulations for a pentamer peptide^{9, 29} which forms a type II turn according to the experimental observation. The sequence of the pentamer peptide is: Tyr-Pro-Gly-Asp-Val. To simplify the demonstration, all simulation conditions were the same as those for the alanine dipeptide simulations described above. A temperature of 300 K and a collision frequency of 1/ps were set for all the simulations. The guiding factor was λ = 0.5 for the SGLD simulation and was λ = 1 for the SGLDfp simulation, so both the simulations have similar conformational searching ability. All simulations were started from an extended conformation and were 200 ns in length.

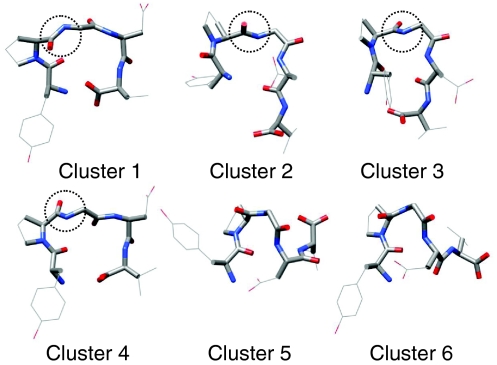
Because a large number of conformations were visited during these simulations, in order to simplify the description, we clustered the conformations to six major clusters using the local maximum clustering method.³⁰ The distances between conformations are calculated as the sum of the difference square of the backbone dihedral angles. Figure 10 shows the representative structures of these six major clusters. Clusters 1 and 4 have a broad turn involving Pro-Gly-Asp wherein the proline carbonyl oxygen points up and points down, respectively. Clusters 2 and 3 have a tight turn involving Pro-Gly wherein the proline carbonyl oxygen points up and points down, respectively. Clusters 5 and 6 form a helical coil wherein the C-terminal points up and points down, respectively.

Figure 10.

The representative conformations of the six major clusters of the pentamer peptide. Backbone atoms are shown as thick sticks and side-chain heavy atoms are shown as thin sticks. Hydrogen atoms are not shown for clarity. Atoms are colored grey, blue, and red for carbon, nitrogen, and oxygen, respectively.

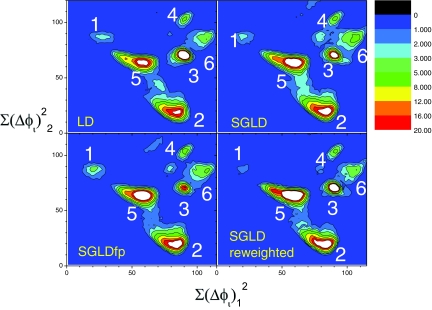
Figure 11 compares the conformational distributions obtained from the LD, SGLD, and SGLDfp simulations. The conformational distributions are shown in two-dimensional contour plots with the distances to the center conformations of clusters 1 and 2 as x coordinates and y coordinates, respectively. Even though the peptide has only five residues, the conformational space is extremely large and the LD simulation of 200 ns may not necessarily properly sample the whole conformational space. All six major clusters can clearly be identified in these simulations, even though the SGLD and SGLDfp simulation results have some trace amounts of other clusters. The density from the SGLD simulation shows broader peaks than those in the LD and SGLDfp results. After reweighting, the SGLD result has peaks as sharp as the LD result. The SGLDfp result resembles the LD result fairly well, again demonstrating that the SGLDfp method can eliminate the perturbation of the SGLD method. Due to the approximations in the SGLD reweighting and in the SGLDfp method, certain deviations from the LD result still remain, especially when the guiding factor is exceptionally large, e.g., larger than 1. The RMSDs from the LD result are 1.44, 1.59, and 0.81 for the SGLD results before and after reweighting and for the SGLDfp result, respectively. The large RMSD for the reweighted SGLD result is caused by a significant fluctuation produced by the reweighting process.

Figure 11.

Conformational distributions in the LD, SGLD, and SGLDfp simulations. Conformational distances from the center conformations of clusters 1 and 2 are used as the x and y coordinates to show the distributions in two dimensions. A distant dependent dielectric constant, ɛ = 4r, is used to describe solvation effect. All simulations are done with γ = 1/ps and T = 300 K. The guiding factors are λ = 0.5 for SGLD and λ = 1 for SGLDfp.

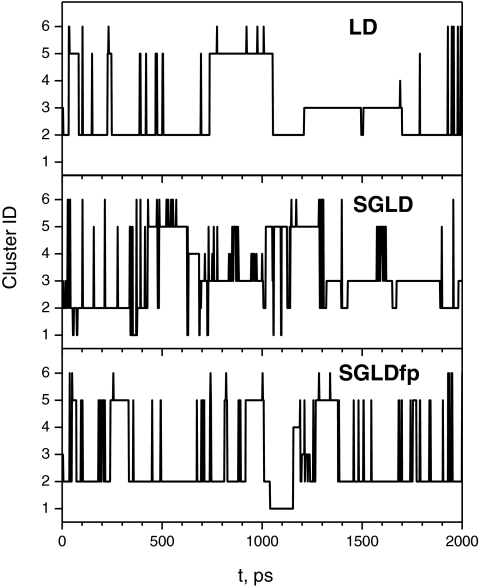
Figure 12 plots the cluster transitions during the first 2000 ps simulations. As can be seen, the LD simulation did not reach cluster 1 during the first 2000 ps simulation and the transitions between clusters were not as frequent as that in the SGLD and SGLDfp simulations. The most frequency transitions occurred between cluster 2 and cluster 5. This agrees with Fig. 11, which shows clusters 2 and 5 are two high density clusters and they are near each other. There are also a significant number of transitions between cluster 2 and cluster 3, but not between cluster 2 and cluster 4, agreeing with Fig. 11 where clusters 2 and 4 are separated by clusters 3, 5, and 6. This example further demonstrates that the SGLDfp method is a suitable approach for protein folding studies in term of its ability to accelerate conformational searching while maintaining the conformational distribution.

Figure 12.

Conformational transitions between the clusters in the first 2000 ps of the LD, SGLD, and SGLDfp simulations. A distant dependent dielectric constant, ɛ = 4r, is used to describe solvation effect. All simulations are done with γ = 1/ps and T = 300 K. The guiding factors are λ = 0.5 for SGLD and λ = 1 for SGLDfp.

CONCLUSIONS

Based on the understanding of the conformational distribution in the SGLD simulation,²² we developed a force-momentum-based self-guided Langevin dynamics simulation method, abbreviated as SGLDfp, to approximately maintain the canonical ensemble distribution while accelerating conformational searching. This method is a general simulation method and can be applied to any studies where a LD simulation can be applied. This method does not need to predetermine important degrees of freedom to achieve accelerated conformational searching. Even though SGLDfp accelerates conformational searching to a less degree than SGLD, it is more convenient than SGLD since it does not require a post-processing step to reweight the visited conformations. In addition, SGLDfp is size extensive, i.e., it can be applied regardless of the system sizes. By contrast, the SGLD reweighting mechanism is difficult to converge for large systems or with large guiding factors. Because SGLDfp does not have such a size limitation, it, therefore, has a wider range of applicability. Since the guiding force is proportional to the collision frequency, the enhancement in conformational searching increases with the collision frequency. For systems with large energy barriers, SGLDfp, as well as SGLD, performs better with large collision frequency. In practical terms, with optimal parameters, SGLD can be used to routinely cross barriers of 20 kT, whereas SGLDfp can be used to cross barriers of 15 kT at a rate LD crosses barriers of 10 kT. Simulation results with a skewed double well system indicate that the guiding factor of 1 or less is recommended to keep acceptable deviations from a canonical ensemble. More details on this will be the subject of a subsequent report. Because SGLDfp can produce approximately the canonical ensemble distribution directly without reweighting, it is more convenient for quantitative simulation studies. For studies requiring a preserved conformational distribution, such as protein folding simulation and the free energy calculation, SGLDfp is a suitable choice to accelerate conformational searching, especially for larger systems where other methods fail. The SGLDfp method can be combined with many other free energy calculation methods, such as the adaptive biasing force method by Darve et al.³¹ and the orthogonal-space-random-walk method by Zheng et al.,^{32, 33, 34} to achieve increased accuracy and efficiency.

APPENDIX: SGLDFP SIMULATION ALGORITHM

To help understand and implement the SGLDfp method, we describe a leap-frog Verlet SGLDfp simulation algorithm below. Assuming the momentum guiding factor, λ^p, is input, a SGLDfp simulation is performed in the following steps:

• (i)Initiate the force guiding factors: λ^f(0) = 0, ξ^f(0) = 0, and the low-frequency variables: ${\tilde{\mathbf{f}}}_i\left(0\right)=0$, ${\tilde{\mathbf{p}}}_i\left(0\right)=0$, ${\tilde{\mathbf{g}}}_i^{\mathrm{p}}\left(0\right)=0$, and ${\tilde{\mathbf{g}}}_i\left(0\right)=0$.
• (ii)
  At time step, t, calculate interaction forces, f_i(t), random forces, R_i(t), and the partial guiding forces, ${{\mathbf{g}}^{\prime }}_i\left(t\right)={\lambda }^{\mathrm{f}}\left(t\right){\tilde{\mathbf{f}}}_i\left(t\right)-{\xi }^{\mathrm{f}}\left(t\right){\tilde{\mathbf{f}}}_i\left(t\right)+{\lambda }_i^{\mathrm{p}}{\gamma }_i{\tilde{\mathbf{p}}}_i\left(t\right)$. The interaction forces, f_i(t), must include any constraint forces as described later in Eq. A20. Random forces, R_i(t), are generated from a Gaussian distribution with zero mean

  $$\rho \left({\mathbf{R}}_i\right)=\frac{1}{\sqrt{4\pi {\gamma }_i{m}_{i}kT}}{e}^{-\frac{{\mathbf{R}}_i^2}{4{\gamma }_i{m}_{i}kT}}.$$

  The low-frequency momentum is calculated using the momentum at the previous half step, p_i(t − (δt/2)),

  $$\begin{array}{c}\hfill {\tilde{\mathbf{p}}}_i\left(t\right)=\left(1-\frac{\delta t}{t_L}\right){\tilde{\mathbf{p}}}_i(t-\delta t)+\frac{\delta t}{t_L}{\mathbf{p}}_i\left(t-\frac{\delta t}{2}\right).\end{array}$$ (A1)

  The low-frequency force is calculated using the force at current step, f_i(t),

  $$\begin{array}{c}\hfill {\tilde{\mathbf{f}}}_i\left(t\right)=\left(1-\frac{\delta t}{t_L}\right){\tilde{\mathbf{f}}}_i(t-\delta t)+\frac{\delta t}{t_L}{\mathbf{f}}_i\left(t\right).\end{array}$$ (A2)
• (iii)
  Calculate the energy conservation factor, ξ^p. The half step velocity, ${\dot{\mathbf{r}}}_i\left(t\right)$, can be expressed in the following form:

  $$\begin{array}{ccc}\hfill {\dot{\mathbf{r}}}_i\left(t\right)& =& {\dot{\mathbf{r}}}_i\left(t-\frac{\delta t}{2}\right)+\frac{\delta t}{2m_i}\left({\mathbf{f}}_i\left(t\right)+{{\mathbf{g}}^{\prime }}_i\left(t\right)+{\mathbf{R}}_i\left(t\right)\right)\hfill \\ & & -\frac{\delta t}{2}\left(1+{\xi }^{\mathrm{p}}{\lambda }_i^{\mathrm{p}}\right){\gamma }_i{\dot{\mathbf{r}}}_i\left(t\right)\hfill \\ \hfill ,\end{array}$$ (A3)

  calculate the friction-free velocity at the half step

  $$\begin{array}{c}\hfill {{\dot{\mathbf{r}}}^{\prime }}_i\left(t\right)={\dot{\mathbf{r}}}_i\left(t-\frac{\delta t}{2}\right)+\frac{\delta t}{2m_i}\left({\mathbf{f}}_i\left(t\right)+{{\mathbf{g}}^{\prime }}_i\left(t\right)+{\mathbf{R}}_i\left(t\right)\right).\end{array}$$ (A4)

  From Eqs. A3, A4, we have

  $$\begin{array}{ccc}\hfill {\dot{\mathbf{r}}}_i\left(t\right)& =& \frac{{{\dot{\mathbf{r}}}^{\prime }}_i\left(t\right)}{1+\frac{(1+{\xi }^{\mathrm{p}}{\lambda }_i^{\mathrm{p}}){\gamma }_i\delta t}{2}}\approx \frac{{{\dot{\mathbf{r}}}^{\prime }}_i\left(t\right)}{1+\frac{{\gamma }_i\delta t}{2}}\hfill \\ & & -\frac{{{\dot{\mathbf{r}}}^{\prime }}_i\left(t\right)}{{\left(1+\frac{{\gamma }_i\delta t}{2}\right)}^2}\frac{{\xi }^{\mathrm{p}}{\lambda }_i^{\mathrm{p}}{\gamma }_i\delta t}{2}.\hfill \end{array}$$ (A5)

  Based on the energy conservation relation (Eq. 13) and neglecting the higher power term of ξ^p, we can solve for the energy conservation factor,

  $$\begin{array}{c}\hfill {\xi }^{\mathrm{p}}=\frac{{\sum }_i^N{{\mathbf{g}}^{\prime }}_i\left(t\right){{\dot{\mathbf{r}}}^{\prime }}_i\left(t\right){\left(1+\frac{{\gamma }_i\delta t}{2}\right)}^{-1}}{{\sum }_i^N{\lambda }_i^{\mathrm{p}}{\gamma }_i{m}_i{\dot{\mathbf{r}}}_i^{\prime 2}\left(t\right){\left(1+\frac{{\gamma }_i\delta t}{2}\right)}^{-2}+\frac{\delta t}{2}{\sum }_i^N{\lambda }_i^{\mathrm{p}}{\gamma }_i{{\mathbf{g}}^{\prime }}_i\left(t\right){{\dot{\mathbf{r}}}^{\prime }}_i\left(t\right){\left(1+\frac{{\gamma }_i\delta t}{2}\right)}^{-2}}.\end{array}$$ (A6)
  The actual guiding force is

  $$\begin{array}{ccc}\hfill {\mathbf{g}}_i^{\mathrm{p}}\left(t\right)& =& {\lambda }_i^{\mathrm{p}}{\gamma }_i({\tilde{\mathbf{p}}}_i\left(t\right)-{\xi }^{\mathrm{p}}{\mathbf{p}}_i\left(t\right))\hfill \\ & =& {\lambda }_i^{\mathrm{p}}{\gamma }_i\left({\tilde{\mathbf{p}}}_i\left(t\right)-\frac{{\xi }^{\mathrm{p}}{m}_i{{\dot{\mathbf{r}}}^{\prime }}_i\left(t\right)}{1+\frac{(1+{\xi }^{\mathrm{p}}{\lambda }_i^{\mathrm{p}}){\gamma }_i\delta t}{2}}\right),\hfill \end{array}$$ (A7)

  $$\begin{array}{c}\hfill {\mathbf{g}}_i\left(t\right)={\lambda }^{\mathrm{f}}{\tilde{\mathbf{f}}}_i\left(t\right)-{\xi }^{\mathrm{f}}{\mathbf{f}}_i\left(t\right)+{\mathbf{g}}_i^{\mathrm{p}}\left(t\right).\end{array}$$ (A8)
• (iv)Update low-frequency variables and accumulators for the calculation of the force guiding factors.
  Low-frequency potential energy

  $$\begin{array}{c}\hfill {\tilde{E}}_{\mathrm{p}}\left(t\right)=\left(1-\frac{\delta t}{t_L}\right){\tilde{E}}_{\mathrm{p}}(t-\delta t)+\frac{\delta t}{t_L}{E}_{\mathrm{p}}\left(t\right).\end{array}$$ (A9)

  Low-frequency guiding forces

  $$\begin{array}{c}\hfill {\tilde{\mathbf{g}}}_i^{\mathrm{p}}\left(t\right)=\left(1-\frac{\delta t}{t_L}\right){\tilde{\mathbf{g}}}_i^{\mathrm{p}}(t-\delta t)+\frac{\delta t}{t_L}{\mathbf{g}}_i^{\mathrm{p}}(\left(t\right),\end{array}$$ (A10)

  $$\begin{array}{c}\hfill {\tilde{\mathbf{g}}}_i\left(t\right)=\left(1-\frac{\delta t}{t_L}\right){\tilde{\mathbf{g}}}_i(t-\delta t)+\frac{\delta t}{t_L}{\mathbf{g}}_i(\left(t\right).\end{array}$$ (A11)

  From the low-frequency momentums, we can calculate the low-frequency temperature

  $$\begin{array}{c}\hfill \tilde{T}\left(t\right)=\frac{1}{N_{\mathrm{DF}}}\sum _i\frac{{\tilde{\mathbf{p}}}_i^2\left(t\right)}{m_i}.\end{array}$$ (A12)

  Update averages for the calculation of the collision factors and energy factors

  $$\begin{array}{c}\hfill FLF=\left(1-\frac{\delta t}{t_{\mathrm{est}}}\right)FLF+\frac{\delta t}{t_{\mathrm{est}}}\sum _i^N{\tilde{\mathbf{f}}}_i\left(t\right)·{\tilde{\mathbf{f}}}_i\left(t\right),\end{array}$$ (A13a)

  $$\begin{array}{ccc}\hfill FHF& =& \left(1-\frac{\delta t}{t_{\mathrm{est}}}\right)FHF+\frac{\delta t}{t_{\mathrm{est}}}\sum _i^N({\mathbf{f}}_i\left(t\right)-{\tilde{\mathbf{f}}}_i\left(t\right))\hfill \\ & & ·({\mathbf{f}}_i\left(t\right)-{\tilde{\mathbf{f}}}_i\left(t\right)),\hfill \end{array}$$ (A13b)

  $$\begin{array}{c}\hfill GLF=\left(1-\frac{\delta t}{t_{\mathrm{est}}}\right)GLF+\frac{\delta t}{t_{\mathrm{est}}}\sum _i^N\left({\tilde{\mathbf{g}}}_i^{\mathrm{p}}\left(t\right)-{\gamma }_i{\tilde{\mathbf{p}}}_i\left(t\right)\right)·{\tilde{\mathbf{f}}}_i\left(t\right),\end{array}$$ (A13c)

  $$\begin{array}{ccc}\hfill GHF& =& \left(1-\frac{\delta t}{t_{\mathrm{est}}}\right)GHF+\frac{\delta t}{t_{\mathrm{est}}}\sum _i^N({\mathbf{g}}_i^{\mathrm{p}}\left(t\right)-{\tilde{\mathbf{g}}}_i^{\mathrm{p}}\left(t\right)\hfill \\ & & -{\gamma }_i({\mathbf{p}}_i\left(t\right)-{\tilde{\mathbf{p}}}_i\left(t\right)))·({\mathbf{f}}_i\left(t\right)-{\tilde{\mathbf{f}}}_i\left(t\right)),\hfill \end{array}$$ (A13d)

  $$\begin{array}{c}\hfill PPLF=\left(1-\frac{\delta t}{t_{\mathrm{est}}}\right)PPLF+\frac{\delta t}{t_{\mathrm{est}}}\sum _i^N{\gamma }_i^2{\tilde{\mathbf{p}}}_i\left(t\right)·{\tilde{\mathbf{p}}}_i\left(t\right),\end{array}$$ (A13e)

  $$\begin{array}{c}\hfill GPLF=\left(1-\frac{\delta t}{t_{\mathrm{est}}}\right)GPLF+\frac{\delta t}{t_{\mathrm{est}}}\sum _i^N{\tilde{\mathbf{g}}}_i\left(t\right)·{\gamma }_i{\tilde{\mathbf{p}}}_i\left(t\right).\end{array}$$ (A13f)

  The collision and energy factors are calculated with the averages

  $$\begin{array}{ccc}& {\lambda }_{\mathrm{lf}}^{\mathrm{p}}=1+\frac{GLF}{FLF},{\lambda }_{\mathrm{hf}}^{\mathrm{p}}=1+\frac{GHF}{FHF},& \hfill \\ \\ & {\chi }_{\mathrm{lf}}=\frac{{\tilde{T}}_0}{\tilde{T}}=1-\frac{GPLF}{PPLF}.\end{array}$$ (A14)

  When ${\tilde{T}}_0$ is available from a previous SGLD simulation with λ = 0, ${\chi }_{\mathrm{lf}}={\tilde{T}}_0/\tilde{T}$ is recommended, otherwise, χ_lf = 1 − GPLF/PPLF has to be used. From χ_lf, we can calculate the high-frequency collision factor: ${\chi }_{\mathrm{hf}}=T-{\chi }_{\mathrm{lf}}\tilde{T}/T-\tilde{T}$.
  The force guiding factors are calculated according to Eqs. 38, 39 with the approximations κ_lf ≈ 1 and κ_hf ≈ 0:

  $$\begin{array}{ccc}\hfill {\lambda }^{\mathrm{f}}(t+\delta t)& =& \left(1-\frac{\delta t}{t_{\mathrm{est}}}\right){\lambda }^{\mathrm{f}}\left(t\right)+\frac{\delta t}{t_{\mathrm{est}}}\hfill \\ & & \times \left(\frac{1}{{\chi }_{\mathrm{lf}}}-\frac{1}{{\chi }_{\mathrm{hf}}}-{\lambda }_{\mathrm{lf}}^{\mathrm{p}}+{\lambda }_{\mathrm{hf}}^{\mathrm{p}}\right),\hfill \end{array}$$ (A15)

  $$\begin{array}{c}\hfill {\xi }^{\mathrm{f}}(t+\delta t)=\left(1-\frac{\delta t}{t_{\mathrm{est}}}\right){\xi }^{\mathrm{f}}\left(t\right)+\frac{\delta t}{t_{\mathrm{est}}}\left({\lambda }_{\mathrm{hf}}^{\mathrm{p}}-\frac{1}{{\chi }_{\mathrm{hf}}}\right).\end{array}$$ (A16)
• (v)
  Advance velocities to the next half time step

  $$\begin{array}{ccc}\hfill {\dot{\mathbf{r}}}_i\left(t+\frac{\delta t}{2}\right)& =& \left(2{\chi }_i-1\right){\dot{\mathbf{r}}}_i\left(t-\frac{\delta t}{2}\right)+{\chi }_i\frac{\delta t}{m_i}\hfill \\ & & \left({\mathbf{f}}_i\left(t\right)+{{\mathbf{g}}^{\prime }}_i\left(t\right)+{\mathbf{R}}_i\left(t\right)\right).\hfill \end{array}$$ (A17)

  Here, the scaling parameter, χ_i, is calculated as

  $$\begin{array}{c}\hfill {\chi }_i={\left(1+\frac{(1+{\xi }^{\mathrm{p}}{\lambda }_i^{\mathrm{p}}){\gamma }_i\delta t}{2}\right)}^{-1}.\end{array}$$ (A18)

  Then, advance positions to the next time step

  $$\begin{array}{c}\hfill {\mathbf{r}}_i(t+\delta t)={\mathbf{r}}_i\left(t\right)+{\dot{\mathbf{r}}}_i\left(t+\frac{\delta t}{2}\right)\delta t.\end{array}$$ (A19)

  If internal coordinates need to be constrained, apply constraining algorithms, such as SHAKE (Ref. ²⁴) or semi-flexible constraint dynamics,²⁵ to obtain constrained positions, ${\mathbf{r}}_i^{\mathrm{CON}}(t+\delta t)$, from r_i(t + δt). The constraint forces must be included in the low-frequency force calculation. The constraint forces are calculated by the following equation:

  $$\begin{array}{c}\hfill {\mathbf{f}}_i^{\mathrm{CON}}(t+\delta t)=\frac{2m_i}{\delta t^2}\left({\mathbf{r}}_i^{\mathrm{CON}}(t+\delta t)-{\mathbf{r}}_i(t+\delta t)\right).\end{array}$$ (A20)
• (vi)Continue to step (ii) with t = t + δt until the end of the simulation.