Moving beyond Watson–Crick models of coarse grained DNA dynamics

Abstract

DNA produces a wide range of structures in addition to the canonical B-form of double-stranded DNA. Some of these structures are stabilized by Hoogsteen bonds. We developed an experimentally parameterized, coarse-grained model that incorporates such bonds. The model reproduces many of the microscopic features of double-stranded DNA and captures the experimental melting curves for a number of short DNA hairpins, even when the open state forms complicated secondary structures. We demonstrate the utility of the model by simulating the folding of a thrombin aptamer, which contains G-quartets, and strand invasion during triplex formation. Our results highlight the importance of including Hoogsteen bonding in coarse-grained models of DNA.

INTRODUCTION

DNA structure possesses several levels of complexity, ranging from the sequence of bases (primary structure) to base-pairing (secondary structure) to its three-dimensional shape (tertiary structure). While the primary structure is typically constant, secondary and tertiary structures fluctuate under thermal energy and are modified by external forces, the action of enzymes, or the presence of a complementary strand. Since the time-scales characterizing these structural dynamics exceed the current capabilities of atomistic simulations,¹ their simulation requires a coarse-grained model.^{2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24} It is reasonable to contend that a minimal model of DNA should at least account for Watson–Crick base pairing and stacking, along with the chemical asymmetry of the backbone (i.e., a $5^{\prime }\text{-}{3}^{\prime }$ directionality). De Pablo and co-workers have used such a model^{13, 14, 24} to gain deep insights into hybridization.^{25, 26, 27}

We show here that restricting hydrogen bonding to Watson–Crick base pairs is insufficient to capture the higher order structure of many sequences of DNA, even for relatively pedestrian systems such as DNA hairpins. Rather, it is essential to include both Watson–Crick and Hoogsteen base pairs.^{28, 29, 30} Hoogsteen bonds stabilize multi-body secondary structure in single-stranded DNA (ssDNA), such as G-quartets^{31, 32} and I-motifs.^{32, 33} They are also the glue that binds triple-stranded DNA. Although the applications of such a model to single- and triple-stranded DNA are apparent, the inclusion of Hoogsteen bonds should also impact simulations of double-stranded DNA (dsDNA). Indeed, while the conventional wisdom embodied in existing coarse-grained models^{2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24} postulates that dsDNA only utilizes Watson–Crick bonds, recent experimental data³⁴ showed transient formation of both A-T and G-C Hoogsteen pairs in double-stranded DNA. Other types of Hoogsteen pairs have not been observed in double-stranded DNA due to excluded volume effects caused by the mismatch. Taken in isolation, Hoogsteen bonds are rather strong; the interaction energy of a Hoogsteen A-T bond (5.2 kcal/mol) compares favorably with the equivalent Watson–Crick bond (5.7 kcal/mol).^{30, 35, 36} The reason why base pairing in double-stranded DNA is dominated by Watson–Crick bonds is the resultant stabilization of excluded volume interactions. Thermal transitions in dsDNA structure, such as melting, hybridization, and bubble formation, will also be affected if the sequence permits Hoogsteen-bonded secondary structure as it transitions to the open state. To capture the complexity of DNA structural dynamics in a coarse-grained model, it is essential to move beyond Watson–Crick base pairs.

Our basic approach to including non-Watson–Crick bonds in a coarse-grained model is illustrated in Fig. 1. Our starting point is a 3-bead representation of each nucleotide; we pick a structure where we represent each nucleotide with a bead for the sugar (S), phosphate (P), and base (B) group. Such a model automatically provides handedness when the DNA is in a helical form.¹³ From a structural standpoint, our model resembles the 3-sites-per-nucleotide (3SPN) model in only the most literal sense; both the 3SPN model from de Pablo and co-workers^{13, 14, 24} and the model we propose here represent each nucleotide as 3 beads. As will be apparent shortly, the force fields for the two models are quite different. The most notable difference is our use of non-spherical bonding potentials, which allows us to avoid the need for dihedral potentials^{7, 13, 14, 15, 16, 24} that introduce an unphysical bias towards the B-form of dsDNA when the DNA is single-stranded.¹³ Rather, we can smoothly move between dsDNA and ssDNA. As a result, it would be inappropriate to view the present model as an extension of the existing 3SPN models.^{13, 14, 24} The spacing between the sugar, phosphate group, and bases, along with their relative sizes, are enforced by a combination of excluded volume interactions and modified harmonic springs; the sum of these potentials creates a relatively deep well that minimizes the fluctuations in these distances.¹⁰ The semi-flexibility of the DNA backbone is enforced by a bending potential between neighboring sugar beads. The sequence dependent structure is captured by base specific potentials. There are two different types of hydrogen bonding interactions, one for Watson–Crick bonds and another for Hoogsteen bonds. Our nomenclature does not distinguish between protonated (reversed-Hoogsteen or wobble pairs) and non-protonated (traditional) Hoogsteen bonds; we simply use the term Hoogsteen bonds in all cases. Stacking interactions in the model occur between bases on the same backbone and enforce a sequence dependence for the interaction in the $5^{\prime }\text{-}{3}^{\prime }$ direction. Cross-stacking interactions occur between bases on a nearby strand when there is Watson–Crick hydrogen bonding between one of the bases involved in the cross-stacking. To enforce the directionality of the hydrogen bonding and stacking/cross-stacking interactions, we have modified their spherical potential functions with a smoothly varying prefactor.^{7, 15, 16, 21} Since the bonds have directionality, all of the base-base interactions (including excluded volume) are enforced at all times in the simulation.

Figure 1.

Coarse-grained model of DNA. Each nucleotide is represented by three beads (Ref. ¹³), one for the phosphate group, one for the sugar and one for the base. The various potentials U_i refer to the different types of interactions, where the hydrogen bonding interaction U_HB includes both Watson–Crick and Hoogsteen bonds. The directionality of the hydrogen bonding and stacking interactions are enforced by an additional prefactor that accounts for the angle θ between the bonding pairs. The fundamental length scale in the model is σ, which corresponds to the phosphate-sugar bond length.

Some coarse-grained models are parameterized from the bottom up,^{2, 3, 4, 5, 6, 7} where the functional form and strength of the potentials are tuned to match trajectories from all atom simulations. We chose a top down approach^{9, 10, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21} for the reasons expounded by Ouldridge et al.²¹ (Naturally, one can also employ a mixture of top down and bottom up approaches.²⁴) After fixing the relative strengths of the base-base interactions with experimental thermodynamic data,^{30, 35, 36} the model has a single free parameter relating the dimensionless temperature to the experimental temperature. We obtain this conversion factor by matching the model predictions for a test sequence to an experimentally obtained melting curve.³⁷ The experimental data used to parameterize the model^{30, 35, 36, 37} were obtained in an aqueous buffer solution. The model thus has implicit electrostatics, similar to others.^{13, 15, 16, 19, 20, 21, 24} Our model is parameterized to match a single ionic strength,^{15, 16, 21} in this case 1X Buffer A,³⁸ which is a model system for in vivo conditions and should be relevant for a number of in vitro biochemical experiments.

Our paper is organized as follows. We begin by describing the model in detail, including its parameterization with experimental data. We test our model by (i) comparing the computed structural properties of double-stranded DNA to A- and B-form DNA and (ii) showing that the model captures melting curves for DNA hairpins that form Hoogsteen bonds in the open state. These problems allow us to assess the quality of our model. We then provide two illustrative examples of the utility of including Hoogsteen bonds, namely, the folding of a thrombin aptamer and triplex formation. We conclude with a detailed discussion of the limitations of our model and possible routes to improving its ability to capture the stability of the double helix and effects related to ionic strength.^{13, 14}

METHODS

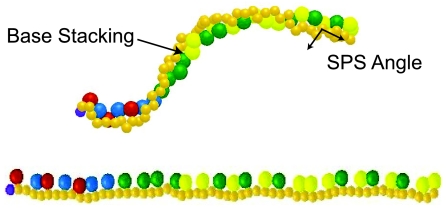
The model, depicted in Fig. 1, is cast in terms of a length σ and energy ε. We will use the degree of freedom embodied in ε to map the simulation temperature to the experimental one.³⁷ We fixed the length scale in the model, σ, to be the bond distance between the sugar and phosphate group. In Fig. 1, the backbone is depicted in a plane. As we can see in Fig. 2, relaxed single-stranded DNA exhibits significant stacking; the bases offset into a single helix conformation in order to maximize the stacking interactions and minimize the excluded volume and backbone bending interactions between consecutive base beads. Although we will see shortly that the phosphate beads only interact through excluded volume and their bonding to the sugars, they are essential to forming a sensible sugar-phosphate-sugar (SPS) angle, which is similar but not equivalent to the glycosyl angle. The importance of the SPS angle will become apparent when we discuss our results for dsDNA in Sec. 3A. For the moment, the important point to note in Fig. 2 is that the equilibrium linear distance between two adjacent sugar beads is less than 2σ. The spontaneous formation of a SPS angle, without the need for a dihedral potential, is a key feature of our model.

Figure 2.

Snapshots from simulations of ssDNA shortly after its initialization as a comb (bottom) and in the relaxed state (top). An example of the sugar-phosphate-sugar (SPS) angle is depicted; this puckering shortens the apparent contour length of the relaxed molecule (top), measured from sugar to sugar, when compared to the completely extended state (bottom and Fig. 1).

Nonspecific interactions

Every bead interacts with the other beads by excluded volume interactions. For each bead i, the interaction with bead j is given by the truncated pairwise Lennard-Jones potential,

$$U_{\mathrm{EV}}\left(r_{ij}\right)=4\epsilon \left[{\left({\displaystyle \frac{\gamma }{r_{ij}}}\right)}^{12}-{\left({\displaystyle \frac{\gamma }{r_{ij}}}\right)}^6\right]+\varepsilon ,$$ (1)

for r_ij ⩽ 2.5γ. The energy U_EV = 0 otherwise. The backbone beads have size σ and the base beads have size 1.5σ. The parameter, γ, in Eq. 1 is calculated with the arithmetic average of the size of the i and j beads. We thus do not distinguish between the different sizes of the bases,¹³ which is a limitation of our model that will be discussed in more detail in Sec. 3E. All bonded beads also interact through the modified harmonic (FENE) potential

$$U_{\mathrm{MH}}\left(r_{ij}\right)=-15\epsilon {\left(\frac{R_0}{\sigma }\right)}^2\ln \left[1-{\left(\frac{r_{ij}}{R_0}\right)}^2\right].$$ (2)

For the backbone-backbone springs, the finite extensible length is 1.5σ, while for the backbone-base springs it is 2.25σ and the parameter, R₀, in Eq. 2 is calculated with the arithmetic average of the finite extensible length for the i and j beads. The combination of excluded volume and spring forces maintains relatively constant extensions between bonded pairs.

Backbone bending

The backbone stiffness is enforced with a bending potential,

$$U_{\mathrm{BB}}\left(\phi \right)=12\epsilon {(1+\cos \phi )}^2,$$ (3)

between all sugar trios along the same backbone. The stiff backbone bending potential has an equilibrium angle of π,^{9, 15, 16} leading to a ssDNA persistence length (calculated from the decay of the autocorrelation function along the vector between consecutive sugar beads) of 1.7 nm. We make this calculation using the sugar beads, rather than including the phosphate beads as well, since the bending energy is defined between sugar trios. Our persistence length thus corresponds to nearly five nucleotides when we account for the SPS angle in Fig. 2.

This value is in line with experimental studies of the flexibility of ssDNA and RNA completed with a variety of approaches; experiments have found values of 0.75 nm via mechanical stretching,³⁹ 1.3 nm utilizing atomic force microscopy,⁴⁰ 1.4 nm from thermal melting profiles,⁴¹ 1.76 nm and 1.82 nm with sedimentation experiments,⁴² 1.5–3.0 nm with fluorescence spectroscopy,⁴³ 2.0–3.0 nm via transient electrical birefringence,⁴⁴ and 3.1–5.2 nm with fluorescence recovery after photobleaching.⁴⁵ The persistence length of ssDNA seems to vary widely due to a variety of factors including the length of the sequences examined, i.e., long (≫100 nucleotides) and short (<100 nucleotides), the model used to examine the data (freely jointed chain or wormlike chain), and the concentration and type of buffer used in each experiment.

Base-base interactions

The sequence dependent interactions have the generic form

$$U_{\mathrm{k}}(r_{ij},\theta )=-{\delta }_{\mathrm{k}}^{ij}{f}_{\mathrm{k}}\left(\theta \right)\epsilon {\left[\exp \left(20\frac{r_{ij}}{\sigma }-30\right)+1\right]}^{-1},$$ (4)

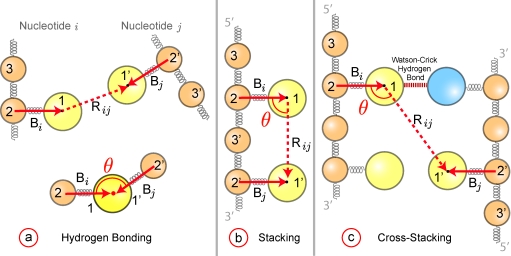
for r_ij ⩽ 10σ. The energy U_k = 0 otherwise. This particular form of the potential has been used elsewhere^{10, 46} to model hydrogen bonding and stacking in DNA, although there is a typographical error in Ref. 10. The parameter ${\delta }_{\mathrm{k}}^{ij}$ describes the strength of a bond of type k between base i and base j. The function f_k(θ) appearing in Eq. 4 accounts for the directionality of the hydrogen bonding interactions (Watson–Crick or Hoogsteen) and the stacking interactions similar to the bead-pin model.^{17, 23} Figure 3 shows how the angle θ is defined for hydrogen bonding, stacking and cross-stacking in terms of the vectors drawn from the backbone to the base, ${\mathbf{B}}_i$ and ${\mathbf{B}}_j$, and the vector drawn between the bases, ${\mathbf{R}}_{ij}$. In Eq. 4, $r_{ij}=\left|{\mathbf{R}}_{ij}\right|$.

Figure 3.

Definition of the angle θ for (a) hydrogen bonding, (b) stacking, and (c) cross-stacking interactions between nucleotide i and nucleotide j. For each nucleotide, the base bead (1), the sugar bead (2) and the phosphate bead (3) are numbered. The vectors ${\mathbf{B}}_i$ and ${\mathbf{B}}_j$ (solid red lines) are drawn from the sugar bead to the base bead. The ${\mathbf{R}}_{ij}$ vector (dashed red line) is drawn between the interacting bases. The top part of (a) shows the nucleotide positions; the bottom part of (a) shows the definition of the angle θ. Both stacking and cross-stacking follow the $5^{\prime }\text{-}{3}^{\prime }$ direction along the backbone. For stacking interactions (b), the nucleotides i and j are contiguous along the backbone. In cross-stacking interactions (c), nucleotide i is involved in Watson–Crick bonding and nucleotide j is displaced in the 5^′ direction from the other Watson–Crick bonded bead. The particular case illustrated in (c) corresponds to the ${\uparrow }_{3\prime }^{5\prime }\begin{array}{c}\mathrm{T}·{\mathrm{A}}_{3\prime }\hfill \\ \mathrm{T}·{\mathrm{T}}_{5\prime }\hfill \end{array}\downarrow$ = 8.8 entry from Table 2.

The hydrogen bonding of some base bead i is computed with all other base beads j ≠ i, which allows us to move smoothly between secondary structure in ssDNA and dsDNA. The value of θ ∈ [0, π] depicted in Fig. 3 is computed from the normalized dot product,

$$\cos \left(\theta \right)=\frac{{\mathbf{B}}_i·{\mathbf{B}}_j}{|{\mathbf{B}}_i\left|\right|{\mathbf{B}}_j|}$$ (5)

and the corresponding modulating function illustrated in Fig. 1 is

$$f_{\mathrm{HB}}\left(\theta \right)=\left\{\begin{array}{ccc}\hfill 0& \hfill \mathrm{for}& \hfill \theta \in [0,\pi /3]\\ \hfill \left|\cos \right(3\theta /2\left)\right|& \hfill \mathrm{for}& \hfill \theta \in [\pi /3,2\pi /3],\\ \hfill 1& \hfill \mathrm{for}& \hfill \theta \in [2\pi /3,\pi ]\end{array}\right.$$ (6)

The full bonding strength is present over an angle of 120°, in light of the mirror symmetry in Fig. 1, which is an approximation of the spread of the hydrogen atoms centered on the coarse-grained bead. The function evolves smoothly between the on/off states, which is important for the triplex formation, and the particular functional form is convenient for computation.^{15, 16} The off state prevents unphysical bonding through the backbone without the need for a cutoff length.

The key differences between stacking/cross-stacking and hydrogen bonding are the limitations on the value of j and the preferred alignment of base i and base j. For stacking, the bead j is displaced from bead i in the 3^′ direction on the chain. For cross-stacking, the i bead is involved in the Watson–Crick bond and the j bead is displaced in the 5^′ direction from the other Watson–Crick bonded bead. The definitions of θ, illustrated in Fig. 3, are computed by

$$\cos \left(\theta \right)=\frac{{\mathbf{B}}_i·{\mathbf{R}}_{ij}}{|{\mathbf{B}}_i\left|\right|{\mathbf{R}}_{ij}|},$$ (7)

and the the corresponding modulating function, sketched in Fig. 1, is

$$f_{\mathrm{S}}\left(\theta \right)=f_{\mathrm{CS}}\left(\theta \right)=\left\{\begin{array}{ccc}\hfill 0& \hfill \mathrm{for}& \hfill \theta \in [0,\pi /6]\\ \hfill \left|\cos \right(3\theta \left)\right|& \hfill \mathrm{for}& \hfill \theta \in [\pi /6,\pi /3],\\ \hfill 1& \hfill \mathrm{for}& \hfill \theta \in [\pi /3,\pi /2]\end{array}\right.$$ (8)

with a mirror symmetry for θ ∈ [π/2, π].

The parameters ${\delta }_{\mathrm{k}}^{ij}$ for hydrogen bonding and stacking are estimated from a range of experimental and computational data in the literature.^{30, 35, 36, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63} Since we eventually choose ε to match the experimental data for hairpin melting curves,³⁷ we only need to determine the relative strengths of each interaction. We first grouped all of the references by the type of measurement, often with several publications per group. All of the groups reporting hydrogen bonding energies included an estimate for the energy of a C-G Watson–Crick hydrogen bond, ${\tilde{U}}_{\mathrm{HB}}^{CG}$, along with values for other hydrogen bonds and/or stacking. We then rescaled all of the data within a given group relative to their reported value for ${\tilde{U}}_{\mathrm{HB}}^{CG}$. One group, which included Ref. 54, reported data for ${\tilde{U}}_{\mathrm{HB}}^{CG}$, ${\tilde{U}}_{\mathrm{S}}^{CG}$ and ${\tilde{U}}_{\mathrm{S}}^{GC}$. We used the latter relationship to rescale the stacking data in the other references. In summary, so long as a group measured either a G-C Watson–Crick hydrogen bond, ${\tilde{U}}_{\mathrm{HB}}^{CG}$, C-G stacking, ${\tilde{U}}_{\mathrm{S}}^{CG}$, or G-C stacking, and ${\tilde{U}}_{\mathrm{S}}^{GC}$ , we can use one of the latter trio to rescale the other hydrogen bonding or stacking data to a relative strength.

To merge these rescaled values into a single set of parameters for ${\tilde{U}}_{\mathrm{k}}^{ij}$ for stacking and hydrogen bonding, we used quantum chemical calculations³⁰ as the guide. The latter calculations provide a rank-order for the strengths of different base-base interactions, and we ensured that our final set of parameters preserves this rank order. There are three possible cases we had to consider to determine the value for a given ${\tilde{U}}_{\mathrm{k}}^{ij}$: (i) If we had multiple values for a single ${\tilde{U}}_{\mathrm{k}}^{ij}$ and they were close, we used the average. By close, we mean that using the average does not affect the rank order. (ii) If we had multiple values for a single ${\tilde{U}}_{\mathrm{k}}^{ij}$ and they were not close, we picked the one that preserves rank order. (iii) If no value for ${\tilde{U}}_{\mathrm{k}}^{ij}$ preserves the rank order, it was excluded from the data set. We did not encounter case (iii).

Although we know the relative bond strengths, the potential in Eq. 4 involves the bond type, the angle of the bond, and the distance between bonded pairs. We conducted trial simulations to determine the appropriate ratio ${\delta }_{\mathrm{S}}^{GC}/{\delta }_{\mathrm{HB}}^{GC}$ such that, at equilibrium, we recover the result ${\tilde{U}}_{\mathrm{S}}^{GC}/{\tilde{U}}_{\mathrm{HB}}^{GC}\approx 2.5$ reported in literature.³⁵ The rescaled base specific parameters, ${\delta }_{\mathrm{k}}^{ij}$, resulting from our literature search and these trial simulations appear in Eq. 4. Note that, although the hydrogen bonding energies are symmetric with respect to ij, the stacking energies depend on the $5^{\prime }\text{-}{3}^{\prime }$ direction.

The values of the ${\delta }_{\mathrm{k}}^{ij}$ parameters for Watson–Crick and Hoogsteen hydrogen bonds^{30, 35, 36, 47, 48, 49, 50, 53, 54, 55, 56} are listed in Table 1. For hydrogen bonding, we do not allow any bonds between base i and i + 2 on the same strand to avoid the formation of one member loops. Note that such loops also incur strong bending and excluded volume penalties, so this restriction may be superfluous. Stacking interactions only occur between contiguous bases on the sequence. For stacking,^{30, 35, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63} the strength (listed in Table 2) depends on the identity of i and j and their order in the $5^{\prime }\text{-}{3}^{\prime }$ sequence on that strand. Note that, when we account for not only the bond type but also the equilibrium bond angle and bond distance, the overall strength of a hydrogen bond interaction is less than half of the overall strength of stacking interactions.^{35, 37} Therefore, even though the noncanonical base pairs have significant hydrogen bonding strengths, they can be considerably destabilized by stacking and cross-stacking interactions.

Table 1.

The base specific hydrogen bonding parameters, ${\delta }_{\mathrm{k}}^{ij}$.

	A	C	G	T
A	3.20	3.64	5.36	4.00
C	3.64	6.12	9.56	2.20
G	5.36	9.56	9.16	4.44
T	4.00	2.20	4.44	2.12

Table 2.

The base specific stacking parameters, ${\delta }_{\mathrm{k}}^{ij}$. The 5^′-(top) base is listed in the left column and the 3^′-(bottom) base pair is listed along the top of the table.

	${\uparrow }_{3^{\prime }}$ A	${\uparrow }_{3^{\prime }}$ C	${\uparrow }_{3^{\prime }}$ G	${\uparrow }_{3^{\prime }}$ T
${}^{5\prime }\uparrow$ A	59.07	72.27	107.91	42.02
${}^{5\prime }\uparrow$ C	115.61	90.86	160.49	107.91
${}^{5\prime }\uparrow$ G	74.58	106.59	90.86	72.27
${}^{5\prime }\uparrow$ T	72.27	74.58	115.61	59.07

Cross-stacking occurs between strands or between noncontiguous bases on the same strand (for example, in the stem of a ssDNA hairpin). These are weak and poorly understood interactions. For cross-stacking between strands (or in a hairpin), we need to consider both bases i and j, as well as their complementary partners. We use a Gō-like potential that turns on the cross-stacking interaction if base i or j is Watson–Crick hydrogen bonded to the complementary strand (or hairpin stem). If one complimentary pair of bases forms a Watson–Crick hydrogen bond, as in Fig. 3, then the two cross-stacking interactions for the dimer are included. The value of the cross-stacking energy is very low when it turns on.

Estimating the value for the cross-stacking energy is not straightforward. We were able to identify one report on cross-stacking energies,³⁵ which included a rubric stating that cross-stacking should be between 10-15% of the stacking energy. We set the ${\delta }_{\mathrm{CS}}^{ij}$ for ${\uparrow }_{3\prime }^{5\prime }\begin{array}{c}\mathrm{G}·{\mathrm{C}}_{3\prime }\hfill \\ \mathrm{C}·{\mathrm{G}}_{5\prime }\hfill \end{array}\downarrow$ to be 15% of the ${\uparrow }_{3\prime }^{5\prime }\begin{array}{c}\mathrm{C}\hfill \\ \mathrm{G}\hfill \end{array}$ dimer and then rescaled the remaining cross-stacking ${\delta }_{\mathrm{CS}}^{ij}$ relative to the corresponding value for ${\uparrow }_{3\prime }^{5\prime }\begin{array}{c}\mathrm{G}·{\mathrm{C}}_{3\prime }\hfill \\ \mathrm{C}·{\mathrm{G}}_{5\prime }\hfill \end{array}\downarrow$. Since we require at least one Watson–Crick interaction in each dimer pair, the possible list of cross-stacking interactions^{30, 35, 49, 50, 51, 64} in Table 3 is much larger than the 16 possible Watson–Crick dimer pairs. If we could not find experimental cross-stacking data, we set the value to zero. Since the cross-stacking interactions are weak, we do not expect the absence of data for some potential pairs to be a major concern.

Table 3.

The base specific cross-stacking parameters, ${\delta }_{\mathrm{k}}^{ij}$. Cross-stacking interactions are only considered if one of the dimer base pairs is a Watson-Crick base pair. The 5^′-(top) base pair is listed in the left column and the 3^′-(bottom) base pair is listed along the top of the table. The table is read so that ${\uparrow }_{3\prime }^{5\prime }\begin{array}{c}\mathrm{A}·{\mathrm{T}}_{3\prime }\hfill \\ \mathrm{C}·{\mathrm{G}}_{5\prime }\hfill \end{array}\downarrow$ =15.9.

	↑AA↓	↑AC↓	↑AG↓	↑AT↓	↑CA↓	↑CC↓	↑CG↓	↑CT↓	↑GA↓	↑GC↓	↑GG↓	↑GT↓	↑TA↓	↑TC↓	↑TG↓	↑TT↓
↑AA↓	–	–	–	8.8	–	–	16.5	–	–	12.1	–	–	11.0	–	–	–
↑AC↓	–	–	–	11.0	–	–	16.5	–	–	16.5	–	–	8.8	–	–	–
↑AG↓	–	–	–	8.8	–	–	15.4	–	–	14.3	–	–	12.1	–	–	–
↑AT↓	11.0	7.7	12.1	11.0	8.8	6.6	15.9	6.6	12.1	14.3	13.2	–	6.4	5.5	–	5.5
↑CA↓	–	–	–	6.6	–	–	11.0	–	–	12.1	–	–	7.7	–	–	–
↑CC↓	–	–	–	7.7	–	–	12.1	–	–	7.7	–	–	6.6	–	–	–
↑CG↓	12.1	12.1	17.6	15.8	16.5	7.7	20.2	11.0	14.3	24.6	15.4	–	14.3	5.5	–	7.7
↑CT↓	–	–	–	7.7	–	–	8.8	–	–	5.5	–	–	5.5	–	–	–
↑GA↓	–	–	–	8.8	–	–	15.4	–	–	17.6	–	–	12.1	–	–	–
↑GC↓	16.5	11.0	15.4	14.1	16.5	12.1	23.9	15.4	15.4	20.2	17.6	–	15.9	8.8	–	13.2
↑GG↓	–	–	–	8.8	–	–	17.6	–	–	15.4	–	–	13.2	–	–	–
↑GT↓	–	–	–	–	–	–	–	–	–	–	–	–	–	–	–	–
↑TA↓	8.8	6.6	8.8	9.7	11.0	7.7	14.1	8.8	8.8	15.8	8.8	–	11.0	7.7	–	8.8
↑TC↓	–	–	–	8.8	–	–	15.4	–	–	11.0	–	–	6.6	–	–	–
↑TG↓	–	–	–	–	–	–	–	–	–	–	–	–	–	–	–	–
↑TT↓	–	–	–	8.8	–	–	13.2	–	–	7.7	–	–	5.5	–	–	–

Simulation algorithm

These potentials are incorporated into a standard Brownian dynamics algorithm. We scale the lengths with σ, the energies with ε, and the time with τ ≡ ξσ²/ε, where ξ is the bead friction coefficient. The friction of each bead is identical and there are no hydrodynamic interactions between beads. The stochastic differential equation is thus

$$\frac{\mathrm{d}{\mathbf{x}}_i}{\mathrm{d}t}=-\frac{\partial U}{\partial {\mathbf{x}}_i}+\sqrt{\frac{2T}{\Delta t}}{\mathbf{r}}_i,$$ (9)

where ${\mathbf{x}}_i$ are the dimensionless bead positions, T = k_BT(K)/ε is the dimensionless temperature in terms of Boltzmann's constant, k_B, and the dimensional temperature, T(K), and Δt is the dimensionless time step. The random numbers, ${\mathbf{r}}_{\mathbf{i}}$, are Gaussian with mean zero and unit variance. The stochastic differential equation is integrated using a predictor-corrector scheme.⁶⁵ We only report time-independent data (qualitative trajectories or thermodynamic data), rendering the choice of friction coefficient one of convenience since it is adsorbed into the time constant. The time step is 0.1τ and the bead positions are saved every 100τ.

To estimate the equilibration time for the double-stranded DNA simulations, we initialized the sequence, 5^′-CCGAGTACGTCGGGCGCTTATAGTG-3^′, as described in Sec. 3A and simulated the coldest dimensionless temperature, T = 0.25. We then computed the average number of bases per turn (calculated from one strand) as a function of time. We considered the duplex equilibrated when this value became constant and used the corresponding time as a conservative estimate for the equilibration of all sequences at all temperatures. We started sampling after two equilibration times and the sampling continued for 8 equilibration times.

We used an even more conservative estimate of the equilibration time for the DNA hairpin melting simulations in Sec. 3B. For a given single-stranded DNA sequence, we first examined the simulation of the coldest dimensionless temperature, T = 0.25, and waited until the first closure event. The BD time step for which this happened was designated as the relaxation time for that sequence. For a simulation of this sequence at a given temperature, we waited until we reached this equilibration time and then sampled for 9 equilibration times. This allowed us to capture many opening and closing events at the melting temperature.

In both the thrombin aptamer study, Sec. 3C, and the triple helix formation study, Sec. 3D, the simulations were continued until the final folded state or stable triplex formation was stable for fifty percent of the total simulation time. The thrombin aptamer was simulated eight times from its initial comb configuration while the triple-helix had three independent simulations. The qualitative trajectories of the triple helix formation did not significantly differ between the three simulations.

RESULTS AND DISCUSSION

We have applied our new model to four different systems. The first pair, dsDNA and ssDNA hairpins, test the model's ability to match or predict experimental data. The second pair, the folding of a thrombin aptamer and triplex formation, highlight two scenarios where Hoogsteen bonds play a crucial role. After reviewing the results of our simulations, we include a comparison with the 3SPN model^{13, 14, 24, 25, 26} and directions for improving our model.

Structure of dsDNA

Our goal in simulating this first system was not to study the mechanism of hybridization per se, but rather to establish that our model spontaneously forms B-DNA over a wide range of sequences and temperatures. Watson–Crick bonds dominate in dsDNA, so this system also demonstrates that Hoogsteen bonds can be included in the model without disrupting the canonical conformation. We used 10 random dsDNA sequences, listed in Table 4, containing 25 base pairs and performed simulations at 5 different dimensionless temperatures, corresponding to a temperature range of 290–315 K based on the conversion factor we will obtain in Sec. 3B. We purposely chose temperatures in which the dsDNA does not melt in order to be better able to examine dsDNA structural characteristics in the canonical state. We will present melting data shortly in the context of ssDNA, which will highlight the importance of Hoogsteen bonds. We initialized the two complementary ssDNA sequences as an anti-parallel ladder, with the backbones straight and the complementary bases separated by 1.5 nm.

Table 4.

List of sequences used to evaluate the dsDNA structure.

Random 25-mer dsDNA Sequences Used
5′-CCGAGTACGTCGGGCGCTTATAGTG-3′
5′-CAGAACACTTTCTACACCCTGACGC-3′
5′-TGCCTGAACGATAAATCCGATGGCT-3′
5′-GGGTTCATCCGCTACCGTGCTCCCT-3′
5′-GTATGCCACGAATACTCTCTGCAGA-3′
5′-TTATCGCTCGAGGTGCTTGGCTGGC-3′
5′-TGTAAGCCACGAATACCGGCCCCGA-3′
5′-GATAAGCGTTTTAGAGTGTCATTTG-3′
5′-TAAGCTTGGGCTGTCTTTTAGGAGG-3′
5′-AAATGAATTCGCTCACGCCCGGTTA-3′

At the start of the simulation, Watson–Crick bonds quickly formed between nearby, complementary bases on opposing strands. These bonds led to local twisting of the chain, with a mixture of right-handed and left-handed structures nucleating at different locations. The twists propagated along the sequence and the chain eventually achieved a homogenous chirality. Of 50 independent simulations conducted with the 10 random dsDNA sequences listed in Table 4, we found that right-handed helices are formed in 62% of the structures. This result is reasonable since our model has no built-in handedness, torsional constraints that favor B-DNA,^{7, 13, 14, 15, 16, 24} bottom up parameterization from an all atom B-DNA model,^{2, 3, 4, 5, 6, 7} or a method to remove the stacking interactions in left-handed twist.²⁰ Indeed, other models of this type lead to equilibrated structures that are sometimes left-handed.^{7, 9, 10}

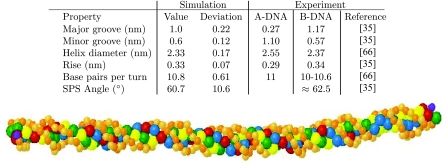
In Fig. 4, we provide a snapshot of the dsDNA configuration from our simulation and the structural data obtained for the right-handed helices, along with representative experimental data for A- and B-DNA.^{35, 66} The results are essentially unchanged if we include the left-handed helices, since the potentials are symmetric with respect to the handedness. The present model produces an overall double-stranded structure that is closest to B-DNA. The simulated structural data, averaged over all sequences and temperatures, agree well with experimental data. We only included data that can be reasonably resolved by the model at our degree of coarse-graining. For example, although it is possible to compute the roll using a multi-bead model for the bases,² we cannot resolve it here because each base is only represented by a single sphere. The major and minor groove spacings were measured between the edges of the excluded volume cutoffs for the relevant beads, rather than from their centers, to correspond to the measurements obtained by NMR.³⁵ These distances are at the limit of what we can resolve at this level of coarse-graining, so the major and minor groove widths should be considered estimates.

Figure 4.

Structural data for dsDNA. The standard deviation is over all sequences and temperatures. The SPS angle measures the angle formed between the phosphate and two sugar beads along the backbone of one of the ssDNA strands in the duplex. A depiction of double-helix DNA is included; the backbone is comprised of the smaller (orange) beads, with the light (orange) beads representing the phosphate beads and the dark (orange) beads representing the sugar beads. The 5^′ end of the sequences is depicted by the dark (purple) beads. The four bases A, C, G, T are represented by the blue, green, red, and yellow beads, respectively. The major and minor groove can be seen in the regular structure of the double helix.

We also estimated the persistence length of a 50 base pair dsDNA using an extrapolation method.⁶⁷ In contrast to our calculation of the persistence length of ssDNA, we constructed the backbone vectors at a length scale corresponding to approximately one turn.^{13, 14, 21} Since we have 10.8 bases per turn (Fig. 4), we constructed vectors between every 11 nucleotides and computed the initial decay of the autocorrelation function. Depending on the reference bead, we obtained a persistence length of 47 ± 8 nm (sugar-to-sugar), 48 ± 7 nm (phosphate-to-phosphate) and 46 ± 10 nm (base-to-base). Although the measurement must be considered a rough estimate, it shows that our model is at least approximately in line with the accepted standard of about 50 nm, or 150 bp.

Any model that includes stacking produces helicity. A particularly notable feature of our model is the sugar-phosphate-sugar (SPS) angle, which is close to but not the same as the sugar pucker (or glycosyl) angle. The 3SPN model^{13, 14, 24} maintains a SPS angle close to the experimental value for B-DNA by imposing a dihedral angle potential. In our model, the SPS angle arises from the directionality of the stacking interactions without the need to also apply a dihedral potential. As would be the case with a spherical potential, the stacking interactions are increased as the bases along one strand move closer together. However, with our directional bonding, the stacking energy is most favorable when the vectors drawn from each sugar to its bonded base are parallel. To maximize the interaction, the backbone flexes and the phosphates are pushed towards the outside of the chain to form the SPS angle. Note that there is no bending penalty for forming a SPS angle because the bending energy is defined between the sugar trios. The result is the formation of a dihedral angle without the need for a dihedral potential. From a computational standpoint, our method and that employed in the 3SPN model^{13, 14, 24} are roughly equivalent; the cost for computing the dihedral angles is somewhat less than that for computing the θ-dependent term appearing in the base-base interactions, but the θ-dependent term provides both the SPS angle and directional bonding.

For studying single-stranded DNA in the in vivo conditions mimicked by Buffer A, our approach appears to offer some advantages compared to the 3SPN models. As noted by Knotts et al.,¹³ constraining a model a priori to favor B-DNA makes it difficult to study transitions to other forms. We suspect that our model does not suffer from the same limitation. It is true that we obtained the various energies for stacking, cross-stacking, and hydrogen bonding from experiments on B-DNA,^{30, 35} so the double-stranded conformation should favor a B-form SPS angle. However, in the absence of Watson–Crick base pairs, the SPS angle changes dramatically in our model. For example, we obtained a SPS angle of 97 ± 52° for the ssDNA sequence 5^′-ATCATGCGATCATCCG-3^′ at a temperature of 340 K. This large deviation in the SPS angle, which results from temporal fluctuations, reflects the flexibility of ssDNA. This allows our model to transition smoothly from ssDNA to dsDNA thereby permitting study of hybridization, melting, and other interchain interactions.

Melting of a DNA hairpin

The second critical test for our model is its ability to capture thermally induced transitions. For this purpose, we considered the seven block polymer hairpins listed in Table 5. Our analysis followed along the lines of prior work.³⁷ To establish the mapping, we first simulated the 5^′-A₅C₅T₅-3^′ hairpin between the dimensionless temperatures T = 0.25 and T = 0.50. The system was initialized as a comb and allowed to relax fully before collecting data. At low temperatures, it takes quite some time for the hairpin to close but the resulting closed state is stable. In prior work,³⁷ we showed that we obtained the same results for the fraction of bound bases independent of whether we start in the open state or the closed state, provided that we wait for the system to equilibrate. As noted in Sec. 2D, we used the time for the largest hairpin to close at the lowest temperature as a very conservative estimate for the equilibration time and use this time for all of the simulations. There are many possible ways for this hairpin to form Watson–Crick base pairs, but we have shown³⁷ that the best way to compare the open/closed state of the system to the experimental data is to time average the number of “correctly” bonded pairs at a given temperature. By correct, we mean that the pairing leads to a completely bonded stem. Since the bonds in the present model are directional, two bases were considered bonded if (i) they possess an allowed angle for hydrogen bonding (see Fig. 1) and (ii) their center-to-center distance was less than 0.3 nm. The simulations produced data at discrete temperatures, which we fit with a sigmoidal function. The experiments were conducted in a common and biologically relevant buffer, Buffer A.³⁸ We then obtained the conversion between the simulation and experimental temperature by shifting the simulated melting curve so that the melting temperature of the simulation, corresponding to the midpoint of the height of the sigmoidal function, aligns with the midpoint in the fluorescence intensity of the experimental data.³⁷ This analysis led to the conversion factor T(K) = 1150 T. Our one degree of freedom was thus used to fit the melting temperature for the 5^′-A₅C₅T₅-3^′ hairpin.

Table 5.

Comparison of simulation and experimental data for DNA hairpin melting.³⁷

		Simulation37		Simulation (here)
	Experiment37
Sequence	Tm(K)	Tm	${\mathrm{R}}_{\mathrm{a}}^2$	Tm	${\mathrm{R}}_{\mathrm{a}}^2$
5′-A5C5T5-3′	341	341	0.995	341	0.996
5′-A5C10T5-3′	337	338	0.942	338	0.979
5′-A7C5T7-3′	328	343	0.450	327	0.940
5′-A7C10T7-3′	330	343	0.540	329	0.942
5′-A5G5T5-3′	329	340	0.622	331	0.928
5′-A5G10T5-3′	341	336	0.713	338	0.902
5′-G5A10C5-3′	338	350	0.514	339	0.915

For each hairpin in Table 5, we determined the simulated melting point and the coefficient of multiple determination adjusted for the number of parameters in the sigmoidal model, ${\mathrm{R}}_{\mathrm{a}}^2$, between the experimental and simulated melting curves. These ${\mathrm{R}}_{\mathrm{a}}^2$ values were obtained from plots similar to Fig. 5. The plots for the other hairpins, which are essentially the same, are included in the Supplemental Information.⁶⁸ While it is difficult to propagate the error in the experimental data, we estimate that it is around ±2 K. The data for the two-bead model^{10, 37} are included in Table 5 for completeness.

Figure 5.

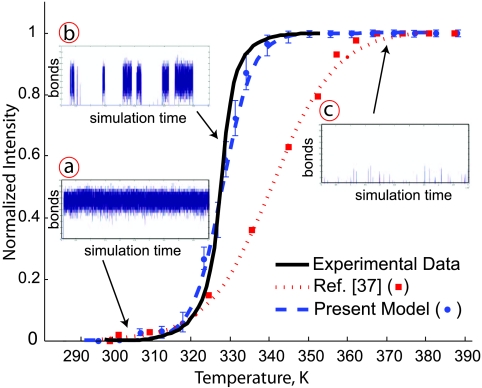
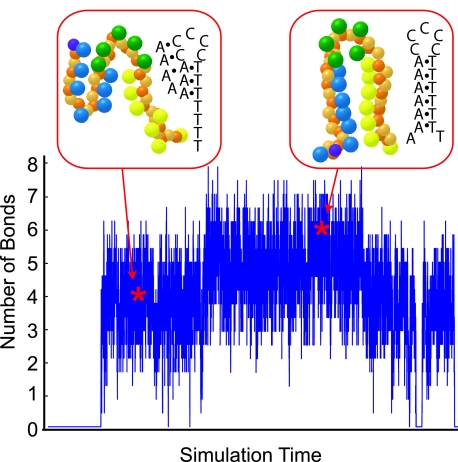
Comparison of the thermodynamics of experimental and simulated hairpin open-close transitions for the sequence 5^′-A₇C₅T₇-3^′. The solid black line is experimental data reported for 1X Buffer A.³⁷ The symbols are the simulation data and the dashed lines are sigmoidal fits to the simulation data for (i) the present model and (ii) simulation data reported in Ref. 37. The insets show the number of correctly aligned bonds for (a) the closed state, (b) the transition and (c) the open state as a function of the simulation time. The amount of data in the trace is 11% of the total sampling time.

By definition, the simulated melting point for the 5^′-A₅C₅T₅-3^′ hairpin is identical to the experimental value. All other simulation data in Table 5, Fig. 5 and the figures in Supplemental Material⁶⁸ can be considered predictive. Given this parameterization, the simulations certainly should capture the melting for the slightly larger loop in 5^′-A₅C₁₀T₅-3^′. Indeed, even the simple two-bead model¹⁰ captures the latter experimental data. The challenge is to capture the data for all sequences, including the width of the transition^{21, 37} and the shoulder.¹³ The very high values of ${\mathrm{R}}_{\mathrm{a}}^2$ achieved by the current model indicate that we indeed accomplished this task. Moreover, the high ${\mathrm{R}}_{\mathrm{a}}^2$ values suggest that no bias was introduced by the arbitrary choice of 5^′-A₅C₅T₅-3^′ for the parameterization. To confirm this conjecture, we repeated the parameterization procedure using each of the other sequences in Table 5. Out of the 42 predicted melting temperatures produced from all possible combinations, the largest difference between simulation and experiment was 3 K.

The present model has a number of improvements compared to the simple two-bead model¹⁰ used in our previous comparison with these experimental data.³⁷ Explicitly, we now have directionality along the backbone, a major/minor groove, experimentally parameterized bonding energies, anisotropic bonding, and non-Watson–Crick bonds. We previously speculated that the main reason why the two-bead model¹⁰ fails to capture the melting transitions of these block-polymer sequences is the absence of Hoogsteen bonds.³⁷ As we can see in Fig. 6, this certainly appears to be the case for the 5^′-A₇C₅T₇-3^′ sequence. At low temperatures, the hairpin is stabilized by Watson–Crick bonds, as expected. When the hairpin opens in Fig. 6, both the adenine and cytosine bases form Hoogsteen bonds, with the cytosines adopting an I-motif.^{32, 33} These Hoogsteen bonds are relatively strong and need to be undone in order to fold into the closed state. They thus represent not only a change in the free energy landscape but non-trivial kinetic traps. While directional bonds are certainly important for modeling long AT or GC tracts,¹⁴ we suspect that Hoogsteen bonds will also be important when these simulations are intended to capture experimental data.

Figure 6.

Detailed trajectory for the number of correct bonds in the stem for the sequence A₇C₅T₇ at a temperature of 327 K, which is near the melting temperature. The snapshots show two examples of the hairpin configurations obtained at the times indicated by the stars. The structure on the left, with 3 paired stem bases, is stabilized by Hoogsteen bonds. The structure on the right shows fraying of the hairpin ends.

Folding of a thrombin aptamer

Aptamers are sequences of ssDNA (or RNA) that bind selectively to proteins. While the methods for isolating aptamers from a random library of nucleic acids^{69, 70, 71} are relatively well developed, the selection method provides little insight into the reasons for their high affinity and specificity towards particular proteins. However, it is reasonable to assume that the secondary and tertiary structures of aptamers substantially contribute to their activity. As a result, coarse-grained simulations could play an important role in understanding aptamer activity. To illustrate the power of such simulations, we looked at the folding pathway of the DNA aptamer 5^′-GGTTGGTGTGGTTGG-3^′, which binds to thrombin, a blood clotting protein.⁷¹ NMR studies⁷² indicated that this aptamer forms a G-quartet. As this structure results from Hoogsteen bonds, the thrombin aptamer is an ideal candidate to study with the present model. Cations such as K⁺ or Na⁺ may stabilize the G-quartet structure.⁷³ Although our model does not have explicit ions, the experimental data used to tune our model^{30, 35, 36, 37} includes these ions and may implicitly account for such electrostatic effects.^{13, 15, 16, 19, 20, 21, 24}

To investigate the folding of this aptamer, we initialized the ssDNA as a comb and performed eight simulation runs. The simulation temperature was 298 K, which corresponds to experiments and should promote the folded state. Figure 7 shows the evolution of the structure as a function of time. We observed two distinct pathways. In both pathways, the distal guanines form a single G-quartet. In Fig. 7, we show the case where this bonding occurred at the 5^′-end (1), but this can also occur at the 3^′-end. In the more common pathway (six of eight simulations), the next bonding step forms a triplex in the interior (2) while leaving the pair of guanines at the other end of the chain unbonded and able to fluctuate (3). To form the final structure (4), the unpaired guanines on the free end need to disrupt the triplex and create a pair of G-quartets. While this folded state (4) is thermodynamically favorable, the kinetics for the final step (3 → 4) are slow compared to the preceding steps. In the less common pathway (two of eight simulations), both distal ends fold in on themselves to create a pair of G-quartets (2^′)s. The entire molecule then folds about the center axis (3^′) to stack the G-quartets (4). In both pathways, the final state, depicted in the wire diagram in Fig. 7, is consistent with NMR data.⁷²

Figure 7.

Folding pathways for the thrombin aptamer, 5^′-G₂T₂G₂TGTG₂T₂G₂-3^′. The numbers indicate steps in the most common pathway (1 → 2 → 3 → 4) and a secondary pathway (1 → 2’ → 3^′ → 4). The wire-frame diagram shows a cartoon of the bead positions at the final snapshot time; the dark (purple) bead denotes the 5^′ end of the DNA molecule.

Strand invasion during triplex formation

Triplex formation plays an important role in the repair of a stalled replication fork or a break in dsDNA. In the simplest model, the strand invasion problem consists of a dsDNA and a ssDNA, where the ssDNA possesses the same sequence as one of the strands in the dsDNA. At the end of the process, the ssDNA is wrapped inside the major groove of the dsDNA and the complex is stabilized by a combination of Watson–Crick and Hoogsteen bonds. The in vivo process is more complicated, since the strand invasion is aided by proteins, such as RecA or Rad51.

Simulating protein free strand invasion provides a particularly stringent test of the capabilities of our model. First, the major groove needs to be wide enough to accommodate the excluded volume of the invading strand. Second, the directionality of the bonding interactions needs to be strong enough to prevent unphysical bonding to multiple sites. Indeed, we frequently found that the spherical potentials appearing in an earlier model¹⁰ led to a collapsed, globular state. Finally, stabilizing the triple-stranded structure requires Hoogsteen bonds.

To demonstrate that our model has the requisite fidelity to capture strand invasion, we used the single-stranded sequence 5^′-ACTCAACCAAGTCATTCTGCGAAT AGTGTATGCGGCGACC-3^′ and a complementary double-strand. The dsDNA was relaxed into the B-form in the absence of the single-strand. We then initialized the ssDNA as a comb. If we define a polar coordinate system at the complementary 5^′-end of the dsDNA with θ = 90° pointing along the backbone of the dsDNA, then the 3^′-end of the ssDNA is located initially at a distance of 1.5 nm and an angle of 150° relative to the 5^′-end of the dsDNA. All beads on the linear ssDNA strand are initially in the plane defined by (i) the line connecting the 5^′ and 3^′ beads of the complementary strand of the dsDNA and (ii) the aforementioned line in the polar coordinate system. This initial condition promotes strand invasion in a reasonable amount of simulation time while allowing thermal motion to stack the ssDNA prior to invasion. The simulation was conducted at a temperature of 285 K.

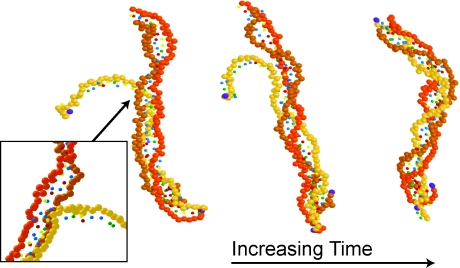
Figure 8 shows several snapshots during the course of the simulation after the ssDNA has begun to disrupt the helical structure of the dsDNA. The ssDNA intially diffused towards the dsDNA. When the two DNAs came into close contact, the presence of the ssDNA opened a bubble in the dsDNA. This bubble allowed for rearrangement of the hydrogen bonding to minimize the energy of the combined Watson–Crick and Hoogsteen interactions between the bases on the three strands. The inset in Fig. 8 highlights the bubble and the invading strand. As this region of the triplex stabilized, the backbone of the invading strand inserted into the major groove and the bubble propagated along the dsDNA. When the bubble reached the opposite side of the dsDNA, it closed to produce the final, triple-stranded state.

Figure 8.

Simulation snapshots during the formation of a triple-stranded DNA. The backbone of the invading strand has the lightest color. For clarity, the base beads are represented as small spheres and the 5^′ backbone beads are dark (purple) spheres. The magnified inset depicts the indicated region of the chain, viewed from behind.

Limitations of the model

Our results thus far have highlighted the advantages of our new model. The structures can smoothly move between a flexible ssDNA and the more constrained dsDNA while still capturing most of the features of the double helix. In the single-stranded state, we are also able to model important physical scenarios that require Hoogsteen bonds, such as G-quartets and I-motifs. However, there are some manifest shortcomings to the model that we discuss here.

The model does not possess any inherent chirality that enforces right-handed double helices. In other models, the chirality has been enforced using dihedral potentials,¹³ which prevent a smooth transition to single-stranded DNA, or by simply turning off the stacking interactions if the helix is left-handed.²⁰ Although we observed a number of left-handed helices, we do not view this as a critical shortcoming of the model. The initial conditions we used in our simulations for dsDNA are unbiased; two opposing combs have no initial chirality. The eventual handedness of the helix is strongly determined by the nucleation of a local region of twist, in particular if this occurs in a GC-rich region. Indeed, when we used the same random numbers but changed the sequence, all of the resulting helices had the same handedness (which happened, by chance, to be right-handed). If our goal was to investigate some property of double-stranded DNA, we simply need to initialize the chain as a right-handed helix. The energy barrier between chirality is enormous and well beyond the time scale for any reasonable isothermal simulation.

The parameterization we use here is only valid for a single ionic strength, since we determined the value of the energy scale ε using experimental data for Buffer A. The model can be modified to account for ionic strengths in the manner proposed by Knotts et al.¹³ First, a screened Debye-Huckel potential needs to be added between phosphate beads. Since electrostatic interactions on the backbone stiffen the DNA,^{74, 75} we then need to adjust the bending potential to recover a persistence length appropriate for single-stranded DNA. If the electrostatic potential is weak compared to the hydrogen bonding, then the value of ε is unaffected by the inclusion of explicit phosphate charges. If not, we can use a multiplicative factor for the ε in Eq. 4 to set the relative strengths, analogous to the 3SPN model.¹³

Perhaps the most critical issue is our use of the same excluded volume interaction, independent of the base identity. For the problems we studied here, this was not an issue but the base sizes will play an important role if the model is used to study mismatches. Our model incorrectly accounts for a non-Watson–Crick mismatch since the hydrogen bonding energies for the Hoogsteen bonds are similar to their Watson–Crick counterparts. In reality, the mismatch should lead to substantial excluded volume interactions, which in turn disrupt the stacking and thus the local stability of the duplex. Fortunately, the remedy to this problem is straightforward — the homogeneous excluded volume interactions need to be replaced by a more realistic model. In the 3SPN model,¹³ for example, different bases are represented by different mass beads and bond lengths. We expect that correcting the bond lengths will be important for accurately capturing the melting of the double helix.

Moving forward, we should also point out an additional issue with our model relative to the 3SPN model,^{13, 14, 24} namely, the use of anisotropic potentials. Most molecular dynamics solvers, such as GROMACS,⁷⁶ only permit spherical potentials. We do not see an easy route towards using spherical potentials in a coarse-grained model and still moving smoothly between double-stranded DNA and single-stranded DNA. Removing the anisotropic potentials requires adding dihedral potentials, which then bias the shape of ssDNA towards the B-form of dsDNA.

CONCLUSIONS

In the present contribution, we have highlighted the importance of including Hoogsteen bonds in coarse-grained models of DNA. The model captures many of the salient features of B-form dsDNA without the need to constrain the backbone via dihedral potential functions. As a result, the SPS angles in the model are not biased towards their double-stranded values and can fluctuate widely in the single-stranded state. Our comparison with experimental hairpin melting data underscores the need to account for Hoogsteen bonding during hybridization of these types of sequences. While the particular block-polymer sequences used here³⁷ exhibit substantial secondary structure in the open state, Hoogsteen-stabilized secondary structures can also play a role in studies of hybridization and bubble formation in conventional dsDNA. The strongest effects should be seen in a GC tract, where the guanines will form a G-quartet and their cytosine counterparts will form an I-motif. In light of recent experimental data,³⁴ it may be necessary to consider Hoogsteen bonds even for relatively simple systems like B-DNA in the fully hybridized state.

In this study we explored the role of Hoogsteen bonds in a relatively simple model of DNA. We expect that it will be straightforward to augment other coarse-grained models with non-Watson–Crick bonds if one wants to study more detailed interactions, such as the role of solvation or ionic strength.^{13, 14, 22, 24, 25, 26} We expect that coarse-grained models incorporating Hoogsteen bonds will be useful in a number of scenarios beyond hybridization of dsDNA or ssDNA hairpins. As the first example, we investigated the folding of an ssDNA aptamer that possesses a G-quartet. There are numerous other aptamers whose secondary and tertiary structure should be affected by Hoogsteen bonding and are thus amenable to simulation using our method. As the second example, we showed how the model could capture the dynamics of strand invasion leading to triplex formation. While the in vivo situation is much more complicated due to the presence of ssDNA binding proteins, the model presented here is the first step towards a sequence-specific, coarse-grained model of DNA repair. Although the model presented here does not include the complex and delicately balanced free energy terms found in all atom systems, this limitation should be balanced against the model's ability to reach long times.