Abstract
Solvation is of fundamental importance to biomolecular systems. Implicit solvent models, particularly those based on the Poisson-Boltzmann equation for electrostatic analysis, are established approaches for solvation analysis. However, ad hoc solvent-solute interfaces are commonly used in the implicit solvent theory. Recently, we have introduced differential geometry based solvation models which allow the solvent-solute interface to be determined by the variation of a total free energy functional. Atomic fixed partial charges (point charges) are used in our earlier models, which depends on existing molecular mechanical force field software packages for partial charge assignments. As most force field models are parameterized for a certain class of molecules or materials, the use of partial charges limits the accuracy and applicability of our earlier models. Moreover, fixed partial charges do not account for the charge rearrangement during the solvation process. The present work proposes a differential geometry based multiscale solvation model which makes use of the electron density computed directly from the quantum mechanical principle. To this end, we construct a new multiscale total energy functional which consists of not only polar and nonpolar solvation contributions, but also the electronic kinetic and potential energies. By using the Euler-Lagrange variation, we derive a system of three coupled governing equations, i.e., the generalized Poisson-Boltzmann equation for the electrostatic potential, the generalized Laplace-Beltrami equation for the solvent-solute boundary, and the Kohn-Sham equations for the electronic structure. We develop an iterative procedure to solve three coupled equations and to minimize the solvation free energy. The present multiscale model is numerically validated for its stability, consistency and accuracy, and is applied to a few sets of molecules, including a case which is difficult for existing solvation models. Comparison is made to many other classic and quantum models. By using experimental data, we show that the present quantum formulation of our differential geometry based multiscale solvation model improves the prediction of our earlier models, and outperforms some explicit solvation model.
INTRODUCTION
One cannot imagine life without water. Indeed, 65–90% of cellular mass is water. Under physiological conditions, almost all important biological processes, such as protein ligand binding, ion transport, signal transduction, gene regulation, transcription, and translation, occur in aqueous environments. Therefore, the first step toward a quantitative description and analysis of the above-mentioned biological processes is a detailed understanding of the solvation process, which refers to the immersion of a molecule from its lowest energy state in vacuum, to an equilibrium state in an aqueous environment. The solvation process involves the mechanical work of inserting a molecule into the solvent, and solvent-solute (intermolecular) interactions at the solvent-solute interface, which is associated with the structural reconstruction of the solvent and solute near the interface. The most important physical observable of a solvation process is the solvation free energy, which is typically modeled as polar and nonpolar contributions. Nonpolar solvation energy involves the surface area effect, the mechanical work and some solvent-solute interactions. The polar solvation energy can be theoretically estimated by a wide variety of approaches ranging from simple phenomenological modifications of Coulomb's law, explicit solvent models that treat the solvent in molecular or atomic details,55 to complex quantum mechanical methods.34, 39, 46, 56 However, for macromolecules, an ab initio description of the solvation process by a full quantum mechanical description of all relevant elemental particles, i.e., electrons and nuclei, and their dynamics, is intractable at present and may still remain unfeasible in the near future. That is due to the excessively large number of degrees of freedom. Multiscale methods, which are able to reduce the number of degrees of freedom, are indispensable in solvation analysis and in the quantitative description of other biological processes in general.76
Based on a mean field approximation for the solvent, implicit solvent models describe the solvent as a dielectric continuum, while the solute molecule is modeled with an atomistic description.5, 24, 32, 38, 59, 62 There are many such two-scale implicit solvent models for the electrostatic analysis of the solvation, including generalized Born (GB) (Refs. 8, 25, and 72) and Poisson-Boltzmann (PB) models.24, 26, 41, 62 Generalized Born methods are very fast but provide only heuristic estimates for polar solvation energies. PB methods can be formally derived from basic theories12, 31, 50 and offer a more accurate method for computing the polar solvation energy.8, 23, 52 In most solvation analysis, the polar solvation energy is complemented by the nonpolar one, which includes contributions from surface tension at the solvent-solute interface, mechanical work of inserting solute molecules into the solvent, and solvent-solute interactions. The reader is referred to two recent papers for review-style elaborated descriptions of the solvation process, solvation models and various applications of solvation methods.16, 17
All implicit solvent models require an interface definition to separate the solute domain from the solvent domain. The solvent-solute interface is typically represented by the van der Waals surface, the solvent accessible surface,42 or the molecular surface (MS) (Ref. 58) in the literature. These definitions are ad hoc in nature and do not account for the interfacial free energy minimization during the solvation process.
Recently, we proposed differential geometry based solvation models to address the above mentioned modeling deficiency in solvation analysis.16, 17, 76 In our approach, the surface free energy is described via the differential geometry of surfaces either in the Eulerian representation,16, 76 or in the Lagrangian representation.17 The solvent-solute interface profile is determined by the first variation of a total free energy functional, which includes polar and nonpolar contributions. The variation based formulation of biomolecular surfaces was introduced by us to construct the minimal molecular surface in 2006.10, 11 Such a formulation makes use of the mean curvature flow. Our geometric flow approach introduced the differential geometry of surfaces to the biomolecular surface analysis. This approach was further extended to potential driven geometric flows, which allow solvent-solute interactions in the surface formation.9 Generalized Laplace-Beltrami equations are derived for generating biomolecular surfaces by the Euler-Lagrange variation. In addition, one of the first partial differential equation (PDE) based biomolecular surface constructions was introduced by us in 2005.77 Our method is conceptually different from PDE based surface smoothing techniques which require a priori given surface. In contrast, our PDE based surface construction does not require a surface to begin with; instead, only atomic information, i.e., atomic coordinates and radii, is needed.
The above mentioned differential geometry based solvation models are important examples of differential geometry based multiscale models.76 Such multiscale models differ conceptually from other conventional multiscale models. Essentially, when there is a real physical separation between two different materials, such as the division between oil and water, and the splitting between protein and solvent, it is natural to incorporate the differential geometry of surfaces to describe the material interface. For this class of systems, it is advantageous to reduce the number of degrees of freedom by describing the material of interest at a fine scale, such as the atomic or the quantum scale, while modeling other materials at a coarse scale, such as the continuum approach. In this way, we have established a general variational framework, in which the total energy functional of a system includes energy contributions from the interface and two materials.
In our earlier differential geometry based solvation models,16, 17, 76 the solute is described as a collection of fixed atomic point charges, which, together with the charge described in the continuum approximation of the surrounding medium, give rise to the total charge source for the Poisson-Boltzmann equation. Fixed point charge models can provide inexpensive approximations, as well as good predictions of many physical and chemical properties. However, it neglects the explicit treatment of polarization effects so that it cannot cover the whole range of properties of interest. In particular, the charge rearrangement in the solute molecule during the solvation process has not been taken into account in the calculation of solvation free energies. It is well-known that the charge rearrangement plays an important role in the solvation process of proteins in various cases.30 Consequently, the highly accurate analysis of solvent-solute surfaces is discounted by the estimation of charge rearrangement during the solvation process. Additionally, our earlier solvation models with fixed charges depend on parameters from the existing molecular mechanical force field parameters,6, 35, 37, 45 which are typically parameterized for certain class of (macro-) molecular systems and may not be appropriate for other classes of molecules. These reasons call for the development of coupling highly accurate solute potentials with a continuum treatment of the solvent.
For computational savings, researchers also proposed polarizable force field (PFF) models combined with a continuum solvent model to treat polarization effects explicitly, such as polarizable multipole Poisson-Boltzmann (PMPB) models,60 fluctuating charge models of generalized-Born calculations,81 etc. The PFF models benefit from the purely classical representation so that the study of large systems can be facilitated. They offer a classical approximation to many-body polarizations.
Generally speaking, a quantum mechanical (QM) description of solute molecules is an ab initio approach to achieve a highly accurate, self-consistent and force field independent charge arrangement during the solvation process. Consequently, the QM description has been incorporated into the classical implicit solvent theory in the past few decades.15, 22, 70, 71 The resulting QM version of continuum model, called quantum mechanical continuum model or polarizable continuum model,7, 14, 18, 20, 36, 68, 70 offers the possibility of carrying out highly accurate quantum calculations in the solute and near the interface. Quantum mechanical continuum model provides a framework to describe the QM effect explicitly in solvent analysis.69 Recently, Mei et al. have proposed a remarkable conductorlike polarizable continuum model to deal with large molecules, such as proteins.47 Notably, Wang et al. have introduced the QM description of solute molecules to the Poisson model for solvation analysis.75 Their results show a good agreement with experimental data.
To integrate a continuum model with a QM description, reaction field potential, i.e., the electric field induced by the polarized solvent, has been introduced as a unifying concept. It is obtained from the electrostatic computation in the framework of continuum models. It also exists in the Hamiltonian of the solute in the quantum calculation.15, 69, 74 Therefore, the quantum formulation of the continuum model involves two problems: (1) the classical electrostatic problem of determining the solvent reaction field potential with the quantum mechanically calculated charge density; (2) the quantum mechanical problem of calculating the electron charge density with fixed nucleus charges in the presence of the reaction field potential. These two problems need to be resolved simultaneously. To carry out these computations, an intuitive self-consistent iterative procedure can be constructed to resolve the quantum problem for the electron distribution and the classic electrostatic problem for the reaction field potential.15, 30, 69, 70, 74
After computing the QM charge density, there are at least two ways to implement the solvation analysis. The first approach is to apply the continuous QM charge density directly to the Poisson-Boltzmann equation as a source term. The second approach is to fit the QM charge density into the atomic point charges, and alternatively use the point charges as the source term.33, 63 Various schemes have been proposed to compute atomic partial charges with certain efficiency and convenience. The simplest way for atomic partial charge assignments is the Mulliken analysis method.49 In Mulliken's approach, the charge is distributed according to the orbital occupation. Many other schemes have also been proposed, including the natural bond orbital analysis, the distributed multipole analysis (DMA), the wavefunction mapping “Class IV” model, the electrostatic potential expansion and analysis, etc.57, 64, 67 At the present time, the most widely used method for estimating atomic partial charges is the least-squared electrostatic potential (ESP) fitting approach. It was first proposed by Momany and has subsequently been implemented in different ways with different choices of grid points where the electrostatic potentials are calculated.48 Examples of such potential-based methods are CHELP, CHELPG, and the Merz-Kollman scheme.13, 19, 21, 65
The quantum mechanical problem of determining the electron charge density can be solved by a variety of theories and algorithms. One of the simplest ab initio approaches is the Hartree-Fock (HF) method, which replaces instantaneous Coulombic electron-electron repulsion interactions with a mean-field average. A variational procedure is used to minimize the energy. An alternative of the HF method is the density functional theory (DFT), which is originated from the Thomas-Fermi model. DFT represents the electronic structure (principally the ground state) of a many-body system as a functional of a single electron density. As usual in many-body electronic structure calculations, the nuclei of the molecule of interest are treated by the Born-Oppenheimer approximation (i.e., as fixed) in DFT to generate a static external potential in which the electrons are moving. The self-consistent iterations are utilized to minimize the total energy of the system. Recently, DFT has become one of the most popular and versatile methods available in computational physics, computational chemistry and computational biology. In all previous QM based implicit solvent models, pre-determined solvent-solute interface models, such as solvent accessible surfaces and MSs are utilized to separate the solvent domain from the solute domain. Since the prediction of implicit solvent models is very sensitive to the definition of solvent-solute interfaces, in many cases, pre-determined solvent-solute interfaces compromises the highly accurate QM description of the solute molecule.
The objective of the present work is to incorporate a quantum mechanical description of charge densities into our earlier differential geometry based solvation models.16, 17 By using this approach, we wish to develop a more accurate and self-consistent multiscale approach for the solvation analysis of both small and large molecules. The advantages of the present quantum formulation of the differential geometry based multiscale solvation model are as follows. First, compared with our earlier solvation models, the present model is able to provide more accurate descriptions of charge rearrangement during the solvation process and leads to a more accurate prediction of the solvation free energies, under the same set of parameters. Note that the accuracy of implicit continuum salvation models relies on parameters such as atomic radii and dielectric constants. Additionally, the present multiscale model reduces the dependence of our earlier solvation models on the existing molecular mechanical force field parameters, which are typically parameterized for certain class of (macro-) molecular systems and may not be appropriate for other class of molecules. Therefore, the present model can be applied to a wider class of problems. Moreover, compared with other existing QM based solvation models,70, 74 the present model avoids the use of unphysical solvent-solute interfaces. The solvent-solute boundary in use is described by the differential geometry of surfaces. Finally, a systematical framework is established to incorporate the polar, nonpolar and quantum energies into a total energy functional. The optimization of the total energy functional leads to coupled governing equations for a set of important state functions, such as the electrostatic potential, the electronic density, and the solvent-solute boundary profile. This set of state functions gives rise to theoretical predictions of the solvation free energy, the electrostatic profile and the solvent-solute interface of the solvent-solute complex.
The rest of this paper is organized as follows. Section 2 is devoted to the theoretical formulation of our differential geometry based quantum model of solvation. We provide a detailed description of various solvation free energy functionals. Three governing equations, i.e., the generalized Poisson-Boltzmann equation, the potential driven geometric flow (i.e., generalized Laplace-Beltrami) equation, and the Kohn-Sham equation are derived from the total energy functional via the Euler-Lagrange variation. Numerical methods and algorithms are presented in Sec. 3, which offers detailed schemes for the solution of the three governing equations. The dynamical coupling of these three equations is achieved by an efficient iterative procedure. A formula for the solvation free energy estimation is also derived from the multiscale total energy functional. The present multiscale model is validated by numerical tests using a number of molecules in Sec. 4. To establish a valid approach, we have examined consistency of the electron density with the PB equation. The unit conversion between conventions used in our PB solver and those in a DFT software package is discussed. The results from the present multiscale mode are compared with those in our previous methods and those in the literature. Applications to three sets of molecules are given in Sec. 4. Some of these sets are computationally challenging. We demonstrate that the present model performs well in the prediction of solvation free energies. This paper ends with a conclusion.
THEORY AND MODEL
Solute-solvent boundary
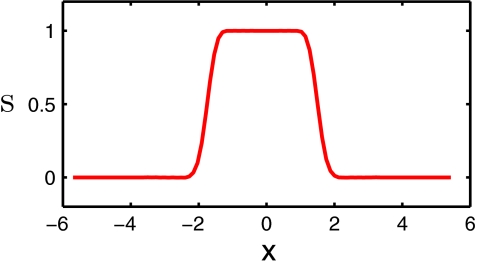
In our model, the solute molecule is described in atomic detail while the solvent molecules are treated as a continuum dielectric medium. As such, the interface between the discrete domain and the continuum domain is naturally described by the differential geometry of surfaces. The computational domain is essentially divided into two (types of) regions, i.e., aqueous solvent domain Ωs and macromolecular domain Ωm. However, from the physical point of view, because electron wavefunctions of the solvent overlap with those of the solute at the atomic scale, Ωs and Ωm should overlap with each other at the boundary of molecules and solvent. As proposed in our previous work,16, 76 we use a characteristic function to characterize this overlapping solvent-solute boundary. Furthermore, the value of function S is one (S = 1) inside the biomolecule domain and zero (S = 0) in the aqueous solvent domain. However, S admits a value between zero and one at the solvent-solute boundary region. The profile of S is illustrated in Fig. 1 for a simple diatomic system. It is clear that there is a smooth transition region at the solvent-solute boundary. Consequently, S is a description function or characteristic function of the solute domain, while (1 − S) is a description function of the solvent domain. In our multiscale model, the evaluation of all the solvent-solute properties should depend on S, which can be deduced from the principle of energy optimization. To this end, we construct a total energy functional to determine all behaviors of the solvation system, which includes the profile of characteristic function S. Sections 2B, 2C, 2D, 2E are devoted to the description of various components of the total energy functional.
Figure 1.
The cross section of S profile for a diatomic system.
Polar free energy functional
The solvation process involves both intermolecular and intramolecular interactions. Solvation analysis has been following certain convention, which may not be precisely consistent with that in other fields. Typically, solvation interactions are classified into the polar type and the nonpolar type. The polar type is often modeled by the Poisson-Boltzmann (PB) equation with appropriate point charges at atomic central positions. In the original electromagnetic theory, the charge source of the electric potential is “free charges.” However, in biophysics, due to their atomistic nature, the point charges are obtained by fitting the electron density distribution of either a charged molecule or a charge-neutral molecule into its atomic centers. Such point charge information is often stored in the database of popular software packages, such as CHARMM.44 Therefore, the polar interactions include both charge and polarization effects inside the molecule. Note that the effect of the rearrangement of electron charges during the solvation process needs to be computed twice, once before and once after the solvation. Polar interactions are also called electrostatic interactions. However, not all electrostatic interactions are described by the PB equation. Strictly speaking, the electrostatic potential solved from the PB equation represents Coulombic type of interactions between charges. However, many other intermolecular interactions, such as London dispersion interactions, Debye (induced dipole) interaction, ion-dipole interactions and dipole-dipole interactions are also electrostatics in origin, and are not directly represented by the PB equation.1, 3, 4, 40, 60
Sharp and Honig,61 and Gilson et al.28 have given a formulation for the electrostatic free energy functional. However, their formulation is based on a given static sharp solvent-solute interface. In the present work, we follow our earlier definition of differential geometry based electrostatic free energy functional16, 76
| (1) |
where Qi is the charge of ith ionic species, Nc is the total number of ionic species, kB is the Boltzmann constant, T is the temperature, and is the bulk concentration of the ith ionic species. Here, εs and εm are the permittivity, or dielectric constants of the solvent and solute domains, respectively. The permittivity ε is one in vacuum, but assumes different values in different environments. In solvation analysis, ε is usually set to 1 or 2 in the solute domain and to 80 in the solvent domain. In Eq. 1, ρtotal is the total charge density of the molecule and is given by
| (2) |
where q is the unit charge of an electron, n(r) is the electron density, nn(r) is the nucleus density, and ZI and RI are the atomic number and the position vector of nucleus I, respectively.
In Eq. 1, the term associated with S is the electrostatic free energy of the solute and that associated with (1 − S) is the electrostatic free energy of the solvent. In our model, the surface function S will be determined by the total energy optimization.
Nonpolar free energy functional
In the solvation model, the polar free energy functional is complemented by the nonpolar free energy functional. To reduce the degrees of freedom of the solvation system, solvent molecules are treated implicitly. Consequently, many well-known intermolecular interactions, such as London dispersion interactions, Debye (induced dipole) interaction, dipole-dipole interactions and van der Waals interactions, are modeled as surface energy, mechanical work, and additional solvent-solute interactions16, 73, 76
| (3) |
where A is the surface area, γ is the surface tension, Vol represents the volume occupied by the molecule of interest, p is the hydrodynamic pressure, ρ0 is the solvent density and is a solvent-solute interaction potential. In general, the solvent density can be a function of position (ρ0 = ρ0(r)) to describe the solvent response to the macromolecule near the solvent-solute boundary. In the present work, we assume a constant bulk solvent density for simplicity. In Eq. 3, the first term is the surface energy. It measures the disruption of intermolecular binding and/or intramolecular bonds that occurs when the surface of a molecule is created in the solvent. The second term is the mechanical work of creating the vacuum of a biomolecular size in the solvent. Both surface energy and mechanical work are hydrophobic in nature. These hydrophobic terms are partially compensated by the third term, an interaction potential, which represents the attractive dispersion and other possible effects near the solvent-solute interface. In our differential geometry based solvation models, this interaction is modeled by the van der Waals potential. However, many other potential forms can be used as well.
In our differential geometry based solvation models, we recast the nonpolar free energy formulation in terms of the surface function S(x). In particular, for the surface area term, we introduce the concept of mean surface area of a family of isosurfaces, which is a set of points {r|S(r) = c, 0 ⩽ c ⩽ 1}. Meanwhile, we make use of the coarea formula from the geometric measure theory to convert the area integral into a global volume integral.76 Finally, the mean surface area can be described by a volume integral and the nonpolar free energy functional can be given as
| (4) |
The reader is referred to our earlier work for mathematical details.16, 17, 76
Quantum mechanical energy functional
In the present multiscale model, we need to evaluate the total charge density ρtotal(r) by quantum mechanical principles or ab initio approaches. However, the ab initio calculation of the electronic structure of a macromolecule is intractable at present due to the large number of degrees of freedom. A vast variety of theories and algorithms have been developed in the literature to reduce the dimensionality of this many-body problem. Here we incorporate the DFT description of the electronic structure of the solute molecule into our differential geometry based solvation model.
Despite the improvement in computer hardware and software for the quantum mechanical calculation, computational costs are still a major concern for the QM simulation of large molecules of interest. Therefore, so-called order-N algorithms,29, 54 in which the computer time and memory scale linearly with the simulated system size, become increasingly important. Though the plane wave basis set has advantages over local basis sets in terms of avoiding basis-set superposition error as well as convergence concerns, it is difficult to be used in the implementation of the O(N) method in DFT. As such, a localized basis set is normally taken to develop fully self-consistent O(N) DFT algorithms. Along this line, a software package named SIESTA (Spanish Initiative for Electronic Simulations with Thousands of Atoms) was developed.2, 66 It is based on a flexible linear combination of atomic orbitals (LCAO) basis set and essentially perfect O(N)scaling when the system is sufficiently large. Therefore, it allows very fast simulations using minimal basis sets and very accurate calculations with complete multiplezeta and polarized bases.53, 54 Moreover, the pseudopotential is used in SIESTA to avoid the calculation of core electrons and to achieve the expansion of a smooth (pseudo-) charge density on a uniform spatial grid domain, which further accelerates the speed of quantum calculations.
Kinetic energy
Combining DFT with our differential geometry based solvation formulation, we define the kinetic energy functional as
| (5) |
where m(r) is the position-dependent electron mass, with h being the Planck constant, and ψj(r) are the Kohn-Sham orbitals. Here, the total electron density n is given by
| (6) |
where the summation is over all the Kohn-Sham orbitals. Note that orbitals {ψj} are subject to the orthonormality constraint
| (7) |
Obviously, Eq. 7 is an approximation which is valid as long as the boundary represented by the characteristic function S is sufficiently far away from atomic centers of the solute molecule. This is true in our model.
Potential energy
Without external potentials, the electrostatic potential energy of nuclei and electrons can be represented by the Coulombic interactions among the electrons and nuclei. There are three groups of electrostatic interactions: interactions between nuclei, interactions between electrons and nuclei, and interactions between electrons. Because of the Born-Oppenheimer approximation, interactions between nuclei do not directly have a impact on the structure of electrons in DFT.
According to the Coulombic law, the repulsive interaction between electrons can be expressed as the Hartree term
| (8) |
where q is again the unit charge of an electron, ε(r) is the position dependent electric permittivity, and r and r′ are positions of two interacting electrons. Equation 8 gives rise to a nonlinear function in terms of electron density n. Therefore, the problem of solving the electronic structure has to be resolved by self-consistent iterations.
Additionally, the attractive interactions between electrons and nuclei are given by
| (9) |
Finally, we write the total potential energy functional as
| (10) |
where the last term EXC is the exchange-correlation potential, which includes all the many-particle interactions in the solute molecule. In general, the exact form of the exchange-correlation potential is not known. There are good approximations in the practical applications, such as the local-density approximation, the local spin-density approximation, and generalized gradient approximations. A detailed elaboration of the exchange-correlation potential is beyond the scope of the present work.
Total free energy functional
Intuitively, it appears that the total free energy functional is the summation of the polar, nonpolar, kinetic and potential energy. However, such a summation will lead to some double counting because of the coupling among different energy terms. For example, the electrostatic energy depends on the charge density, which, in turn, depends on the kinetic and potential energies of electrons. Additionally, the electrostatic potential serves as a variable in the polar energy functional, meanwhile it serves as a known input in the potential energy of electrons. To see this connection, we need to solve the Poisson equation in vacuum (ε = 1)
| (11) |
where ϕv is the electrostatic potential in vacuum and with nv(r) being the electron density in vacuum. The solution of Eq. 11 is
| (12) |
Note that Eq. 12 is the exact total Coulombic potential of electron-electron interactions and electron-nucleus interactions. As such, we do not need to include Uee[n] and Uen[n] terms in the total free energy functional.
Finally, we propose a multiscale total free energy functional for biomolecules at equilibrium
| (13) |
where the first row is the nonpolar energy functional, the second and third rows account for the electrostatic energy functional and the last row is the electronic energy functional. As discussed above, the term ρtotalϕ also contributes to the Coulombic potentials of electron-electron and electron-nucleus interactions. This total free energy functional provides a starting point for the derivation of governing equations and a basis for the evaluation of solvation free energies.
Governing equations
The total free energy functional 13 is a function of characteristic function S, electrostatic potential ϕ and electron density n. The governing equations of these quantities can be obtained by the first variation of the total free energy functional 13. From the mathematical point of view, there should exist optimal functions S(r), ϕ(r) and a set of orbitals {ψj} at the equilibrium state in which the solvation free energy is optimized. The variational procedure for S(r), ϕ(r) and {ψj} is described below.
First, by the variation of Eq. 13 with respect to the electrostatic potential ϕ, we have
| (14) |
The Euler-Lagrange equation is used in the above variation. Equation 14 is the generalized Poisson-Boltzmann (GPB) equation16, 76
| (15) |
where the dielectric function is given by
| (16) |
This is a smooth function. It is clear that the GPB equation utilizes a smooth dielectric profile. There is a smooth transition region for the dielectric function to change from εs to εm. Therefore, the solution procedure of the present GPB equation 15 avoids many numerical difficulties of solving elliptic equations with discontinuous coefficients79, 80, 82, 84, 85 in the classical PB equation. Furthermore, in a solvent without salt, the GPB equation is simplified to be the generalized Poisson equation
| (17) |
Both Eqs. 15, 17 are similar to our earlier results.16, 76 However, in the present multiscale model, the charge source ρtotal is to be determined by solving the Kohn-Sham equations, rather than by the fixed charges ρfix = ∑jqjδ(r − rj), with qj being the total fixed charge of the jth solute atom.
Additionally, by the variation of Eq. 13 with respect to the surface function S, we have
| (18) |
In Eq 18, is a generalized Laplace-Beltrami operator, which is a generalization of the usual Laplacian operator to a smooth manifold of macromolecular surface.9, 76 In general, γ can be a function of the position γ = γ(r) to account for the surface hydrophobicity at different locations of the macromolecule. For simplicity, it is treated as a constant in our present computation. By solving Eq. 18, we obtain a “physical solvent-solute boundary” (S). As discussed in earlier work,9, 11, 16, 76 the solution of this elliptic partial differential equation (PDE) can be attained via a parabolic PDE
| (19) |
where the generalized “potential” V is defined as
| (20) |
where the electronic potentials in the last row do not contribute much to V at equilibrium. This is due to the fact that they are essentially confined inside the solute molecular domain. Note that Eq. 19 has the same structure as the potential driven geometric flow equation defined in our earlier work.9, 16, 76 As t → ∞, the initial profile of S evolves into a steady state solution, which solves the original Eq. 18 with an optimal surface function S.
Finally, to derive the equation for the electronic wavefunctions, we need to incorporate the constraint as shown in Eq. 7 into the total energy functional. This can be done easily with a family of Lagrange multipliers . Therefore, by the variation of Eq. 13 with respect to the wavefunction and applying the constraint, we have
| (21) |
where the Lagrange multiplier constants Ei have been interpreted as energy expectation values. Equation 21 is the Kohn-Sham equation in which the effective Kohn-Sham potential is defined as
| (22) |
where and qϕ is the potential contribution from Coulombic interactions. It is to be calculated by the GPB equation 14 with a given total charge density. Apparently, Eq. 21 does not directly depend on the surface function S, so that existing DFT packages can be used in our computations with a minor modification as described in Sec. 3C.
It seems that the generalized Poisson-Boltzmann equation 15, the generalized Laplace-Beltrami equation 19 and the Kohn-Sham equation 21 are strongly coupled to each other. Therefore, these three equations have to be solved by appropriate iterative procedures. This aspect is discussed in Sec. 3.
NUMERICAL METHODS AND ALGORITHMS
Solution of the generalized Laplace-Beltrami equation
The solution of the generalized Laplace-Beltrami equations has been studied and used in our earlier work,11, 16 including detailed discretization schemes. Here, we give a brief description of the solution procedure for Eq. 19. First of all, to solve the Laplace-Beltrami equation, the expression of solvent-solute interaction potential Uss must be prescribed explicitly. Although Uss includes many unspecified interactions, we consider the following form:
| (23) |
where is the potential due to the ith atom in the solute molecule. One possible choice of is the following Lennard-Jones (L-J) 6-12 pair potential
| (24) |
where ɛi is the well-depth parameter, and σi and σs are solute atomic and solvent radii, respectively. Here r is the point of interest and ri is a position vector of an atom in the solute molecule. The L-J potential can be divided into attractive term Uatt and repulsive term Urep in different ways. It can be a “6-12” decomposition as follows:
| (25) |
Alternatively, it can also be a “WCA” decomposition based on the original WCA model43
| (26) |
| (27) |
As indicated in our earlier work,16 the WCA attractive potential provides good results for solvation. Therefore, all the calculations in the present study are carried out by using the WCA decomposition.
Additionally, a necessary step in solving Eq. 19 is to determine all the physical parameters involved. Because of the choice of the polar and nonpolar separation and the continuum representation of solvent in our model, not all parameters from the literature are suitable. In particular, surface tension γ serves as a fitting parameter in our model due to its ambiguity in atomic-scale models.43, 51, 73 Therefore, we rewrite the generalized potential driven geometric flow equation as
| (28) |
where Vγ = V/γ. Then, in addition to the Lennard Jones parameters εi, σs and σi, other parameters including p/γ, ρs/γ, εs/γ, and εm/γ need to be pre-determined in the solution of the generalized potential driven geometry flow equation.
Equation 28 is solved with the Dirichlet boundary condition S(r, t) = 0, ∀r ∈ ∂Ω. For the initial value of S, we consider
| (29) |
where we define the domain enclosed by the solvent accessible surface to be , with ri and rp being atomic van der Waals radius and the probe radius, respectively. Here, Ri is the atomic center position vector of the ith solute atom and Na denotes the total number of atoms for a given macromolecule. To protect the van der Waals surface and make the computation more efficient, we only update the values of S(x, y, z, t) at the points in between the domains of van der Waals surface and the solvent accessible surface; i.e., (x, y, z) ∈ Dsa/DvdW, where DvdW is the domain enclosed by the van der Waals surface . Numerically, to avoid possible zeros in the denominator of Eq. 28 we add a very small number, i.e., 10−7, into the denominator expression, which does not affect results in practice.
For simplicity, the widely used explicit Euler scheme can be applied to the solution of the generalized Laplace-Beltrami equation for the time integration. The Euler scheme can be combined with the second order central difference scheme for the spatial discretization.11 Nevertheless, this algorithm is not very efficient, because a very small time stepping size is required to guarantee the stability of the time integration. An alternative direction implicit (ADI) scheme was constructed in our earlier work.9, 16 The ADI scheme is second order in both spatial and time discretizations. It builds in a fast O(N) Thomas algorithm to solve the tridiagonal linear system and thus is very efficient. The ADI algorithm is unconditionally stable and allows a much larger time stepping size than that of the explicit Euler scheme. In the present work, the ADI algorithm is adopted for the solution of the generalized potential driven geometric flow equation 19.
Note that from Eq. 19 we know that the surface evolution depends on the electron charge density, which spreads over a large area wherever the electronic distribution is nonzero. In principle, this implies that the solution of the generalized Laplace-Beltrami equation requires the input of wavefunctions and the charge density. However, since the electron density decays rapidly away from atomic centers, non-neglected values can only be found in the region inside the solute van der Waals surface. As such, the terms associated with charge density ntotal and wavefunctions do not have significant contributions to the time evolution of surface function S, which occurs outside the van der Waals surface. As such, the terms associated with the electron density or wavefunctions are neglected in the numerical simulation of the Laplace-Beltrami equation. Moreover, in the present study, we only consider a solvent environment without mobile ions. Therefore, the term associated with mobile ions is omitted in the present numerical simulation.
Solution of the generalized Poisson-Boltzmann equation
In solvation analysis, the generalized PB equation 17 is subject to the Dirichlet boundary condition27
| (30) |
where qj is the total fixed charge of the jth solute atom. One option is to use the point charges from a force field model such as CHARMM. However, in the present work, we consider the following Dirichlet boundary condition:
| (31) |
where the boundary condition is nonlinear—it depends on the electron density n and thus needs to be implemented iteratively.
The standard second order center difference scheme is applied in this study to solve Eq. 17. An accurate solution can be obtained due to the continuous dielectric definition ε(S). Let the pixel (i, j, k) represent the position (xi, yj, zk). The discretized form of Eq. 17 is
| (32) |
where hx, hy and hz are the grid spacings at x, y and z directions, respectively. Here, ρtotal(i, j, k) is the charge density at grid point (xi, yj, zk), which is calculated from the electronic charge density n(r) and nucleus density nn. The implementation of ρtotal will be discussed in the next paragraph. As such, the discretized PB equation can be converted into the standard linear algebraic equation system of the form AX = B, where X is the solution of interest, A is the discretization matrix and B is the source term associated with the charge density. It has been shown previously that the PB solver is able to deliver the designed second-order accuracy.16
On the right hand side of Eq. 32, the charge density at each grid point should be given. As an efficient approach, atomic charges have been widely used to approximate the charge density of electrons and nuclei, especially for large molecules of general interest. Therefore, the point charge approach has gained much popularity in PB solvers as well as PB applications.6, 35, 37, 45 Nevertheless, charge assignment at atomic centers is a nontrivial issue. The deficiencies of the atomic point charge approach have been discussed in the Introduction. The direct implementation of the quantum mechanical charge density can avoid errors caused by the atomic point charge approximation. Moreover, this approach frees us from the electrostatic potential fitting process. To carry it out in the finite difference scheme, the total charge density ρtotal(i, j, k), which consists of the electron density n(r) and nucleus density nn, needs to be prescribed at each grid point of the computational domain. In particular, the nucleus density nn(r), which is considered as stationary and located at the center of atoms, can be distributed to the nearest eight neighboring grid points by the second order interpolation (i.e., the trilinear mapping). The distributed nucleus core point charges are converted into the nucleus charge density by dividing point charges with the volume of the unit grid. Finally, the total charge density at each grid point is obtained by the summation of nucleus density and the electronic charge density which is directly taken from the quantum mechanical calculation.
However, a new issue arises from the above treatment of nuclei. Since each nucleus core charge is split into its eight neighboring grid points, it is easy to find out that short range interactions are biased and self-interaction energies are artificially introduced. This is due to the interactions of grid charges within one single atom. It exists even in the absence of solvent and any other charges. Apparently, this is a pure artifact due to the finite difference approach and must be eliminated. Within the partial charge approach the artifact can be canceled out mainly by calculating the PB equation twice, one in vacuum and the other in the solvent. It turns out that this strategy also works well here. Numerical tests regarding this cancellation of self-interaction energies are demonstrated later. It is important to point out that numerically if one implements the quantum mechanical calculation with a non-frozen core method, the remaining error from the self-interaction cancellation is still too large to be neglected. In other words, the above cancellation strategy may fail when one applies a non-frozen core approach. Therefore, frozen core approaches, such as pseudopotential methods, must be applied in our quantum calculations here. Because frozen core approaches dramatically reduce the number of charges in each nucleus and thus implicitly decease implementation errors.
The biconjugate gradient method is a good choice in solving the PB equation. However, as we have demonstrated in our previous work,16 the combination of stabilized biconjugate gradient method (BiCG) and the blocked Jacobi preconditioner (BJAC) from PETSc (http://www.mcs.anl.gov/petsc/petsc-as/), as well as the combination of the orthomin method (OM) and the incomplete LU factorization preconditioner (ILU) from SLATEC (http://people.sc.fsu.edu/~burkardt/f_src/slatec/slatec.html), speeds up the process of the PB solution. In this study, we apply the combination of ILU and OM from SLATEC. In our iteration procedure, the prior electrostatic potential is taken as a good initial guess for the followed linear system solving procedure. It turns out that this treatment makes the generalized PB solver converge much faster than simply setting the initial guess to be 0.16 Additionally, the convergence tolerance is set to be 10−4 as a good balance between the accuracy and efficiency.
Solution of the generalized Kohn-Sham equation
The generalized Kohn-Sham equation 21 admits all-electron and all-nucleus potentials. The direct solution of Eq. 21 is very expensive for macromolecules. Therefore, further simplifications are necessary. In particular, because classical DFT methods have been developed in the past few decades, the solution of Eq. 21 needs to make use of existing DFT methods.
Note that the Coulombic potential functionals shown in Eqs. 8, 9 involve spatially varying dielectric constants, which reflect the solvation process. The related spatially varying electrostatic potential is built in the generalized Poisson-Boltzmann equation 15, whose solution gives rise to the electrostatic potential energy qϕ used in the generalized Kohn-Sham equation 21. In contrast, the standard Kohn-Sham equation is for a molecular system in vacuum and its Coulombic potentials are of the form of qϕv where ϕv is given by Eq. 12 with the total charge density in vacuum described in Sec. 3D. The effective potential in the generalized Kohn-Sham equation 21 can be written as
| (33) |
where
| (34) |
is called the reaction field potential. Here ϕ0 is the solution of the Poisson equation in the homogeneous medium with the charge source ρtotal(r)
| (35) |
where ρtotal(r) is obtained from the generalized Kohn-Sham equation 21. In Eq. 33, is the Kohn-Sham potential
| (36) |
In the present work, is represented by the traditional Kohn-Sham potential. Consequently, a variety of computational techniques developed for the traditional Kohn-Sham DFT can be utilized in the present work. What we need to do for solving the generalized Kohn-Sham equation 21 is to add a reaction field potential qϕRF to an existing Kohn-Sham DFT solver.
The most important issues in the solution of the Kohn-Sham equation are the selection of the exchange-correlation potential and the use of the pseudopotential. The pseudopotential approach eliminates the complicated effects of core electrons and allows the expansion of a smooth (pseudo-) charge density on a uniform spatial grid. In this approach, the chemically active valence electrons are dealt with explicitly, while the core electrons are ‘frozen’ and considered together with the nuclei as fixed nonpolarizable ion cores. With the pseudopotential approximation, the formalism of the total energy functional needs to be modified, which leads to the following expression of a Kohn-Sham effective potential66
| (37) |
where VH(r) and VXC(r) are total Hartree and exchange-correction potentials, respectively. Here, and are the local part and the nonlocal part of the pseudopotential of atom I. For elaborated discussions of the above potentials, we refer the reader to an excellent review.66
In the present work, SIESTA (Spanish initiative for the electronic structure of thousands of atoms), a quantum mechanical package of high efficiency, is utilized for solving our generalized Kohn-Sham equation 21. SIESTA possesses the ability to perform DFT simulations of more than a thousand atoms. The details of the package have been extensively described.66 It develops a self-consistent density functional method using the standard norm-conserving pseudopotential and a flexible numerical linear combination of atomic orbital (LCAO) basis sets with an essentially perfect O(N) scaling, in which the computer CPU time and memory scale linearly with the simulated system size. Note that normally linear scaling kicks in when the system is sufficiently large. The exchange and correlation are treated within the Kohn-Sham DFT. Both the local density approximation and local spin density approximation (LDA/LSDA), as well as the generalized gradient approximation (GGA) are allowed. Moreover, SIESTA permits very fast simulations by using minimal basis sets and very accurate calculations with complete multiple-zeta and polarizable bases. Therefore, it can provide a general scheme to perform quantum calculations with requirements ranging from being very fast to being very accurate. For all of the simulations in the present work, the default double-ζ plus single polarization (DZP) bases are used. The MeshCutoff is set as 125 Rydberg and the LDA is applied. The SolutionMethod is set to be “diagon.”’
Evaluation of the solvation free energy
The solvation free energy is the energy required or released from the transfer of a unit of solute molecules from vacuum to a solvent. By definition, it is calculated by the difference between the total energies in solution and in vacuum,
| (38) |
where ϕv is the electrostatic potential in vacuum and nv is the solute electronic density in vacuum, which is defined in terms of the electronic wavefunctions of the solute in vacuum
| (39) |
In Eq. 38, Gtotal[S, ϕ, n] is given in Eq. 13 and Gvacuum[ϕv, nv] denotes the total energy functional in vacuum
| (40) |
where is the total charge density in vacuum. For simplicity, we have omitted the ionic density in Eq. 38. Note that the variation of Gvacuum[ϕv, nv] gives rise to the standard Poisson equation 11 and the standard Kohn-Sham equation
| (41) |
where and are appropriate eigenvalues and eigenfunctions of Hamiltonian .
However, there is a technical difficulty in the direct evaluation of Gtotal[S, ϕ, n]. Namely, the integration of the quantum mechanical terms in Eq. 13 requires the S function profile, which is not involved in most Kohn-Sham DFT software packages. Therefore, in the present work, we evaluation the solvation free energy by the following approximation
| (42) |
where Gnp, ΔGp and ΔGQM are the nonpolar, polar and quantum mechanical contributions, respectively. The nonpolar solvation free energy does not exist in vacuum, and its form in solution is given by
| (43) |
By using the Gauss’ divergent theorem and integration by parts, it is easy to show that the polar solvation energy is given by
| (44) |
Similarly, the polar solvation energy in vacuum is . Therefore, one may compute the change of the polar solvation energy by . However, this expression leads to a situation that the quantum mechanical contribution ΔGQM cannot be evaluated in SIESTA because of the lack of required potential terms. Additionally, such an expression is inconsistent with the conventional electrostatic solvation free energy of the form
| (45) |
Therefore, in the present solvation analysis ΔGp is calculated by Eq. 45, which leads to two remaining electrostatic potential terms . These terms are combined with the rest of the quantum energy functionals to compute the change of the quantum mechanical energy as
| (46) |
where . Note that wavefunctions {ψj} are computed with the full Hamiltonian in the solution. The main advantage of the quantum mechanical energy change given in Eq. 46 is that it can be easily computed by using existing DFT software packages as discussed in Sec. 3C.
The current formula of the solvation free energy is systematically derived from the framework of the differential geometry based solvation model. It consists of the nonpolar energy Gnp, the electrostatic solvation free energy ΔGp, and the change of the solute self-energy ΔGQM due to the redistribution of electrons in the solvation process. It is of interest to see that the formulation of the present solvation analysis is consistent with that in the literature,69, 74, 75 which is basically computed by using a good chemical intuition. The reliability and accuracy of the current model are further validated by a comparison between the present prediction and experimental data, as well as that in the literature in Sec. 4.
Dynamical coupling of involved PDE equations
As described in Sec. 2F, on the one hand, the total charge density in the solution is obtained by solving the Kohn-Sham equation in the presence of the reaction field potential ϕRF = ϕ − ϕ0, which is computed by solving the PB equation and the Poisson equation, i.e., Eqs. 15, 35. On the other hand, the solution of the PB equation requires the quantum mechanically calculated charge density, the surface profile S, and the dielectric profile ε(S), which are generated by solving the generalized Laplace-Beltrami equation (LBE). Moreover, the potential in the generalized Laplace-Beltrami equation contains the terms associated with the electrostatic potential from the PB equation and the charge density from the Kohn-Sham equations. In principle, the Laplace-Beltrami equation, the generalized PB and Kohn-Sham equations need to be solved simultaneously until the convergence is reached, i.e., the solvation energy of two runs agrees with each other within a prescribed tolerance. This can be achieved via a self-consistent iteration procedure.
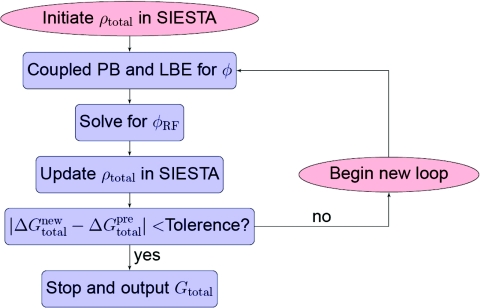
In practice, we adopt an inner-outer iterative strategy to implement the self-consistent procedure. The inner iterations concern the solution of the coupled generalized PB equation and the Laplace-Beltrami equation. These iterations have been carried out in our previous work,16 except for the different representation of the continuous charge density. In the present work, the inner iterations are combined with the solution of the Kohn-Sham equation during the outer iterations. More details are described in the following and can be seen from a work flow chart in Fig. 2 as well.
Figure 2.
Flowchart of the numerical solution of the coupled PDEs.
Step 0: (Generation of the solute quantum energy in vacuum and initialization of the charge density): We carry out a quantum mechanical calculation in vacuum with SIESTA to obtain an initial total charge density. The solute quantum energy in vacuum is recorded for computing ΔGQM in the output step.
Step 1: (Inner iteration of the coupled PB and Laplace-Beltrami equations): Given a total charge density distribution, as described previously,16 a temporary electrostatic potential ϕ can be generated by solving the generalized PB equation with a temporary S. It is followed by the evolution of time-dependent generalized Laplace-Beltrami equation for a number of time iterations. With the updated intermediate S, one can update the electrostatic potential via the PB equation. This cycle repeats until the electrostatic solvation energy converges within a pre-determined criterion. Note that the relaxation algorithm should be used to guarantee the convergence.16
Step 2: (Generation of a reaction field potential): Solve the PB equation in a homogeneous medium with the same total charge density as that in the previous step. Then the reaction field potential ϕRF is obtained by the difference between the electrostatic potential from the previous step and the current Poisson calculation in the homogeneous medium.
Step 3: (Solution of the Kohn-Sham equation): Run the SIESTA program again to obtain a new total charge density by incorporating the computed reaction field potential into the Kohn-Sham Hamiltonian.
Step 4: (Calculation of the solvation energy and convergence check): Calculate the total solvation free energy with the resulting ϕ, S and {ψj}. Go back to Step 1 until it converges. When convergence is reached, one ends the iteration and outputs the solvation free energy.
To output the charge density in SIESTA, one needs to set SaveRho to be true in the input fdf file, while SpinPolarized is false according to the fact that all tested molecules in this work are neutral and that most of neutral molecules possess zero net spin. Eventually, SIESTA generates an XV file to store lattice vectors and atomic positions, together with an RHO file to record the values of the charge quantity on the grid points. However, the standard input for our PB solver is a Gaussian CUBE format file which contains the origin, grid spacing, atomic coordinates and charge densities. Therefore, a CUBE formate file must be created based on the information from the XV file and RHO file to transfer the charge density data from SIESTA to the PB solver. It can be carried out by a subroutine grid2cube.x, which is included in the SIESTA package. During the translation, the coordinates of the origin are shifted to make the molecule roughly appear at the center of the computational domain.
After the reaction field potentials are obtained by the PB solver, they are regarded as an external solvent potential effect and must be incorporated into the Kohn-Sham quantum calculation in SIESTA. As such, reaction field potentials have to be passed into SIESTA during the self-consistent iteration process. It can be done by adding them into the variable of total potential named Vscf in the subroutine file dhscf.F under “Siesta-3.0-b/Src”. Therefore, a data translation procedure is required to pass the reaction field potential from the PB solver into SIESTA. Furthermore, attention needs to be paid to the unit conversion. In particular, the unit of distance used in SIESTA is Bohr, while it is Angstrom in the PB solver. The units of potential are ec/Angstrom and Rydberg/ec in the present PB solver and in SIESTA, respectively. Here ec denotes the fundamental charge used as the unit of a point charge in both the PB solver and SIESTA.
VALIDATION AND APPLICATIONS
This section provides validation and applications for the proposed model and computational algorithms. The performance of SIESTA has been tested and described in the literature.66 The generalized Laplace-Beltrami equation 19 has the same differential operator as our earlier mean curvature flow11 except for the extra source terms. Previously, we have numerically proved that the explicit Euler algorithm delivers the reliability and convergence of the solution of the Laplace-Beltrami equation, and the finite central difference scheme is of second-order convergence in space.9 For the PB solver, given the partial charges, it has also been numerically proved to be of second-order convergence.16 However, here the source term in the PB equation is no longer represented by the partial charges adopted from existing molecular mechanical force fields, such as AMBER or CHARMM. In this work, the source term is represented by the charge density obtained directly from the quantum calculation. There are new concerns from this different charge strategy. First of all, regarding the distribution of nucleus charges, which are much larger than partial charges, it is crucial to know whether the self-interaction energy artifact within a single atom leads to non-neglected bias even after the treatment of the energy cancellation. Secondly, it is important to check whether the implementation is correct in terms of the data translation and unit conversion between different solvers during the self-consistent iteration procedure. Based on these considerations, we examine the cancellation of self-interaction artificial energy and continue to check the data translation and unit conversion between the PB solver and SIESTA in the Appendices. In this section, we demonstrate the overall accuracy of our model in the calculation of solvation free energies, as well as the solvent effect on the solute electronic structure, by a comparison with experimental data.
We consider three types of applications in this section. First, we apply our new multiscale model to a set of 24 small molecules. Then, a challenging set of 16 molecules is studied. Finally, three larger molecules are taken for efficiency and robustness test. The Dirichlet boundary condition is used for both the generalized Poisson-Boltzmann equation and the generalized Laplace-Beltrami equation as in our previous calculations.11, 27, 78, 83
Accuracy of solvation free energies computed by the present model
Besides the data translation and unit conversion, the overall accuracy of the present model still needs to be further verified by comparing with experimental data. In particular, it is of crucial importance to check the accuracy of the total solvation energy as well as the solvent effect on the solute electronic structure. The contribution of the solvation free energy from the polarization of electron cloud can be decomposed into two parts. As shown in Table 1, prior to the polarization, the solvent interacts with the solute based on its vacuum electronic distribution which gives rise to the electrostatic solvation energy using the vacuum charge density. When the polarization takes place, the electron cloud is redistributed to reach a more favorable interaction with the solvent. This generates a gain for the solvation free energy . However, the redistribution of the electron cloud leads to the change of the interactions between electrons and nuclei and those between electrons. It causes an unfavorable decrease in the solvation energy (ΔGQM). Therefore, the total energy contribution of the polarization is calculated by the sum of ΔGQM and ΔΔGp. Table 1 summarizes the numerical results of the total solvation free energy and the decomposition for three small molecules. Here, ΔGtotal = ΔGp + Gnp + ΔGQM. As demonstrated in the table, the total solvation energies fit experimental data74 very well. Moreover, it is expected from the classical linear response theory that the loss from the distortion of electron cloud is equal to about half of the gain from the solute-solvent interaction energy.69 It is evident that our results are quantitatively in accord with the theory. The slightly higher ratio (about 0.6) may be caused by the change in the exchange-correction energy term within the DFT calculations.
Table 1.
Solvation free energy (kcal/mol) and its decomposition.
| Compound | ΔGp | ΔΔGp | ΔGQM | ABS(ΔGQM/ΔΔGp) | ΔGtotal | Exptl74 | |
|---|---|---|---|---|---|---|---|
| Water | −6.25 | −7.55 | −1.30 | 0.86 | 0.66 | −6.31 | −6.30 |
| Methanol | −5.18 | −6.18 | −1.00 | 0.63 | 0.63 | −4.98 | −5.11 |
| NH3 | −3.86 | −5.12 | −1.26 | 0.87 | 0.69 | −3.79 | −4.29 |
Solvation free energies of 24 small molecules
Encouraged by the successful reproduction of the solvation free energies for the above three small molecules, we apply the present differential geometry based multiscale model and algorithms to the solvation analysis of an extended set of 24 small neutral organic molecules. In this application, all geometric structures are taken from the Pubchem database (http://pubchem.ncbi.nlm.nih.gov). The required pseudopotential input files for SIESTA in the psf format are conveniently produced through a pseudopotential generator web (http://www.tddft.org/programs/octopus). Atomic radii for the LB equation are adopted from a new parametrization of ZAP-9 used by Nicholls51 and in our previous studies.16 Specifically, the radii of hydrogen, carbon, oxygen, nitrogen, chlorine, fluorine and sulfur are set to be 1.1 Å, 1.87 Å, 1.76 Å, 1.40 Å, 1.82 Å, 2.4 Å and 2.15 Å, respectively. Note that different surface definitions in implicit solvent models should have their own optimal radii set.73 In particular, it is found numerically that a continuous dielectric definition based model is supposed to have radii of slightly larger values than those of a sharp interface based model.16 Therefore, we multiply the radii from ZAP-9 by a factor. In practice, a factor of 1.1 is used for all atomic radii in a molecule of more than 14 atoms. However, if a molecule has less than 15 atoms, the factor is given by a formula 1.02 + (Max(0, Na-5))*0.008, where Na represents the total number of atoms. Numerically it turns out that the solvation energy predictions are sensitive to the radii factor for small molecules with less than 15 atoms. In this case, the fewer atoms, the smaller factor.
In our calculation, since the polarization is treated explicitly with the quantum mechanical calculation, we set the dielectric constant in the solute region as εm = 1, while εs = 80 for the solvent region. Other parameters are set in a similar way as in our previous work:16 We choose ρ0/γ = 2 and take into account the pressure by setting p/γ = 0.2. Note that in the numerical simulation, all ratio parameters here are treated as dimensionless. For L-J parameters, σs is chosen to be 0.65 Å and σi is the solute atomic radii.73 Due to the continuum representation of solvent in our model, the 6-12 Lennard Jones potential formula 24 differs from the standard version—the distance used in our formula is no longer the distance between the centers of solute atoms and the centers of solvent atoms but the distance between a specific position in the solvent region and the centers of solute atoms. Therefore, the setting of well depth ɛi differs from the ones taken from AMBER or OPLS force fields. As we did in the previous work,16 it is determined by an equality, that is, if r is on the vdW surface of the atom. Here the constant Di should have different values for various types of atoms. For simplicity we use a uniform constant D = 1.0 to determine the value of ɛi. The grid dimension is the same in both the PB solver and SIESTA, and it depends on the MeshCutoff energy value in SIESTA, which is 125 Rydberg in current simulations. The time stepping of is used, where hx is the grid spacing at the x direction. Finally, γ = 0.0065 kcal/(mol Å2) obtained from the previous work16 is applied to compute the total nonpolar solvation energy.
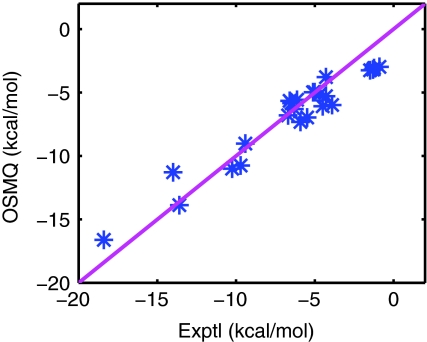
Table 2 summarizes the numerical results of the solvation free energies of 24 molecules. The root mean square error (RMS) of 1.31 kcal/mol is obtained, which indicates a very good agreement between the present prediction and experimental data.74 The agreement can also be seen from Fig. 3. Moreover, to examine the consistency, the ratio of ΔΔGp and ΔGQM is computed and listed in Table 3. It is evident that the numerical ratio is always about 0.6. Therefore, the reliability and consistency of the present model have been illustrated.
Table 2.
Comparison of solvation free energies (kcal/mol) obtained from the present model and experimental data for 24 small molecules.
| Compound | Na | Gnp | ΔGp | ΔGQM | ΔGtotal | Exptl74 | Error |
|---|---|---|---|---|---|---|---|
| Ethanol | 9 | 0.74 | −6.33 | 0.61 | −4.98 | −5.01 | 0.03 |
| Propionamide | 12 | 1.02 | −12.19 | 2.14 | −9.03 | −9.41 | 0.38 |
| H2O | 3 | 0.39 | −7.55 | 0.86 | −6.31 | −6.30 | −0.01 |
| Phenol | 13 | 1.21 | −7.88 | 1.01 | −5.66 | −6.60 | 0.94 |
| Methanethiol | 6 | 0.7 | −4.29 | 0.50 | −3.08 | −1.24 | −1.84 |
| Propionic acid | 11 | 1.02 | −7.73 | 0.87 | −5.84 | −6.47 | 0.63 |
| Acetamide | 9 | 0.82 | −14.23 | 2.65 | −10.76 | −9.71 | −1.05 |
| Acetonitrile | 10 | 0.87 | −8.23 | 1.36 | −5.99 | −3.9 | −2.09 |
| Ethanethiol | 9 | 0.87 | −4.53 | 0.47 | −3.19 | −1.3 | −1.89 |
| Aniline | 14 | 1.23 | −9.34 | 1.15 | −6.97 | −5.49 | −1.48 |
| Methanol | 6 | 0.57 | −6.18 | 0.63 | −4.98 | −5.11 | 0.13 |
| Acetic acid | 8 | 0.83 | −8.67 | 1.03 | −6.81 | −6.7 | −0.11 |
| 1-methylcytosine | 16 | 1.32 | −23.9 | 5.96 | −16.62 | −18.4 | 1.78 |
| Pyridine | 11 | 0.98 | −7.61 | 1.49 | −5.14 | −4.7 | −0.44 |
| 9-methyladenine | 18 | 1.45 | −18.5 | 3.17 | −13.88 | −13.6 | −0.28 |
| 1-methyluracil | 15 | 1.28 | −15.35 | 2.78 | −11.29 | −14.0 | 2.72 |
| NH3 | 4 | 0.46 | −5.12 | 0.87 | −3.79 | −4.29 | 0.50 |
| 4-cresol | 16 | 1.35 | −7.94 | 1.00 | −5.58 | −6.13 | 0.55 |
| 4-Methylimidazole | 12 | 1.04 | −15.88 | 3.84 | −11.00 | −10.25 | −0.76 |
| Methylethyl sulfide | 12 | 1.03 | −4.83 | 0.55 | −3.25 | −1.49 | −1.76 |
| n-Butylamine | 16 | 1.08 | −7.19 | 0.81 | −5.29 | −4.29 | −1.00 |
| 3-Methylindole | 19 | 1.42 | −10.40 | 1.66 | −7.32 | −5.91 | −1.41 |
| Methylamine | 7 | 0.54 | −7.70 | 1.07 | −6.09 | −4.5 | −1.59 |
| Benzene | 12 | 1.20 | −4.69 | 0.51 | −2.98 | −0.9 | −2.08 |
| RMS error | 1.31 | ||||||
| Average error | 1.06 |
Figure 3.
Correlation between experimental data and the present optimized surface model with quantum correction (OSMQ) in solvation free energies of 24 small molecules.
Table 3.
Solvation free energy (kcal/mol) decomposition for a set of 21 molecules.
| Compound | ΔGp | ΔΔGp | ΔGQM | ABS(ΔGQM/ΔΔGp) | |
|---|---|---|---|---|---|
| Ethanol | −5.42 | −6.33 | −0.91 | 0.61 | 0.67 |
| Propionamide | −8.84 | −12.19 | −3.35 | 2.14 | 0.64 |
| Phenol | −6.30 | −7.88 | −1.58 | 1.01 | 0.64 |
| Methanethiol | −3.44 | −4.29 | −0.85 | 0.50 | 0.59 |
| Propionic acid | −6.31 | −7.73 | −1.42 | 0.87 | 0.62 |
| Acetamide | −10.13 | −14.23 | −4.10 | 2.65 | 0.65 |
| Acetonitrile | −6.04 | −8.23 | −2.19 | 1.36 | 0.62 |
| Ethanethiol | −3.77 | −4.53 | −0.76 | 0.47 | 0.62 |
| Aniline | −7.52 | −9.34 | −1.82 | 1.15 | 0.63 |
| Acetic acid | −7.01 | −8.67 | −1.66 | 1.03 | 0.62 |
| 1-methylcytosine | −14.68 | −23.90 | −9.22 | 5.96 | 0.65 |
| Pyridine | −5.3 | −7.61 | −2.31 | 1.49 | 0.64 |
| 9-methyladenine | −13.42 | 18.50 | −5.08 | 3.17 | 0.62 |
| 1-methyluracil | −10.88 | −15.35 | −4.47 | 2.78 | 0.62 |
| 4-cresol | −6.40 | −7.94 | −1.54 | 1.00 | 0.65 |
| 4-Methylimidazole | −10.03 | −15.88 | −5.85 | 3.84 | 0.66 |
| Methylethyl sulfide | −3.94 | −4.83 | −0.89 | 0.55 | 0.62 |
| n-Butylamine | −5.96 | −7.19 | −1.23 | 0.81 | 0.66 |
| 3-Methylindole | −7.80 | −10.40 | −2.60 | 1.66 | 0.64 |
| Methylamine | −6.10 | −7.70 | −1.60 | 1.07 | 0.67 |
| Benzene | −3.72 | −4.69 | −0.97 | 0.52 | 0.53 |
Solvation free energies of 16 molecules
Application of the set of 24 small molecules has shown that the proposed solvation model works well for the solvation free energy calculation of small molecules. One motivation for developing the present optimized surface model with the quantum charge density is to deal with a relatively challenging set of compounds, which was studied by Nicholls et al.51 and in our earlier work16 where the PB theory and fixed partial charges were used. This set is
challenging to compute because of the existence of polyfunctional or interacting polar groups, which lead to strong solvent-solute interactions. The challenge has been illustrated numerically in the previous work.16, 51 In particular, with the OpenEye-AM1-BCC v1 charge and corresponding optimized ZAP 9 radii, the root mean square error (RMS) obtained by Nicholls et al. is 1.71 ± 0.05 kcal/mol via an explicit solvent model. The smallest RMS error of their single - conformer Poisson-Boltzmann approach is 1.87 ± 0.03 kcal/mol.51 By using our previous optimized surface model (OSM) with OpenEye-AM1-BCC v1 charges, a better performance in the solvation calculation could be attained. However, RMS error was still 1.76 kcal/mol. Large errors from benzamides can not be avoided if both OpenEye-AM1-BCC v1 charge and ZAP 9 radii are used in the PB approaches. Errors from the calculation of benzamides were still between 3.5 and 4.0 kcal/mol.
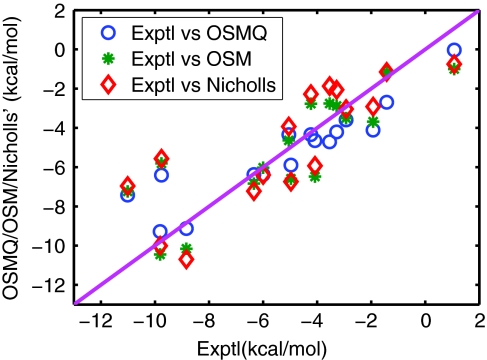
Therefore, aiming at possible improvements, we introduce quantum mechanical corrections to take care of the charge density. As we did before, structure data of this set of 16 molecules is taken from the paper of Nicholls et al.51 In particular, atomic coordinates are taken from their supporting information, which have already been optimized by using Gaussian03 package in vacuum with B3LYP/6-31G**. The atomic radii are still based on their new parametrization ZAP-9 and multiplied by a common factor 1.1. All other parameters needed in current model are set in the same way as described for the above set of 24 molecules. Note that in the previous papers,16, 51 the set contains 17 molecules. Here we remove a compound (benzyl bromide) because it has atomic species Br for which we can not obtain a proper pseudopotential file from the mentioned pseudopotential generator website. Since errors from the calculation of benzyl bromide was about 1 kcal/mol which is much lower than RMS, exclusion of benzyl bromide should make the RMS increase.
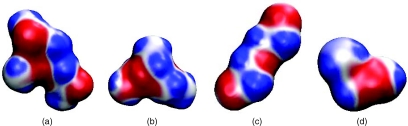
The results are summarized in Table 4 which lists the values of solvation free energies for different components and gives a comparison of total solvation free energies between calculated and experimental values.51 One can also see the correlation between calculated and experimental data from Fig. 5. It shows that the RMS error of 16 molecules from the present model is 1.50 kcal/mol, which is much better than that from the explicit method of 1.71 kcal/mol.51 It is also better than our earlier OSM result of 1.76 kcal/mol.16 Therefore, a conclusion can be reached that nontrivial improvement is made using the charge density directly computed from quantum mechanical calculations. Figure 4 depicts the surface electrostatic potentials of four compounds at their corresponding isosurfaces S = 0.50. These surface potential profiles correlate with the surface electron density distribution and chemical properties of the molecules.
Table 4.
Comparison of free energies (kcal/mol) for 16 compounds.
| Compound | Gnp | ΔGp | ΔGQM | ΔGtotal | Exptl51 | Error |
|---|---|---|---|---|---|---|
| glycerol triacetate | 2.24 | −12.73 | 1.35 | −9.13 | −8.84 | −0.29 |
| benzyl chloride | 1.35 | −6.29 | 0.82 | −4.11 | −1.93 | −2.19 |
| m-bis(trifluoromethyl)benzene | 2.24 | −2.63 | 0.36 | −0.03 | 1.07 | −1.10 |
| N,N-dimethyl-p-methoxybenzamide | 1.97 | −11.24 | 1.85 | −7.42 | −11.01 | 3.58 |
| N,N-4-trimethylbenzamide | 1.86 | −9.79 | 1.52 | −6.41 | −9.76 | 3.35 |
| bis-2-chloroethyl ether | 1.45 | −6.34 | 0.55 | −4.34 | −4.23 | −0.11 |
| 1,1-diacetoxyethane | 1.65 | −8.47 | 0.92 | −5.90 | −4.97 | −0.93 |
| 1,1-diethoxyethane | 1.50 | −6.22 | 0.52 | −4.20 | −3.28 | −0.92 |
| 1,4-dioxane | 1.00 | −6.00 | 0.66 | −4.35 | −5.05 | 0.70 |
| diethyl propanedioate | 1.81 | −9.08 | 0.89 | −6.38 | −6.00 | −0.38 |
| dimethoxymethane | 1.03 | −5.11 | 0.48 | −3.59 | −2.93 | −0.66 |
| ethylene glycol diacetate | 1.59 | −9.00 | 1.03 | −6.38 | −6.34 | 0.04 |
| 1,2-diethoxyethane | 1.54 | −6.85 | 0.61 | −4.70 | −3.54 | −1.16 |
| diethyl sulfide | 1.22 | −4.32 | 0.41 | −2.69 | −1.43 | −1.26 |
| phenyl formate | 1.37 | −6.91 | 0.89 | −4.65 | −4.08 | −0.57 |
| imidazole | 0.95 | −14.10 | 3.29 | −9.86 | −9.81 | −0.05 |
| RMS error | 1.50 | |||||
| Average error | 1.08 |
Figure 5.
Correlation between experimental data51 and the present optimized surface model with quantum mechanics (OSMQ) in solvation free energies of 16 compounds.
Figure 4.
Illustration of surface electrostatic potentials of four small compounds at their corresponding isosurfaces S = 0.50. (a) Glycerol triacetate; (b) 1,1-diethoxyethane; (c) bis-2-chloroethyl ether; (d) dimethoxymethane.
Unfortunately, as shown in Table 4, errors from two amide compounds are still quite large. This problem leads us to further explore the source of their errors. Note that in this work, structural parameters are pre-determined and have not been optimized during the quantum calculation of the electronic density profile. Therefore, the aforementioned large errors must be due to the structural parameters. To prove this we carry out the present solvation analysis of the 16 compounds based on the structural data provided from the Pubchem database (http://pubchem.ncbi.nlm.nih.gov/). Our new results are listed in Table 5. Indeed, errors from two amide compounds are significantly reduced. However, the RMS error of the set (i.e., 1.50 kcal/mol) is exactly the same as that generated from the computation by using ZAP-9 structural parameters,51 because of larger errors from other compounds.
Table 5.
Free energies (kcal/mol) for 16 compounds using structures from Pubchem data.
| Compound | Gnp | ΔGp | ΔGQM | ΔGtotal | Exptl51 | Error |
|---|---|---|---|---|---|---|
| glycerol triacetate | 2.33 | −13.01 | 1.44 | −9.23 | −8.84 | −0.39 |
| benzyl chloride | 1.34 | −6.10 | 0.81 | −3.94 | −1.93 | −2.01 |
| m-bis(trifluoromethyl)benzene | 2.22 | −3.29 | 0.41 | −0.66 | 1.07 | −1.73 |
| N,N-dimethyl-p-methoxybenzamide | 1.94 | −12.00 | 2.04 | −8.02 | −11.01 | 2.99 |
| N,N-4-trimethylbenzamide | 1.85 | −10.59 | 1.77 | −6.97 | −9.76 | 2.79 |
| bis-2-chloroethyl ether | 1.44 | −5.85 | 0.58 | −3.82 | −4.23 | 0.41 |
| 1,1-diacetoxyethane | 1.66 | −8.51 | 0.90 | −5.94 | −4.97 | −0.97 |
| 1,1-diethoxyethane | 1.53 | −6.07 | 0.58 | −3.96 | −3.28 | −0.68 |
| 1,4-dioxane | 1.05 | −5.13 | 0.49 | −3.59 | −5.05 | 1.46 |
| diethyl propanedioate | 1.83 | −11.78 | 1.62 | −8.33 | −6.00 | −2.33 |
| dimethoxymethane | 1.06 | −4.61 | 0.34 | −3.21 | −2.93 | −0.28 |
| ethylene glycol diacetate | 1.68 | −9.63 | 1.4 | −6.91 | −6.34 | −0.57 |
| 1,2-diethoxyethane | 1.72 | −5.68 | 0.44 | −3.52 | −3.54 | −0.02 |
| diethyl sulfide | 1.22 | −4.57 | 0.51 | −2.84 | −1.43 | −1.41 |
| phenyl formate | 1.35 | −6.61 | 0.90 | −4.36 | −4.08 | −0.28 |
| imidazole | 0.82 | −13.16 | 2.97 | −9.28 | −9.81 | −0.53 |
| RMS error | 1.50 | |||||
| Average error | 1.18 |
Note that our approach belongs to the so called “blind test”51 in which the same set of atomic parameters is used for all compounds. Certainly, our errors can be further reduced if atomic parameters are chosen based on molecular information. As such, one is allowed to use different atomic parameters based on the chemical constitution and function groups of a molecule. For example, carbons within the same molecule can have different atomic radii. However, such approaches can no longer be called a “blind test” as discussed by Nicholls et al.51
Solvation free energies of 3 larger molecules
The overall accuracy of the proposed model has been examined by the above two sets of small molecules. Reliability, robustness and consistency have been shown numerically. As far as efficiency is concerned, the proposed model is expected to be slower than traditional continuum models in the solvation analysis due to the additional QM calculations. However, the computational cost of the present model can be much less than that of the traditional QM calculation and existing quantum mechanical continuum solvation models. This is due to the following three reasons. First, implicit description of the solvent is adopted to dramatically reduce the number of degrees of freedom. Second, the time-consuming quantum calculation has been accelerated by the pseudopotential and minimum basis set in the framework of a linear scaling density functional theory in SIESTA. Furthermore, EPS charge fitting process, which depends on the definition of partial charges and the choices of sampling points, is avoided in this model, we directly use charge density instead. Therefore, it is believed that with powerful computer facilities, the current model can be a good choice to handle complex systems such as large drug molecules, amino acids as well as moderately large proteins. To examine the performance of this model for larger molecules, three molecules are chosen, including phorbol (54 atoms), Staurosporine (66 atoms, a potent protein kinase C inhibitor which enhances cAMP-mediated responses in human neuroblastoma cells), and phorbol12,13-dibutyrate (71 atoms, an effective activator of calcium-activated, phospholipid-dependent protein kinase C). Solvation free energies of these molecules are computed and the computational cost is recorded with two quad-core Xeon 2.3 GHz processors. Our results are listed in Table 6. It is also shown that the ratios of ΔΔGp and ΔGQM are still about 0.6, which is consistent with those in smaller molecule calculations. In Figure 6, we illustrate the surface electrostatic potentials for the three compounds. The isosurface S = 0.50 is chosen for the plot. As shown in our earlier work,16 different isosurfaces may exhibit different electrostatic characteristic.
Table 6.
Solvation free energies (kcal/mol) of 3 large molecules and corresponding CPU time.
| Compound | ΔΔGp | ΔGQM | ABS(ΔGQM/ΔΔGp) | Gnp | ΔGtotal | Time (hour) | |
|---|---|---|---|---|---|---|---|
| phorbol | −17.69 | −3.02 | 1.94 | 0.64 | 3.24 | −15.53 | 0.44 |
| phorbol12,13-dibutyrate | −20.00 | −4.94 | 2.91 | 0.59 | 4.60 | −17.43 | 0.97 |
| Staurosporine | −18.71 | −8.39 | 4.78 | 0.57 | 3.79 | −18.53 | 0.82 |
Figure 6.
Illustration of surface electrostatic potentials of three compounds at their corresponding isosurfaces S = 0.50. (a) Phorbol; (b) Phorbol12,13-dibutyrate; (c) Staurosporine.
CONCLUSION
Solvation itself is an elementary process in nature, that has a great impact on other more sophisticated physical, chemical, and biological processes. The importance of the understanding of solvation cannot be overemphasized. In a series of work we have proposed differential geometry based solvation models.16, 17, 76 A key ingredient of these models is that the interface, which separates the solvent domain from the continuum domain, is described by the differential geometry of surfaces. A variational framework is constructed for the total free energy functional which consists of polar and nonpolar contributions. The polar solvation energy was computed by the Poisson-Boltzmann equation with partial charges adopted from molecular mechanical force fields. Generally speaking, partial charges in force fields are parameterized for a certain class of molecules and may not be accurate for others. Additionally, the fixed charge pattern cannot describe the charge arrangement during the solvation process. This drawback limits the accuracy and utility of our earlier solvation models. The present work surpasses such a limitation by incorporating quantum density into our earlier models.
We believe that solvation is subject to the fundamental law of physics. As such, all the important state functions, including the quantum density of the solute, must be determined by a multiscale total free energy functional, which has the contribution from the quantum mechanical energy of electrons at the finest scale. Therefore, we construct a new multiscale total free energy functional which includes the electron kinetic energies and potential energies. Apart from the earlier two governing equations, i.e., the generalized Poisson-Boltzmann equation for the electrostatic potential and the generalized Laplace-Beltrami equation for the solvent-solute boundary, one additional governing equation, the Kohn-Sham equation for electronic structures, is also derived from the total energy functional by the Euler-Lagrange variation. The solution of these three governing equations gives rise to the desirable minimal free energy of solvation.
Numerical methods and algorithms are discussed for the solution of three coupled partial different equations (PDEs). The Poisson-Boltzmann and the Laplace-Beltrami equations (i.e., a generalized Laplace-Beltrami equation) are solved in a similar manner as that in earlier approaches.16, 17 The Kohn-Sham equation is solved twice, one for the solute in vacuum and another in solution. By means of the reaction field potential, we can relate our Kohn-Sham Hamiltonian in both situations to the standard one, so that existing computational software packages can be utilized. The present work has developed a protocol to make use of SIESTA (Spanish Initiative for the Electronic Structure of Thousands of Atoms), an efficient linear scaling DFT package, for the solution of the electronic density. Appropriate iteration procedures are developed to dynamically couple three governing equations and ensure the convergence of the solution.
The present multiscale model is validated by the solvation analysis of realistic molecules whose experimental solvation free energies are available. We have particularly analyzed the stability and consistency of the present model when atomic partial charges in our previous Poisson solver are replaced by the continuous density distribution. Note that the Dirichlet to Neumann mapping technique was used in our earlier Poisson solver to efficiently handle the charge singularities.27 Whereas, such a technique cannot be utilized in the present work. It turns out that the present approach is able to deliver accurate solvation energies.
The present multiscale model is applied to three sets of molecules. One of these sets is considered as a challenging set for which many existing models do not work sufficiently well. The present model shows an improvement upon our earlier models16, 17 and outperforms an explicit solvation method.51 The computational efficiency of the present model can be a concern, as quantum mechanical calculations are involved. We demonstrate that for a molecule with about 60 atoms, the computation of the present multiscale model can be finished within an hour by using a two-processor personal computer.
A further improvement of the present multiscale solvation model is to account for the solvent structure modifications due to solvent-solute interactions. This improvement can be done with traditional integral equation methods or liquid density functional theory.76 This aspect is under our consideration.
ACKNOWLEDGMENTS
The authors thank Dr. Wei Li for useful discussions of quantum calculations. This work was supported in part by NSF Grant Nos. DMS-0616704 and CCF-0936830, and NIH Grant No. R01GM-090208.
APPENDIX A: VALIDATION OF THE CANCELLATION OF SELF-INTERACTION ENERGY
As described earlier, the use of the finite difference scheme in the solution of the Poisson-Boltzmann equation results in the artifact of self-interaction energy which needs to be removed. Although it is common to assign the partial charge at the center of each atom to mimic the effect of electrostatic interactions, this approach also artificially introduces self-interaction energy by using the finite difference scheme. It is known that the cancellation of self-interaction energy works fine with the partial charge formalism by computing the PB equation twice. However, the direct use of the quantum mechanical charge density in the PB equation gives different outcomes. Because the magnitude of distributed nucleus charges is much larger than that of partial charges, the direct use of the quantum mechanic charge density leads to much larger self-interaction energy in the finite difference scheme. Therefore, the accuracy of the PB solver for the reaction field potential and the solvation calculation heavily depend on the cancellation procedure. To our knowledge, with the direct use of the quantum charge density in the PB equation, no numerical test has been done for the impact of self-interaction, neither has the performance of the artifact energy cancellation been examined. To validate our approach, we test 16 small molecules whose partial charges can be obtained from the literature. The details of structure data and parameter setting are described in Sec. 4. In particular, a uniform grid size 0.25 Å is applied to the computation with the partial charge approach. However, in quantum calculation the grid dimension is the same both in the PB solver and in SIESTA. It is automatically generated in SIESTA by setting the MeshCutoff equal to 125 Rydberg. Therefore, the grid size in the present simulation is no longer uniform and varies with different molecules. Take the water molecule as an example, when cutoff energy is 125 Rydberg, the grid size is hx × hy × hz = 0.1190 Å× 0.1192 Å× 0.1182 Å, which is fine enough for the solvation calculation. Table 7 lists the total electrostatic energies both in vacuum and in solution for these 16 molecules, together with the electrostatic solvation free energies which are the difference between the total electrostatic energies in vacuum and in solution. It is found that, as expected, the self-interaction energies with the quantum charge density are much larger than those with the partial charge treatment. The former is hundreds of times larger than the latter. However, through the cancellation, the electrostatic solvation free energies are very close to each other. It can be concluded that most of the self-interaction energy artifact can be removed in the present finite difference scheme with either the fixed partial charge source or the charge density source. Therefore, the direct use of the quantum charge density in the PB solver with the finite difference scheme is validated. Note that although the total electrostatic energies vary under different mesh cutoff energies, the resulting electrostatic solvation free energies show convergence.
Table 7.
Comparison of total electrostatic energy (kcal/mol) and electrostatic solvation energy (kcal/mol) obtained with the partial charge approach and with the direct use of charge density.
| Partial Charge approach |
Charge density approach |
||||||
|---|---|---|---|---|---|---|---|
| Compound | Vacuum | Solution | ΔGp | Vacuum | Solution | ΔGp | |
| glycerol triacetate | 2443.64 | 2456.10 | −12.46 | 704426.41 | 704439.14 | −12.73 | |
| benzyl chloride | 210.88 | 215.93 | −5.04 | 341037.68 | 341043.97 | −6.29 | |
| m-bis(trifluoromethyl)benzene | 1472.87 | 1476.12 | −3.25 | 669772.11 | 669774.74 | −2.63 | |
| N,N-dimethyl-p-methoxybenzamide | 1068.47 | 1077.68 | −9.21 | 533551.77 | 533563.01 | −11.24 | |
| N,N-4-trimethylbenzamide | 866.22 | 873.91 | −7.69 | 396325.28 | 396335.07 | −9.79 | |
| bis-2-chloroethyl ether | 315.5 | 319.77 | −4.23 | 478232.71 | 478239.05 | −6.34 | |
| 1,1-diacetoxyethane | 1754.93 | 1763.19 | −8.25 | 471728.52 | 471736.99 | −8.47 | |
| 1,1-diethoxyethane | 613.59 | 618.04 | −4.45 | 332415.49 | 332421.71 | −6.22 | |
| 1,4-dioxane | 316.81 | 322.47 | −5.65 | 286515.14 | 286521.15 | −6.00 | |
| diethyl propanedioate | 1726.22 | 1734.06 | −7.84 | 434796.12 | 434805.20 | −9.08 | |
| dimethoxymethane | 517.65 | 522.18 | −4.55 | 258225.34 | 258230.45 | −5.11 | |
| ethylene glycol diacetate | 1768.99 | 1777.45 | −8.46 | 434943.17 | 434952.17 | −9.00 | |
| 1,2-diethoxyethane | 484.14 | 488.46 | −4.32 | 343486.83 | 343493.67 | −6.85 | |
| diethyl sulfide | 133.21 | 135.59 | −2.39 | 223784.37 | 223788.70 | −4.32 | |
| phenyl formate | 876.50 | 884.3 | −7.85 | 328961.95 | 328968.86 | −6.91 | |
| imidazole | 944.38 | 955.65 | −11.27 | 199535.85 | 199549.02 | −13.16 | |
APPENDIX B: VALIDATION OF DATA TRANSLATION AND UNIT CONVERSION
In this section, we demonstrate the reliability of data translation and unit conversion between the PB solver and SIESTA by comparing the results from the current calculations with those from the literature. As stated before, the solution of the PB solver depends on the input of the quantum charge density from SIESTA. The polarization of electron cloud, in turn, requires the input of the reaction field potential obtained from the solution of the PB solver. Therefore, the reliability of charge density data passed into the PB solver can be tested by the solution of the PB equation. Meanwhile, the validity of reaction field potential values is illustrated via the change of the solute self-energy due to the polarization of electrons. For comparison, results by Wang et al.75 are used because of the similarity in energy decomposition in the solvation analysis. In their work, they studied the polarization of electron cloud during the solvation process as well. A quantum mechanical calculation based on density functional theory and the Poisson-Boltzmann equation was implemented. Finally, by chemical analysis the solvation free energy was also decomposed into an electrostatic solvation free term, a change term in the solute self-energy and a nonpolar term. The software UHBD together with a pre-determined solvent excluded surface were used for the solution of the PB equation in their work.75 Table 8 displays the comparison in solvation free energy components for three small molecules which are water, NH3 and methanol. It is evident that the results of solvation components from two different methods are comparable to each other. This consistency proves the appropriate data translation process used in different forms of computation domains, as well as the correct unit conversion between the PB solver and SIESTA.
Table 8.
Comparison of solvation energy components between present results (OSMQ) and those of Wang et al. (Ref. 75) for three small molecules.
| ΔGp (kcal/mol) |
ΔGQM (kcal/mol) |
Gnp (kcal/mol) |
||||||
|---|---|---|---|---|---|---|---|---|
| Compound | OSMQ | Wang et al. | OSMQ | Wang et al. | OSMQ | Wang et al. | ||
| Water | −7.55 | −7.36 | 0.86 | 1.01 | 0.39 | 0.59 | ||
| Methanol | −6.18 | −5.53 | 0.63 | 0.77 | 0.57 | 0.77 | ||
| NH3 | −5.12 | −6.77 | 0.87 | 0.92 | 0.46 | 0.63 | ||
References
- Abrashkin A., Andelman D., and Orland H., Phys. Rev. Lett. 99, 077801 (2007). 10.1103/PhysRevLett.99.077801 [DOI] [PubMed] [Google Scholar]
- Artacho E., J. Phys.: Condens. Matter 20, 064208 (2008). 10.1088/0953-8984/20/6/064208 [DOI] [PubMed] [Google Scholar]
- Azuara C., Lindahl E., Koehl P., Orland H., and Delarue M., Nucleic Acids Res. 34, W38 (2006). 10.1093/nar/gkl072 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Azuara C., Orland H., Bon M., Koehl P., and Delarue M., Biophysical Journal 95, 5587¨C5605 (2008). 10.1529/biophysj.108.131649 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baker N. A., “Biomolecular applications of Poisson-Boltzmann methods,” in Reviews in Computational Chemistry, edited by Lipkowitz K. B., Larter R., and Cundari T. R. (Wiley, Hoboken, NJ, 2005), Vol. 21. [Google Scholar]
- Baker N. A., Sept D., Joseph S., Holst M. J., and McCammon J. A., Proc. Natl. Acad. Sci. U.S.A. 98(18), 10037 (2001). 10.1073/pnas.181342398 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barone V., Cossi M., and Tomasi J., J. Chem. Phys. 107, 3210 (1997). 10.1063/1.474671 [DOI] [Google Scholar]
- Bashford D. and Case D. A., Annu. Rev. Phys. Chem. 51, 129 (2000). 10.1146/annurev.physchem.51.1.129 [DOI] [PubMed] [Google Scholar]
- Bates P. W., Chen Z., Sun Y. H., Wei G. W., and Zhao S., J. Math. Biol. 59, 193 (2009). 10.1007/s00285-008-0226-7 [DOI] [PubMed] [Google Scholar]
- Bates P. W., Wei G. W., and Zhao S., arXiv:q-bio/0610038v1, [q-bio.BM], 2006.
- Bates P. W., Wei G. W., and Zhao S., J. Computat. Chem. 29(3), 380 (2008). 10.1002/jcc.20796 [DOI] [PubMed] [Google Scholar]
- Beglov D. and Roux B., J. Chem. Phys. 104(21), 8678 (1996). 10.1063/1.471557 [DOI] [Google Scholar]
- Besler B. H., J. Merz, K. M., and Kollman P. A., J. Comput. Chem. 11, 431 (1990). 10.1002/jcc.540110404 [DOI] [Google Scholar]
- Cances E., Mennucci B., and Tomasi J., J. Chem. Phys. 107, 3032 (1997). 10.1063/1.474659 [DOI] [Google Scholar]
- Chen J., Noodleman L., Case D., and Bashford D., J. Phys. Chem. 98, 11059 (1994). 10.1021/j100094a013 [DOI] [Google Scholar]
- Chen Z., Baker N. A., and Wei G. W., J. Comput. Phys. 229, 8231 (2010). 10.1016/j.jcp.2010.06.036 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen Z., Baker N. A., and Wei G. W., “Differential geometry based solvation models II: Lagrangian formulation,” J. Math. Biol. (in press). 10.1007/s00285-011-0402-z [DOI] [PMC free article] [PubMed]
- Chiba M., Fedorov D. G., and Kitaura K., J. Comput. Chem. 29, 2667 (2008). 10.1002/jcc.21000 [DOI] [PubMed] [Google Scholar]
- Chirlian L. E. and Francl M. M., J. Comput. Chem. 8, 894 (1987). 10.1002/jcc.540080616 [DOI] [Google Scholar]
- Cossi M., Barone V., Cammi R., and Tomasi J., Chem. Phys. Lett. 255, 327 (1996). 10.1016/0009-2614(96)00349-1 [DOI] [Google Scholar]
- Cox S. R. and Williams D. E., J. Comput. Chem. 2, 304 (1981). 10.1002/jcc.540020312 [DOI] [Google Scholar]
- Cramer C. J. and Truhlar D. G., Chem. Rev. 99, 2161 (1999). 10.1021/cr960149m [DOI] [PubMed] [Google Scholar]
- David L., Luo R., and Gilson M. K., J. Comput. Chem. 21(4), 295 (2000). [DOI] [Google Scholar]
- Davis M. E. and McCammon J. A., Chem. Rev. 94, 509 (1990). 10.1021/cr00101a005 [DOI] [Google Scholar]
- Dominy B. N. and C. L.BrooksIII, J. Phys. Chem. B 103(18), 3765 (1999). 10.1021/jp984440c [DOI] [Google Scholar]
- Fogolari F., Brigo A., and Molinari H., J. Mol. Recog. 15(6), 377 (2002). 10.1002/jmr.577 [DOI] [PubMed] [Google Scholar]
- Geng W., Yu S., and Wei G. W., J. Chem. Phys. 127, 114106 (2007). 10.1063/1.2768064 [DOI] [PubMed] [Google Scholar]
- Gilson M. K., Davis M. E., Luty B. A., and McCammon J. A., J. Phys. Chem. 97(14), 3591 (1993). 10.1021/j100116a025 [DOI] [Google Scholar]
- Goedecker S., Rev. Mod. Phys. 71, 1085 (1999). 10.1103/RevModPhys.71.1085 [DOI] [Google Scholar]
- Gogonea V. and Merz K. M., J. Phys. Chem. A 103, 5171 (1999). 10.1021/jp990266w [DOI] [Google Scholar]
- Holm C., Kekicheff P., and Podgornik R., Electrostatic Effects in Soft Matter and Biophysics, NATO Science Series (Kluwer Academic, Boston, 2001). [Google Scholar]
- Honig B. and Nicholls A., Science 268(5214), 1144 (1995). 10.1126/science.7761829 [DOI] [PubMed] [Google Scholar]
- Hu H., Lu Z. Y., and Yang W. T., J. Chem. Theory Comput. 3, 1004 (2007). 10.1021/ct600295n [DOI] [PubMed] [Google Scholar]
- Husowitz B. and Talanquer V., J. Chem. Phys. 126(5), 054508, (2007). 10.1063/1.2432327 [DOI] [PubMed] [Google Scholar]
- Im W., Beglov D., and Roux B., Comp. Phys. Commun. 111(1-3), 59 (1998). 10.1016/S0010-4655(98)00016-2 [DOI] [Google Scholar]
- Improta R., Barone V., Scalmani G., and Frisch M. J., J. Chem. Phys. 125, 054103 (2006). 10.1063/1.2222364 [DOI] [PubMed] [Google Scholar]
- Jayaram B., Sprous D., and Beveridge D. L., J. Phys. Chem. B 102(47), 9571 (1998). 10.1021/jp982007x [DOI] [Google Scholar]
- Jinnouchi R. and Anderson A. B., Phys. Rev. B 77, 245417 (2008). 10.1103/PhysRevB.77.245417 [DOI] [Google Scholar]
- Kamerlin S. C. L., Haranczyk M., and Warshel A., J. Phys. Chem. B 113, 1253 (2009). 10.1021/jp8071712 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koehl P., Orland H., and Delarue M., Phys. Rev. Lett. 102, 087801 (2009). 10.1103/PhysRevLett.102.087801 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lamm G., “The Poisson-Boltzmann equation,” in Reviews in Computational Chemistry, edited by Lipkowitz K. B., Larter R., and Cundari T. R. (Wiley, Hoboken, NJ, 2003), pp 147–366. [Google Scholar]
- Lee B. and Richards F. M., J. Mol. Biol. 55(3), 379 (1971). 10.1016/0022-2836(71)90324-X [DOI] [PubMed] [Google Scholar]
- Levy R. M., Zhang L. Y., Gallicchio E., and Felts A. K., J. Am. Chem. Soc. 125(31), 9523 (2003). 10.1021/ja029833a [DOI] [PubMed] [Google Scholar]
- A. D.MacKerellJr., Bashford D., Bellot M., R. L.DunbrackJr., Evanseck J. D., Field M. J., Fischer S., Gao J., Guo H., Ha S., Joseph-McCarthy D., Kuchnir L., Kuczera K., Lau F. T. K., Mattos C., Michnick S., Ngo T., Nguyen D. T., Prodhom B., W. E.ReiherIII, Roux B., Schlenkrich M., Smith J. C., Stote R., Straub J., Watanabe M., Wiorkiewicz-Kuczera J., Yin D., and Karplus M., J. Phys. Chem. B 102(18), 3586 (1998). 10.1021/jp973084f [DOI] [PubMed] [Google Scholar]
- Madura J. D., Briggs J. M., Wade R. C., Davis M. E., Luty B. A., Ilin A., Antosiewicz J., Gilson M. K., Bagheri B., Scott L. R., and McCammon J. A., Comput. Phys. Commun. 91(1-3), 57 (1995). 10.1016/0010-4655(95)00043-F [DOI] [Google Scholar]
- Marenich A. V., Cramer C. J., and Truhlar D. G., J. Chem. Theory. Comput. 4(6), 877 (2008). 10.1021/ct800029c [DOI] [PubMed] [Google Scholar]
- Mei Y., Ji C. G., and Zhang J. Z. H., J. Chem. Phys. 125, 094906 (2006). 10.1063/1.2345201 [DOI] [PubMed] [Google Scholar]
- Momany F. A., J. Phys. Chem. 82, 592 (1978). 10.1021/j100494a019 [DOI] [Google Scholar]
- Mulliken R. S., I. J. Chem. Phys. 23, 1833 (1955). 10.1063/1.1740588 [DOI] [Google Scholar]
- Netz R. R. and Orland H., Eur. Phys. J. E 1(2-3), 203 (2000). 10.1007/s101890050023 [DOI] [Google Scholar]
- Nicholls A., Mobley D. L., Guthrie P. J., Chodera J. D., and Pande V. S., J. Med. Chem. 51(4), 769 (2008). 10.1021/jm070549+ [DOI] [PubMed] [Google Scholar]
- Onufriev A., Bashford D., and Case D. A., J. Phys. Chem. B 104(15), 3712 (2000). 10.1021/jp994072s [DOI] [Google Scholar]
- Ordejon P., Phys. Stat. Sol. 217, 335 (2000). [DOI] [Google Scholar]
- Ordejon P., Artacho E., and Soler J. M., Phys. Rev. B 53, 10441 (1996). 10.1103/PhysRevB.53.R10441 [DOI] [PubMed] [Google Scholar]
- Ponder J. W. and Case D. A., Adv. Protein Chem. 66, 27 (2003). 10.1016/S0065-3233(03)66002-X [DOI] [PubMed] [Google Scholar]
- Reddy M. R., Singh U. C., and Erion M. D., J. Comput. Chem. 28(2), 491 (2007). 10.1002/jcc.20510 [DOI] [PubMed] [Google Scholar]
- Reed A. E., Curtiss L. A., and Weinhold F., Chem. Rev. 88, 899 (1988). 10.1021/cr00088a005 [DOI] [Google Scholar]
- Richards F. M., Ann. Rev. Biophys. Bioeng. 6(1), 151 (1977). 10.1146/annurev.bb.06.060177.001055 [DOI] [PubMed] [Google Scholar]
- Roux B. and Simonson T., Biophys. Chem. 78(1-2), 1 (1999). 10.1016/S0301-4622(98)00226-9 [DOI] [PubMed] [Google Scholar]
- Schnieders M. J., Baker N. A., Ren P., and Ponder J. W., J. Chem. Phys. 126, 124114 (2007). 10.1063/1.2714528 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharp K. A. and Honig B., J. Phys. Chem. 94, 7684 (1990). 10.1021/j100382a068 [DOI] [Google Scholar]
- Sharp K. A. and Honig B., Annu. Rev. Biophys. Biophys. Chem. 19, 301 (1990). 10.1146/annurev.bb.19.060190.001505 [DOI] [PubMed] [Google Scholar]
- Sigfridsson E. and Ryde U., J. Comput. Chem. 19(4), 377 (1998). [DOI] [Google Scholar]
- Simmonett A. C., Gilbert A. T. B., and Gill P. M. W., Mol. Phys. 103, 2789 (2005). 10.1080/00268970500187910 [DOI] [Google Scholar]
- Singh U. C. and Kollman P. A., J. Comput. Chem. 5, 129 (1984). 10.1002/jcc.540050204 [DOI] [Google Scholar]
- Soler J. M., J. Phys.: Condens. Matter 14, 2745 (2002). 10.1088/0953-8984/14/11/302 [DOI] [Google Scholar]
- Stone A. J. and Alderton M., Mol. Phys. 56, 1047 (1985). 10.1080/00268978500102891 [DOI] [Google Scholar]
- Takano Y. and Houk K. N., J. Chem. Theory Comput. 1(1), 70 (2005). 10.1021/ct049977a [DOI] [PubMed] [Google Scholar]
- Tannor D. J., Marten B., Murphy R., Friesner R. A., Sitkoff D., Nicholls A., Ringnalda M., Goddard W. A., and Honig B., J. Am. Chem. Soc. 116, 11875 (1994). 10.1021/ja00105a030 [DOI] [Google Scholar]
- Tomasi J., Mennucci B., and Cammi R., Chem. Rev. 105, 2999 (2005). 10.1021/cr9904009 [DOI] [PubMed] [Google Scholar]
- Tomasi J. and Persico M., Chem. Rev. 94, 2027 (1994). 10.1021/cr00031a013 [DOI] [Google Scholar]
- Tsui V. and Case D. A., J. Am. Chem. Soc. 122(11), 2489 (2000). 10.1021/ja9939385 [DOI] [Google Scholar]
- Wagoner J. A. and Baker N. A., Proc. Natl. Acad. Sci. U.S.A. 103(22), 8331 (2006). 10.1073/pnas.0600118103 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang M. L. and Wong C. F., J. Phys. Chem. A 110, 4873 (2006). 10.1021/jp0565195 [DOI] [PubMed] [Google Scholar]
- Wang M. L., Wong C. F., Liu J. H., and Zhang P. X., Chem. Phys. Lett. 442, 464 (2007). 10.1016/j.cplett.2007.05.092 [DOI] [Google Scholar]
- Wei G. W., Bull. Math. Biol. 72, 1562 (2010). 10.1007/s11538-010-9511-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wei G. W., Sun Y. H., Zhou Y., and Feig M., arXiv:math-ph/0511001v1 (2005).
- Yu S., Geng W., and Wei G. W., J. Chem. Phys. 126, 244108 (2007). 10.1063/1.2743020 [DOI] [PubMed] [Google Scholar]
- Yu S. and Wei G. W., J. Comput. Phys. 227, 602 (2007). 10.1016/j.jcp.2007.08.003 [DOI] [Google Scholar]
- Yu S., Zhou Y., and Wei G. W.. J. Comput. Phys. 224(2), 729 (2007). 10.1016/j.jcp.2006.10.030 [DOI] [Google Scholar]
- Zhao D., Yu L., Gong L., Liu C., and Yanga Z.. J. Chem. Phys. 134, 194115 (2011). 10.1063/1.3590718 [DOI] [PubMed] [Google Scholar]
- Zhao S. and Wei G. W., J. Comput. Phys. 200(1), 60 (2004). 10.1016/j.jcp.2004.03.008 [DOI] [Google Scholar]
- Zhou Y. C., Feig M., and Wei G. W., J. Comput. Chem. 29, 87 (2008). 10.1002/jcc.20769 [DOI] [PubMed] [Google Scholar]
- Zhou Y. C. and Wei G. W., J. Comput. Phys. 219(1), 228 (2006). 10.1016/j.jcp.2006.03.027 [DOI] [Google Scholar]
- Zhou Y. C., Zhao S., Feig M., and Wei G. W., J. Comput. Phys. 213(1), 1 (2006). 10.1016/j.jcp.2005.07.022 [DOI] [Google Scholar]