Dynamics of tandem bubble interaction in a microfluidic channel

Abstract

The dynamics of tandem bubble interaction in a microfluidic channel (800 × 21 μm, W × H) have been investigated using high-speed photography, with resultant fluid motion characterized by particle imaging velocimetry. A single or tandem bubble is produced reliably via laser absorption by micron-sized gold dots (6 μm in diameter with 40 μm in separation distance) coated on a glass surface of the microfluidic channel. Using two pulsed Nd:YAG lasers at λ = 1064 nm and ∼10 μJ/pulse, the dynamics of tandem bubble interaction (individual maximum bubble diameter of 50 μm with a corresponding collapse time of 5.7 μs) are examined at different phase delays. In close proximity (i.e., interbubble distance = 40 μm or γ = 0.8), the tandem bubbles interact strongly with each other, leading to asymmetric deformation of the bubble walls and jet formation, as well as the production of two pairs of vortices in the surrounding fluid rotating in opposite directions. The direction and speed of the jet (up to 95 m/s), as well as the orientation and strength of the vortices can be varied by adjusting the phase delay.

INTRODUCTION

The interaction of cavitation bubbles in a fluid medium or near a boundary occurs frequently in a wide range of engineering and biomedical applications (Blake and Gibson, 1987; Pishchalnikov et al., 2003; Mitragotri, 2005). Bubble–bubble interaction with resultant violent collapse of the bubble and subsequent shock wave emission or high-speed liquid jet formation have been associated with erosion damage on solid surfaces in hydraulic machinery (Arndt, 1981) and certain adverse effects on cells and tissue exposed to diagnostic and therapeutic ultrasound (Miller, 1987). However, the power of cavitation has also been harnessed in biomedical applications to improve the disintegration of kidney stones in shock wave lithotripsy (Xi and Zhong, 2000), to facilitate targeted drug and gene delivery (Mitragotri, 2005), and to enhance the efficacy of high-intensity focused ultrasound in cancer therapy (Kennedy, 2005).

Several groups have investigated the dynamics of bubble–bubble interaction using laser-based experimental systems with high spatial and temporal precision in bubble generation. Lauterborn and Hentschel (1985) showed examples of the interaction of two bubbles of similar size in water, demonstrating mutual attraction of the bubbles with reentrant jet formation toward each other. Blake et al. (1993) examined the interaction of two different-sized bubbles in water near a solid boundary. Their results demonstrate that the mutual interaction between two bubbles in close proximity is as important as the presence of a rigid boundary in determining the overall behavior of the bubbles (i.e., migration, asymmetric deformation, jet formation, and bubble splitting). Sato and Tomita (1998) studied non-spherical motion of two laser-generated bubbles near a solid boundary. By adjusting the time delay (and thus the phase difference) between the two bubbles, they were able to control the direction of jet formation either toward or away from the boundary. Within an optimal range of phase delay, they were able to increase the jet speed produced by the tandem bubble interaction compared to its counterpart from a single bubble of similar size near the boundary.

The general features of bubble–bubble interaction observed experimentally have been captured by model simulations based on potential flow and the boundary element method (BEM) (Blake et al., 1993; Sato and Tomita, 1998) and similarities with a single bubble oscillation either near a rigid or soft boundary were noted (Blake and Gibson, 1987). The BEM approach has also been used to describe the dynamical interaction in a multi-bubble cloud (Chahine and Duraiswami, 1992). Moreover, Ilinskii et al. (2007) have investigated bubble–bubble interaction in an acoustic field based on Lagrangian and Hamiltonian mechanics, demonstrating coupled pulsation with translational motions. Higher order surface disturbances of the bubble can also be introduced to model jet formation (Kurihara et al., 2010).

In recent years, there has been a growing interest in tandem bubble interaction in microfluidic devices (Chen et al., 2006; Chen and Lin, 2008; Chang et al., 2010) with potential applications in directional and localized membrane poration on single cells (Sankin et al., 2010), characterization of material properties of nanotubes (Quinto-Su et al., 2010), and cell sorting (Lautz et al., 2010). In all these previous studies, cavitation bubbles were produced by laser-induced rapid heating of fluids containing color dyes. In some cases, the dye (such as Trypan blue) was used not only to enhance laser absorption but also to serve conveniently as a biomarker for cell membrane permeabilization (Le Gac et al., 2007). However, since most of the dyes are either cytotoxic or non-biocompatible their presence in the fluid medium could severely limit the utility of these methods in biomedical and biotechnological applications.

In this study, we describe a method for controlled generation of tandem bubbles in a microfluidic channel with patterned gold dots decorated on its glass substrate. In the following sections, we will first summarize briefly the theoretical background for the mutual interaction between two oscillating bubbles. Then, the protocol for micropatterning of gold dots on a glass surface, and the fabrication of a microfluidic chip will be described together with experimental methods for high-speed imaging of bubble dynamics and flow visualization via particle imaging velocimetry (PIV). Finally, we will present the results of laser-generated single and tandem bubble in the microfluidic channel with particular emphasis on the effects of phase delay on the dynamics of tandem bubble interaction and jet formation.

THEORETICAL BACKGROUND

The mutual interaction between two oscillating bubbles in water can be described by the secondary Bjerknes forces (Mettin et al., 1997; Lauterborn and Kurz, 2010). In the simplest case, the pressure field (p₁) produced by a spherically oscillating bubble (referred as bubble 1 or B₁) is given by

$$p_1=\frac{\rho }{r}\frac{d}{\mathit{dt}}(R_1^2{\stackrel{·}{R}}_1),$$ (1)

where ρ is the density of water, r is the radial coordinate, R₁ is the time-varying radius of B₁, and the overdot denotes time derivative. A second bubble (B₂) located at an inter-bubble distance d from B₁ will experience a time-varying radiation force (F₁₂) produced by p₁ given by

$${\mathit{F}}_{12}=-V_2\nabla p_1,$$ (2)

where V₂ is the volume of B₂. Integrating Eq. 2 over a period of the volume oscillation of the bubble, one can determine the secondary Bjerknes force by

$${\mathit{F}}_{\mathrm{B}}=〈{\mathit{F}}_{12}〉=-\frac{\rho }{4\pi d^2}〈{\stackrel{·}{V}}_1{\stackrel{·}{V}}_2〉{\mathbf{e}}_r,$$ (3)

where the angular brackets denote time average, V₁ is the volume of B₁, and e_r is the unit vector along the radial direction. It has been shown that the secondary Bjerknes forces of two spherically oscillating bubbles are symmetric: $〈{\mathit{F}}_{12}〉=-〈{\mathit{F}}_{21}〉$ (Mettin et al., 1997).

The most significant implication of Eq. 3 is that when two bubbles oscillate in-phase, they attract each other. In contrast, when oscillating out-of-phase, they repel each other.

MATERIALS AND METHODS

Patterning of micron-sized gold dots on a glass surface

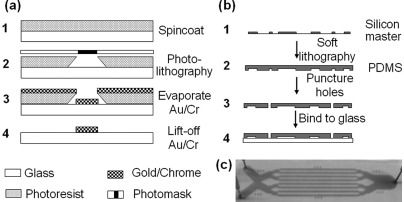
It has been shown previously that vapor microbubbles can be generated via laser-induced localized heating of metal surfaces immersed in water (Yang, 2007) or nanoparticle dispersed tissue mimicking materials (Farny et al., 2005). To produce tandem bubbles with precision in nucleation sites and desirable spatial distribution, a glass surface was treated by coating it with an array of paired gold dots having a separation distance of 40 μm using metal lift-off technique (Schoning et al., 2005). Briefly, as shown in Fig. 1a, a thin layer of photoresist (NFR 015, Sunnyvale, CA) was first spin-coated on a 1-mm-thick microscopic glass slide (#48300, VWR International). A chrome master photomask (Photo Sciences) with designed patterns was then used to perform photolithography on the coated layer of photoresist using a lithography mask aligner (MA6/BA6, Karl Suss). An array of paired gold dots of 6 μm in diameter and 15 nm thick was deposited on the glass surface using an electron beam evaporator (PVD 75, Kurt Lesker) preceded by a 2-nm-thick chrome underlayer deposition in order to enhance the adhesion between the glass surface and the gold dots. The 6-μm-diameter gold dots were selected to ensure sufficient area for laser absorption while providing a small enough target (<the focal spot of the laser beam) for easy alignment and consistency in bubble generation.

Figure 1.

(Color online) Schematic diagrams showing the protocols for (a) patterning of micron-sized gold dots on a glass surface using metal lift-off technique and (b) fabrication of PDMS–glass microfluidic chips. (c) A photograph of the integrated microfluidic chip with individual channels filled with a blue solution. Blunt needles are connected to the ports punctured on the PDMS.

Based on the Drude free-electron theory (Johnson and Christy, 1972), the attenuation coefficient (α) of an incident laser pulse at near-infrared wavelengths by a metal nanolayer can be estimated by

$$\ln (1-\alpha )\propto -n_{e}a{\lambda }^3,$$ (4)

where n_e is the electron density in the metal, λ is the laser wavelength, and a is the metal thickness. This leads to an estimated maximum absorption of about 70% by the gold nanolayer at 1064 nm wavelength. It is worth noting that while a thicker layer of gold deposition on the glass surface will increase laser absorption, it will also generate more insoluble gas and metal debris during plasma formation, making the resultant bubble dynamics less reproducible.

Fabrication of the microfluidic chips

To construct a microfluidic chip, the glass slide with patterned gold dots on the surface was bound with a polydimethyl-siloxane [(PDMS), which has an elastic modulus of 1.8 MPa (Schneider et al., 2008)] block containing several microchannels [Fig. 1b]. The PDMS (Sylagard 184, Dow Corning) microchannels were produced from a silicon master mold (Stanford Microfluidic Foundry) using soft lithography technique (Duffy et al., 1999). Each channel was designed to have a cross section of 800 × 21 μm (width × height), allowing for injection and exchange of different fluid media (e.g., for cell culture and bioassays). Fluid access ports (1 mm in diameter) were punctured at the ends of the PDMS microchannel, which has a nominal length of 25 mm [Fig. 1c]. The surfaces of the glass substrate and the PDMS slab (2 mm thick) were hydrophilized in an oxygen plasma asher (K-1050X, Emitech), aligned using position pins, and brought into conformal contact. The integrated chip was then baked on a hot plate to strengthen the bonding at the glass–PDMS interface. Using a syringe, the microchannels in the microchip were filled with de-ionized water. A unique advantage of the microchip design is that multiple test sites can be created within each channel, thus providing a high-throughput platform for assessing tandem bubble interaction under a variety of experimental conditions.

Laser-induced microbubble(s) in the microfluidic channel

The fabricated microfluidic chip was placed on the stage of an experimental system constructed from an inverted microscope (Axio Observer D1, Zeiss) described previously (Sankin et al., 2010). Two Q-switched Nd:YAG lasers of 1064 nm wavelength and 5 ns pulse duration [MiniLase I (laser 1) and Orion (laser 2), New Wave Research] were focused through a 63 × objective (LD Plan Neofluar, Zeiss) and projected on a pair of gold dots (Fig. 2). Alignment of the laser foci with the gold dots was facilitated by a rotating slide holder (H22ROTS, Prior Scientific) in combination with the x–y translational stage of the microscope. Bubble dynamics and the flow field around the pulsating bubble(s) can be visualized through the same objective via high-speed cameras connected to the microscope. In this study, the output power of each laser was adjusted to be ∼10 μJ so that the maximum bubble diameter produced from individual gold dots is 50.0 ± 0.9 μm (mean ± standard deviation, n = 12).

Figure 2.

(Color online) A schematic diagram of the experimental setup for laser-generated tandem microbubble in a microfluidic channel (inter-bubble distance d = 40 μm). The mid-point between the pair of gold dots is chosen as the origin “O” of a Cartesian x–y–z coordinate system, where the positive direction of the y axis is pointed from B₂ (y = −20 μm) to B₁ (y = +20 μm) and the z-axis is from glass (z < 0) to PDMS (z > 25 μm).

The non-dimensional standoff distance (γ) between a pair of equal-sized tandem bubbles can be defined by the ratio of the inter-bubble distance (d) divided by the maximum diameter of the individual bubbles (2R_max) (Khoo et al., 2009),

$$\gamma =\frac{d}{2R_{\max }}.$$ (5)

In this study, γ was kept constant at 0.8, corresponding to a strong mutual interaction between the tandem bubbles due to the secondary Bjerknes force. However, the phase delay between the oscillations of the two bubbles can be adjusted using a digital delay generator (BNC 555, Berkeley Nucleonics) that controls the timing of the trigger signals to the two lasers. The time delay τ between individual laser pulses was monitored by a photodiode (DET210, Thorlabs) connected to an oscilloscope (500 MHz WaveRunner 6050A, LeCroy).

High-speed imaging and flow visualization

The dynamics of laser-generated single or tandem bubble oscillation in the microfluidic channel were captured using a high-speed camera (Imacon 200, DRS Hadland) operated at 50 ns exposure time and a framing rate of 1 or 10 × 10⁻⁶ frames/s. Backlight illumination was provided by a fiber-optic coupled xenon flash lamp with 200 μs pulse duration (ML1000, Dyna-Lite). To facilitate the visualization of flow motion generated by the bubble oscillation via PIV, 2 μm polystyrene beads (R0200, Duke Scientific) were added as neutral buoyancy tracers in the fluid medium at a concentration of 1 × 10⁹ beads/ml. The trajectories of the tracers were recorded by a second high-speed camera (Phantom V7.3, Vision Research) operated at 1 μs exposure time and 20 000 frames/s. The acquired image sequences (at 1.5 pixel/μm resolution) were processed offline by DaVis7 software (LaVision, GmbH) using a 16 × 16 pixel interrogation window with 50% overlap to determine the velocity and vorticity fields averaged over every 50 μs after the tandem bubble interaction.

RESULTS AND DISCUSSION

Dynamics of a single bubble

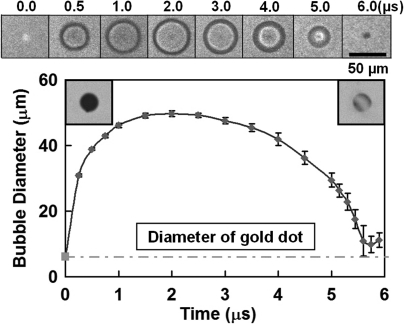
The generation of a cavitation bubble via laser-irradiation of a 6 μm gold dot on a glass surface is highly localized and reproducible. A representative high-speed imaging sequence of laser-induced single bubble oscillation in the microfluidic channel is shown in Fig. 3, together with a bubble diameter vs time plot obtained from 12 measurements using individual gold dots. The strong absorption of the incident laser pulse by the gold dot leads to the instantaneous creation of a plasma (at t = 0 s), which expands rapidly to form a vapor bubble of a maximum projected diameter (in the x–y plane) of 50 μm in 2 μs. The rapid initial increase in the projected bubble diameter may be related to the creation of a hemispherical bubble around the gold dot, which is gradually transformed, upon further expansion, into a cylindrical bubble constrained by the top and bottom surfaces of the microfluidic channel. Thereafter, the bubble starts to collapse, reaching a minimum size in about 3.7 μs, followed by a slight rebound. Overall, the collapse time of the bubble (T_c) in the PDMS–glass microchannel is 5.7 μs. In comparison, using the same experimental setup, T_c of a bubble with a 50 μm maximum diameter in a glass–glass microchannel of 25 μm height was found to be 8.8 μs. The difference is likely attributed to the compliance of the PDMS boundary, which is known to shorten the collapse time of a bubble in close proximity (Brujan et al., 2001); in contrast, a rigid boundary (i.e., glass) can lengthen the collapse of a similar bubble (Blake and Gibson, 1987).

Figure 3.

(Color online) Dynamics of a single bubble oscillation produced by laser absorption from a single gold dot patterned on the glass bottom of a microfluidic channel (the brighter interior in the collapse phase compared to the expansion phase may suggest a transition from an initial 3D hemispherical expansion to a two-dimensional cylindrical collapse of the bubble). The insets in the upper-left and upper-right corners of the plot show a gold dot before and after a single cavitation event, respectively, demonstrating thermal ablation and cavitation damage to the gold layer.

Dynamics of tandem bubble: The effects of phase delay

General features of tandem bubble oscillation

In our experiment, two equal-sized laser-generated bubbles (R_max = 25 μm) are created in close proximity to each other (d = 40 μm or γ = 0.8). Therefore, strong interaction due to the secondary Bjerknes force between the two bubbles is observed, leading to asymmetric bubble deformation and axial jet formation (Fig. 4). In particular, we focus on the effects of the time delay (τ, varying from 0 and T_c) between the generation of the two bubbles on their dynamic interaction and subsequent jet and vortex formation in the surrounding fluid.

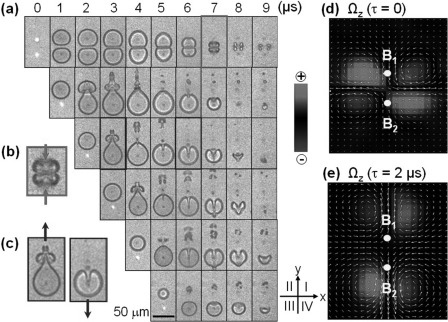
Figure 4.

(Color online) (a) Laser-generated tandem bubble oscillation and jet formation produced inside the PDMS–glass microchannel at an inter-bubble time delay of 0, 1, 2, 3, 4, 5 μs (from top to bottom). High-speed imaging sequences were taken with a framing rate of 1 × 10⁶ frames/s; (b) jet formation from in-phase tandem bubble oscillation; (c) jet formation from out-of-phase tandem bubble oscillation; and vorticity field averaged over t = 100–150 μs after (d) in-phase and (e) out-of-phase tandem bubble oscillation.

The general features of tandem bubble oscillation are investigated by high-speed photography at a framing rate of 1 × 10⁶ frames/s. As shown in Fig. 4a (first row), when the two bubbles are generated simultaneously, i.e., in-phase, both B₁ and B₂ start to expand concurrently after the plasma formation. The proximal walls of the two bubbles quickly approach each other and become stagnated and flattened along the mid-plane between the two bubbles, while their distal walls continue to expand outward for about 3 μs. Upon maximum expansion, the tandem bubble begins to collapse in unison toward the flattened proximal walls in the mid-plane. Because of their larger curvatures, the sections of the distal walls along the axis of the tandem bubble collapse much more rapidly than the rest of the bubble surface (see t = 5–7 μs), leading to the formation of two axial jets moving toward each other [see Fig. 4b]. The collision of the two axial jets in the mid-plane breaks up the tandem bubble into two pairs of small daughter tandem bubbles that move away from each other along the x axis.

The dynamics of in-phase tandem bubble interaction is analogous to a single bubble oscillation near a rigid boundary (that serves as a mirror of the single bubble), with the centroids of the bubbles and/or axial jets migrating toward each other (or toward the boundary) (Blake and Gibson, 1987; Quinto-Su and Ohl, 2009). This observation is supported by the progressive thinning of the gap between the proximal walls of the tandem bubble, not only during the initial expansion but also in the collapse phase when the mutual attraction associated with the secondary Bjerknes force increases significantly with decreased inter-bubble distance and much more rapidly changed bubble volume [see Eq. 3]. Furthermore, the collapse time of the tandem bubble is lengthened (T_c = 7.5 μs) compared to its counterpart of a single bubble (T_c = 5.7 μs). This observation is consistent with the findings of previous studies (Lauterborn, 1982; Blake and Gibson, 1987; Quinto-Su and Ohl, 2009).

In contrast, when two equal-sized bubbles are generated at different times within a single oscillation period, the characteristics of the tandem bubble interaction change dramatically. As shown in Fig. 4a, the original symmetric geometry (in the projected x–y plane) in B₁ oscillation is disrupted immediately after the generation of B₂ (with a time delay τ varying from 1 to 5 μs in the second to sixth rows), whose radial oscillation, in turn, is also severely distorted. In general, the two bubbles are found to oscillate mostly out-of-phase and therefore, repel each other by the secondary Bjerknes force. This mutual interaction leads to the formation of axial jets moving away from each other [see, e.g., Fig. 4c], and the breakdown of B₁ into several smaller daughter bubbles drifting along the axis of the tandem bubble (or y axis). The detail of the interaction and characteristics of the jet formation depends on the phase delay between the two bubbles, which, for example, can provide a means to optimize the tandem bubble interaction for maximizing the resultant jet velocity.

In particular at τ = 2 μs [the third row in Fig. 4a], B₁ has just reached its maximum expansion and is ready to collapse when B₂ is produced. Therefore, the two bubbles oscillate completely out-of-phase (i.e., anti-phase), resulting in the collapse of B₁ being greatly accelerated by the concomitant expansion of B₂ with a significantly shortened T_c of 3.7 μs.

The dynamics of anti-phase tandem bubble interaction is analogous to a single bubble oscillation near a free surface (that serves as a deformable boundary of constant pressure), with the centroids of the bubbles and/or axial jets migrating away from each other (or the free surface) (Blake et al., 1987). Our observation of the tandem bubble interaction in a narrow fluid gap (a quasi-two-dimensional configuration) is similar to the general features of tandem bubble interacting in free field [a three-dimensional (3D) configuration] (Sato and Tomita, 1998). The primary difference is in the geometry of the bubble (cylindrical vs spherical) and associated dependency of the strength of the Bjerknes attraction (1/d vs 1/d²) (Chahine, 1982; Quinto-Su and Ohl, 2009).

The flow field around the tandem bubble during t = 100–150 μs has been characterized by PIV, which reveals a pattern of streamlines that is consistent with the deformation of the bubbles, jet formation, and subsequent displacement of the bubble remnants. Furthermore, the PIV results shown in Figs. 4d, 4e demonstrate the formation of two pair of vortices around the center of the tandem bubble (i.e., the origin of the x–y–z coordinate system O). The two pairs of vortices associated with the tandem bubble oscillating in-phase tend to stay close to each other with the vortices rotating counterclockwise in quadrants I and III, yet clockwise in quadrants II and IV [Fig. 4d]. In contrast, the two pairs of vortices generated by the anti-phase oscillating tandem bubble rotate in the opposite direction of their in-phase counterpart and gradually drift outward away from each other [Fig. 4e]. It has been observed that these long-lasting vortices can sustain the movement of bubble remnants for more than 150 μs. During t = 100 and 150 μs, the magnitude of the maximum vorticity produced by the anti-phase tandem bubble oscillation is 2.8 × 10³·s⁻¹, compared to 1.8 × 10³·s⁻¹ produced by the in-phase tandem bubble oscillation. These findings support the potential utility of tandem bubbles in various biological and biotechnology applications, such as single cell membrane poration (Sankin et al., 2010) and directional displacement of microparticles and suspended cells in a microfluidic device (Lautz et al., 2010).

Effects of phase delay on tandem bubble interaction

The effects of the phase delay on the dynamics of tandem bubble interaction and jet formation are examined in detail at a framing rate up to 10 × 10⁶ frames/s (Fig. 5). Several interesting features can be noticed. First, the rapid expansion and subsequent elongation of B₂ toward B₁ as a result of their mutual interaction causes an asymmetric deformation of the proximal walls of the tandem bubble, leading to the formation of a first liquid jet (J₁) inside the collapsing B₁ [see, e.g., t = 1.3–1.6 μs in Fig. 5a]. The proximal walls of the two bubbles appear to be separated by a thin layer of liquid even when J₁ is piercing through the interior of B₁ [see, e.g., t = 2.3–2.6 μs in Fig. 5b]. This observation is consistent with the results of potential flow modeling of tandem bubble interaction in three dimensions, which also suggest the formation of a high pressure region between the asymmetrically deformed proximal bubble walls that drives the development of J₁ (Sato and Tomita, 1998). Second, B₁ breaks up into several small daughter bubbles upon collapsing into a minimum volume shortly before or after J₁ pierces through the distal wall of B₁. Subsequently, the remnants of B₁ are carried away from the center of the tandem bubble along the y axis by the resultant vortex flow [see also Fig. 4e]. Third, T_c of B₁ is found to vary significantly with the phase delay between the two bubbles. The minimum in T_c for B₁ (i.e., 3.8 μs) is produced at an inter-bubble time delay of τ = 2 μs, which, interestingly, also correlates to the largest elongation of B₂ produced [see t = 3.0 μs in Fig. 5b; the elongation is measured by the ratio of the maximum bubble diameter along the y axis over its counterpart along the x axis]. Fourth, upon maximum expansion B₂ starts to collapse with its highly elongated proximal wall contracting rapidly backward, forming a second jet (J₂) piercing through the interior of B₂ toward its distal wall (see, e.g., t = 4.3–6.5 μs in Fig. 5c]. The push-and-pull action of the tandem bubble (more specifically of B₂, as shown in Fig. 5) has been coined the “catapult” effect (Fong et al., 2009).

Figure 5.

Dynamics of laser-generated tandem bubble oscillation and jet formation produced inside the PDMS–glass microchannel at an inter-bubble time delay of (a) 1 μs, (b) 2 μs, (c) 3 μs, and (d) 4 μs. High-speed imaging sequences were taken with a framing rate up to 10 × 10⁶ frames/s.

Temporal development of the tandem bubble oscillation

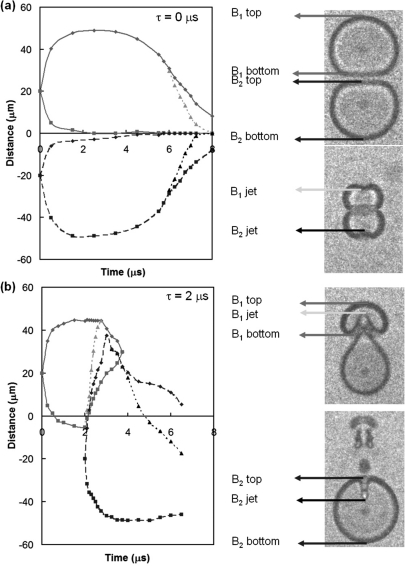
The dynamics of tandem bubble oscillation can be further illustrated by the temporal variations of its boundaries along the y axis. Based on the data shown in Fig. 5, the locations of the top and bottom poles of the bubbles as well as the tip locations of the jets over time are plotted. For the in-phase oscillation [Fig. 6a], the proximal walls of the bubbles move toward each other and stagnate in the mid-plane while the distal walls expand outward more extensively before collapsing in unison back toward the mid-plane [see also the first row in Fig. 4a]. The oscillations of the two bubbles are merely mirror images of each other, as well as the two axial jets, which move faster than the collapse of the remaining portions of the distal walls of the bubbles. In contrast, the expansion and collapse of the two bubbles in the anti-phase oscillation [Fig. 6b] are significantly different from each other in terms of bubble collapse time and maximum axial elongation. For example, the extrusion of the proximal surface of B₂ is clearly coupled with the advance of the tip of J₁ inside the collapsing B₁. However, the advance of the tip of J₂ inside the collapsing B₂ is largely decoupled with the rebound (or re-expansion) of B₁ because of its rapid break up due to surface instability. Consequently, the speed of J₂ in general is found to be significantly slower than J₁ (Fig. 7). Furthermore, the diagram illustrates clearly the lengthening or shortening in collapse time when the tandem bubble oscillates either in-phase or out-of-phase, respectively.

Figure 6.

(Color online) Temporal development of the top and bottom poles of the tandem bubble along the y axis (see the coordinates in Fig. 2): (a) in-phase oscillation, (b) anti-phase oscillation. Solid lines: B₁ top and B₁ bottom; dashed lines: B₂ top and B₂ bottom; dotted lines: B₁ jet tip and B₂ jet tip.

Figure 7.

(Color online) Relation between jet velocity and time delay between the generation of the first and second bubbles. J₁ and J₂ indicate the jets from the collapse of the first and second bubbles, respectively. The jet speed is averaged within 500 ns after the initiation of the collapse of each bubble, the results are obtained from six individual measurements.

Jet velocity

Figure 7 shows the dependency of jet velocity on the time delay (τ) between the generations of the two bubbles. The speed of J₁ was measured by averaging the tip displacement on the proximal wall of B₁ over the first 500 ns starting from the initial expansion of B₂. The results show that the maximal speed of J₁ (95 ± 7 m/s) is reached at τ = 2 μs for the anti-phase bubble oscillation, which is likely correlated with the most efficient energy transfer from B₂ to B₁ (Chang et al., 2010). The speed of J₂ was measured by averaging the tip displacement on the proximal wall of B₂ over the first 500 ns from the initial collapse of B₂. The speed of J₂ was found to increase progressively from τ = 1 to 4 μs.

SUMMARY

In this study, we have developed a method for generating tandem bubbles in a microfluidic channel via laser absorption by patterned micron-sized gold dots. The dynamics of single bubble oscillation produced in such a microchannel are highly reproducible, allowing for a detailed examination of the tandem bubble interaction with various phase delays. In close proximity (γ = 0.8), the coupled oscillation of the tandem bubble produces asymmetric deformation of the bubble walls, leading to axial jet formation either toward or away from each other depending on the phase relationship between the two bubbles. The rotational direction and strength of the resultant vortices around the tandem bubble, as well as the axial jet speed, can also be adjusted and controlled by changing the phase delay. Since this method of tandem bubble generation is non-toxic and biocompatible, it may provide a versatile platform for exploring a diverse range of biomedical and biotechnology applications ranging from targeted drug/gene delivery to cell manipulation and sorting in high-throughput microfluidic systems.