Examining Agreement and Longitudinal Stability Among Traditional and Response-to-Intervention-Based Definitions of Reading Disability Using the Affected-Status Agreement Statistic

Abstract

Rates of agreement among alternative definitions of reading disability and their 1- and 2-year stabilities were examined using a new measure of agreement, the affected-status agreement statistic. Participants were 288,114 first through third grade students. Reading measures were Dynamic Indicators of Basic Early Literacy Skills Oral Reading Fluency and Nonsense Word Fluency, and six levels of severity of poor reading were examined (25th, 20th, 15th, 10th, 5th, and 3rd percentile ranks). Four definitions were compared, including traditional unexpected low achievement and three response-to-intervention-based definitions: low achievement, low growth, and dual discrepancy. Rates of agreement were variable but only poor to moderate overall, with poorest agreement between unexpected low achievement and the other definitions. Longitudinal stability was poor, with poorest stability for the low growth definition. Implications for research and practice are discussed.

An agreed-on definition of reading disability serves as an essential foundation for reading research. Whether the comparison involves behavioral, cognitive, or biological variables, studies that compare reading disabled individuals to control groups require ways of defining those with reading disabilities. Without an agreed-on definition that can be implemented reliably and validly, understanding the nature, causes, and best treatments for reading disability is unlikely. Similarly, an agreed-on definition is essential for practice. The idea that whether or not one is considered to have a reading disability and be eligible for assistance might vary depending on one’s zip code is unsettling at the very least.

How best to conceptualize and define reading disability has long been a contentious issue (Rutter & Yule, 1975), and it remains so today. The traditional conceptualization of reading disability has focused on the presence of unexpected difficulty in reading. The common operational definition of unexpected difficulty became a discrepancy between an individual’s IQ score and his or her achievement score in reading. For example, the U.S. government adopted an eligibility definition of learning disabilities based on a “severe discrepancy” between ability and achievement (U.S. Office of Education, 1977); this definition was used to determine who was eligible for special services through the Education for All Handicapped Children Act of 1975. This discrepancy definition is also incorporated into the current edition of the Diagnostic and Statistical Manual of Mental Disorders (American Psychiatric Association, 2000).

During the past three decades, researchers have questioned the adequacy of the discrepancy definition of learning disabilities in general and of reading disabilities in particular. When children identified as learning disabled by the discrepancy definition have been compared to children who have low achievement in reading (typically at the 25th percentile or below) but do not have a significant IQ–achievement discrepancy, these two groups have not been found to differ on a variety of cognitive variables including verbal and nonverbal short-term memory, rapid naming, visual attention, and speech production (Fletcher et al., 1994). An analysis of growth in reading ability from first to ninth grade found that discrepant children and low-achieving children had similar growth patterns, with both groups characterized by a plateau in growth at a lower level than children without problems in reading (Francis, Shaywitz, Stuebing, Shaywitz, & Fletcher, 1996). A meta-analysis of 46 studies comparing discrepant and low-achieving students concluded that these two groups were not significantly different on the reading-related constructs of phonological awareness, rapid naming, verbal short-term memory, and vocabulary, though there did appear to be significant differences between the two groups on other measures related to overall cognitive abilities (Stuebing et al., 2002). Another meta-analysis examining 86 studies of IQ-discrepant and low-achieving students concluded that the IQ-discrepant group exhibited greater impairment in reading ability than the low-achieving group and that this difference was most notable on timed tests (D. Fuchs, Fuchs, Mathes, & Lipsey, 2000).

Additional research has focused on the role of intelligence in predicting responsiveness to instruction in students who are learning disabled. Although researchers generally agree that the IQ–achievement discrepancy method is no longer the preferred method of diagnosing learning disabilities, there is disagreement on whether or not a student’s IQ is relevant with regard to special education. A recent meta-analysis reported that IQ predicted 12% to 15% of the variance in reading comprehension (D. Fuchs & Young, 2006). However, a follow-up meta-analysis concluded that IQ predicted only 1% to 3% of the variance in response to the reading intervention (Stuebing, Barth, Molfese, Weiss, & Fletcher, 2009).

In 2004, the Individuals with Disabilities Education Act (IDEA) was reauthorized and broadened the definition of learning disabilities. The new IDEA regulations no longer mandate the use of the discrepancy-based definition of learning disabilities (although they do not prohibit it either) and now permit the use of a response to intervention (RTI) model. With an RTI model, the process of identifying students with learning disabilities begins by identifying students who do not appear to be responsive to effective reading instruction provided in the students’ regular classroom setting. Intervention is then provided to students who have not responded adequately to effective regular classroom instruction. Students who do not respond adequately to intervention are then considered to be learning disabled (D. Fuchs & Fuchs, 2006).

One challenge in implementing an RTI model is deciding what constitutes inadequate RTI. Some variants of the RTI model focus on students’ rate of growth in reading ability. For example, Vellutino et al. (1996) proposed a “median split” model that began by identifying a group of “poor readers” based on teacher ratings of each student’s reading ability. The poor readers then received an intervention consisting of 30 minutes of daily one-to-one tutoring for 15 weeks. The authors calculated slopes representing growth and identified nonresponders as those whose slopes were below the median. A similar approach is represented by the “slope-discrepancy model” (D. Fuchs, Fuchs, & Compton, 2004). Using this model, at-risk students were identified on the basis of a beginning of school year screening. They were provided reading intervention, and slopes were used to quantify growth. The slope-discrepancy model diverges from the median split model in that nonresponsiveness is not determined by a median split but rather in reference to classroom, school, district, state, or national norms.

Other RTI approaches involve identifying students with learning disabilities based on a one-time assessment. The “final benchmark” (Good, Simmons, & Kame’enui, 2001) method sets a benchmark score that suggests need for additional intervention. All children are tested at a specific time point such as the middle or end of the school year, and those who score below the benchmark are considered learning disabled. The authors provided recommended benchmarks based on a longitudinal study of children in Oregon from kindergarten to third grade.

The “normalization” (Torgesen et al., 2001) method selects an at-risk group of students to receive a tutoring intervention. Torgesen and colleagues (2001) chose for their at-risk group students who were diagnosed with a learning disability by the discrepancy method and who had Word Attack and Word Identification scores significantly below average. At the end of the Tier 2 tutoring, children who scored below a standard score of 90 on either the Word Attack or Word Identification test were categorized as nonresponders. Both the “final benchmark” and “normalization” approaches are forms of low achievement cutoff, differing only on the criteria they use to set the cut point between normal learners and learning disabled students.

Finally, the “dual discrepancy” (L. S. Fuchs & Fuchs, 1998; Speece & Case, 2001) model combines both measurement of student growth as well as a onetime assessment. The procedure begins by testing all children in the classroom at multiple time points over several weeks or months. Children who are one standard deviation or more below the classroom average on both slope and their last score on the assessment are considered for additional educational services and may be considered learning disabled.

Thus, there are a variety of RTI models used to categorize children in terms of reading disability. It is important to understand the extent to which the alternative operational definitions of nonresponders identify the same or different students. If the same students are identified by the alternative definitions of nonresponders, then it may not matter which particular definition is used; the different models may provide essentially the same answer. Alternatively, if there is relatively little overlap in students identified by the alternative definitions, then it would seem critical to carry out studies designed to directly compare the reliability and validity of the different classification models to identify a common, agreed-on definition. In addition to comparing the different RTI models to one another, it is also important to compare RTI-based definitions to the traditional IQ–achievement discrepancy model to assess whether these two approaches identify the same or different students. If the traditional and RTI-based definitions identify the same students, use of one versus the other may lead to similar conclusions. However, if the traditional and RTI-based definitions identify different students, determining which definition is preferred is essential.

Although several methods of implementing the RTI model have been proposed, little research has compared the various methods. D. Fuchs et al. (2004) compared a variety of alternative definitions of RTI in samples of first and second grade students. At-risk students were identified on the basis of screening measures given at the beginning of the year. The intervention used in measuring RTI was Peer-Assisted Learning Strategies (D. Fuchs, Fuchs, Mathes, & Simmons, 1997). They reported that the alternative RTI-based predictors generated largely different groups of poor readers. Barth et al. (2008) compared the performance of three alternative RTI-based methods of assessing RTI (slope, final status, and dual discrepancy) across both different cut points (scoring 0.5, 1.0, and 1.5 standard deviations below the mean of typically achieving students) and two measures (Test of Word Reading Efficiency—Torgesen, Wagner, & Rashotte, 1999; Continuous Monitoring of Early Reading Skills—Mathes, Torgesen, & Herron, in press). The sample consisted of 399 first-grade students. Agreement was measured using kappa, and the results were that agreement among the 808 possible combinations of methods, cut points, and measures was poor. Only 15% of the kappas calculated reached the minimal level of agreement of .40, and much of the agreement detected by the kappas was agreement that individuals were not poor readers as opposed to agreement that individuals were poor readers. It is important to follow up these studies for three reasons. First, given the importance of the issue of approaches to identifying nonresponders, studies with larger samples are essential. Sample sizes of the existing studies were modest, especially because the numbers of nonresponders are less than the total sample sizes. Second, neither of the studies just reviewed addressed the longitudinal stability of the classification decisions. Approaches that lead to more stable classification decisions should be preferred over ones that yield less stable ones. Third, the statistics that were used to quantify agreement appear to overestimate agreement that individuals are nonresponders.

Prior to examining agreement and longitudinal stability among alternative definitions in the present study, we briefly review the statistics used that are routinely used to quantify agreement and introduce a new statistic that measures agreement that individuals have a disorder such as reading disability.

Quantifying Agreement Between Two Methods of Classification

To what extent do two methods agree on whether an individual has a reading disability? Answering this question is not straightforward. Consider the hypothetical situation presented in Table 1. This is a two-by-two table that describes agreement between two methods of classifying 100 individuals as either having reading disability or being adequate readers. The methods agree that 6 individuals have reading disability (cell a) and 88 are adequate readers (cell d). The methods disagree about the remaining 6 individuals, 2 of whom are considered to have reading disability by Method B but not by Method A (cell b) and 4 of whom are considered to have reading disability by Method A but not by Method B (cell c). What is the best way to describe the degree to which the two methods agree about whether individuals have reading disability?

Table 1.

Hypothetical Comparison Between Two Methods of Classification

	Method A
Method B	Reading Disability	Adequate Reader	Total
Reading disability	(a) 6	(b) 2	8
Adequate reader	(c) 4	(d) 88	92
Total	10	90	100

Overall Agreement

The simplest measure of agreement is overall proportion of agreement. Methods A and B agree on 94 (cell a plus cell d) out of the 100 cases, for an overall proportion of agreement of .94. Unfortunately, overall proportion of agreement is inflated by chance. For disorders with low base rates such as reading disability, the inflation by chance is substantial.

Cohen’s Kappa

Cohen’s kappa is proportion of agreement corrected for chance. Kappa describes the proportion of agreement that exceeds agreement that would occur by chance and thus is preferred over the previously mentioned overall agreement. The formula for kappa is

$$\mathrm{\kappa }=\frac{\text{Pr}(a)-\text{Pr}(e)}{1-\text{Pr}(e)}.$$

In the formula, κ represents kappa, Pr(a) represents the actual proportion of agreement, and Pr(e) represents the proportion of agreement expected on the basis of chance. For the data in Table 1, we already determined that the overall proportion of agreement—Pr(a)—was .94. Agreement expected on the basis of chance is calculated by multiplying base rates as follows. For Method A, the base rate for reading disability is 10 out of 100 or .10, and adequate reader was diagnosed 90 out of 100 times or .90. For Method B, reading disability was diagnosed 8 out of 100 times or .08, and adequate reader was diagnosed 92 out of 100 times or .92. The probability that both methods would have diagnosed reading disability because of chance is .10 times .08 or .008. The probability that both methods would have diagnosed adequate reader because of chance is .90 times .92 or .828. The overall proportion of agreement expected on the basis of chance is the sum of these two probabilities: .008 + .828 = .836. Putting the values of .94 and .836 in the kappa formula above gives

$$\mathrm{\kappa }=\frac{\text{Pr}(a)-\text{Pr}(e)}{1-\text{Pr}(e)}=\frac{.94-.836}{1-.836}=\frac{.104}{.164}=.634.$$

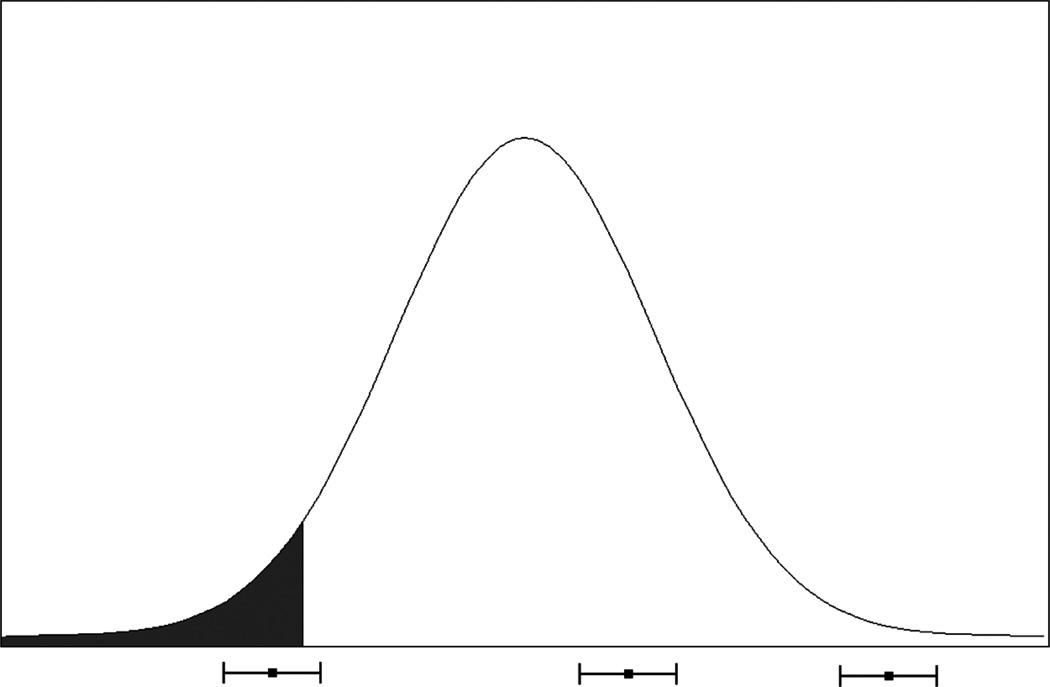
Although kappa corrects overall proportion of agreement for chance, it has an important limitation. Kappa overestimates the level of agreement between methods that individuals have reading disability. Kappa averages agreement above chance that individuals have reading disability and agreement above chance that individuals are adequate readers. Under normal conditions, agreement that individuals do not have developmental dyslexia is higher than is agreement that they do (Barth et al., 2008). The reason for this can be understood by referring to Figure 1, which shows a distribution of scores and a cut point used to categorize individuals as having a reading disability. Scores for three individuals are represented on the x-axis. Measurement error is represented in the figure by error bars around the true scores of the three individuals. For the individual whose true score is near the cut point, measurement error can cause the individual’s observed score to be below the cut point on one assessment and above the cut point on a second assessment. As can be seen in Figure 1, for categories such as reading disability with relatively low base rates, most of the individuals with reading disability necessarily will score near the cut point. In contrast, adequate readers can be far from the cut point. The result is that measurement error is less likely to cause fluctuation in categorization for adequate readers compared to individuals with reading disability. Because kappa averages agreement about both having reading disability and being an adequate reader, it is an overestimate of agreement that an individual has reading disability and an underestimate of agreement that an individual is an adequate reader. This holds for any disorder that has a base rate less than 50% of the population.

Figure 1.

The effects of measurement error on scores near a cut point

Affected-Status Agreement Statistic

To measure agreement between methods that individuals are affected by a target condition such as reading disability in a way that is not inflated by agreement that individuals are not affected, we developed the affected-status agreement statistic. Affected-status agreement is the proportion of students classified as having reading disability by both definitions being compared out of the group of students classified as reading disabled by either definition. For example, suppose that 100 students were identified as having reading disability by either the low achievement or low growth definitions and that 50 of these 100 students were identified by both definitions. The affected-status agreement would then be 50 divided by 100, or .50. Referring back to Table 1, affected-status agreement would be calculated by dividing cell a by the sum of cells a, b, and c. For the present example, the affected-status agreement would be 6 divided by the sum of 6 + 2 + 4, or .50. It is interesting to compare the kappa value of .634 to the affected-status agreement statistic of .50. The difference in these two values represents the inflation of kappa by accuracy for classifying adequate readers. Note that there are situations for which there is as much interest in accuracy for classifying adequate readers as there is in accuracy for classifying individuals with reading disability. For these circumstances, kappa is a useful statistic. However, when the question is how well two methods agree on whether an individual has reading disability, the affected-status agreement statistic is preferred.

The affected-status agreement statistic is a proportion with a known standard error and confidence interval. The formula for the standard error of affected-status agreement is

$$\mathit{\text{SE}}=\sqrt{\frac{A_{\mathit{\text{SA}}}(1-A_{\mathit{\text{SA}}})}{N}}.$$

For this formula, SE is the standard error, A_SA is the affected-status agreement statistic, and N is the N for the three cells that make up the affected-status agreement statistic. For the example in Table 1,

$$\mathit{\text{SE}}=\sqrt{\frac{A_{\mathit{\text{SA}}}(1-A_{\mathit{\text{SA}}})}{N}=}\sqrt{\frac{.5(1-.5)}{12}=}.14.$$

To calculate the 95% confidence interval, 1.96 times the standard error is added to and subtracted from the obtained affected-status agreement statistic. For the present example, the 95% confidence interval corresponds to .50 plus or minus .14(1.96). This equals .50 plus or minus .27, or from .23 to .77. The confidence interval can be used to answer two questions about the value of the affected-status agreement statistic. The first question—whether the level of agreement is significantly greater than 0—is answered by determining whether the confidence interval contains 0. Because it does not in our case, we can conclude that the affected agreement statistic value of .50 is significantly greater than 0 at the .05 level of confidence. The second question—whether the level of agreement is significantly less than perfect—is answered by determining whether the confidence interval contains 1. Because it does not in our case, we can conclude that the affected agreement statistic value of .50 is significantly less than its maximum possible value of 1 at the .05 level of confidence.

Chance-Corrected Affected-Status Agreement Statistic

Like sensitivity and positive predictive value, the affected-status agreement statistic does not correct for chance agreement. However, a chance-corrected affected-status agreement statistic is available. To find the chance-corrected affected-status agreement, the first step is to find agreement expected because of chance. For the data presented in Table 1, finding the agreement expected because of chance for each cell requires multiplying their corresponding base rates. These calculations are presented in Table 2. Because the affected-status agreement statistic is calculated by dividing cell a by the sum of cells a, b, and c, the following formula is used to calculate how much of affected-status agreement would be because of chance:

$$A_{\mathit{\text{SA}}}(e)=\frac{.008}{.008+.092+.072}=.047.$$

Table 2.

Calculating Agreement Expected Because of Chance

	Method A
Method B	Developmental Dyslexia	Adequate Reading	Proportions
Developmental dyslexia	(a) .10(.08) = .008	(b) .90(.08) = .072	.08
Adequate reading	(c) .10(.92) = .092	(d) .90(.92) = .828	.92
Proportions	.10	.90	1.00

To calculate chance-corrected affected-status agreement, the obtained values are substituted into the following equation:

$$\mathit{\text{Corr}}{A}_{\mathit{\text{SA}}}=\frac{A_{\mathit{\text{SA}}}(a)-A_{\mathit{\text{SA}}}(e)}{1-A_{\mathit{\text{SA}}}(e)}=\frac{.5-.047}{1-.047}=\frac{.453}{.953}=.48.$$

Note how little a difference there is between the value of affected-status agreement (.5) and chance-corrected affected-status agreement (.48). Recall that when kappa was used to correct overall agreement for agreement because of chance, the difference was considerable. For the present example, overall agreement was .94 and kappa was .634. This represents a drop in agreement of 33%. Most of the drop is attributable to chance agreement that individuals are adequate readers (cell d). Because agreement that individuals are adequate readers does not figure in the affected-status agreement statistic, the difference between the original and chance-corrected versions of the affected-status agreement statistic is minimal.

The goal of the present study was to carry out a large-scale comparison of four definitions of reading disability using the affected-status agreement statistic. One definition was a traditional unexpected low achievement definition that relied on discrepancy between measures of ability and achievement. The remaining three definitions were based on an RTI approach: low achieving (similar to final benchmark and normalization), low growth (similar to median split and slope discrepancy), and dual discrepancy. In addition, we investigated the longitudinal stability of each classification definition over 1- and 2-year periods. Finally, we investigated agreement and stability at different levels of reading problem severity to assess whether the alternative definitions would converge on the same students as the reading problem became more severe.

Method

Data Collection

Data were collected on first-through third-grade children from districts throughout the state of Florida who were attending Reading First schools. Reading First is the largest federal initiative in the history of the United States designed to improve the reading performance of poor readers. All participating schools had to select from among five basal reading series that met criteria for effective instructional practice. Professional development and reading coaches were made available to teachers to support effective instruction, including use of progress monitoring measures to inform instruction and for grouping students on the basis of similar instructional needs.

The data used in this study were obtained using Florida’s Progress Monitoring and Reporting Network (PMRN) maintained by the Florida Center for Reading Research. The PMRN is a centralized data collection and reporting system through which Reading First schools in Florida report reading data and receive reports of the data for instructional decision making. Trained assessors (not the classroom teachers) collected the progress monitoring data and entered the data into the PMRN’s web-based data entry facility. These assessors were trained by a statewide network of master trainers who were themselves trained by professionals at the Florida Center for Reading Research. The training was provided to assessors using a train-the-trainer approach, and the training included a fidelity of implementation check prior to collection of data. In addition, school districts were required to retest a small percentage of students within each grade to allow evaluation of intertester reliabilities. If the test–retest reliabilities fell outside expected bounds, the district was asked to determine the reason for it and to retrain the assessors at the school involved.

Participants

The sample consisted of 288,114 students from across the state who were in first, second, or third grade in the fall of 2003, 2004, or 2005 and had received at least one of our target measures at least once during the school year. Because of the longitudinal nature of our sample, many of the students assessed in first grade were also assessed in second and third grades. This fact allowed for the evaluation of the stability of reading disorder classification over time. The number of students with available data at each grade level is presented below when discussing the various methods of categorization. Maximum likelihood was used to handle missing data (Raudenbush & Bryk, 2002). Of the participants, 48% were female and 76.5% were eligible for free or reduced-price lunch, and the ethnic breakdown was as follows: 32.0% White, 36.2% Black, 25.1% Hispanic, 3.7% mixed race, 1.3% Asian, and 0.3% Native American (percentages do not add up to 100.0% because of missing data).

Measures

The reading measures included a measure of fluency for reading connected text and a measure of fluency for decoding nonsense words.

Dynamic Indicators of Basic Early Literacy Skills (DIBELS) Oral Reading Fluency (5th ed.; ORF)

This measure (Good, Kaminski, Smith, Laimon, & Dill, 2001) assesses oral reading fluency for reading grade-level connected text. This test is individually administered and assesses the number of words read accurately in 1 minute. The ORF was administered four times, during the months of September, December, February, and April, during first, second, and third grades. Performance was measured at each time point by having students read three passages aloud for 1 minute each, with the cue to “be sure to do your best reading.” Words omitted and substituted and hesitations of more than 3 seconds were scored as errors. Words self-corrected within 3 seconds were scored as accurate. The assessor noted errors, and the number of correct words read per minute was used as the score. The median of the scores from the three test passages was used as the final data point for each assessment period. The median alternate-form reliability for oral reading of passages is .94 (Good, Kaminski, Smith, & Bratten, 2001). Test–retest reliability for the ORF was calculated for a subset of students from the PMRN and was .96 (Catts, Petscher, Schatschneider, Bridges, & Mendoza, 2009).

DIBELS Nonsense Word Fluency (NWF)

This individually administered measure requires the child to read vowel–consonant and consonant–vowel–consonant single-syllable pseudowords. All pseudowords had short vowel sounds. The NWF was also administered four times, during the months of September, December, February, and April, during first and second grades. After a practice trial, the examiner instructs the child to read the “make-believe” words as quickly and accurately as possible. If the child does not respond within 3 seconds, the examiner prompts with “next?” The stimuli are presented in 12 rows of five words each. Alternate-forms reliability has been reported to range from .83 to .94, and predictive and concurrent criterion-related validity coefficients with reading have been reported in the range from r = .36 to r = .91 (Speece, Mills, Ritchey, & Hillman, 2003). A subset of students from the PMRN were found to have test–retest reliability of .86 (Catts et al., 2009). The scoring guidelines gave credit for correctly producing individual phonemes or for producing the pseudoword as a blended unit. Thus, if the nonsense word was “vab,” 3 points were awarded if the child said /v/ /a/ /b/ or “vab.”

Peabody Picture Vocabulary Test (3rd ed.; PPVT)

This measure (Dunn & Dunn, 1997) assesses receptive vocabulary and listening comprehension. The test is individually administered and requires the student to point to the picture that best matches the word spoken by the assessor. Each item consists of four pictures as response options on the page, and items are presented in ascending difficulty. The PPVT was administered once a year during the month of February during first, second, and third grades. Median split-half reliabilities of the PPVT are .94 for both forms of the test. The median test–retest reliability is .93, and the median alternate-forms reliability ranges from .88 to .96. Furthermore, the PPVT is highly correlated with measures of IQ, and it has a correlation of .96 with the Verbal IQ score from the third edition of the Wechsler Intelligence Scales for Children (Dunn & Dunn, 1997; see Note 1).

Procedures

Scores on the ORF and NWF measures were used to classify children as reading disabled using the four definitions, each applied at six levels of severity of the reading problem: 25th percentile, 20th percentile, 15th percentile, 10th percentile, 5th percentile, and 3rd percentile. These six levels of severity were chosen because there is not currently a consensus as to where the cut off for classifying students as learning disabled should be set. For example, the “normalization” method (Torgesen et al., 2001) suggests identifying students with a standard score below 90, which is at the 25th percentile. Other methods, such as “dual discrepancy” (L. S. Fuchs & Fuchs, 1998; Speece & Case, 2001), suggest a cutoff of 1 standard deviation below the mean, which corresponds to about the 16th percentile. Still others may suggest cutoffs at 1.5 or 2 standard deviations below the mean. Rather than select only one of these cut points, a range of points was compared to provide a more thorough examination of agreement rates among various methods.

Unexpected low achievement (ULA)

This definition was included to represent the traditional discrepancy method of diagnosing learning disabilities. The PPVT was used as a proxy for IQ with the ORF and NWF scores used as achievement measures. Regression analyses were completed with end-of-year ORF or NWF scores as the dependent variable and PPVT scores as the predictor. Students who did not have both PPVT and end-of-year ORF or NWF scores were excluded from the analysis. Residuals were obtained, and the distribution of residuals was used to identify students who met the ULA definition. Students were then compared based on their residual scores, and those who were below the specified percentile levels were considered reading disabled. There were 123,556 students with available first-grade PPVT and ORF scores, and 123,555 students had first-grade PPVT and NWF scores. In second grade, 119,503 students were classified based on PPVT and ORF scores, and 119,499 students had been administered the PPVT and NWF. For third grade, 123,554 students had scores on both the PPVT and ORF.

Low achievement (LA)

Similar to the final benchmark and normalization implementations of RTI, this definition classified children based on their score at one time point, namely, the end of the school year. Children were considered reading disabled if they fell below the specified percentile on the reading fluency measure. Those who did not have end-of-year ORF or NWF scores were excluded from the analysis. For both the ORF and NWF, there were 124,850 students with first grade scores. In second grade, 120,657 students completed the ORF and 120,656 students completed the NWF. Third grade ORF scores were available for 125,154 students.

Low growth (LG)

The LG definition was based on the child’s slope of reading fluency gains over the year, similar to the slope-discrepancy and median split RTI methods. Growth curve modeling was used to estimate each student’s slope, and students were classified as learning disabled if their slope fell below the specified percentiles. The benefit of growth curve modeling is that students who did not have complete data at all four time points during the school year could still be included in the analysis and the growth curve would be created based on the available data. Students who had no ORF or NWF scores for a given school year were excluded. For both the ORF and NWF, 136,280 students had available first-grade data and 131,231 students had second-grade data. Third-grade ORF scores were available for 136,423.

Dual discrepancy (DD)

The DD definition combined the student’s slope of growth over the year with the end-of-year score on reading fluency. This method utilized the growth curve estimates of both slope and end-of-year intercept; therefore, the only children excluded were those who had no ORF or NWF scores during the school year. Although this approach is typically implemented by setting a cut point on both slope and end-of-year score, we chose to modify that approach to make it more comparable to our other classification models. To allow for comparisons of students identified by the four models, it is necessary to classify approximately the same number of children at each percentile. Therefore, the slope and end-of-year intercept estimates were converted to z scores and summed to create a DD score that equally weighted slope and end-of-year intercept. Children were then classified based on the percentile cutoffs as they corresponded to these DD scores, yielding approximately the same number of students at each cutoff as in the other three methods. The number of students with available data for this method was the same as for the LG method.

Students were classified as reading disabled or not based on these four definitions, with the classifications being made separately for each grade and reading fluency measure. Therefore, children were categorized based on their ORF from Grade 1, ORF from Grade 2, ORF from Grade 3, NWF from Grade 1, and NWF from Grade 2.

We compared agreement among all possible pairs of alternative definitions using the affected-status agreement statistic. We examined the longitudinal stability of the four alternative definitions in a similar manner. For each definition, stability was defined using the affected-status agreement statistic by dividing the number of students classified as reading disabled at both time points by the total number of students classified as reading disabled at either time point. If, for example, 1,600 students were classified as reading disabled using the LG definition in either first or second grade, and if 1,200 of these 1,600 students were identified as reading disabled by the LG definition in both grades, the value of the affected-status agreement statistic over time would be 1,200 divided by 1,600, or .75.

Results and Discussion

Agreement Among the Models

Table 3 presents the affected-status agreement values among alternative definitions for NWF in first and second grades and ORF in first through third grades. Agreement between the traditional unexpected LA and the three RTI-based definitions of LG, LA, and DD was poor, though at greater than chance levels of agreement. Using our metric for determining rates of agreement, the chance rates of agreement for two different definitions to agree on a reading disability diagnosis at the 25th, 20th, 15th, 10th, 5th, and 3rd percentiles are 14.0%, 11.0%, 7.0%, 5.0%, 3.0%, and 1.7%, respectively. For example, at the 3rd percentile, the median affected-status agreement values between ULA definition and the three RTI-based definitions were 25%, 23%, and 25% for the LA, LG, and DD definitions, respectively. With decreasing severity of the reading problem, agreement increased, with observed agreement rates at the 25th percentile that were roughly double in magnitude of those at the 3rd percentile. The results did not support the idea that the alternative definitions would converge on the same group of poor readers as severity of the reading problem increased.

Table 3.

Agreement Rates for Classifying Students as Reading Disabled Using Four Alternative Definitions at Six Levels of Severity

Comparison	3rd Percentile	5th Percentile	10th Percentile	15th Percentile	20th Percentile	25th Percentile
ULA vs. LA
NWF Grade 1	31	37	44	51	56	61
NWF Grade 2	23	30	41	50	58	63
ORF Grade 1	9	13	26	37	46	54
ORF Grade 2	25	36	50	57	62	64
ORF Grade 3	37	45	54	57	59	61
ULA vs. LG
NWF Grade 1	29	33	41	46	51	56
NWF Grade 2	21	28	37	46	53	59
ORF Grade 1	9	14	25	36	45	53
ORF Grade 2	23	31	42	47	50	51
ORF Grade 3	31	36	39	41	42	44
ULA vs. DD
NWF Grade 1	28	32	40	46	51	56
NWF Grade 2	21	28	38	46	54	60
ORF Grade 1	8	13	26	37	46	53
ORF Grade 2	25	35	49	55	60	61
ORF Grade 3	38	45	52	54	55	56
LA vs. LG
NWF Grade 1	71	66	66	67	69	72
NWF Grade 2	51	55	60	66	71	74
ORF Grade 1	49	54	65	73	77	81
ORF Grade 2	48	55	58	61	61	60
ORF Grade 3	54	53	50	48	48	49
LA vs. DD
NWF Grade 1	76	73	73	74	75	78
NWF Grade 2	69	69	71	75	78	81
ORF Grade 1	74	76	80	84	86	88
ORF Grade 2	75	78	80	83	83	82
ORF Grade 3	81	81	79	76	74	74
LG vs. DD
NWF Grade 1	75	71	73	74	76	79
NWF Grade 2	59	62	69	73	77	81
ORF Grade 1	64	68	79	84	86	89
ORF Grade 2	63	69	71	71	70	70
ORF Grade 3	63	62	59	60	61	63

Note: ULA = unexpected low achievement; LA = low achievement; LG = low growth; DD = dual discrepancy; ORF = Oral Reading Fluency; NWF = Nonsense Word Fluency.

There are two possible reasons why agreement might increase with decreasing severity of the reading problem. The first is that an increased base rate associated with decreasing severity would increase chance agreement. For example, two completely independent characteristics with base rates of 70% will yield a chance agreement near 50%. However, because the least severe level of reading was at the 25 percentile and the affected-status agreement statistic is not affected by chance agreement that individuals are not affected, chance agreement cannot explain the doubling of agreement rates with decreasing severity of the reading problem. Most of the increase in agreement is expected because of a related phenomenon. Cases with a true score close to the cutoff score can change categories on repeated measurement because of measurement error (Francis et al., 2005). On one occasion, the observed score can be below the cutoff score, and on the next occasion it can be above the cutoff score. With very low cutoff scores associated with more severe reading problems, affected cases will have scores that are relatively closer to the cutoff score because of the proximity of the cutoff score to the lowest possible score. When the cutoff score is increased with decreasing severity of the reading problem, the scores of affected cases can be farther from the cutoff score and therefore be less likely to be on the other side of the cutoff score because of measurement error.

Turning to the three RTI-based definitions, the median affected-status agreement rate between the LA and LG definitions was 51% at the 3rd percentile level of severity, increasing to 72% at the 25th percentile. This level of affected-status agreement was considerably higher than that between the traditional ULA and the RTI-based definitions, although relatively low nonetheless. Higher levels of affected-status agreement were found between the DD definition and the LA and LG definitions. The median affected-status agreement rate between the DD and LA definitions was 75% at the 3rd percentile, increasing to 81% at the 25th percentile. Median affected-status agreement between the DD and LG definitions was 63% at the 3rd percentile, increasing to 79% at the 25th percentile. The higher agreement rates between the DD and both LA and LG definitions compared to that between LA and LG probably reflects the part–whole relations between the DD and both LA and LG definitions. Being identified with the DD definition necessarily required meeting the LA and LG definitions.

In general, rates of affected-status agreement were similar across grade levels and reading measures with one exception. For the ULA definition, affected-status agreement rates for oral reading fluency increased with increasing grade level for the two lowest percentiles of reading. Looking at the first two columns of Table 3, the affected-status agreement rates between ULA and the three RTI-based definitions are rank ordered by grade. This may represent a floor effect in oral reading fluency at lower levels of performance.

Longitudinal Stability

Turning to longitudinal stability of the alternative definitions, affected-status agreements within definitions across years are presented in Table 4. It was possible to examine longitudinal stability of definitions using NWF from first to second grades and longitudinal stability of definitions based on ORF from first to second, first to third, and second to third grades.

Table 4.

Agreement Rates Over Time for Classifying Students as Reading Disabled Using the Four Alternative Definitions

Comparison	3rd Percentile	5th Percentile	10th Percentile	15th Percentile	20th Percentile	25th Percentile
ULA
NWF Grades 1 to 2	14	17	22	27	31	35
ORF Grades 1 to 2	18	22	30	37	43	48
ORF Grades 1 to 3	14	18	27	33	37	40
ORF Grades 2 to 3	35	39	44	47	50	53
LA
NWF Grades 1 to 2	26	25	25	29	33	37
ORF Grades 1 to 2	39	41	45	48	50	53
ORF Grades 1 to 3	38	41	39	39	39	43
ORF Grades 2 to 3	54	56	55	55	56	58
LG
NWF Grades 1 to 2	14	14	18	22	26	30
ORF Grades 1 to 2	16	22	28	30	33	34
ORF Grades 1 to 3	17	20	20	21	22	24
ORF Grades 2 to 3	22	26	25	26	27	29
DD
NWF Grades 1 to 2	24	24	27	30	33	37
ORF Grades 1 to 2	28	32	37	42	45	48
ORF Grades 1 to 3	30	35	35	35	35	37
ORF Grades 2 to 3	42	46	47	47	47	47

Note: ULA = unexpected low achievement; LA = low achievement; LG = low growth; DD = dual discrepancy; ORF = Oral Reading Fluency; NWF = Nonsense Word Fluency.

In general, the longitudinal stability was low for all of the definitions. The affected-status agreement rates were largely below 50%, indicating that more than half of the children who are identified as reading disabled by one of these methods in one grade will not be considered reading disabled in another grade. The LG definition in particular showed the worst stability rates, perhaps a consequence of the lower reliability of measures of growth relative to measures of status under typical conditions.

General Discussion

Overall, these results suggest relatively low agreement between traditional ULA and RTI-based definitions of reading disability and only modest agreement among alternative RTI-based definitions.

Two limitations in the design of the present study need to be considered, as they might have implications for interpreting the results. First, our measure of RTI was based on response to general classroom instruction, as opposed to response to an intensive intervention that we provided. Second, our measures of reading were brief progress monitoring tasks. Although they have been shown to have adequate reliability and validity, it is possible the results might have been different had other longer assessments been used. However, our results are in line with those of other studies that did involve intervention and that used longer assessments (Barth et al., 2008; D. Fuchs et al., 2004). In fact, our results yielded 164 out of 276 comparisons with an affected-status agreement rate greater than .40, a rate of about 59%, compared to Barth et al.’s (2008) results of 15% of kappa values greater than .40.

Poor longitudinal stability was found for all of the definitions. Some of this instability can be attributed to using cut scores in relatively continuous distributions. Francis et al. (2005) demonstrated using analyses of both simulation data and an existing longitudinal data set that measurement error can have a substantial effect on reducing longitudinal stability. When calculating agreement rates for Francis et al.’s data using the affected-status agreement statistic, stability rates for both LA and LA plus IQ–achievement discrepancy classifications of learning disabilities were about 44% for their existing longitudinal data and ranged from 14% to 36% for the simulated data.

Another possible source of longitudinal instability is the role of instruction. More specifically, if larger numbers of students are classified as reading disabled at Time 1 than at Time 2, the movement of students out of the reading disabled category may be the result of instruction rather than a lack of stability in the assessment method. However, this was not the case in our study. Because we created our cutoffs based on percentiles relative to the rest of the sample and had similar sample sizes at each time point, approximately the same number of students were classified as reading disabled at each time point.

The fact that different definitions of reading disability result in largely different groups of individuals being classified has implications for both research and practice. Lacking an agreed-on, reliable, and valid definition of reading disability presents a significant obstacle in the path toward understanding the nature, identification, and best treatments for reading disability. One preliminary suggestion based on our results is that future RTI-based definitions should favor decisions based on status (LA) rather than on growth, which was a less reliable measure within our sample. A critical goal for future research is to compare the reliability and validity of classification based on the traditional and alternative RTI-based definitions. Such studies have yet to be done despite the fact that RTI-based identification approaches are already being implemented. Ideally, such research would pave the way toward a consensus revised model for identification of learning disabilities.

A problem for professional practice is that whether a student is determined to have a reading disability may vary depending on which definition is used. A related problem, given the low agreement rates between traditional unexpected achievement and RTI-based definitions, is that schools that are now adopting RTI-based methods of diagnosing learning disabilities must be prepared for an influx of students newly diagnosed as learning disabled by RTI-based definitions who were not identified using the traditional definition. In addition, schools will have to determine how to handle students who were previously considered learning disabled based on the traditional definition but do not meet the RTI standard for being classified as learning disabled. These results suggest that the number of students in each of these two categories will be substantial.

Biographies

Jessica S. Brown Waesche, Ph.D., is an Assistant in Research at the Florida Center for Reading Research. Her current interests include learning disabilities and quantitative methods.

Chris Schatschneider, Ph.D., is a Professor of Psychology at Florida State University and is an Associate Director of the Florida Center for Reading Research. His current interests include early reading development, methodology, and statistics.

Jon K. Maner, Ph.D., is an Associate Professor of Psychology at Florida State University. His current interests involve social cognition, evolutionary psychology, and quantitative methods.

Yusra Ahmed is a graduate student in the Developmental Psychology program at Florida State University. Her current interests include learning disabilities and the developmental relationship between reading and writing skills.

Richard Wagner, Ph.D., is the Robert O. Lawton Distinguished Research Professor of Psychology at Florida State University. He holds the W. Russell and Eugenia Morcom Chair, and is Associate Director of the Florida Center for Reading Research. His current interests include reading and writing-related learning disabilities.