Numeracy Skills in Patients With Degenerative Disorders and Focal Brain Lesions

Abstract

Objective: To characterize the numerical profile of patients with acquired brain disorders. Method: We investigated numeracy skills in 76 participants—40 healthy controls and 36 patients with neurodegenerative disorders (Alzheimer dementia, frontotemporal dementia, semantic dementia, progressive aphasia) and with focal brain lesions affecting parietal, frontal, and temporal areas as in herpes simplex encephalitis (HSE). All patients were tested with the same comprehensive battery of paper-and-pencil and computerized tasks assessing numerical abilities and calculation. Degenerative and HSE patients also performed nonnumerical semantic tasks. Results: Our results, based on nonparametric group statistics as well as on the analysis of individual patients, and all highly significant, show that: (a) all patients, including those with parietal lesions—a key brain area for numeracy processing—had intact processing of number quantity; (b) patients with impaired semantic knowledge had much better preserved numerical knowledge; and (c) most patients showed impaired calculation skills, with the exception of most semantic dementia and HSE patients. Conclusion: Our results allow us, for the first time, to characterize the numeracy skills in patients with a variety of neurological conditions and to suggest that the pattern of numerical performance can vary considerably across different neurological populations. Moreover, the selective sparing of calculation skills in most semantic dementia and HSE suggest that numerical abilities are an independent component of the semantic system. Finally, our data suggest that, besides the parietal areas, other brain regions might be critical to the understanding and processing of numerical concepts.

Neuropsychological studies of patients with brain lesions offer an insight into the organization and the neural basis of cognitive processes. To date, no studies have provided an overview on numeracy skills in different neurological populations. To outline the patterns of spared and impaired numeracy abilities, we investigated numeracy skills in 36 patients with a variety of neurodegenerative pathologies and with focal brain lesions. Moreover, to clarify the relation between numerical and arithmetical conceptual knowledge, considered part of semantic memory, and other types of nonnumerical knowledge, we also administered patients a set of semantic tasks.

Numeracy Skills in Patients With Degenerative Brain Disorders

Although an increasing number of studies have explored numerical abilities in patients with Alzheimer's disease (e.g., Girelli, Luzzatti, Annoni, & Vecchi, 1999; Mantovan, Delazer, Ermani, & Denes, 1999; Noel & Seron, 1993, 1995; see Girelli & Delazer, 2001 for a review), far fewer have done so in patients with semantic dementia (e.g., Cappelletti, Butterworth, & Kopelman, 2001, 2006; Crutch & Warrington, 2002; Diesfelt, 1992; Julien, Thompson, Neary, & Snowden, 2008; Julien, Neary, & Snowden, 2010). Moreover, to date, there are no studies on patients with progressive aphasia and there are only very few investigating numerical processing in patients with the frontal variant of frontotemporal dementia, which focused primarily on arithmetical skills and on dot counting (e.g., Halpern et al., 2004; Crutch & Warrington, 2002). The existing literature on numeracy skills in these populations is briefly reviewed here.

The results of group studies exploring numeracy skills in patients with Alzheimer's disease (AD) are mixed, reporting either calculation impairments at the early stages of the illness (e.g., Cano et al., 1998; Carlomagno et al., 1999; Deloche et al., 1995; Grafman, Kempen, Rosenberg, Salazar, & Boller, 1989; Kaufmann & Delazer, 1998; Pesenti, Seron, & van der Linden, 1994), or selectively preserved calculation abilities (e.g., Diesfeldt, 1993; Girelli et al., 1999; Mantovan et al., 1999; Remond-Besuchet et al., 1999). A few single-case studies on AD focused on subjects' transcoding skills, that is, reading, writing, and the transformation of numbers from alphabetic or Arabic formats. These studies reported intrusion errors that AD patients often make when writing number words or Arabic numbers, for instance “43” → “forty3” instead of 43 (Della Sala, Gentileschi, Gray, & Spinnler, 2000; Kessler & Kalbe, 1996; Noel & Seron, 1993, 1995; Tegnér & Nyback, 1990; Thioux et al., 1998). These errors have been explained in terms of a transcoding-specific impairment, together with a more general impairment of inhibitory processes (Macoir, Audet, Lecomte, & Delisle, 2002; Thioux et al., 1998).

With reference to one of the most established theoretical models of numerical cognition, the Triple Code Model (Dehaene & Cohen, 1995), it seems that the existing studies of AD patients have focused mainly on the verbal and the Arabic representational codes outlined in the model. The verbal code is used to manipulate number words (as in transcoding) and to perform arithmetical operations (e.g., multiplications), whereas the Arabic code is used to manipulate Arabic numbers again in transcoding and multidigit calculation. However, a critical aspect missing from existing studies on AD patients is whether the third and most important component of the Triple Code Model, that is, the analog magnitude code, is preserved in these patients.

Until very recently, information on the ability to manipulate magnitude was also missing from patients with semantic dementia. The very few studies investigating numeracy skills in semantic dementia patients reported that: (a) preserved numerical knowledge typically dissociates from impaired nonnumerical knowledge (e.g., Cappelletti et al., 2001; Cappelletti, Butterworth, & Kopelman, 2006; Crutch & Warrington, 2002; Diesfeldt, 1993; Jefferies, Patterson, Jones, Bateman, & Lambon-Ralph, 2004; Jefferies, Bateman, Lambon-Ralph, 2005; Julien et al., 2008, 2010; Zamarian, Karner, Benke, Donnemiller, & Delzer, 2006), and that (b) numeracy skills continued to be better preserved in the context of severely deteriorated semantic knowledge (Cappelletti, Morton, Kopelman, & Butterworth, 2005).

Numeracy Skills in Patients With Focal Brain Lesions

Many studies have investigated numeracy skills in patients with focal lesions (for a review, see Cappelletti & Cipolotti, 2010), which have mainly reported difficulties in performing arithmetical operations (e.g., Fasotti, Eling, & Bremer, 1992; Fasotti, Eling, & van Houtem, 1994; Lucchelli & De Renzi, 1993) or in transcoding (e.g., Basso, Burgio, & Caporali, 2000). For instance, studies in patients with frontal lesions explored their calculation skills given that frontal lobes are thought to be primarily involved in planning and monitoring arithmetical operations rather than in manipulating numerical quantity (e.g., Dehaene & Cohen, 1995; Dehaene, Piazza, Pinel, & Cohen, 2003; Lucchelli & De Renzi, 1993, but see Revkin et al., 2008). However, little is known about other numerical abilities besides calculation.

To our knowledge, there are no studies exploring numerical processing in patients with herpes simplex encephalitis (HSE). These patients often show impaired semantic knowledge (e.g., Kopelman, 2000; Lambon Ralph, Lowe, & Rogers, 2007; Mazzoni, Pollera Orsucci, & Giraldi, 1996; Sartori & Lombardi, 2004), but it is not known whether this semantic impairment extends to numerical knowledge as well. Establishing whether numerical and nonnumerical knowledge may dissociate in HSE is important to evaluate the extent to which these types of knowledge are independent or related aspects of semantic understanding.

Patients with parietal lesions are the most interesting to investigate in terms of their numerical skills, given the evidence suggesting the involvement of the parietal areas in numerical processing (e.g., Cappelletti, Lee, Freeman, & Price, 2010; Dehaene et al., 2003, for a review). Perhaps the most striking case of number deficit has been reported in a patient with left parietal lesion who was selectively impaired in all number tasks except when numbers 1 to 4 were involved (Cipolotti, Butterworth, & Denes, 1991). Although not so severe, other cases of impaired number skills following left parietal lesions have been reported (Ashkenazi, Henik, Ifergane, & Shelef, 2008; Dehaene & Cohen, 1997; Lemer, Dehaene, Spelke, & Cohen, 2003; Rosselli & Ardilla, 1989; Polk, Reed, Keenan, Hogarth, & Anderson, 2001; Warrington, 1984; Wood et al., 2006); however, not all parietal lesions result in numerical impairments (Cappelletti & Cipolotti, 2010), leaving open the question whether and to what extent the parietal lobes are critically involved in processing numbers.

The Present Study

The present study is a prospective investigation that attempts: (a) to characterize the numerical profile of neurological patients with degenerative disorders and focal brain lesions affecting the parietal, temporal, and frontal brain areas; and (b) to examine the relationship between numerical and nonnumerical knowledge within semantic memory in patients with degenerative disorders and in those with HSE. Unfortunately, the quality of our patients' brain images, which were collected primarily for clinical purposes and using different scanners, did not allow us to apply modern-style neuroimaging analyses. In the absence of more detailed information, the patients' brain lesions were therefore classified according to relatively general anatomical criteria. Nevertheless, the main purpose and the novelty of our study was to characterize the numeracy profile in different clinical populations.

Because of the fundamental differences in the etiology of degenerative and focal lesion patients, we predicted that numeracy skills in these patients may differ. Specifically, we hypothesized that numeracy skills in patients with focal lesion may be more preserved than in degenerative patients. This is because degenerative disorders imply the deterioration of a wider network of connections relative to a static lesion, and this may have implications for patients' cognitive skills. Therefore, performance in patients with degenerative and focal lesions was analyzed independently. We also hypothesized that patients with both degenerative and focal lesions may be more impaired in arithmetic tasks relative to tasks assessing quantity processing such as number comparison. This is because number comparison relies on the core knowledge of quantity, whereas arithmetic requires additional skills such as memory of simple facts and procedures besides working memory and executive functions, which may be more vulnerable to brain lesions. Finally, we hypothesized that numerical and nonnumerical semantic knowledge may be distinct.

Participants

Neurological patients

A total of 16 patients with neurodegenerative conditions were studied: (a) eight with probable AD; (b) three with semantic dementia, SD (temporal variant of frontotemporal dementia); (c) three with the frontal variant of frontotemporal dementia (FTD); and (d) two with progressive nonfluent aphasia (PA). A total of 20 patients with focal brain damage were studied: (a) six subjects with parietal lesions; (b) nine with HSE affecting primarily the left temporal areas; and (c) five with frontal lesions. The 36 patients were recruited from the Neuropsychiatry and Memory Disorders Clinic at St. Thomas Hospital in London, England (Kopelman, 1996), and from the Neurology Department at St. Bortolo Hospital in Vicenza, Italy. See Table 1 for the demographic details of the patients recruited and for the proportion of patients with lesions affecting the left or the right hemisphere.

Table 1. Demographic Data of Control Participants and Patients.

In the case of neurodegenerative disorders, patients were recruited if they: (a) conformed as closely as possible to the clinical features of dementia of Alzheimer type, of semantic dementia, of progressive aphasia, or the frontal variant of frontotemporal dementia (e.g., Snowden, Goulding, & Nearly, 1989); (b) showed magnetic resonance imaging or computer tomography brain scans consistent with the clinical diagnosis; and (c) had been initially diagnosed in the 18–24 months before this study was carried out. In the case of focal brain lesions, patients were recruited according to the location of their lesions shown on their brain scans. Lesion location was established by a consultant neuroradiologist and was corroborated by a medically qualified member of our team. Patients were classified as belonging to a specific subgroup (e.g., parietal) on the basis of the brain area that was mainly affected by the lesion. Focal lesions affected either the left or the right hemisphere (see Table 1). Patients with alcohol-related cognitive impairment, a history of moderate or severe head trauma, or primary psychiatric disorders were excluded from the study. Patients with visual or auditory impairments, which could interfere with performance on cognitive tasks, were also excluded.

Control subjects

Thirty, healthy, right-handed British (16 women) and 10 Italian (four women) were studied as controls. Controls were age- and education-matched to the patients (British: mean age = 60.7 years, SD = 5.1; mean education = 9.9 years, SD = 1.8; Italian: mean age = 68.3 years, SD = 4.2; mean education = 10.3 years, SD = 2.8). Controls performed all the number tasks. A subgroup of these controls (n = 20) also performed the semantic tasks. Because there was no performance difference between English and Italian controls—no Task × Group interaction, F(1, 38) = .022, p < .88, ns—the overall group of controls was compared to patients.

For all participants, consent was obtained according to the Declaration of Helsinki and the study was approved by the local ethics committee.

Statistical Analysis

Considering the nonhomogeneous variance of some of the patients' data and the incidence of ceiling scores in the control group, 6 types of nonparametric analyses were performed.

Analysis 1 used the Kruskal–Wallis test to compare the performance of patients grouped by type, that is, degenerative and focal lesions relative to controls for each of the main number tasks used. Pairwise Mann–Whitney U tests were used to investigate further group differences.

Analysis 2 was based on the Brunner–Munzel test, a nonparametric rank-based test that takes into account the unequal size of some of the patients' subgroups and the variability of their performance (Brunner & Munzel, 2000; computed on http://www.r-project.org/).

Analysis 3 explored the performance of individual patients relative to controls using the one-tailed significance test based on the statistical approach of Crawford and colleagues (Crawford, Howell, & Garthwaite, 1998; Crawford & Garthwaite, 2002). This test treats an individual patient as a sample, affording the comparison of the patient with the control group (Crawford et al., 1998; Crawford & Garthwaite, 2002).

Analysis 4 examined whether there were dissociations between different number and maths tasks in each patient relative to controls. This was done using the Revised Standardized Difference Test (Crawford & Garthwaite, 2005), which compares each patient's discrepancy in two tasks with the control sample.

Analysis 5 explored the errors made by patients in transcoding and in calculation tasks. For these error analyses, we first identified five types of transcoding errors and four types of calculation errors. We then examined whether errors made by patients with degenerative and focal lesion as well as by each subgroup of patients differed significantly from controls and the contribution of the different subgroup of patients to each error made.

Analysis 6 explored participants' performance in the number comparison task. This was done first by correlating each subgroup's slope relative to the control group similar to the original approach of Moyer and Landauer (1967). A further analysis of the distance effect was performed following Lorch and Myers' approach (1990) whereby the regression estimate of the distance effect's slope is calculated for each participant and then used in a t test to indicate whether they differed from zero. Individual slopes were also compared to the control group using the Crawford and Garthwaite's (2002) approach.

The Wilcoxon signed-ranks test was used to compare performance across numerical and nonnumerical semantic tasks.

In all analyses, the exact test option for small samples was used. Moreover, adjustment for multiple comparisons for the group of patients with degenerative and focal lesion patients was made using a Bonferroni correction. Results are only treated as significant if they achieve p < .012 for patients with degenerative disorders and p < .017 for patients with focal lesion.

Because there was no significant difference between patients with left and right parietal lesions in any of the tasks performed, all p > .1, ns, performance was averaged across these patients.

Neuropsychological Background

All patients were administered a neuropsychological battery to assess intellectual functioning, memory, and executive abilities. Either the National Adult Reading Test (NART, Nelson & Willison, 1991) or Raven's Progressive Matrices (Raven, 1965) was administered to estimate premorbid levels of functioning in patients with degenerative disorders. Italian patients were administered Raven's Progressive Matrices (Raven, 1965) and not the NART. The Wechsler Adult Intelligence Scale–Revised was used to assess verbal and performance IQ of patients with focal lesions (Wechsler, 1981).

Memory functions were assessed with the verbal Digit Span (Wechsler, 1987), the Recognition Memory Test (RMT, Warrington, 1984), and the Logical Memory Test of the Wechsler Memory Scale−Revised (WMS-R, Wechsler, 1987). The RMT allows for the evaluation and comparison of verbal and visual recognition memory whereas the WMS-R Logical Memory Test assesses immediate and delayed recall of verbal material.

Picture naming was tested either with the Graded Naming Test (McKenna & Warrington, 1980) in British patients or with pictures selected from the Snodgrass and Vanderwart set (1980) in Italian patients. Executive functions were also assessed. Specifically, the ability to form abstract concepts and to use feedback were tested using the Wisconsin Card Sorting Test (Nelson, 1976), phonemic fluency using Controlled Oral Word Association (letters F, A, and S; Spreen & Strauss, 1998), and set shifting using the Trail-Making test (Reitan & Wolfson, 1985) only in patients with degenerative disorders. In addition, patients with degenerative disorders were also administered the Mini–Mental State Examination (MMSE, Folstein et al., 1975) to screen for mental impairment.

Results

All patients with degenerative disorders had weak performance in the IQ tests, suggesting a mild degree of intellectual underfunctioning. The only exception was patients with semantic dementia, who obtained a reasonable score in the Raven's Progressive Matrices. Short-term memory as well as visual and verbal memory functions were impaired. All patients performed poorly on the phonemic fluency test (“FAS”), and on other tests assessing executive functions. MMSE scores corresponded to a mild level of cognitive decline (see Table 2).

Table 2.

Patients with focal lesions performed poorly on the IQ tests, with the exception of patients with HSE. Short-term memory was preserved but visual memory functions were impaired. Nominal functions were relatively preserved. Patients with frontal lesions performed poorly on the phonemic fluency test, which is known to be sensitive to frontal lobe dysfunction (see Table 2).

Experimental Investigation

Numerical and calculation skills were examined in all patients. Our number and calculation battery was constructed with a structure similar to that of other batteries available for clinical purposes (e.g., Delazer, Girelli, Granà, & Domahs, 2003; Deloche et al., 1994). In addition, nonnumerical semantic knowledge was tested in all patients with neurodegenerative disorders and in patients with HSE.

Below is a list of the tests used and a short description of each; for more details, see also Appendices A and B and Cappelletti et al. (2001).

Procedure

Stimuli

Stimuli for the numerical and calculation tasks were single or multidigit numerals presented in Arabic or in verbal format (written or spoken). When visually presented, numerals were printed in font 24 on separate cards presented individually to participants. For these paper-and-pencil tasks, responses were unspeeded, the only exception being the Graded Difficulty Calculation Task (see below).

For the number comparison task, the stimuli consisted of white Arabic numbers presented on a black background of a S2VP Sony laptop. The task was controlled using the Cogent Graphics toolbox (http://www.vislab.ucl.ac.uk/Cogent/) and Matlab software. The viewing distance was approximately 0.5 m. Each trial started with a central fixation cross presented for 200 ms after which single-digit Arabic numbers from 1 to 9 (excluding 5) were presented one at a time until response or for a maximum of 2000 ms. Once subjects' responses in each trial were recorded, approximately one second elapsed before the next trial began. There were 2 blocks of 64 single-digit Arabic numbers each. Participants had to decide whether each number was larger or smaller than 5. In one block, they were asked to press a left key of the keyboard if the number presented was smaller than 5 and a right key if the number was larger than 5. The instructions were reversed for the following block and the order of the instructions was counterbalanced across participants. Both accuracy and reaction times were recorded.

For the nonnumerical semantic tasks, stimuli were 48 pictures and their corresponding names selected from the Snodgrass and Vanderwart's set of black-and-white line drawings (Snodgrass & Vanderwart, 1980). Stimuli were depicted on separate cards, presented individually to participants. The stimuli were chosen to represent six semantic categories: three living categories (i.e., vegetables, body parts, animals) and three man-made categories (i.e., tools, furniture, means of transport). A few items were adapted for the patients recruited in Italy. There was no time constraint to produce an answer.

Experimental Tasks

Number tasks

Numeracy skills were tested with the following tasks: (a) number and quantity comprehension, that is, number comparison and number composition with tokens. Number comparison offers a measure of number comprehension when participants' response times as well as accuracy are collected, as we did for our patients; (b) knowledge of number sequence and order with counting, what number comes before and after a given one; and (c) transcoding, that is, reading, writing, and transforming numbers from one format to another, for instance “two” or “TWO” to “2” or the opposite.

Calculation tasks

Calculation abilities were tested with the following tasks: (a) arithmetical facts, that is, orally presented single-digit arithmetical operations (addition, subtraction, multiplication, and division problems); (b) multidigit calculation, that is, the Graded Difficulty Arithmetic Test (Jackson & Warrington, 1986), consisting of orally presented multidigit addition and subtraction problems; (c) multidigit written calculation, with operations presented and to be solved in written format; and (d) approximation, that is, arithmetical operations presented with multiple-choice selection of results; participants were required to chose the result approximately correct for each operation without exact calculation.

Unfortunately, tasks assessing nonsymbolic numerosity (e.g., dots in a display) were not administered to our patients.

Nonnumerical semantic tasks

Nonnumerical semantic knowledge was tested with the following tasks: (a) picture naming; (b) classification, requiring participants to group pictures according to the six superordinate categories (vegetables, body parts, animals, tools, furniture, means of transport); (c) matching, requiring participants to match a given name with the picture corresponding to it (e.g., word cat to the picture of a cat); (d) semantic features, requiring participants to indicate the functional and perceptual features defining objects, for example, color of a tomato or function of a knife; and (e) semantic fluency, consisting of producing words belonging to the six semantic categories (vegetables, body parts, animals, tools, furniture, means of transport).

Results

Quantity Processing

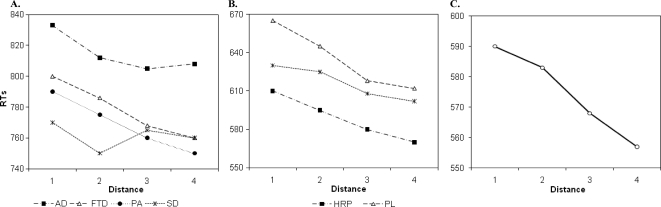
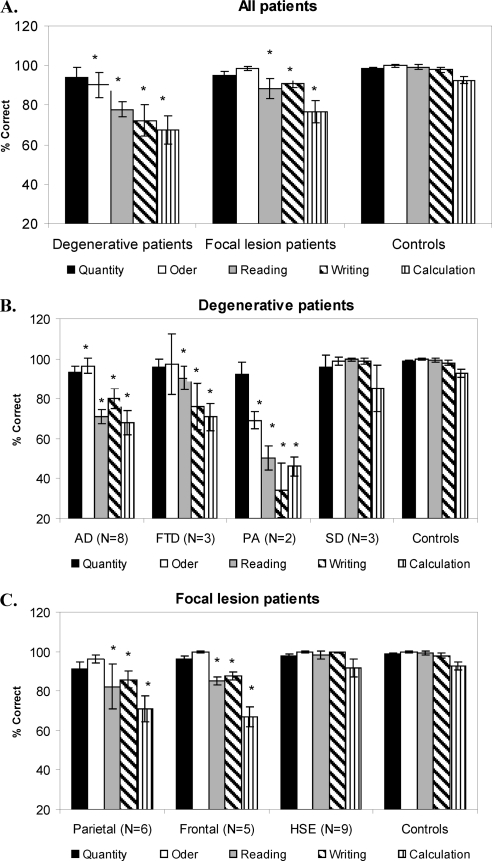
All patients with degenerative and focal lesions were accurate at processing number quantity (see Table 3), as also confirmed by the Brunner−Munzel Test, which takes into account the intergroup variability and the small size of some of the subgroups (see Appendix C). With the exception of patients with HSE, all the others were slower than controls (see Table 3), although their response times decreased as a function of the numerical distance from the target number to the reference number “5”, AD: r² = .74, p > .01; FTD: r² = .82, p > .04; PA: r² = .69, p > .002; semantic dementia: r² = .83, p > .004; parietal: r² = .81, p = .008; frontal: r² = .72, p > .03; HSE: r² = .87, p = .005 (see Figures 2A and 2B). This indicates a normal “distance effect” (Moyer & Landauer, 1967), typically indicating preserved quantity processing. Moreover, by using the Lorch and Myers method based on the individual patients' regression estimates of the distance effect, we showed that the distance effect was indeed significant in each subgroup of patients (see Table 3). Comparison of each patient's coefficient to the individual slopes of the control group was also performed based on the Crawford and Garthwaite's (2002) approach. This further confirmed that there was no significant difference between patients and controls, therefore showing that even at the individual level the numerical distance effect was maintained in our patients (see Table 3).

Table 3.

Figure 2. Performance of patients with (A) degenerative disorders, (B) focal brain lesions, and of (C) controls in the number comparison task.

A further analysis explored whether there was any advantage (i.e., faster reaction times) in responding to small numbers with the left hand and large numbers than with the right hand (i.e., the Spatial-Numerical Association of Response Codes effect, Dehaene et al., 1993). A repeated-measures analysis of variance revealed a significant main effect of response mapping, that is, small numbers answered with left hand relative to the right hand and the opposite for large numbers, F(1, 29) = 23.3, p < .001, which did not interact with group, F(6, 29) = 0.14, p = .7, ns. Further pairwise comparison showed that faster RTs were observed for the small number → left key and large number → right key mappings relative to the opposite mappings (small number → right key and large number → left key) in all patients, t(35) = 3.98, p = .007, which indicates that a spatial representation of numbers was maintained.

Order Processing

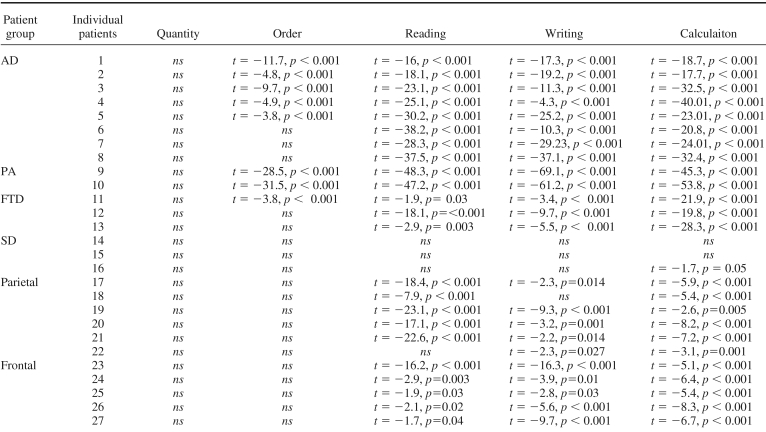
Relative to controls, order processing was impaired only in patients with AD and PA and preserved in the patients with all other degenerative and focal lesions (see Figure 1A, 1B, 1C and Table 3). Analysis of individual patients relative to controls based on the approach of Crawford and colleagues (Crawford et al., 1998; Crawford & Garthwaite, 2002) showed that most of patients with AD (i.e., 5 of 8) and all patients with PA were impaired in processing numerical order (see Appendix D). AD's impairment was further confirmed in an analysis based on the Brunner−Munzel Test (see Appendix C).

Figure 1. Performance of: (A) all patients and control subjects, (B) patients with degenerative disorders, and (C) patients with focal lesions in number and calculation tasks. Asterisks indicate a significant difference in performance relative to control subjects.

Transcoding

Reading and writing were generally impaired, except in patients with semantic dementia and HSE (see Figures 1A, 1B, 1C and Table 4). An analysis of individual patients relative to controls, based on the approach of Crawford and colleagues (Crawford et al., 1998; Crawford & Garthwaite, 2002), showed that all patients with AD, PA, and FTD as well as most patients with parietal and all frontal lesions were impaired in transcoding (see Table 4 and Appendix D), and this was also corroborated in the analysis based on the Brunner−Munzel Test (see Appendix C).

Table 4.

Error Analysis

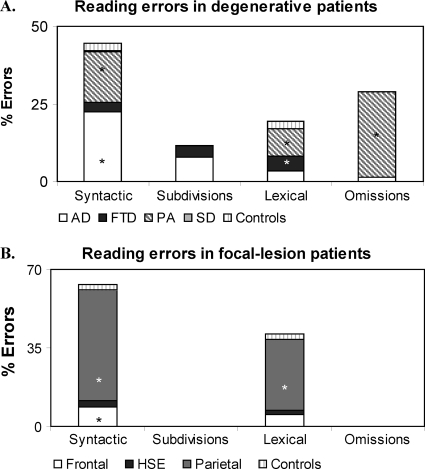
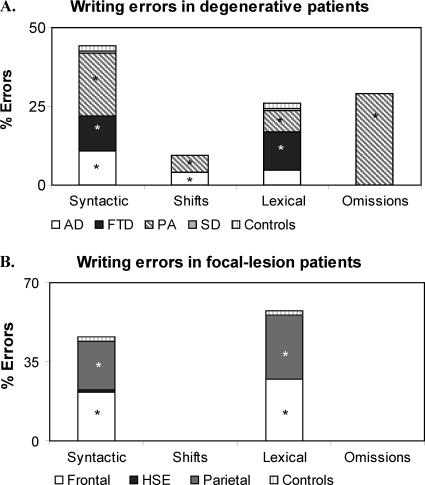
In reading and writing numbers, three types of errors were identified using the Deloche and Seron classification (1982): (a) syntactic errors, which consist of the wrong assembly of the elements in the number string, for example, number “905” read as “nine thousand and five” or the spoken number “thirty thousand and 27” written as “327”; (b) lexical errors, which consist of the replacement of one or more of the correct digits in a number with other digits belonging to the same number class, for example, number “505” read or written as “five hundred and two”; (c) subdivisions, consisting of separating numbers in subparts, for example, “30027” read as “thirty-zero-twenty-seven”; and (d) omissions and partial answers. In addition, in writing numbers to dictation or from a written input, there were also (e) shifting errors, when part or all the format of the input is reproduced into the format of the output, for example, the spoken input “forty-nine” written as “FORTY-NINE” instead of the requested “49” (complete lexical shift), or a mixture of numerals and number words, for example, “FORTY9” (partial lexical shift) (Thioux et al., 1998).

In reading numbers, most errors made by patients with degenerative lesions were syntactic (42.3%), followed by omissions (29.04%), lexical (17.0%), and subdivisions (11.6%). Patients with focal lesions made syntactic (61.08%) and lexical errors (38.92%) and but no omissions and subdivision errors (see Figure 3B and Table 4). In writing numbers, patients with degenerative lesions made syntactic (42.6%), omissions (29%), lexical (25.2%), and shifts errors (4.2%) (see Figure 4A and Table 4), whereas patients with focal lesions made only lexical and syntactic errors (55.7 and 44.3%, respectively) but no omission or shift errors (see Figure 4B and Table 4).

Figure 3. Errors in reading numbers made by patients with (A) degenerative disorders and (B) focal brain lesions. Asterisks indicate a proportion of errors significantly higher relative to control subjects (see Table 4 for more details of the statistical analyses performed).

Figure 4. Errors in writing numbers made by patients with (A) degenerative disorders and (B) focal brain lesions. Asterisks indicate a proportion of errors significant higher relative to control subjects (see Table 4 for more details of the statistical analyses performed).

Different subgroups of patients with degenerative and focal lesions differed from controls in the errors made in reading and writing numbers (see Figure 3A and Table 4). The contribution of each subgroup of patients to the each type of error made is illustrated in Figures 3 and 4.

Calculation

Calculation was impaired in all patients with degenerative and focal lesions, with the exclusion of most patients with semantic dementia and all patients with HSE (see Figures 1, Table 5, and Appendixes C and D). Patients with semantic dementia showed good accuracy, although the procedures they used were often long and consisted of decomposing each arithmetical operation in simpler steps. For instance, “53 × 19” could either be performed as “(53 × 20) − 53” or as “(50 × 19) + (3 × 19)”. When these noncanonical procedures led to correct results, a correct score was assigned. An analysis of individual patients relative to controls, based on the approach of Crawford and colleagues (Crawford et al., 1998; Crawford & Garthwaite, 2002), showed that all patients with AD, PA, and FTD as well as patients with parietal and frontal lesions and one of 3 patients with semantic dementia were impaired in calculation (see Table 5 and Appendix D).

Table 5.

Error Analysis

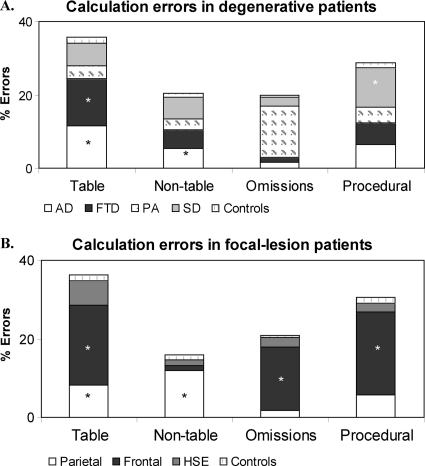
Four types of errors were identified in performing simple and multidigit calculation: (a) table errors, when results belong to other time tables, for example “3 × 4” = 8; (b) nontable errors, when results do not belong to time tables, for example, “3 × 4” = 11; (c) procedural errors, for example, operations unfinished, borrowing or carrying not performed; and (d) omissions.

Patients with degenerative disorders made mainly table and procedural errors (34.3% and 27.4%, respectively); nontable errors and omissions occurred in almost equal proportion (19.3 and 19%, respectively, see Figure 5A). Patients with focal lesions also made mainly table and procedural errors (34.8 and 29.2%, respectively) followed by omissions and nontable errors (20.4 and 14.6% respectively, see Figure 5B). Different subgroups of patients with degenerative and focal lesions differed from controls in the errors made in calculation (see Table 5).

Figure 5. Errors in calculation tasks made by patients with (A) degenerative disorders and (B) focal brain lesions. Asterisks indicate a proportion of errors significant higher relative to control subjects (see Table 5 for more details of the statistical analyses performed).

Comparison Between Patients With Degenerative Disorders and Focal Lesions and Between Number and Calculation Tasks Within Each Group

Patients with degenerative disorders and focal lesions were directly compared to test whether they differed in any of the main numerical abilities tested. No differences were found in quantity, transcoding, or calculation tasks, respectively, U = 108, p = .78, ns; U = 113, p = .1, ns; U = 138, p = .4, ns; the only difference between the two groups was in order tasks, U = 39, p = .001. We also directly compared patients' performance in quantity and calculation tasks; results showed that all patients were better in the former task than the latter, AD: Z = 5.2, p < .001; FTD: Z = 7.1, p < .001; PA: Z = 4.3, p < .001; SD: Z = 5.2, p < .001; parietal lesion: Z = 4.7, p < .001; frontal lesion: Z = 4.38, p < .001; HSE: Z = 4.9, p < .001.

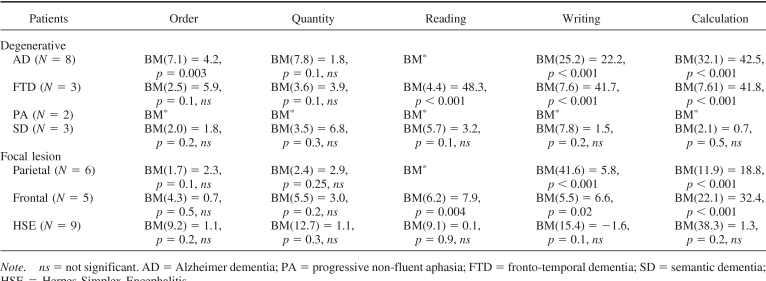
With the exception of patients with semantic dementia, in patients with the other degenerative disorders quantity dissociated from order processing (but not in patients with FTD), as well as from transcoding and maths. Likewise, quantity dissociated from transcoding and maths in patients with parietal and frontal lesions but not in patients with HSE.

Order processing dissociated from both transcoding and maths in all patients excluding patients with semantic dementia and HSE; finally, transcoding and maths dissociated in all patients with degenerative disorders and focal lesions, except those with AD and HSE (see Table 6).

Table 6.

Combined with previous analyses, these dissociations indicate that quantity was more strongly or at least equally preserved relative to other numerical skills and maths in all patients. These dissociations also show that although calculation and transcoding were damaged in most patients relative to controls, the patients were not equally impaired; however, the direction of this dissociation, that is, whether calculation was worse than transcoding or vice versa, was not consistent across the subgroups of patients.

Nonnumerical Semantic Tasks

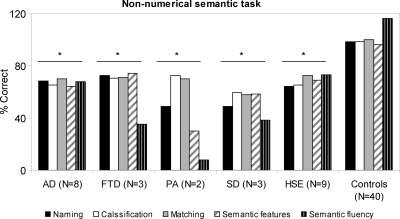
Relative to controls, patients with degenerative disorders were impaired in all the semantic tasks administered, Kruskal−Wallis effect of group: naming, χ²(4) = 51.23, p < .001; classification, χ²(4) = 38.2, p < .03; matching, χ²(4) = 34.07, p = .04; semantic features, χ²(4) = 48.11, p < .001; semantic fluency, χ²(4) = 43.39, p = .025. In each semantic task, each subgroup of patients with degenerative disorders was significantly impaired relative to controls (all p between .05 and .003, see Figure 6). Likewise, patients with HSE were impaired in all the semantic tasks administered relative to controls, Kruskal–Wallis effect of group: naming, χ²(1) = 11.1, p < .001; classification, χ²(1) = 22.12, p < .001; matching, χ²(1) = 8.4, p < .04; semantic features, χ²(1) = 15.6, p = .023; semantic fluency, χ²(1) = 20.5, p < .01.

Figure 6. Performance of patients with degenerative disorders (AD, FTD, PA, SD), patients with HSE, and control subjects in nonnumerical semantic tasks. Asterisks indicate a significant difference in performance relative to control subjects (see text for more details of the statistical analyses performed). Note that in the semantic fluency task the number of items produced is reported rather than the percentage correct.

Patients' performance in numerical and semantic tasks was directly compared to test whether their understanding of numerical and nonnumerical concepts differed relative to controls. Numerical knowledge was better preserved than nonnumerical knowledge in patients with degenerative disorders and with HSE, Z scores number-semantic tasks AD: Z = 6.1, p = .043; FTD: Z = 5.3, p < .02; PA: Z = 7.5, p = .03; semantic dementia: Z = 8.2, p < .001; HSE: Z = 4.3, p = .025.

Discussion

This study aimed to characterize the numeracy profile of 36 patients with acquired brain disorders. Below, we discuss our four main findings, which can be summarized as follows. First, all patients with degenerative disorders and focal lesions showed intact processing of number quantity. Second, most patients with degenerative disorders and focal lesions were impaired in calculation tasks (with the exception of most patients with semantic dementia and all patients with HSE). Third, performance in number order and transcoding was heterogeneous across groups. Fourth, patients with impaired semantic knowledge showed much better preserved numerical knowledge. There was no difference between patients with degenerative disorders and focal lesions in all numerical abilities, with the exception of order processing. No firm conclusions on the contribution of different brain regions to numeracy could be reached because our patients' brain images came from various sources; however, the main aim of our study was to characterize the numerical profile of our patients.

Quantity Processing Is Preserved

All our patients were accurate at comparing numerical quantities, including patients with lesions affecting the parietal lobes, a key brain area for numerical processing. The ability to process number quantity is an important index of how magnitude is represented and is a typical finding in the literature of numerical cognition (Butterworth, 1999; Dehaene, 1997; Moyer & Landauer, 1967). In clinical and experimental settings, number quantity skills are normally measured by asking participants to indicate the larger in magnitude between two numbers, usually administered in the form of paper-and-pencil, time-unconstrained number comparison task. Typically, most patients are reported to perform flawlessly on this task, and very few cases of impaired quantity processing have been described so far (e.g., Ashkenazi et al., 2008; Cipolotti et al., 1991; Dehaene & Cohen, 1995; Delazer, Benke, Trieb, Schocke, & Ischebeck, 2006; Koss et al., 2010; Lemer et al., 2003).

The scarcity of patients with impaired number comparison may seem surprising, given that several cases have been reported with numerical and calculation impairments. This is particularly unexpected in the case of patients with lesions to the parietal areas, because these brain regions have been suggested to be strongly implicated in numeracy skills (e.g., Dehaene et al., 2003). Various reasons may explain why only a few patients show impaired number quantity processing, even in the case of parietal lesions. First, number comparison may be considered a very easy task, which may explain why most patients are good at it. However, dissociations have been reported in performing number comparison relative to other tasks with similar difficulty level, such as parity judgment or judgment of objects' size (e.g., Cipolotti et al., 1991; Lemer et al., 2003; Polk et al., 2001). Second, administering quantity comparison tasks by paper-and-pencil methods may not be sensitive enough to reveal any numerical impairment. This may be because patients showing preserved accuracy might nevertheless use basic strategies to perform this task like counting rather than accessing numbers automatically. Such strategies may only be revealed in the pattern of reaction times but not in accuracy scores. Our study overcame this problem by measuring both accuracy and reaction times. Even with this additional measure, we showed that quantity processing was preserved in our patients, as indicated by a normal distance effect, namely, faster response times as the numerical distance between two numbers increased. By investigating quantity processing in patients with degenerative disorders and focal lesions, our study complements previous investigations that focused on the verbal and Arabic representational codes outlined in previous theoretical models of numerical cognition (e.g., Dehaene & Cohen, 1995). Moreover, all patients performed better in quantity tasks relative to calculation, possibly because quantity processing is a more deeply rooted, core number skill compared to calculation, a more education-based ability, also depending on other cognitive skills such as working memory and attention.

As mentioned above, preserved ability to compare number quantities was also observed in patients with parietal lesions. Brain lesions in these patients affected either the right or the left parietal lobe and therefore contralesional parietal areas may have been sufficient to maintain intact number quantity processing. This hypothesis finds support in some theoretical accounts of numerical cognition, suggesting that some numerical skills such as number comparison can be implemented either in the left or in the right parietal regions (e.g., Dehaene & Cohen, 1997). However, the left and right parietal areas do not always compensate, as indicated by single cases of impaired numerical skills, including number quantity, following unilateral parietal lesions (e.g., Ashkenazi et al., 2008; Cipolotti et al., 1991; Lemer et al., 2003) or degenerative processes affecting the parietal lobes specifically (e.g., Delazer et al., 2006; Koss et al., 2010). The fact that parietal lesions result in numerical impairments in some patients but not others may depend on how the brain recovers or compensates after a lesion or a degenerative process. For instance, it is possible that other brain areas, besides the parietal ones, become involved in numerical processing following a brain lesion, as suggested in the concept of “degeneracy” (Price & Friston, 2002). Degeneracy is the proposal that multiple brain areas may be able to perform the same cognitive task such that, when damage occurs to a brain region that is primarily involved in a task, “alternative” regions may become available to maintain residual performance. Although our data do not allow us to test whether this was the case in our patients, it is possible that number comparison is preserved even in patients with parietal lesions because other brain areas may be able to perform this task. Support for this hypothesis comes from neuropsychological studies tracking patients' performance in a variety of numerical tasks including number comparison following stroke (Basso, Caporali, & Faglioni, 2005; Delazer & Butterworth, 1997). In one of these studies, the patient's distance effect was abnormal (i.e., longer reaction times for more distant numbers) only immediately after stroke but it recovered in the following weeks (Delazer & Butterworth, 1997), whereas other studies showed spontaneously recovery from acalculia in the majority of the patients investigated (Basso et al., 2005; Caporali, Burgio, & Basso, 2000). Further study is needed to support the hypothesis that quantity processing can be performed by different areas of the brain capable of taking over the function of lesioned areas.

Calculation Skills Are Impaired in Most Patients

Our patients with degenerative disorders and focal lesions were impaired in performing calculation, with the exception of most patients with semantic dementia and all patients with HSE. Impairment was observed for oral and written arithmetical operations as well as calculation approximation. Our error analysis showed that table and procedural errors were those most frequently made.

It may be argued that calculation was impaired in our patients simply because it is a complex task, as it requires preserved knowledge of arithmetical facts and procedures, besides preserved attention and working memory and the ability to plan and monitor the execution of the operations. However, our error analysis suggests that distinct components of the arithmetic processing were differentially impaired across patients. For instance, patients with AD and parietal lesions were more impaired at retrieving arithmetical facts relative to executing arithmetical operations. In contrast, patients with frontal lesions were impaired at both retrieving arithmetical facts and at executing operations. Finally, patients with semantic dementia seemed mostly impaired at executing arithmetical operations, because most of their errors were procedural. Therefore, although calculation is more complex than other number tasks because it involves multiple components and additional cognitive resources, the error analysis allowed us to identify which of these components were specifically impaired in different neurological populations.

Of particular interest was calculation performance of the patients with semantic dementia. These patients were generally able to perform arithmetical operations, including multidigit ones, despite impaired arithmetical procedures and partly impaired simple facts. This impairment indirectly revealed intact understanding of the meaning of arithmetical operations, that is, arithmetical conceptual knowledge (Hittmair-Delazer, Semenza, & Denes, 1994) in all our patients with semantic dementia, who developed alternative algorithms which were successfully used to process arithmetical operations (Cappelletti et al., 2001, 2005). Although dissociation between arithmetical conceptual knowledge and other numerical abilities has been previously reported (Delazer & Benke, 1997; Hittmair-Delazer et al., 1994), such a dissociation has only recently been described in the context of a progressive cognitive disorder.

Moreover, performance in calculation in patients with semantic dementia showed not just preserved understanding of arithmetical operations, but also the ability to adapt the algorithms to contingent impairments, showing flexible and skilled mastery of arithmetical conceptual knowledge (Cappelletti et al., 2005). Although this result is consistent with previous research (e.g., Diesfeldt, 1993; Crutch & Warrington, 2002), other recent studies have shown that the preservation of arithmetical knowledge depends on the integrity of semantic memory and can be modulated by personal experience with numbers (Julien et al., 2008, 2010). We suggest that the apparent discrepancy between these studies and our results may be explained in terms of individual variability and practice with numbers. It is possible that in our patients' numerical knowledge was still preserved, despite poor semantic memory, because they had a strong interest for numbers, either because of their profession or personal interests, which we documented in two of the three patients with semantic dementia (Cappelletti et al., 2001, 2005). It is also possible that longitudinal investigations may have revealed patterns of impairments in numerical knowledge more similar to those recently reported in other patients with semantic dementia. We did not find evidence of impaired arithmetical knowledge in any of the patients with semantic dementia that we studied longitudinally (Cappelletti et al., 2005), although unfortunately we could not examine the long-term performance of the other two patients with semantic dementia.

Heterogeneous Performance in Number Order and Transcoding Tasks

Performance in number order and transcoding varied considerably across patients. For instance, number order was only impaired in patients with AD (although marginally) and in patients with PA, and was preserved in all other patients. Impairment in patients with PA was not simply due to difficulties in verbal output. Indeed, even when presented with multiple written choices, patients with PA were impaired at indicating the number coming before or after another one. Previous research on numerical order supports that: (a) order and quantity are “both sides of the same coin” (Jacob & Nieder, 2008) because they share a common representation in the brain (Franklin & Jonides, 2009); or alternatively that (b) processing order and quantity information require at least partially different cognitive mechanisms (e.g., Cheng & Butterworth., forthcoming; Tang, Ward, & Butterworth, 2008; Turconi, Jemel, Rossion, & Seron, 2004; Zorzi, Di Bono, & Fias, 2011). Although the small size of some of the patient groups suggests the need for further investigations, our results showing preserved quantity processing and impaired order processing in some of the patients are novel for two reasons: (a) they reinforce the idea that processing numerical order and quantity are distinct; and (b) they indicate that order processing can be impaired also in patients with degenerative disorders, therefore adding to the existing literature that reports difficulties in processing number order only in a few patients with focal lesions (e.g., Turconi & Seron, 2002).

Number reading and writing were impaired in all patients with the exception of those with semantic dementia and HSE, with patients with PA and parietal lesions contributing to most of the errors made. This heterogeneous performance may be due to the fact that different components are involved in transcoding, for instance, the mastering of lexical and syntactic rules, besides other cognitive skills such as working memory, and these components may be differently affected by different brain lesions.

Numerical Knowledge Is Better Preserved Than Nonnumerical Semantic Knowledge

A striking dissociation emerged in all our patients with degenerative disorders and with HSE, whose understanding of numbers and arithmetic was significantly better preserved relative to their comprehension of nonnumerical concepts. This dissociation was especially notable in patients with semantic dementia, who showed severe degradation of semantic knowledge and yet well-preserved understanding of numerical and arithmetical principles. The subgroup of patients with semantic dementia included only three participants, and our results were consistent across two patients, with one patient marginally different from controls, suggesting that further study is needed to corroborate our results. Nevertheless, our findings reinforce previous evidence that, despite cognitive decline, arithmetical conceptual knowledge remains better preserved in patients with degenerative disorders (see also Cappelletti et al., 2001, 2006; Crutch & Warrington, 2002; Diesfeldt, 1993; Jefferies et al., 2004, 2005; Zamarian et al., 2006). Selectively preserved number knowledge has been reported in the context of preserved general semantics (Delazer & Benke, 1997; Hittmair-Delazer et al., 1994; McCloskey, Caramazza, & Basili, 1985; Sokol & McCloskey, 1990, 1991; Sokol, McCloskey, & Cohen, 1989; Warrington, 1982). In contrast, our data offer a new prospective, because they showed a dissociation between numerical and nonnumerical conceptual knowledge. Moreover, this dissociation also emerged in some patients with focal lesions, that is, HSE. These patients have been previously studied in terms of their nonnumerical semantic knowledge, which is often impaired (e.g., Kopelman, 2000; Lambon Ralph et al., 2007; Mazzoni et al., 1996; Pietrini et al., 1988; Sartori & Lombardi, 2004), but no studies have yet focused on numerical knowledge in patients with HSE.

Better preserved numerical knowledge relative to nonnumerical knowledge might be seen in terms of numbers being high-frequency items whose repeated use may facilitate their access and understanding. However, we showed that our patients' impaired semantic knowledge also extended to other high-frequency items. For instance, patients failed to name the picture of a “key” or of a “car”, which have the same frequency of the numbers “twenty” and “five”, respectively. Numbers might have also been better preserved in our patients because they are typically learnt in a sequence that may facilitate remembering them. However, it seems unlikely that this feature alone explains patients' better understanding of numerical concepts because other ordered categories, such as months or days of the week, were also partially impaired (e.g., Cappelletti et al., 2001). Moreover, the fact that numbers are represented in a sequence does not seem to account for the well-preserved knowledge of arithmetical concepts that some of our patients (i.e., those with semantic dementia and HSE) showed. In principle, it may also be possible that the patients' impaired semantic knowledge could be due to the diversity of their cognitive impairments, involving memory, attention, and visuospatial skills. Although we cannot preclude that these damages may have contributed to the semantic impairments, it seems that, if this were the case, a similar impairment should have emerged in performing numerical tasks, which also require attention and memory skills to be performed. Instead, we suggest that numerical concepts were better preserved than other concepts because they represent a distinct semantic category within the semantic system, which was selectively spared in most of our patients (see also Cappelletti et al., 2001).

Conclusion

The results of our study offer for the first time an overview on numeracy skills in patients with different degenerative disorders and focal brain lesions. Our data showed that all patients had intact processing of number quantity, and that those patients with impaired semantic knowledge had much better preserved numerical knowledge. In contrast, most patients were impaired in calculation tasks (with the exception of most patients with semantic dementia and those with HSE) and showed a heterogeneous pattern of performance in tasks assessing number order and transcoding. Moreover, our data suggest that, besides the parietal areas, other brain regions might be critical for the understanding and processing of numerical concepts.

A. Numerical Tasks Performed (see also Cappelletti et al., 2001)

Number Tasks

Number and Quantity Comprehension

Number comparison

Participants have to indicate whether each single-digit Arabic numerals presented on the computer screen was larger or smaller than the reference number “5”. Accuracy and reaction times are recorded. One point assigned for each correct answer.

Composing the value of numerals with tokens

Participants are orally presented with a number and asked to select tokens composing the value of the number. Target numbers are up to 3-digit numerals and tokens are colored plastic circles representing number 100, 20, 10, 5, and 1. One point assigned for each correct answer.

Knowledge of Number Sequence and Order

Counting sequences

Participants are asked to count verbally both forward and backward from 20 to 1 and vice-versa. One point assigned for each correct answer.

What comes before/next

Participants have to indicate what number comes before or after an orally presented number (up to 4-digit). One point assigned for each correct answer.

Transcoding

Reading Arabic numerals and number words

Participants are required to read aloud Arabic numerals (up to 6-digit numerals) and number words (corresponding to up to 5-digit numerals). One point assigned for each correct answer.

Writing Arabic numerals and number words to dictation

Participants have to write to dictation Arabic numerals (up to 6-digit numerals). One point assigned for each correct answer.

Transcoding from written number words to Arabic numerals

Participants are required to write the Arabic numerals corresponding to a visually presented number word (up to 4-digit numerals). One point assigned for each correct answer.

Transcoding from Arabic numerals to written number words

Participants are required to write the number word corresponding to a given Arabic numeral (up to 4-digit numerals). One point assigned for each correct answer.

Calculation Tasks

Arithmetic facts

All problems are verbally presented and verbally answered. Problems are tested, blocked by operation (addition, subtraction, multiplication, division). In each block of operation, some rule-based problems are included (addition: n + 0; subtraction: n − n, n − 0; multiplication n × 0, n × 1; division n ÷ n, n ÷ 1). One point assigned for each correct answer.

Mental calculation

(Graded difficulty arithmetic test, Jackson & Warrington, 1986). Multidigit addition and subtraction problems are verbally presented and verbally answered. Operands include 1-, 2-, and 3-digit numerals. One point assigned for each correct answer provided within 10 seconds.

Written calculation

Progressively more difficult multidigit problems (addition, subtraction, multiplication, division) presented in Arabic format to be solved by written procedures. Operands include 1-, 2-, and 3-digit numerals. One point assigned for each correct answer.

Approximation

Multidigit addition, subtraction, and multiplication presented with four false answers. Participants required choosing the answer closest to the correct result as fast as possible and without calculating it. One point assigned for each correct answer.

B. Semantic Tasks Performed (see also Cappelletti et al., 2001)

Picture Naming

Black-and-white pictures selected from the Snodgrass and Vanderwart's set (Snodgrass & Vanderwart, 1980) are presented to participants who are asked to provide the name of the object depicted. One point is assigned for each correct answer.

Classification

A set of pictures of objects or their names (e.g., “cat”, “carrot”, “hammer”) are presented one at a time to participants who are asked to classify them into the appropriate semantic category (e.g., “animals”, “vegetables”, “tools”, respectively). One point is assigned for each correct answer.

Matching

A set of pictures are presented to participants who are asked to indicate which picture correspond to a given name. One point is assigned for each correct answer.

Semantic Features

Participants are asked to indicate the functional or perceptual features of objects. One point is assigned for each correct answer.

Semantic Fluency

For each given semantic category, subjects are asked to provide as many names as possible in 1 minute. One point is assigned for each correct name produced.