The mirror game as a paradigm for studying the dynamics of two people improvising motion together

Abstract

Joint improvisation is the creative action of two or more people without a script or designated leader. Examples include improvisational theater and music, and day-to-day activities such as conversations. In joint improvisation, novel action is created, emerging from the interaction between people. Although central to creative processes and social interaction, joint improvisation remains largely unexplored due to the lack of experimental paradigms. Here we introduce a paradigm based on a theater practice called the mirror game. We measured the hand motions of two people mirroring each other at high temporal and spatial resolution. We focused on expert actors and musicians skilled in joint improvisation. We found that players can jointly create novel complex motion without a designated leader, synchronized to less than 40 ms. In contrast, we found that designating one player as leader deteriorated performance: The follower showed 2–3 Hz oscillation around the leader's smooth trajectory, decreasing synchrony and reducing the range of velocities reached. A mathematical model suggests a mechanism for these observations based on mutual agreement on future motion in mirrored reactive–predictive controllers. This is a step toward understanding the human ability to create novelty by improvising together.

Many human activities are performed together by two or more persons, but the basic mechanisms underlying joint action (1–3) are still largely unknown. Recent work has addressed well-defined joint actions such as finger tapping (4, 5), rocking in chairs (6), or lifting a wooden plank together (7), showing phenomena of synchronization and hysteresis (8). There is much less study of improvised action that is open-ended (9, 10). Examples of such joint action occur when musicians, dancers, or actors improvise together (11), and also in day-to-day experience such as two people locked in an engaging conversation (12, 13) or two toddlers in play (14). Subjective reports by joint improvisers describe moments of high performance in which improvisers do not know who is leading and who is following (15–17). These reports raise interesting questions: How does joint improvisation work? Does improvising together indeed lead to better performance? And does joint improvisation differ from simply following an improvising leader?

Despite the importance of joint improvised action in social interactions and creative processes, it has rarely been studied, due to a lack of experimental paradigms. Here we present an experimental system for studying joint improvised action, based on the mirror game, a fundamental practice in improvisation theater (18, 19) and dance/movement therapy (20). In the mirror game, two players imitate each other, producing coherent dance-like motion that seems choreographed. The game can be viewed as a simple paradigm in which two people create motion together de novo.

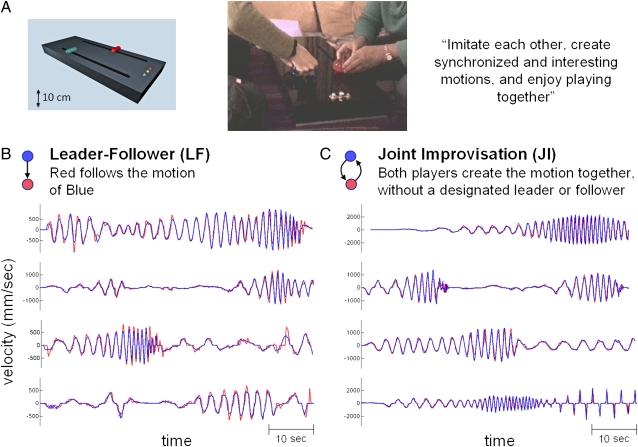
We adapted the mirror game using a custom device for measuring motion in one dimension (Materials and Methods). Two players faced each other holding handles (Fig. 1A) that can move along parallel tracks 55 cm long. The players were told that this is a collaborative game whose purpose is to enjoy creating motion together that is synchronized and interesting. The mirror game proceeded with two types of rounds: In leader–follower (LF) rounds, one player was leading and the other was following. In joint-improvisation (JI) rounds, the players moved together without a designated leader. A set of lights indicated the type of round. Each game had nine rounds of 1 min, counterbalanced between LF and JI rounds. Motion was tracked at a spatial resolution of 1 mm and temporal resolution of 20 ms. We tested expert improvisers—actors and musicians with over 10 y of experience in joint improvisation. We also tested people without prior experience in improvisational arts.

Fig. 1.

A one-dimensional mirror game shows complex, coordinated improvised motion. (A) In the mirror game, the motion of two players moving handles along tracks is sampled at 50 Hz and at a spatial resolution of 0.94 mm. (B) Examples of velocity traces in rounds where the leader and follower are designated (LF rounds). Here the leader is the blue player. (C) Examples of velocity traces in joint improvisation rounds, with no designated leader and follower (JI rounds). The data for all experimental rounds are provided in SI Appendix, Fig. 24.

Results

Players Create Complex and Highly Synchronized Motion Together.

In all games, we found complex movement behavior (Fig. 1 B and C; the full dataset is shown in SI Appendix). Players performed sinusoidal-like motions of varying amplitude and frequency. Often, amplitude and frequency showed continuous or abrupt changes: 27% of the rounds had periods of clear crescendos and diminuendos. Some rounds showed stops of varying duration with interspersed staccato motion.

To analyze the motion, we segmented it into periods between zero-velocity events (n = 1,888 segments in the dataset; Materials and Methods). We measured the difference between the times in which players reached zero velocity, dT (Fig. 2A). We found that dT in most cases (76%) was smaller than 180 ms, with 29% of segments showing timing differences of less than 40 ms (SI Appendix, Fig. 1). These differences are considered too fast to be controlled by visual feedback alone (21). This indicates that the behavior is not purely reactive but rather has a predictive component, as discussed in the model below.

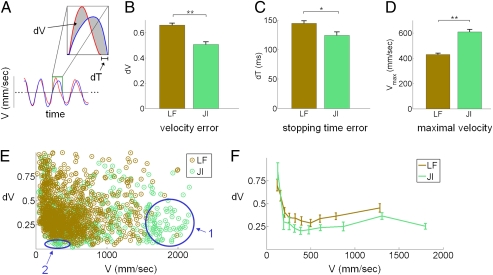
Fig. 2.

Joint improvised motion by experts is more synchronized and rapid than leader–follower motion. (A) Two measures of synchronicity of the motions of the two players. The velocity traces are segmented to periods between zero-velocity events. For each segment, the relative velocity error (dV) and the timing difference between zero-velocity events (dT) are computed. (B) Relative velocity error between players, dV, averaged over all segments. (C) Mean temporal differences between zero-velocity events of the two players, dT, averaged over all segments. (D) Maximal velocity averaged over all segments. (E) Relative velocity error in all segments, as a function of average segment velocity. Brown and green dots correspond to LF and JI rounds, respectively. Areas 1 and 2 are regions reached primarily in JI rounds and not in LF rounds. (F) Relative velocity error as a function of velocity. Shown is median dV in equal-sized velocity bins, with SEs computed by bootstrapping (*P < 0.01, **P < 0.001).

Experts Perform Better Without a Designated Leader.

We next asked whether having a designated leader affects the motion, compared with having no designated leader. For this purpose, we compared LF to JI rounds. Note that this comparison is done within player pairs and thus controls for differences between players and pairs.

We measured the synchronization of the two players by computing the mean relative difference in velocity (dV) and the timing differences between zero-velocity events (dT) (Fig. 2A; Materials and Methods). We also measured the range of velocities achieved by the players. We found that experts show better synchronization—a lower dV and dT—and a larger range of velocities without a designated leader than when a leader was designated (Fig. 2 B–D; dV, P < 0.001; dT, P < 0.01; V_max, P < 0.001; qualitatively similar results were obtained for relative error in position; SI Appendix, Fig. 2). This finding relates to a recent study on synchronized finger tapping, in which higher synchrony was achieved when the tappers heard each other (performing as a coupled unit) than when hearing was unidirectional (5).

JI rounds were distinct from LF rounds in showing accurate high-velocity segments (area 1 in Fig. 2E; dV < 0.5) as well as very accurate low-velocity segments (area 2 in Fig. 2E; dV < 0.1). The increased synchrony of JI rounds relative to LF rounds is found also when binning data according to velocity (Fig. 2F) or frequency (SI Appendix, Fig. 3). In JI rounds, players were able to move together accurately at frequencies approaching ω_max∼2.5 Hz (SI Appendix, Fig. 4), at the top end of the previously reported range of stable visually guided synchronization to computer-generated signals (22, 23).

We also measured the complexity of the motion, using both a wavelet-based complexity measure (SI Appendix, Figs. 5 and 6) and a measure based on human raters who scored the complexity of time traces (SI Appendix, Figs. 7 and 8). Both assays showed that the motion in JI rounds is as complex as that in LF rounds.

In sum, moving together is better for expert improvisers: With no designated leader, they reached lower errors in velocity and stopping times, and a wider range of velocities, than when a leader was designated.

Experts Can Enter a State of Co-leadership.

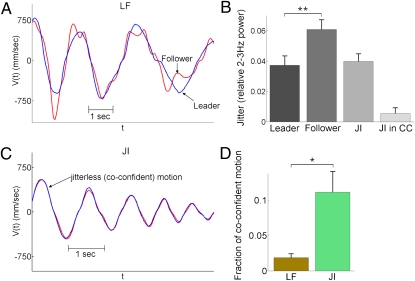
We next sought to understand the mechanisms that underlie the better performance in JI compared with LF rounds. We found a characteristic difference between these conditions, related to the high-frequency component of the motion. The follower in LF rounds displayed a jittery motion, which oscillated at a frequency of 2–3 Hz around the leader's trajectory (Fig. 3A and SI Appendix, Fig. 9). Thus, rather than lagging behind the leader, the follower overshoots and undershoots the leader's motion with a characteristic frequency. This jittery motion is similar to the 1–2 Hz jitter found in studies of manual tracking of computer-generated oscillating targets (24), and is thought to originate from a reactive controller that adjusts the motion of the follower based on the perceived tracking error (25). We quantified the jitter of each player by the relative Fourier root-mean-square (rms) power in the 2–3 Hz band. Followers had higher jitter than leaders in 91% of LF rounds in the study (Fig. 3B; P < 0.01).

Fig. 3.

Followers demonstrate 2–3 Hz oscillation (jitter) around the leader's smooth trajectory, whereas joint improvisation shows periods of coconfident motion without such jitter. (A) In LF rounds, the follower shows jitter around the leader's smooth trajectory. (B) Mean jitter of the follower is higher than that of the leader. Jitter in JI motion is similar to that of the leader in LF motion. (C) JI rounds show periods of coconfident (CC) motion in which both players show almost no jitter (<0.01; B). (D) Percentage of time in coconfident motion is higher in JI than in LF rounds (*P < 0.05, **P < 0.01).

Thus, high jitter may serve as a mark of followership, whereas leaders perform nonjittery motion that may be called, borrowing a term from drawing, a confident line.

In contrast to LF rounds, we found that JI rounds displayed periods in which both players showed synchronized, confident lines, with little jitter (Fig. 3C and SI Appendix, Fig. 9). In these coconfident periods, the players created motion together without showing marks of followership. To quantify these coconfident periods, we measured the percentage of time that both players showed relatively jitterless motion (periods of nonzero motion longer than 2 s in which the Fourier rms power in the 2–3 Hz band of the difference between the players’ velocities is less than 10% of their mean velocity). JI rounds showed 12% of such coconfident motion, whereas LF rounds showed 2% (Fig. 3D, P = 0.013).

The average duration of coconfident periods in JI rounds was 4.6 s (SI Appendix, Fig. 10). Out of the 27 JI rounds in our dataset, 10 rounds (37%) had periods of coconfident motion, covering on average 12.3 s. One of the JI rounds showed coconfident motion for 42 s (SI Appendix, Fig. 11). The coconfident motion was as complex as the motion of leaders in LF rounds (SI Appendix, Fig. 12). The coconfident periods were among the most synchronized in the dataset (mean dV = 0.12, mean dT = 38 ms). However, the rest of the JI motion (the noncoconfident motion) was still significantly more synchronized on average than LF motion (SI Appendix, Figs. 13–15).

These findings may indicate that expert improvisers can perform JI, at least part of the time, not by repeatedly switching roles of leader and follower, but by managing to agree on motions together.

As a control, we also tested novices without improvisation experience. We found that novices showed significantly lower precision, less accurate timing, and smaller range of velocities than experts (SI Appendix, Figs. 16–18). In contrast to experts, they performed JI more poorly than LF rounds (SI Appendix, Figs. 19–21), and showed high jitter in both LF and JI rounds (SI Appendix, Fig. 22). This highlights the difficulty of the JI task, which requires not only tracking but also initiating motion together.

Mathematical Model Suggests a Mechanism Based on Mirrored Reactive–Predictive Controllers.

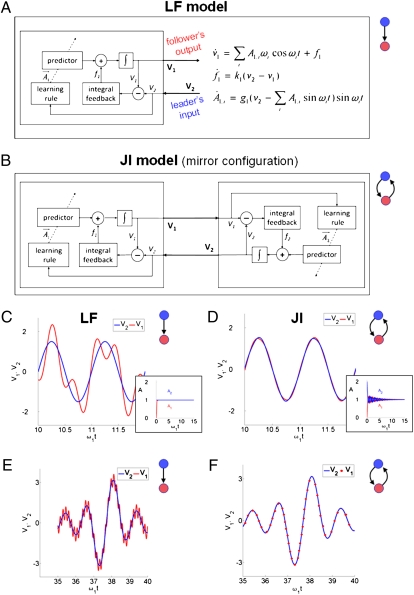
To gain further insight, we sought a simple mechanism based on control theory that can capture the present observations: (i) Show jitter when tracking a motion, but (ii) show jitterless accurate motion when two controllers are placed in a mirror configuration. We present an illustrative model whose properties can be exactly solved (Fig. 4).

Fig. 4.

Control model for the mirror game. (A) A reactive–predictive controller produces output motion υ₁ that tracks the input motion υ₂. The controller has a reactive unit (integral feedback, f₁) that compares υ₁ with υ₂, and a predictive unit that generates an expectation of the future motion. (B) Two reactive–predictive controllers in a mirror configuration, where the output of one is the input of the other. (C) A single controller tracks an input signal with jitter. Here the predictor has a single frequency, ω. (D) Mirrored controllers converge to precise jitterless motion. Initial conditions are A₁(0) = 2, A₂(0) = 0, υ₁(0) = 0, υ₂(0) = 0. (Insets) Predictor amplitudes A₁ and A₂ converge, so that controllers end up agreeing on future motion. Here k₁ = k₂ = 1, g₁ = g₂ = 10. (E and F) Same as C and D for a predictor with five frequencies (ω₁,…,ω₅ = 0.025, 0.05, 0.075, 0.1, 0.125). F shows the motion of mirrored controllers, after a transient time, in response to initial conditions A_i,1(0) = A_i,2(0) = 0,υ₁(0) = 0,υ₂(0) = 1. E is the motion of a single controller receiving the motion of F as input.

Our model uses reactive and predictive controllers as basic elements. We chose this model following common practice in modeling human tracking of moving objects (26, 27), robotic control, and human–robot interaction.

Reactive control corrects motion according to the perceived difference between the hand and the tracked object. The reactive controllers compared the input and output velocities, with time constants k₁ and k₂, for the two players. Predictive control includes an internal model of future motion, and learns the predicted motion by updating this internal model based on the motion of the tracked object. The predictor has an internal model that learns the amplitudes A_i(t) of a Fourier series 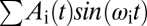. This predictor can thus represent any reasonably smooth motion, including one with temporal changes in amplitude and frequency. Both players had their own internal model, A_i,1(t) and A_i,2(t).

In the LF condition, a single controller tracked a given input υ₂(t) (Fig. 4A). Solving the model analytically showed jittery tracking similar to that observed in the present human data for LF rounds. The jitter is due to the inability of the reactive controller to precisely follow a dynamic signal (Fig. 4 C and E). [Note that it is possible to design a controller that follows such motion without jitter (26); however, here we chose a controller that shows jitter as observed]. The jitter frequency was determined by the time constant of the reactive controller, 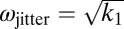. Jittery tracking was reached after a transient time determined by the rate constant g of the learning equation of the predictor.

The JI condition was modeled by two such controllers in a mirror configuration such that the output velocity of one controller is the input for the other (Fig. 4B). This resulted in joint motion that, after a transient time, lacked jitter and showed precise tracking up to high frequencies (Fig. 4 D and F and SI Appendix, Fig. 23). Tracking only broke down at frequencies higher than a critical frequency .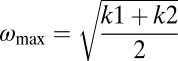

The model thus predicts that the maximal frequency possible in JI rounds is similar to the jitter frequency in LF rounds, ω_jitter ⋍ ω_max, in agreement with the present human data in which both frequencies are about 2.5 Hz, as described above.

We note that these qualitative conclusions are valid for a wide range of model parameters and do not require tuning of parameters. The model suggests that the author of the joint motion is the implicit agreement of the two predictors about future motion: The two predictors converge to equal amplitudes in their internal model A_i,1 = A_i,2 (Fig. 4D, Inset).

Discussion

This study presents an experimental paradigm for studying joint improvised motion based on the mirror game. We find that expert improvisers show better precision and performance when there is no designated leader than when a leader is designated. When a leader was designated, the follower showed a 2–3 Hz oscillation, which we term “jitter,” around the leader's smooth trajectory. When no leader was designated, experts showed periods when both players performed smooth, synchronized, complex motion with almost no jitter. Thus, they performed joint improvisation, at least in part, like two leaders in agreement. A model of mirrored controllers captures some of these observations, and suggests that the choreography in joint improvisation emerges from spontaneously generated implicit agreement on future motion.

These results indicate that people can enter a state of joint improvisation in which both lead the motion, and in which performance is high. This may correspond to the moments of togeth-erness reported by improvising musicians and actors (15–17). Moments of togetherness are rare in life, and are probably even more rare under experimental conditions. We therefore focused on expert improvisers to increase the probability of finding such moments in an experimental setting. In this context, we note that novices did not seem to enter the co-leadership state in the mirror game, and had lower overall performance, particularly when no leader was designated. Future studies can explore what conditions and training may enhance the likelihood of entering states of togetherness.

The mirror game, involving mutual motor imitation, may tap into a fundamental mechanism of human interaction. Mirroring is a basic form of social communication (28), thought to be involved in the establishment of parent–baby bonds (29) and to enhance children's play (14) and rapport between people (30). The mirror game offers a scenario in which two people create novel behavior together that is simple enough to study quantitatively. The present approach thus offers an empirical window for exploring the dynamic, cognitive, and physiological aspects of joint improvised action.

Materials and Methods

Subjects.

Twelve expert improvisers [six males and six females, age mean (SEM) 49.4 (2.9)] had at least 10 y of experience in playback theater (31, 32) (n = 9), movement improvisation (n = 1), or jazz music (n = 2). Individuals participated in one (n = 8), two (n = 3), or four (n = 1) games. The research protocol was reviewed and approved by the president and fellows of Harvard College, on behalf of the Harvard University Committee on the Use of Human Subjects.

Setup.

Custom hardware was developed for measuring motions of a pair of players in the one-dimensional mirror game. Players moved handles along parallel tracks 545.2 mm long. Handle positions were measured by an encoder at a spatial resolution of 0.94 mm and temporal resolution of 20 ms. The handles were clear plastic ellipsoids (length 101 mm, width 52 mm) colored red and blue. Handle tips were 71 mm apart. Data were recorded on a laptop computer using dedicated software. Two colored lights, red and blue, located at the side of the system (right side of blue player), indicated the type of round. A bell sound indicated the start and end of each round.

Procedure.

Players sat facing each other holding the handles comfortably with both hands. The system was placed on a low table (height 0.5 m). Each round started with either the red light turning on (for “red leader” LF rounds), the blue light (for “blue leader” LF rounds), or both lights turning on (for JI rounds). Two seconds after these lights, a bell sound indicated the start of the round. The end of the round was indicated by all lights turning off, and the same sound. Trials were separated by a 10-s pause in which players were instructed to relax and, if they wished, remove their hands from the handles. Nine rounds, each lasting 60 s, were counterbalanced in the following order: blue, red, JI, red, JI, blue, JI, blue, and red. An extra JI round of 180 s followed the first nine rounds. This last round was not used for the results reported in this study. The results remain qualitatively the same if the 180-s JI round is included in the analysis.

Before the actual game, a practice game consisting of three 15-s rounds (blue, red, and JI) was used to acquaint players with the procedure. Before this practice, the game and the procedure were explained to the players (see full instructions in SI Appendix). Subjects were instructed that the goal of the game is to “imitate each other, create synchronized and interesting motions, and enjoy playing together.” The experimenter emphasized that the game is not a competition, and that the goal is to enjoy creating motions together. The experimenter was not present in the room during the game. At the end of the game, players were debriefed and any additional questions were answered.

Data Analysis.

Velocity signal (position derivative smoothed by median-Gaussian filter over five temporal samples) was segmented, with segments defined as periods longer than 300 ms between zero-velocity events, with end-to-end distance longer than 28 mm. Few very long segments (>8 s) were removed (n = 17, 0.9% of total segments). In total, segments covered 65% of the experimental data, the rest being chiefly times of zero motion. Accuracy was measured in corresponding pairs of segments from the two players. A corresponding pair was defined as having the start and end of movement of the two players within 400 ms of each other. Spatial accuracy dV was defined as the mean relative difference in velocity over all samples i in the segment: 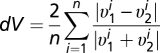. Temporal accuracy dT was defined as the time difference between segment end points. Maximal velocity V_max was defined as the average of the maximal velocities of the two players in the segment.

Jitter was evaluated with a bandpass filter centered at 2.5 Hz, divided by rms of total velocity, in a moving window of size 0.67 s. To define coconfident motion, we used jitter as a criterion, seeking periods of motion when both players have little jitter. Coconfident periods were defined as periods of nonzero motion longer than 2 s in which the Fourier rms power in the 2–3 Hz band of the difference between the players’ velocities is less than 10% of their mean velocity. Fraction of coconfident motion is expressed relative to total time of nonzero motion.

Jitter is motion with frequencies in the 2–3 Hz band overlaid on lower-frequency motion. Thus, for detecting coconfident motion, we could not analyze motion whose main spectral component was in high frequency—such motion does not have sizable low-frequency components, and hence it is not possible to define jitter. In the detection of coconfident motion, we therefore excluded motion in which more than 70% of the total power was in frequencies above 1.5 Hz. This excluded motion comprises 3.6% of the motion in LF rounds and 3.8% in JI rounds. Within this high-frequency motion, there exist periods of good synchrony, as evidenced by low-velocity error (dV < 0.3; SI Appendix, Fig. 3), which are not captured by the present coconfident motion detector.

Solution of Control Model.

Consider for simplicity the model with a single predictor frequency ω. The LF rounds are modeled by leader “input” velocity υ₂ = A₂sin(ωt), with constant amplitude A₂. The derivative of the follower velocity is 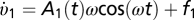, with integral feedback control 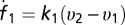and learning rule dA₁/dt = g(υ₂ − A₁sin(ωt))sin(ωt), which derives from minimizing the error E = 1/2(υ₂ − A₁(t)sin(ωt))² by hill climbing, dA₁/dt = −gdE/dA₁. The solution is 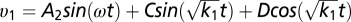, showing jitter with frequency 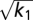around the leader's motion. JI rounds are modeled by mirroring two controllers, so that 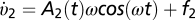, , 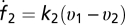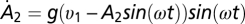. The solution at long times for the velocity difference approaches zero, υ₁ − υ₂ → 0, as long as 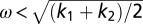, as can be shown by solving for u = υ₁ − υ₂, in the limit of slowly varying a = A₁ − A₂. This results in a linear driven oscillator equation ü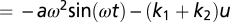, whose solution is u = −(aω²/(k₁ + k₂ − ω²))sin(ωt). The resulting equation for the predictor amplitude difference is then , so that a (and consequently u) converges to zero, because 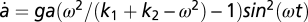, which is a first-order decay equation with a nonpositive time-dependent rate, as long as 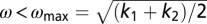. Instability occurs when ω > ω_max. For a multifrequency predictor (Fig. 4 E and F), a similar but more involved analysis shows the same conclusions. Transient time τ for the velocities to converge to jitterless motion in the mirror configuration is longer than 1/g, and depends on frequencies. It is solved in SI Appendix, Fig. 23, showing at low frequencies gτ ∼ (ω_max/ω)², and near ω_max gτ ∼ ω_max/(ω_max − ω). Thus, the transient time diverges at very low frequencies and very near to ω_max. It is minimal, gτ_min ⋍ 6, at a frequency ω* ⋍ 0.9ω_max, possibly corresponding to the highly synchronized motion of area 2 in Fig. 2E. The present model differs from the class of models that have been used to describe aspects of collective behavior such escape panic (33) and bird flocking (34). These models use a reactive element but lack a predictor element. Jitter due to the reactive controller may relate to the inner critic concept of improvisation (10, 11).