Large-area optoelastic manipulation of colloidal particles in liquid crystals using photoresponsive molecular surface monolayers

Abstract

Noncontact optical trapping and manipulation of micrometer- and nanometer-sized particles are typically achieved by use of forces and torques exerted by tightly focused high-intensity laser beams. Although they were instrumental for many scientific breakthroughs, these approaches find few technological applications mainly because of the small-area manipulation capabilities, the need for using high laser powers, limited application to anisotropic fluids and low-refractive-index particles, as well as complexity of implementation. To overcome these limitations, recent research efforts have been directed toward extending the scope of noncontact optical control through the use of optically-guided electrokinetic forces, vortex laser beams, plasmonics, and optofluidics. Here we demonstrate manipulation of colloidal particles and self-assembled structures in nematic liquid crystals by means of single-molecule-thick, light-controlled surface monolayers. Using polarized light of intensity from 1,000 to 100,000 times smaller than that in conventional optical tweezers, we rotate, translate, localize, and assemble spherical and complex-shaped particles of various sizes and compositions. By controlling boundary conditions through the monolayer, we manipulate the liquid crystal director field and the landscape of ensuing elastic forces exerted on colloids by the host medium. This permits the centimeter-scale, massively parallel manipulation of particles and complex colloidal structures that can be dynamically controlled by changing illumination or assembled into stationary stable configurations dictated by the “memorized” optoelastic potential landscape due to the last illumination pattern. We characterize the strength of optically guided elastic forces and discuss the potential uses of this noncontact manipulation in fabrication of novel optically- and electrically-tunable composites from liquid crystals and colloids.

Reconfigurable self-assembly of micrometer- and nanometer-sized particles of various shapes and chemical compositions is of great interest from the standpoints of both fundamental science and practical applications (1–14). The use of anisotropic liquid crystal (LC) fluids as host media for such colloidal self-assembly is currently perhaps one of the most promising approaches (2–14). It not only allows one to engender anisotropic long-range interaction forces and achieve oriented self-assembly guided by the long-range orientational order of the LC host (2), but also enables control of the medium-mediated interparticle forces by means of varying temperature, applying external fields, and utilizing the response of LC alignment to the presence of various chemical substances (3–14). Properties of such tunable self-assembled LC-based composite micro- and nanostructured materials can be further engineered by controlling positions and orientations of constituent particles of desired material compositions, shapes, and sizes (6), which is important for LC usage beyond the conventional display applications. For example, optical metamaterials are a new class of typically nanofabricated composites that can be engineered to have unprecedented optical properties, such as negative refraction of light (15–20). They consist of ordered arrays of predesigned structural units that play the role of “building blocks,” similar to that of molecules and atoms in conventional condensed matter systems (15–17). Optical control of such building blocks may potentially provide the means for large-scale fabrication and all-optical device applications of metamaterials (20). However, conventional optical manipulation does not simultaneously achieve the required high resolution and the large-area control, owing to the need for tight focusing of high-power beams (21–23). Although high-throughput, large-area optical manipulation has been achieved by use of optically-directed electrophoretic, dielectrophoretic, and other forces (23–30), these approaches are often restricted to specific types of particles, require application of fields in addition to the use of light, and cannot be applied to large-area manipulation in anisotropic LC fluids (30).

In this work, we decorate confining plates of LC cells with photoresponsive surface monolayers of azobenzene-containing dMR (derivative of Methyl Red) and demonstrate high-throughput large-area manipulation of fluid-borne particles. Light of intensity from 1,000 to 100,000 times smaller than that in laser tweezers allows us to perform rotational and translational noncontact manipulation of particles and colloidal superstructures with varying sizes, shapes, and compositions. This is achieved by controlling surface boundary conditions for the LC alignment through the illumination of photoresponsive azobenzene-based surface monolayers (31–36). The optical control of the landscape of ensuing elastic forces and noncontact manipulation can be achieved on centimeter scales and are of interest for fabrication of novel optically and electrically-tunable LC-based composites.

Results and Discussion

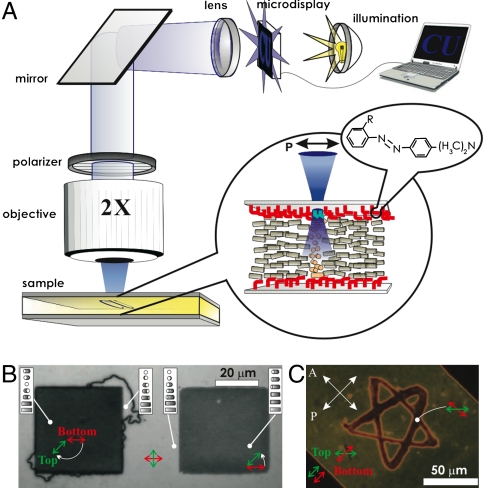
Liquid crystals are complex fluids with orientational ordering of anisotropic nanometer-sized molecules described by the director N with nonpolar symmetry (N ≡ -N) (1, 37). From the standpoint of optical properties, they are uniaxial crystals with an optical axis along N (37). External fields and surface boundary conditions can cause spatial patterns of molecular alignment described by the coordinate-dependent director field N(r). Display and electrooptic applications of LCs typically involve rubbing of polyimide-coated confining substrates to set boundary conditions for the large-scale uniform alignment described by the far-field director N₀, (2–14, 37) although optical alignment is also broadly used (31–36). When the LC is confined between glass plates with molecular monolayers, boundary conditions for N(r) can be set by controlling the orientation of the surface-bound dMR molecules in the so-called “trans” conformation state (Fig. S1). Linearly polarized light in the violet-blue part of the optical spectrum promotes the alignment of trans-state dMR and N(r) at the LC-dMR interface orthogonal to the polarization direction (Fig. 1A) (31–36). The desired N(r) structures (Fig. 1 B and C) can be obtained either by projecting light patterns by using a microdisplay (Fig. 1A) or by computer-programmed scanning of a 488 nm Ar laser beam using a setup shown in Fig. S2. By adjusting the focus to coincide with one of the two LC-dMR interfaces, one can independently define boundary conditions for N(r) at both surfaces (Fig. 1C). N(r) in the sample bulk adopts to satisfy these light-controlled surface boundary conditions, as seen from polarizing optical microscopy images (Fig. 1 B and C). One can induce different amounts of director twist across the cell, typically up to the maximum twist angle of about 3π/2, at which propagation of line defects relieves the strong twist distortions by transforming it into a less twisted state to minimize the elastic energy (Fig. S3). Lateral dimensions of the light-controlled N(r)-structures can be varied from about a micrometer to millimeters and larger, depending on pattern projection and objective lenses (if any). This dynamic optical control of N(r) permits manipulation of positions, orientations, and assembly of micro- and nano-sized particles (Figs. 2–4).

Fig. 1.

Light-controlled patterned alignment of liquid crystals via dMR surface monolayers. (A) A schematic showing the projection of a computer-controlled light pattern onto the dMR monolayer by use of a microdisplay and an objective lens. dMR molecules of the monolayer are bound to the surface by the functional group denoted by R (Fig. S1) and align with their trans-state azobenzene groups perpendicular to the linear polarization of the incident light (Inset), setting boundary conditions for N. (B) Polarizing microscopy image of coexisting LC domains with twist configurations shown in the insets by use of cylinders depicting the structure across the cell; N(r) between the dMR alignment directions at the bottom (red) and top (green) surfaces is twisted clockwise by 135° and counterclockwise by 45° in the left and right square-shaped domains, respectively; the bright areas between the squares have ± 90°-twist. (C) Independent control of boundary conditions at the top and bottom surfaces generates a star-shaped twist domain within a larger, differently twisted domain while maintaining a uniform N in the bottom left and top right corners of the image. Image (B) is taken between crossed polarizer P and analyzer A parallel to its edges and image (C) for orientations marked by white arrows.

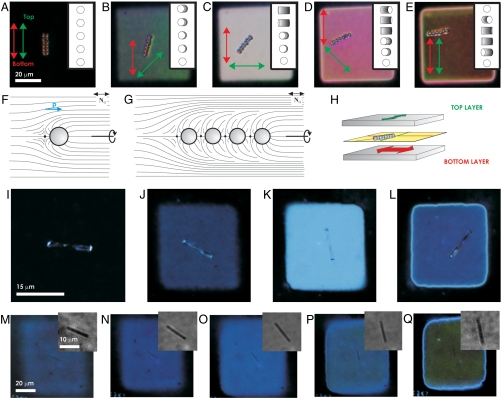
Fig. 2.

Optoelastic manipulation of colloidal rods and chains of spheres. (A–E) A self-assembled chain of dipolar 2 μm silica spheres dynamically controlled through the continuous rotation of the trans-state dMR molecules defining N at the surfaces. (F–G) N(r) around (F) a single dipolar sphere and (G) a chain of self-assembled spheres. (H) A schematic depicting the chain in the midplane of a cell with 90°-twisted N(r) across the cell as it rotates by half of the twist angle; chains, such as the one in (E), often rotate to an angle slightly smaller than a half of the N(r)-twist angle due to a combination of a small gravity-induced shift of the chain from the cell midplane downward and the proximity of the boundary between the twisted and untwisted domains. (I–Q) Rotational manipulation applied to (I–L), a glass rod of 3 μm in diameter and (M–Q), a silver rod of 100 nm in diameter. The insets in (M–Q), show fragments of the same images but with an enhanced contrast.

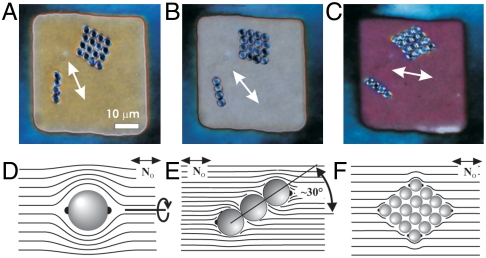
Fig. 3.

Light-directed self-assembly and control of colloidal architectures. (A–C) Self-assembled chain-like and diamond-shaped colloidal architectures of 3 μm melamine resin spheres rotating with N in the cell midplane (marked by a white arrow). (D–F) Schematics of N(r) surrounding (D) a single spherical particle with tangential surface anchoring, (E) a chain of such particles aligned at about 30° to the far-field director N₀ and (F) their diamond-shaped self-assembled structure with the long axis along N. We note that twisting of N(r) breaks the quadrupolar symmetry of director distortions around the particles with tangential surface anchoring. Each particle within the colloidal self-assembled structures has two boojums (black dots), although only some of them are shown in (E, F).

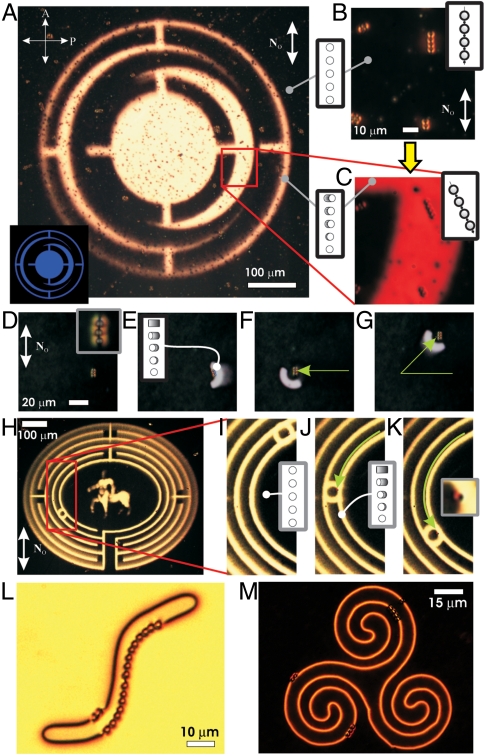
Fig. 4.

Large-scale optoelastic rotation and translation of colloids and their chains. (A) Large-scale projection of a pattern shown in the inset for massively parallel manipulation through the control of a dMR monolayer; N within the illuminated regions is twisted by 45° throughout the LC cell thickness. (B, C) Dipolar chains in a cell with (B) uniform and (C) twisted director structures before and after illumination, respectively. (D–G) Manipulation of a self-assembled dipolar colloidal chain via a continuous lateral translation of an illuminated region along the green arrows; the inset in (D) shows an enlarged view of the chain. (H) A twisted domain in the form of a labyrinth surrounded by a uniform N and used for the large-scale manipulation. (I–K) enlarged images of the labyrinth showing a particle trapped at the interface between the twisted and uniform domains [shown clearly in the inset of (K)] and translated for about 1 mm along one of the labyrinth pathways. (L, M) Individual colloids and their chains of different lengths trapped in the complex-shaped optoelastic traps formed between sample regions with different amounts of director twist controlled through polarized sample illumination; the particle trapping potential landscape can be dynamically reconfigured by varying light illumination patterns and can be also kept long-term constant without sample illumination. The dynamically controlled uniform and twisted N(r)-structures across the cell in marked regions are shown in the insets of (A, B, C, I, J). The far-field uniform director N₀ is marked by white double arrows.

Colloidal inclusions set vertical boundary conditions for N(r) at the surfactant-treated surfaces (Fig. 2F) and tangential conditions at the surfaces of bare colloids used in our studies (Fig. 3D). Director distortions and topological defects, such as the hyperbolic bulk point defect (Fig. 2F) or surface point defects called boojums (Fig. 3D), match these boundary conditions with the far-field director N₀. The ensuing N(r)-structures have either dipolar or quadrupolar symmetry (Figs. 2F and 3D, respectively). Elastic interactions between colloids with dipolar N(r) lead to the formation of chains of particles interspaced by point defects and directed along N₀ (Fig. 2 A and G), resembling interactions between electrostatic dipoles that form chains along electric field lines (2). Colloidal quadrupoles form chains at an angle of about 30° with respect to N₀ or diamond-shaped crystallites with one diagonal along N₀ (Fig. 3) (3, 4). All studied particles and structures elastically repel from both confining plates and localize in the cell midplane or close to it (13). Gradual rotation of the linear polarization direction of illumination light focused onto one of the dMR monolayers induces a twist of N across the sample thickness (Fig. 2 A–E). As light traverses through the cell with twisted N, its linear polarization follows the director twist (due to the so-called “Mauguin regime” of light propagation) (37), so that transmission of polarizing microscopy light between crossed polarizers reaches a maximum when N is twisted by π/2 (Fig. 2C) and a new local minimum when N twists by π (Fig. 2E). Particles and their structures, such as the dipolar colloidal chains (Fig. 2 A–E and Fig. S4), follow the rotation of N due to its twist while staying in the cell midplane (Fig. 2H). Similar rotation is achieved for glass microrods (Fig. 2 I–L), silver (Fig. 2 M–Q) and other nanorods (Fig. S5), as well as self-assembled chains and crystallites of particles with tangential boundary conditions (Fig. 3).

Optoelastic control of particles and their self-assembled architectures can be extended to large sample areas and to thousands of colloids without compromising resolution or robustness (Fig. 4). For example, we rotate preselected particles and their chains within illuminated regions of the projected pattern (Fig. 4A, Inset) by rotating the linear polarization of the illumination light to an angle two times the desired chain alignment angle (Fig. 4 A–C). By optically inducing elastic distortions next to colloidal particles or their assemblies, we localize them in a trap region with the strongest gradient of N(r) and then translate by continuously advancing the boundary conditions and, thus, the ensuing N(r)-pattern (Fig. 4 D–G). Optoelastic manipulation on large lateral lengthscales (not accessible to conventional laser tweezers) is demonstrated by translating an individual particle along an optically generated labyrinth-like structure of N(r) distortions (Fig. 4 H–K). This optoelastic control is applied to particles of various compositions and with shapes ranging from spheres to nanowires having facetted sidewalls that are simultaneously rotated and translated independently from each other (Fig. 4 and Figs. S4–S6).

What are the underpinning physical mechanisms that allow for the large-area low-intensity noncontact optical manipulation? Colloidal particles can either induce distortions of N(r) or barely perturb it, depending on their size and LC molecular interactions at their surfaces. In the latter case, characteristic for particles with small submicrometer size or with weak surface boundary conditions, placing a colloidal sphere of radius R in a region of the LC with preexisting twist elastic distortions across the sample thickness h reduces the elastic energy by ΔU = 2πK₂₂Δφ²R³/(3h²), where Δφ is the twist angle of N and K₂₂ is the twist Frank elastic constant (1, 37). This effect resembles both dielectrophoretic and conventional optical trapping: particles localize in optically manipulated regions with the strongest gradient of N(r) to reduce the elastic energy, just like high-dielectric-constant particles localize in the regions with the strongest gradients of electric field in dielectrophoretic and optical traps. The dynamically controlled region with large Δφ is an optoelastic trap that manipulates particles when the illuminated pattern is translated laterally. For particles with R≥50 nm and typical K₂₂ = 5 pN, ΔU is much larger than k_BT, thus permitting the robust translational optoelastic manipulation (Fig. 5A and Figs. S4 and S6), in addition to rotational manipulation (Figs. 2–4 and Fig. S5). The condition U ∼ (5–10)k_BT for reliable trapping (21) yields the minimum R ∼ 10 nm for trapping in cells with h ∼ (3–5) R. Even smaller colloids can be trapped in point or line singularities with isotropic defect cores; however, this type of manipulation is outside of the scope of this work.

Fig. 5.

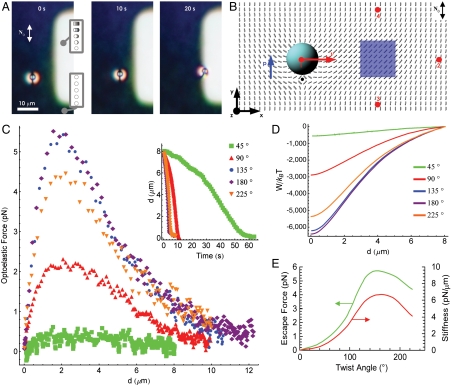
Optoelastic trapping force exerted on a colloidal particle by light-controlled twist distortions. (A) A series of video frames showing attraction of a dipolar colloid to a twist-domain optoelastic trap formed within a sample with uniform N₀; the elapsed time is marked on the frames. (B) Computer-simulated N(r) in the midplane of a cell with a dipolar particle and an elastic distortion induced by rotating N at one of the confining surfaces by π/2 (with respect to N₀) within the illuminated region (blue); the elastic dipole moment p and velocity v are marked by the blue and red arrows, respectively. (C) Optoelastic trapping force and (D) interaction energy vs. trap-particle distance for the various twist angles; the inset in (C) shows the experimentally measured trap-particle distance vs. time for different angles of director twist across the cell within the optoelastic trap. (E) Optoelastic escape force (green curve) and trap stiffness (red curve) vs. twist of N across the cell in the trap.

Colloids with strong boundary conditions induce dipolar or quadrupolar director distortions (Figs. 2F and 3D) that mediate their anisotropic interactions with each other and with the light-controlled N(r)-structures to minimize the elastic energy. Particle-trap interactions can be tuned from attractive to repulsive by controlling the symmetry of light-induced N(r)-distortions using dMR monolayers. For example, a particle with a dipolar N(r)-structure interacts attractively with the twisted domain shown in Fig. 5A, in order to eliminate the region of strong elastic distortions between the particle and the trap (Fig. 5B). A particle with the same orientation of the elastic dipole moment p in the position #2 experiences repulsion, because elastic distortions of the particle and the trap do not match and elastic energy decreases with increasing separation. Reversing the twist handedness in the domain or flipping p to point along the negative y-direction causes repulsion of a particle from the initial position #1 but attraction from the position #2, consistent with the corresponding elastic distortions. Particles always weakly attract to the optoelastic trap from the initial positions #3 and #4, regardless of twist handedness and orientation of p parallel or antiparallel with respect to N₀; they tend to localize at the corners of the optoelastic trap, again, consistent with the symmetry of corresponding elastic distortions. Similar to the case of conventional optical trapping in LCs (30), the equilibrium spatial localization of particles within the optoelastic trap depends on the overall N(r). The trapped particles with dipolar elastic distortions typically localize at the interface of twisted and untwisted LC domains (Fig. 5A and Fig. S4), where the N(r)-structure around the particle matches that of the domain boundary. Particles with higher symmetry, quadrupolar N(r) tend to localize in the central part of the twisted domains, where they displace the elastic-energy-costly LC region (Fig. S3 H and I).

Optoelastic trap-particle interactions are rather long-range, unlike those due to optical gradient forces in conventional laser trapping. This is due to the long-range nature of N(r)-distortions induced by the traps and particles with strong boundary conditions. Depending on the symmetry of N(r) in the optoelastic trap, these interactions—at large distances—qualitatively resemble dipole-dipole or dipole-quadrupole interactions in electrostatics. At short distances, the optoelastic force increases linearly with the particle’s displacement Δr from the equilibrium trapping position, exhibiting Hookean behavior F_oel = -k_oelΔr, where k_oel is the stiffness of the optoelastic trap (Fig. 5C). The peak value of attractive force occurs when Δr is comparable to the particle size and, in analogy with the conventional optical manipulation, it can be called the “escape force,” since it determines the external force needed to remove a particle from this optoelastic trap (Fig. 5 C and E). Although exerted forces depend on particle size and shape, cell thickness, and the involved N(r)-distortions, typical binding energies are within 100–10,000 k_BT, escape force within 0.1–10 pN, and k_oel within 0.1–10 pN/μm (Fig. 5 C–E). Maximum achievable optoelastic forces are about an order of magnitude lower than maximum optical gradient forces in conventional tweezers. Although the strength of optoelastic forces can be controlled at constant intensity by varying the light polarization alone, this control is more difficult than in conventional tweezers having trapping force proportional to the laser power that can be easily tuned. Because of this, the optoelastic method can have only limited uses in quantitative studies of interparticle colloidal forces, especially in the case of weak forces below 0.1 pN.

Optoelastic manipulation can be used for noncontact control of inclusions of different material compositions, regardless of their refractive index or other properties. This manipulation is not restricted to the use of high numerical aperture objectives, or any objectives for that matter. Since trapping of particles and exerted forces are determined by light-controlled elastic distortions within the nematic fluid, optoelastic control is independent of the exact mechanisms of projecting the dMR-guiding light patterns, as long as the resolution of images is larger than—or comparable to—the minimum size of distorted regions in a uniformly aligned LC. This minimum size depends on the competition of bulk elastic and surface anchoring energies described by the so-called anchoring extrapolation length l_e = K/W = (0.1–2) μm, where K is an average Frank elastic constant and W is the surface anchoring coefficient.

Similar to the case of conventional optical trapping, it is of interest to consider if gravity can set limitations on the size and type of particles manipulated by use of optoelastic forces. The gravitational force 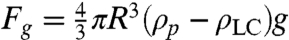, can be significant, especially for inorganic particles with density ρ_p much larger than the density of the LC, ρ_LC, where g is the acceleration gravity. However, the gravitational force is balanced by elastic forces that repel colloids from bounding plates with strong planar boundary conditions (13, 38, 39). The elastic repulsive force between a dipolar colloid (Fig. 2F) and a substrate decays with distance d as F_er ∝ K(R/d)⁴. Such elastic interaction with the confining surfaces tends to localize the particle in the cell midplane while gravity tends to displace the particle away from it (SI Text). Using the balance of elastic and gravitational forces, we have estimated the displacement of colloids from the cell midplane vs. particle size and particle-LC density mismatch (Fig. S8). Surprisingly, gravity sets no limits on the size of particles that can be manipulated using this approach. This is due to the fact that elastic forces increase with the particle size as ∝ R⁴ and easily overcome the gravitational force, which scales as ∝ R³, for large particles. The upper limit on the size of manipulated inclusions is set by the cell gap and the distance up to which the LC alignment can be reliably controlled (hundreds of microns).

Another important advantage of our approach is that—once elastic distortions are optically generated—the particles can be kept entrapped without the use of optical illumination or other external influence, which is impossible in the case of conventional optical trapping and other techniques. The LC cells preserve optically induced alignment and can maintain the landscape of optical trapping potential for long periods of time (months), as demonstrated for individual particles and colloidal chains of different length in Fig. 4 L and M. One can therefore form complex structures of patterned LC alignment and particles that can be dynamically changed by projecting time-varying illumination patterns or can be made stable over long time by use of the property of the LC/dMR system to “memorize” the last projected light pattern and the trapping potential landscape. On the other hand, because of the exquisite sensitivity of our manipulation technique, even ambient light can alter the “memorized” optoelastic trapping patterns in the cell; precautions are needed to avoid unwanted exposure to light to which dMR is sensitive.

To conclude, we have demonstrated a unique approach for large-scale optical manipulation of nano- and micro-sized objects that utilizes azobenzene-containing surface monolayers. This noncontact control of mesoscopic inclusions in LCs is of interest from the standpoint of light-guided self-assembly of tunable optical metamaterials and other reconfigurable nano- and micro-structured composites. Optoelastic manipulation will expand the available means of direct fundamental study of liquid crystalline colloidal dispersions (2–14, 30, 40), control of localized particle-like excitations in LCs (41), and generation of novel beams with phase singularities by use of light-directed liquid crystals (42). Although the optoelastic method cannot be used in biological manipulation and in quantitative force measurements, it provides a powerful experimental platform needed for the development of optically addressed information displays, composite materials, and all-optical devices.

Materials and Methods

Sample Preparation.

The nematic LC material pentylcyanobiphenyl (5CB) was obtained from Frinton Labs. The melamine resin and silica spheres (3 and 2 μm in diameter, respectively), silver nanorods (100 nm in diameter), and glass microrods (3 μm in diameter) were redispersed from aqueous dispersions to methanol and then to the LC by solvent exchange (SI Text). To obtain vertical boundary conditions for the LC molecular alignment on the surface of particles, we have treated the silica spheres with the surfactant [3-(trimethoxysilyl)propyl]octadecyl-dimethylammonium chloride (DMOAP). For this, we dispersed silica spheres in a 5 wt.% aqueous solution of DMOAP and sonicated it for 30 min. The particles were extracted via centrifugation at 3,000 rotations per minute and replacement of the solvent with deionized water. This process was repeated 5 times and the remaining water was then evaporated on a hot stage at about 120 °C for 10 h. The particles were added to the LCs and the obtained dispersion was again sonicated for 3 h to break colloidal aggregates.

To fabricate cells, glass plates of 1 mm or 0.15 mm in thickness were thoroughly cleaned by using detergents, deionized water, several organic solvents and plasma cleaning (supporting online material). To obtain the photosensitive surface monolayer on the glass plates, we submerged them into approximately 1 wt.% solution of 2-(4-dimethylamino-phenylazo)-N-(3-triethoxysilane-propyl)-benzamide (dMR) (43) in toluene at elevated temperature of 45 °C for 90 min to facilitate surface bonding of the dMR molecules. This was followed by a toluene rinse to wash away the excess dMR, blowing with dry nitrogen, and curing at 115 °C for 2 h. The glass cells were formed using plates bound by epoxy mixed with monodisperse spherical spacers of 4–20 μm in diameter to set the gap thickness. The cells were filled with the LC colloidal dispersions by capillary action and sealed with epoxy.

Image Projection.

We use an illumination system (Fig. 1A) consisting of a microdisplay with 1,024 × 768 pixels (EMP-730, Epson) that controls transmitted light intensity on a pixel-by-pixel basis, an objective lens, and a lamp light source with a blue filter (since the dMR is the most sensitive to violet and blue light, we use blue light for the patterned illumination). For imaging purposes, this system is integrated with an Olympus BX51 upright polarizing optical microscope. The desired dynamic illumination patterns are typically generated using animations in Microsoft PowerPoint, similar to the case of common overhead projection of presentations, except that the projection is done to much smaller areas using different optics and typically coupling to an optical microscope (Fig. 1). For some illumination experiments, we use scanning mirrors and a 488 nm Ar laser of a confocal imaging system FV-300 built around Olympus IX81 inverted microscope (Fig. S2). In both approaches, we project linearly polarized light of power within 1–100 μW onto the sample. This light is used to manipulate individual or multiple particles (tens of thousands) and their self-assembled structures at the same time and on the lateral scales ranging from microns to millimeters (Figs. 2–5). In both systems, we used objective lenses of numerical aperture within NA = 0.1–1.4 and with magnifications ranging from 2× to 100×. To avoid modification of the controlled N(r) patterns while imaging by means of transmission-mode polarizing microscopy, we minimized exposure of samples to white light by reducing exposure time and intensity while using maximum sensitivity of the Spot 14.2 Color Mosaic Camera (from Diagnostic Instruments, Inc.); alternatively, we used an optical filter that blocks visible light in the blue and violet ranges of the optical spectrum, to which the dMR is most sensitive (Fig. S1).