Curvature-driven capillary migration and assembly of rod-like particles

Abstract

Capillarity can be used to direct anisotropic colloidal particles to precise locations and to orient them by using interface curvature as an applied field. We show this in experiments in which the shape of the interface is molded by pinning to vertical pillars of different cross-sections. These interfaces present well-defined curvature fields that orient and steer particles along complex trajectories. Trajectories and orientations are predicted by a theoretical model in which capillary forces and torques are related to Gaussian curvature gradients and angular deviations from principal directions of curvature. Interface curvature diverges near sharp boundaries, similar to an electric field near a pointed conductor. We exploit this feature to induce migration and assembly at preferred locations, and to create complex structures. We also report a repulsive interaction, in which microparticles move away from planar bounding walls along curvature gradient contours. These phenomena should be widely useful in the directed assembly of micro- and nanoparticles with potential application in the fabrication of materials with tunable mechanical or electronic properties, in emulsion production, and in encapsulation.

Fluid interfaces are remarkable sites for directed migration and assembly of particles (1–6). When particles distort an interface, spontaneous, long-range interactions occur owing to capillary energy, given by the product of the surface tension and the area of the distortion. When distortions induced by neighboring particles overlap, the interfacial area decreases, resulting in capillary interactions that cause particles to attract and assemble. This effect, responsible for clustering of cereal in a bowl of milk (7), is now an important means for microparticle assembly at otherwise planar fluid interfaces, in particular for anisotropically shaped objects, which assemble with preferred orientations (4, 6, 8–13). At planar interfaces, the magnitude of the interaction is determined by the particle geometry, size, and surface energies. Hence, once the particles are placed at the interface, the strength of resulting capillary interactions is fixed. Assembly occurs at random locations on the interface determined by sites of initial encounter between the particles. In this work, we show that interface curvature can be employed as an external field to direct the location at which particles assemble. The phenomenon is entirely controlled by the coupling between geometry and capillarity. Therefore, it can be applied to colloids made of any material.

When an anisotropic particle is placed on a curved fluid interface, capillary interactions arise, as the area of the interface then depends on the particle’s orientation with respect to the principal axes and its location in a curvature gradient, resulting in torques (5, 14) and forces (5) on the particle. Because fluid interfaces can be molded and reconfigured using pinning sites, confinement, or applied fields, curvature-driven capillary interactions are potentially powerful means to amplify the magnitude of interactions and to direct microparticle assembly. Although these effects have been predicted in theory, they remain largely unexplored in experiment. In our recent work, we demonstrated the alignment of rod-like particles along principle axes of curvature. Here, we extend our earlier work by showing that particles can be driven along well-defined paths at interfaces owing to interactions driven by imposed gradients in the curvature field. Curvature gradients diverge at corners. We exploit this effect to create “hot spots” for particle assembly that have not been predicted previously, and demonstrate particle migration, orientation, and assembly at these preferred sites.

In the small slope limit, the interaction of the microparticle-induced deformation with the curvature field is akin to that of a multipole in an applied electric field (3, 15, 16). Microparticles of negligible weight distort the interface if the contact line (where fluid subphase, superphase, and particle meet) is undulated. Such contact lines can be generated by surface roughness, chemical heterogeneities (3, 17, 18), or by shape anisotropy (4, 6, 8–13). The resulting particle-induced deformation of the interface is a quadrupolar mode (3). These deformations are particularly pronounced for rod-like microparticles (4, 6, 10–14), which must bend the interface to satisfy their wetting conditions at the three-phase contact line. Furthermore, the axes of the quadrupolar deformation mode correspond to the major and minor axes of a rod-like particle, so alignments are readily evident. For these reasons, we use cylindrical microparticles to demonstrate curvature-driven orientation, migration, and assembly. We tailor interfacial landscapes to create curvature fields that orient, align, and steer microparticles. Although we exploit particle shape to deform the interface, theory suggests that these effects should occur for any microparticle with an undulated contact line on a planar interface—i.e., for particles with patchy wetting owing to roughness or chemical heterogeneities (3). Indeed, recent theory suggests that even smooth spheres in curved interfaces will create quadrupolar deformations and sense curvature gradients (19).

We create interface shapes with curvature fields of increasing complexity to isolate different features of the particle migration/rotation mechanism. For this purpose, we designed a set of experiments in which the interface is pinned at vertical microposts. By changing the shape of the micropost cross-section, we tailor the interface shape in a controlled manner. Particle trajectories are compared to a theoretical framework based on representing the particle-induced deformation as a quadrupole.

Results and Discussion

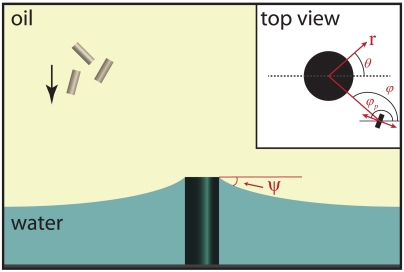
We first create an interface with a radial gradient in Gaussian curvature that drives particle orientation and migration along a straight path to sites of high curvature. To mold the interface shape, we use a vertical cylindrical micropost of height H_m = 300 μm and radius R_m = 131 μm fabricated from the epoxy resin SU-8 (see SI Text for experimental details). As shown schematically in Fig. 1, water is deposited so that its contact line is pinned at the top edges of the micropost, and the interface height decays with distance r from the micropost center with a slope at the contact line equal to - tan ψ, where 14° ≤ ψ ≤ 22°, as determined from a side view of the interface. Near the micropost (within several micropost radii) the interface shape h_m(r) is well approximated as a minimal surface 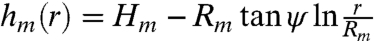. This surface has principal curvatures ± 1/R_c that depend on position and decrease with distance from the micropost as r^-2. In polar coordinates (r,θ) centered at the post, the principal directions of curvature are circles of constant r and radial lines of constant θ. Oil (hexadecane) is gently placed atop the water and micropost to prevent evaporation of the water layer and to preserve the interface shape.

Fig. 1.

Schematic of a curved oil–water interface with slope - tan ψ formed around a circular micropost. Cylindrical microparticles sediment through the oil phase, attach to the interface, and create deformations that interact with the interface curvature field. (Inset) Top view of the micropost with polar coordinates (r,θ) and of the particle-induced deformation, approximated as a quadrupole. The angle φ_p indicates the orientation of the quadrupolar rise axis, represented as a two-headed arrow. The angle φ indicates the orientation of the principal axis of curvature.

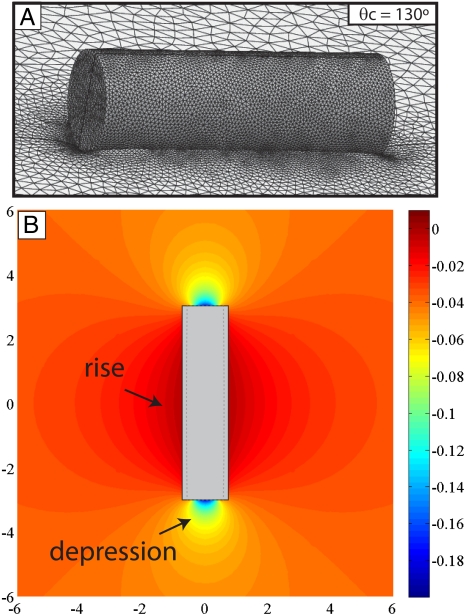
We study the behavior of cylindrical microparticles on this interface. The microparticles, also fabricated from the epoxy resin SU-8, have radius R_p = 5 ± 1 μm and aspect ratio Λ = L_p/2R_p in the range 2.0 ≤ Λ ≤ 3.0, where L_p is the particle length. The contact angle of water-SU-8-hexadecane is θ_c = 130° as determined by the sessile drop method. When these particles are located on the fluid interface, they deform it to satisfy the wetting conditions at the contact line where water, oil, and particle meet. The corresponding particle-induced deformation on an otherwise planar interface, determined numerically (see SI Text for details), is shown in Fig. 2. The deformation about the cylinder has an elongated quadrupolar structure, with depression at the planar end faces, and weak rise along the curved sides. Far from the microparticle, this deformation field can be described as a quadrupolar deformation mode in polar coordinates (3, 4, 6). Closer to the microparticle, the deformation field can be described as an elongated quadrupolar deformation most readily described in elliptical coordinates (6, 13). Within roughly three particle radii of the microparticle surface, near-field details dominate (6). The main features of the results in this work can be captured by approximating the particle-induced deformation field as a quadrupolar mode in either polar or elliptic coordinates (see SI Text and related Figs. S1 and S2).

Fig. 2.

Particle-induced deformation field around a cylindrical microparticle of aspect ratio Λ = 3.0 and contact angle θ_c = 130 ° on an otherwise planar interface determined numerically. (A) Side view. (B) Isoheight map. The deformation field has a quadrupolar structure with interface depression near the flat ends of the cylinder and rise along the curved sides.

To study the interaction of these microparticles with the curved interface, the microparticles are placed in the oil phase, where they sediment and attach to the interface in a side-on configuration (i.e., with their major axis tangent to the interface) (6, 20). Once attached, the particles are no longer affected by gravity, as the Bond number associated with the particle 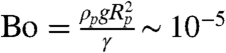, which measures the relative magnitude of gravity to surface tension, where ρ_p is the density of the particle, g is acceleration due to gravity, and γ is the interfacial tension.

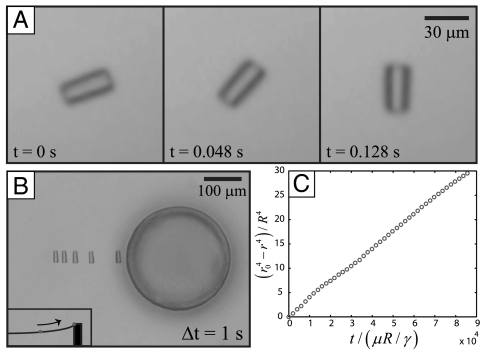
A typical particle trajectory for this simple case is shown in Fig. 3. Once attached to the curved interface, the particle rotates rapidly to orient along the principal axes (14) (Fig. 3A). Thereafter, it accelerates along a radial line toward the micropost, indicating that the force on the particle increases with proximity to the micropost (see Fig. 3B and Movie S1).

Fig. 3.

Particle rotation and migration along a curved interface. (A) Sequential images of a microparticle immediately after attachment to the interface. The particle rotates rapidly (within 0.128 s) to align its quadrupolar axes along the principal axes of the host interface. (B) Time-lapsed images of the microparticle position every 1.0 s. (C) The particle position r(t) obeys a power law r ∼ t^1/4.

The underlying mechanism for this migration is fundamentally different from that examined in prior work on bubbles (21) and heavy spherical particles (22–25), which follow gradients in interface height. In those studies, buoyant particles migrate uphill and heavy particles migrate downhill, like beads on a string, to minimize their gravitational potential energy. In our case, the gravitational potential of the particle is negligible. Furthermore, the Laplace pressure gradients owing to mean curvature gradients are negligible, so there are no pressure differences to drive the motion. Rather, migration is induced by changes in interfacial energy, which, in the superposition approximation can be expressed as

[1]

Here, ∇∇h₀ is the curvature tensor of the undisturbed host interface h₀ evaluated at the particle position and Π is the quadrupole moment tensor, a property of the particle-induced disturbance (see SI Text) (3, 26). The quadrupole moment tensor is independent of the curvature, and the particle thus follows gradients in interface curvature. For the results in Fig. 3, the curvature is maximum at the micropost, so particles migrate uphill. The quadrupole moment tensor is

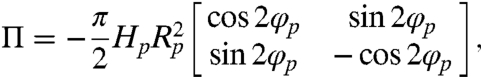[2]

where φ_p defines the orientation of the quadrupolar rise axis, R_p is the particle radius, and H_p is the deformation amplitude, which can be extracted from the simulated interface deformation around the particles (6). The curvature tensor is

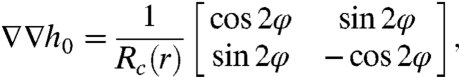[3]

where φ is the angle defining the orientation of the principal axes of curvature at r. Carrying out the scalar product between the two matrices in Eqs. 2 and 3, the energy becomes

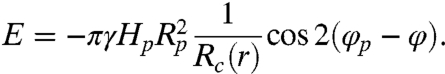[4]

We have derived Eq. 4 previously to understand the curvature-driven alignment of rod-like particles along principal axes in the absence of migration (14). This functional form also corresponds to the energy of interaction between a monopolar and quadrupolar distortion (27, 28) (see SI Text). This energy drives particle rotation, with a torque 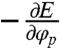comparable in magnitude to the capillary energy itself, to align the quadrupolar rise axes of the particle-induced deformation along the principal axes of the interface (i.e., φ_p = φ) (5, 14). The energy also drives particle translation with a radial capillary force 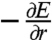. The relatively large torque compared to the force allows the particles to migrate while maintaining the “optimal” orientation φ_p = φ throughout its trajectory.

Recalling that 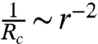, the expression for the curvature capillary energy in Eq. 4 implies a power law relationship between the radial location of the particle and time. The Reynolds number Re associated with the particle motion is small (Re ≤ 1.7 × 10^-3), so inertia is negligible and the migration rate is determined by a balance of the capillary force and the viscous drag F_drag = C_D6πμR_pU, where C_D is a drag coefficient of order unity, μ is the viscosity of the oil phase, and 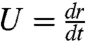is the particle velocity. This balance implies r ∼ t^1/4, which is confirmed by our experiments as shown in Fig. 3C. Because the curvature capillary energy is balanced by viscous dissipation, the magnitude of the interaction energy can be inferred according to

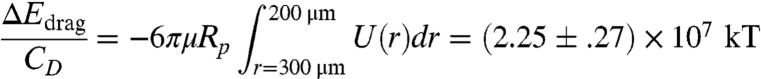for representative trajectories along host interfaces with Ψ = 22° for cylinders of radius 5 μm. Thus, curvature gradients provide remarkable energies for directed particle motion. These energies should remain significant for particles of much smaller scale; Eq. 4 suggests that

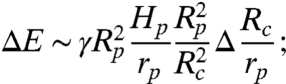thus, for similar geometries (i.e., fixing aspect ratios 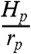and 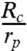), curvature-driven fluxes should remain significant for particles as small as tens of nanometers. For interfaces that present steeper curvature gradients relative to the particle dimension than in this experiment, curvature migration can remain significant at even smaller scales.

The particle rotation and migration reported in Fig. 3 are closely related to the motion of insects up curved menisci (29, 30). Insects located at fluid interfaces create distortions owing to their weight and by displacing their appendages or bending their bodies to excite capillary force distributions around their centers of mass. The resulting insect-induced disturbances resemble capillary monopoles owing to the insect weight, which would drive migration downhill, and capillary quadrupoles, which we show follow curvature gradients. The insects rotate and migrate to sites of high meniscus curvature upon creating these quadrupolar disturbances.

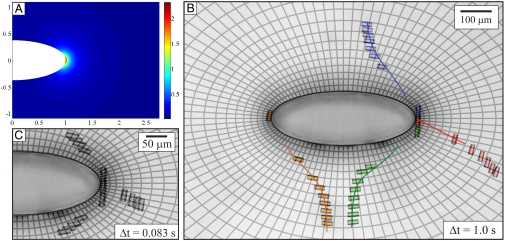
In our second experiment, we create a curvature field to steer particles along complex trajectories. We create this field by pinning the fluid interface to a micropost with an elliptical cross-section having height H_m = 300 μm, major axis a = 350 μm, and minor axis b = 135 μm with interface slope ψ ≈ 18° at the pole of the ellipse (i.e., at the point of intersection of the major axis with the contact line). We describe the shape of the interface in elliptic coordinates (s_m,t_m) centered at the micropost. The coordinate lines s_m and t_m are ellipses and hyperbolae, respectively; s₀ is the ellipse that conforms to the contact line. In these coordinates, the interface shape around the micropost can be described as an elliptical monopole (see SI Text). The corresponding curvature field is shown in Fig. 4A. Far from the micropost, curvature gradients resemble those around the circular micropost because the elliptical monopole converges to the polar monopole for s_m≫s₀. However, near the micropost, curvature gradients vary along the contour of the micropost from a minimum value at the minor axis to a maximum value at the poles.

Fig. 4.

Particle migration near an elliptical micropost. (A) Interface curvature field. The curvature is maximum near the poles of the micropost. (B) Top view of particle migration. Contours of constant s_m (ellipses) and t_m (hyperbolae) indicate the principal axes at each location. Time-lapsed images are shown for four particles; the particles attached to the interface in the following order (false color images): red, green, blue, and orange. Along each trajectory, particles align with their major axes tangent to contours of constant s_m. Trajectories agree with prediction based on pair potential (solid line). (C) Time-lapsed images. Particles accelerate near the poles of the micropost.

When microparticles attach to this interface, they align rapidly along the principal axes of the host interface, which are parallel to the coordinate lines, and veer toward the high curvature sites at the poles, as shown in Fig. 4B and Movie S2, maintaining their alignment with the principal axes along their path. Microparticle positions are reported in time-lapsed images every 1.0 s in Fig. 4B; the coordinate lines are also shown to indicate the principal axes of curvature at each location. Particle velocities vary nonmonotonically as they migrate through the complex curvature gradient field. Acceleration is highly pronounced near the pole of the micropost, as shown in the time-lapse images at 0.083-s intervals in Fig. 4C. The local curvature gradient, which is proportional to the particle velocity, increases as this site is approached. Finally, upon arriving in the vicinity of the pole, particles assemble influenced by particle–particle and particle–curvature interactions (6, 14). These results demonstrate that interfacial curvature can be tailored to steer particles to a given location and to create complex, curved trajectories that are not simply parallel to bounding surfaces.

We derive a closed-form expression for the capillary energy E (see SI Text) by modeling the particle-induced deformation as an elliptical quadrupole and calculating the curvature tensor corresponding to the elliptical monopole. This expression defines the energy gradient landscape around the particle and allows us to predict particle trajectories to within the drag coefficients for rotation and migration, which are unknown for nonspherical particles that excite undulations at an interface. We use tabulated values for the rotational drag coefficient for an immersed cylinder and a fitted value for the drag coefficient for migration extracted from the data in Fig. 3 (see SI Text). The predicted particle trajectories compare favorably to experiment (Fig. 4B).

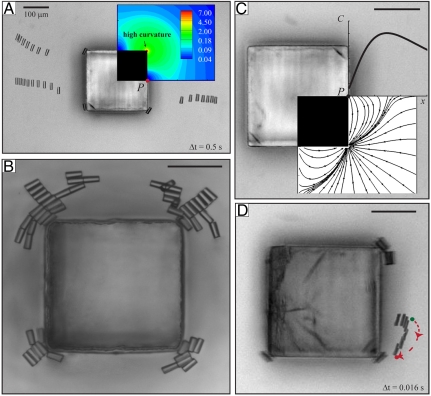
In our final experiment, we generate steep curvature gradients at specific sites to define “docking sites” for migration and assembly and to create assemblies that are not simply close-packed structures. A square micropost with sides of length L = 250 μm is used to pin the water interface under the oil layer. The curvature field is shown in Fig. 5A. Near the corners of the micropost, the interface curvature changes rapidly. Curvatures diverge at infinitely sharp corners, similar to the divergence of an electric field gradient near a pointed conductor (15); this divergence is limited by the finite radius of curvature of the corner in experiment and by the finite mesh size in the simulations discussed below.

Fig. 5.

Particle migration near a square micropost. (A) Time-lapsed images every 0.5 s showing microparticle trajectories. (Inset) Curvature field as determined numerically from the linearized Young–Laplace equation with slope ψ = 18° at point P. Steep curvature gradients are apparent near corners. (B) Complex structures formed by aggregated particles near the corners of the micropost. (C) Curvature gradient field creates a repulsive capillary interaction. (Inset) Curvature, denoted C, varies nonmontonically with distance from point P. (D) Time-lapsed image of microparticle tracing a curved trajectory along predicted curvature gradients. (Scale bars: 100 μm.)

When a microparticle attaches to this interface, it migrates toward the corners (Fig. 5A and Movie S3). When several particles are introduced to the system, they form complex structures at the corners owing to particle–particle and particle–curvature interactions, as shown in Fig. 5B. We have previously shown that, on planar surfaces, cylindrical particles assemble end-to-end with high reliability to make straight, rigid chains. Near the square microposts, the particles form curved assemblies, with end-to-end and side-to-side assemblies evident. Notably, in this figure (and in all experiments in which particles interacted with square microposts), the interface in the neighborhood of the micropost side midpoint remains devoid of particles. This particle-free zone develops because of a repulsive capillary force created by curvature gradients directed locally outward from the pillar, as shown in Fig. 5C, which depicts the curvature gradient field. These curvature gradients can be understood by considering the interface near the midpoint of the micropost side (indicated by the point P in Fig. 5). For a minimal surface, owing to symmetry arguments, the curvature is zero at P. Far from the pillar, the interface curvature decays like that around a circular micropost. Thus, along a ray perpendicular to the pillar passing through P, the curvature varies nonmonotonically; it first increases from zero, then decays as r^-2 (see Fig. 5C, Inset). The curvature gradient thus points away from the micropost near P, generating a local repulsion. Meanwhile, the curvature increases near the corner. The resulting curvature gradient field features curved paths shown in Fig. 5C. A time-stamped image of a particle tracing the predicted curved trajectory in this vicinity is shown in Fig. 5D and Movie S4.

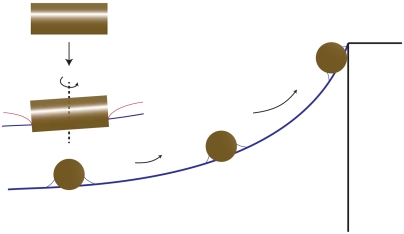
Capillary interactions between microparticles at otherwise planar interfaces have been explained by treating particle-induced deformations as capillary multipoles of various order. The convention for attraction between capillary multipoles differs from electrostatics in that regions of capillary rise (positive capillary charges) attract each other, as do regions of capillary depression (negative capillary charges). Although this simple rubric captures the far-field interactions among the microparticles at planar interfaces, it does not fully capture the curvature-driven interactions that we report here. Rather, the particle motion in these experiments can be understood in terms of the schematic shown in Fig. 6. Around any point, the host interface is shaped like a saddle. The undulated contact lines created by particles are also saddle-like. To minimize surface area, the particle must do two things. It must sit astride the host surface with the appropriate orientation and slide along the host interface to minimize the difference between the curvature of its deformation field and that of the host. This mechanism explains both the torque and the migration along nontrivial paths following the curvature gradients.

Fig. 6.

Schematic illustrating particle rotation and migration. Left to right, the particle rotates to orient its saddle-like contact line on the saddle-like host interface. Thereafter, the particle migrates to minimize the difference between the curvature of the particle-induced deformation and that of the host interface.

In conclusion, we have demonstrated that curvature gradients in fluid interfaces interact with particle-induced deformations to orient particles and drive them to sites of high curvature. The curvature field can be treated as an external field. Like external magnetic or electric fields, the curvature field can be tuned to create desired outcomes. To demonstrate this concept, we have tailored curvature fields to create attractive and repulsive sites, and used them to assemble microparticles into complex configurations. Because interface topography can be readily reconfigured, control over curvature provides a route to the dynamic control of microparticle assembly with potential application in emerging fields such as metamaterials (31, 32).

Materials and Methods

Additional information can be found in the SI Text, which includes the derivation of closed-form expressions for curvature-driven capillary interactions used to calculate the particle trajectories in Figs. 3 and 4; details for lithographic fabrication of particles and microposts; experimental details on the use of pinning sites to define the shape of host interfaces and methods for particle deposition on interfaces; details for simulations of interface shape; details regarding optical microscopy and particle tracking; and data analysis for calculation of particle trajectories and measurement of drag coefficients.