Carbon and sulfur back flux during anaerobic microbial oxidation of methane and coupled sulfate reduction

Abstract

Microbial degradation of substrates to terminal products is commonly understood as a unidirectional process. In individual enzymatic reactions, however, reversibility (reverse reaction and product back flux) is common. Hence, it is possible that entire pathways of microbial degradation are associated with back flux from the accumulating product pool through intracellular intermediates into the substrate pool. We investigated carbon and sulfur back flux during the anaerobic oxidation of methane (AOM) with sulfate, one of the least exergonic microbial catabolic processes known. The involved enzymes must operate not far from the thermodynamic equilibrium. Such an energetic situation is likely to favor product back flux. Indeed, cultures of highly enriched archaeal–bacterial consortia, performing net AOM with unlabeled methane and sulfate, converted label from ¹⁴C-bicarbonate and ³⁵S-sulfide to ¹⁴C-methane and ³⁵S-sulfate, respectively. Back fluxes reached 5% and 13%, respectively, of the net AOM rate. The existence of catabolic back fluxes in the reverse direction of net reactions has implications for biogeochemical isotope studies. In environments where biochemical processes are close to thermodynamic equilibrium, measured fluxes of labeled substrates to products are not equal to microbial net rates. Detection of a reaction in situ by labeling may not even indicate a net reaction occurring in the direction of label conversion but may reflect the reverse component of a so far unrecognized net reaction. Furthermore, the natural isotopic composition of the substrate and product pool will be determined by both the forward and back flux. This finding may have to be considered in the interpretation of stable isotope records.

Microbial catabolic pathways and their rates in habitats and cultures are frequently measured by adding isotopically labeled substrate and quantifying the rate of label appearance in the product pool. Such label flux is usually regarded as unidirectional and thus, assumed to represent the rate of substrate conversion. However, in enzyme kinetics, like in chemical kinetics, the concept of bidirectionality or reversibility of biochemical reactions is a long-established feature (1–5).* Hence, if substrate is converted to product through a multistep pathway and each reaction occurs with a back reaction, some steady flux of the terminal product by intermediate pools back to the substrate pool should occur. Such back flux is measurable by isotope labeling of the product and measuring label appearance in the vanishing substrate pool. This finding would, in principle, be analogous to the established measurement of isotope exchange to gain insights into basic enzyme mechanisms (1–5).

Like in enzymatically catalyzed single reactions, one expects that the back flux through the entire chain (sequence) of individual catabolic reactions should be more significant the less exergonic the overall reaction becomes, because an individual reaction within the sequence cannot be more exergonic (more irreversible) than the overall reaction. A weakly exergonic catabolism (energy metabolism) is common in strictly anaerobic microorganisms (6–11). Still, the possibility of product back flux in anaerobes has been largely neglected and treated only in relatively few labeling studies. The perhaps best-known example is the conversion of added ¹⁴C-methane to ¹⁴C-carbon dioxide during net methane formation by various methanogenic archaea (12–16). The enzymatic key reaction of this back flux, the methyl carbon exchange between added ¹³CH₄ and its direct precursor ¹²CH₃-coenzyme M, was recently quantified in an enzymatic assay, with all reaction partners present at equilibrium concentrations (that is, without net methane formation or consumption) (17). Furthermore, conversion of added ³⁵S-sulfide to ³⁵S-sulfate during net reduction with lactate by Desulfovibrio has been observed (18). The incorporation of added ¹⁴CO₂ into the carboxyl group of acetate during oxidation through the Wood–Ljungdahl (carbon monoxide dehydrogenase) pathway in an anaerobe is an example of partial product back flux (19, 20).

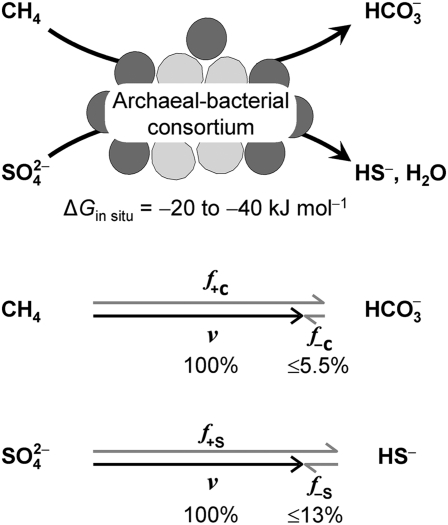
These studies indicate reversibility and operation close to thermodynamic equilibrium of specific substrate–product reaction sequences within an overall catabolism (that encompasses electron acceptor and donor). Here, we show reversibility of an entire anaerobic catabolism, including electron donor as well as the electron acceptor, and present a refined quantitative data evaluation to reveal the extent of back flux. The examined process is the anaerobic oxidation of methane with sulfate (AOM) (1),

which is energetically characterized by(Eq. 2)

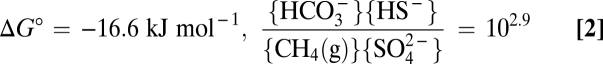and thus one of the least exergonic processes sustaining life (ΔG in situ is often between −20 and −40 kJ mol⁻¹) (21–23). It should, therefore, be associated with noticeable reversibility. AOM is of great environmental significance, because it counteracts methane release from marine sediments into the oxic biosphere (refs. 24 and 25 and references therein). It is catalyzed by consortia of phylogenetically distinct Euryarchaeota [anaerobic methanotrophs (ANME groups)] and associated Deltaproteobacteria; the latter are assumed to perform sulfate reduction (26–30). Labeling studies using natural sediment samples with AOM activity provided hints of ¹⁴CO₂ conversion to ¹⁴CH₄ during net AOM by the indigenous consortia (31–33). The mode of coupling, which does not seem to involve conventional anaerobic intermediates such as H₂ or acetate, remains a matter of discussion (SI Text, Anaerobic Oxidation of Methane as Enzymatically Catalyzed System and Fig. S1) (21, 23, 34–37).

Axenic AOM consortia have not been isolated so far. To clearly show reversibility of AOM and exclude microbial use of substrates other than methane and sulfate, we used essentially detritus-free marine AOM consortia that had been highly enriched by repeated transfer and growth with CH₄ and SO₄²⁻ as the only added energy source.

Results

Characterization of Enriched AOM Cultures.

The sediment-free, methane-consuming, and sulfide-producing enrichment cultures were first characterized with respect to the occurring phylotypes and unequivocal AOM activity to verify suitability for the isotope back flux studies. The abundant cells were archaea (ANME-2 groups) and Deltaproteobacteria (95–99% of detectable cells according to DAPI and specific 16S rRNA probing) (38, 39). Specific (dry mass related) activities for methane consumption and sulfide formation were ∼0.3 and 2.0 mmol g⁻¹ d⁻¹ in the Hydrate Ridge (HR) and Isis Mud Volcano (MV) enrichment cultures, respectively (39). Substrate labeling experiments with ¹⁴CH₄ and ³⁵SO₄²⁻ and product label quantification performed in this study yielded a molar ratio between formed CO₂ and H₂S of 0.96/1 (HR) and 1.07/1 (MV) in accordance with expression 1† (Table S1). From previous chemical analysis of incubations without methane, it is known that net methane production is marginal (i.e., <0.05% of the AOM rate) (39). The rate of net sulfide production without methane was <5% of the rate achieved in the presence of methane (Table S2). This finding showed that background methanogenesis and sulfate reduction with endogenous compounds, residual detrital matter, or dead cell carbon were essentially absent or very small, respectively. These cultures were, therefore, ideal to study the flux of labeled inorganic carbon and sulfide into the pools of methane and sulfate, respectively, when these compounds were present as substrates.

Sulfur and Carbon Back Fluxes.

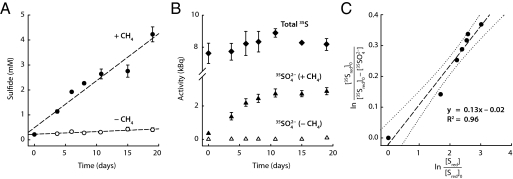
For convenience, product label back fluxes during net AOM were determined as rates relative to the culture volumes (rather than to biomass). Increase in sulfide concentration yielded methane-dependent sulfate reduction rates of 190 μmol L⁻¹ d⁻¹ (MV) (Fig. 1A) and 120 μmol L⁻¹ d⁻¹ (HR) (SI Text, Time Course Experiment with Consortia from Hydrate Ridge and Fig. S2A). In experiments with labeled sulfide, the overall ³⁵S activity was constant during the whole time series. Increasing amounts of tracer were recovered in the ³⁵SO₄²⁻ pool of AOM-active samples. However, in contrast to constant sulfate reduction rates (Fig. 1A and Fig. S2A), label transfer from the sulfide to the sulfate pool decreased during the course of the experiment because of the significant dilution of the ³⁵S-sulfide label with steadily forming unlabeled sulfide (Fig. 1B and Figs. S2B and S3). This dilution was taken into consideration by refined data evaluation (Materials and Methods and SI Text, Calculation of Reverse Reaction Rate). The determined rates of sulfur back flux were 7% and 13% (HR and MV, respectively) of the AOM rate based on chemical quantification (Figs. 1C and 2, Fig. S2C, and Table S2). The flux of ³⁵S label from the sulfide to the sulfate pool was negligible when AOM was prevented by omission of methane (Fig. 1B and Fig. S2B).

Fig. 1.

Time course experiment: the addition of labeled sulfide (product) to highly enriched, detritus-free consortia from Isis MV that perform anaerobic oxidation of methane. (A) Developing sulfide concentrations in the presence (•) and absence (○) of methane. (B) Development of ³⁵S-activity in the sulfate pool during incubation with (▲) and without (△) methane as electron donor. The total ³⁵S-activity (◆, sulfate + sulfide) is also indicated. The shown radiolabel was determined after incubation at the same time to eliminate the effect of decay. (C) Double logarithmic plot according to Eq. 16 to calculate the reverse rate; dotted line marks the 95% confidence interval.

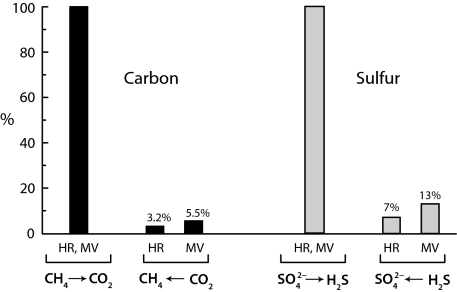
Fig. 2.

Comparison of reverse (back flux) to net reactions (set to 100%) during the anaerobic oxidation of methane with sulfate by highly enriched consortia from HR and Isis MV. Data analysis underlying sulfur back flux is in Fig. 1.

The calculated rates of the back flux of dissolved inorganic carbon (DIC; CO₂, HCO₃⁻, and CO₃²⁻) to methane (DIC → CH₄) were 3.2% and 5.5% (HR and MV, respectively) of the net AOM rate (Fig. 2 and Table S1). This finding is at least one order of magnitude higher than the methane–carbon back flux (CH₄ → DIC) during net methanogenesis in methanogenic cultures (0.001–0.36%) (12–14). The ratios between sulfur and carbon back fluxes were 2.2 and 2.4 (HR and MV, respectively) and thus, nearly identical for the two enrichment cultures. We also measured the flux of ¹⁴C label from the inorganic carbon pool to methane, whereas the net oxidation reaction was prevented by omission of sulfate in the presence of methane. Label from ¹⁴C-inorganic carbon still appeared in the methane pool at rates of 2.4% and 2.3% (HR and MV, respectively) of the AOM rate with sulfate (Table S1).

Discussion

As expected, our ³⁵S- and ¹⁴C-labeling results clearly showed substantial fluxes of sulfide back to sulfate and bicarbonate back to methane during AOM, and they confirm the reversibility of an entire catabolic process with low-energy yield. Such catabolic reversibility is viewed from a more general kinetic and thermodynamic perspective with respect to implications in the biogeochemical study of in situ catabolic rates and isotope patterns of biologically redox-active elements.

Concept of Catabolic Back Flux.

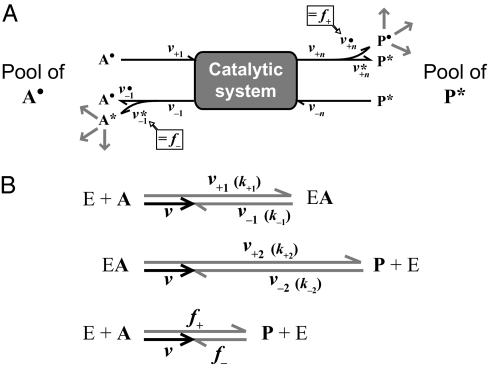
A catabolic pathway in cells of a prokaryotic species or community represents a complex sequence of many enzymatic reactions and intermediates (intercellular; in communities, they are also extracellular). If the subsequent reactions occur with reversibility and are viewed from the molecular perspective (that is, regarding microstates stochastically) at a given moment, the larger fraction of the enzyme molecules of each reaction performs the forward reaction, whereas a smaller fraction simultaneously performs the reverse reaction. The resulting macrostate is a system with substrate uptake and reoutput and product output and reuptake. For convenience, this finding is illustrated in Fig. 3 for a simple overall reaction, A ⇌ P, with indication of the rates (v) and label (*) added to the product pool; the unlabeled (^•) element is also indicated. Substrate reoutput (v₋₁) not only includes the part derived from product (v*₋₁) but also substrate that never reached the product side (v^•₋₁). In a steady state, the sum of the uptake rates must equal the sum of the release rates (i.e., v₊₁ + v_−n = v₋₁ + v_+n), which leads to the net rate v (Eq. 3):

Fig. 3.

Depiction of forward and back flux during the net reaction A → P in a steady state catalytic system with reversible but otherwise unknown internal reactions. Such a system can consist of an entire pathway (A) or a single enzymatic reaction (B; E + A → EA → P + E) (Figs. S4 and S5). All reactions, including uptake or binding and release, are reversible. Arrows indicate rates (velocities). The forward (v₊) and back (v₋) rates correspond to individual steps in a catalytic system. The index n refers to the number of forward and backward fluxes (B; n = 2 for a single enzymatic reaction) (Fig. S5). A description of abbreviations is given in Table S3. (A) Catalytic system: the fate of substrate and product is followed by the different labels (A^•, P*) of the initial pools. Release of A and P includes both the returned fraction that never reached the other side (v^•_–1, v*_+n), and the fraction directly derived from the other side (v^•_+n, v*_–1). Forward (f₊) and back (f₋) flux are the concentrations (amounts per investigated volume) of P^• and A* most recently derived per time from A^• and P*, respectively. Hence, return to the side of their origin with progressing reaction is neglected by examining a short time interval (A* in A^• and P^• in P* remaining very dilute). (B) Vector model for rates in a single enzymatic reaction (E + A → EA → P + E) (Fig. S5). The sizes of rates are indicated by lengths of arrows. The same net rate (v) is the difference of uptake (binding) and release of substrate (v₊₁, v₋₁) and product (v₊₂, v₋₂) as well as the difference between forward and back flux (f₊, f₋). The rate constants for a single enzymatic reaction, k₊₁, k₋₁, k₊₂, k₋₂, and the actual concentrations determine v₊₁, v₋₁, v₊₂, v₋₂, respectively. The vector model was calculated for the enzymatic reaction using (in rate units): v₊₁ = 6, v₋₁ = 4, v₊₂ = 9, v₋₂ = 7; result: v = 2, f₊ = 4.15, f₋ = 2.15 (Eqs. S35 and S36).

The rates of substrate formation from product (v*₋₁) and product formation from substrate (v^•_+n) are experimentally accessible by isotope labeling. For better distinction, we designate these particular rates v^•_+n = f₊ and v*₋₁ = f₋. Net disappearance of substrate, v = v₊₁ − v^•₋₁ − f₋, and mass conservation, v₊₁ −v^•₋₁ = f₊, yield for the net rate (Eq. 4)

Hence, the net rate is expressed by three pairs of rates (Eqs. 3 and 4; for single enzyme shown in Fig. 3B), with f₊, f₋, and v being experimentally accessible. During net reaction A → P, there are the inequalities (5 and 6)

and

Flux Rates and Free Energy.

Thermodynamic values such as free energies are based on macroscopic time-independent equilibria, and they cannot, in principle, predict reaction rates, which are determined by molecular mechanisms. However, the actual free energy change (more precisely, the change in chemical potential) and rate of a reaction are both determined (at constant temperature) by concentrations (strictly speaking, by activities in the case of chemical potentials). The thermodynamic and kinetic treatment of a reaction must, therefore, meet each other at equilibrium, where the free energy as well as the net reaction rate (resulting from concentration-dependent forward and back reaction) is zero. This connection‡ has been a basic aspect in enzyme kinetics (1, 3–5, 40). A similar analytical treatment of the connection between energetics and kinetics of the here investigated microbial catabolic system is presently impossible in view of its complexity and the largely unknown enzymes and intermediates. To substantiate the initial argument that the reverse flux must increase relatively with decreasing free energy, we present this connection for a simple enzymatic reaction, again formulated with one substrate, A, and one product, P. Furthermore, only a lumped enzyme-bound state, EA, appears in the reaction (Fig. 3 and SI Text, Thermodynamics and Kinetics in Catabolism); kinetic constants are designated as k.

As for a reversible, two-step purely chemical reaction, formulation of equilibrium conditions (SI Text, Thermodynamics and Kinetics in Catabolism) yields k₊₁k₊₂/(k₋₁k₋₂) = [P]_e/[A]_e (the parameters [P]_e and [A]_e indicate concentrations at equilibrium). This leads to the Haldane relationship. Its common formulation includes the experimentally accessible Michaelis (composite) constants K_m+ = (k₋₁ + k₊₂)/k₊₁ and K_m− = (k₋₁ + k₊₂)/k₋₂ for the forward and reverse reactions, respectively, which are obtained through multiplying nominator and denominator with k₋₁ + k₊₂. By designating k₊₂ = k_cat+ and k₋₁ = k_cat− (catalytic constants for product and substrate formation, respectively) and expressing the equilibrium constant, K_e, through the standard free energy change, ΔG° (SI Text, Thermodynamics and Kinetics in Catabolism), the Haldane relationship can be expressed as (Eq. 7)

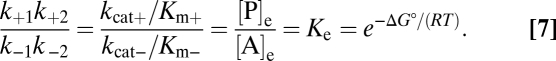A certain imprecision lies in the fact that concentrations (in kinetics) and activities (in thermodynamics) are treated here as numerically equivalent.

Under nonequilibrium conditions, the net reaction rate v ≠ 0 results from the individual rates or fluxes (Eq. 3 or 4, respectively), which are determined by the actual concentrations, [A] and [P], and the kinetic rate constants, k₊₁, k₊₂, k₋₁, and k₋₂. The latter again are connected by Eq. 7. [A] and [P] also determine the actual free energy, ΔG < 0. This finding leads to a connection between the flux ratio, f₋ and f₊, and the actual free energy (where the standard free energy, ΔG°, no longer appears; derivation in SI Text, Thermodynamics and Kinetics in Catabolism) (Eq. 8):

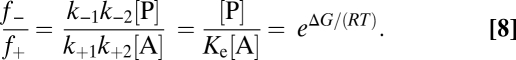With Eq. 4, the back flux can be also related to the net rate (Eq. 9):

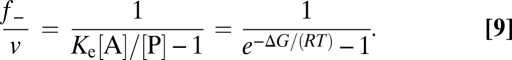Eqs. 8 and 9 express that forward and back flux catalyzed by an enzyme at given substrate and product concentrations cannot vary independently of each other (because the kinetic constants cannot vary independently) (Eq. 7). The equations also show that the back flux relative to the forward flux or net rate becomes the more relevant the closer the reacting system is to the thermodynamic equilibrium. Marginal to essentially no back flux can only be expected for strongly exergonic linear reaction sequences (very negative ΔG).

Remarks on Back Flux Through an Entire Catabolism with Special Reference to AOM.

Accordingly, relevant product back flux is expected in microbial cells or cell communities catalyzing cascades of enzymatic reactions through a weakly exergonic catabolism. A catabolism operating not far from the thermodynamic equilibrium can only include reactions that are at least as close to the equilibrium [that is, that cannot be strongly energy-dissipating (irreversible)]. The process in our experiments, AOM, is one of the least exergonic catabolic processes. Under the incubation provided in this study, the calculated free energy change (21) for AOM is only −25 to −35 kJ mol⁻¹. The range in natural habitats is often −20 to −40 kJ mol⁻¹ (22, 23). The free energy actually dissipated by the in vivo catabolism is less negative than these calculated values because of coupling to energy conservation. Such coupling may be an important factor contributing to catabolic reversibility and back flux. Largely irreversible, energy-dissipating reactions during AOM are expected only in the anabolism (biosynthesis).

Sulfur back flux was at least two times as fast as carbon back flux during AOM. This finding shows that back fluxes (and forward fluxes) of electron acceptor and electron donor are not necessarily stoichiometrically coupled. This finding is in contrast to the ratio of their net rates, which in a steady state must always reflect the overall stoichiometry. Hence, the pathways of the electron acceptor and electron donor may be differently close to the equilibrium. This finding is analogous to enzymatic reactions with two (or more) substrates and two (or more) products, where isotope exchange rates may differ between substrate–reactant pairs depending on their mechanisms and individual rate constants (3, 4).

The extent of the relative reverse reactions in the 20 °C (293 K; MV) enrichment was higher than in the 12 °C (285 K; HR) enrichment (Fig. 2). Because the equilibrium constant, K_e (T, p), and hence also free energy change of a reaction (at given concentrations) are temperature-dependent, the extent of the reverse reaction relative to the forward or net reaction must be generally influenced by temperature. A thermodynamic prediction of this tendency is appealing. The equilibrium constants at two different temperatures (indices 1 and 2; T₂ > T₁) can be related to each other by (Eq. 10)

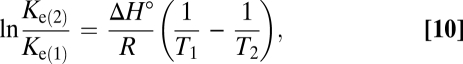where ΔH° is the standard enthalpy change of the reaction.¶ With ΔH° = −11.4 kJ mol⁻¹ (assumed to be the same for 285, 293, and 298 K) for AOM, the ratio of the equilibrium con-stant of AOM at the two temperatures in this study is K_{e(293 K)}/K_{e(285 K)} = 0.88 (that is, <1). The extent of the reverse reactions is inversely proportional to the equilibrium constants (Eqs. 8 and 9). Therefore, the extent of the reverse reactions of AOM at higher temperature to the extent at a lower temperature should be >1 (that is, reversibility should indeed increase with temperature). Still, a more refined quantitative treatment is presently not possible, because the catabolic reaction of AOM (1) is composed of sequential and parallel reactions. The above ΔH° is that of net AOM, whereas the enthalpies of the pathways of carbon and sulfur that constitute AOM and were examined separately as bulk reactions in this study are unknown.

Microbial Substrate–Product Interconversion Without Net Reaction?

Enzymes continue catalyzing the forward and back reaction also when the equilibrium is reached (that is, if the net reaction is v = 0). This principle was recently applied to show methyl incorporation from ¹³CH₄ into methyl-coenzyme M by the purified terminal enzyme of methanogenesis (17). Hence, also multiple enzyme systems like microbial cells should catalyze interconversion of substrates and products (that is, exchange of labeled elements between them) in the absence of a net reaction. Indeed, when in our experiments methane and inorganic carbon were present whereas sulfate was essentially depleted so as to prevent net AOM, carbon back flux was still observed, albeit at a lower rate than during net AOM. However, if vice versa sulfate and sulfide were present without methane addition, sulfur label exchange was not observed. One explanation for the latter observation could be that sulfide back flux at low concentrations as prevailing in this particular experiment is a first-order process, allowing only marginal, barely detectable label back flux. Another explanation could be that arrest of the net reaction results in the depletion or inactivation of a coreactant or another component needed for an operative sulfur pathway. Forward and backward fluxes through intact in vivo systems are certainly more delicate than through a single enzymatic reaction, and understanding of the possibilities and conditions of substrate–product interconversion through various microbial pathways requires more detailed physiological investigations.

Consideration of Product Back Flux in Natural Habitats.

Many environmentally relevant and microbial-mediated chemical reactions occur close to equilibrium conditions. Our findings have implications for studies of environmental processes at low-energy yields (for instance, in anoxic systems such as AOM environments or the deep biosphere). Microbial catabolic activity in natural habitats is often measured by examining the flux of added isotope label from substrate to product pool rather than by determining the net rate of product accumulation by chemical quantification. Tracer conversion rates in the opposite of net AOM or net methanogenesis have been reported from experiments with marine sediments (31, 33), bacterial mats (32), and methanogenic sludge (16, 41); however, these studies could not exclude the possibility of co-occurrence of methanogenesis and AOM. If back flux occurs, label flux from substrate will not be identical to the microbial net rate. In most cases, this effect (5–10%) will be hidden in the normal uncertainty and variability of radiotracer measurements. However, highly accurate net rate determination by isotope labeling would have to include both forward and back flux measurement to yield the net rate. Moreover, detection of a reaction in situ by labeling does not necessarily indicate a net reaction occurring in the direction of label conversion; it may represent the back flux during the opposite reaction and thus, a pseudoreaction; hence, dominance of the opposite reaction would have to be excluded, which was extensively discussed for methanogenesis vs. AOM (23). Nevertheless, as in biochemical studies of single enzyme reactions (17, 42), isotope probing of back fluxes at near equilibrium conditions may provide means of probing catabolic mechanisms at the community level.

Finally, reverse reactions are important also for the understanding of stable isotope fractionation (43–45). So far, the reversibility of sequential individual catabolic reactions but not the reversibility of an entire catabolism as a whole has been examined in isotope fractionation studies (18, 43, 46–49) (i.e., at least one step in a sequence of catabolic reactions was considered to be unidirectional). This treatment allowed determination of isotope effects according to a Rayleigh isotope fractionation equation. However, if an entire sequence of catabolic reactions is reversible, which it must be near equilibrium, the Rayleigh treatment is no longer valid, because the isotope composition of the reaction product (e.g., sulfide) affects the isotope composition of the reactant (e.g., sulfate). In the case of sulfate reduction, this effect has recently been observed in laboratory culture experiments (50). Our study and a recent study where discrepancies between bulk sulfate reduction rates and ³⁵S transfer from sulfate to sulfide were found (51) show that isotope fractionation between a reactant and a product under in situ conditions (e.g., AOM) may not be determined solely by kinetic isotope fractionation but also by the isotope composition of the product pool. A specific case of such bidirectional isotope fractionation may be that absence of net reaction could result in an equilibrium isotope fraction that reflects the highest thermodynamic stability of the involved isotopologues. Recent studies on pure cultures of sulfate reducing Bacteria indeed show that sulfur isotope fractionations approach equilibrium isotope fractionation values (52), implying that isotope exchange between product and substrate pools may, rather, be the rule than the exception for metabolism under low-energy condition. Refined measurements of isotope fractionations, which may also depend on the type of microorganisms (39), would be needed to explore the significance of the reverse reaction for stable isotope signatures under different settings of environmental and chemical parameters.

Materials and Methods

Origin, Enrichment, and Preparation of Cultures for Experiments.

The investigated enrichment cultures originated from anoxic sediment of two marine methane seep areas, HR (Cascadia Margin, Oregon, NE Pacific; 044° 34.2′N, 125° 08.7′W; August 2000) and Isis MV sediment (Eastern Mediterranean Sea; 032° 21.7′N, 031° 23.4′E; September 2003). Sediments had been sampled during the R/V Sonne (SO-148/1, 2000) and R/V L'Atalante (NAUTINIL, 2003) expeditions, respectively. The methane-consuming, sulfide-producing cultures were enriched in anoxic synthetic seawater medium (53), with methane and sulfate as the only energy sources through repeated transfer (over some years) from sediment. Thereby, loosely flocculating cell aggregates were propagated, whereas the sediment matrix with detritus was continuously diluted out (confirmed by microscopic survey and microbial staining). Consortia of Archaea (ANME-2 groups) and Deltaproteobacteria were abundant (95–99% of detectable cells according to DAPI and specific 16S rRNA probing) (38, 39). These highly enriched consortia with their inherently slow growth (38) were available only in limited quantities and therefore, were used sparingly. Subsequently, experiments with ¹⁴C-bicarbonate and ³⁵S-sulfide labeling were carried out at different times, and the batches available at one time differed from the batches at another time with respect to cell density and volumetric activity. Within an experiment at a given time, however, the same enrichment batch was distributed equally to establish equal volumetric activities. Before the radiotracer studies, cultures were allowed to settle; the sedimented microorganisms were transferred to new medium with sulfate and sulfide additions. Aliquots were then transferred to culture tubes incubated at their temperature optima (HR, 12 °C; MV, 20 °C) (21, 39).

Incubation Experiments with ³⁵S-Label.

To measure the sulfate reduction rate by labeling, resuspended enrichments were distributed in amounts of 1 mL in 5-mL tubes. Tubes were completely filled (headspace-free) with anoxic synthetic seawater medium that was saturated with unlabeled CH₄ (under a gas phase of 150 kPa). Tubes were sealed with elastic butyl rubber. Controls were prepared with N₂ instead of CH₄ or with sterilized (20 g formaldehyde L⁻¹) cultures. A solution of ³⁵S-Na₂SO₄ (Amersham) was injected into a 5-mL culture tube. The specific activity in the medium was 5.5 × 10⁸ Bq mol⁻¹ (total sulfate concentration, 28 × 10⁻³ mol L⁻¹, for rate determination was assumed to be constant throughout the experiment). After 4 d, sulfide was recovered by a standard chromium reduction distillation method using a zinc acetate trap followed by scintillation counting. To preserve the settled cultures, 4 mL supernatant culture medium were transferred anoxically to 20 mL zinc acetate solution (0.9 M) to stop the reaction and fix sulfide. Radiolabeled ³⁵S product (total reduced inorganic sulfur) was separated from the radiolabeled reactant (³⁵SO₄^2–) by reduction with Cr²⁺ and cold distillation (54). The radioactivity of both pools was quantified by scintillation counting (scintillation mixture; LumaSafe Plus; scintillation counter, 2900TR LSA; Packard).

³⁵S-sulfide for labeling experiments was freshly generated from ³⁵S-Na₂SO₄ by bacterial reduction. Desulfovibrio vulgaris (DSM 2119) was incubated in a 20-mL tube containing 10 mL anoxic freshwater medium (53), H₂ gas (with 20% CO₂; 150 kPa total pressure) as electron donor, and 5 × 10⁻³ mol L⁻¹ Na₂SO₄ with an adjusted label activity of 1.25 × 10¹¹ Bq mol⁻¹. After complete reduction of sulfate, the culture was mixed with anoxic H₃PO₄ (5 mL at 1 mol L⁻¹). A slow N₂ stream was passed through the solution and headspace, through anoxic citrate buffer (10 mL at 0.1 mol L⁻¹, pH 4), and finally, through anoxic solutions of ZnCl₂ (15 mL at 0.4 mol L⁻¹) to trap sulfide. The collected ZnS suspension (a total of 75 mL) was acidified with H₃PO₄ (60 mL at 1 mol L⁻¹) under an N₂ headspace in an anoxic 156-mL vial to release labeled sulfide. The preparation through a gas phase and citrate buffer avoided transfer of other sulfur species that may have been present as impurities in the Desulfovibrio culture.

Labeled H₂S gas in N₂ was withdrawn in portions of 0.2 mL (6–9 kBq), injected into the headspace of 16-mL incubation vials with 10 mL medium and culture suspension, and for 24 h, equilibrated with the aqueous phase. Then, methane (200 kPa) was injected, and samples were incubated on a rotary shaker. After 0, 3, 6, 8, 11, 15, and 19 d, four culture tubes (replicates) were used for analysis; 8 mL culture medium (biomass was maintained) were transferred to an anoxic zinc acetate solution (0.25 mol L⁻¹; 6 mL per tube) to fix sulfide. Total ³⁵S was determined in 100-μL aliquots from the ZnS suspension. ³⁵SO₄²⁻ was determined after thorough removal of ZnS by centrifugation (15 min, 2,500 × g) and ultrafiltration (Anotop 25 membrane filter, 0.02-μm pores; Whatman). Removal of ZnS was verified in filtrate aliquots by acidification with HCl (7 mol L⁻¹; 0.5 mL per mL), purging with N₂, and scintillation counting.

To analyze possible formation of ³⁵S-thiosulfate from labeled sulfide, unlabeled thiosulfate (final concentration of 1 mmol L⁻¹) was added to filtrate aliquots. Sulfate and thiosulfate were separated by an ion chromatograph (Waters) equipped with an IC-Pak anion exchange column (50 × 4.6 mm) and conductivity detector. The eluent was isophthalic acid (1 mmol L⁻¹, pH 4.5) in 10% aqueous methanol (10%, vol/vol; flow rate = 1.0 mL min⁻¹). The separated fractions were checked for ³⁵S. However, ³⁵S-thiosulfate was not detectable. Resulting samples with ³⁵S-label were mixed with LumaSafe Plus (Lumac LSC) and analyzed by liquid scintillation counting (TR-2900; Caberra-Packard).

Incubation Experiments with ¹⁴C-Label.

Resuspended enrichments were prepared similar to the sulfate reduction labeling experiment (see above). Controls were prepared with N₂ instead of CH₄ or without sulfate or with sterilized (20 g formaldehyde L⁻¹) cultures. CH₄ oxidation and back flux were measured by injecting ¹⁴CH₄ (American Radiolabeled Chemicals) or ¹⁴C-NaHCO₃ (Perkin-Elmer), respectively, from aqueous solutions with high specific activity. Final specific activities in the medium were 6.5 × 10⁸ Bq mol⁻¹ for CH₄ (total concentration = 1.5 × 10⁻³ mol L⁻¹) and 4.5 × 10⁸ Bq mol⁻¹ for inorganic carbon (total concentration = 30 × 10⁻³ mol L⁻¹). After 4 d of incubation, 4 mL culture medium were fixed by transfer to 6 mL NaOH (0.6 mol L⁻¹) in a sealed glass vial (20 mL). Total methane was determined using a 5890A gas chromatograph (Hewlett Packard) equipped with a stainless steel Porapak-Q column (183 m × 3.2 mm, 80/100 mesh; Agilent) and flame ionization detector. Radioactivity of carbonate or methane was determined after separating both fractions. Methane was stripped off with air, oxidized at 850 °C with CuO, and trapped in 2-phenylethylamine base solution. Through acidification, carbonate was transferred into gaseous phase and again trapped in 2-phenylethylamine (55). Trap solutions were mixed with Ultima Gold XR (Perkin-Elmer) and analyzed in a 2900TR LSA liquid scintillation counter (TR-2900; Canberra-Packard).

Additional Analyses.

Sulfide was determined colorimetrically using the methylene blue formation reaction in a miniaturized assay (56).

Determination of Reverse Reaction Rate.

In catabolic conversion of substrate product with reversibility, A ⇌ P, forward and back flux (in the Introduction) are f₊ and f₋ (moles volume⁻¹ time⁻¹). When product label, P*, is added, appearance of A* reveals the back flux. If the label is a radioisotope with noticeable decay, error in label quantification is avoided by measuring radioactivity in all samples at the same time after the experiment; the specific isotope decay rate is independent of the chemical composition. The infinitesimal concentration d[A*] formed during an infinitesimal time dt depends on f₊ and f₋, heavy isotope discrimination in each direction (α₋, α₊; ≥1), and the proportion of label in total product and substrate (brackets indicate concentrations) (Eq. 12):

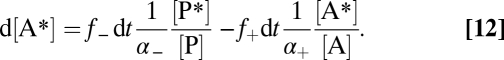Treatment is simplified by assuming that α₋, α₊ ∼ 1 and that the label proportion in the reactant pool remains very low ([A*]/[A] << [P*]/[P]), and therefore, return by f₊ can be neglected. Eq. 12 then yields (Eq. 13)

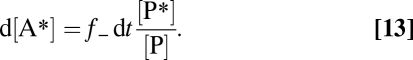P* is increasingly diluted by steadily forming unlabeled P (SI Text, Calculation of the Reverse Reaction Rate and Fig. S3). If an increase Δ[A*] is measured after a short enough incubation time, Δt, during which [P*]/[P] remains essentially constant, Eq. 13 can be simplified and rearranged to (Eq. 14)

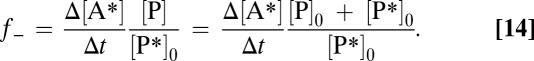[P]₀ is the initial product concentration, and [P*]₀ is the initial label concentration. If [P*]₀ << [P]₀, Eq. 14 is simplified to (Eq. 15)

Such treatment is similar to the common determination of substrate fluxes in habitats by labeling and measuring product label (57, 58). We applied Eq. 15 to evaluate ¹⁴C back fluxes in the methane–bicarbonate system. Back flux of inorganic carbon during AOM was determined, and ¹⁴CH₄ recovered from ¹⁴C-bicarbonate after 4 d of incubation (endpoint measurement), applying Eq. 15 with Δ[A*] = [¹⁴CH₄], [P]₀ = 0.031 mol L⁻¹, and [P*] = [H¹⁴CO₃] added (C_inorg calculated from added NaHCO₃/CO₂ buffer). A high concentration of C_inorg was initially added as NaHCO₃ (30 mmol L⁻¹; a common natural buffer for cultivation of AOM consortia and many other anaerobes). Based on the net AOM rate derived from methane-dependent sulfide formation, C_inorg increased during incubation from 30 (initial) to ≤30.4 mmol L⁻¹.

In contrast to the concentration of bicarbonate, the concentration of sulfide was low at the beginning (<0.5 mmol L⁻¹). This concentration is advisable for cultivation of anaerobes, because sulfide can be inhibitory. However, now dilution of product label during AOM was significant, and [P] in Eq. 13 is expressed as a function of time. Assuming that the net rate, v, of A → P is largely independent of [A] (zero-order behavior, which is common in many microbial batch incubations) and that cell growth is negligible during incubation, the experimental data follow a straight-line fit with the slope f₋/v when displayed according to (derivation in SI Text, Calculation of the Reverse Reaction Rate) (Eq. 16)

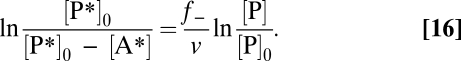Assuming the aforementioned prerequisites (negligible isotope fractionation, concentration-independent rates, and label concentration in the sulfate pool remaining low), we applied Eq. 16 with [P*]₀ = [H₂³⁵S] added and [A*] = [³⁵SO₄²⁻], [P] = [S_red], and [P]₀ = [S_red]₀ (S_red is chemically quantified sulfide). It has to be noted that the label concentration in the sulfate pool increases to the end of the incubation experiment to a level where label flux from the sulfate pool to the sulfide pool may no longer be negligible; application of Eq. 16 would then result in underestimation of the back flux. Chemical isotope exchange of ³⁵S between sulfide and zerovalent sulfur (e.g., elemental S or polysulfide S) (59) would dilute the specific activity of the sulfide pool (i.e., the effect would be the same). However, the linear trends for the data plotted in Fig. 1C and Fig. S2C indicate that the effect of such a label flux to the end of the experiment is within the error of the determined back fluxes (Table S2).