Aerodynamic performance of a hovering hawkmoth with flexible wings: a computational approach

Abstract

Insect wings are deformable structures that change shape passively and dynamically owing to inertial and aerodynamic forces during flight. It is still unclear how the three-dimensional and passive change of wing kinematics owing to inherent wing flexibility contributes to unsteady aerodynamics and energetics in insect flapping flight. Here, we perform a systematic fluid-structure interaction based analysis on the aerodynamic performance of a hovering hawkmoth, Manduca, with an integrated computational model of a hovering insect with rigid and flexible wings. Aerodynamic performance of flapping wings with passive deformation or prescribed deformation is evaluated in terms of aerodynamic force, power and efficiency. Our results reveal that wing flexibility can increase downwash in wake and hence aerodynamic force: first, a dynamic wing bending is observed, which delays the breakdown of leading edge vortex near the wing tip, responsible for augmenting the aerodynamic force-production; second, a combination of the dynamic change of wing bending and twist favourably modifies the wing kinematics in the distal area, which leads to the aerodynamic force enhancement immediately before stroke reversal. Moreover, an increase in hovering efficiency of the flexible wing is achieved as a result of the wing twist. An extensive study of wing stiffness effect on aerodynamic performance is further conducted through a tuning of Young's modulus and thickness, indicating that insect wing structures may be optimized not only in terms of aerodynamic performance but also dependent on many factors, such as the wing strength, the circulation capability of wing veins and the control of wing movements.

1. Introduction

Flying insects, in general, perform flapping wing flight to create aerodynamic forces to stay airborne and for forward and darting flight. The high-lift unsteady aerodynamic effects in the flapping wing have been unveiled until now to mainly include mechanisms of the leading edge vortex (LEV) [1], the clap and fling [2], the wake capture and the rotational circulation [3]. A key tool in flapping wing flight, the insect wing, is a flexible structure that often changes its shape dynamically during flight [4], and hence the wing deformation owing to fluid and inertial forces is usually passive because insect wings, unlike birds and bats, lack intrinsic musculature [5].

The aerodynamics and structural dynamics of the insect flapping wing are strongly coupled, which often leads to a complex fluid–structure interaction (FSI) problem. In the past decade, most experimental studies using dynamically scaled models and/or computational studies based on Navier–Stokes solutions (e.g. [3,6–10]) have been performed under an assumption that the wing is rigid and flat undergoing flapping motions based on the wing kinematics at the wing base. More recently, the in-flight deformation of insect wings and its role on the aerodynamic performance of insect flight have been studied by means of recent advances in high-tech equipment such as high speed digital video cameras and auto-tracking and reconstruction techniques for wing kinematics (e.g. [11–13]), the digital particle image velocimetry (DPIV) for flow measurement (e.g. [14,15]) and computational analyses (e.g. [16–20]). Most of these studies report interesting results associated with flapping wing aerodynamics in terms of three-dimensional deformations with wing twist and camber. Mountcastle & Daniel [15] measured flow fields around rotating fresh and dried wings of a hawkmoth by using DPIV and found that the fresh wing could impart the momentum into surrounding fluid more effectively than the dried wing. Young et al. [20] analysed a forward flight of locust by using a commercial computational fluid dynamics (CFD) solver and by prescribing the three-dimensional wing shape changes based on measurements. They found that the twisted and cambered wing could transfer momentum to the wake efficiently and hence modify the direction of aerodynamic force vectors appropriately.

Insect wings are often composed of a variety of complex components, which co-determine their flexibility [4,21]. The three-dimensional wing shape and the timing of deformation during flapping flight significantly depend on wing structures, which very likely, as a result of evolution, is a design capable to enhance the aerodynamic performance. A computational FSI analysis that is performed by coupling a CFD solver and a computational structural dynamics (CSD) solver [22] may be a straightforward and effective approach to resolve this highly nonlinear problem, because it is capable of providing detailed information on both flow fields and structural dynamics of flexible wings and hence to evaluate the flexible wing aerodynamic performance. The most recent FSI analysis-based studies of flapping or heaving wings (e.g. [16,18,19]), however, are limited to highly simplified kinematic and/or structural models of oscillating foils and/or flapping wings. In this study, we present for the first time, to our knowledge, a computational FSI-based analysis of hawkmoth hovering flight by constructing a realistic structural wing-body model, which takes into account the vein distribution and anisotropy of hawkmoth wing. We address how the three-dimensional and passive changes of wing kinematics owing to inherent wing flexibility contribute to unsteady aerodynamics and energetics in insect flapping flight, and furthermore, how the wing stiffness affects the aerodynamic performance.

2. Material and methods

(a). FSI modelling of hawkmoth hovering

An integrated computational framework of the FSI analysis specified for insect flapping flight is established by coupling an in-house CFD-based insect dynamic flight simulator [6] and a newly developed finite-element method based CSD solver. This computational model integrates the realistic wing–body morphology, the realistic wing–body kinematics, the flapping wing aerodynamics including wing–wing and wing–body interactions and the structural dynamics of flexible wings [23].

(i). Morphological, kinematic and aerodynamic modelling of hawkmoth hovering

Flexible wing aerodynamics in insect flapping flight is studied by modelling a hawkmoth, Manduca sexta undergoing hovering flight. A realistic wing–body morphological model for CFD and CSD analyses is constructed based on the images as shown in figure 1a,b, by tracing the outline of wings and body of the hawkmoth, Agrius convolvuli, a species close to M. sexta [24] because M. sexta does not live in Japan. Details can be found in the electronic supplementary material and Liu [6]. We scale the wing shape using the mean chord length of M. sexta, and the influence of geometric differences is assumed to be negligibly small in this study. Note that, while hawkmoths are four-winged, for simplicity, we model the fore- and hind-wings as a single pair of wings considering the highly synchronized motion observed in flapping flight, which may enhance the chordwise-wing stiffness slightly.

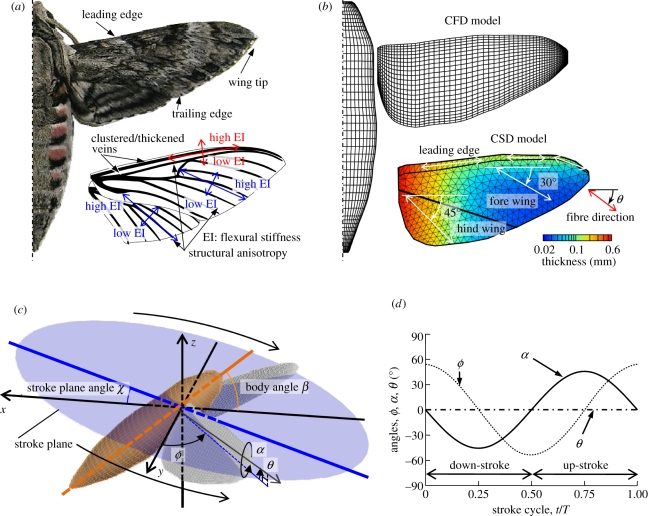
Figure 1.

(a) A hawkmoth Agrius Convolvuli with a generalized wing venation including fore- and hind-wings. EI, flexural stiffness. (b) A computational model for CFD and CSD analyses. (c) Definition of a global coordinate system (x, y, z), body angle β, stroke plane angle χ and wing position parameters within stroke plane: positional angle ϕ, elevation angle θ and feathering angle α. (d) Simplified kinematics at wing base for FSI analysis. ϕ, positional angle; α, feathering angle; θ, elevation angle.

Hovering kinematics of the flapping wings and body of the hawkmoth, M. sexta, are represented by the stroke plane angle χ, the body angle β and the three angles (the positional angle ϕ, the elevation angle θ and the feathering angle α) of wing stroke within the stroke plane, which are defined and illustrated in figure 1c [6,25]. Because the body motion in hovering is negligibly small [25], the insect body is fixed as tethered in this study.

The wing deformation owing to inertial forces, aerodynamic forces and ‘physical’ wing–body interactions is, in general, inherently included in the measured wing kinematics. Hence, subtraction of the wing deformation is essentially difficult, and a simplified harmonic wing kinematics is hereby used as an input at the wing base. The passive wing deformation owing to wing flexibility is then predicted computationally and the aerodynamic performance is compared with that of rigid wings. The three angles representing wing movements for the FSI analysis are approximated in a sinusoidal form as shown in figure 1d, such that:

2.1

where ω is the angular frequency; the coefficients (ϕ′_c1, α′_s1) are determined from the measured kinematic data ([23,25]; the electronic supplementary material). The aerodynamic performance of flexible wings with the wing base kinematics (equation 2.1) is evaluated and compared with that of rigid wings, which flap with both the prescribed wing base kinematics and the wing tip kinematics based on the FSI results of flexible wings.

Reynolds number Re and reduced frequency k are defined by

2.2

where ν is the kinematic viscosity of air (1.5 × 10⁻⁵ m² s⁻¹) and f is the flapping frequency. The mean chord length c_m is used as the reference length, and the reference velocity U is defined by a mean wing tip velocity (U = 2ΦfR, where Φ is the wing beat amplitude and R is the wing length) in hovering flight. For hawkmoth, Manduca, c_m = 18.3 mm and R = 48.3 mm. Wing and body kinematic models are based on the experimental data of the hovering hawkmoth, Manduca [7]: positional, feathering and elevation angles are plotted as in figure 1c; the body angle χ = 39.8°; the stroke plane angle β = 15°; wing stroke amplitude Φ = 2 rad; and f = 26.1 Hz. Hence, the Reynolds number is calculated to be approximately 6300 and the reduced frequency k is 0.3.

(ii). Structural modelling of flexible wings

The hawkmoth wing structure is mainly supported by wing veins and membrane. The wing veins are clustered and thickened around the wing base and leading edge as illustrated in figure 1a, which together shape the wing: they are tapered towards the wing tip and trailing edge, and hence the zones cannot be assumed to be rigid [26,27]. A thin and flexible membrane is placed between the veins; the directional arrangement of the wing veins and the difference of bending stiffness between the veins and membrane usually result in a high anisotropy of macroscopic flexural stiffness of hawkmoth wings [28]. Thus, the time varying wing shape in terms of spanwise- and chordwise-bending and twist is, in general, determined by the three-dimensional arrangement of these components over the wing.

In this study, we build up a computational structural model as depicted in figure 1b, by taking into account the anisotropy and distribution of bending stiffness. The wing model is validated through a comparison of dynamic wing deformations with measurements (the electronic supplementary material; [23]). Note that both nonlinearity of wing stiffness owing to three-dimensional wing structures and nonlinear structural components are neglected here because of the poor database in the literature, though they often exhibit flexibility in ventral bending but stiffness in dorsal bending (‘one-way hinge’) [4,26,27].

Furthermore, we investigate the wing stiffness effect by scaling the whole wing stiffness EI proportional to an original stiffness EI_moth from 3EI_moth, 2EI_moth, EI_moth/2 down to EI_moth/3. The EI is modulated by Young's modulus and thickness under an assumption that the stiffness of a thin wing structure is proportional to Young's modulus and the thickness cubic [29]. Note that the thickness affects not only stiffness but also mass distribution, while Young's modulus can adjust the stiffness independently.

(b). Definition of wing deformations

The deformed flexible wing based on FSI analysis usually shows a skewed shape even with a flat initial shape, which may be decomposed into three types of deformations: the spanwise bending, the twist and the camber [4]. To investigate how each separated individually and hence simplified deformation affects the aerodynamic performance of flapping wings, we hereby redefine these deformations through interpolation with a square-least method (the electronic supplementary material) and compare their aerodynamic performances.

(c). Evaluation of hovering aerodynamic performance

Time varying vertical and horizontal forces (F_v, F_h) are non-dimensionalized by

2.3

where ρ is the density of air (1.23 kg m⁻³), S_w is the plan form area of a single wing and C_v and C_h denote the non-dimensional vertical and horizontal force coefficients, respectively. The muscle-mass-specific aerodynamic power (P_a) is calculated based on instantaneous aerodynamic forces and moving velocities of each cell [6]. Following Lehmann & Dickinson [30] and Aono et al. [31], we also assume that the mass of flight muscle contributes to 30 per cent of the total body mass.

Aerodynamic efficiency of hovering flight has been defined by using the minimum power required for hovering, which is derived on a basis of the Rankin–Froude momentum (RFm) theory, divided by the aerodynamic power required for moving the wing in air [32]. While the RFm efficiency is very useful to clarify the energetics of various kinds of insects, it is usually difficult to accurately estimate the ‘real’ efficiency for moving the wing in surrounding fluid because of the complex unsteady vortex structures around flapping wings. However, the power requirement can be predicted computationally in a more accurate way. For instance, the efficiency of forward movement in flying insects or swimming fishes can be calculated by using a product of instantaneous moving velocity of their bodies and thrust forces as induced power P_ind [33]. In the case of hovering flight, the power that is received by the fluid can be used as the induced power of hovering flight, which is hereby calculated directly by the vertical aerodynamic forces and the averaged vertical flow velocities on a closed-loop virtual surface, wrapping each of the flapping wing pairs (electronic supplementary material, figure S3). The aerodynamic efficiency of hovering flight η is then calculated by dividing the mean induced power 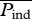with the mean aerodynamic power 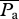(the electronic supplementary material; [23]).

3. Results

(a). In-flight deformation of hawkmoth's wings

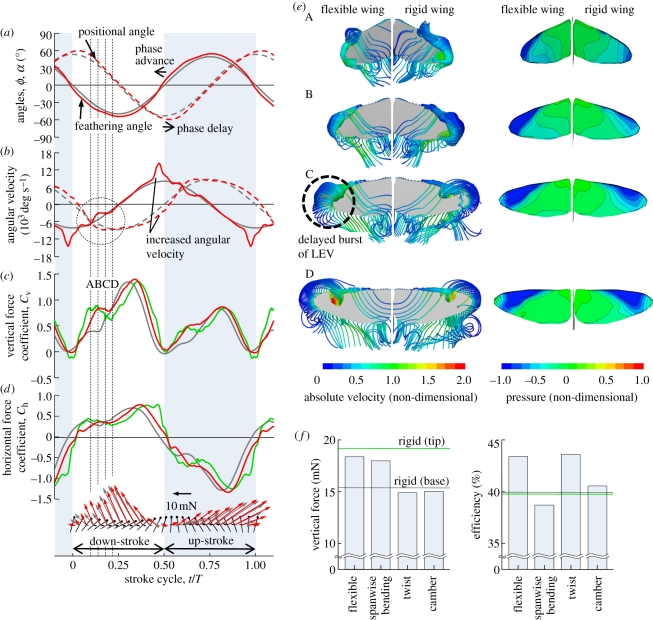
Figure 2a shows the time-varying positional and feathering angles of flexible and rigid wings at a cross section of 0.8 R. The time-varying wing shape and deformations in terms of the spanwise bending, the twist and the camber are visualized and shown in the electronic supplementary material, movie and figure S4; time-courses of deformations at a cross section of 0.8 R are also shown in the electronic supplementary material, figure S5 (red line). While the spanwise bending and the twist angle vary smoothly, there exists a rapid increase in distal area. The flexible wing shows pronounced deformations in spanwise bending and twist immediately after stroke reversal (electronic supplementary material, figures S4 and S5) and then a nose-down twist with a maximum of approximately 12° at the wing tip relative to the wing base. Willmott & Ellington [25] reported that the portion of hawkmoth wing in the distal area (forewing) displays a variable twist with maxima of 15°–20°. While the present unified fore- and hind-wing model may somehow underestimate the elastic wing deformation, the computed twist is reasonable compared with the measurements. The wing model also shows some positive camber, which, although less than 2 per cent, is relatively small compared with the measured cambers of large insects, such as locusts [11].

Figure 2.

Time-courses of (a) positional and feathering angles at 0.8 R, (b) angular velocities, (c) vertical and (d) horizontal force coefficients of flexible and rigid wings. Terms of (base) and (tip) represent the basic kinematics in equation (2.1) and the FSI analysis-based kinematics, respectively. At the bottom of (d), aerodynamic force vectors (red and grey for flexible and rigid wings, respectively) are also illustrated, where a small vector coloured black at each cross section denotes the instantaneous moving direction and the velocity of a rigid wing. (e) Instantaneous streamlines and pressure contours on upper surfaces of flexible and rigid wings at instants A, B, C and D as shown in (c). (f) Time-averaged vertical aerodynamic force and efficiency generated by a flexible wing, a rigid wing and three rigid wing models with prescribed spanwise bending, twist and camber based on FSI analysis. (a,b) Red line, flexible wing; grey line, rigid wing. (c,d) Red line, flexible wing; grey line, rigid wing (base); green line, rigid wing (tip).

The spanwise bending and twist are large during translation, but show small peaks before the subsequent stroke reversal (electronic supplementary material, figures S4 and S5). Such deformation leads to significant changes in wing-tip kinematics. First, the flexible wing shows an advanced phase in feathering angle, but a delayed phase in positional angle at the wing tip (figure 2a). This indicates that the wing deformation leads to an advanced phase of wing rotation, from a sinusoidal wave to a more realistic one involving high-order harmonics, which is suggested to be capable of serving as a source of the additional circulation and hence enhance the force production in flapping wings [3]. Second, the translational and rotational velocities at a cross section of 0.8 R, as plotted in figure 2b, increase remarkably, in particular before stroke reversal.

(b). Aerodynamic performance of flexible wings

Time-courses of vertical and horizontal force coefficients and aerodynamic force vectors generated by flexible and rigid wings are plotted in figure 2c,d, where the force vectors (red and grey for flexible and rigid wings, respectively) are projected onto the x–z plane (figure 1c,d). While both rigid and flexible wings can produce large forces during the down- and up-stroke, the vertical aerodynamic forces are smaller at the up-stroke than at the down-stroke owing to an inclined stroke plane.

It is seen that, while both flexible and rigid wings show a plateau in the vertical aerodynamic force production at early down-stroke, the flexible wing obviously creates more force than the rigid wing and the force vectors contribute more to the vertical force components (figure 2c,d). Instantaneous streamlines and pressure contours on the wing surfaces are illustrated in figure 2e during an interval where four instants are marked as A, B, C and D (figure 2c). At early down-stroke, when the wing proceeds to late pronation undergoing a pitch-down rotation, the LEV and the trailing edge vortex (TEV) grow in size and in strength stretching from the wing base towards the wing tip; the TEV subsequently detaches from the wing, forming a starting vortex but connecting to the LEV and the wing tip vortex (TV) at the wing tip at A (figure 2e). Subsequently, the TV of the rigid wing becomes unstable at C, gradually separating and shedding from the wing surface, which correspondingly results in a shrink pattern of negative pressure contours at the wing tip. By contrast, the LEV and the TV on the flexible wing seem to be more stable than those of the rigid wing with an enlarged negative pressure region at B and C (figure 2e). When the TV breaks down and separates from the wing, the LEV still keeps growing with a strong negative pressure region at D (figure 2e) until the vertical aerodynamic forces generated by both flexible and rigid wings become almost even immediately after the wing turns to decelerate. However, it is interesting to find that at late down-stroke the flexible wing eventually reaches a higher force peak than the rigid wing (figure 2c). When the wing approaches early supination, the aerodynamic force decreases owing to the breakdown/shedding of the LEV and the translational deceleration. Here, the flexible wing can also create larger forces than the rigid wing.

To quantify the hovering aerodynamic performance, we calculate the time-averaged vertical and horizontal aerodynamic forces, the aerodynamic power, the induced power and the aerodynamic efficiency in a complete wing stroke, which are summarized in table 1. It is seen that both flexible and rigid wings can produce sufficient lift forces to support the weight of the hawkmoth (14.7 mN, [6]). Compared with the rigid wing, the flexible wing generates larger vertical forces at both the down- and up-stroke while horizontal forces are large at the up-stroke but small at the down-stroke. Interestingly, while the flexible wing can apparently generate approximately 22 per cent larger vertical force than the rigid wing does, 14 per cent more muscle-mass-specific aerodynamic power is required for the flexible wing-based hovering flight. The induced power that can be interpreted as the momentum imparted to the vertical direction, however, shows a remarkable net increase by more than 24 per cent in the case of the flexible wing, which obviously leads to an increase in the aerodynamic efficiency by approximately 3.4 per cent.

Table 1.

Time-averaged vertical and horizontal forces acting on wings and body at down- (F_{v, down}, F_{h, down}) and up-stroke (F_{v, up}, F_{h, up}), in a complete wing-beat cycle (F_v, F_h), vertical force to mass ratio of hawkmoth (14.7 mN), muscle-mass-specific aerodynamic and induced powers of a single flexible or rigid wing (P_a′, P_ind′), and aerodynamic efficiencies (η).

	vertical force (mN)			horizontal force (mN)			vertical force-mass ratio, Fv/M	aerodynamic power, Pa′ (W kg−1)	induced power, Pind′ (W kg−1)	aerodynamic efficiency, η (%)
	Fv, down	Fv, up	Fv	Fh, down	Fh, up	Fh
flexible	23.8	13.1	18.4	12.9	−24.4	−5.7	1.25	95.3	41.4	43.4
rigid (base)	20.8	9.9	15.4	13.5	−22.2	−4.4	1.05	83.3	33.3	40.0
rigid (tip)	26.3	12.9	19.2	14.8	−26.0	−5.7	1.31	108.9	43.3	39.8

To investigate how the wing deformations based on the FSI analysis (figure 2a) affect the aerodynamic performance, we further computed the vertical and horizontal forces of a rigid wing model with the deformed wing kinematics prescribed. It is seen that time courses of the aerodynamic forces are similar with those of the flexible wing, but a pronounced difference is observed in particular after the plateau when the wing approaches stroke reversal (figure 2c,d). Figure 2f shows the time-averaged vertical forces and efficiencies of the flexible wing, the rigid wing and a rigid wing model with the separated deformations in terms of the spanwise bending, the twist and the camber. Correspondingly, time courses of the bending angles, the vertical force coefficients and the mean aerodynamic force vectors at the down- and up-stroke are plotted in the electronic supplementary material, figure S5 and also summarized in the electronic supplementary material, table S3.

Note that a rigid wing model with the prescribed wing tip kinematics can create a large vertical aerodynamic force of 19.2 mN comparable with that of the flexible wing (table 1), but results in a significant drop in aerodynamic efficiency of 39.8 per cent (figure 2f). Compared with the rigid wing based on the wing base kinematics (equation (2.1)), the rigid wing model with the prescribed spanwise bending (electronic supplementary material, figure S5a) shows an obvious increase in vertical force with a similar tendency as observed in the flexible wing (figure 2c). However, this rigid wing model clearly adds more pain on power requirement by 108.5 W kg⁻¹ (electronic supplementary material, table S3) and hence has a decrease in efficiency of 38.7 per cent (figure 2f). By contrast, the twist effect probably leads to an increase in the efficiency, for instance, the rigid wing with the prescribed twist shows a higher efficiency of 43.6 per cent at the same level of the flexible wing, although it actually results in a decrease in vertical force (figure 2f). This is because the input power (72.9 W kg⁻¹) is largely reduced by the wing twist. On the other hand, the camber effect seems to hardly extend influence on the aerodynamic force and efficiency (figure 2f).

(c). Wing stiffness effect on aerodynamic performance of flexible wings

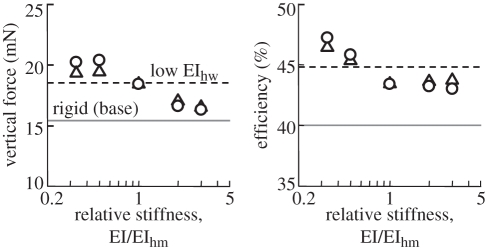
A systematic study on wing stiffness effect was then conducted in terms of Young's modulus and wing thickness as illustrated in the electronic supplementary material, figure S6, which shows the time-varying bending angles, twist angles and cambers at 0.8 R from the wing base. It is seen that the amplitude and the phase delay of wing deformations are increased with decreasing Young's modulus or thickness. Flapping angles and vertical force coefficients are further illustrated in the electronic supplementary material, figure S7, which shows a strong correlation between the wing stiffness and the aerodynamic force production. Figure 3 illustrates the wing stiffness effect on the mean vertical force and efficiency: lower wing stiffness or a relatively flexible wing seems to be capable of creating larger aerodynamic forces as well as higher efficiencies.

Figure 3.

Wing stiffness effect on vertical aerodynamic force and efficiency of flexible wings. Circles, Young's modulus; triangles, thickness.

(d). Wake structures induced by flexible wings

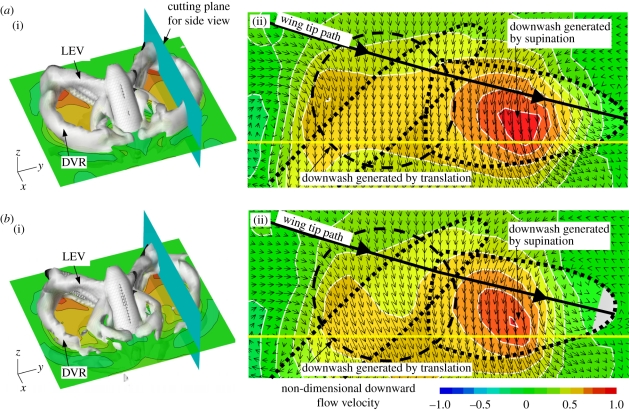
We further compare wake structures between the rigid and flexible wings in terms of vortex dynamics and downwash at the end of the down-stroke (figure 4a,b), in which, normalized by c_m/U, the iso-vorticity surface with a magnitude of Ω = 1.5 is visualized in a three-dimensional structure. The vorticity Ω is defined by the curl of a velocity vector v: Ω = curl v. A close-up view of the downwash is visualized in terms of velocity vectors and downward velocity contours at a cutting plane of 0.6 R from the wing base. Similar vortex structures and wake topologies are observed in both rigid and flexible wings: the down-stroke vortex ring (DVR) is formed from the LEV, the TV, the TEV and the root vortex. Since the LEV and the TV play a key role in the force production of hovering flight, influence of the vortex structures near the body can be negligible [34]. An intense hovering downwash is formed flowing through the centre of the DVR [6,35]. However, there does exist pronounced discrepancy between the flexible and rigid wings: the direction of air-flow generated by the flexible wing approaches the vertical direction more than that of the rigid wing. Moreover, much stronger downward flows with larger vertical velocities are observed around the flexible wing, which correspond with the downwashes generated by both translation and rotation (supination) of the wing.

Figure 4.

Wake structures generated at down-stroke about (a) flexible and (b) rigid wings. (i) Iso-vorticity surface (coloured grey) is plotted with a magnitude of Ω = 1.5; and downwash at a horizontal plane (x–y plane) and (ii) at a cutting plane of 0.6 R from the wing base are visualized in terms of velocity vectors and downward velocity contours. Note that LEV and DVR stand for the leading-edge vortex and the down-stroke vortex ring, respectively.

4. Discussion

Our FSI analysis of a hovering hawkmoth with flexible wings reveals that wing flexibility can increase downward flow in wake and hence aerodynamic forces, and even further enhances aerodynamic efficiency. Note that the present FSI-based wing deformations may be underestimated because of the strong connection between fore- and hind-wings. We have carried out an extensive study on this problem in Nakata & Liu [23], by modelling a flexible wing model with different fore- and hind-wing stiffness and an approximately 10 per cent stiffness of the hind wing EI_hw so as to reduce the physical interaction between the fore- and hind-wings. While the spanwise bending observed is similar to that of the flexible wing model (electronic supplementary material, figure S4), the maximum wing twist angle computed is increased up to 17°, in good agreement with the measurements [25]. Furthermore, obtained with almost the same vertical force, the efficiency is calculated to be 44.8 per cent, greater than that of the flexible wing model (43.4%). Note that compared with the wing stiffness effect as illustrated in figure 3, such an increase in efficiency owing to the stiffness reduction of the hind wing is apparently small and limited. Therefore, the present fore- and hind-wing model with uniform wing stiffness is capable of reasonably predicting and evaluating the aerodynamic performance of flexible wings with dynamic wing deformations.

It should also be noted that the camber computed by our model is small. There is still no study reporting detailed wing deformations of the hovering hawkmoth, but large insects, for instance locusts, often show variable wing cambers of 8 per cent in the forewing and 10 per cent in the hindwing [11]. One possible reason that the computed camber is relatively small may be because the inherent cambers of the hawkmoth wing (up to 4% in spanwise and 5% in chordwise, [26]) as well as the complex structural components are not taken into account in this study. The present model, however, successfully avoids the negative camber as observed in other studies [19,36], probably because of the use of the realistic properties and anisotropy of wing stiffness. Possible mechanisms for the development of such positive camber can be found in the literature [21,37]. With respect to the camber effects, we will carry out an extended study in our future work.

(a). Lift enhancement by wing flexibility

(i). Delayed burst of leading edge vortex

Aerodynamic and inertial forces applied on a flapping wing can result in passive wing deformations, which are probably responsible for stabilizing and hence delaying the breakdown of the LEV/TV during wing translation. As illustrated in figure 2c, both flexible and rigid wings show a similar high peak of vertical force immediately after the wing turns to decelerate. This is because the LEV keeps growing and attaching coherently onto the wing surface even after the LEV breaks down with the TV shedding off the wing surface [6,35]. However, there does exist pronounced discrepancy at early down-stroke, where the flexible wing obviously creates more vertical forces than the rigid wing (figure 2c). At instance A, a stronger LEV as a portion of horseshoe vortex is observed near the wing tip of the flexible wing, which grows rapidly over instances of B, C and D, resulting in a larger and stronger negative pressure region on the wing surface (figure 2e). Very probably, the spanwise bending of the flexible wing induced during pronation creates this LEV at an earlier timing than that of the rigid wing (electronic supplementary material, figure S5a), which leads to a fast and steep increase in vertical force at A–B (figure 2c). The LEV then keeps growing for a while up to instance D before approaching the middle down- and up-stroke. During the interval, although the inertial force becomes very small (electronic supplementary material, figure S4i), the spanwise bending and twist, and hence the angular velocities, show significant variations near the wing tip (B and C, marked circle in figure 2b). These wing deformations very probably stabilize the LEV and hence result in a delayed burst (breakdown) at D compared with that of the rigid wing at C (figure 2e). This delayed burst even further influences the development of the LEV after the breakdown and subsequently the flexible wing reaches a higher force peak than the rigid wing (figure 2c). Furthermore, a nose-down twist (figure 2a–c and electronic supplementary material, figures S4 and S5) can result in a pronounced direction change of spanwise wing cross sections, and hence the direction of force vectors (figure 2) as well as the downwashes (figure 4).

(ii). Phase advance and angular velocity increase

The inherent structural flexibility and anisotropy distribution in insect wings in general, lead to wing twist and camber during flapping flight, which are known to change dynamically in magnitude and distribution (e.g. locusts [11]; hawkmoth [38]; hoverflies [13]). This means that any input and/or control of the wing kinematics being exerted at the wing base may output different wing kinematics at the wing tip passively because of the dynamic shape changes. Here, we find that the timing of the wing twist is adjusted in a passive, but adaptive way to advance the phase of wing rotation (figure 2a). This phenomenon is also observed in a two-dimensional FSI study of Diptera with a simplistic structural model by Ishihara et al. [18], in which the torsion flexibility is concentrated on the leading edge as an elastic spring. Our three-dimensional FSI analysis further reveals that the spanwise flexibility can cause a spanwise bending and hence delays the timing of stroke reversal at the wing tip (figure 2a). Appropriate combination of the chord- and span-wise deformation leads to a relative phase advance of rotation in flexible wings, which can strengthen the vortex ring and the downwash as well as the rotational circulation, while modifying the wing attitude to benefit from the wake capture [3].

In addition, the wing deformations may lead to increasing angular velocities of positional and feathering angles mostly in the distal area of the flapping wings (figure 2b), which can augment the circulation around insect wings [39]. In this study, compared with the rigid wing movements, we find a jump in the angular velocities of positional and feathering angles in the flexible wing (figure 2b). This is because the inertial force, which may dominate wing deformations of large insects [40], can be increased by the deceleration of positional angles, and the elastic energy stored in the form of bending and twist is released rapidly during late down- and up-stroke. Such elastic energy release in flexible wing flapping very probably makes the flexible wing catch up with the rigid wing when approaching the end of the down- and up-stroke.

Obviously, the relative phase advance and the angular velocity increase correspond with a larger vertical force (figure 2c) rather than that of the rigid wing during wing rotation. Hence, the spanwise bending is responsible for the most vertical forces produced immediately before stroke reversal (figure 2f and the electronic supplementary material, figure S5). Furthermore, the rigid wing model with the deformed wing kinematics prescribed (figure 2c,f) does provide concrete evidence that not only the three-dimensional wing configuration, but also the variation in wing kinematics can enhance the aerodynamic force production. In relation to the downwash and the force production, our results (figure 4) indicate that the stronger downward flow is created timely when the wing experiences a rapid stroke reversal where larger forces are created (figure 2c), which is also confirmed experimentally by Mountcastle & Daniel [15].

(b). Flexible wing aerodynamics and energetics: importance of elastic deformation

Our results indicate that the dynamic elastic deformation of flapping wings owing to inherent wing flexibility can improve aerodynamic performance of insect hovering flight effectively. We find that the high lift or large force enhancement mechanism may result in a necessarily larger power requirement, but significantly higher efficiency as well. Young et al. [20] performed a CFD analysis of locust forward flight with prescribed realistic wing kinematics and the virtual kinematics in which the elastic deformation was subtracted. They confirmed an increase in aerodynamic force and efficiency, but a decrease in input power, which was thought to be owing to the wing deformations. Here, we can also confirm the decrease in input power of the rigid wing model with a prescribed twist (electronic supplementary material, table S3) and the increase in efficiency (figure 2f). The discrepancy between our and Young et al.'s [20] study is thought to be caused by the FSI analysis-based spanwise bending (figure 2f). This indicates that three-dimensional spanwise and chordwise deformations should be taken into account in accurately evaluating flexible wings' energetics.

The aerodynamic efficiency is a measure of how much of the input power for moving a wing in air is used for the transfer of vertical momentum into surrounding fluid and hence for the vertical force production. Another important finding in this study is the efficiency enhancement mechanism in flexible wings even though it requires more input power. This is because the wing kinematics at the wing tip is modified passively, but favourably owing to the elastic wing deformation even with an input of relatively inefficient wing kinematics at the wing base. Note that the wing base in hovering has low velocity and is ineffective for aerodynamic force production. This suggests that there may exist an optimal distribution of wing kinematics between the wing base and wing tip, which should be more efficient in creating vertical aerodynamic forces. A rigid and flat wing can create higher aerodynamic forces with appropriately tuned wing kinematics than that of a flexible wing in some cases [41], but cannot achieve high efficiency by the distributed kinematics. Hence, the elastic wing deformation is thought to be a key in tuning optimal wing kinematics spanwise in insect flapping flight. Our rigid wing models with the FSI-based wing kinematics prescribed strongly support this hypothesis. We see that large vertical forces can be produced comparable with that of the flexible wing and that a rigid and flat wing model used in previous studies is capable of evaluating the aerodynamic force production for insect flapping flight. However, the aerodynamic efficiency easily drops to a lower level of the rigid wing model based on the wing base kinematics by equation (2.1). This points to the importance of the dynamic spanwise distribution of wing kinematics in enhancing the aerodynamic efficiency, and thus confirms that the elastic wing deformation is an effective way to achieve higher aerodynamic performance in insect flapping flight.

(c). Relationship between wing stiffness and wing structure optimization

In this study, the inherent flexibility in the insect wing is confirmed to be able to enhance the aerodynamic performance of flapping wings. By tuning the wing stiffness, we further find that there may exist an optimal wing structure, e.g. in terms of Young's modulus and/or thickness, by which an optimized aerodynamic efficiency can be achieved. We expected that such a wing structure optimization might occur in our realistic model of the hawkmoth hovering with realistic Young's modulus and wing thickness. The extensive study on the wing stiffness effect (figure 3), however, indicates that with thinner veins and the same Young modulus, our hovering hawkmoth model can fly more effectively at a smaller stiffness than it is. The incompleteness in the current FSI model may be a reason that it leads to such a gap between this virtual computational model and reality. On the other hand, it may also be reasonable to consider the role of insect wing structure in a way that it must create aerodynamic forces to stay airborne while making an effective response to the control input at the wing base without wing failure or serious fracture while circulating the fluid inside [42]. If the vein thickness is reduced, its structural strength will be decreased because of the reduction in cross-section area, which may lead to a structural wing failure. Furthermore, with increasing wing flexibility, the control of wing kinematics may become more complicated. Therefore, the inherent flexibility of insect wings may not need to be optimized merely from the viewpoint of aerodynamics because the structural design of insect wings is the result of compromise among many factors.