Selection in Insurance Markets: Theory and Empirics in Pictures

From the large scale social insurance programs of Social Security and Medicare to the heavily regulated private markets for property and casualty insurance, government intervention in insurance markets is ubiquitous. The fundamental theoretical reason for such intervention, based on classic work from the 1970s, is the problem of adverse selection. But despite the age and influence of the theory, systematic empirical examination of selection in actual insurance markets is a relatively recent development. Indeed, in awarding the 2001 Nobel Prize for the pioneering theoretical work on asymmetric information, the Nobel committee noted this paucity of empirical work (Bank of Sweden, 2001).

Over the last decade, however, empirical work on selection in insurance markets has gained considerable momentum, and a fairly extensive (and still growing) empirical literature on the topic has emerged. This research has found that adverse selection exists in some insurance markets but not in others. It has also uncovered examples of markets that exhibit “advantageous selection” – a phenomenon not considered by the original theory and that has different consequences for equilibrium insurance allocation and optimal public policy than the classical case of adverse selection. Researchers have also taken steps toward estimating the welfare consequences of detected selection and of potential public policy interventions.

In this essay, we present a graphical framework for analyzing both theoretical and empirical work on selection in insurance markets. This graphical approach, which draws heavily on Einav, Finkelstein, and Cullen (2010), provides both a useful and intuitive depiction of the basic theory of selection and its implications for welfare and public policy, as well as a lens through which one can understand the ideas and limitations of existing empirical work on this topic.

We begin by using this framework to review the “textbook” adverse selection environment and its implications for insurance allocation, social welfare, and public policy. We then discuss several important extensions to this classic treatment that are necessitated by important real world features of insurance markets, and which can be easily incorporated in the basic framework. Finally, we use the same graphical approach to discuss the intuition behind recently developed empirical methods for testing for the existence of selection and examining its welfare consequences. We conclude by discussing some important issues that are not well-handled by this framework and which, perhaps not unrelatedly, have been little addressed by the existing empirical work; we consider these fruitful areas for additional research. Our essay does not aim at reviewing the burgeoning empirical literature on selection in insurance markets. However, at relevant points in our discussion we point the interested reader to recent papers that review or summarize recent findings.

Adverse and Advantageous Selection: A Graphical Framework

The Textbook Environment for Insurance Markets

We start by considering the textbook case of insurance demand and cost, in which perfectly competitive, risk-neutral firms offer a single insurance contract that covers some probabilistic loss, risk-averse individuals differ only in their (privately-known) probability of incurring that loss, and there are no other frictions in providing insurance such as administrative or claim-processing costs. Thus, more in the spirit of Akerlof (1970) and unlike the well known environment of Rothschild and Stiglitz (1976), firms compete in prices but do not compete on the coverage features of the insurance contract. We return to this important simplifying assumption in the end of this essay.

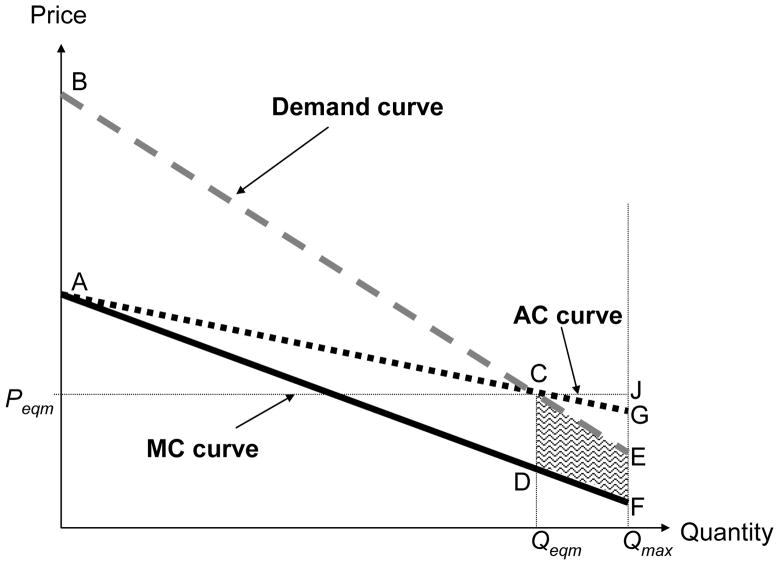
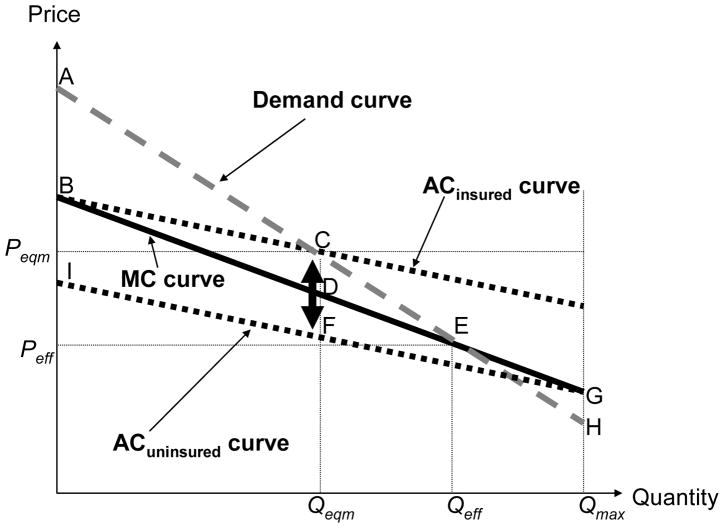
Figure 1 provides our graphical representation of this case, and illustrates the resulting adverse selection as well as its consequences for insurance coverage and welfare. The figure considers the market for a specific insurance contract. Consumers in this market make a binary choice of whether or not to purchase this contract, and firms in this market compete only over what price to charge for the contract.

FIGURE I.

Adverse selection in the textbook setting

The vertical axis indicates the price (and expected cost) of that contract, and the horizontal axis indicates the quantity of insurance demand. Since individuals face a binary choice of whether or not to purchase the contract, the “quantity” of insurance is simply the fraction of insured individuals. With risk-neutral insurance providers and no additional frictions, the social (and firms’) costs associated with providing insurance are the expected insurance claims—that is, the expected payouts on policies.

Figure 1 shows the market demand curve for the insurance contract. Because individuals in this setting can only choose the contract or not, the market demand curve simply reflects the cumulative distribution of individuals’ willingness to pay for the contract. While this is a standard unit demand model that could apply to many traditional product markets, the textbook insurance context allows us to link willingness to pay to cost. In particular, a risk averse individual’s willingness to pay for insurance is the sum of her expected cost and her risk premium.

In the textbook environment, individuals are homogeneous in their risk aversion (and all other features of their utility function). Therefore, their willingness to pay for insurance is increasing in their risk type—that is, their probability of loss, or expected cost—which is privately known. This is illustrated in Figure 1 by plotting the marginal cost (MC) curve as downward sloping: those individuals who are willing to pay the most for coverage are those that have the highest expected cost. This downward sloping MC curve represents the well-known adverse selection property of insurance markets: the individuals who have the highest willingness to pay for insurance are those who are expected to be the most costly for the firm to cover.

The link between the demand and cost curve is arguably the most important distinction of insurance markets (or selection markets more generally) from traditional product markets. The shape of the cost curve is driven by the demand-side customer selection. In most other contexts, the demand curve and cost curve are independent objects; demand is determined by preferences and costs by the production technology. The distinguishing feature of selection markets is that the demand and cost curves are tightly linked since the individual’s risk type not only affects demand but also directly determines cost.

The risk premium is shown graphically in the figure as the vertical distance between expected cost (the MC curve) and the willingness to pay for insurance (the demand curve). In the textbook case, the risk premium is always positive, since all individuals are risk-averse and there are no other market frictions. As a result, the demand curve is always above the MC curve and it is therefore efficient for all individuals to be insured (Q_eff = Q_max). Absent income effects, the welfare loss from not insuring a given individual is simply the risk premium of that individual, or the vertical difference between the demand and MC curves.

When the individual-specific loss probability (or expected cost) is private information to the individual, firms must offer a single price for pools of observationally identical, but in fact heterogeneous, individuals. Of course, in practice firms may vary the price based on some observable individual characteristics (such as age or zip code). Thus, Figure 1 can be thought of as depicting the market for coverage among individuals who are treated identically by the firm.

The competitive equilibrium price will be equal to firms’ average cost at that price. This is a zero profit condition; offering a lower price will result in negative profits, and offering higher prices than competitors will not attract any buyers. The relevant cost curve the firm faces is therefore the average cost (AC) curve, which is also shown in Figure 1. The (competitive) equilibrium price and quantity is given by the intersection of the demand curve and the AC curve (point C).

The fundamental inefficiency created by adverse selection arises because the efficient allocation is determined by the relationship between marginal cost and demand, but the equilibrium allocation is determined by the relationship between average cost and demand. Because of adverse selection (downward sloping MC curve), the marginal buyer is always associated with a lower expected cost than that of infra-marginal buyers. Therefore, as drawn in Figure 1, the AC curve always lies above the MC curve and intersects the demand curve at a quantity lower than Q_max. As a result, the equilibrium quantity of insurance will be less than the efficient quantity (Q_max) and the equilibrium price will be above the efficient price, illustrating the classical result of under-insurance in the presence of adverse selection (Akerlof, 1970; Rothschild and Stiglitz, 1976). That is, it is efficient to insure every individual (MC is always below demand) but in equilibrium the Q_max – Q_eqm individuals with the lowest expected costs remain uninsured because the AC curve is not always below the demand curve. These individuals value the insurance at more than their expected costs, but firms cannot insure these individuals and still break even.

The welfare cost of this under-insurance depends on the lost surplus (the risk premium) of those individuals who remain inefficiently uninsured in the competitive equilibrium. In Figure 1, these are the individuals whose willingness to pay is less than the equilibrium price, P_eqm. Integrating over all these individuals’ risk premia, the welfare loss from adverse selection in this simple framework is given by the area of the “dead-weight loss” trapezoid CDEF.

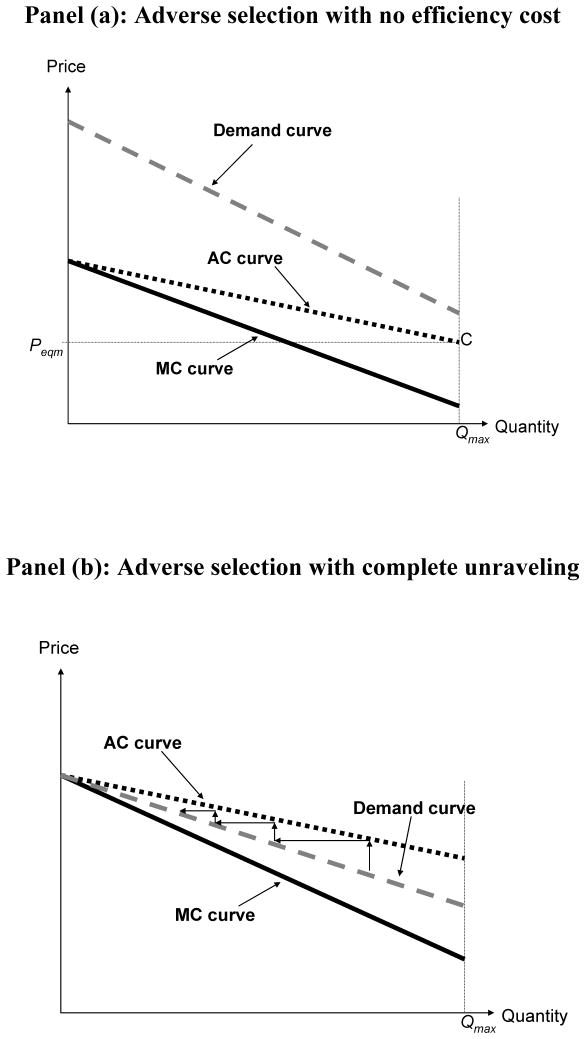
Even in the textbook environment, the amount of under-insurance generated by adverse selection, and its associated welfare loss, can vary greatly. Figure 2 illustrates this point by depicting two specific examples of the textbook adverse selection environment, one that produces the efficient insurance allocation and one that produces complete unraveling of insurance coverage. The efficient outcome is depicted in Panel (a). While the market is adversely selected (that is, the MC curve is downward sloping), the AC curve always lies below the demand curve. This leads to an equilibrium price P_eqm, that, although it is higher than marginal cost, still produces the efficient allocation (Q_eqm = Q_eff = Q_max). This situation can arise, for example, when individuals do not vary too much in their unobserved risk (that is, the MC and consequently AC curve is relatively flat) and/or individuals’ risk aversion is high (that is, the demand curve lies well above the MC curve).

FIGURE 2. Specific Examples of extreme cases.

The case of complete unraveling is illustrated in Panel (b). Here, the AC curve always lies above the demand curve even though the MC curve is always below it. ¹ As a result, the competitive equilibrium is that no individual in the market is insured, while the efficient outcome is for everyone to have insurance. One could also use Panel (b) to illustrate the potential death spiral dynamics that may lead to such unraveling. For example, if insurance pricing is naively set but dynamically adjusted to reflect the average cost from the previous period (which is, in fact, a fairly common practice in many health insurance settings), the market will gradually shrink until it would unravel. This convergent adjustment process is illustrated by the arrows in Panel (b). Cutler and Reber (1998) provide an empirical case study of a death spiral of this nature in the context of a health insurance plan offered to Harvard University employees.

Public Policy in the Textbook Case

Our graphical framework can also be used to illustrate the consequences of common public policy interventions in insurance markets. The canonical solution to the inefficiency created by adverse selection is to mandate that everyone purchase insurance. In the textbook setting, this produces the efficient outcome in which everyone has insurance. However, the magnitude of the welfare benefit produced by an insurance purchase requirement can vary dramatically depending on the specifics of the market. The two extreme examples presented in Figure 2 illustrate this point, but even in intermediate cases captured by Figure 1 the magnitude of the welfare loss (area CDEF) is highly sensitive to the shape and location of the cost and demand curves and is therefore ultimately an empirical question.²

Another commonly discussed policy remedy for adverse selection is to subsidize insurance coverage. We can use Figure 1 to illustrate. Consider, for example, a lump sum subsidy toward the price of coverage. This would shift demand out, leading to a higher equilibrium quantity and less underinsurance. The welfare loss would still be associated with the area between the original (pre-subsidy) demand curve and the MC curve, and would therefore unambiguously decline with any positive subsidy. A large enough subsidy (greater than the line segment GE in Figure 1) would lead to the efficient outcome, with everybody insured.

A final common form of public policy intervention is regulation that imposes restrictions on the characteristics of consumers over which firms can price discriminate. Some regulations require “community rates” that are uniform across all individuals, while others prohibit insurance companies from making prices contingent on certain observable risk factors, such as race or gender. For concreteness, consider the case of a regulation that prohibits pricing on the basis of gender. Recall that Figure 1 can be interpreted as applying to a group of individuals who must be treated the same by the insurance company. When pricing based on gender is prohibited, males and females are pooled into the same market, with a variant of Figure 1 describing that market. When pricing on gender is allowed, there are now two distinct insurance market – described by two distinct variants of Figure 1 – one for women and one for men, each of which can be analyzed separately. A central issue for welfare analysis is whether, when insurance companies are allowed to price on gender, consumers still have residual private information about their expected costs. If they do not, then the insurance market within each gender-specific segment of the market will exhibit a constant (flat) MC curve, and the equilibrium in each market will be efficient. In this case, policies that restrict pricing on gender are unambiguously welfare decreasing since they create adverse selection where none existed before. However, in the more likely case that individuals have some residual private information about their risk that is not captured by their gender, each gender-specific market segment would look qualitatively the same as Figure 1 (with downward sloping MC and AC curves). In such cases, the welfare implications of restricting pricing on gender could go in either direction; depending on the shape and position of the gender-specific demand and cost curves relative to the gender-pooled ones, the sum of the areas of the “deadweight loss” trapezoids in the gender-specific markets could be larger or smaller than the area of the single deadweight loss trapezoid in the gender-pooled market.³

Departures from the Textbook Environment

Although the textbook treatment of insurance markets may give rise to dramatically different magnitudes of the welfare costs arising from adverse selection, the qualitative findings are robust. Under the textbook assumptions, private information about risk always produces under-insurance relative to the efficient outcome, and mandatory insurance coverage is always a welfare-improving policy intervention. However, these robust qualitative results only hold in this textbook case. They may be reversed with the introduction of either or both of two important features of actual insurance markets: 1) insurance “loads” or administrative costs of providing insurance, and 2) preference heterogeneity.

Consider first a loading factor on insurance, for example in the form of additional administrative cost associated with selling and servicing insurance, perhaps due to costs associated with advertising and marketing, or with verifying and processing claims. Many insurance markets display evidence of nontrivial loading factors, including long-term care insurance (Brown and Finkelstein, 2007), annuity markets (Friedman and Warshawsky, 1990; Mitchell et al., 1999; Finkelstein and Poterba, 2002), health insurance (Newhouse, 2002), and automobile insurance (Chiappori et al., 2006).⁴

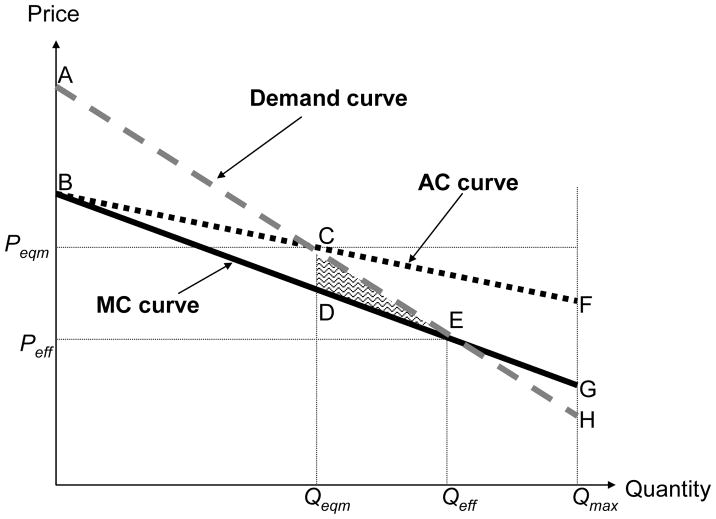
The key implication of such loads is that it is now not necessarily efficient to allocate insurance coverage to all individuals. Even if all individuals are risk averse, the additional cost of providing an individual with insurance may be greater than the risk premium for certain individuals, making it socially efficient to leave such individuals uninsured. This case is illustrated in Figure 3, which is similar to Figure 1, except that the cost curves are shifted upward reflecting the additional cost of insurance provision.⁵

FIGURE 3.

Adverse selection with additional cost of providing insurance

Figure 3 is drawn in a way that the MC curve crosses the demand curve “internally” (that is, at a quantity lower than Q_max), at point E, which depicts the socially efficient insurance allocation. It is efficient to insure everyone to the left of point E (since their willingness to pay for insurance exceeds their expected cost), but socially inefficient to insure anyone to the right of point E since their willingness to pay is less than their expected cost. In this situation, it’s efficient to keep Q_max – Q_eff individuals uninsured.

The introduction of loads does not affect the basic analysis of adverse selection, but it does have important implications for its standard public policy remedies. The competitive equilibrium is still determined by the zero profit condition, or the intersection of the demand curve and the AC curve (point C in Figure 3), and in the presence of adverse selection (downward sloping MC curve) this leads to under-insurance relative to the social optimum (Q_eqm < Q_eff), and to a familiar dead-weight loss triangle CDE.

However, with insurance loads, the textbook result of an unambiguous welfare gain from mandatory coverage no longer obtains. As Figure 3 shows, while a mandate that everyone be insured “regains” the welfare loss associated with under-insurance (triangle CDE), it also leads to over-insurance by covering individuals whom it is socially inefficient to insure (that is, whose expected costs are above their willingness to pay). This latter effect leads to a welfare loss given by the area EGH in Figure 3. Therefore whether a mandate improves welfare over the competitive allocation depends on the relative sizes of triangles CDE and EGH; this is turn depends on the specific market’s demand and cost curves, and is therefore an empirical question.

A second important feature of real-world insurance markets not captured by the textbook treatment is preference heterogeneity: that is, the possibility that individuals may differ not only in their risk but also in their preferences, such as their willingness to bear risk (risk aversion). The classical models (like Rothschild and Stiglitz, 1976) make the simplifying and theoretically-attractive assumption that individuals have the same preferences, and may vary only in their (privately known) expected costs. As a result, willingness to pay for insurance is an increasing function of expected costs.

In practice, of course, individuals may differ not only in their expected cost but also in their preferences. Indeed, recent empirical work has documented substantial preference heterogeneity in different insurance markets, including automobile insurance (Cohen and Einav, 2007), reverse mortgages (Davidoff and Welke, 2007), health insurance (Fang, Keane, and Silverman, 2008), and long-term care insurance (Finkelstein and McGarry, 2006). The existence of unobserved preference heterogeneity opens up the possibility of advantageous selection, which produces opposite results to the adverse selection results just discussed.⁶

Consider for example heterogeneity in risk aversion, in addition to the original heterogeneity in risk (expected cost). All else equal, willingness-to-pay for insurance is increasing in risk aversion and in risk. If heterogeneity in risk aversion is small, or if those individuals who are high risk are also more risk averse, the main insights from the textbook analysis remain. But if high-risk individuals are less risk averse and the heterogeneity in risk aversion is sufficiently large, advantageous selection may emerge. Namely, the individuals who are willing to pay the most for insurance are those who are the most risk averse, and in the case described these are also those individuals associated with the lowest (rather than the highest) expected cost. Indeed, it is natural to think that in many instances individuals who value insurance more may also take action to lower their expected costs: drive more carefully, invest in preventive health care, and so on.

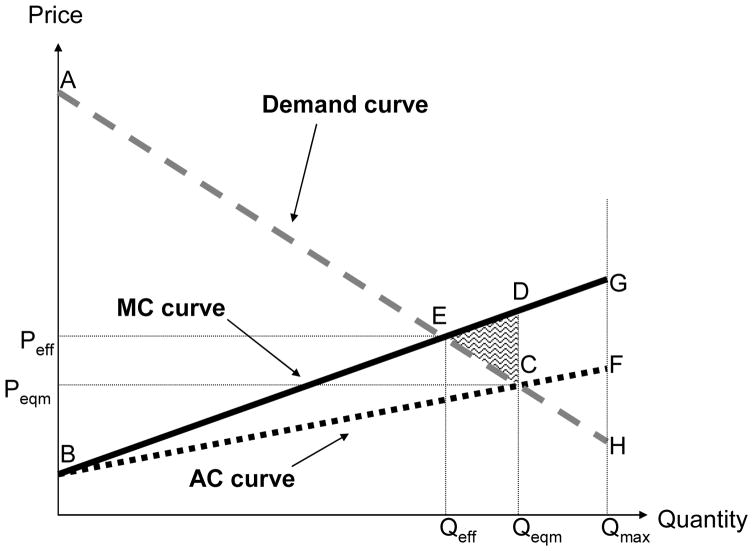
Figure 4 provides our graphical illustration of such advantageous selection and its consequences for insurance coverage and welfare. In contrast to adverse selection, advantageous selection is defined by an upward sloping MC (and AC) curve.⁷ As price is lowered and more individuals opt into the market, the marginal individual opting in has higher expected cost than infra-marginal individuals. Since the MC curve is upward sloping, the AC curve will lie everywhere below it. If there were no insurance loads (as in the textbook situation), advantageous selection would not lead to any inefficiency; the MC and AC curves would always lie below the demand curve, and in equilibrium all individuals in the market would be covered, which would be efficient.

FIGURE 4.

Advantageous selection

With insurance loads, however, advantageous selection generates the mirror image of the adverse selection case, also leading to inefficiency, but this time due to over-insurance rather than underinsurance. Figure 4 depicts this case. The efficient allocation calls for providing insurance to all individuals whose expected cost is lower than their willingness to pay—that is, all those who are to the left of point E (where the MC curve intersects the demand curve) in Figure 4. Competitive equilibrium, as before, is determined by the intersection of the AC curve and the demand curve (point C in Figure 4). But since the AC curve now lies below the MC curve, equilibrium implies that too many individuals are provided insurance, leading to over-insurance: there are Q_eqm – Q_eff individuals who are inefficiently provided insurance in equilibrium. These individuals value the insurance at less than their expected costs, but competitive forces make firms reduce the price in order to attract these individuals and at the same time attracting more profitable infra-marginal individuals. Again, the area of the dead-weight loss triangle CDE quantifies the extent of the welfare loss from this over-insurance.

From a public policy perspective, advantageous selection calls for the opposite solutions relative to the tools used to combat adverse selection. For example, given that advantageous selection produces “too much” insurance relative to the efficient outcome, public policies that tax existing insurance policies (and therefore raise P_eqm toward P_eff) or outlaw insurance coverage (mandate no coverage) could be welfare-improving. Although there are certainly taxes levied on insurance policies, to our knowledge advantageous selection has not yet been invoked as a rationale in public policy discourse, perhaps reflecting the relative newness of both the theoretical work and empirical evidence. To our knowledge, advantageous selection was first discussed by Hemenway (1990), who termed it “propitious” selection. De Meza and Webb (2001) provide a theoretical treatment of advantageous selection and its implications for insurance coverage and public policy.

Advantageous selection is not merely a theoretical possibility. It has recently been documented in several insurance markets, with different sources of individual heterogeneity that give rise to it. Finkelstein and McGarry (2006) document advantageous selection in the market for long-term care insurance and provide evidence that more cautious individuals invest more in precautionary behavior and are less likely to use a nursing home, but at the same time are more likely to purchase long-term care insurance. Fang, Keane, and Silverman (2008) document advantageous selection in the market for Medi-gap coverage, which provides private health insurance that supplements Medicare for the elderly, but show that in the case of Medi-gap, cognition may be the driving force: individuals with higher cognitive ability are often able to make better decisions, which can translate into both greater coverage and at the same time lower health care expenditures.

Advantageous selection provides a nice example of the interplay in the selection literature between theory and empirical work. The original adverse selection theory motivated empirical work testing for the existence of adverse selection. This empirical work in turn provided examples of advantageous selection (which the original theory had precluded), suggesting the need for important extensions to the theory. We now turn to a more detailed discussion of how the existing empirical work can be viewed through the graphical framework we have developed.

Empirical Work on Selection: A Graphical View

Empirical research on selection in insurance markets has flourished over the last decade. This empirical literature began, quite naturally, by asking how we can test for whether the classic adverse selection models apply in real-world insurance markets. In other words, what would selection look like in the data, when or if it exists? Empirical research has now progressed from trying to detect the existence (and nature) of selection toward attempts to quantify its welfare consequences and those of potential public policy interventions. We can use our graphical framework to understand the intuition and limitations of this research program.

“Positive Correlation” Tests For Adverse Selection

Using our graphical framework, testing for adverse selection essentially requires us to test whether the MC curve is downward sloping. Making inference about marginal individuals is difficult, however. As a result, the early empirical approaches developed strategies that attempt to get around this difficulty by, instead, focusing on comparing averages.

The graphical depictions of adverse selection in Figure 1 (or Figure 3) suggests one way to examine whether adverse selection is present in a particular insurance market: compare the expected cost of those with insurance to the expected cost of those without (or compare those with more insurance coverage to those with less coverage).

To see this idea more clearly, consider Figure 5. Here we start with the adverse selection situation already depicted in Figure 3, denoting the AC curve shown in previous figures by AC_insured to reflect the fact that it averages over those individuals with insurance, and adding one more line: the AC_uninsured curve. The AC_uninsured curve represents the average expected cost of those individuals who do not have insurance. That is, the AC_insured curve is derived by averaging over the expected costs of the insured (averaging “from the left”, starting at Q = 0) while the AC_uninsured curve is produced by averaging over the expected costs of the uninsured (averaging “from the right”, starting at Q = Q_max). A downward-sloping MC curve implies that AC_insured is always above AC_uninsured, with the average costs of the insured at Q_max equal to the average costs of the uninsured at Q = 0 (because both represent the average costs of the full population), and the marginal cost curve intersecting AC_insured at Q = 0 and AC_uninsured at Q = Q_max.

FIGURE 5.

The “positive correlation” test for selection

Thus, at any given insurance price, and in particular at the equilibrium price, adverse selection implies that the average cost of insured individuals is higher than the average cost of uninsured, and the difference in these averages is given by line segment CF in Figure 5 (the thick arrowed line in the figure). This basic insight underlies the widely used “positive correlation” test for asymmetric information. The test measures the distance between point C (average costs of those who in equilibrium are insured) and point F (average costs of those who in equilibrium are not insured). The results are consistent with the existence of adverse selection if the average cost of the insured (point C) is statistically greater than those of the uninsured (point F).

The test has typically been implemented by comparing proxies for expected costs across individuals with different insurance coverage, controlling as needed for important confounding factors (as we discuss below). Many of these empirical papers use data from a single company, and examine average claims across individuals who are offered the same contracts but who choose more or less coverage. Our graphical framework naturally extends to the choice of more vs. less coverage (as opposed to any vs. no insurance). Indeed, the recent burgeoning of empirical work on selection likely reflects at least in part researchers’ increasing success in obtaining access to insurance company data, which has greatly improved their ability to examine questions of private information empirically.

Perhaps due in part to its not-so-demanding data requirement, variants of the positive correlation test have been quite popular; the test requires “only” that one observe the average expected costs of individuals (who are observationally identical to the firm) with different amounts of insurance coverage. There is now a large literature studying how average costs vary across different coverage options in a broad range of insurance markets, including health, life, automobile, and homeowner insurance. The results have been mixed. In some markets, researchers have found evidence consistent with adverse selection—that is, higher average costs for individuals with greater insurance coverage—while in others they have found evidence of advantageous selection—defined by a negative relationship between insurance coverage and average costs—or have been unable to reject the null of symmetric information, meaning no difference in average costs. Cohen and Siegelman (2010) provide a recent review of this literature.

Challenges in Applying the Positive Correlation Test

Although applying the simple positive correlation test is reasonably straightforward, one has to confront certain challenges. Researchers have generally been quite careful to acknowledge these issues and in some cases to find creative ways that get around them. We mention here three common issues that often come up in applications, again referring to our graphical framework for intuition.

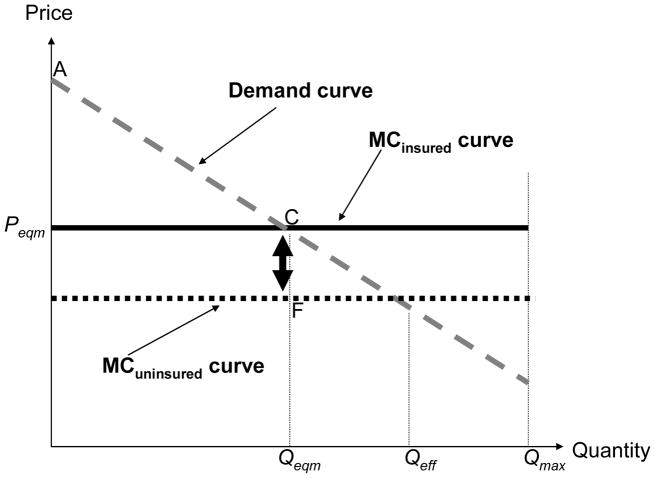
A first important limitation of the positive correlation test is that comparing expected costs across individuals with and without insurance may confound adverse selection and moral hazard. Both adverse selection and moral hazard can generate a positive correlation between insurance coverage and claims, but these are two very different forms of asymmetric information with very different implications for public policy. With adverse selection, individuals who have private information that they are at higher risk self-select into the insurance market, generating the positive correlation between insurance coverage and observed claims. As already discussed, the government has several potential welfare-improving policy tools to possibly address such selection. With moral hazard, individuals are identical before they purchase insurance, but have incentives to behave differently after. Those with greater coverage have less incentive to take actions that reduce their expected costs, which will generate a relationship between insurance coverage and observed claims. Unlike in the case of adverse selection, the government typically has no advantage over the private sector at reducing the welfare costs of moral hazard.

Figure 6 shows how moral hazard can produce the same “positive correlation” property as adverse selection produces in Figure 5. Specifically, Figure 6 provides a graphical representation of an insurance market with moral hazard but no selection. The lack of selection is captured by the flat MC curves. Moral hazard is captured by drawing two different MC curves, as opposed to the single MC curve we have drawn in the figures so far. The MC_insured curve represents the expected cost of insured individuals, and corresponds to the MC curves we have been drawing in all previous figures. The MC_uninsured curve represents the expected cost of these same individuals, if they were uninsured. Moral hazard, which takes the form of greater expected costs when a given individual has insurance than when she does not, implies that MC_insured is greater than MC_uninsured for each individual (or, graphically, point-by-point).⁸ The vertical difference between MC_insured and MC_uninsured is a graphical way to quantify moral hazard in terms of expected cost.

FIGURE 6.

The “positive correlation” test for moral hazard

Figure 6 is drawn for a case in which there is no adverse selection: individuals have the same expected cost, the MC curves are flat, and the demand curve is downward sloping due to other factors (for example, heterogeneity in risk aversion). Yet, a comparison of expected costs between the insureds and uninsureds would lead to the same quantity (line segment CF) as in Figure 5. However, while in Figure 5 the positive correlation arose due to adverse selection, in Figure 6 this same positive correlation is generated entirely by moral hazard. ⁹

Therefore, in situations where moral hazard could be an important factor, the positive correlation test is a joint test of either adverse selection or moral hazard. Finding a positive correlation would reject the null (of symmetric information) either due to the presence of adverse selection or moral hazard (or both). Moreover, finding no correlation could be either due to no asymmetric information or due to the existence of both moral hazard and advantageous selection, which offset each other. On the other hand, a convincing finding of a negative correlation is still informative, as it would be consistent with advantageous selection, even in the presence of moral hazard.

A second important consideration in applying the positive correlation test is the set of covariates that are being conditioned out. As a starting point, one must condition on the consumer characteristics that determine the prices offered to each individual. That is, a proper implementation of the positive correlation test requires that we examine whether, among a set of individuals who are offered coverage options at identical prices, those who buy more insurance have higher expected costs than those who do not. In the absence of such conditioning, it is impossible to know whether a correlation arises due to demand (different individuals self select into different contracts) or supply (different individuals are offered the contracts at different prices by the insurance company). Only the former is evidence of selection. As a result, some of the most convincing tests are those carried out using insurance company data, where the researcher knows (rather than assumes) the full set of characteristics that the insurance company uses for pricing. Absent data on individually-customized prices, which is sometimes difficult to obtain, one may instead try to flexibly control for all individual characteristics that affect pricing (Chiappori and Salanie, 2000).

A yet more nuanced decision is whether one should control for a larger set of covariates (when available). In addition to the consumer characteristics that determine their choice set (that is, the specific contracts and their prices), one could attempt to control for other observed variables that are not used (due to regulation or any other reason), for other observable variables that are not observed by the firm (some may be observable to the firm with additional cost, others may be observable only to the researcher), and so on. Whether such variables should be used as covariate is less obvious and is likely to depend on the question that one would like to answer. One needs to recognize that the interpretation of a positive correlation can vary depending on such decision. For example, one may find positive correlation only because firms are not allowed to incorporate race into pricing. If this positive correlation disappears when race is controlled for, one may want to be careful about the precise meaning of the term “asymmetric information” (since race is known to the insurance company even if not used in pricing) even though the implications for market equilibrium and inefficiency may be the same.

A final important consideration in applying the test concerns the measurement of costs. Figure 5 suggests that the theoretical object one would like to observe is that of expected cost. Expectations are, of course, difficult to observe, so researchers often use proxies for it.

The most direct proxy would use the average realized costs. With enough data, realized costs of the insured converge to the expected costs, precisely capturing the theoretical object. In practice, however, realized costs may be tricky. For example, when comparing insured to uninsured individuals, one obviously does not observe the “claims” of the uninsured. Even when comparing claims of individuals who choose more or less coverage within a given company, certain realized (social) costs are less likely to be claimed by individuals with less coverage. For example, there is a range of possible claim amounts that are worth claiming under low deductible, but would not provide any benefits for (and are unlikely to be filed by) individuals covered by a higher deductible.

There are several potential strategies for trying to detect differences in real behavior as opposed to differences in claiming behavior. One option is to focus on a subset of realized claims that are less prone to insurance coverage influencing decisions to file a claim: for example, by focusing on multiple-car accidents in the context of automobile insurance. Alternatively, one might use data external to the firm: for example, by examining mortality certificates in the context of annuities or life insurance. The latter has the ancillary benefit that such “external” data are observed for the uninsured population as well.

Another approach is to identify individual characteristics that are not priced by insurance companies but are known to be associated with expected cost, such as age or gender in the context of employer-provided health insurance. An ancillary benefit of this approach is that it also gets around the issue of moral hazard. A limitation of this approach, however, is that it can only be applied in situations in which – in conflict with textbook economics – pricing is not affected by an important risk factor. In such settings, one might reasonably wonder whether the original concerns about the efficiency loss from adverse selection and the potential public policy remedies are at all relevant.

Beyond Testing: Quantifying Selection Effects

The importance and influence of the seminal theoretical work on selection in insurance markets stemmed in large part from its findings that selection could impair the efficient operation of competitive insurance markets and potentially open up scope for welfare-improving government intervention. Detecting selection is therefore only a first step. If selection is empirically detected, it is natural to ask whether the welfare costs it generates are large or small, and what might be the welfare consequences of specific government policies. These are fundamentally empirical questions, and our graphical framework is useful for guiding attempts to quantify these welfare constructs.

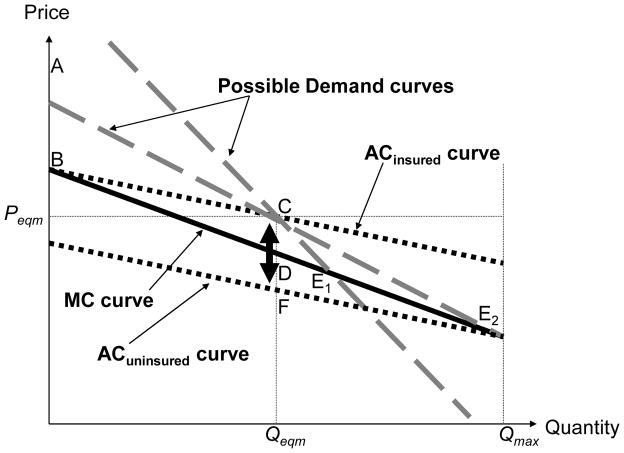
We begin by debunking a common (mis)perception that the very same empirical objects that are used for the positive correlation test (described earlier) can also be informative about the welfare costs associated with selection. It may be appealing to imagine that markets that appear “more adversely selected”—that is, ones in which there is a larger difference between the expected costs of insureds and uninsureds—experience greater welfare loss associated with that selection. Unfortunately, Figure 7 illustrates that without additional assumptions, comparisons of expected costs are not that informative about underlying efficiency costs. Figure 7 starts with the situation depicted in Figure 3. Once again, the equilibrium difference in expected costs between the insureds and uninsureds is given by the distance between points C and F, and the welfare loss from adverse selection is given by the area of the deadweight loss triangle CDE. However, here we have drawn two possible demand curves, each of which give rise to the same equilibrium point (point C), while keeping the MC and AC curves unchanged. ^10,11 By design, the two demand curves generate the same equilibrium point, thereby producing the same difference in expected costs between the insureds and uninsureds (line segment CF in Figure 7). However, these demand curves generate different efficient outcomes, meaning different points at which the two demand curves intersect the MC curve, denoted in the figure by points E₁ and E₂. As a result, they produce different-sized welfare losses, given by the corresponding triangles CDE₁ and CDE₂. This example thus illustrates how deadweight loss triangles of different sizes can be generated even though the “extent of adverse selection” as measured by the difference in average costs is the same.

FIGURE 7.

The “positive correlation” and its (non)relation to welfare costs of selection

One way to make some progress in quantifying the welfare consequences of selection or of potential public policy is to use bounds which are based on easily observable objects. For example, suppose we would like to bound the welfare cost of selection. We use Figure 1 (adverse selection) for this discussion, but it is easy to imagine an analogous discussion for the advantageous selection shown in Figure 4. Suppose first that we observe only the price of the insurance sold in the market. If we are willing to assume that we observe the competitive equilibrium price (P_eqm), we can obtain a (presumably not very tight) upper bound of the welfare cost of selection, given by P_eqm × Q_max. Intuitively, because adverse selection leads to underinsurance the worst possible scenario is when nobody is insured but everybody should be insured. Since the equilibrium price must exceed the willingness-to-pay for insurance by the uninsureds (otherwise they would have purchased insurance), the price provides an upper bound on the per-individual welfare loss.

Additional data may help tighten the bound. If we also observe the (equilibrium) share of uninsured individuals (that is, Q_max − Q_eqm), the upper bound for the welfare loss can be tightened to P_eqm (Q_max − Q_eqm). Finally, if we also have all the data elements needed for the positive correlation test – so that we also observe the expected costs of the uninsureds and denote it by X – we can further tighten this upper bound to (P_eqm – X) (Q_max − Q_eqm) (equal to area CDFJ in Figure 1).¹²

Substantially more progress can be made in estimating the welfare consequences of selection (or of potential public policy interventions) if we have one additional data element beyond what is required for the positive correlation test. This additional element, which is so heavily used in other subfields of applied microeconomics, is identifying variation in insurance prices.

To see how useful price variation may be for welfare analysis, one can imagine the ideal experiment of randomly varying the price at which insurance is offered to large pools of otherwise identical individuals. For each pool, we would then observe the fraction of individuals who bought insurance and the average realized costs of insured individuals. In such an ideal situation, we can use the data generated to “trace out” the demand curve and the AC curve in our graphical analysis, and to derive the MC curve, thus producing the three essential curves behind all of the welfare analysis in our graphical framework. ¹³

Observing the MC curve arguably addresses the key challenge for empirically analyzing insurance markets which, as noted earlier, is to identify the marginal individuals. Indeed, with knowledge of the MC curve, AC curve, and demand curve, it is straightforward to compute the welfare loss of adverse selection or any other object of interest within the graphical framework we propose, such as the welfare effects of the various public policy interventions we analyzed earlier. This is the basic point advanced in Einav, Finkelstein, and Cullen (2010), who empirically illustrate this idea in the context of employer-provided health insurance. They also provide some discussion of possible sources of such identifying pricing variation, including field experiments, experimentation by firms, and pricing variation driven by various common forms of insurance regulation.

Such pricing variation has two related ancillary benefits. First, it provides a direct test of both the existence and nature of selection based on the slope of the estimated MC curve. We can reject the null of symmetric information if we can reject the null of a constant MC curve. Moreover, a finding that the MC curve is downward (upward) sloping suggests the existence of adverse (advantageous) selection. Crucially, unlike the “positive correlation” test, this “cost curve” test of selection is not affected by the existence (or lack thereof) of moral hazard. To see why this is true, recall that the AC curve from which the MC curve is derived is defined as the average costs of all those individuals who buy a specific insurance contract. Because the cost curves are defined over a sample of individuals who all have the same insurance contract, differences in the shape of the cost curve are not directly affected by moral hazard. ¹⁴

This insight suggests a step-by-step approach to analysis of selection in insurance markets if one has access to identifying pricing variation, in addition to the data on average costs of those with different insurance coverage. In the first step, the simple correlation test can be used to see if one can reject the null of symmetric information (in favor of either a positive or negative correlation). In the second step, if the null of symmetric information is rejected, the identifying pricing variation can then be used to estimate the cost curves and thus detect whether selection—as distinct from moral hazard—exists and whether it is adverse or advantageous. Finally, if selection is detected, its welfare cost can be estimated, and the welfare consequences of potential public policy interventions weighed, by bringing the estimated demand curve into the analysis as well.

There is yet another important benefit from identifying pricing variation, although it is not the focus of this essay, which is that it allows one to test for and quantify moral hazard. To see this, we can again consider what the ideal experiment might be. To analyze moral hazard, one would randomly allocate insurance to some individuals and allocate no insurance to others. But this is essentially the experiment generated by identifying pricing variation: those individuals who are assigned high prices are less likely to have insurance, while those who are assigned low prices are more likely to be insured. One can then test and quantify the moral hazard effect of insurance by projecting any observed behavior of interest on whether an individual is insured or not, using the identifying source of price variation as an instrument for insurance coverage. Moreover, one can go further and, instead of only quantifying the average moral hazard effect, use the estimated demand curve for insurance to quantify the heterogeneity of moral hazard as a function of the individual’s willingness to pay for insurance. Such analysis may address important questions that go well beyond the current state of the empirical literature on average moral hazard effects in insurance markets to examine whether high risk individuals are such because their underlying risk is higher—for example, because they are chronically ill—or because their behavioral response to insurance is greater—for example, because they are deterred from seeing a doctor unless their out-of-pocket cost is sufficiently low. To our knowledge, this has not yet been investigated.

Finally, we note that an attractive feature of our graphical framework is that it provides a transparent way to assess the relative contribution of the data and of any underlying theoretical or statistical assumptions in giving rise to the empirical estimates. An example may be useful. Consider Figure 3, and suppose we are interested in estimating the area of the deadweight loss triangle CDE. For this particular object of interest, we require estimates of the demand curve and cost curves at the range that is between Q_eqmx and Q_eff, while other parts of the curves are less important. A researcher who has excellent price variation that identifies the curves for infra-marginal buyers (to the left of Q_eqmx) would need to rely heavily on theoretical or statistical assumptions to extrapolate the curves to the relevant region, and would need to perform robustness checks to evaluate alternative models that may imply different extrapolations. In contrast, if the price variation spans the relevant region, sensitivity to modeling assumptions may be less of a concern.

To the extent that more limited (or nonexistent) pricing variation requires greater modeling assumptions for the welfare analysis, one nice feature of insurance markets is that the theory underlying individual choices of insurance coverage is well developed and much tested (in the laboratory and in the field). Thus, this is a context where perhaps more than others, relying on theoretical restrictions may be quite credible. Einav, Finkelstein and Levin (2010) provide a recent review of modeling approaches to welfare analysis in insurance markets and some of the recent findings.

Concluding Comments

The graphical framework we have presented provides a unified approach for understanding both the conceptual welfare issues posed by selection in insurance markets and potential government intervention, as well as the existing empirical efforts to detect selection and measure its welfare consequences. However, this framework has abstracted from several constructs that are potentially of interest. Some are very easily handled by simple extensions of the framework, others much less so.

We start with the easier issues. Although for expositional simplicity we focused on the binary choice of “whether or not to buy insurance,” the same graphical analysis can easily be applied to a choice between more or less coverage. It can also be used to analyze choices across more than two contracts, although a multi-dimensional graphical approach is less appealing. Finally, it is straightforward to relax our maintained assumption of perfectly competitive insurance markets – which in many markets may not bear much resemblance to reality. One could carry out a similar analysis using alternative pricing assumptions which lead to a different equilibrium point (instead of the average cost pricing arising from perfect competition). Welfare could then be analyzed by comparing the new equilibrium point with the efficient allocation, although of course now it must be recognized that any welfare cost conflates both those created by selection and those created by imperfect competition.

A more difficult set of issues relates to the focus of the analysis on the pricing distortions arising from selection while abstracting from the possibility that selection can distort the set of insurance contracts that are offered. In other words, we have assumed that insurance companies compete over the price of a given set of insurance contracts. In practice, insurance companies also set the coverage features of the insurance contract (deductibles, covered events, and so on) and selection pressures may well affect the set of contract features offered in equilibrium. Admittedly, abstracting from this potential consequence of selection may miss a substantial component of its welfare implications and may explain why most of the empirical work to date on the welfare costs of selection has tended to find relatively modest welfare effects. Einav, Finkelstein and Levin (2010) provide more discussion and description of this point.

Allowing the contract space to be determined endogenously in a selection market raises challenges on both the theoretical and empirical front. On the theoretical front, we currently lack clear characterizations of the equilibrium in a market in which firms compete over contract dimensions as well as price, and in which consumers may have multiple dimensions of private information (like expected cost and risk preferences). From an empirical standpoint, the challenge is that if adverse selection greatly reduces the set of offered contracts, estimating the welfare loss from the contracts not offered may require the researcher to go quite far out of sample. While these challenges are far from trivial and may explain why there has been relatively little work of either type on this topic to date, we view this direction as an extremely important – and likely fruitful – topic for further research. As with the research to date on selection in insurance markets, we expect that there will be a useful complementarity between theoretical and empirical progress moving forward.