Simulating indoor concentrations of NO₂ and PM_2.5 in multi-family housing for use in health-based intervention modeling

Abstract

Residents of low-income multi-family housing can have elevated exposures to multiple environmental pollutants known to influence asthma. Simulation models can characterize the health implications of changing indoor concentrations, but quantifying the influence of interventions on concentrations is challenging given complex airflow and source characteristics. In this study, we simulated concentrations in a prototype multi-family building using CONTAM, a multi-zone airflow and contaminant transport program. Contaminants modeled included PM_2.5 and NO₂, and parameters included stove use, presence and operability of exhaust fans, smoking, unit level, and building leakiness. We developed regression models to explain variability in CONTAM outputs for individual sources, in a manner that could be utilized in simulation modeling of health outcomes. To evaluate our models, we generated a database of 1000 simulated households with characteristics consistent with Boston public housing developments and residents, and compared the predicted levels of NO₂ and PM_2.5 and their correlates with the literature. Our analyses demonstrated that CONTAM outputs could be readily explained by available parameters (R² between 0.89 and 0.98 across models), but that one-compartment box models would mischaracterize concentrations and source contributions. Our study quantifies the key drivers for indoor concentrations in multi-family housing and helps to identify opportunities for interventions.

Introduction

Pediatric asthma prevalence and the frequency of severe attacks have been shown to be elevated in low-income urban populations (Crain et al., 1994; Joseph et al., 1996; Spiegel et al., 2006; Moorman et al., 2007). While asthma has a complex etiology, multiple studies and expert reports (NAS, 2000; EPA, 2004; EPA, 2006; Sharma et al., 2007) have focused on the potential influence of indoor environmental exposures. Interventions that can reduce indoor exposures and consequent health implications are therefore of great interest.

While there is an extensive empirical literature on indoor pollutant concentrations and predictors, one of the challenges of this literature is that it is difficult to disentangle the various contributing factors and to quantify the tradeoffs between indoor and outdoor sources given changes in ventilation or other household characteristics. For example, measurement studies demonstrated that NO₂ tends to have greater concentrations indoors in the presence of gas stoves (Lee et al., 1998; Zota et al., 2005), indicating that efforts to improve venting of gas stoves or to increase ventilation in general will reduce NO₂ concentrations. However, increasing general ventilation increases indoor NO₂ concentrations from outdoor sources, particularly in urban settings with high traffic. For pollutants with multiple indoor and outdoor sources such as NO₂ and PM_2.5 the quantitative effect of specific interventions on the relative influence of indoor and outdoor sources is challenging to ascertain from field studies. This challenge is further exacerbated in multi-pollutant contexts, where similar root causes could influence concentrations of multiple contaminants.

For these reasons, models simulating indoor concentrations are often applied. Indoor concentrations of airborne contaminants can be estimated by basic principles, where concentrations are a function of penetration efficiency, air exchange rate (AER, also termed air change rate), decay rate, indoor source strength and unit volume (Long et al., 2001; Pepper and Carrington, 2009). However, many low-income urban residents live in multi-family housing, where conditions can be more complex and may not be well represented by a single compartment model. For example, the airflow in multi-story apartment buildings lacking mechanical ventilation generally moves from lower-level to upper-level apartments, leading lower-level apartments to generally have more outdoor air, lower humidity, and draftier conditions, while upper-level apartments have higher humidity and pollutant levels (NAS, 2000). In a building with central air conditioning or window AC units the reverse would occur during the cooling season. Moreover, indoor sources vary substantially across apartments and over time, including between-season and within-season differences.

More detailed simulation models of the residential environment have been developed to model indoor air quality (IAQ) in a variety of building types, including complex environments like multi-family housing. One well-validated simulation tool that has been applied extensively is CONTAM (NIST, Gaithersburg, MD) (http://www.bfrl.nist.gov/IAQanalysis/), a multi-zone airflow and contaminant transport program that has been used for applications such as modeling the effect of indoor environmental interventions on concentrations of multiple contaminants in inner-city housing (Emmerich and Howard-Reed, 2005b) and the effect of air cleaning systems on indoor concentrations of PM_2.5 (Myatt et al., 2008; Macintosh et al., 2010). Outputs from this model include time-resolved ventilation rates, pollutant concentrations, and relative humidity for individual units within a building. For this model, 209 prototype buildings (single family and multi-family) have been constructed to be representative of the US housing stock as a whole, and these prototype buildings are embedded within the CONTAM model and are available for use (Persily et al., 2006).

While CONTAM and similar models are ideal in many respects, these models cannot necessarily be integrated directly within models simulating the health consequences of indoor environmental interventions. For example, in discrete event simulation models (DEM) – used to model a complex system which evolves over time given changes in state variables that occur at defined points in time (Law and Kelton, 2000) – IAQ would need to be characterized on an hourly basis for years across thousands or millions of homes with varying characteristics across numerous interventions. This is computationally and logistically challenging with models such as CONTAM. However, if approaches could be developed to extract the findings from CONTAM in a manner that is both physically interpretable and applicable in health risk simulation models, then the insights from these more complex multi-compartment models can be integrated with DEM models and used to design interventions.

In this study, we used CONTAM to simulate a range of building characteristics and occupant behaviors and determine their influence on indoor relative humidity, NO₂ and PM_2.5 concentrations related to various source types. We then built regression models to predict relative humidity and indoor NO₂ and PM_2.5 concentrations by source type based on housing characteristics, occupant behavior, and meteorological conditions. To evaluate these regression models, we constructed a sample of 1000 homes based on characteristics consistent with Boston public housing developments and their residents, and compared estimated pollutant concentrations and relative source contributions with values reported in the IAQ literature. This application informs our ultimate objective to simulate the health benefits of indoor environmental interventions in low-income multi-family housing in Boston. This approach provides a mechanism for developing indoor exposure models in the context of discrete event simulation or other health risk assessment studies.

Materials and methods

Simulation model

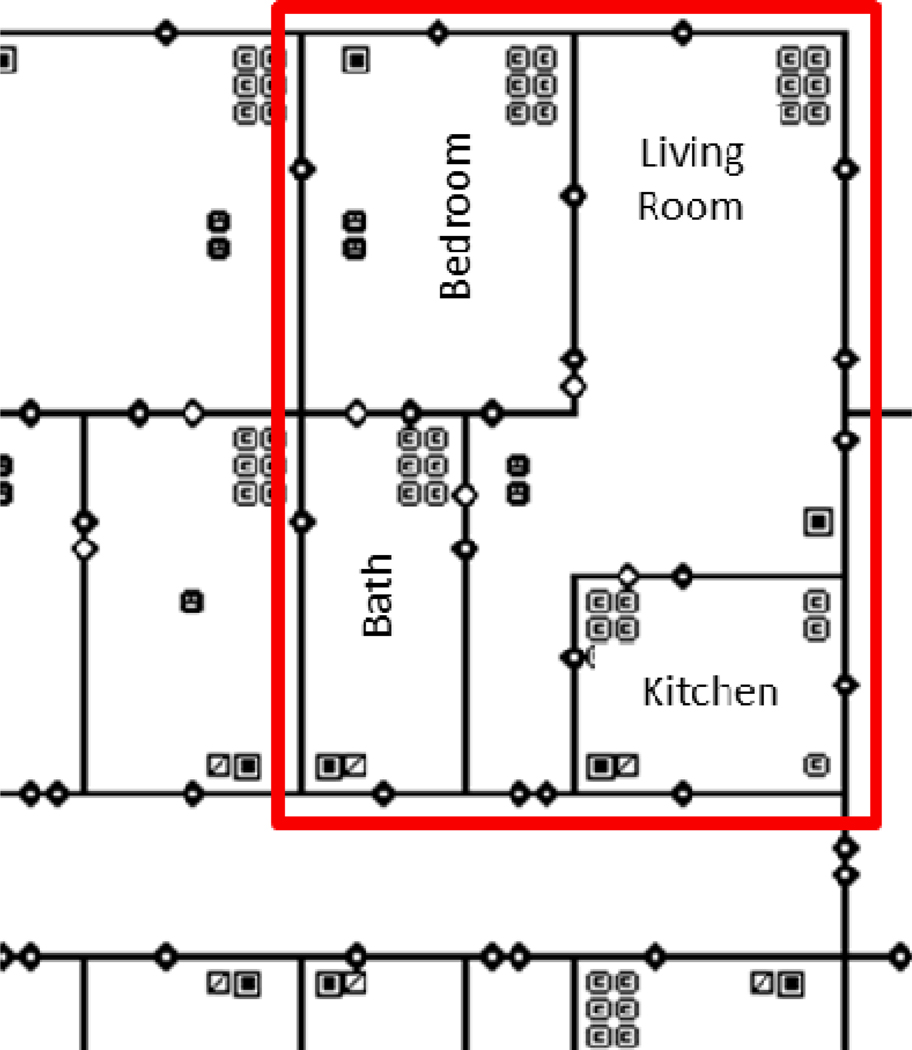
We used CONTAM 2.4c to estimate pollutant concentrations and relative humidity in a typical multi-family housing unit under a range of conditions. We selected the template for apartment building 26 to simulate a building typical of Boston public housing – 4 stories, 1940–1969 construction, and naturally ventilated (Persily et al., 2006). A family of 2 adults and 2 children were simulated living in each 65.3 m² apartment, which included a bedroom, bathroom, living room, and kitchen (Figure 1).

Figure 1.

CONTAM schematic of simulated apartment unit in a multifamily building.

Contaminant sources and sinks

We modeled NO₂ and PM_2.5 as contaminants in CONTAM, given literature linking both to lung function decrements among asthmatic children (Horak et al., 2002; Delfino et al., 2004; Gauderman et al., 2004; Trenga et al., 2006; Delfino et al., 2008). Based on a review of the literature (Özkaynak et al., 1996; Lee et al., 1998; Zota et al., 2005), we focused on sources of each pollutant anticipated to be the dominant contributors in most cases. Sources of NO₂ included gas stoves used for cooking, gas stoves used for supplemental heating in the winter, and outdoor infiltration; sources of PM_2.5 included smoking, cooking, and outdoor infiltration. PM_2.5 emissions from the oven when used to heat the house were considered negligible. Removal rates for deposition and decay were estimated for each room by multiplying the rates by air density at standard temperature and pressure, and by room volume. Table 1 presents the emission and decay/removal rates used for each contaminant source. In addition, we modeled relative humidity as a potential proxy of mold growth, given that mold or persistent moisture has also been associated with lung function in asthmatic children (Williamson et al., 1997). Indoor sources of relative humidity included occupant behaviors such as breathing, showering, cooking, and dish washing (Table 1).

Table 1.

Contaminant source and sink emission rates and schedules used as inputs for CONTAM simulations.

Contaminant source	Emission/removal rate	Reference	Schedule
PM2.5 from cigarettes (ETS)	0.33 mg/min (10 mg/cig* 2 cig/hr)	(Klepeis et al., 2003)	7:00–19:00, 1 cigarette smoked every half hour
ETS PM2.5 deposition	−0.1 h−1	(Klepeis and Nazaroff, 2006)	24 hours
PM2.5 from cooking	1.56 mg/min	(Burke et al., 2001)	Weekday: 7:00–7:30, 12:00–12:30, 17:30–18:30 Weekend: 8:30–9:30, 11:30–12:30, 17:30–18:30a
PM2.5 deposition from cooking and outdoors	−0.19 h−1	(Long et al., 2001)	24 hours
NO2 from gas stove during cooking	56 µg/sec	(Persily, 1998)	Same as PM2.5 cooking schedule
NO2 from using oven for heating	28 µg/sec	(Persily, 1998)	6:00–22:00 daily during winter
NO2 decay from all sources	−0.87 h−1	(Emmerich and Persily, 1996)	24 hours
Water vapor from showering	670 mg/s	(Persily, 1998)	10 minute showers @ 6:00 & 6:30 on weekdays; 9:00 and 9:30 on weekends
Water vapor from cooking	138.9 mg/s	(Persily, 1998)	Same as PM2.5 cooking schedule
Water vapor from dishwasher	83.3 mg/s	(Persily, 1998)	19:00–20:00 daily
Water vapor from breathing
Children	Awake: 11.1 mg/s	(Persily, 1998)	6:30–20:00 on weekdays, 8:00–20:00 on weekends
	Sleeping: 6.11 mg/s		20:00–6:30 on weekdays, 20:00 to 8:00 on weekends
Adults	Awake: 15.3 mg/s	(Persily, 1998)	6:00–22:00
	Sleeping: 8.42 mg/s		22:00–6:00

^aIn simulations where the stove was used twice a day only usage during breakfast and dinner hours was simulated

Outdoor air pollution and meteorological data

Boston hourly air pollution data were obtained from state monitors recorded between 01/01/1995 and 10/31/2009. For PM_2.5 data were available from the Harrison Av./Dudley Square station located in the Roxbury neighborhood of Boston. For NO₂ the data available was the average of three monitors located in Boston (Harrison Av., Kenmore Sq., and Breman Street) and two monitors in nearby urban communities (Chelsea, Lynn). We constructed a file with hourly averages over 365 days of mean NO₂ and PM_2.5 concentrations using all the data available between 1995 and 2009 at the time of our analysis. Hourly values of solar radiation and weather conditions (e.g. temperature, relative humidity, wind speed and direction) for a typical year were downloaded from the TMY2 dataset (1961– 1990: Typical Meteorological Year 2, National Solar Radiation Data Base, National Renewable Energy Laboratory). While there are modest mismatches in time, this approach provides a reasonably representative set of hourly outdoor pollutant and meteorological conditions.

CONTAM simulations

We conducted a factorial design to allow us to span the array of conditions that might be observed in low-income multi-family housing. The key dimensions in our CONTAM factorial design were gas stove use (2 times/day or 3 times/day), apartment location (1^st floor or 4^th floor), season (spring, summer, fall, winter), exhaust fan use in the bathroom during showering and in the kitchen during cooking (on/off), and house leakiness (wall leakage area per unit area: 1.2, 3.7, 5.0, or 13.1 cm²/m²– hereafter described as leakiness categories 1 through 4). We ran CONTAM across all combinations of these above dimensions. The lowest category of wall leakage area approximated the LEED Green Building Rating System airtightness standard of 8.1 cm² of leakage area per 9.3 m² of enclosure area, corresponding to an average air exchange of 0.33 h⁻¹. The next two wall leakage values corresponded to average air exchange rates of approximately 0.85 and 1.2 h⁻¹, consistent with measurements in Boston public housing units (Zota et al., 2005). The highest leakiness category was intended to represent a house with significant leakage, consistent with a home with open windows all day (Johnson, 2002). Fan airflows were 85 m³/h and 170 m³/h for the bathroom and kitchen respectively. All cases were simulated for 7-day periods each season. Temperature indoors was set to 298K – while higher than the typical indoor set point, empirical studies in Boston public housing have found systematic overheating and measured average daily temperatures between 296 and 301K (Brugge et al., 2003). Variables were only modified in the apartments under study (2 out of 16 apartments). In the remaining apartments variables were kept constant: the bathroom and kitchen fan were always operated during cooking and showering events, the stove was used for 3 cooking periods per day, the oven was not used for supplemental heat in the winter, and no dishwasher was operated. The CONTAM output files included mixing ratios (mass of water vapor per unit mass of dry air, used to calculate relative humidity), air pollutant concentrations per room per source, and flow rates into and out of each apartment wall, in half hour time increments.

Statistical analysis

We used SimReadW (NIST, Gaithersburg, MD) to convert CONTAM output files to text and Excel files. We used SAS (Proc Means, version 9.1, SAS Institute Inc., Cary, NC) to calculate 24-hour average indoor pollutant concentrations per source and pollutant across all apartment rooms. Mixing ratio values were converted to relative humidity values using ASHRAE psychrometric equations (ASHRAE, 2009).

We built regression models using SAS (Proc GLM) where the dependent variable was the log-transformed daily 24-hour average relative humidity or pollution concentration per source and per pollutant (NO₂ from cooking, NO₂ from using the oven to heat the house, NO₂ from outdoors, PM_2.5 from cooking, PM_2.5 from smoking, and PM_2.5 from outdoors). To make our regression models physically interpretable, we built predictors consistent with IAQ modeling equations or concepts.

For NO₂ and PM_2.5, we first built predictors based on the standard single-compartment box model utilized previously (Özkaynak et al., 1997; Long et al., 2001; Baxter et al., 2007).

$$C_{\mathit{\text{in}}}=\underset{\text{outdoor}}{\underbrace{\frac{Pa}{a+k}{C}_{\mathit{\text{out}}}}}+\underset{\text{indoor}}{\underbrace{\frac{E/V}{a+k}}}$$ (eq. 1)

where P = penetration efficiency (dimensionless), a = AER (h⁻¹), k = decay rate (h⁻¹), E = source strength (µg/h), V = unit volume (m³).

For infiltration from outdoors, the box model term is a product of outdoor concentrations and Pa/(a+k). For PM_2.5, we assumed that P = 0.99 and k = 0.18 h⁻¹ in the summer and spring, and that P = 0.8 and k = 0.19 h⁻¹ in the fall and winter, as estimated elsewhere (Long et al., 2001). For NO₂, we assumed that P = 1 and that k = 0.87 h⁻¹ (Emmerich and Persily, 1996).

For indoor sources, concentrations should be predicted well by a term that corresponds to E/(a+k). We omitted unit volume, as the unit volume is constant across runs. For indoor sources where source strength did not vary across runs (PM_2.5 from ETS and NO₂ from supplemental heating), the term used as a predictor in our regression model was therefore 1/(a+k). For cooking, for which utilization did vary across runs, the term was E/(a+k), where E=the NO₂ or PM_2.5 source strength associated with the stove. For PM_2.5 generated by ETS, we used a k of 0.1 h⁻¹ (Klepeis and Nazaroff, 2006).

After conducting univariate regressions of log-transformed NO₂ and PM_2.5 concentrations from CONTAM as a function of these predictors, we constructed multivariate linear regression models using stepwise regression, including covariates that were significant at p < 0.05. Candidate covariates included terms that could explain differences between multi-compartment CONTAM outputs and the predictors derived from box model concepts. This included unit level, given the influence of a stack effect (warm air moving upward in the building due to temperature-driven differences in air density); fan presence and operability, which can vent concentrations from cooking and other specific sources; season, given possible additional influences of indoor-outdoor temperature differences; 24-hour average AER, given the possibility of ventilation effects not fully captured by the simple box model predictor; and outdoor pollutant concentrations.

For relative humidity, CONTAM cannot track separate sources, and predictors such as temperature are expected to dominate; therefore, the focus on predictors derived from the structure of Equation 1 was not directly relevant. We built a single multivariate regression model for the log-transformed total relative humidity, incorporating the following indoor and outdoor covariates: outdoor temperature/humidity, season, fan use, apartment level, inverse AER, and an interaction term between stove use and fan use as candidate predictors. Model-building was conducted in a stepwise fashion as described above.

Simulating concentrations in Boston public housing

To evaluate the applicability and interpretability of our regression models, we developed a program in R (R 2.12.1, The R foundation of Statistical Computing) to generate households that mimicked characteristics typical of Boston public housing. We assigned the houses characteristics based on previously published literature on Boston public housing or inner-city housing and simulated an ensemble of houses (n=1000) for a year. Household characteristics included:

• In 34% of houses with children at least 1 adult smokes (Digenis-Bury et al., 2008), with 50% of them light smokers and 50% heavy smokers,

• 89% of households own a gas stove (Kattan et al., 1997),

• 38% use the stove for heating in the winter (Brugge et al., 2001), assuming that the supplemental heat was turned on only on days when the 24-hour average outdoor temperature was below 273K,

• 13% have a working exhaust fan in the kitchen (Kattan et al., 1997),

• 20%, 50% and 30% of units fall in leakiness categories 1 through 3 respectively (Zota et al., 2005); in the summer, the AER associated with each leakiness category increased by 0.4 h⁻¹ to simulate window opening, which was the change in AER reported in the heating versus non-heating season by Zota et al.

• Cooking time was estimated as 16 minutes per stove use (32 min/day and 48 min/day for households where cooking occurred 2X/day and 3X/day respectively), based on current values reported in the EPA Exposure Factors Handbook (EPA, 2009).

Each day a random value was drawn from normal distributions of outdoor NO₂ and PM_2.5 (averaged from Boston hourly pollution data as described above), outdoor temperature and relative humidity (averaged from TMY2 data), and AER (calculated from CONTAM simulation output, stratified by season and leakiness category), and these values were used to estimate indoor relative humidity and NO₂ and PM_2.5 by source. We evaluated the distribution of concentration outputs, in aggregate and by source type, and compared these results with values reported in the indoor pollution literature.

Results

Eight hundred and ninety six values of 24-hour average pollutant concentrations and relative humidity were simulated in CONTAM (4 leakiness categories × 2 apartment levels × 2 fan settings × 2 daily stove uses × 4 seasons × 7 days). Table 2 shows the range of values generated for each source of PM_2.5 and NO₂. Values are high, reflecting the simulated activity patterns where all households had a gas stove, a heavy smoker, used the oven for heating during the winter, and cooked on the stove 2 or 3 times a day. The values are clearly not representative of typical annual averages, but represent the distributions generated with our factorial design. 24-hour average simulated indoor relative humidity was 31.4% (SD= 12.9), 69.8% (SD= 14.5), 44.8% (SD=13.5), and 20.1% (SD= 8.9) for spring, summer, fall, and winter respectively.

Table 2.

24-hour average NO₂ and PM_2.5 concentrations generated using CONTAM to simulate an apartment building with different levels of air exchange rates, location in building, kitchen and bathroom fan presence and operability, use of stove, and seasons. All households had a gas stove, a heavy smoker, and used the oven for supplemental heat in the winter.

	Mean	Standard Deviation	25th percentile	Median	75th percentile
NO2 (µg/m3)
Total	96.0	38.8	62.8	86.3	120.0
Heating house with oven (winter only)	89.8	39.0	48.4	83.3	129.3
Cooking	61.4	37.2	30.6	49.1	87.6
Outdoors	15.9	7.2	8.4	15.0	23.0
PM2.5 (µg/m3)
Total	103.7	60.8	57.6	88.9	136.5
ETS	43.1	26.6	21.0	39.2	58.7
Cooking	52.9	41.4	23.8	42.3	71.1
Outdoors	7.7	1.8	6.5	6.9	8.6

Table 3 shows the NO₂ regression models derived from the CONTAM simulation runs for each source, including a univariate R² term per covariate as well as a partial model R² for the stepwise multivariate model. Table 4 presents the same models for PM_2.5. Model R² ranged between 0.89 and 0.98.

Table 3.

Regression models predicting indoor NO₂ concentrations from cooking, heating the house with the oven, and outdoors, from a database of apartments in a multi-family building simulated with CONTAM.

Dependent variable: log (NO2 from cooking (µg/m3))				Model R2=0.89
	Estimate (β)	Standard Error	t value	P value	Univariate R2	Partial R2
Intercept	3.03	0.03	93.5	<.0001	-	-
Fan off	0.98	0.01	68.8	<.0001	0.60	0.60
Box model term 1a	0.47	0.02	28.0	<.0001	0.29	0.86
AERb	−0.06	0.01	−9.9	<.0001	0.20	0.87
Lower level	−0.23	0.02	−14.3	<.0001	0.01	0.89
Dependent variable: log (NO2 from heating in winter(µg/m3))				Model R2= 0.98
	Estimate (β)	Standard Error	t value	P value	Univariate R2	Partial R2
Intercept	3.56	0.03	106.6	<.0001	-	-
Box model term 2c	1.91	0.05	38.1	<.0001	0.92	0.92
AER	−0.11	0.01	−22.2	<.0001	0.82	0.96
Lower level	−0.16	0.01	−11.1	<.0001	0.13	0.98
Fan off	0.05	0.01	4.1	<.0001	0.004	0.98
Dependent variable: log (NO2 from outdoors(µg/m3))				Model R2=0.90
	Estimate (β)	Standard Error	t value	P value	Univariate R2	Partial R2
Intercept	0.83	0.03	25.3	<.0001	-	-
Infiltration term*NO2 outd	141.71	2.58	54.9	<.0001	0.86	0.86
AER	−0.02	0.01	−3.7	0.0002	0.50	0.87
Season: Fall	0.16	0.02	8.7	<.0001	0.13	0.87
Season: Spring	0.08	0.02	4.6	<.0001	-	-
Season: Summer	0.14	0.02	7.1	<.0001	-	-
Lower level	0.21	0.01	15.2	<.0001	0.06	0.90

^aBox model term 1=stoveuse/(aer+kNO₂)

^bAER= air exchange rate or air change rate

^cBox model term 2= 1/(aer+kNO₂)

^dInfiltration term= p*aer/(aer+kNO₂)

Table 4.

Regression models predicting indoor PM_2.5 concentrations from cooking, environmental tobacco smoke (ETS), and outdoors, from a database of apartments in a multi-family building simulated with CONTAM.

Dependent variable: log (PM2.5 from cooking (µg/m3))				Model R2=0.91
	Estimate (β)	Standard Error	t value	P value	Univariate R2	Partial R2
Intercept	2.95	0.03	111.3	<.0001	-	-
Fan off	1.02	0.02	62.9	<.0001	0.43	0.43
Box model term 1	0.24	0.01	38.5	<.0001	0.43	0.83
AER	−0.15	0.01	−23.1	<.0001	0.32	0.87
Lower level	−0.38	0.02	−21.0	<.0001	0.01	0.91
Dependent variable: log (PM2.5 from ETS (µg/m3))				Model R2=0.93
	Estimate (β)	Standard Error	t value	P value	Univariate R2	Partial R2
Intercept	3.64	0.02	149.0	<.0001	-	-
AER	−0.31	0.01	−55.9	<.0001	0.75	0.75
Box model term 2	0.48	0.01	44.4	<.0001	0.66	0.86
Lower level	−0.48	0.02	−31.1	<.0001	0.04	0.92
Season: Fall	−0.04	0.02	−2.3	0.0218	0.04	0.93
Season: Spring	0.04	0.02	2.0	0.0458	-	-
Season: Summer	−0.17	0.02	−8.3	<.0001	-	-
Dependent variable: log (PM2.5 from outdoors (µg/m3))				Model R2=0.91
	Estimate (β)	Standard Error	t value	P value	Univariate R2	Partial R2
Intercept	0.80	0.02	35.6	<.0001	-	-
Infiltration term*PM2.5 out	0.13	0.002	53.3	<.0001	0.59	0.59
Season: Fall	−0.03	0.01	−2.9	0.0045	0.39	0.76
Season: Spring	−0.21	0.01	−21.3	<.0001	-
Season: Summer	−0.42	0.01	−30.8	<.0001	-
AER	0.04	0.003	14.7	<.0001	0.14	0.76
Lower level	0.28	0.01	36.4	<.0001	0.01	0.91

^aBox model term 1= stoveuse/(aer+kPM_2.5)

^bAER= air exchange rate

^cBox model term 2= 1/(aer+kETS)

^dInfiltration term= p*aer/(aer+kPM_2.5)

The term derived from the single-compartment box model was positive and statistically significant in all models, though its predictive power varied across models. The lowest predictive power in multivariate models was seen for NO₂ and PM_2.5 from cooking, given the importance of an operating kitchen fan in predicting indoor concentrations.

The box model term performed quite well for NO₂ from gas stove heating (in a model fit to a subset of winter observations) and from infiltration from outdoors, with slightly weaker performance for PM_2.5 from ETS and infiltration from outdoors.

Even with the inclusion of a term derived from box model concepts, a separate term for AER was statistically significant in all multivariate models. The term had modest explanatory power in most cases, especially for infiltration from outdoors, but added significantly to predictive power for NO₂ from cooking and PM_2.5 from ETS. For all indoor sources, the AER term had a negative coefficient, indicating a potential systematic bias when applying the box model term in isolation.

In addition, level (upper, lower) was significant in all models, with a negative coefficient for indoor sources (i.e., higher concentrations at the upper level) and a positive coefficient for infiltration from outdoors. Season demonstrated modest predictive power in a subset of models, and none of the meteorological covariates (temperature, relative humidity) were significant.

Table 5 shows the regression model predicting indoor relative humidity. The regression model for indoor relative humidity had an R² of 0.94 (Table 5), and included season and inverse AER as well as the meteorological covariates outdoor relative humidity and temperature. Fan use and lower level of the building were significant in the multivariate model but they contributed less than 1% to the model R².

Table 5.

Regression models predicting indoor RH, from a database of apartments in a multi-family building simulated with CONTAM.

Dependent variable: log(RH indoors)				Model R2= 0.94
	Estimate (β)	Standard Error	t value	P value	Univariate R2	Partial R2
Intercept	2.07	0.03	75.8	<.0001	-	-
Temperature outdoors	0.02	0.001	20.1	<.0001	0.72	0.72
Season: Fall	0.01	0.02	0.3	0.7732	0.68	0.73
Season: Spring	−0.10	0.01	−7.3	<.0001	-	-
Season: Summer	0.20	0.03	5.8	<.0001	-	-
1/AERa	0.13	0.003	37.1	<.0001	0.28	0.85
RH outdoors	0.01	0.0003	37.0	<.0001	0.18	0.93
Lower level	−0.08	0.01	−9.0	<.0001	0.005	0.94
Fan off	0.03	0.01	4.0	<.0001	0.003	0.94

^aAER= air exchange rate

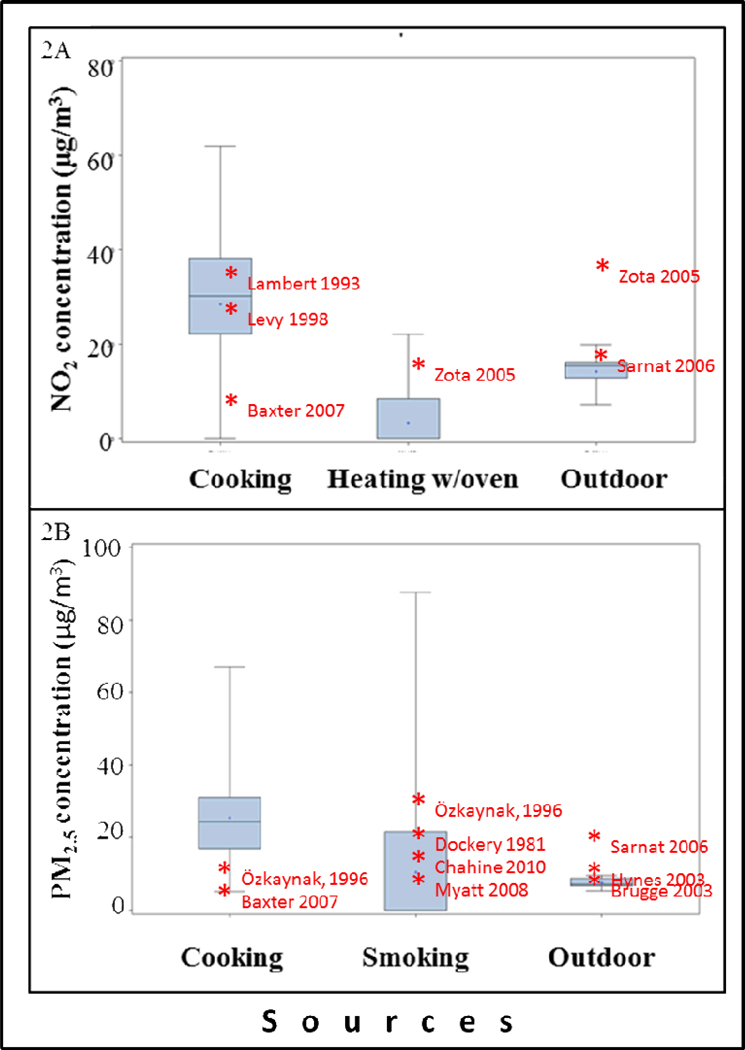
For the simulated population of 1000 households with characteristics typical of inner city housing, mainly Boston public housing, Figures 2A and 2B present box plots of 24-hour daily averages of NO₂ and PM_2.5 contributions per source, with the asterisks representing concentrations reported in the literature for each pollutant and source. For NO₂, cooking contributes more than either heating with the oven or infiltration from the outdoors, with a mean contribution of 28.4 µg/m³ (versus 3.3 µg/m³ for heating with the oven and 14.1 µg/m³ for infiltration from outdoors). Similarly, for PM_2.5, cooking is the largest contributor to modeled indoor concentrations, with a mean contribution of 25.6 µg/m³ (versus 10.5 µg/m³ for smoking and 7.6 µg/m³ for infiltration from outdoors). Mean AER over the simulated year was 0.53, 1.2, and 1.6 h⁻¹ for leakiness categories 1, 2, and 3, respectively. These values are slightly larger than the AERs corresponding with the wall leakage values, consistent with the influence of window opening in the summer and other ventilation pathways, and remain within the range of values reported for this type of housing (Zota et al., 2005).

Figure 2.

24-hour daily averages of A) NO₂ and B) PM_2.5 contributions per source from a sample of 1000 simulated households, estimated using regression models with input characteristics typical of Boston public housing. The asterisks represent typical concentrations reported in the literature for each pollutant and source (Dockery and Spengler, 1981; Lambert et al., 1993; Özkaynak et al., 1996; Levy et al., 1998; Brugge et al., 2003; Hynes et al., 2003; Zota et al., 2005; Sarnat et al., 2006; Baxter et al., 2007; Myatt et al., 2008; Chahine et al., 2010).

While this rank ordering is true when comparing median concentrations, there is significant variability across simulated homes in relative source contributions, especially for indoor sources. When we compared quartiles of simulated indoor and outdoor NO₂ and PM_2.5 concentrations, residents’ exposure in the lowest NO₂ quartile was 3% from heating the house with a gas oven in the winter, 29% from cooking with a gas stove, and 68% from outdoors. On the other hand, in the highest quartile, 12% of the exposure was from using the gas oven to heat the house, 68% from cooking with a gas stove, and 20% from outdoors. Of note, this represents the distribution on an annual average basis – the contribution from heating the home with a gas oven is significantly greater during the coldest days of the winter, and zero the rest of the year. For PM_2.5, residents from households in the lowest quartile were exposed to PM_2.5 principally from cooking (62%), followed by outdoor concentrations (37%) and smoking (1%); exposure in the highest quartile came from cooking (46%), smoking (44%) and outdoors (10%).

In the highest NO₂ quartile almost 100% of households owned a gas stove, used the gas oven for supplemental heating in the winter, and didn’t operate the fan while cooking. Conversely, in the lowest quartile only 44% of households owned a gas stove and 49% didn’t operate the fan while cooking. In both NO₂ quartiles there was a wide distribution of AER. For PM_2.5, households in the lowest quartile were mostly non-smoking (98%) and used the stove twice a day (74%), while in the highest quartile 91% were either light or heavy smokers, and 64% used the stove three times a day. Fewer households were classified as high AER in the high versus low PM_2.5 quartiles.

Discussion

The regression models describing the CONTAM simulation outputs explained between 89% and 98% of variability and were able to capture the distribution of concentrations predicted by CONTAM. Beyond their predictive power, the regression models were physically interpretable and provided some interesting insights about the value-added of more complex IAQ modeling. Specifically, if CONTAM pollutant concentration outputs were perfectly correlated with estimates from a simple one-compartment box model, it would imply that a one-compartment model would have no greater uncertainty than CONTAM itself. However, a regression parameter based on one-compartment box model concepts was not the only predictor of indoor pollution, reinforcing that multi-family housing indoor air pollution dynamics are complex, and justifying the need to use advanced simulation programs (even given the subsequent need to develop regression models from these programs) to more accurately predict indoor concentrations. The box model parameter explained between 29% and 92% of the indoor pollution variability, depending on the modeled source.

As would be expected, operating a kitchen fan during cooking had a large impact on NO₂ and PM_2.5 concentrations (explaining 60% and 43% of the variability in multivariate models, respectively). This effect is uncertain given limitations in CONTAM, where kitchen exhaust fans are operated as general room exhaust, and not as a point-source exhaust with empirical data on capture efficiency. The assumption that the room is well-mixed with general exhaust may underestimate the influence of an operable exhaust fan proximate to the combustion source, but the lack of a formal term for capture efficiency could overestimate the removal rate. In spite of these uncertainties, other studies have shown that having an operable fan during cooking has a large impact on indoor air pollutants (Li et al., 2006), making fan operation and maintenance a target for intervention studies. The true effect of the fan would depend on airflow, how well the fan is running, and its capture efficiency, and these factors should be included in future intervention models. Other studies have shown that having an operable fan during cooking has a large impact on indoor air pollutants (Li et al., 2006), making fan operation and maintenance a target for intervention studies. For all indoor pollutant sources (cooking, ETS, heating) and for relative humidity, higher concentrations were modeled in the upstairs apartments compared to downstairs. Apartment level was likely a proxy for stack effect during the heating season or periods of stove use. For outdoor concentrations this trend was reversed, due to the stack effect moving air with lower concentrations of outdoor pollutants from the downstairs apartment to the upstairs, and replacing it with outdoor air.

AER was the third variable that was a significant predictor in all models, an interesting finding given its inclusion in the box model parameter. While the explanation for the independent significance of this term is not immediately obvious, it was generally in the anticipated direction for air exchange rates (i.e., for indoor sources higher AER produced lower pollution concentrations, though the coefficient was positive for outdoor PM_2.5 and negative for outdoor NO₂). This indicates that the simple box model does not fully capture the influence of air exchange rates in multi-family housing. With the exception of ETS PM_2.5, once the box model term was included, the independent AER term was significant but only improved the model R² by 1% to 4%. For ETS PM_2.5 AER improved the model R² by 20%. Both AER and season, which was significant in some of the models, likely explained residual variability due to unmeasured meteorological conditions or housing characteristics.

Outdoor temperature was the most significant predictor of indoor relative humidity (R² = 0.72). In the multivariate model an inverse term for AER explained 12% of the variability after controlling for season and outdoor temperature. This likely represents the influence of infiltration, with higher air exchange rates (and greater ventilation) associated with lower indoor relative humidity. Outdoor relative humidity was less significant both in univariate and multivariate models. Season, apartment level, and fan presence and operability were significant covariates but only marginally improved the model R² as their effects were mostly accounted for by the other covariates.

While we were able to explain the vast majority of variability in CONTAM outputs, this does not by itself imply that the CONTAM estimates themselves are accurate. Our regression models are only useful for health risk simulation if the estimated concentrations are reasonable. Formal external validation is not possible given the hypothetical nature of our investigation and somewhat unique characteristics of our target population, but we can compare our estimated source contributions for households characteristic of low-income multi-family housing with corresponding values from the literature.

For PM_2.5 from ETS, we estimated mean 24-hour average concentrations of 20.6 µg/m³ (SD=8.8) for households with light smokers (12 cigarettes/day) and 39.4 µg/m³ (SD=16.1) for households with heavy smokers (24 cigarettes/day). These estimated values assumed that the smoker was in the house the entire time they smoked. Once this fact is accounted for, and given the small unit sizes in our study, these values are in general agreement with previously published simulation studies as well as values measured in field studies. Modeling data from the American Housing Survey, Chahine et al. estimated a mean concentration of 16.3 µg/m³ ETS PM (SD=16.9) in households with smokers, where the daily mean number of cigarettes smoked was 14.9 (Chahine et al., 2010). Using CONTAM, Myatt et al. modeled a median and mean concentration of ~12 µg/m³ and ~17.5 µg/m³ respectively, based on smoking 8 cigarettes/day (Myatt et al., 2008). Klepeis et al. used a box model and reported concentrations between 6.6 and 49 µg/m³ with smokers consuming 30 cigarettes/day indoors and outdoors (Klepeis and Nazaroff, 2006). In field studies, Dockery et al found that contact with one smoker adds 20 µg/m³ to PM_2.5 personal exposure (Dockery and Spengler, 1981); and Ozkaynak et al. found 30 µg/m³ higher PM_2.5 concentrations in homes with smokers (Özkaynak et al., 1996) compared to non-smokers.

Turning to PM_2.5 associated with cooking, there is more variability in the empirical literature and more challenges in comparing studies given the importance of exhaust fan use, cooking time, and type of cooking (i.e., frying vs. grilling vs. boiling). We estimated that households with a working fan had mean PM_2.5 contributions from cooking of 10.9 µg/m³ (SD=4.3), versus 27.8 µg/m³ (SD=11.1) in houses with non-working fans. In contrast, Baxter et al found that cooking with a gas stove more than 1 hour/day increased PM_2.5 on average 5.7 µg/m³ (Baxter et al., 2007), Özkaynak reported an increase in personal exposure of 13 µg/m³ in households that cooked for more than 1 minute (Özkaynak et al., 1996), and Brunekreef et al found that cooking increased indoor PM_2.5 concentrations by 11.65 µg/m³ in Amsterdam and by 1.86 µg/m³ in Helsinki (Brunekreef et al., 2005). Our estimates appear somewhat higher than these studies. This could be due to our high percentage of homes without a kitchen exhaust fan (the published studies did not report details on whether an exhaust fan was in use), or related to appreciable uncertainty in PM_2.5 cooking emission rates. We used 1.56 mg/min as reported by Burke et al, but values have been reported as low as 0.0017 mg/min and as high as 17 mg/min (Emmerich and Persily, 1996; Özkaynak et al., 1996; Persily, 1998; Burke et al., 2001; He et al., 2004; Olson and Burke, 2006). While this imposes some challenges in interpreting and utilizing our outputs, our modeling structure is such that we could rapidly test alternative emission rates and adjust in the event that relevant validation data were available. Moreover, given the smaller residence volumes in our simulation as compared to many previous studies, a more significant influence would be expected from any indoor source.

For NO₂, the most significant contribution to concentrations was cooking with a gas stove, which contributed an average of 28.4 µg/m³ (SD=14.5). When stratified by kitchen exhaust fan use, in households with a working fan cooking contributed 11.5 µg/m³ (SD=5.9) versus 31 µg/m³ (SD=0.01) in households with non-working fans. In comparison, field studies have shown that households that use gas stoves have 11.1–37.1 µg/m³ higher concentrations than households with electric stoves (Moschandreas, 1992; Lambert et al., 1993; Lee et al., 1998), and households using a gas stove more than 1 hour/day increased NO₂ concentrations by 10.6 µg/m³ (Baxter et al., 2007). Moreover, the total NO₂ ratio in houses with working fans versus non-working fans in our study was 1.7, similar to the ratio of 1.4 reported elsewhere (Li et al., 2006), with the slightly higher values potentially attributable to unit size as well as factors such as AER.

Finally, for NO₂ from heating with a gas stove, comparisons with values in the literature are more challenging, given limited reporting and relatively coarse information available in the literature. Our mean NO₂ contributions from the stove during the winter were 13.4 µg/m³, including homes that did and did not use the gas oven for supplemental heating. We assumed that the 38% of houses that used the oven for heating in the winter always had it on when the average 24-hour temperature outdoors was below 273°K, although use is likely more sporadic depending on the heating system performance and operation. In a study in Boston public housing, Zota et al measured indoor NO₂ values 31.6 µg/m³higher during the heating season compared to non-heating season, attributable to both lower air exchange rates during the winter and the use of gas stoves for supplemental heating. Univariate regression models estimated an average contribution from heating with gas stoves of 14.9 µg/m³, across observations including the heating and non-heating season. Our estimates are therefore reasonably consistent with the empirical literature.

The average fractions of pollutants that penetrated indoors were 0.4 (range 0.2–0.5) and 0.6 (range: 0.4–0.8) for NO₂ and PM_2.5 respectively, reflecting losses due to deposition and decay. The PM_2.5 fractions are similar to those reported in other studies: 0.7 (Özkaynak et al., 1996), ~0.65 (Long et al., 2001), and 0.8 (Baxter et al., 2007). For NO₂ our values were lower than those reported in the literature: 0.5 (Monn et al., 1997), 0.7 (Levy et al., 1998), 0.6 (Lee et al., 1998), 0.5 (Baxter et al., 2007).

There are some limitations to our approach. We constrained the CONTAM simulation to model a constant indoor temperature of 298K because of the inability to vary temperature in real-time in a manner that corresponded with occupant behaviors, potentially not capturing variations in pollutant concentrations driven by outdoor/indoor temperature differences. We accounted for window opening during the summer by adjusting the AER directly, rather than incorporating an hourly window opening schedule, which only grossly captures variations in pollutants and excludes potential hourly variations. We likely overestimated the moisture content in the air by not adjusting for water vapor storage in building materials and furnishings, a phenomenon which has been modeled with moderate success, and is still undergoing improvement (Emmerich et al., 2002). However, CONTAM has been extensively tested and validated, including in applications to quantify the effects of interventions on multiple contaminants in a townhouse (Emmerich et al., 2005), the effect of central forced-air heating and cooling on indoor air quality (Emmerich and Persily, 1996), and the effect of air cleaning systems on multiple indoor pollutants (Myatt et al., 2008; Macintosh et al., 2010). Another limitation is the use of regression models to explain the complex dynamics of air movement in the building, which may not capture some extreme cases, though the extremely high R² indicates that we do not have substantial outliers. Finally, given the small unit volumes assumed in our analysis and our focus on a small multi-family dwelling consisting entirely of corner units, the quantitative findings regarding source contributions may not generalize to other homes, though the analytical approach could be readily extended to these settings.

In spite of these issues, our modeling approach would allow us to estimate the effectiveness of interventions on populations with different housing and behavioral characteristics without having to simulate each scenario in CONTAM, which often involves significant time and effort, and without relying solely on simple box models that may not capture important dynamics in multi-family housing. For example, to calculate the effect of fixing all the kitchen fans in Boston public housing, we simulated a new random set of 1000 households, and set the percent of working fans to 100%. Results showed that on average total NO₂ concentrations would drop from 45.9 µg/m³ to 31.8 µg/m³ (−31%) and PM_2.5 concentrations would drop from 42 µg/m³ to 28.8 µg/m³ (−34%). This type of analysis can be used directly in simulation models estimating the exposure and health risk implications of housing-based interventions, informing future policy initiatives. The modeling approach we presented can be used to study the effect of interventions on individual pollution sources and total pollution concentrations. The methods can be applied to any building type and pollutant, and when coupled with estimates of the costs of interventions and the health benefits of concentration changes, can directly inform policy decisions regarding indoor environmental interventions.

Practical implications.

Many low-income urban asthmatics live in multi-family housing that may be amenable to ventilation-related interventions such as weatherization or air sealing, wall and ceiling hole repairs, and exhaust fan installation or repair, but such interventions must be designed carefully given their cost and their offsetting effects on energy savings as well as indoor and outdoor pollutants. We developed models to take into account the complex behavior of airflow patterns in multi-family buildings, which can be used to identify and evaluate environmental and non-environmental interventions targeting indoor air pollutants which can trigger asthma exacerbations.