Altitudinal Variation at Duplicated β-Globin Genes in Deer Mice: Effects of Selection, Recombination, and Gene Conversion

Abstract

Spatially varying selection on a given polymorphism is expected to produce a localized peak in the between-population component of nucleotide diversity, and theory suggests that the chromosomal extent of elevated differentiation may be enhanced in cases where tandemly linked genes contribute to fitness variation. An intriguing example is provided by the tandemly duplicated β-globin genes of deer mice (Peromyscus maniculatus), which contribute to adaptive differentiation in blood–oxygen affinity between high- and low-altitude populations. Remarkably, the two β-globin genes segregate the same pair of functionally distinct alleles due to a history of interparalog gene conversion and alleles of the same functional type are in perfect coupling-phase linkage disequilibrium (LD). Here we report a multilocus analysis of nucleotide polymorphism and LD in highland and lowland mice with different genetic backgrounds at the β-globin genes. The analysis of haplotype structure revealed a paradoxical pattern whereby perfect LD between the two β-globin paralogs (which are separated by 16.2 kb) is maintained in spite of the fact that LD within both paralogs decays to background levels over physical distances of less than 1 kb. The survey of nucleotide polymorphism revealed that elevated levels of altitudinal differentiation at each of the β-globin genes drop away quite rapidly in the external flanking regions (upstream of the 5′ paralog and downstream of the 3′ paralog), but the level of differentiation remains unexpectedly high across the intergenic region. Observed patterns of diversity and haplotype structure are difficult to reconcile with expectations of a two-locus selection model with multiplicative fitness.

WHEN functionally distinct alleles are maintained as a balanced polymorphism, each of the associated genetic backgrounds accumulates its own set of neutral mutations. The partitioning of nucleotide variation between alternative allele classes results in elevated levels of diversity and linkage disequilibrium (LD), and this characteristic signature provides a possible means of identifying balanced polymorphisms in genomic survey data (Charlesworth 2006). The chromosomal extent of the elevated diversity and haplotype structure is jointly determined by the age of the selected polymorphism and the frequency of crossing over, as recombination provides a conduit for genetic exchange between alternative allele classes (Strobeck 1983; Hudson and Kaplan 1988; Kaplan et al. 1988; Schierup et al. 2000; Charlesworth et al. 2003; Nordborg and Innan 2003; Wiuf et al. 2004). In the case of spatially varying selection, alternative alleles will be present at different frequencies in locally adapted populations. This increases between-population components of diversity and LD relative to within-population components. Consequently, spatially varying selection on a given polymorphism is expected to produce a localized peak of between-population diversity, and the elevated differentiation at linked sites will decline as a function of genetic map distance from the selected site (Charlesworth et al. 1997; Feder and Nosil 2010).

Over a broad range of population sizes and migration rates, recombination is expected to limit the peak of differentiation to a relatively narrow window spanning the selected polymorphism (Feder and Nosil 2010). The signature of selection may be further eroded by gene conversion, which provides a second conduit for genetic exchange between selectively maintained allele classes. Peaks of differentiation may be most readily detectable in cases where epistatic selection maintains coadapted combinations of alleles at linked genes. This is because the selective elimination of recombinant chromosomes reduces the effective rate of crossing over between the selected loci (Ishii and Charlesworth 1977). In cases in which two or more linked genes jointly contribute to fitness variation, theoretical results suggest that it may be possible to detect the effects of epistatic selection by analyzing patterns of silent-site diversity in the intergenic region and in the external flanking regions (Kelly 2000; Kelly and Wade 2000; Barton and Navarro 2002; Navarro and Barton 2002; Chevin et al. 2009; Takahasi 2009).

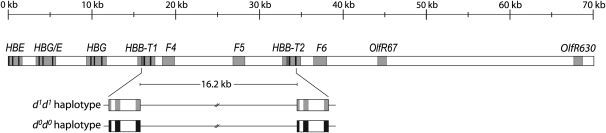
An empirical test of these predictions requires a system where allelic polymorphism at linked genes is associated with fitness variation under natural conditions. The tandemly duplicated globin genes of the deer mouse (Peromyscus maniculatus) are well suited to this purpose, as genetic variation in hemoglobin function mediates the adaptive fine tuning of blood–oxygen affinity in mice that are native to different elevational zones (Snyder 1981, 1985; Snyder et al. 1982, 1988; Chappell and Snyder 1984; Chappell et al. 1988; Storz 2007; Storz et al. 2007a, 2009, 2010a; Storz and Kelly 2008; Storz and Moriyama 2008). The two tandemly duplicated β-globin genes of these mice exhibit especially intriguing patterns of altitudinal variation and haplotype structure (Storz et al. 2009). These two genes, HBB-T1 and HBB-T2, encode the β-chain subunits of adult hemoglobin and are separated by 16.2 kb of noncoding DNA on chromosome 1 (Hoffmann et al. 2008a). In highland and lowland populations of deer mice from Colorado, the HBB-T1 and HBB-T2 genes segregate the same pair of functionally distinct alleles due to a history of interparalog gene conversion (Storz et al. 2009, 2010a). At both HBB-T1 and HBB-T2, the two alternative alleles are distinguished by four amino acid substitutions: 62 (Ala/Gly), 72 (Gly/Ser), 128 (Ser/Ala), and 135 (Ala/Ser). The d¹ allele class is defined by the four-site amino acid combination 62Gly/72Gly/128Ala/135Ala, and the d⁰ allele class is defined by the alternative four-site combination 62Ala/72Ser/128Ser/135Ser. The HBB-T1 and HBB-T2 genes exhibit striking haplotype structure, as alleles of the same functional type are in perfect coupling-phase LD: one chromosome harbors the d¹ allele at both paralogs, and the alternative chromosome harbors the d⁰ allele at both paralogs. The alternative two-locus haplotypes also exhibit pronounced frequency differences between elevational zones: the d¹d¹ haplotype is nearly fixed at high altitude, and the alternative d⁰d⁰ haplotype predominates at low altitude (Storz et al. 2009, 2010a). In previous surveys, all sampled mice were d⁰d⁰/d⁰d⁰ double homozygotes, d⁰d⁰/d¹d¹ double heterozygotes, or d¹d¹/d¹d¹ double homozygotes. Recombinant d⁰d¹ or d¹d⁰ chromosomes were never observed in highland or lowland population samples, but it is possible that such haplotypes would be recovered by additional sampling at intermediate elevations.

A multilocus analysis of nucleotide diversity and LD indicated that the altitudinal differences in HBB haplotype frequencies reflect a history of divergent selection between highland and lowland populations (Storz et al. 2009). Moreover, functional experiments revealed that the two-locus HBB haplotype that predominates at high altitude (d¹d¹) is associated with increased hemoglobin–oxygen affinity, which helps safeguard arterial oxygen saturation under conditions of severe hypoxia (Storz et al. 2009, 2010a,b). Allelic differences in hemoglobin–oxygen affinity are caused by differences in intrinsic oxygen-binding affinity, as well as differences in the sensitivity to allosteric cofactors that stabilize the low-affinity, deoxygenated conformation of the hemoglobin tetramer. Thus, the altitudinal patterns of allele frequency variation can be related to fitness-related differences in hemoglobin function (reviewed by Storz and Wheat 2010).

The objectives of this study were (i) to characterize the altitudinal pattern of allele frequency variation and haplotype structure at the HBB genes; (ii) to determine whether the elevated level of altitudinal differentiation at the HBB genes extends to closely linked loci; and (iii) to gain insight into the nature of selection that may be responsible for maintaining the two-locus haplotype structure at the HBB genes. To accomplish these objectives, we analyzed allele frequency variation at the HBB genes in mice sampled across a steep altitudinal gradient, and we conducted a multilocus analysis of nucleotide polymorphism and LD in mice with different genetic backgrounds at the HBB genes. Using two sets of mice that were alternative double homozygotes at the two HBB paralogs (d¹d¹/d¹d¹ and d⁰d⁰/d⁰d⁰), we compared levels and patterns of nucleotide variation at a total of 16 autosomal loci: the two divergently selected HBB genes, eight additional linked loci that span the β-globin gene cluster on chromosome 1, and six unlinked autosomal loci. Finally, we conducted a forward-time simulation study tailored to the design of the empirical population genetic analysis. We used the simulation results to assess whether the observed LD between the two HBB paralogs could be maintained by spatially varying selection that acts independently on each gene (multiplicative fitness effects).

Materials and Methods

Samples

We sampled a total of 178 deer mice from nine localities along an altitudinal transect that spanned the interface between the southern Rocky Mountains and the Great Plains of North America. This altitudinal transect spanned 3727 m of vertical relief over a linear distance of 617 km, from the crest of the Colorado Front Range to the prairie grassland of central Kansas. The collection localities, elevations, and sample sizes were as follows (from highest to lowest): (1) summit of Mt. Evans, Clear Creek Co., Colorado, 4347 m (n = 49); (2) Summit Lake, Clear Creek Co., Colorado, 3911 m (n = 10); (3) South Fork of Lost Creek, near Bailey, Park Co., Colorado, 3013 m (n = 7); (4) Niwot Ridge, Boulder Co., Colorado, 2900 m (n = 12); (5) Ward, Boulder Co., Colorado, 2733 m (n = 5); (6) Mesa Reservoir, Boulder Co., Colorado, 1672 m (n = 12); (7) Nunn, Weld Co., Colorado, 1578 m (n = 15); (8) Bonny Reservoir, Yuma Co., Colorado, 1158 m (n = 53); and (9) Fort Larned National Monument, Pawnee Co., Kansas, 620 m (n = 15). Mice were live-trapped and handled in accordance with guidelines approved by the University of Nebraska Institutional Animal Care and Use Committee (IACUC no. 07-07-030D). After killing each mouse, the heart, liver, and kidney were snap-frozen in liquid nitrogen and stored at −80° prior to DNA extraction. Skins and skulls or alcohol-preserved specimens were deposited in the vertebrate collection at the Denver Museum of Nature and Science (Denver, CO).

Study design for the analysis of DNA sequence variation

As described previously (Storz and Kelly 2008), we sequenced six unlinked autosomal loci in a panel of 30 mice: 15 specimens from the high-altitude endpoint of the transect (Mt. Evans, CO) and 15 specimens from a low-altitude prairie grassland locality (Yuma Co., CO). This set of unlinked loci included β-fibrinogen, LCAT, RAG1, AP5, vimentin, and rhodopsin. Polymorphism data from these six loci were used to estimate parameters of an isolation-with-migration model of population structure (see below). As described previously (Storz et al. 2009), we cloned and sequenced both alleles of the HBB-T1 and HBB-T2 genes in a subset of 26 mice from the same panel. This yielded 52 experimentally phased sequences per gene (104 sequences in total). The cloning protocol enabled us to reconstruct complete diploid genotypes for the HBB-T1 and HBB-T2 paralogs of each mouse, and we were also able to determine the exact haplotype phase of all heterozygous sites. These data were used to analyze levels and patterns of intragenic LD within each of the two HBB paralogs.

The random sample of 26 mice that were used in the survey of HBB polymorphism included eight d¹d¹/d¹d¹ double homozygotes from the high-altitude population sample and seven d⁰d⁰/d⁰d⁰ double homozygotes from the low-altitude sample. To boost the sample size for double homozygotes in each two-locus genotype class, we cloned and sequenced the HBB-T1 and HBB-T2 genes from three additional specimens: one d¹d¹/d¹d¹ mouse from the high-altitude sample and two d⁰d⁰/d⁰d⁰ mice from the low-altitude sample. This yielded a constructed sample of 18 mice that were double homozygotes for alternative two-locus HBB haplotypes (nine d¹d¹/d¹d¹ mice and nine d⁰d⁰/d⁰d⁰ mice). We then used this constructed sample of double homozygotes to survey nucleotide polymorphism at eight additional linked loci that spanned the β-globin gene cluster on chromosome 1 (Figure 1). The physical positions of these loci were determined by reference to the sequence of a bacterial artificial chromosome (BAC) clone that contained the complete β-globin gene cluster of P. maniculatus (GenBank accession number EU204642; Hoffmann et al. 2008a). Of the eight “linked loci,” the first three loci in the 5′ to 3′ direction are embryonic β-like globin genes: the ε-globin gene (HBE), the chimeric γ/ε-globin gene (HBG/E), and the γ-globin gene (HBG), which is located immediately upstream of the HBB-T1 gene. The next two noncoding loci, F4 and F4 (for fragments 4 and 5, respectively), are located in the intergenic region between HBB-T1 and HBB-T2, and the third noncoding locus, F6 (fragment 6), is located immediately downstream of HBB-T2. The sequenced loci that are furthest downstream from the β-globin gene cluster are both olfactory receptor genes, OlfR67 and OlfR630. Since all sequenced specimens were d¹d¹/d¹d¹ or d⁰d⁰/d⁰d⁰ double homozygotes, SNP alleles at each of the five flanking loci have a known linkage phase relative to the alternative two-locus HBB haplotypes. The multilocus data for the panel of d¹d¹/d¹d¹ and d⁰d⁰/d⁰d⁰ double homozygotes were used to analyze patterns of diversity and LD across the β-globin gene cluster (including the HBB-T1 and HBB-T2 genes).

Figure 1 .

Genomic structure of the β-globin gene cluster in the deer mouse. The HBE, HBG/E, and HGB genes encode the β-chain subunits of embryonic hemoglobin, and the HBB-T1 and HBB-T2 genes encode the β-chain subunits of adult hemoglobin. Shaded regions denote regions targeted for the resequencing survey of nucleotide polymorphism; F4, F5, and F6 are segments of noncoding DNA; and OlfR67 and OlfR630 are olfactory receptor genes.

Sequences for the six unlinked loci were already available for 15 of the 18 mice in the constructed panel of d¹d¹/d¹d¹ and d⁰d⁰/d⁰d⁰ double homozygotes. For the purpose of making comparisons with the two HBB paralogs and the other eight linked loci on chromosome 1, we cloned and sequenced both alleles from each of the six unlinked loci in the remaining specimens so that we had complete 16-locus genotypes for all 18 mice in the panel (32 sequenced alleles per mouse). To summarize the new sequence data that were collected for this study: we cloned and sequenced all eight linked loci in 18 mice (288 sequenced alleles), and we cloned and sequenced HBB-T1, HBB-T2, and the six unlinked loci in 3 mice (6 experimentally phased sequences per locus, 48 sequences total). All new sequences were deposited in GenBank under the accession numbers JN711139–JN711405.

Allele-specific PCR assay

We used an allele-specific PCR assay to identify d⁰/d⁰, d⁰/d¹, and d¹/d¹ genotypes at each of the two HBB paralogs in all 178 deer mouse specimens. In the case of HBB-T1, the primers HBBF (5′ GGG CAG GGC ATA TAA AGT AGA G 3′) and HBBT1R (5′ TCT CTA GGG GAC AAC TGA CCT 3′) were used to amplify a ∼1.3-kb DNA fragment that spanned the complete coding region. A 1:1000 dilution of the resultant HBBF/HBBT1R PCR product was then used as template for two allele-specific PCR reactions that discriminate between the d⁰ and d¹ allele classes. The primers ChrF (5′ AGT TTA GAT GGA AGG TA 3′) and Chr1R (5′ CAG CTG AAT CTT ACT GGA AAT 3′) were used to amplify d⁰-type alleles and the primers Chr2F (5′ TGA YTT CTT KTT CTC YAG TAA A 3′) and ChrR (5′ TCA CGA TCA TAT TGC CCA GGA 3′) were used to amplify d¹-type alleles. In the case of HBB-T2, the HBBF primer was used in combination with HBBT2R (5′ TCT CTG GAG ACA AAT AAG CTT TGC 3′) to amplify a DNA fragment that spanned the complete coding region, and we then performed allele-specific PCR assays to discriminate between the d⁰ and d¹ allele classes, as described above. The primer pair HBB-Chr1F (5′ TGT TGW GTT GAC TTG CAA CCG 3′) and ChrR was used to amplify d⁰-type alleles, and the primer pair HBB-Chr2F (5′ TGT TGA GTT GAC TTG CAA CCT 3′) and ChrR was used to to amplify d¹-type alleles. The HBB-T1 and HBB-T2 genes were PCR amplified using High-Fidelity PCR master mix (Roche Molecular Diagnostics, Basel, Switzerland) using the following protocol: 94° (120 sec) initial denaturing, 58° (30 sec), 72° (60 sec) 30×, and a final extension at 72° (120 sec). The subsequent allele-specific PCR reactions were performed using ABgene Thermo-Start Taq DNA polymerase and ReddyMix PCR reagents (Thermo Fisher Scientific, Rockford, IL) using the following protocol: 94° (120 sec) initial denaturing, 58° (30 sec), 72° (60 sec) 30×, and a final extension at 72° (120 sec).

PCR, cloning, and sequencing

PCR and cloning protocols for the HBB-T1 and HBB-T2 paralogs are described in Storz et al. (2009) and those for the six unlinked loci are described in Storz et al. (2007a) and Storz and Kelly (2008). Each of the eight linked loci was PCR amplified using High-Fidelity PCR master mix with the following thermalcycling protocol: 94° (120 sec) initial denaturing, [94° (10 sec), 50°–60° (70 sec), 68° (120 sec)] 10 cycles, [94° (15 sec), 50°–60° (30 srec), 68° (120 sec)] 20 cycles and a final extension step at 72° (7 min). Primer sequences and chromosomal coordinates for each locus are provided in Table S1. Automated DNA sequencing of PCR products was performed on an ABI 3730 capillary sequencer using Big Dye chemistry (Applied Biosystems, Foster City, CA).

Analysis of population structure

To characterize population structure across the altitudinal gradient we used genotypic data for the two HBB genes to compute Weir and Cockerham’s (1984) estimators of F-statistics: f (= F_IS), F (= F_IT), and θ (= F_ST). To assess whether observed genotype frequencies deviated from Hardy–Weinberg expectations we used randomization tests based on the inbreeding coefficients, f and F. To test for deviations from Hardy–Weinberg equilibrium (HWE) in population samples from individual localities, a null distribution of f values was generated by permuting alleles among individuals within each sample. To test for deviations from HWE at the total population level, a null distribution of F-values was generated by permuting alleles among individuals in a pooled sample from all localities. We used a similar randomization procedure to test the null hypothesis that genotypes at one HBB gene were independent of genotypes at the other gene, and in each case the log-likelihood ratio G-statistic was used as the test statistic.

To gain insight into the history of the deer mouse populations under consideration, we estimated six population genetic parameters using the “isolation-with-migration analytic” model implemented in the program IMa (Hey and Nielsen 2007). We restricted the IMa analyses to the six unlinked autosomal loci that were sequenced from the 15 highland (Mt. Evans) specimens and the 15 lowland (Yuma Co.) specimens. The parameter estimates included the divergence time (t) between the highland and lowland populations, two migration rates (m₁, the migration rate from the lowland population into the highland population; m₂, the migration rate from the highland population into the lowland population), and three effective population sizes (q₁, effective size of the highland population; q₂, effective size of the lowland population; q_A, effective size of the ancestral population). Because IMa assumes no intralocus recombination, we restricted our analysis to the largest nonrecombining block of sequence for each locus.

We initially performed a series of preliminary IMa runs with flat priors for each parameter. On the basis of results of these preliminary runs, we defined upper bounds for each prior that encompassed the entire posterior distribution for each parameter estimate (Won and Hey 2005). Using these prior distributions, we then performed two replicate IMa runs with identical priors, but different random number seeds to assess convergence in parameter estimates. All of the IMa analyses were performed using a burn-in of 100,000 steps and five Markov-coupled chains with geometric heating (g1 = 0.8; g2 = 0.9). The program was allowed to run until the effective sample size for each parameter estimate was >45 (∼8 × 10⁷ steps). Visual inspection of parameter trend lines suggested proper chain mixing, and the parameter estimates were highly similar between replicate runs, suggesting convergence of parameter estimates.

Analysis of intragenic LD in the HBB paralogs

We conducted an analysis of LD within the HBB-T1 and HBB-T2 paralogs using the original panel of 26 highland and lowland mice (n = 52 chromosomes per gene). We used the squared allele–frequency correlation, r², to measure LD between pairs of SNPs and we used Fisher’s exact test to determine the probability of obtaining estimates of LD that were more extreme than the observed values under the null hypothesis of linkage equilibrium. The analysis included only biallelic SNPs in which the minor allele was present at least twice in the sample. We used nonlinear regression to model the decay of intragenic LD as a function of physical distance under a model of recombination-drift equilibrium that incorporated mutation (Hill and Weir 1988). Specifically, we used a nonlinear regression model based on the Gauss–Newton algorithm, as implemented in the nls function of the R statistical computing package (http://www.r-project.org). To summarize the effects of recombination on intragenic LD, we also computed the ZZ test statistic of Rozas et al. (2001), which measures the difference between the average r² between adjacent nucleotide polymorphisms and the average of pairwise r² values across the entire gene. To compute confidence intervals of the ZZ test statistic we conducted 10,000 coalescent simulations (with no recombination) that were conditioned on the observed number of segregating sites. We inferred the linkage phase of d⁰ and d¹ alleles between the two HBB paralogs using the program PHASE (Stephens et al. 2001; Stephens and Donnelly 2003). We inferred two-locus haplotypes in samples from individual localities and in the total pooled sample. All of the PHASE analyses were run for 10,000 steps with a 1000 step burn-in and a thinning interval of 10.

Analysis of clinal variation across the altitudinal transect

We estimated the center and width of the altitudinal cline in two-locus HBB haplotype frequencies using the program Clinefit (Porter et al. 1997). In the Clinefit analysis we used a burn-in of 200 parameter tries per step, and following the burn-in we saved 20,000 replicate steps with 20 replicates run between saves.

Multilocus analysis of sequence variation within and between genotype classes

For comparisons between the alternative genotype classes, we compiled sequences from the two HBB genes, the eight linked loci, and the six unlinked loci for the 18 d⁰d⁰/d⁰d⁰ and d¹d¹/d¹d¹ mice. DNA sequences were aligned and assembled into contigs using ClustalX (Thompson et al. 1997) and Sequencher (Gene Codes, Ann Arbor, MI). Summary statistics of nucleotide polymorphism and LD were computed with the program SITES (Hey and Wakeley 1997) and custom programs written in C (available upon request). To assess the prevalence of recombination within each locus, we used the four-gamete test of Hudson and Kaplan (1985) to estimate R_M, the minimum number of recombination events in the history of the sample. We computed two different measures of DNA sequence variation: nucleotide diversity, π (the average number of pairwise differences between sequences) and Watterson’s (1975) estimator of the scaled mutation rate, θ_W (= 4Nu, where N is the effective population size and u is the mutation rate per nucleotide). To measure levels of intralocus LD, we used a generalized version of Kelly’s (1997) Z_nS that accommodates nucleotide polymorphisms with more than two alleles. Finally, we used the nucleotide data to compute F_ST (Hudson et al. 1992, Equation 3) and δ_ST (Nei and Kumar 2000, Equation 12.74) as locus-specific measures of nucleotide differentiation between the two genotype classes, and we used Z_g (Storz and Kelly 2008, Equation 3) to measure the between-sample component of LD. Finally, we used D_xy (Nei and Kumar 2000, Equation 12.65) as a measure of nucleotide divergence between the two HBB paralogs on both the d⁰d⁰ and d¹d¹ haplotype backgrounds.

Simulation study

We conducted forward simulations under separate models of equilibrium and nonequilibrium population structure. The equilibrium model is an elaboration of that presented in Storz and Kelly (2008). As described previously, the simulator tracks evolution within a population composed of 400 diploid individuals subdivided between two demes of equal size (representing the high- and low-altitude populations). The two demes exchange migrants at rate m. Molecular evolution was modeled within a chromosomal region containing four linked loci. Each locus is 1000 bp in length and the recombination rate between loci is r_L. Given the average recombination rate estimated for house mice (0.63 cM/Mb; Shifman et al. 2006), we used r_L = 0.005 for the 16.2-kb interval separating the two HBB paralogs in P. maniculatus. The first and third loci along this chromosome contain a polymorphic site (nucleotide position 500) that is subject to spatially varying selection. At each selected locus, there are two functionally distinct alleles, A₀ and A₁. In the highland population, the fitnesses of A₀A₀, A₀A₁, and A₁A₁ are 1, 1 − s/2, and 1 − s, respectively, at each locus. The opposite selection regime applies within the lowland population. The value for s was chosen to maintain an equilibrium frequency of the locally favorable allele at approximately 0.9, consistent with the empirical data.

All sites were subject to reversible mutation between the four nucleotide bases and recombination occurred with equal probability between each pair of adjacent sites in the sequence. Each simulation run was initiated with all individuals heterozygous (A₀/A₁) at each selected locus and homozygous at all other sites. We allowed the population to evolve for 50N generations before sampling sequences. This burn-in allowed mutation, selection, migration, and genetic drift to reach statistical equilibrium. Subsequent to the burn-in, we randomly sampled until obtaining 18 individuals that were double homozygotes at the two selected loci. This scheme emulates the empirical sample configuration. Given the sample of 36 chromosomes per locus, we calculated S, π, δ_ST, Z_nS, and Z_g in addition to measures of LD between pairs of linked loci.

Sampling was repeated at intervals of N/4 generations until 1000 samples were taken from a simulation run. We aggregated samples from 10 independent runs to produce estimates for each parameter combination. To parameterize the simulation model, we used empirical results from the survey of six unlinked nuclear loci. These loci suggest that the scaled neutral mutation rate, 4Nu, is ∼0.012/site, the scaled recombination rate, 4Nr, is ∼0.03, and the scaled migration rate, 4Nm, is ∼18.0 (Storz and Kelly 2008). Our base value for the rate of gene conversion, g, was 0.1 × 4Nr, in accordance with experimental data from the β-globin gene cluster in mammals (Holloway et al. 2006). We assumed that gene conversion affected only the selected loci (which were stand-ins for the two HBB paralogs) and that allelic and nonallelic gene conversion occur at equal rates. The former assumption is justifed by the well-documented pattern in the α- and β-globin gene families of mammals that nonallelic gene conversion is almost exclusively restricted to coding sequence (Storz et al. 2007b 2008; Hoffmann et al. 2008a,b; Opazo et al. 2008, 2009; Runck et al. 2009, 2010). We also assume that the conversion tract spans the entire sequence of the recipient gene, which again is consistent with empirical data for mammalian β-globin genes (Borg et al. 2009).

To explore the effects of nonequilibrium population structure, we also conducted simulations under an isolation-with-migration model that was parameterized with results from the IMa analysis. In these simulations, we used the same genetic parameters (with respect to mutation, recombination, gene conversion, etc.) as described above for the equilibrium model. We initiated each run with a single ancestral population of a specified size and allowed this population to reach mutation-drift balance at tracked loci. The population was then subdivided into two descendant subpopulations, and the locally beneficial A₁ allele was introduced at each of the two selected loci (mimicking mutation followed by interparalog gene conversion). At each of the two selected loci, fitnesses of the A₀A₀, A₀A₁, and A₁A₁ genotypes were identical to those described previously for the equilibrium model. The highland and lowland populations evolved for t generations before sequences were sampled according to the strategy described above. The relative sizes of the ancestral and descendant populations and the time since divergence were taken from the IMa analysis. Since the locally beneficial A₁ allele was initially present as a single copy, it was lost due to drift in the great majority of simulation runs. We rejected and restarted all simulation runs in which the A₁A₁ haplotype failed to attain a frequency of >0.5 in the highland population within t/2 generations. The A₁A₁ haplotype always eventually attained high frequency (usually >0.99) in simulations that satisfied this criterion.

Results

We first present empirical results of the analysis of polymorphism and LD at the HBB genes, along with the multilocus analysis of DNA sequence variation between the alternative HBB genotype classes. We then present results of the simulation study to compare the observed patterns of nucleotide variation with those expected under a two-locus model of spatially varying selection with multiplicative fitness.

Altitudinal variation in two-locus haplotype frequencies

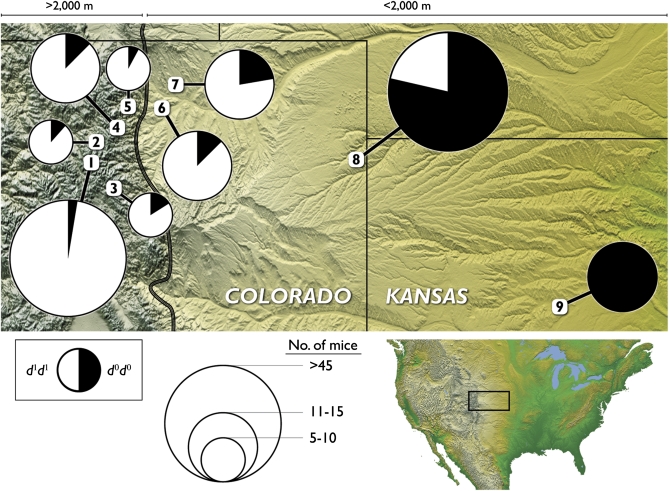
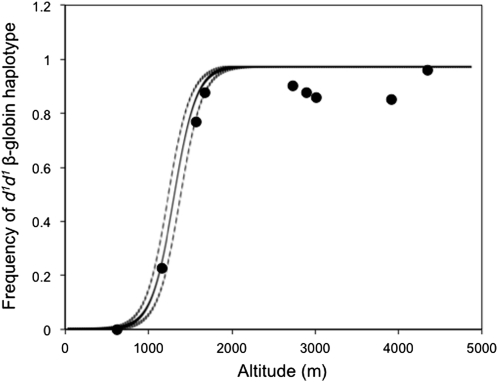
The HBB-T1 and HBB-T2 paralogs were both characterized by steep altitudinal clines in allele frequency. At both genes, the d¹ allele was nearly fixed in the sample from the high-altitude endpoint of the transect (frequency 0.959) and the d⁰ allele was fixed at the low-altitude endpoint. Measures of genotypic LD revealed a highly nonrandom association between alleles at the two HBB paralogs (P < 0.0001). Consistent with previous surveys from a single pair of high- and low-altitude localities (Storz et al. 2009, 2010a), the observed genotype frequencies indicated that all sampled mice were either d⁰d⁰/d⁰d⁰ double homozygotes, d⁰d⁰/d¹d¹ double heterozygotes, or d¹d¹/d¹d¹ double homozygotes. When analyzed as a single pooled sample, the linkage phase of two-locus HBB haplotypes could be resolved unambiguously (posterior probability = 1.0 for all 178 individuals). Haplotype phase could also be resolved with high posterior probability (0.90–1.0) for all but one individual when they were analyzed at the level of individual sampling localities. Thus, the available data for the two HBB paralogs indicate that alleles of the same functional type were in perfect coupling-phase LD. Consequently, the clinal pattern of altitudinal variation can be described in terms of two-locus haplotype frequencies (Figures 2 and 3). The estimated center of the altitudinal cline was 1320 m above sea level (95 C.I. = 1246–1399 m) and the estimated cline width was 562 m (95 C.I. = 329–808 m).

Figure 2 .

Spatial variation in two-locus haplotype frequencies at the HBB genes in P. maniculatus. Sampling localities are numbered in decreasing order of elevation, from 4347 m to 620 m above sea level.

Figure 3 .

Altitudinal cline in two-locus HBB haplotype frequencies in P. maniculatus sampled across the interface between the Great Plains and the southern Rocky Mountains of North America.

Population structure

When sequences were binned into d⁰ and d¹ allele classes, neither of the HBB paralogs exhibited departures from Hardy–Weinberg genotype frequencies at the level of individual sampling localities (F_IS = −0.153 for both genes, P > 0.05). However, in the total sample, both genes exhibited a pronounced excess of homozygotes due to population structure (F_IT = 0.525, P < 0.001). As shown in Figure 2, the high- and low-altitude endpoints of the transect were characterized by nearly fixed differences (F_ST = 0.938), and a high level of genetic differentiation was apparent across the transect as a whole (F_ST = 0.588).

The model-based analysis of population structure at the reference loci assumed that the observed levels of genetic differentiation between mice from the mountains and the plains reflects a history of geographic isolation combined with relatively low levels of recurrent gene flow. IMa estimates of population genetic parameters are presented in Table 1 and graphical depictions of the posterior probability densities for each parameter estimate are presented in Supporting Information, Figure S1. Because IMa produces estimates that are scaled to the neutral mutation rate (μ), we converted the scaled parameter estimates to demographic parameters by assuming a neutral mutation rate of 4.91 × 10⁻⁹/site/year (Geraldes et al. 2008). The estimated divergence time (t) was ∼600,000 generations bp, and estimates of the subsequent rate of migration between the highland and lowland populations were low in both directions. Although the estimated lowland → highland migration rate (m₁ = 1.6 × 10⁻⁷) was 2 orders of magnitude greater than the highland → lowland migration rate (m₂ = 1.8 × 10⁻⁹), the HPD intervals for both estimates broadly overlapped (Figure S1). The estimated effective size of the highland population was significantly larger than that of the ancestral population, suggesting a past history of demographic expansion at high elevation following population divergence. Estimates of effective sizes for the highland (q₁), lowland (q₂), and ancestral populations (q_A) were approximately 2.4 × 10⁶, 1.5 × 10⁶, and 4.7 × 10⁵ individuals, respectively.

Table 1 . Estimates of population genetic parameters under an isolation-with-migration model.

Parameter	Scaled estimate	Demographic estimate
Highland Ne (q1)	3.47 (1.54–8.25)	2.4 × 106 individuals (1.1 × 106–5.7 × 106)
Lowland Ne (q2)	2.12 (0.81–4.67)	1.5 × 106 individuals (5.6 × 105–3.3 × 106)
Ancestral Ne (qA)	0.68 (0.19–1.37)	4.7 × 105 individuals (1.3 × 105–9.5 × 105)
Migration rate (lowland → highland; m1)	0.45 (0.00–5.24)	1.6 × 10−7 migrants/generation (1.8 × 10−9–1.9 × 10−6)
Migration rate (highland → lowland; m2)	0.005 (0.00–4.34)	1.8 × 10−9 migrants/generation (1.8 × 10−9–1.6 × 10−6)
Divergence time (t)	0.21 (0.10–0.43)	5.8 × 105 generations (2.9 × 105–1.2 × 106)

Parameter estimates are scaled to the neutral mutation rate (μ) and were converted to demographic parameters by assuming a neutral substitution rate of 4.91 × 10⁻⁹/site/year for autosomal genes (Geraldes et al. 2008). Numbers in parentheses are the 90% highest posterior density intervals for the parameter estimates.

Levels and patterns of LD

At the HBB-T1 gene, Fisher’s exact test revealed significant LD between 1425 of 2576 pairwise comparisons (584 of which remained statistically significant after Bonferroni correction), and at the HBB-T2 gene, significant LD was observed between 1355 of 2710 such comparisons (530 of which remained significant after Bonferroni correction). HBB-T1 and HBB-T2 both showed evidence for a history of intragenic recombination (R_m = 8 and 12, respectively).

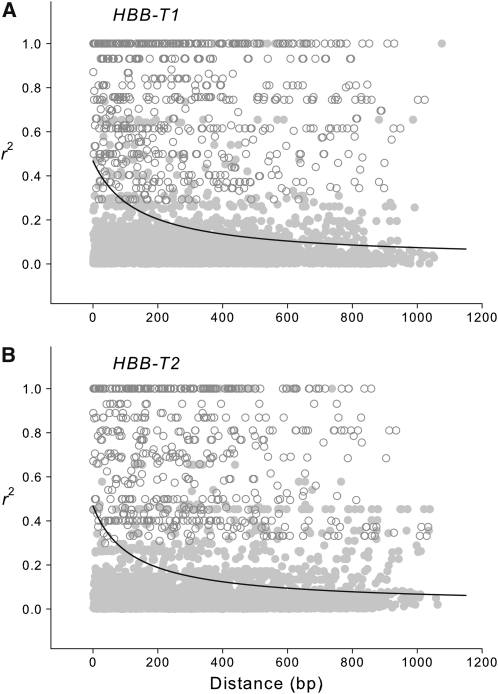
To assess the chromosomal extent of possible “divergence hitchhiking” effects (Charlesworth et al. 1997; Via 2009; Feder and Nosil 2010), we measured rates of decay of intragenic LD at each of the two β-globin genes. If LD decays to near background levels within each individual gene, then spatially varying selection at the HBB-T1 and HBB-T2 genes cannot be expected to have much of an effect on flanking loci. At both HBB-T1 and HBB-T2, mean r² declined to less than 0.1 within 800 bp (Figure 4). Although a small number of nonrandom associations persisted for site pairs separated by up to 1 kb, it is clear that LD does not extend very far into flanking chromosomal regions. Consistent with these results, estimated values of the ZZ test statistic were significantly positive for both HBB-T1 and HBB-T2 (ZZ = 0.054 and 0.047, respectively; P < 0.05 in both cases), indicating that intragenic recombination has played an important role in randomizing pairwise associations between polymorphisms within each gene.

Figure 4 .

Rate of decay of LD within the (A) HBB-T1 and (B) HBB-T2 genes. The fitted lines represent nonlinear regressions of r² against physical distance using a mutation–recombination–drift model. Open symbols denote estimates of LD for pairs of polymorphic sites that remained statistically significant after correction for multiple comparisons.

Nucleotide diversity and LD within and between genotype classes

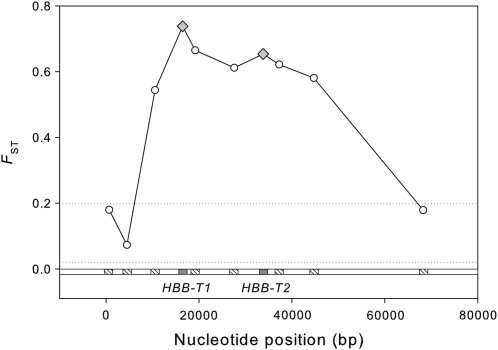
Comparison between the d⁰d⁰/d⁰d⁰ and d¹d¹/d¹d¹ genotype classes revealed high levels of nucleotide differentiation and LD at the two HBB paralogs and the most closely linked loci relative to the set of unlinked loci (Table 2). The especially high levels of nucleotide differentiation at the HBB paralogs extended across the 16.2-kb intergenic region, and dropped away in the upstream and downstream flanking regions (Figure 5). All of the linked and unlinked loci showed evidence of intralocus recombination although the two HBB paralogs and closely linked loci (HBG, F4, F5, F6) were characterized by higher levels of intralocus LD, as indicated by the uniformly higher Z_nS values (Table 3). Interlocus LD was also highest for the two HBB paralogs and closely linked loci and was lowest in pairwise comparisons involving the most distal loci (e.g., HBE and HBG/E at the 5′ end and OlfR630 at the 3′ end of the surveyed region; Figure S2).

Table 2 . Locus-specific measures of silent site diversity and LD between d¹d¹/d¹d¹ vs. d⁰d⁰/d⁰d⁰ genoytpe classes.

Locus	Fixed differences	Shared polymorphisms	FST	Zg
Linked loci
HBE	0	24	0.184	0.007
HBG/E	0	32	0.073	0.003
HBG	2	12	0.544	0.053
HBB-T1	18	0	0.738	0.110
F4	21	4	0.665	0.070
F5	3	18	0.612	0.106
HBB-T2	13	0	0.654	0.094
F6	17	0	0.622	0.151
OlfR67	1	11	0.581	0.074
OlfR630	0	4	0.179	0.008
Unlinked autosomal loci
β-Fibrinogen	0	4	0.027	0.002
LCAT	0	12	0.070	0.004
RAG1	0	7	0.197	0.007
AP5	0	10	0.045	0.003
Vimentin	0	24	0.084	0.002
Rhodopsin	0	49	0.087	0.003

Figure 5 .

Interlocus variation in nucleotide differentiation between highland and lowland mice with different genetic backgrounds at the HBB-T1 and HBB-T2 genes. Open hatched squares denote the following loci (from left to right): HBE, HBG/E, HBG, F4, F5, F6, OlfR67, and OlfR630. The horizontal dotted lines denote the maximum and minimum F_ST values for the unlinked reference loci in the same panel of mice.

Table 3 . Summary of nucleotide polymorphism and LD at seven linked loci that span the β-globin gene cluster and six unlinked autosomal loci.

	Genotype class	Na	L (bp)	Sb	π (Sil)	θW/bp (Sil)	RMin	ZnS
Linked loci
HBE	d1d1/d1d1	18	1489.1	44	0.0080	0.0080	13	0.073
	d0d0/d0d0	18	1504.2	35	0.0057	0.0064	7
HBG/E	d1d1/d1d1	18	1706.0	78	0.0093	0.0113	14	0.108
	d0d0/d0d0	18	1683.6	77	0.0118	0.0119	4
HBG	d1d1/d1d1	18	1409.0	31	0.0062	0.0064	4	0.102
	d0d0/d0d0	18	1409.0	26	0.0040	0.0054	2
HBB-T1	d1d1/d1d1	18	1210.0	61	0.0132	0.0147	7	0.158
	d0d0/d0d0	18	1210.0	19	0.0034	0.0046	1
F4	d1d1/d1d1	18	1317.9	101	0.0195	0.0223	9	0.140
	d0d0/d0d0	18	1389.0	8	0.0015	0.0017	0
F5	d1d1/d1d1	18	1367.0	87	0.0246	0.0185	8	0.229
	d0d0/d0d0	18	1367.0	45	0.0043	0.0096	1
HBB-T2	d1d1/d1d1	18	1195.0	63	0.0167	0.0153	3	0.161
	d0d0/d0d0	18	1195.0	15	0.0044	0.0037	1
F6	d1d1/d1d1	18	991.0	100	0.0451	0.0293	2	0.379
	d0d0/d0d0	18	991.0	1	0.0003	0.0003	0
OlfR67	d1d1/d1d1	18	982.0	20	0.0057	0.0059	2	0.115
	d0d0/d0d0	18	982.0	15	0.0059	0.0044	1
OlfR630	d1d1/d1d1	18	990.4	29	0.0036	0.0047	4	0.118
	d0d0/d0d0	18	996.2	17	0.0038	0.0029	4
Unlinked loci
β-Fibrinogen	d1d1/d1d1	18	589.0	19	0.0050	0.0094	2	0.045
	d0d0/d0d0	18	589.0	19	0.0061	0.0094	0
LCAT	d1d1/d1d1	18	452.0	15	0.0115	0.0090	3	0.057
	d0d0/d0d0	18	426.2	18	0.0108	0.0123	5
RAG1	d1d1/d1d1	18	1164.4	19	0.0035	0.0040	4	0.079
	d0d0/d0d0	18	1168.6	18	0.0029	0.0030	3
AP5	d1d1/d1d1	18	361.5	16	0.0128	0.0113	5	0.061
	d0d0/d0d0	18	369.0	20	0.0143	0.0134	7
Vimentin	d1d1/d1d1	18	724.0	46	0.0119	0.0185	4	0.052
	d0d0/d0d0	18	724.0	72	0.0222	0.0289	4
Rhodopsin	d1d1/d1d1	18	1199.3	87	0.0170	0.0211	15	0.039
	d0d0/d0d0	18	1242.7	113	0.0190	0.0264	8

Estimates of π, θ_W, and Z_nS are based on variation at silent sites. Estimates of Z_nS are based on the pooled sample of d¹d¹/d¹d¹ and d⁰d⁰/d⁰d⁰ genotype classes.

^aNumber of sampled chromosomes.

^bNumber of segregating sites.

In the total sample of d⁰d⁰ and d¹d¹ haplotypes (n = 72 chromosomes), comparison between the HBB-T1 and HBB-T2 paralogs revealed six fixed differences and 36 shared polymorphisms at silent sites (D_xy = 0.0313). Levels of interparalog divergence were roughly similar on each of the separate haplotype backgrounds: D_xy = 0.0287 and 0.0260 for the d⁰d⁰ and d¹d¹ haplotypes, respectively.

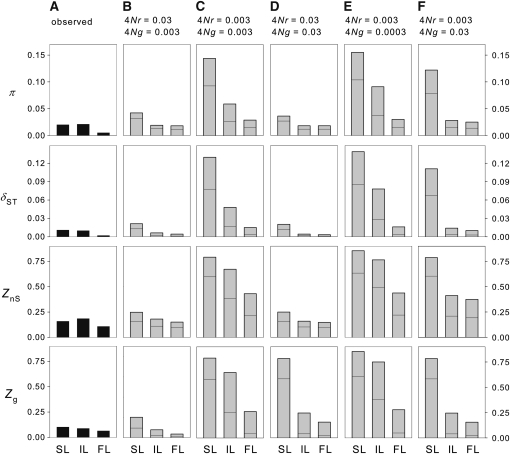
Simulation results

The simulation study was designed to replicate the observed patterns of nucleotide diversity and LD. To compare the empirical results with the simulation results, we summarized empirical measures of diversity and LD for three classes of loci: the selected loci (an average value for the two HBB paralogs), the intergenic loci (an average value for F4 and F5), and the flanking loci (an average value for HBG and OlfR67; Figure 6A). Simulations under the equilibrium model of population structure revealed that spatial variation in fitness rankings can be expected to produce a pronounced locus-specific increase in both the overall nucleotide diversity (π) and the between-population component of diversity (δ_ST) relative to the intergenic locus and the flanking locus (Figure 6, B–F). The same discrepancy was observed for intragenic LD (Z_nS) and the between-population component of intragenic LD (Z_g). However, as shown in Figure 6, there were certain features of the empirical data that were not replicated over a broad range of parameter values for the scaled rates of recombination and interparalog gene conversion (4N_r and 4N_g, respectively). The simulations revealed that the various measures of nucleotide diversity and LD were highest for the selected loci, intermediate for the intergenic locus, and lowest for the flanking locus. The discrepancy between the intergenic locus and the flanking locus was greatest when a reduced rate of recombination (4N_r = 0.003) was combined with low rates of gene conversion (4N_g = 0.003–0.0003; Figure 6C, E). In comparison with the empirical data, the simulated data exhibited consistently larger discrepancies in measures of diversity and LD between the intergenic locus and the selected loci. The empirical data also exhibited consistenly higher levels of LD between pairs of loci across the entire chromosomal region than was evident in the simulations.

Figure 6 .

Observed values (A) and simulated values (B–F) of four summary statistics of nucleotide diversity and LD (π, δ_ST, Z_nS, and Z_g) for three classes of loci: selected loci (SL), intergenic loci (IL), and flanking loci (FL). In each of the four rows of column A, the bars represent empirical measures of diversity and LD for the “selected loci” (an average value for the two HBB paralogs), the intergenic loci (an average value for F4 and F5), and the flanking loci (an average value for HBG and OlfR67; see Figure 1). In each row of columns B–F, the bar for each locus represents the 0.95 percentile of the simulated distribution of a given statistic and the horizontal line denotes the median value. The values shown in B–F derive from simulations with different combinations of values for the scaled rate of recombination between adjacent sites (4N_r) and the scaled rate of gene conversion between the selected loci (4N_g).

Consistent with the simulation-based expectations, empirical measures of diversity and LD dropped off in the flanking regions (i.e., upstream of HBB-T1 and downstream of HBB-T2; Figure 5, 6). But contrary to the simulation-based expectations, empirical measures of diversity and LD remained relatively high across the intergenic region, suggesting a reduction in the effective rate of recombination between the two HBB paralogs. Elevated rates of gene conversion (4Ng = 0.03) improved the fit to some features of the data (e.g., by reducing diversity within the selected genes), but simultaneously reduced the fit to other features of the data (e.g., reduced Z_nS across the intergenic region and reduced levels of interparalog divergence).

The initial simulation analysis assumed that the populations were at statistical equilibrium with regard to the effects of mutation, migration, selection, and drift. To evaluate whether nonequilibrium population structure might improve the fit between observed and expected patterns, we performed additional simulations that were parameterized with results of the IMa analyis (Table 1). However, simulations under this isolation-with-migration model did not provide an improved fit to the data (Table S2). The IMa estimates (Table 1) suggested an ancestral population size that was substantially smaller than current population sizes. This requires a substantially elevated neutral mutation rate (relative to what we estimated previously on the basis of equilibrium assumptions; Storz and Kelly 2008) because the level of nucleotide variation would be largely determined by the effective size of the ancestral population. This is due to the relatively recent time since divergence and subsequent expansions of the descendant subpopulations. Simulations of molecular evolution under this demographic scenario do not yield dramatic differences in measures of diversity and LD between the selected loci and the flanking loci (Table S2). For most parameter combinations, the equilibrium model of population structure generally provided a better fit to the data than the isolation-with-migration model. In summary, over a broad range of demographic and historical scenarios, the observed patterns of nucleotide variation and LD cannot be easily reconciled with a multiplicative fitness scheme at linked loci.

Discussion

The survey of β-globin polymorphism in deer mice from the southern Rockies and the Great Plains revealed a steep altitudinal cline in two-locus haplotype frequencies. The two-locus HBB haplotype that increases in frequency as a function of altitude (d¹d¹) is associated with increased hemoglobin-oxygen affinity (Storz et al. 2009, 2010a; Natarajan et al. 2011), which enhances pulmonary oxygen loading under hypoxia. Thus, the deer mouse β-globin polymorphism represents a rare case in which the spatial patterning of allele frequency variation across an environmental gradient can be related to adaptive functional properties of the encoded protein.

Patterns of variation at unlinked autosomal loci revealed a substantial level of population structure across the surveyed region of central North America, corroborating results of previous phylogeographic studies (Gering et al. 2009). However, relative to the unlinked reference loci, the HBB genes and other closely linked loci exhibited significantly higher levels of nucleotide differentiation and LD between the high- and low-altitude population samples. The elevated levels of divergence at the HBB genes relative to other linked and unlinked loci suggest that the steepness of the observed altitudinal cline cannot be explained by a history of admixture between genetically distinct populations that have come into secondary contact. Moreover, the rapid decay of intragenic LD (Figure 4) and the reduced levels of differentiation at external flanking loci (Figure 5) indicate that the observed pattern of clinal variation at the HBB genes cannot be attributed to the indirect effects of spatially varying selection at one or more linked loci. Given the combined functional and population-genetic evidence for spatially varying selection on the two-locus HBB polymorphism in deer mice, results of our multilocus analysis of nucleotide polymorphism across the β-globin gene cluster provide empirical insights into the chromosomal extent of divergence hitchhiking.

As shown in Figure 5, high levels of nucleotide differentiation at the two HBB paralogs drop away quite rapidly in the external flanking regions upstream of HBB-T1 and downstream of HBB-T2, and values for the most distal loci (HBE, HBG/E, and OlfR630) fall within the range of values for unlinked reference loci. In conjunction with the rapid decay of intragenic LD within both HBB paralogs, this pattern suggests that divergence hitchhiking effects do not extend much beyond 15–20 kb. This is consistent with patterns of diversity and LD at tandemly duplicated α-globin genes in the same panel of mice (Storz and Kelly 2008) and is also largely consistent with results of recent analytic and simulation results (Feder and Nosil 2010).

Reconciling patterns of long-range and short-range LD

The observed LD at both HBB paralogs is at least partly attributable to population structure, as the variance in allele frequencies between the high- and low-altitude samples augments the covariance in allele frequencies between polymorphic sites within each gene. Even in the absence of epistatic interactions, theoretical results indicate that spatially varying selection on linked loci can generate substantial LD when the intergenic recombination fraction is of the same magnitude as the selection coefficients for the two loci (Slatkin 1975). For this reason, significant LD between a clinally varying pair of linked loci cannot be construed as prima facie evidence for epistatic selection (Nei and Li 1973; Li and Nei 1974; Feldman and Christiansen 1975; Slatkin 1975). In the case of the deer mouse β-globin polymorphism, however, the analysis of haplotype structure revealed a paradoxical pattern whereby perfect LD between the two HBB paralogs (which are separated by 16.2 kb) is maintained in spite of the fact that LD within both paralogs decays to background levels over physical distances of <1 kb. Indeed, the simulation results indicate that observed levels of nucleotide diversity and LD at the intergenic loci are more similar to those of the two HBB paralogs than expected under a model of multiplicative fitness effects. Below we discuss possible causes and consequences of the observed two-locus haplotype structure.

Epistatic selection as a possible cause of haploytpe structure

Excess LD between the two HBB paralogs suggests the possibility that the effective rate of intergenic recombination is reduced by epistatic selection. In this system, epistasis for fitness (if it exists) could possibly be explained by an interaction effect between alternative β-chain hemoglobin variants and/or a nonlinear relationship between gene dosage and physiological performance.

Since members of the β-globin gene family are under the transcriptional control of cis-acting regulatory elements that are located far upstream of the structural genes (∼20 kb in deer mice; Hoffmann et al. 2008a), there would seem to be ample scope for interaction effects between distal and proximal cis-regulatory mutations or between cis-acting regulatory mutations and amino acid mutations in the coding region. Indeed, epistatic interactions between closely linked regulatory and structural mutations have been documented for a number of well-characterized enzyme polymorphisms that are implicated in local adaptation [e.g. Adh polymorphism in Drosophila melanogaster (Laurie and Stam 1994) and Ldh polymorphism in killifish, Fundulus heteroclitus (Crawford and Powers 1992)].

In certain human populations that are native to malarial regions, there is solid evidence that epistatic selection is maintaining coadapted combinations of alleles at tandemly linked β-like globin genes. The well-known sickle-cell amino acid polymorphism in the adult HBB gene plays a key role in resistance to falciparum malaria. Homozygotes for the 6βVal mutant (the S allele) have an elevated resistance, but suffer from chronic anemia; homozygotes for the wild-type 6βGlu (the A allele) are susceptible to malaria, but have normal hemoglobin concentrations. The A/S heterozygotes have highest fitness in malarial environments because they typically have only slightly reduced hemoglobin concentrations, and hemoglobin that incorporates the S-type β-chain subunits (α₂β^S₂) is prone to polymerization at low cellular oxygen tensions, which in turn promotes the clearance of parasite-infected “sickled” red blood cells from the circulation. The fitness trade-off between anemia and susceptibility to malaria is modulated by the expression of the closely linked ^Aγ- and ^Gγ-globin (HBG) genes, which are normally expressed only during fetal development. Since the postnatal expression of fetal hemoglobin (α₂γ₂) ameliorates the effects of sickle-cell anemia, alleles at the HBG genes that are associated with the adult persistence of fetal hemoglobin increase the fitness of homozygotes for the S allele at the adult HBB gene (Nagel 2001; Nagel and Steinberg 2001). In human populations from malarial regions of the Mediterranean, the Middle East, and the Indian subcontinent, long-range LD between the HBG and HBB genes appears to be attributable to epistatic selection that maintains coupling-phase LD between the “persistence of fetal hemoglobin” allele at one or both of the fetal HBG genes and the S allele at the adult HBB gene (Nagel and Steinberg 2001; Steinberg 2001). For these reasons, the β-globin gene cluster has been cited as an example of a coadapted gene complex or “supergene,” in which “…the frequencies of alleles at different loci are mutually adjusted with respect to one another by natural selection favoring epistatic combinations with high fitness” (Templeton 2006, p. 395).

We have no experimental evidence to confirm that the two-locus HBB haplotype structure in deer mice is maintained by a similar form of epistastic selection between regulatory and structural polymorphisms. Since embryonic globin genes are not expressed in the adult red blood cells of mice from highland or lowland environments (Storz et al. 2010a), there is no obvious basis for epistatic interactions between the HBB genes and embryonic β-like globin genes. Moreover, results of the population genetic analysis are not consistent with epistatic selection involving long-range interactions between the HBB genes and distant cis-acting regulatory elements. As shown in Figure 5, the most distal flanking genes (HBE and HBG/E at the far 5′ end of the surveyed region, and OlfR630 at the far 3′ end) exhibit the lowest levels of nucleotide differentiation between the d⁰d⁰ and d¹d¹ haplotype backgrounds. Levels of overall nucleotide diversity and LD show the same basic pattern (Tables 2 and 3), which is not consistent with the idea that the β-globin gene cluster constitutes a coadapted gene complex. If epistatic selection were maintaining coadapted combinations of alleles between the HBB paralogs and distant cis-acting regulatory sites, then levels of nucleotide diversity and LD would be expected to persist upstream of the HBB-T1 gene and/or downstream of the HBB-T2 gene. Results of the population genetic analysis suggest that if the two-locus HBB haplotype structure in deer mice is being maintained by epistatic selection, then the interacting sites are probably located in or near the HBB genes themselves.

Consequences of linkage for local adaptation

Given that the divergent fine tuning of hemoglobin–oxygen affinity has been shown to play a key role in the local adaptation of deer mice to different elevational zones (Snyder 1981, 1985; Snyder et al. 1982, 1988; Chappell and Snyder 1984; Chappell et al. 1988; Storz 2007; Storz and Kelly 2008; Storz et al. 2007a, 2009, 2010a), the observed LD between the two HBB paralogs also has important implications for the ability of allele frequencies (and hence, the population mean phenotype) to “track” spatial changes in the environment. Theory developed by Slatkin (1975) demonstrated that linkage can improve prospects for adaptation to local conditions when genotypes at a pair of linked genes undergo concordant transitions in fitness rankings across an environmental gradient. This hypothetical scenario is perfectly in line with the two-locus β-globin polymorphism in deer mice since the same d⁰ and d¹ alleles are segregating at each of the two HBB paralogs. Slatkin’s (1975) theoretical results indicate that the spatial scale at which allele frequencies can respond to local selection is reduced by as much as 30% when the intergenic recombination fraction is of the same magnitude as the selection coefficient. As stated by Slatkin (1975, p. 793): “…tighter linkage between two loci will allow the gene frequencies at both loci to respond to smaller scale changes in the environment than they would in the absence of linkage….” These results are especially relevant to a consideration of local adaptation to different elevational zones, as altitudinal gradients are characterized by especially fine-grained spatial variation in environmental factors such as temperature and oxygen tension.]